下载文档原格式
第4章效用4.1复习笔记1．序数效用论（1）序数效用论序数效用论指用序数来表示消费者偏好次序的理论。
序数效用论者认为，效用不能用基数表示，而只能用序数第一、第二、第三等表示消费者的偏好顺序和效用水平。
（2）序数效用论的假设①消费者对两种商品的任意两个组合A、B 能明确地说出自己的偏好。
②消费者的偏好具有传递性。
③消费者对数量多的两种商品组合的偏好永远大于对数量少的两种商品组合的偏好。
（3）序数效用函数序数效用函数为每个可能的消费束指派一个数字（效用水平），当且仅当()()1212,,x x y y 时，()()1212,,u x x u y y > ；当且仅当()()1212,,x x y y 时，()()1212,,u x x u y y = 。
效用函数的数值，只在对不同商品束进行排列时才有意义；任意两个商品束之间的效用差额的大小是无关仅要的。
（4）无差异曲线无差异曲线是指所有具有相同效用水平的消费束构成的集合。
（5）效用函数的单调变换如果()f x 是单增的函数，则效用函数()()U'x f U x =⎡⎤⎣⎦就被称作是()U x 的单调变换。
（6）效用函数的单调变换原理效用函数的单调变换与原来的效用函数代表相同的偏好，如图4-1所示。
图4-1单调变换不改变消费者的无差异曲线的位置和形状（7）效用函数的存在性定理假定消费者的偏好具有完备性、反身性、传递性、连续性和强单调性，那么就存在一个能代表该偏好的连续效用函数。
（8）一般商品、厌恶品和中性品如果()U x 关于x 单增，则称x 是一般商品；如果()U x 关于x 单减，则称x 是厌恶品；如果()U x 关于x 不变，则称x 是中性品。
2．效用函数的几个例子（1）完全替代的效用函数如图4-2所示()1212U x x ax bx =+，图4-2完全替代的效用（2）完全互补的效用函数如图4-3所示(){}1212min ,U x x ax bx =，图4-3完全互补的效用（3）拟线性偏好的效用函数如图4-4所示()()1212U x x v x x =+，图4-4拟线性效用（4）柯布-道格拉斯效用函数()11212a aU x x x x -=，（5）不变替代弹性的效用函数()()11212,1u x x A x x ρρρδδ⎡⎤=+-⎣⎦特别地，当替代参数1ρ=时，CES 效用函数就变为完全替代的效用函数。
Intermediate Microeconomics:A Modern Approach (8th Edition)Hal R. Varian范里安中级微观经济学：现代方法（第8版）完美中文翻译版）含全部习题详细解答）第3章：偏好（含全部习题详细解答偏好（曹乾译（东南大学caoqianseu@）3偏好在第2章我们已看到，消费者行为的经济模型很简单：人们在能购买得起的商品束中选择最优的消费束最优的消费束．．．．．．。
上一章说明了“能够买得起”的含义，本章则旨在说明“最优商品束”的概念。
我们把消费者选择的东西称为消费束．．．（consumption bundles ）。
消费束是我们研究选择问题中涉及到的全部全部．．商品（或服务）。
“全部”二字值得强调：当分析消费者选择问题时，一定要将涉及到的商品全部包含在消费束的定义中。
如果我们是在最宽泛的水平上研究消费者选择问题，我们不仅需要知道消费者可能消费的所有商品，还需要知道消费的时间，地点以及在什么样情形下消费的。
毕竟人们不仅关心今天的食物数量，还关心明天的食物数量。
大西洋里的小船和撒哈拉沙漠里的同样的小船，意义是不同的，类似的还有晴天的雨伞与阴雨天的雨伞。
通常将不同场所或环境中的“同种”商品视为不同的商品，因为消费者在这样的情形下对商品的评价会不同。
然而，当我们关注的是简单的消费选择问题时，相关的商品通常非常明显。
我们经常采用前面介绍过的思想：只使用两种商品进行分析，而将其中一种商品视为“所有其他的商品”。
这样做的好处是，我们可以重点关注一种商品和所有其他商品之间的权衡问题。
这样，在涉及很多商品的消费选择问题时，我们仍可以使用二维图形进行分析。
因此，可以假设消费束只包含两种商品，令),(21x x 表示消费束，其中1x 代表某种商品，2x 代表另外一种商品。
有时可将这个消费束简写为X 。
3.1消费者的偏好假设给定两个消费束),(21x x 和),(21y y ，消费者可按照他自己的意愿对这两个消费束排序。
范⾥安《微观经济学：现代观点》（章节题库-选择）【圣才出品】第5章选择⼀、判断题 1．某消费者的效⽤函数为u （x ，y ）＝（x ＋2）（y ＋1），如果他所消费的商品x 和商品y 都增加⼀倍，那么商品x 和商品y 的边际替代率仍保持不变。
（）【答案】F【解析】边际替代率为：//u x MRS u y ??=-??当u （x ，y ）＝（x ＋2）（y ＋1）时，MRS ＝－（y ＋1）/（x ＋2）；当u （x ，y ）＝（2x ＋2）（2y ＋1）时，MRS ＝－2（2y ＋1）/[2（2x ＋2）]＝－（2y ＋1）/[2（x ＋1）]。
商品x 和商品y 的边际替代率发⽣变化。
2．在最优选择处，消费者的⽆差异曲线和预算线⼀定是相切的。
（）【答案】F【解析】最优选择处，⽆差异曲线和预算线可以相切，也可以不相切。
在凸性偏好和内部最优的条件下，相切是最优选择的充分条件，即相切处⼀定是最优选择，但最优选择不⼀定是相切的。
在边界最优的情况下，如商品完全替代的情况下，⽆差异曲线与预算线是相交的，⽽不是相切的。
3．已知⼀元钱的边际效⽤为5个单位，⼀⽀钢笔的边际效⽤为35个单位，则消费者需要⽤6元来买这⽀钢笔。
（）【答案】F 【解析】基数效⽤论中效⽤最⼤化条件为MU/P ＝λ，本题中35/6＞5，消费者需要7元来购买这⽀钢笔。
4．某消费者的效⽤函数为u （x ，y ）＝x ＋4y 1/2，商品x 的价格为1元/单位，商品y 的价格为2元/单位。
如果他的收⼊从100元增加到150元，他对商品y 的消费将增加超过10%，但少于50%。
（）【答案】F【解析】根据效⽤最⼤化的条件//x y P u x P u y= 可得：1/（2y －1/2）＝1/2，即y ＝1。
当收⼊变动时，消费者对y 的消费不变。
5．某消费者效⽤函数为u （x ，y ）＝max{x ，y}，如果商品x 的价格与商品y 的价格相等，该消费者会选择购买等量的x 和y 。
![微观经济学：现代观点(范里安 著)48题及答案[精品文档]](https://img.taocdn.com/s1/m/d15c0ce971fe910ef12df8a5.png)
第一部分 消费者选择理论1.有两种商品，x1和x2，价格分别为p1和p2，收入为m 。
当11x x ≥时，政府加数量税t,画出预算集并写出预算线2. 消费者消费两种商品（x1，x2），如果花同样多的钱可以买（4，6）或（12，2），写出预算线的表达式。
3．重新描述中国粮价改革（1）假设没有任何市场干预，中国的粮价为每斤0。
4元，每人收入为100元。
把粮食消费量计为x ，在其它商品上的开支为y ，写出预算线，并画图。
（2）假设每人得到30斤粮票，可以凭票以0。
2元的价格买粮食，再写预算约束，画图。
（3）假设取消粮票，补贴每人6元钱，写预算约束并画图。
4． 证两条无差异曲线不能相交5． 一元纸币（x1）和五元纸币（x2）的边际替代率是多少？ 6． 若商品1为中性商品，则它对商品2的边际替代率？7. 写出下列情形的效用函数，画出无差异曲线，并在给定价格（p 1，p 2）和收入（m ）的情形下求最优解。
（1）x 1=一元纸币，x 2=五元纸币。
（2）x 1=一杯咖啡，x 2=一勺糖, 消费者喜欢在每杯咖啡加两勺糖。
8. 解最优选择 （1）21212(,)u x x x x =⋅（2）12u x x =+9. 对下列效用函数推导对商品1的需求函数，反需求函数，恩格尔曲线；在图上大致画出价格提供曲线，收入提供曲线；说明商品一是否正常品、劣质品、一般商品、吉芬商品，商品二与商品一是替代还是互补关系。
（1）212x x u += （2）()212,m in x x u =（3）ba x x u 21⋅=（4） 12ln u x x =+,10. 当偏好为完全替代时，计算当价格变化时的收入效用和替代效用（注意分情况讨论）。
11. 给定效用函数 (,)x y xy =，p x =3，p y =4，m=60，求当p y 降为3时价格变化引起的替代效应和收入效应。
12. 用显示偏好的弱公理说明为什么Slutsky 替代效应为负。
第4章 效 用1．一个效用函数自乘奇数次是单调变换。
那么该效用函数自乘偶数次还是单调变换吗？（提示：考虑 ()2f u u =这种情况）答：一个效用函数自乘偶数次后还是不是单调变换取决于效用函数的取值。
分析如下： 通常情况下，()12,0u u x x =≥，因此()2f u u =是（正的）单调变换，也就是说()2f u u =是单调递增的函数。
但是，也有可能存在()12,0u u x x =≤的情况。
比如，给某消费者两种商品，但这两种商品都是厌恶品，在这种情形下，他的效用不可能为正，即()12,0u u x x =≤。
所以，该情形下()2f u u =就不是（正的）单调变换。
根据分析需要，不考虑负单调变换的情形。
2．下面哪些是单调变换？ （1）213u v =-； （2）21/u v =-； （3）21/u v =； （4）ln u v =； （5）v u e -=-； （6）2u v =；（7）20u v v =>，； （8）20u v v =<，。
答：（1）是（正的）单调变换。
（2）在0v >时是单调变换，0v <时不是单调变换。
（3）在0v >时不是单调变换，0v <时是单调变换。
（4）是单调变换（此题暗含着0v >的假设，否则ln u v =无定义）。
（5）是单调变换。
（6）在0v >时是单调变换，0v <时不是单调变换。
（7）是单调变换。
（8）不是单调变换。
总结：单调变换的函数应是增函数；单调变换分为正单调变换和负单调变换，正单调变换后的效用函数能同样代表原偏好，负单调变换后的效用函数不能代表原偏好；单调变换不影响效用函数的边际替代率。
3．如果偏好是单调的，经过原点的射线与每一条无差异曲线只会相交一次。
请严格地证明。
（提示：如果它同某条无差异曲线相交两次，会出现什么情况呢？）证明：采用反证法，假设经过原点的射线方程为()()0f x ax a =>，它同某无差异曲线相交于两点()12,x x 和()12,y y ，由于()12,x x 和()12,y y 同在直线()f x ax =上，所以在1122x y x y >>，和1122x y x y <<，之中，必有其一成立，不妨假设是1122x y x y >>，，根据偏好的单调性，这就意味着()()1212,,x x y y ，这就和()12,x x 与()12,y y 在同一条无差异曲线上相矛盾。
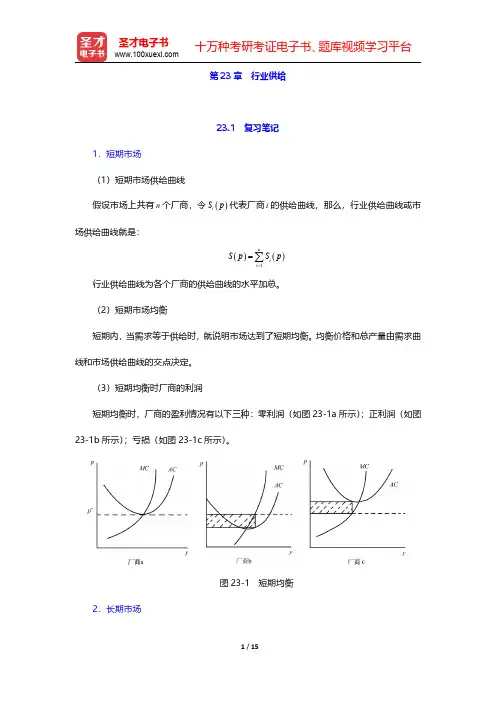
第23章行业供给23.1复习笔记1．短期市场（1）短期市场供给曲线假设市场上共有n 个厂商，令()i S p 代表厂商i 的供给曲线，那么，行业供给曲线或市场供给曲线就是：()()1ni i S p S p ==∑行业供给曲线为各个厂商的供给曲线的水平加总。
（2）短期市场均衡短期内，当需求等于供给时，就说明市场达到了短期均衡。
均衡价格和总产量由需求曲线和市场供给曲线的交点决定。
（3）短期均衡时厂商的利润短期均衡时，厂商的盈利情况有以下三种：零利润（如图23-1a 所示）；正利润（如图23-1b 所示）；亏损（如图23-1c 所示）。
图23-1短期均衡2．长期市场（1）长期竞争性均衡的实现条件第一，行业中的厂商都达到利润最大化；第二，所有厂商的经济利润为零；第三，产品的价格是厂商供给量与消费者需求量相等时的价格。
（2）长期竞争性均衡的实现途径及其动态分析一方面是行业内企业数量的调整，表现为厂商进入或退出某行业；另一方面是厂商对生产规模的调整。
3．长期供给曲线（1）长期供给曲线长期中，厂商基于长期成本函数和市场价格来选择是否进入该行业。
只要市场均衡价格高于长期平均成本的最低点，就会有新的厂商进入该行业并相应增加行业总供给。
因此，长期行业供给曲线逐渐由一个锯齿形状趋向于最低平均成本的水平线，如图23-2所示。
在一个竞争性市场中，单个厂商占市场总供给的份额非常小。
因此，可以把长期行业供给曲线就看为是等于最低平均成本的水平线。
图23-2近似的长期供给曲线完全竞争厂商的长期均衡出现在LAC曲线的最低点。
这时，生产的平均成本降到长期平均成本的最低点，商品的价格也等于最低的长期平均成本。
即完全竞争厂商的长期均衡条件为：==（利润最大化的条件，且是效率最优的）P LMC SMC==（经济利润为零）P LAC SAC（2）零利润的含义首先，这里的利润是指经济利润，而非会计利润；其次，经济利润为零，但会计利润有可能为正；再者，如果一个行业只能赚取零利润，并不是说该行业已经消失，而是说该行业不存在诱导新厂商进入的吸引力；最后，在利润为零的长期均衡中，该行业的生产是有效的（社会福利最大化），所以该行业是成熟的。
Intermediate Microeconomics:A Modern Approach (8th Edition)Hal R. Varian范里安中级微观经济学：现代方法（第8版）完美中文翻译版）含全部习题详细解答）第4章：效用（含全部习题详细解答效用（曹乾译（东南大学caoqianseu@）4效用在维多利亚时代，哲学家和经济学家轻率地把“效用”作为衡量一个人总体福利（well-being ）的指标。
他们用效用数值衡量一个人的幸福程度。
在这种思想下，自然可认为消费者做出选择的目的是使他们的效用最大（使他们尽可能地幸福）。
问题在于这些古典经济学家从未真正地阐述过怎样衡量效用。
我们应该如何量化不同消费选择下的效用“数额”？某人的效用与另外一人的效用相同吗？额外一颗糖块的效用是额外一根胡萝卜效用的两倍，这句话到底是什么意思？效用是人们希望最大化的“东西”，这里的“东西”是指什么？由于这些概念难以准确界定，现代经济学家已经抛弃了上述老套的观点，即他们不再把效用看成幸福的衡量指标。
取而代之的是，他们用消费者偏好．．．．．（consumer preferences ）重新改写了消费者行为理论，效用仅仅被当作为一种描述偏好的方法一种描述偏好的方法．．．．．．．．．。
经济学家逐渐认识到，对于选择行为而言，效用最要紧的事情是一个商品束的效用是否比另外一个商品束的高，至于高多少并不重要。
起初，偏好是用效用定义的：说一个商品束),(21x x 比另外一个商品束),(21y y 更受偏好，表示x 商品束比y 商品束效用更高。
但现在我们的观点正好反过来。
消费者的偏好偏好．．是研究选择行为的最基本工具，效用只是描述偏好的一种方法。
效用函数．．．．（utility function ）是对每个可能的消费束都赋予数值的一种方法，这种方法要做到对于更受偏好的消费束，赋值更大。
也就是说，消费束),(21x x 比),(21y y 更受偏好当且仅当前者的效用值要比后者大：用符号表示，),(),(2121y y x x f 当且仅当),(),(2121y y u x x u >.效用赋值的唯一重要性能是它是如何对商品束排序排序．．的。
Intermediate Microeconomics:A Modern Approach (8th Edition)Hal R. Varian范里安中级微观经济学：现代方法（第8版）完美中文翻译版）含全部习题详细解答）第3章：偏好（含全部习题详细解答偏好（曹乾译（东南大学caoqianseu@）3偏好在第2章我们已看到，消费者行为的经济模型很简单：人们在能购买得起的商品束中选择最优的消费束最优的消费束．．．．．．。
上一章说明了“能够买得起”的含义，本章则旨在说明“最优商品束”的概念。
我们把消费者选择的东西称为消费束．．．（consumption bundles ）。
消费束是我们研究选择问题中涉及到的全部全部．．商品（或服务）。
“全部”二字值得强调：当分析消费者选择问题时，一定要将涉及到的商品全部包含在消费束的定义中。
如果我们是在最宽泛的水平上研究消费者选择问题，我们不仅需要知道消费者可能消费的所有商品，还需要知道消费的时间，地点以及在什么样情形下消费的。
毕竟人们不仅关心今天的食物数量，还关心明天的食物数量。
大西洋里的小船和撒哈拉沙漠里的同样的小船，意义是不同的，类似的还有晴天的雨伞与阴雨天的雨伞。
通常将不同场所或环境中的“同种”商品视为不同的商品，因为消费者在这样的情形下对商品的评价会不同。
然而，当我们关注的是简单的消费选择问题时，相关的商品通常非常明显。
我们经常采用前面介绍过的思想：只使用两种商品进行分析，而将其中一种商品视为“所有其他的商品”。
这样做的好处是，我们可以重点关注一种商品和所有其他商品之间的权衡问题。
这样，在涉及很多商品的消费选择问题时，我们仍可以使用二维图形进行分析。
因此，可以假设消费束只包含两种商品，令),(21x x 表示消费束，其中1x 代表某种商品，2x 代表另外一种商品。
有时可将这个消费束简写为X 。
3.1消费者的偏好假设给定两个消费束),(21x x 和),(21y y ，消费者可按照他自己的意愿对这两个消费束排序。
即消费者可以认为一个消费束严格好于另外一个消费束，或者认为这两个消费束无差异。
我们用符号f 表示严格偏好．．．．(strict preference)，因此),(),(2121y y x x f 表示消费者严格偏好),(21x x 胜于),(21y y ，意思是说他肯定想要消费束X 而不是消费束Y 。
这种偏好关系提供了判断消费者选择哪个消费束的依据。
如果消费者偏好消费束X 胜于消费束Y ，那么他会选择消费束X 。
因此，偏好的思想是基于消费者行为行为．．之上的。
为了判断某消费者是否偏好某个消费束胜于另一个消费束，我们可以提供给他这两个消费束，观察他的选择行为。
如果他原本可以选择),(21y y ，但他总是选择),(21x x ，那么可知他偏好),(21x x 胜于),(21y y 。
如果消费者认为两个消费束是无差异．．．的．（indifferent ），我们记为),(~),(2121y y x x ，其中符号~表示无差异。
无差异的意思是说消费者根据自己的偏好，认为这两个消费束提供的满足程度是一样的。
我们用符号−f 表示弱偏好．．．（weak preference ）, ),(),(2121y y x x −f 意思是说消费者对前者的偏好胜于后者或者消费者对于这两个消费束无差异，简单地说就是消费者认为前者至少．．和后者一样好。
严格偏好、弱偏好和无差异不是三个独立的概念，它们互相相关！例如，若果),(),(2121y y x x −f 并且),(),(2121x x y y −f ，则),(~),(2121y y x x 。
即，如果消费者认为消费束X 至少和消费束Y 一样好，并且并且．．消费束Y 至少和消费束X 一样好，则消费者一定对这两个消费束是无差异的。
类似地，如果),(),(2121y y x x −f ，但),(~),(2121y y x x 不成立，则),(),(2121y y x x f 。
这只不过是说如果消费者认为消费束X 至少和消费束Y 一样好，但这两个消费束对他来说不是无差异的，则他认为消费束X 严格好于消费束Y 。
3.2关于偏好的假设经济学家通常对消费者偏好的“一致性(consistency)”作出一些假设。
例如，某情形下，既有),(),(2121y y x x f 又有),(),(2121x x y y f ，这样的偏好即使不说是矛盾的，也是不理性的。
因为这意味着消费者认为消费束X 比Y 好，但又反过来认为消费束Y 比X 好。
因此需要对偏好关系作出某些假设。
有些假设非常基本，通常被称为消费者理论的“公理”。
此处我们给出消费者偏好的三条公理。
完备性．．．（complete ）公理。
假设任何两个消费束都可以比较，即给定消费束X 和消费束Y ，必有),(),(2121y y x x −f 或者),(),(2121x x y y −f ，或者二者都成立，在最后一种情形中，消费者对于这两个消费束是无差异的。
反身性．．．（reflexive ）公理。
假设任何消费束都至少和它本身一样好，即),(),(2121x x x x −f 。
传递性．．．（transitive ）公理。
如果),(),(2121y y x x −f 并且),(),(2121z z y y −f ，则),(),(2121z z x x −f 。
换句话说，如果消费者认为消费束X 至少和Y 一样好，而且消费束Y 至少和Z 一样好，则他认为消费束X 至少和Z 一样好。
第一个公理即完备性公理，几乎难以反驳，至少对于经济学家通常研究的选择问题来说是这样的。
我们说任何两个消费束可以比较，只不过想表明消费者能在这二者中作出取舍。
你也许会想到极端情形比如生或死的选择，这类问题中对选项的排序很困难甚至无法排序，幸好经济学基本不研究这样的选择问题。
第二个公理即反身性公理，是平凡的（trivial ）（一）。
任何消费束当然和同样的消费束至少一样好。
父母偶尔会发现小孩的行为违背了反身性公理，但对于大多数成人的行为来说，这个假设似乎是合理的。
第三个公理即传递性公理，问题相对大些。
人们并没搞清偏好的传递性是否为偏好的必要．．属性。
从纯逻辑的角度看，偏好的传递性假设无法做到让人信服。
事实上，传递性是对人们选择行为作出的假设，而不是纯逻辑的论断。
当然，这个假设是否符合基本逻辑事实并不是问题的关键，关键在于这个假设能否合理地准确刻画消费者的选择行为。
如果某个消费者说他认为消费束X 比Y 好，Y 比Z 好，Z 比X 好。
怎么评价他？我们通常认为他不正常。
更重要的是，如果给上述消费者三个消费束X ，Y 和Z ，他如何选出最喜欢的？他很难作出选择，因为无论他选哪个消费束，都还有比这个消费束更好的消费束。
如果我们想研究消费者的“最佳”选择问题，必须假设偏好满足传递性公理。
如果偏好不是传递的，就可能出现无法作出最优选择的情形。
3.3无差异曲线偏好的三个公理是消费者理论的基石，如果再加上其他一些技术性的假设，我们就能用数学构建起整个消费者理论的大厦。
然而，借助图形分析更加直观，但我们先要引入刻画偏好的一个工具，这就是无差异曲线．．．．．（indifference curve ）。
图3.1：弱偏好集弱偏好集。
阴影区域的所有消费束都至少和),(21x x 一样好。
（一）trivial （平凡的），数学用语，是指某东西（例如向量空间）的结构非常简单，不值一提（但又不得不提）。
有时我们也会遇到下列说法：某方程的某个解是平凡的。
这是说这个解非常简单。
请看图3.1，我们用横轴和纵轴分别表示商品1和商品2的消费数量。
任选一个消费束),(21x x ，用阴影标记出所有比),(21x x 更好或者一样好的消费束。
这些消费束称为弱偏好．．．集．（weakly preferred set ）。
在弱偏好集边界上的消费束与),(21x x 一样好，这些消费束组成了无差异曲线．．．．．。
对于任何一个消费束都可以画出经过这点的无差异曲线。
经过某个消费束的无差异曲线包含了所有与该消费束一样好的消费束。
使用无差异曲线刻画偏好时，在同一条无差异曲线上的消费束是无差异的。
不同无差异曲线上的消费束怎样比较？在图形上如果只给你几条无差异曲线，你无法比较不同无差异曲线上的消费束。
因此，有时候人们在无差异曲线上标记一些小箭头，指出哪个方向上的消费束更受偏好。
我们一般不这么做，除非在容易混淆的情形时，我们才用箭头标记。
如果我们对偏好不作出进一步的假设，你可以画出任意形状的无差异曲线。
即使如此，无差异曲线仍具有一个重要的性质：不同无差异曲线不同无差异曲线．．．．．．．（代表不同偏好水平代表不同偏好水平））．．．．．．．．．．不能相交．．．．。
也就是说，不可能出现类似图3.2的情形。
为了证明上述结论，在图形上任意选取三个消费束：X ，Y 和Z ，使得X 只位于其中一条无差异曲线上，Y 只位于另一条无差异曲线上，Z 位于上述两条无差异曲线的交点处。
由于不同无差异曲线代表不同的偏好水平，因此假设X 严格好于Y 。
由图可知，Z X ~以及Y Z ~，由传递性公理可知Y X ~。
但这与我们的假设Y X f 矛盾。
这就说明无差异曲线不能相交。
图3.2：无差异曲线不能相交无差异曲线不能相交。
如果相交，消费束X ，Y 和Z 必然两两无差异，因此这三个消费束就不能位于不同的无差异曲线上。
无差异曲线还有其他什么样的性质吗？一般来说，答案为：并不多。
无差异曲线是描述偏好的一种方法。
几乎任何“合理的”偏好都能用无差异曲线描述。
你要掌握的技巧是给你一种偏好类型，你能找到相应的无差异曲线形状来描述它。
下面我们就介绍这些知识。
3.4偏好的例子我们利用例子来考察偏好和无差异曲线之间的对应关系。
我们先给出一些偏好类型，然后看看什么样形状的曲线能描述这样的偏好。
给定偏好类型，构建相应无差异曲线的通用程序如下。
首先，画好横纵坐标，任意画出一个点，代表消费束),(21x x 。
现在假设给消费者一些商品1（1x ∆），则新消费束为),(211x x x ∆+。
你来回答怎样改变改变．．商品2的数量才能恰好使消费者还在原来的无差异曲线上。
假设商品2的变化量为2x ∆。
现在问题变为“给定商品1的消费量变化1x ∆，2x ∆为多大时， ),(2211x x x x ∆+∆+和),(21x x 这两个消费束恰好无差异？”一旦你知道如何移动),(21x x ，你就画出了一小段无差异曲线。
再画出一个消费束，重复以上步骤…直到你画出比较全面的无差异曲线形状。
完全替代两种商品是完全替代．．．．（perfect substitute ）的，如果消费者愿意按固定固定．．比率将一种商品替换为另一种。
