离散数学习题集十五套 答案

离散数学试题及答案一、选择题1. 在集合论中，下列哪个选项表示两个集合A和B的并集？A. A ∩ BB. A ∪ BC. A - BD. A × B答案：B2. 命题逻辑中，下列哪个符号表示逻辑非？A. ∧B. ∨C. ¬D. →答案：C3. 在有向图中，如果存在一条从顶点u到顶点v的路径，那么称顶点v为顶点u的：A. 祖先B. 后代C. 邻居D. 连接点答案：B二、填空题1. 一个命题函数P(x)表示为“x是偶数”，那么其否定形式为________。

答案：x是奇数2. 在关系R上，如果对于所有的a和b，如果(a, b)∈R且(b, a)∈R，则称R为________。

答案：自反的三、简答题1. 简述什么是等价关系，并给出其三个基本性质。

答案：等价关系是一种特殊的二元关系，它满足自反性、对称性和传递性。

自反性指每个元素都与自身相关；对称性指如果a与b相关，则b也与a相关；传递性指如果a与b相关，b与c相关，则a与c也相关。

2. 解释什么是图的连通分量，并给出如何判断一个图是否是连通图。

答案：连通分量是指图中最大的连通子图，即图中任意两个顶点之间都存在路径。

判断一个图是否是连通图，可以通过深度优先搜索或广度优先搜索算法遍历整个图，如果所有顶点都被访问，则图是连通的。

四、计算题1. 给定命题公式P：((p → q) ∧ (r → ¬p)) → (q ∨ ¬r)，证明P是一个重言式。

答案：通过使用命题逻辑的等价规则和真值表，可以证明P在所有可能的p, q, r的真值组合下都为真，因此P是一个重言式。

2. 给定一个有向图G，顶点集合V(G)={1, 2, 3, 4}，边集合E(G)={(1, 2), (2, 3), (3, 4), (4, 1), (2, 4)}。

找出所有强连通分量。

答案：通过Kosaraju算法或Tarjan算法，可以找到图G的强连通分量，结果为{1, 4}和{2, 3}。

《离散数学》试题及答案一、选择题（每题5分，共25分）1. 设集合A={1,2,3,4,5}，B={2,4,6,8,10}，则A∩B的结果是（）A. {1,2,3,4,5}B. {2,4}C. {1,3,5}D. {1,2,3,4,5,6,8,10}答案：B2. 下列关系中，哪个是等价关系？（）A. ≤B. ≠C. |D. ≠答案：A3. 设图G有5个顶点，每两个顶点之间都有一条边相连，则图G的边数是（）A. 5B. 10C. 15D. 20答案：C4. 下列哪一个图是欧拉图？（）A. 无向图B. 有向图C. 树D. 环答案：D5. 下列哪一个命题是正确的？（）A. 若p→q为真，则p为真B. 若p∧q为假，则p为假C. 若p∨q为真，则q为真D. 若p→q为假，则p为假答案：B二、填空题（每题5分，共25分）1. 设集合A={a,b,c,d}，B={c,d,e}，则A-B=________。

答案：{a,b}2. 设p是命题“今天是晴天”，q是命题“我去公园玩”，则命题“如果今天不是晴天，那么我不去公园玩”可以表示为________。

答案：¬p→¬q3. 设图G有n个顶点，e条边，则图G的度数之和为________。

答案：2e4. 一个连通图至少有________个顶点。

答案：25. 设图G的邻接矩阵为A，则A的转置矩阵表示________。

答案：图G的转置图三、判断题（每题5分，共25分）1. 离散数学是研究离散结构的数学分支。

（）答案：正确2. 两个集合的笛卡尔积是这两个集合的直积。

（）答案：正确3. 有向图中，顶点u和顶点v之间的长度为2的路径是指路径上有3条边。

（）答案：错误4. 树是一种无向图。

（）答案：正确5. 哈夫曼编码是一种贪心算法。

（）答案：正确四、应用题（每题25分，共50分）1. 设集合A={1,2,3,4,5}，B={2,4,6,8,10}，C={3,6,9,12,15}，求A∪(B∩C)。

习题参考解答习题1.11、（3）P：银行利率降低Q：股价没有上升P∧Q（5）P：他今天乘火车去了北京Q：他随旅行团去了九寨沟PQ（7）P：不识庐山真面目Q：身在此山中Q→P，或～P→～Q（9）P：一个整数能被6整除Q：一个整数能被3整除R：一个整数能被2整除T：一个整数的各位数字之和能被3整除P→Q∧R ，Q→T2、（1）T （2）F （3）F （4）T （5）F（6）T （7）F （8）悖论习题 1.31（3）)()()()()()(R P Q P R P Q P R Q P R Q P →∨→⇔∨⌝∨∨⌝⇔∨∨⌝⇔∨→（4）()()()(())()(()())(())()()()()P Q Q R R P P R Q R P P R R P Q R P P R P R Q R Q P ∧∨∧∨∧=∨∧∨∧=∨∨∧∧∨∧=∨∧∨∧∨∧∨=右2、不， 不， 能习题 1.41(3) (())~((~))(~)()~(~(~))(~~)(~)P R Q P P R Q P P R T P R P R Q Q P R Q P R Q →∧→=∨∧∨=∨∧=∨=∨∨∧=∨∨∧∨∨、主合取范式)()()()()()()()()()()()()()())(())(()()(())()())(()((Q P R P Q R P Q R R Q P R Q P R Q P Q P R Q P R P Q R P Q R R Q P R Q P R Q P R Q P Q Q P R P P Q R R R Q Q P P R Q R P P Q R P P Q R P ∧∧∨∧⌝∧∨⌝∧⌝∧∨∧⌝∧⌝∨⌝∧∧⌝∨⌝∧⌝∧⌝=∧∧∨⌝∧∧∨∧⌝∧∨⌝∧⌝∧∨∧⌝∧⌝∨∧⌝∧⌝∨⌝∧∧⌝∨⌝∧⌝∧⌝=∨⌝∧∧∨∨⌝∧⌝∧∨∨⌝∧∨⌝∧⌝=∧∨⌝∧∨⌝=∨⌝∧∨⌝=→∧→ ————主析取范式(2) ()()(~)(~)(~(~))(~(~))(~~)(~)(~~)P Q P R P Q P R P Q R R P R Q Q P Q R P Q R P R Q →∧→=∨∧∨=∨∨∧∧∨∨∧=∨∨∧∨∨∧∨∨ 2、()~()(~)(~)(~~)(~)(~~)P Q R P Q R P Q P R P Q R P Q R P R Q →∧=∨∧=∨∧∧=∨∨∧∨∨∧∨∨∴等价3、解：根据给定的条件有下述命题公式：（A →（C ∇D ））∧～（B ∧C ）∧～（C ∧D ）⇔（～A ∨（C ∧～D ）∨（～C ∧D ））∧（～B ∨～C ）∧（～C ∨～D ）⇔（（～A ∧～B ）∨（C ∧～D ∧～B ）∨（～C ∧D ∧～B ）∨（～A ∧～C ）∨（C ∧～D ∧～C ）∨（～C ∧D ∧～C ））∧（～C ∨～D ）⇔（（～A ∧～B ）∨（C ∧～D ∧～B ）∨（～C ∧D ∧～B ）∨（～A ∧～C ）∨（～C ∧D ∧～C ）） ∧（～C ∨～D ）⇔（～A ∧～B ∧～C ）∨（C ∧～D ∧～B ∧～C ）∨（～C ∧D ∧～B ∧～C ）∨ （～A ∧～C ∧～C ）∨（～C ∧D ∧～C ∧～C ）∨（～A ∧～B ∧～D ）∨（C ∧～D ∧～B ∧～D ）∨（～C ∧D ∧～B ∧～D ）∨（～A ∧～C ∧～D ）∨ （～C ∧D ∧～C ∧～D ）（由题意和矛盾律）⇔（～C ∧D ∧～B ）∨（～A ∧～C ）∨（～C ∧D ）∨（C ∧～D ∧～B ）⇔（～C ∧D ∧～B ∧A ）∨ （～C ∧D ∧～B ∧～A ）∨ （～A ∧～C ∧B ）∨ （～A ∧～C ∧～B ）∨ （～C ∧D ∧A ）∨ （～C ∧D ∧～A ）∨（C ∧～D ∧～B ∧A ）∨（C ∧～D ∧～B ∧～A ）⇔（～C ∧D ∧～B ∧A ）∨ （～A ∧～C ∧B ∧D ）∨ （～A ∧～C ∧B ∧～D ）∨（～A ∧～C ∧～B ∧D ）∨ （～A ∧～C ∧～B ∧～D ）∨（～C ∧D ∧A ∧B ）∨ （～C ∧D ∧A ∧～B ）∨ （～C ∧D ∧～A ∧B ）∨ （～C ∧D ∧～A ∧～B ）∨（C ∧～D ∧～B ∧A ）∨（C ∧～D ∧～B ∧～A ） ⇔（～C ∧D ∧～B ∧A ）∨ （～A ∧～C ∧B ∧D ）∨ （～C ∧D ∧A ∧～B ）∨ （～C ∧D ∧～A ∧B ） ∨（C ∧～D ∧～B ∧A ）⇔（～C ∧D ∧～B ∧A ）∨ （～A ∧～C ∧B ∧D ）∨（C ∧～D ∧～B ∧A ） 三种方案：A 和D 、 B 和D 、 A 和C习题 1.51、 （1）需证()(())P Q P P Q →→→∧为永真式()(())~(~)(~())~~(~)(()(~))~(~)(~)()P Q P P Q P Q P P Q P P P Q P Q TP Q P Q T P Q P P Q →→→∧=∨∨∨∧∨=∨∨∧∨=∨∨∨=∴→⇒→∧（3）需证S R P P →∧⌝∧为永真式SR P P T S F S R F S R P P ⇒∧⌝∧∴⇔→⇔→∧⇔→∧⌝∧3A B A B ⇒∴→ 、为永真式。

离散数学习题答案习题一1. 判断下列句子是否为命题？若是命题说明是真命题还是假命题。

（1）3是正数吗？（2）x＋1=0。

（3）请穿上外衣。

（4）2＋1＝0。

（5）任一个实数的平方都是正实数。

（6）不存在最大素数。

（7）明天我去看电影。

（8）9＋5≤12。

（9）实践出真知。

（10）如果我掌握了英语、法语，那么学习其他欧洲语言就容易多了。

解：（1）、（2）、（3）不是命题。

（4）、（8）是假命题。

（5）、（6）、（9）、（10）是真命题。

（7）是命题，只是现在无法确定真值。

2. 设P表示命题“天下雪”，Q表示命题“我将去书店”，R表示命题“我有时间”，以符号形式写出下列命题。

（1）如果天不下雪并且我有时间，那么我将去书店。

（2）我将去书店，仅当我有时间。

（3）天不下雪。

（4）天下雪，我将不去书店。

解：（1）（┐P∧R）→Q。

（2）Q→R。

（3）┐P。

（4）P→┐Q。

3. 将下列命题符号化。

（1）王皓球打得好，歌也唱得好。

（2）我一边看书，一边听音乐。

（3）老张和老李都是球迷。

（4）只要努力学习，成绩会好的。

（5）只有休息好，才能工作好。

（6）如果a和b是偶数，那么a+b也是偶数。

（7）我们不能既游泳又跑步。

（8）我反悔，仅当太阳从西边出来。

（9）如果f(x)在点x0处可导，则f(x)在点x0处可微。

反之亦然。

（10）如果张老师和李老师都不讲这门课，那么王老师就讲这门课。

（11）四边形ABCD是平行四边形，当且仅当ABCD的对边平行。

（12）或者你没有给我写信，或者信在途中丢失了。

解：（1）P：王皓球打得好，Q：王皓歌唱得好。

原命题可符号化：P∧Q。

（2）P：我看书，Q：我听音乐。

原命题可符号化：P∧Q。

（3）P：老张是球迷，Q：老李是球迷。

原命题可符号化：P∧Q。

（4）P：努力学习，Q：成绩会好。

原命题可符号化：P→Q。

（5）P：休息好，Q：工作好。

原命题可符号化：Q→P。

（6）P：a是偶数，Q：b是偶数，R：a+b是偶数。

精品文档离散数学习题答案习题一及答案：（ P14-15 ）14、将下列命题符号化：（ 5）李辛与李末是兄弟解：设 p：李辛与李末是兄弟，则命题符号化的结果是p（ 6）王强与刘威都学过法语解：设 p：王强学过法语； q：刘威学过法语；则命题符号化的结果是p q （ 9）只有天下大雨，他才乘班车上班解：设 p：天下大雨； q：他乘班车上班；则命题符号化的结果是q p（ 11）下雪路滑，他迟到了解：设 p：下雪； q：路滑； r ：他迟到了；则命题符号化的结果是( p q)r15、设 p： 2+3=5.q：大熊猫产在中国 .r：太阳从西方升起 .求下列复合命题的真值：（ 4）(p q r )(( p q)r )解： p=1， q=1，r=0 ，(p q r )(110)1，((p q)r )((11)0)(00)1(p q r )(( p q)r ) 1 1119、用真值表判断下列公式的类型：（ 2）( p p)q解：列出公式的真值表，如下所示：p q p qp) ( p p)q( p001111011010100101110001由真值表可以看出公式有 3 个成真赋值，故公式是非重言式的可满足式。

20、求下列公式的成真赋值：精品文档（ 4）( p q)q解：因为该公式是一个蕴含式，所以首先分析它的成假赋值，成假赋值的条件是：( p q)1p0q0q0所以公式的成真赋值有： 01，10， 11。

习题二及答案：（ P38）5、求下列公式的主析取范式，并求成真赋值：（ 2）(p q) (q r )解：原式( p q) q r q r( p p) q r( p q r ) ( p q r )m3m7，此即公式的主析取范式，所以成真赋值为011， 111。

6、求下列公式的主合取范式，并求成假赋值：（ 2）( p q) ( p r )解：原式( pp r ) ( p q r )( p q r )M 4，此即公式的主合取范式，所以成假赋值为 100。

离散考试题与答案一、选择题1. 下列哪个不是离散数学的基本概念？A. 集合B. 二进制C. 图论D. 函数答案：C2. 设A = {1, 2, 3, 4}，B = {3, 4, 5, 6}，则A ∩ B = ?A. {1, 2}B. {3, 4}C. {5, 6}D. {3, 4, 5, 6}答案：B3. 在一个完全图中，有多少条边？A. nB. n(n-1)/2C. n(n+1)/2D. 2n答案：B4. 若f(x) = x^2 + 3x，则f(-2)的值为？A. -4B. -2C. 0D. 2答案：C5. 若A = {a, b, c}，B = {b, c, d}，则A - B = ?A. {a, b, c}B. {b, c, d}C. {a, d}D. {}答案：A二、填空题1. 设f(x) = x^2 + 5，求f(-3)的值。

答案：162. 设A = {1, 2, 3}，B = {3, 4, 5}，则A ∪ B = ？答案：{1, 2, 3, 4, 5}3. 在一个有向图中，若存在一条从顶点A到顶点B的路径，并且从B到A也存在一条路径，则该图称为_____图。

答案：强连通图4. 二进制数11111111转换为十进制的结果为______。

答案：2555. 若给定集合A = {1, 2, 3, 4}，则集合A的所有子集的个数为______。

答案：16三、简答题1. 解释集合的并、交和差的运算。

答案：集合的并运算指的是将两个集合中的所有元素合并成一个新的集合，新集合中的元素包括原来两个集合中的所有元素，但不重复。

集合的交运算指的是求出两个集合中共有的元素，构成一个新的集合。

集合的差运算指的是在一个集合中去除另一个集合中的元素，得到一个新的集合。

2. 什么是图论？答案：图论是研究图及其在各个领域中的应用问题的一门学科。

图由若干个顶点及连接这些顶点的边构成，图论主要研究图的性质、结构和算法问题。

3. 什么是函数？答案：函数是一种将每个输入值唯一对应到输出值的关系。

1、设A ={1，{2}，4，5}，B ={2，{5}}，则A - B ={1，{2}，4，5}，A ⊕B ={1，{2}，4，5,2，{5}}.2、n K 是n 阶无向完全图，则n K 有 n*(n-1)/2 条边.3、一棵树有2个6度点、3个4度点、3个2度点，其它的都是1度，则T 中有___18___片树叶.4、图G 如右图所示，点割集有{d}、{a}边割集_{(a,d)}、 {(f,e) (f,d)}．波兰符号法表达式=**+*+÷211242311.设个体域{}1,2D =，与公式()xA x ∃等价的命题公式是()()12A A ∨5、计算命题公式()q p r →→⌝的主析取范式、成真赋值、成假赋值。

()()02346q p rp q rm m m m m ⇔⌝⌝∨∨⌝⇔⌝∧∨⌝⇔∨∨∨∨成真赋值：000， 010，011，100， 110成假赋值：001， 101，111. 6计算命题公式()()p q r q ∨→⌝→的主析取范式、成真赋值、成假赋值。

()()()0123467p q r q p q q rm m m m m m m ⇔⌝∨∨∨⇔⌝∧⌝∨∨⇔∨∨∨∨∨∨成真赋值：000， 001 ，010，011，101， 110， 111成假赋值：100 7. 画出下图G 的最小生成树，并计算其权值。

图不惟一（略），权为19即是正确答案 W(T)=19图不惟一（略）,权为13即为正确答案W(T)=138. 点着色学生会下设6个委员会, 第一委员会={张, 李, 王}, 第二委员会={李, 赵, 刘}, 第三委员会={张, 刘, 王}, 第四委员会={赵,刘, 孙}, 第五委员会={张, 王}, 第六委员会={李, 刘, 王}. 每个月每个委员会都要开一次会, 为了确保每个人都能参加他所在的委员会会议, 这6个会议至少要安排在几个不同时间段?解：(点着色问题)至少要安排在4个不同的时间段第1时段:一,四第2时段:二,五第3时段:三第4时段:六9、计算机系期末安排6门选修课程的考试，课程编号为1到6。

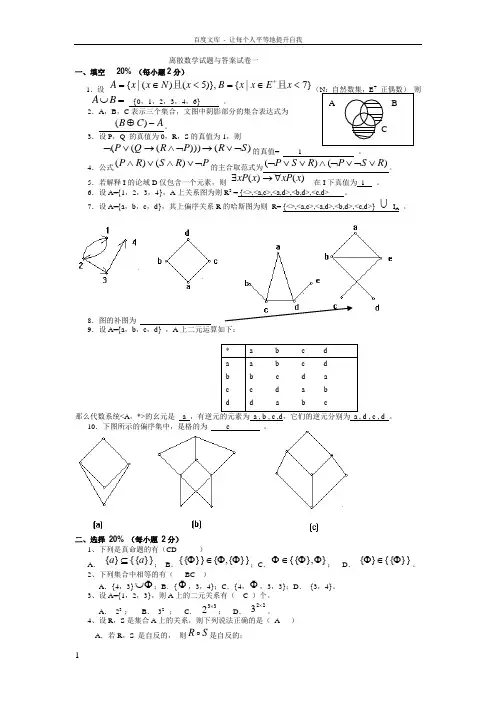
离散数学试题与答案试卷一一、填空20% （每小题2分）1．设}7|{)},5()(|{<∈=<∈=+xExxBxNxxA且且（N：自然数集，E+正偶数）则=⋃BA{0，1，2，3，4，6} 。

2．A，B，C表示三个集合，文图中阴影部分的集合表达式为ACB-⊕)(。

3．设P，Q 的真值为0，R，S的真值为1，则)()))(((SRPRQP⌝∨→⌝∧→∨⌝的真值= 1 。

4．公式PRSRP⌝∨∧∨∧)()(的主合取范式为)()(RSPRSP∨⌝∨⌝∧∨∨⌝。

5．若解释I的论域D仅包含一个元素，则)()(xxPxxP∀→∃在I下真值为1 。

6．设A={1，2，3，4}，A上关系图为则R2 = {<>,<a,c>,<a,d>,<b,d>,<c,d> 。

7．设A={a，b，c，d}，其上偏序关系R的哈斯图为则R= {<>,<a,c>,<a,d>,<b,d>,<c,d>}IA。

8．图的补图为9．设A={a，b，c，d} ，A上二元运算如下：* a b c dabcda b c db c d ac d a bd a b c那么代数系统<A，*>的幺元是 a ，有逆元的元素为a , b , c ,d，它们的逆元分别为 a , d , c , d 。

10．下图所示的偏序集中，是格的为 c 。

二、选择20% （每小题2分）1、下列是真命题的有（CD）A．}}{{}{aa⊆；B．}}{,{}}{{ΦΦ∈Φ；C．}},{{ΦΦ∈Φ；D．}}{{}{Φ∈Φ。

2、下列集合中相等的有（BC ）A．{4，3}Φ⋃；B．{Φ，3，4}；C．{4，Φ，3，3}；D．{3，4}。

3、设A={1，2，3}，则A上的二元关系有（ C ）个。

A．23 ；B．32 ；C．332⨯；D．223⨯。

4、设R，S是集合A上的关系，则下列说法正确的是（A ）A．若R，S 是自反的，则SR 是自反的；A BCB ．若R ，S 是反自反的， 则S R 是反自反的；C ．若R ，S 是对称的， 则S R 是对称的；D ．若R ，S 是传递的， 则S R 是传递的。

《离散数学》题库与答案一、选择或填空（数理逻辑部分）1、下列哪些公式为永真蕴含式( )(1)⌝Q=>Q→P (2)⌝Q=>P→Q (3)P=>P→Q (4)⌝P∧(P∨Q)=>⌝P答：在第三章里面有公式（1）是附加律，（4）可以由第二章的蕴含等值式求出（注意与吸收律区别）2、下列公式中哪些是永真式( )(1)(┐P∧Q)→(Q→⌝R) (2)P→(Q→Q) (3)(P∧Q)→P (4)P→(P∨Q)答：（2），（3），（4）可用蕴含等值式证明3、设有下列公式，请问哪几个是永真蕴涵式( )(1)P=>P∧Q (2) P∧Q=>P (3) P∧Q=>P∨Q(4)P∧(P→Q)=>Q (5) ⌝(P→Q)=>P (6) ⌝P∧(P∨Q)=>⌝P答：（2）是第三章的化简律，（3）类似附加律，（4）是假言推理，（3），（5），（6）都可以用蕴含等值式来证明出是永真蕴含式4、公式x((A(x)B(y，x))z C(y，z))D(x)中，自由变元是( )，约束变元是( )。

答：x,y, x,z（考察定义在公式x A和x A中，称x为指导变元，A为量词的辖域。

在x A和x A的辖域中，x的所有出现都称为约束出现，即称x 为约束变元，A中不是约束出现的其他变项则称为自由变元。

于是A(x)、B(y，x)和z C(y，z)中y为自由变元，x和z为约束变元，在D(x)中x 为自由变元）5、判断下列语句是不是命题。

若是，给出命题的真值。

( )(1)北京是中华人民共和国的首都。

(2) 陕西师大是一座工厂。

(3) 你喜欢唱歌吗 (4) 若7+8＞18，则三角形有4条边。

(5) 前进！ (6) 给我一杯水吧！答：（1）是，T （2）是，F （3）不是（4）是，T （5）不是（6）不是（命题必须满足是陈述句，不能是疑问句或者祈使句。

）6、命题“存在一些人是大学生”的否定是( )，而命题“所有的人都是要死的”的否定是( )。

《离散数学》练习题和参考答案《离散数学》练习题和参考答案一、选择或填空（数理逻辑部分）1、下列哪些公式为永真蕴含式？( )(1)⌝Q=>Q→P (2)⌝Q=>P→Q (3)P=>P→Q (4)⌝P∧(P∨Q)=>⌝P 答：（1），（4）2、下列公式中哪些是永真式？( )(1)(┐P∧Q)→(Q→⌝R) (2)P→(Q→Q) (3)(P∧Q)→P (4)P→(P∨Q) 答：（2），（3），（4）3、设有下列公式，请问哪几个是永真蕴涵式?( ) (1)P=>P∧Q (2) P∧Q=>P (3) P∧Q=>P∨Q(4)P∧(P→Q)=>Q (5) ⌝(P→Q)=>P (6) ⌝P∧(P∨Q)=>⌝P 答：（2），（3），（4），（5），（6）4、公式∀x((A(x)→B(y，x))∧∃z C(y，z))→D(x)中，自由变元是( )，约束变元是( )。

答：x,y, x,z5、判断下列语句是不是命题。

若是，给出命题的真值。

( )北京是中华人民共和国的首都。

(2) 陕西师大是一座工厂。

(3) 你喜欢唱歌吗？ (4) 若7+8＞18，则三角形有4条边。

(5) 前进！ (6) 给我一杯水吧！答：（1）是，T （2）是，F （3）不是（4）是，T （5）不是（6）不是6、命题“存在一些人是大学生”的否定是( )，而命题“所有的人都是要死的”的否定是( )。

答：所有人都不是大学生，有些人不会死7、设P：我生病，Q：我去学校，则下列命题可符号化为( )。

(1) 只有在生病时，我才不去学校 (2) 若我生病，则我不去学校(3) 当且仅当我生病时，我才不去学校(4) 若我不生病，则我一定去学校答：（1）P↔（4）QP→⌝P⌝⌝（2）QQ→P⌝→（3）Q8、设个体域为整数集，则下列公式的意义是( )。

(1) ∀x∃y(x+y=0) (2) ∃y∀x(x+y=0)答：（1）对任一整数x存在整数 y满足x+y=0（2）存在整数y 对任一整数x满足x+y=09、设全体域D是正整数集合，确定下列命题的真值：(1) ∀x∃y (xy=y) ( ) (2) ∃x∀y(x+y=y) ( ) (3) ∃x∀y(x+y=x) ( ) (4) ∀x∃y(y=2x) ( )答：（1） F （2） F （3）F （4）T10、设谓词P(x)：x是奇数，Q(x)：x是偶数，谓词公式∃x(P(x)∨Q(x))在哪个个体域中为真?( )(1) 自然数(2) 实数 (3) 复数(4) (1)--(3)均成立答：（1）11、命题“2是偶数或-3是负数”的否定是（）。

《离散数学》试题及标准答案解析⼀、填空题1设集合A,B，其中A＝{1,2,3}, B= {1,2}, 则A - B＝____________________; ρ(A) - ρ(B)＝ __________________________ .2. 设有限集合A, |A| = n, 则 |ρ(A×A)| = __________________________.3.设集合A = {a, b}, B = {1, 2}, 则从A到B的所有映射是__________________________ _____________, 其中双射的是__________________________.4. 已知命题公式G＝?(P→Q)∧R，则G的主析取范式是_________________________________________________________________________________________.6设A、B为两个集合, A= {1,2,4}, B = {3,4}, 则从A?B＝_________________________; A?B＝_________________________;A－B＝ _____________________ .7. 设R是集合A上的等价关系，则R所具有的关系的三个特性是______________________, ________________________, _______________________________.8. 设命题公式G＝?(P→(Q∧R))，则使公式G为真的解释有__________________________，_____________________________, __________________________.9. 设集合A＝{1,2,3,4}, A上的关系R1= {(1,4),(2,3),(3,2)}, R2= {(2,1),(3,2),(4,3)}, 则R1?R2 = ________________________,R2? R1 =____________________________, R12 =________________________.10. 设有限集A, B，|A| = m, |B| = n, 则| |ρ(A?B)| = _____________________________. 11设A,B,R是三个集合，其中R是实数集，A = {x | -1≤x≤1, x∈R}, B = {x | 0≤x < 2, x∈R},则A-B = __________________________ , B-A =__________________________ , A∩B = __________________________ , .13.设集合A＝{2, 3, 4, 5, 6}，R是A上的整除，则R以集合形式(列举法)记为__________________________________________________________________.14. 设⼀阶逻辑公式G = ?xP(x)→?xQ(x)，则G的前束范式是__________________________ _____.16. 设谓词的定义域为{a, b},将表达式?xR(x)→?xS(x)中量词消除，写成与之对应的命题公式是__________________________________________________________________________.17. 设集合A＝{1, 2, 3, 4}，A上的⼆元关系R＝{(1,1),(1,2),(2,3)}, S＝{(1,3),(2,3),(3,2)}。

离散数学试题与答案试卷一3、设A={1，2，3}，则A 上的二元关系有（ c ）个。

A ． 23 ；B ． 32 ；C ． 332⨯； D ． 223⨯。

5、设A={1，2，3，4}，P （A ）（A 的幂集）上规定二元系如下|}||(|)(,|,{t s A p t s t s R =∧∈><=则P （A ）/ R=（ d ）A ．A ；B ．P(A) ；C ．{{{1}}，{{1，2}}，{{1，2，3}}，{{1，2，3，4}}}；D ．{{Φ}，{2}，{2，3}，{{2，3，4}}，{A}}试卷二试题与答案1、 设S={a 1 ，a 2 ，…，a 8}，B i 是S 的子集，则由B 31所表达的子集是 6、设 ,+ 为普通加法和乘法，则（ a ）>+< ,,S 是域。

A ．},,3|{Q b a b a x x S ∈+== B ．},,2|{Z b a n x x S ∈==C ．},12|{Z n n x x S ∈+== D ．}0|{≥∧∈=x Z x x S = N 。

1、 设R 是A 上一个二元关系，)},,,(),(|,{R b c R c a A c A b a b a S >∈<>∈<∈∧∈><=且有对于某一个试证明若R 是A 上一个等价关系，则S 也是A 上的一个等价关系。

（9分）一、 证明 46%1、（9分）（1） S 自反的A a ∈∀，由R 自反，),(),(R a a R a a >∈<∧>∈<∴，S a a >∈∴<,（2） S 对称的传递对称定义R Sa b R R b c R c a S R b c R c a S b a Ab a >∈⇒<>∈<∧>∈<⇒>∈<∧>∈<⇒>∈<∈∀,),(),(),(),(,,（3） S 传递的定义传递S Sc a R R c b R b a R c e R e b R bd R d a Sc b S b a Ac b a >∈⇒<>∈<∧>∈<⇒>∈<∧>∈<∧>∈<∧>∈<⇒>∈<∧>∈<∈∀,),(),(),(),(),(),(,,,,由（1）、（2）、（3）得；S 是等价关系。

《失散数学》题库与答案一、选择或填空（数理逻辑部分）1、以下哪些公式为永真包含式？( )(1) Q=>Q→P(2)Q=>P→Q(3)P=>P→Q(4)P (P Q)=> P答：在第三章里面有公式（1）是附带律，（4）能够由第二章的包含等值式求出（注意与汲取律差别）2、以下公式中哪些是永真式？ ( )(1)(┐PQ)→(Q→R)(2)P→(Q→Q)(3)(P Q)→P(4)P →(P Q)答：（2），（3），（4）可用包含等值式证明3、设有以下公式，请问哪几个是永真蕴涵式 ?( )(1)P=>P Q(2)P Q=>P(3)P Q=>PQ(4)P (P→Q)=>Q(5)(P→Q)=>P(6)P(P Q)=> P答：（2）是第三章的化简律，（3）近似附带律，（4）是假言推理，（3），（5），（6）都可以用包含等值式来证明出是永真包含式4、公式 x((A(x) B(y，x)) zC(y，z)) D(x)中，自由变元是( ) ，拘束变元是() 。

答：x,y, x,z （观察定义在公式xA和xA中，称x为指导变元，A为量词的辖域。

在xA和xA的辖域中，x的全部出现都称为拘束出现，即称x为拘束变元，A中不是拘束出现的其余变项则称为自由变元。

于是A(x)、B(y，和zC(y，z)中y为自由变元，x和z为拘束变元，在D(x)中x为自由变元）5、判断以下语句能否是命题。

假如，给出命题的真值。

( )(1)北京是中华人民共和国的国都。

(2)陕西师大是一座工厂。

(3)你喜爱唱歌吗？(4)若7+8＞18，则三角形有4条边。

(5)行进！(6)给我一杯水吧！1答：（1）是，T （2）是，F （3）不是（4）是，T （5）不是（6）不是（命必足是述句，不可以是疑句或许祈使句。

）6、命题“存在一些人是大学生”的否认是( ) ，而命题“全部的人都是要死的”的否认是( ) 。

可编辑修改精选全文完整版离散数学习题答案习题一：P121.判断下列句子哪些是命题？在是命题的句子中，哪些是简单命题？哪些是真命题？哪些命题的真值现在还不知道？(1)中国有四大发明。

(2)5是无理数。

(3)3是素数或4是素数。

(4)x2+3<5，其中x是任意实数。

(5)你去图书馆吗？(6)2与3都是偶数。

(7)刘红与魏新是同学。

(8)这朵玫瑰花多美丽呀！(9)吸烟请到吸烟室去！(10)圆的面积等于半径的平方乘π。

(11)只有6是偶数，3才能是2的倍数。

(12)8是偶数的充分必要条件是8能被3整除。

(13)2025年元旦下大雪。

1、2、3、6、7、10、11、12、13是命题。

在上面的命题中，1、2、7、10、13是简单命题；1、2、10是真命题；7的真值现在还不知道。

2.将上题中是简单命题的命题符号化。

(1)p：中国有四大发明。

(2)q：5是无理数。

(7)r：刘红与魏新是同学。

(10)s：圆的面积等于半径的平方乘π。

(1)t：2025年元旦下大雪。

3.写出下列各命题的否定式，并将原命题及其否定式都符号化，最后指出各否定式的真值。

“5是有理数”的否定式是“5不是有理数”。

解：原命题可符号化为：p：5是有理数。

其否定式为：非p。

非p的真值为1。

4.将下列命题符号化，并指出真值。

(1)2与5都是素数。

(2)不但π是无理数，而且自然对数的底e也是无理数。

(3)虽然2是最小的素数，但2不是最小的自然数。

(4)3是偶素数。

(5)4既不是素数，也不是偶数。

a：2是素数。

b：5是素数。

c：π是无理数。

d：e是无理数。

f：2是最小的素数。

g：2是最小的自然数。

h：3是偶数。

i：3是素数。

j：4是素数。

k：4是偶数。

解：（1）到（5）的符号化形式分别为a∧b，c∧d，f∧非g，h∧i，非j∧非k。

这五个复合命题的真值分别为1，1，1，0，0。

5.将下列命题符号化，并指出真值。

a：2是偶数。

b：3是偶数。

c：4是偶数。

离散数学试题与答案试卷一一、填空 20% （每小题2分）1．设 }7|{)},5()(|{<∈=<∈=+x E x x B x N x x A 且且（N ：自然数集，E + 正偶数） 则 =⋃B A 。

2．A ，B ，C 表示三个集合，文图中阴影部分的集合表达式为 。

3．设P ，Q 的真值为0，R ，S 的真值为1，则)()))(((S R P R Q P ⌝∨→⌝∧→∨⌝的真值= 。

4．公式P R S R P ⌝∨∧∨∧)()(的主合取范式为 。

5．若解释I 的论域D 仅包含一个元素，则 )()(x xP x xP ∀→∃ 在I 下真值为 。

6．设A={1，2，3，4}，A 上关系图为则 R 2 = 。

7．设A={a ，b ，c ，d}，其上偏序关系R 的哈斯图为则 R= 。

8．图的补图为 。

9．设A={a ，b ，c ，d} ，A 上二元运算如下：那么代数系统<A ，*>的幺元是 ，有逆元的元素为 ，它们的逆元分别为 。

10．下图所示的偏序集中，是格的为 。

二、选择 20% （每小题 2分）1、下列是真命题的有（ ） A ． }}{{}{a a ⊆；B ．}}{,{}}{{ΦΦ∈Φ；C ． }},{{ΦΦ∈Φ；D ． }}{{}{Φ∈Φ。

2、下列集合中相等的有（ ）A ．{4，3}Φ⋃；B ．{Φ，3，4}；C ．{4，Φ，3，3}；D ． {3，4}。

3、设A={1，2，3}，则A 上的二元关系有（ ）个。

A ． 23 ； B ． 32 ； C ． 332⨯； D ． 223⨯。

4、设R ，S 是集合A 上的关系，则下列说法正确的是（） A ．若R ，S 是自反的， 则S R 是自反的； B ．若R ，S 是反自反的， 则S R 是反自反的； C ．若R ，S 是对称的， 则S R 是对称的； D ．若R ，S 是传递的， 则S R 是传递的。

5、设A={1，2，3，4}，P （A ）（A 的幂集）上规定二元系如下|}||(|)(,|,{t s A p t s t s R =∧∈><=则P （A ）/ R=（ ）A．A ；B．P(A) ；C．{{{1}}，{{1，2}}，{{1，2，3}}，{{1，2，3，4}}}；D．{{Φ}，{2}，{2，3}，{{2，3，4}}，{A}}6、设A={Φ，{1}，{1，3}，{1，2，3}}则A上包含关系“⊆”的哈斯图为（）7、下列函数是双射的为（）A．f : I→E , f (x) = 2x ；B．f : N→N⨯N, f (n) = <n , n+1> ；C．f : R→I , f (x) = [x] ；D．f :I→N, f (x) = | x | 。

.离散1一、选择题（每题2分，共20分） CABBB DACDA二、填空题（每题2分，共20分）1.n222.a∨b=1，a∧b=03.x*(xΔy)=x xΔ(x*y)=x4. 无回路5. 大项的合取所组成6. (∃x)⌝ P(x) (∀x)⌝ P(x)7.68.对任意的a,b G∈,有(a*b)*(a*b)=(a*a)*(b*b)9.βγ10. {<1，2>，<3，3>,<1，3>，<4，2>}，{<1,4>,<2,2>}三、判断题（每题1分，共10分）×√√×××××√√四、解答题（5小题，共30分）1.(5分）给定无孤立点图G，若存在一条路，经过图中每边一次且仅一次，该条路称为欧拉路；如果一个图有欧拉路，则这个图能一笔画出。

2.（8分）各4分，步骤对，结果错，适当扣分，如果求出其一个，另一个直接写出，也不扣分。

只有结果，且结果对，给一半分，只有结果，且结果错，不给分。

解：主析取式:(┐P∧┐Q∧R)∨(┐P∧┐Q∧┐R)∨(P∧Q∧R)∨(P∧┐Q∧R)∨(┐P∧Q∧R)主合取式:（┐P∨Q∨R）∧（┐P∨┐Q∨R）∧（P∨┐Q∨R）3.（5分）由无向树的性质可知，无向树的顶点数是边数加1，又知无向图所有顶点的度之和为边数的2倍。

（1分）令1度顶点个数为x,则顶点数为2+1+3+x，所有顶点的度之和为x+2*2+3+3*4，（2分）从而有x+2*2+3+3*4=2*(2+1+3+x-1)，解之得x=9,即有9个1度的点。

（2分）4.（7分）解：5. （5分）⎪⎪⎪⎪⎪⎭⎫⎝⎛=1100110100100101R M （2分）,（2分）,具有自反，对称性质（1分）五、证明（3小题，共20分）1. （10分）每步约1分，没有P,T 标识扣3分,没有序号扣3分。

证明过程：（1）P →R P （2）⌝R →⌝P T （1）E （3）P ∨Q P （4）⌝P →Q T （3）E （5）Q →S P （6）⌝P →S T （4）（5）I （7）⌝R →S T （2）（6）I （8）R ∨S T （8）E 2. （5分）。