2016年秋季新版浙教版七年级数学上学期6.7、角的和差同步练习1

角的和差一、基础过关1.下列关于角的说法正确的个数是( )①角是由两条射线组成的图形；②角的边越长,角越大；③在角一边延长线上取一点D；④角可以看作由一条射线绕着它的端点旋转而形成的图形。

A.1个B.2个C.3个D.4个2.下列4个图形中,能用∠1,∠AOB,∠O三种方法表示同一角的图形是( )3.已知∠1=36°45′,则∠1的余角是（）A.53°55′B.53°15′C.143°55D.63°15′4.如果一个角的补角是150°，则这个角的度数是（）A.30°B.60°C.90°D.120°5.任意一个锐角的补角比它的余角（）A.大90°B.大180°C.小90°D.小180°6.已知∠1和∠2互为余角，且∠2与∠3互补，∠1=65°，则∠3=（）A.65°B.25°C.115°D.1557.下列哪个角不能由一副三角板作出( )A.105ºB.15ºC.175ºD.135º二、综合训练1.23°45ˊ+24°15ˊ=_______；100°2ˊ33"-14°14ˊ53"=_______．2.若∠1 =50°，则它的余角是，它的补角是。

3.若∠α =110°，则它的补角是，它的补角的余角是。

4.如图，AOB是一条直线，∠AOD∶∠DOB＝3∶1，OD平分∠COB。

则∠DOC的度数为_____。

参考答案一、基础过关1.C2.B3.A4.A5.A6.D7.C二、综合训练1.47°60ˊ 85°47ˊ40"2.40°130°3.70°20°4.67.5°。

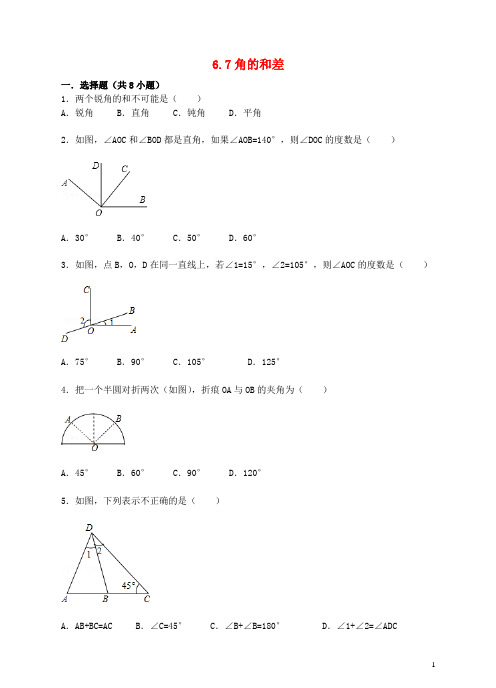
6.7角的和差一．选择题（共8小题）1．两个锐角的和不可能是（）A．锐角 B．直角 C．钝角 D．平角2．如图，∠AOC和∠BOD都是直角，如果∠AOB=140°，则∠DOC的度数是（）A．30° B．40° C．50° D．60°3．如图，点B，O，D在同一直线上，若∠1=15°，∠2=105°，则∠AOC的度数是（）A．75° B．90° C．105° D．125°4．把一个半圆对折两次（如图），折痕OA与OB的夹角为（）A．45° B．60° C．90° D．120°5．如图，下列表示不正确的是（）A．AB+BC=AC B．∠C=45° C．∠B+∠B=180°D．∠1+∠2=∠ADC6．如图，小明将自己用的一副三角板摆成如图形状，如果∠AOB=155°，那么∠COD等于（）A．15° B．25° C．35° D．45°7．已知∠AOB=70°，以O为端点作射线OC，使∠AOC=42°，则∠BOC的度数为（）A．28° B．112° C．28°或112° D．68°8．用一副三角板不可以拼出的角是（）A．105° B．75° C．85° D．15°二．填空题（共6小题）9．∠α+∠β=90°，且∠α=2∠β，则∠α=，∠β=．10．已知∠AOB=50°，∠BOC=30°，则∠AOC= ．11．如图，∠AOC和∠DOB都是直角，如果∠DOC=28°，那么∠AOB= ．12．如图，已知∠COB=2∠AOC，OD平分∠AOB，且∠COD=20°，则∠AOB的度数为．13．如图，将一副直角三角板叠在一起，使直角顶点重合于点O，则∠AOB+∠DOC= 度．14．如图，点O是直线AD上的点，∠AOB，∠BOC，∠COD三个角从小到大依次相差25°，则这三个角的度数是．三．解答题（共3小题）15．如图，已知OD平分∠AOB，射线OC在∠AOD内，∠BOC=2∠AOC，∠AOB=114°．求∠COD 的度数．16．已知在平面内，∠AOB=70°，∠BOC=40°，求∠AOC的度数．17．如图，OM是∠AOC的平分线，ON是∠BOC的平分线．（1）如图1，当∠AOB=90°，∠BOC=60°时，∠MON的度数是多少？为什么？（2）如图2，当∠AOB=70°，∠BOC=60°时，∠MON= （直接写出结果）．（3）如图3，当∠AOB=α，∠BOC=β时，猜想：∠MON= （直接写出结果）．6.7角的和差参考答案与试题解析一．选择题（共8小题）1．解：∵锐角一定大于0°，且小于90°，∴两个角的和不可能是平角．故选D．2．解：如右图所示，∵∠AOC=∠BOD=90°，∠AOB=140°，∴∠AOD=∠AOB﹣∠BOD=140°﹣90°=50°，∴∠DOC=∠AOC﹣∠AOD=90°﹣50°=40°．故选B．3．解：∵∠2=105°，∴∠BOC=180°﹣∠2=75°，∴∠AOC=∠1+∠BOC=15°+75°=90°．故选：B．4．解：把一个半圆对折两次后展开（如图），∠AOD=∠DOC=∠COE=∠EOB=45°；∠AOC=∠DOE=∠COB=90°；故选：C．5．解：A、看图可知AB+BC=AC；B、∠1+∠2=∠ADC，∠C可能等于45°；C、不正确，写法不规范，应该是∠ABD+∠CBD=180°D、看图可知，∠1+∠2=∠ADC．故选C．6．解：∵三角板的两个直角都等于90°，所以∠BOD+∠AOC=180°，∵∠BOD+∠AOC=∠AOB+∠COD，∵∠AOB=155°，∴∠COD等于25°．故选B．8．解：已知一副三角板各角的度数是30度，60度，45度，90度，可以拼出的度数就是用30度，60度，45度，90度相加减，45°+60°=105°，30°+45°=75°，45°﹣30°=15°，显然得不到85°．故选：C．二．填空题（共6小题）9．解：∵∠α+∠β=90°，且∠α=2∠β，∴，解得∠α=60°，∠β=30°，故答案为60°、30°．10．解：当OC在∠AOB内部，因为∠AOB=50°，∠BOC=30°，所以∠AOC为20°；当OC在∠AOB外部，因为∠AOB=50°，∠BOC=30°，所以∠AOC为80°；故∠AOC为20°或80°．11．解：∵∠AOC=∠DOB=90°，∠DOC=28°，∴∠AOB=∠AOC+∠DOB﹣∠DOC，=90°+90°﹣28°，=152°．故答案为：152°12．解：∵∠COB=2∠AOC，OD平分∠AOB，且∠COD=20°，∴设∠COB=2∠AOC=2x，∠AOD=∠BOD=1.5x，∴∠COD=0.5x=20°，∴x=40°，∴∠AOB的度数为：3×40°=120°．故答案为：120°．13．解：如右图所示，∵∠AOD+∠COD=90°，∠COD+∠BOC=90°，∠BOD=∠COD+∠BOC，∠AOD+∠BOD=∠AOB，∴∠AOD+∠COD+∠COD+∠BOC=180°，∴∠AOD+2∠COD+∠BOC=180°，∴∠AOB+∠COD=180°．故答案是180．14．解：设∠AOB=x，∠BOC=x+25°，∠COD=x+50°，∵∠AOB+∠BOC+∠COD=180°，∴3x+75°=180°，x=35°，∴这三个角的度数是35°，60°，85°，故答案为35°，60°，85°．三．解答题（共3小题）15．解：∵OD平分∠AOB，∠AOB=114°，∴∠AOD=∠BOD==57°．∵∠BOC=2∠AOC，∠AOB=114°，∴∠AOC=．∴∠COD=∠AOD﹣∠AOC=57°﹣38°=19°．16．解：分两种情况考虑：（1）当∠BOC在∠AOB外部时，∠AOC=∠AOB+∠BOC═70°+40°=110°；（2）当∠BOC在∠AOB内部时，∠AOC=∠AOB﹣∠BOC═70°﹣40°=30°，则∠AOC的度数为110°或30°．17．解：（1）如图1，∵∠AOB=90°，∠BOC=60°，∴∠AOC=90°+60°=150°，∵OM平分∠AOC，ON平分∠BOC，∴∠MOC=∠AOC=75°，∠NOC=∠BO C=30°∴∠MON=∠MOC﹣∠NOC=45°．（2）如图2，∵∠AOB=70°，∠BOC=60°，∴∠AOC=70°+60°=130°，∵OM平分∠AOC，ON平分∠BOC，∴∠MOC=∠AOC=65°，∠NOC=∠BOC=30°∴∠MON=∠MOC﹣∠NOC=65°﹣30°=35°．故答案为：35°．。

6.5-6.7 角与角的度量、角的大小比较及角的和差一、选择题（共15小题；共75分）1. 下列四个角中，最有可能与70∘角互补的是 ( )A. B.C. D.2. 已知∠α=35∘，则∠α的补角的度数是 ( )A. 55∘B. 65∘C. 145∘D. 165∘3. 如图，OA是北偏东30∘方向的一条射线，若射线OB与射线OA垂直，则OB的方位角是 ( )A. 北偏西30∘B. 北偏西60∘C. 东偏北30∘D. 东偏北60∘4. 已知∠α=35∘，则∠α的余角的度数是 ( )A. 55∘B. 45∘C. 145∘D. 135∘5. 已知：如图所示，直线AB、CD相交于O，OD平分∠BOE，∠AOC=42∘，则∠AOE的度数为 ( )A. 126∘B. 96∘C. 102∘D. 138∘6. 在直线AB上任取一点O，过点O作射线OC,OD，使OC⊥OD，当∠AOC=30∘时，∠BOD的度数是 ( )A. 60∘B. 120∘C. 60∘或90∘D. 60∘或120∘7. 如图，某轮船在O处，测得灯塔A在它北偏东40∘的方向上，渔船B在它的东南方向上，则∠AOB的度数是 ( )A. 85∘B. 90∘C. 95∘D. 100∘8. 在∠AOB的内部任取一点C，作射线OC，则一定存在 ( )A. ∠AOB>∠AOCB. ∠AOB<∠BOCC. ∠BOC>∠AOCD. ∠AOC>∠BOC9. ∠α=39∘22ʹ，则∠α的补角为 ( )A. 39∘22ʹB. 139∘22ʹC. 140∘38ʹD. 50∘38ʹ10. 钟表 1 点 20 分时，时针与分针所成的角是 ( )A. 150度B. 80度C. 120度D. 90度11. 如果∠α和∠β互补，且∠α>∠β，则下列表示∠β的余角的式子中：① 90∘−∠β；② ∠α−90∘；③ 12(∠α+∠β)；④ 12(∠α−∠β)．正确的有 ( )A. 4个B. 3个C. 2个D. 1个12. 一个角的补角是它的余角的3倍，则这个角的度数是 ( )A. 30∘B. 45∘C. 60∘D. 75∘13. 如图，已知∠AOB=40∘，∠AOC=90∘，OD平分∠BOC，则∠AOD的度数是 ( )A. 20∘B. 25∘C. 30∘D. 35∘14. 足球射门，不考虑其他因素，仅考虑射点到球门AB的张角大小时，张角越大，射门越好．如图的正方形网格中，点A，B，C，D，E均在格点上，球员带球沿CD方向进攻，最好的射点在( )A. 点CB. 点D或点EC. 线段DE（异于端点）上一点D. 线段CD（异于端点）上一点15. 若∠1，∠2互为补角，且∠1>∠2，则∠2的余角是 ( )A. 12(∠1+∠2) B. ∠1−90∘ C. 12∠1−∠2 D. 12(∠2−∠1)二、填空题（共15小题；共75分）16. 若∠α=39∘21ʹ，则∠α的补角为．17. 如图，A，O，B在一直线上，∠AOC=∠BOC，若∠1=∠2，则图中互余的角共有对．18. 40.5∘=40∘ʹ19. 计算：50∘−15∘30ʹ=．，则这个角为．20. 一个角的补角与它的余角的4倍的和等于周角的171821. 画一个∠AOB，使∠AOB=30∘，再作OC⊥OA，OD⊥OB，则∠COD的度数是．22. 如图所示，在锐角∠AOB内部，画1条射线，可得3个锐角；画2条不同射线，可得6个锐角；画3条不同射线，可得10个锐角；⋯．照此规律，画6条不同射线，可得锐角个．23. 一副三角板按如图所示方式重叠，若图中∠DCE=35∘25ʹ，则∠ACB=．24. 如图所示，OM，ON分别是∠BOC和∠AOC的平分线，∠AOB=84∘．① ∠MON=度；② 当OC在∠AOB内绕点O转动时，∠MON的值改变．（填“会”或“不会”）25. 一个角的补角比它的余角的2倍大40度，则这个角的度数为度．26. 如图，已知∠EOC是平角，OD平分∠BOC，在平面上画射线OA，使∠AOC和∠COD互余，若∠BOC=50∘，则∠AOB是．27. 如图，在∠AOB内以点O为端点的射线有n条，则图中共有个角．28. 计算：0.3∘=ʹ，900ʹ=∘，75∘15ʹ36ʹ=∘．29. 在平角∠AOB的内部引n条射线．（1）当n=1时，图中共有个小于平角的角．（2）当n=2时，图中共有个小于平角的角．（3）当n=3时，图中共有个小于平角的角．（4）当n=k时，图中共有个小于平角的角．30. 已知∠AOB=α，∠BOC=β，（α>β），且OD，OE分别为∠AOB，∠BOC的角平分线，则∠DOE的度数为或（结果用α，β的代数式表示）．三、解答题（共5小题；共65分）31. 已知一个角的补角等于这个角的余角的4倍，求这个角的度数．32. 如图，O在直线AC上，OD是∠AOB的平分线，OE在∠BOC内．Ⅰ若OE是∠BOC的平分线，则有OD⊥OE，试说明理由；∠EOC，∠DOE=72∘，求∠EOC的度数．Ⅱ若∠BOE=1233. 如图，有A、B、C、P四个点，根据以下要求画图（保留画图痕迹）Ⅰ（1）画直线AB；（2）画线段BC；（3）画射线AP；Ⅱ若点B在点A正东方向，那么点P在点A的方向；Ⅲ在射线AP上取线段AD，使AD=AB+BC（尺规作图）；Ⅳ在平面上确定一点O，使AO+BO+CO+DO长度最短，这是根据原理．34. 如图，直线AB与CD相交于点O，OP是∠BOC的平分线，OE⊥AB，OF⊥CD．Ⅰ如果∠AOD=40∘，那么根据，可得∠BOC=度．Ⅱ图中除直角外，还有相等的角吗?请写出三对：（i）；（ii）；（iii）．Ⅲ求∠POF的度数．35. 如图1，已知∠AOB=150∘，∠AOC=40∘，OE是∠AOB内部的一条射线，且OF平分∠AOE．Ⅰ若∠EOB=10∘，则∠COF=；Ⅱ若∠COF=20∘，则∠EOB=；Ⅲ若∠COF=n∘，则∠EOB= ---（用含n的式子表示）．Ⅳ当射线OE绕点O逆时针旋转到如图2的位置时，请把图补充完整；此时，∠COF与∠EOB 有怎样的数量关系?请说明理由．答案第一部分1. D2. C3. B4. A5. B6. D7. C8. A9. C 10. B11. B 12. B 13. B 14. C 15. B第二部分16. 140∘39ʹ．17. 418. 3019. 34∘30ʹ20. 40∘21. 30∘或150∘22. 2823. 144∘35ʹ24. 42；不会25. 4026. 115∘或15∘27. (n+1)(n+2)228. 18；0.25；75.2629. （1）2；（2）5；（3）9；（4）k(k+3)230. 12α−12β或12α+12β第三部分31. 设这个角为x，则它的补角为(180∘−x)，余角为(90∘−x)．由题意得180∘−x=4(90∘−x)．解得x=60∘．答：这个角的度数为60∘．32. （1）∵OD、OE分别是∠AOB和∠BOC的平分线，∴∠DOB=12∠AOB，∠BOE=12∠BOC，∴∠DOB+∠BOE=12(∠AOB+∠BOC)=90∘，∴OD⊥OE．（2）设∠BOE=x．∵∠BOE=12∠EOC，∴∠EOC=2x．∵∠DOE=72∘，∴∠DOB=12∠AOB=72−x，∴2(72−x)+x+2x=180，解得x=36∘．∴∠EOC=72∘．33. （1）（2）南偏东30∘（3）AD即为所求．（4）连接AC，BD交点即为O．是根据两点之间线段最短原理．34. （1）对顶角相等；40（2）（i）∠AOD=∠BOC；（ii）∠COP=∠BOP；（iii）∠EOC=∠BOF （3）因为OP是∠BOC的平分线，∠BOC=20∘．所以∠COP=12因为∠DOF+∠BOF+∠COP+∠BOP=180∘，∠DOF=90∘，∠COP=20∘，所以∠BOF+∠BOP=180∘−90∘−20∘=70∘．故∠POF=∠BOF+∠BOP=70∘．35. （1）30∘（2）30∘（3）70∘−2n∘（4）画图∠EOB=70∘+2∠COF（仅写出结论，没写理由得1分）设∠COF=n∘，则∠AOF=∠AOC−∠COF=40∘−n∘．又OF平分∠AOE，所以∠AOE=2∠AOF=80∘−2n∘．所以∠EOB=∠AOB−∠AOE=150∘−(80∘−2n∘)=(70+2n)∘即∠EOB=70∘+2∠COF．。

浙教新版七年级上学期《6.7 角的和差》同步练习卷一．选择题（共27小题）1．如图，OB是∠AOC内部的一条射线，把三角尺的角的顶点放在点O处，转动三角尺，当三角尺的边OD平分∠AOB时，三角尺的另一边OE也正好平分∠BOC，则∠AOC的度数为（）A．100°B．110°C．120°D．130°2．如图，点O在直线AB上，OC平分∠AOD，若∠COD＝∠BOD，则∠COB 的度数为（）A．115°B．105°C．95°D．85°3．借助常用的直角三角尺，能画出一些度数的角，下列选项中不能画出的角是（）A．15°B．100°C．165°D．135°4．用一副三角板可以画出的最大锐角的度数是（）A．85°B．75°C．60°D．45°5．已知∠AOB＝70°，以O端点作射线OC，使∠AOC＝28°，则∠BOC的度数为（）A．42°B．98°C．42°或98°D．82°6．如图，点O在直线AB上，OD是∠AOC的平分线，OE是∠COB的平分线．若∠DOC＝70°，则∠BOE的度数是（）A．30°B．40°C．25°D．20°7．如图，O是直线AB上一点，OD平分∠BOC，∠COE＝90°，若∠AOC＝40°，则∠DOE为（）A．15°B．20°C．30°D．45°8．在同一平面内，若∠BOA＝50.3°，∠BOC＝10°30′，则∠AOC的度数是（）A．60.6°B．40°C．60.8°或39.8D．60.6°或40°9．如图，∠AOC＝∠BOD＝80°，如果∠AOD＝140°，那么∠BOC等于（）A．20°B．30°C．50°D．40°10．如图，已知点M是直线AB上一点，∠AMC＝52°48′，∠BMD＝72°19′，则∠CMD等于（）A．49°07′B．54°53′C．55°53′D．53°7′11．如图，已知∠BOC＝2∠AOB，OD平分∠AOC，∠BOD＝14°，则∠AOB 的度数为（）A．14°B．28°C．32°D．40°12．用一副三角板可以画出一些指定的角，下列各角中，不能用一副三角板画出的是（）A．15°B．75°C．85°D．105°13．把两块三角板按如图所示那样拼在一起，则∠ABC等于（）A．70°B．90°C．105°D．120°14．把一副三角板按照如图所示的位置摆放，则形成两个角，设分别为∠α、∠β，若已知∠α＝65°，则∠β＝（）A．15°B．25°C．35°D．45°15．如图，点C、O、B在同一条直线上，∠AOB＝90°，∠AOE＝∠DOB，则下列结论：①∠EOD＝90°；②∠COE＝∠AOD；③∠COE＝∠DOB；④∠COE+∠BOD＝90°．其中正确的个数是（）A．1B．2C．3D．416．如图，∠AOC和∠DOB都是直角，如果∠AOB＝150°，那么∠DOC＝（）A．30°B．40°C．50°D．60°17．已知两角之比为2：1，且这两角之和为直角，则这两个角的大小分别为（）A．70°，22°B．60°，30°C．50°，40°D．55°，35°18．如图，点B，O，D在同一直线上，若∠DOC＝105°，则∠BOC的度数是（）A．75°B．90°C．105°D．125°19．在同一平面内，∠AOB＝70°，∠BOC＝40°，则∠AOC的度数为（）A．110°B．30°C．110°或150°D．30°或110°20．如图，点O在直线AB上，射线OC、OD在直线AB的同侧，∠AOD＝40°，∠BOC＝50°，OM、ON分别平分∠BOC和∠AOD，则∠MON的度数为（）A．135°B．140°C．152°D．45°21．如图，∠AOB＝30°，OB平分∠AOC，OC平分∠BOD，OD平分∠COE，则∠COE＝（）A．30°B．45°C．60°D．90°22．把一副三角板按如图所示那样拼在一起，那么∠ABC的度数是（）A．150°B．135°C．120°D．105°23．如图，是一副特制的三角板，用它们可以画出一些特殊角．在54°、60°、63°、72°、99°、120°、144°、150°、153°、171°的角中，能画出的角有（）A．7个B．8个C．9个D．10个24．如图，将一副三角板叠放在一起，使直角的顶点重合于O，则∠AOC+∠DOB ＝（）A．90°B．120°C．160°D．180°25．如图，OC是∠AOB的平分线，OD是∠AOC的平分线，且∠COD＝25°，则∠AOB等于（）A．50°B．75°C．100°D．120°26．如图，将长方形纸片ABCD的角C沿着GF折叠（点F在BC上，不与B，C重合），使点C落在长方形内部点E处，若FH平分∠BFE，则∠GFH的度数α是（）A．90°＜α＜180°B．0°＜α＜90°C．α＝90°D．α随折痕GF位置的变化而变化27．α，β都是钝角，甲、乙、丙、丁计算，（α+β）的结果依次为50°，26°，72°，90°，其中有正确的结果，则计算正确的是（）A．甲B．乙C．丙D．丁二．填空题（共6小题）28．如图，若∠3：∠2＝2：5，且∠2﹣∠1＝12°，∠3等于．29．将一张长方形纸片按如图所示的方式折叠，BD、BE为折痕，若∠ABE＝34°，则∠DBC为度．30．已知∠AOB＝80°，∠BOC＝50°，OD是∠AOB的角平分线，OE是∠BOC 的角平分线，则∠DOE＝．31．将一副三角板如图摆放，若∠BAE＝135°17′，则∠CAD的度数是．32．如图所示，点C，O，D在同一条直线上，∠AOC＝40°，∠BOD＝50°，OM，ON分别是∠AOC，∠BOD的平分线，则∠MON＝．33．如图，直线AB、CD相交于点O，∠DOE＝∠BOE，OF平分∠AOD，若∠BOE＝28°，则∠EOF的度数为．三．解答题（共17小题）34．如图，∠AOB＝120°，点C为∠AOB内部一点，OD平分∠BOC，OE平分∠AOD（1）如果∠AOC＝30°，依题意补全图形；（2）在（1）的条件下，求∠EOC的度数；（3）如果∠AOC＝α（0°＜α＜120°），直接用含α的代数式表示∠EOC的度数．35．如图OC是∠AOB内部的一条射线，∠BOC＝2∠AOC，OD平分∠AOC．（1）若∠AOB＝120°，求∠BOC和∠BOD的度数；（2）画出∠BOC的平分线OE，说明∠DOE＝∠AOB．36．如图1所示：已知，∠AOB＝90°，∠BOC＝30°，OM平分∠AOC，ON 平分∠BOC．（1）∠MON═；（2）如图2，∠AOB＝90°，∠BOC＝x°，仍然分别作∠AOC、∠BOC的平分线OM、ON，能否求出∠MON的度数若能，求出其值；若不能，说明理由．（3）如图3，若∠AOB＝α，∠BOC＝β（α、β均为锐角，且α＞β），仍然分别作∠AOC、∠BOC的平分线OM、ON，能否求出∠MON的度数．若能，求∠MON的度数．（4）从（1）、（2）、（3）的结果中，你发现了什么规律？37．如图1，O为直线AB上一点，过点O作射线OC，∠AOC＝30°，将一直角三角板的直角顶点放在点O处，一边ON在射线OA上，另一边OM与OC 都在直线AB的上方．现将图25﹣1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周．（1）如图2，若经过t秒后，线段OM恰好平分∠BOC，此时∠COM＝°；∠AON＝°；t＝秒；（2）在（1）的条件下，线段ON是否平分∠AOC？请说明理由；（3）如图3，若三角板在转动的同时，射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周，那么经过多长时间OC平分∠MON？38．如图，已知∠AOB＝90°，∠EOF＝60°，OE平分∠AOB，OF平分∠BOC，求∠COB和∠AOC的度数．39．如图，已知∠AOB＝90°，射线OC绕点O从OA位置开始，以每秒4°的速度顺时针方向旋转；同时，射线OD绕点O从OB位置开始，以每秒1°的速度逆时针方向旋转．当OC与OA成180°时，OC与OD同时停止旋转．（1）当OC旋转10秒时，∠COD＝°．（2）当OC与OD的夹角是30°时，求旋转的时间．（3）当OB平分∠COD时，求旋转的时间．40．如图所示，已知∠AOB＝90°，∠BOC＝30°，OM平分∠AOC，ON平分∠BOC；（1）求∠MON；（2）∠AOB＝α，∠BOC＝β，求∠MON的度数．41．如图，已知∠AOC＝60°，∠BOD＝90°，∠AOB是∠DOC的3倍，求∠AOB的度数．42．如图，直线AB，CD相交于点O，OA平分∠EOC．（1）若∠EOC＝70°，求∠BOD的度数；（2）若∠EOC：∠EOD＝2：3，求∠BOD的度数．43．如图，已知∠BOC＝2∠AOC，OD平分∠AOB，且∠AOC＝40°，求∠COD 的度数．44．已知∠AOB＝54°，从O点引出一条射线OC，∠BOC＝14°．求∠AOC的度数．45．已知O为直线AB上的一点，∠COE是直角，OF平分∠AOE．（1）如图1，若∠COF＝34°，则∠BOE＝；若∠COF＝m°，则∠BOE＝；∠BOE与∠COF的数量关系为．（2）当射线OE绕点O逆时针旋转到如图2的位置时，（1）中∠BOE与∠COF 的数量关系是否仍然成立？请说明理由．46．已知：如图，∠AOB是直角，∠AOC＝40°，ON是∠AOC的平分线，OM 是∠BOC的平分线．（1）求∠MON的大小；（2）当锐角∠AOC的大小发生改变时，∠MON的大小是否发生改变？为什么？47．如图，O为直线DA上的一个点，∠AOB＝130°，OE是∠AOB的平分线，∠COB＝90°，求∠AOC和∠COE的度数．48．下列各小题中，都有OE平分∠AOC，OF平分∠BOC．（1）如图①，若点A、O、B在一条直线上，∠EOF＝；（2）如图②，若点A、O、B不在一条直线上，∠AOB＝140°，则∠EOF＝；（3）由以上两个问题发现：当∠AOC在∠BOC的外部时，∠EOF与∠AOB的数量关系是∠EOF＝；（4）如图③，若OA在∠BOC的内部，∠AOB和∠EOF还存在上述的数量关系吗；请简单说明理由；49．已知点O在直线AB上，OD平分∠AOC，OE平分∠BOC．（1）若OC⊥AB于点O，如图1，直接写出∠DOE的度数为；OD与OE 的位置关系是；（2）若OC与AB不垂直，如图2，其它条件不变，（1）中的结论还成立吗？若成立，请说明你的猜想是正确的；若不成立，请说明理由；（3）如图2，若∠AOD＝40°，请你利用（2）中得到的结论，求∠BOE的度数．50．如图，已知OE平分∠AOC，OF平分∠BOC（1）若∠AOB是直角，∠BOC＝60°，求∠EOF的度数．（2）若∠AOC＝x°，∠EOF＝y°，∠BOC＝60°，请用x的代数式来表示y．（直接写出结果就行）．浙教新版七年级上学期《6.7 角的和差》同步练习卷参考答案与试题解析一．选择题（共27小题）1．如图，OB是∠AOC内部的一条射线，把三角尺的角的顶点放在点O处，转动三角尺，当三角尺的边OD平分∠AOB时，三角尺的另一边OE也正好平分∠BOC，则∠AOC的度数为（）A．100°B．110°C．120°D．130°【分析】根据角平分线的定义得到∠BOD＝∠AOB，∠BOE＝∠BOC，则∠EOD＝∠AOB+∠BOC＝∠AOC，然后把∠EOD＝60°代入计算即可．【解答】解：∵OD边平分∠AOB，OE平分∠BOC，∴∠BOD＝∠AOB，∠BOE＝∠BOC，∴∠EOD＝∠AOB+∠BOC＝∠AOC，∵∠EOD＝60°，∴∠AOC＝2×60°＝120°．故选：C．【点评】本题考查了角的计算：1°＝60′，1′＝60″．关键是根据角平分线的定义解答．2．如图，点O在直线AB上，OC平分∠AOD，若∠COD＝∠BOD，则∠COB 的度数为（）【分析】根据角平分线的定义得到∠AOC＝∠COD，根据平角的定义列方程即可得到结论．【解答】解：∵OC平分∠AOD，∴∠AOC＝∠COD，∵∠COD＝∠BOD，∴∠AOC＝∠COD＝∠BOD，∵∠AOC+∠COD+∠BOD＝180°，∴∠BOD+∠BOD+∠BOD＝180°，∴∠BOD＝30°，∠COD＝75°，∴∠COB＝∠COD+∠BOD＝105°，故选：B．【点评】本题考查了角的计算，角平分线的定义，平角的定义，求得∠BOD＝30°是解题的关键．3．借助常用的直角三角尺，能画出一些度数的角，下列选项中不能画出的角是（）A．15°B．100°C．165°D．135°【分析】先分清一副三角尺，各个角的度数分别为多少，然后将各个角相加或相减即可得出答案．【解答】解：A、利用45°和30°的角可以画出15°的角，故本选项错误；B、＝，不合题意，即借助常用的直角三角尺，能画出一些度数的角，不能画出100度的角，故本选项正确；C、利用90°、45°和30°组合即可画出165°的角，故本选项错误；D、利用90°和45°组合即可画出165°的角，故本选项错误；故选：B．【点评】此题主要考查了用三角板直接画特殊角，关键掌握用三角板画出的角的规律：都是15°的倍数．4．用一副三角板可以画出的最大锐角的度数是（）【分析】根据三角板原有的30°、45°、60°、90°四种角，依据可以直接画出的角和利用和或差画出的角，即可得到结论．【解答】解：用一副三角板可以画出：30°、45°、60°、75°、15°，五个锐角，其中最大的锐角为75°．故选：B．【点评】本题主要考查了角的计算，按照直接画出和通过角的求和或求差作出的角即可得出所有情况．5．已知∠AOB＝70°，以O端点作射线OC，使∠AOC＝28°，则∠BOC的度数为（）A．42°B．98°C．42°或98°D．82°【分析】根据题意画出图形，利用分类讨论思想求解即可．【解答】解：如图，当点C与点C1重合时，∠BOC＝∠AOB﹣∠AOC＝70°﹣28°＝42°；当点C与点C2重合时，∠BOC＝∠AOB+∠AOC＝70°+28°＝98°．故选：C．【点评】本题考查的是角的计算，在解答此题时要注意进行分类讨论，不要漏解．6．如图，点O在直线AB上，OD是∠AOC的平分线，OE是∠COB的平分线．若∠DOC＝70°，则∠BOE的度数是（）A．30°B．40°C．25°D．20°【分析】根据角平分线的定义求出∠AOC，根据邻补角的定义求出∠BOC，根据角平分线的定义计算即可．【解答】解：∵OD是∠AOC的平分线，∴∠AOC＝2∠COD＝140°，∴∠BOC＝180°﹣∠AOC＝40°，∵OE是∠COB的平分线，∴∠BOE＝∠BOC＝20°，故选：D．【点评】本题考查的是角平分线的定义、角的计算，掌握角平分线的定义、结合图形正确进行角的计算是解题的关键．7．如图，O是直线AB上一点，OD平分∠BOC，∠COE＝90°，若∠AOC＝40°，则∠DOE为（）A．15°B．20°C．30°D．45°【分析】先根据平角的定义求出∠BOC＝140°，再由OD平分∠BOC，根据角平分线的定义求出∠COD＝∠BOC＝70°，即可求出∠DOE＝20°．【解答】解：∵∠AOC＝40°，∴∠BOC＝180°﹣∠AOC＝140°，∵OD平分∠BOC，∴∠COD＝∠BOC＝70°，∵∠COE＝90°，∴∠DOE＝90°﹣70°＝20°．故选：B．【点评】本题考查了角平分线的定义；弄清各个角之间的数量关系是解决问题的关键．8．在同一平面内，若∠BOA＝50.3°，∠BOC＝10°30′，则∠AOC的度数是（）A．60.6°B．40°C．60.8°或39.8D．60.6°或40°【分析】分OC在∠AOB内部和∠AOB外部两种情况分别求解可得．【解答】解：∠AOC＝∠BOA+∠BOC＝50.3°+10°30′＝50.3°+10.5°＝60.8°或∠AOC＝∠BOA﹣∠BOC＝50.3°﹣10°30′＝50.3°﹣10.5°＝39.8°，故选：C．【点评】本题主要考查角的计算，解题的关键是掌握分类讨论思想的运用和角度的转换．9．如图，∠AOC＝∠BOD＝80°，如果∠AOD＝140°，那么∠BOC等于（）A．20°B．30°C．50°D．40°【分析】先求出∠COD的度数，然后根据∠BOC＝∠BOD﹣∠COD，即可得出答案．【解答】解：∵∠AOC＝80°，∠AOD＝140°，∴∠COD＝∠AOD﹣∠AOC＝60°，∵∠BOD＝80°，∴∠BOC＝∠BOD﹣∠COD＝80°﹣60°＝20°．故选：A．【点评】本题主要考查了角的计算能力，熟练掌握角相互间的和差关系是基础．10．如图，已知点M是直线AB上一点，∠AMC＝52°48′，∠BMD＝72°19′，则∠CMD等于（）A．49°07′B．54°53′C．55°53′D．53°7′【分析】根据∠AMC＝52°48′，∠BMD＝72°19′和∠CMD＝180°﹣∠AMC ﹣∠BMD，代入计算即可．【解答】解：∵∠AMC＝52°48′，∠BMD＝72°19′，∴∠CMD＝180°﹣∠AMC﹣∠BMD＝180°﹣52°48′﹣72°19′＝54°53′；故选：B．【点评】此题考查了角的计算，掌握平角的定义是本题的关键，是一道基础题．11．如图，已知∠BOC＝2∠AOB，OD平分∠AOC，∠BOD＝14°，则∠AOB 的度数为（）A．14°B．28°C．32°D．40°【分析】根据∠BOC＝2∠AOB，OD平分∠AOC，∠BOD＝14°，可以得到∠AOB与∠AOD的关系，从而与∠BOD建立关系，得到∠AOB的度数．【解答】解：∵已知∠BOC＝2∠AOB，OD平分∠AOC，∴∠AOC＝3∠AOB＝2∠AOD，∴∠AOD＝1.5∠AOB，∴∠AOD﹣∠AOB＝0.5∠AOB＝∠BOD＝14°，∴∠AOB＝28°，故选：B．【点评】本题考查角的计算、角平分线的定义，解题的关键是找出各个角之间的关系，与已知条件建立关系．12．用一副三角板可以画出一些指定的角，下列各角中，不能用一副三角板画出的是（）A．15°B．75°C．85°D．105°【分析】一副三角板中的度数有：90°、60°、45°、30°；用三角板画出角，无非是用角度加减法，根据选项一一分析，排除错误答案．【解答】解：A、15°的角，45°﹣30°＝15°；B、75°的角，45°+30°＝75°；C、85°的角，不能直接利用三角板画出；D、105°的角，45°+60°＝105°．故选：C．【点评】此题考查的知识点是角的计算，关键是用三角板直接画特殊角的步骤：先画一条射线，再把三角板所画角的一边与射线重合，顶点与射线端点重合，最后沿另一边画一条射线，标出角的度数．13．把两块三角板按如图所示那样拼在一起，则∠ABC等于（）A．70°B．90°C．105°D．120°【分析】∠ABC等于30度角与直角的和，据此即可计算得到．【解答】解：∠ABC＝30°+90°＝120°．故选：D．【点评】本题考查了角度的计算，理解三角板的角的度数是关键．14．把一副三角板按照如图所示的位置摆放，则形成两个角，设分别为∠α、∠β，若已知∠α＝65°，则∠β＝（）A．15°B．25°C．35°D．45°【分析】按照如图所示的位置摆放，利用∠α、∠β和直角正好在一条直线上，用平角减去直角再减去65°即可得出答案．【解答】解：如图所示，一副三角板按照如图所示的位置摆放，则∠α+∠β+90°＝180°，即∠β＝180°﹣90°﹣65°＝25°．故选：B．【点评】此题主要考查学生对角的计算的理解和掌握，解答此题的关键是利用∠α、∠β和直角正好在一条直线上，难度不大，是一道基础题．15．如图，点C、O、B在同一条直线上，∠AOB＝90°，∠AOE＝∠DOB，则下列结论：①∠EOD＝90°；②∠COE＝∠AOD；③∠COE＝∠DOB；④∠COE+∠BOD＝90°．其中正确的个数是（）A．1B．2C．3D．4【分析】结合图形，根据平角的定义、余角的性质和等量代换可以进行判断，注意运用角的和差的运算．【解答】解：∵∠AOB＝90°∴∠AOD+∠BOD＝90°∵∠AOE＝∠DOB∴∠AOE+∠AOD＝90°，即∠EOD＝90°∴∠COE＝∠AOD，∠COE+∠BOD＝90°∴①②④正确．故选：C．【点评】解题时注意运用余角的性质：同角的余角相等．16．如图，∠AOC和∠DOB都是直角，如果∠AOB＝150°，那么∠DOC＝（）A．30°B．40°C．50°D．60°【分析】根据图象∠AOB等于两个直角的和减去∠COD计算．【解答】解：∠DOC＝90°+90°﹣∠AOB＝180°﹣150°＝30°．故选A．【点评】本题注意，∠COD是两个直角重叠的部分．17．已知两角之比为2：1，且这两角之和为直角，则这两个角的大小分别为（）A．70°，22°B．60°，30°C．50°，40°D．55°，35°【分析】由两角之比是2：1，即可设这两个角分别为：2x°，x°，又由两角之和为直角，即可得方程：2x+x＝90，解此方程即可求得答案．【解答】解：设这两个角分别为：2x°，x°，根据题意得：2x+x＝90，解得：x＝30．则这两个角分别为：60°，30°．故选：B．【点评】此题考查了角的计算．解题时注意掌握方程思想的应用．18．如图，点B，O，D在同一直线上，若∠DOC＝105°，则∠BOC的度数是（）A．75°B．90°C．105°D．125°【分析】根据邻补角的定义解答即可．【解答】解：∵点B，O，D在同一直线上，∠DOC＝105°，∴∠BOC＝180°﹣105°＝75°，故选：A．【点评】本题考查的角的计算，解题的关键是邻补角的定义．19．在同一平面内，∠AOB＝70°，∠BOC＝40°，则∠AOC的度数为（）A．110°B．30°C．110°或150°D．30°或110°【分析】分OC在∠AOB内和OC在∠AOB外两种情况考虑，依此画出图形，根据角与角之间结合∠AOB、∠BOC的度数，即可求出∠AOC的度数．【解答】解：当OC在∠AOB内时，如图1所示．∵∠AOB＝70°，∠BOC＝40°，∴∠AOC＝∠AOB﹣∠BOC＝30°；当OC在∠AOB外时，如图2所示．∵∠AOB＝70°，∠BOC＝40°，∴∠AOC＝∠AOB+∠BOC＝110°．故选：D．【点评】本题考查了角的计算，分OC在∠AOB内和OC在∠AOB外两种情况考虑是解题的关键．20．如图，点O在直线AB上，射线OC、OD在直线AB的同侧，∠AOD＝40°，∠BOC＝50°，OM、ON分别平分∠BOC和∠AOD，则∠MON的度数为（）A．135°B．140°C．152°D．45°【分析】根据题意可求出∠COD＝90°，再根据角平分线的性质即可求出∠MON 的度数．【解答】解：易知：∠COD＝180°﹣∠AOD﹣∠BOC＝90°，∵OM、ON分别平分∠BOC和∠AOD，∴∠NOD＝∠AOD＝20°，∠COM＝∠BOC＝25°，∴∠MON＝20°+25°+90°＝135°故选：A．【点评】本题考查角度计算，涉及角平分线的性质，解题的关键是求出∠COD的度数，本题属于基础题型．21．如图，∠AOB＝30°，OB平分∠AOC，OC平分∠BOD，OD平分∠COE，则∠COE＝（）A．30°B．45°C．60°D．90°【分析】直接利用角平分线的性质分别得出∠BOC，∠COD，∠EOD的度数，进而得出答案．【解答】解：∵∠AOB＝30°，OB平分∠AOC，∴∠AOB＝∠BOC＝30°，∵OC平分∠BOD，∴∠DOC＝∠BOC＝30°，∵OD平分∠COE，∴∠DOE＝∠COD＝30°，∴∠COE＝2∠COD＝60°．故选：C．【点评】此题主要考查了角的计算以及角平分线的性质，正确得出∠COD的度数是解题关键．22．把一副三角板按如图所示那样拼在一起，那么∠ABC的度数是（）A．150°B．135°C．120°D．105°【分析】∠ABC等于30度角与直角的和，据此即可计算得到．【解答】解：∠ABC＝30°+90°＝120°，故选：C．【点评】本题考查了角度的计算，理解三角板的角的度数是关键．23．如图，是一副特制的三角板，用它们可以画出一些特殊角．在54°、60°、63°、72°、99°、120°、144°、150°、153°、171°的角中，能画出的角有（）A．7个B．8个C．9个D．10个【分析】一副三角板中的度数，用三角板画出角，无非是用角度加减法，逐一分析即可．【解答】解：54°＝90°﹣36°，则54°角能画出；60°不能写成36°、72°和45°、90°的和或差的形式，不能画出；63°＝90°﹣72°+45°，则63°可以画出；72°可以利用三角板的72°角直接画出；99°＝90°+45°﹣36°，则99°角能画出；120°不能写成36°、72°和45°、90°的和或差的形式，不能画出；144°＝72°+72°，则144°角能画出；150°不能写成36°、72°和45°、90°的和或差的形式，不能画出；153°＝72°+72°+45°﹣36°，则153°可以画出；171°＝90°+36°+45°，则171°可以画出．总之，能画出的角有7个．故选：A．【点评】此题考查的知识点是角的计算，关键是用三角板直接画特殊角的步骤：先画一条射线，再把三角板所画角的一边与射线重合，顶点与射线端点重合，最后沿另一边画一条射线，标出角的度数．24．如图，将一副三角板叠放在一起，使直角的顶点重合于O，则∠AOC+∠DOB ＝（）A．90°B．120°C．160°D．180°【分析】因为本题中∠AOC始终在变化，因此可以采用“设而不求”的解题技巧进行求解．【解答】解：设∠AOD＝a，∠AOC＝90°+a，∠BOD＝90°﹣a，所以∠AOC+∠BOD＝90°+a+90°﹣a＝180°．故选：D．【点评】本题考查了角度的计算问题，在本题中要注意∠AOC始终在变化，因此可以采用“设而不求”的解题技巧进行求解．25．如图，OC是∠AOB的平分线，OD是∠AOC的平分线，且∠COD＝25°，则∠AOB等于（）A．50°B．75°C．100°D．120°【分析】根据角的平分线定义得出∠AOD＝∠COD，∠AOB＝2∠AOC＝2∠BOC，求出∠AOD、∠AOC的度数，即可求出答案．【解答】解：∵OC是∠AOB的平分线，OD是∠AOC的平分线，∠COD＝25°，∴∠AOD＝∠COD＝25°，∠AOB＝2∠AOC，∴∠AOB＝2∠AOC＝2（∠AOD+∠COD）＝2×（25°+25°）＝100°，故选：C．【点评】本题考查了对角平分线定义和角的计算等知识点的应用，主要考查学生运用角平分线定义进行推理的能力和计算能力，题目较好，难度不大．26．如图，将长方形纸片ABCD的角C沿着GF折叠（点F在BC上，不与B，C重合），使点C落在长方形内部点E处，若FH平分∠BFE，则∠GFH的度数α是（）A．90°＜α＜180°B．0°＜α＜90°C．α＝90°D．α随折痕GF位置的变化而变化【分析】根据折叠的性质可以得到△GCF≌△GEF，即∠CFG＝∠EFG，再根据FH平分∠BFE即可求解．【解答】解：∵∠CFG＝∠EFG且FH平分∠BFE．∠GFH＝∠EFG+∠EFH∴∠GFH＝∠EFG+∠EFH＝∠EFC+∠EFB＝（∠EFC+∠EFB）＝×180°＝90°．故选：C．【点评】本题主要考查了折叠的性质，注意在折叠的过程中存在的相等关系．27．α，β都是钝角，甲、乙、丙、丁计算，（α+β）的结果依次为50°，26°，72°，90°，其中有正确的结果，则计算正确的是（）A．甲B．乙C．丙D．丁【分析】本题是对钝角定义的考查，求解时可根据定义求得结果．【解答】解：∵α，β都是钝角，所以大于90°，小于180°，∴180°＜（α+β）＜360°，∴30°＜（α+β）＜60°，则只有50°符合要求．故选：A．【点评】本题是钝角的定义的考查，利用不等式的性质求解．二．填空题（共6小题）28．如图，若∠3：∠2＝2：5，且∠2﹣∠1＝12°，∠3等于32°．【分析】根据比例可设∠3＝2x，∠2＝5x，利用方程和平角解答即可．【解答】解：∵∠3：∠2＝2：5，设∠3＝2x，∠2＝5x，∵∠1+∠2+∠3＝180°，∠2﹣∠1＝12°，可得：5x﹣12°+5x+2x＝180°，解得：x＝16，所以∠3＝2×16°＝32°，故答案为：32°【点评】本题考查角度计算，解题的关键是熟练利用平角的定义和方程解答．29．将一张长方形纸片按如图所示的方式折叠，BD、BE为折痕，若∠ABE＝34°，则∠DBC为56度．【分析】根据翻折的性质可知，∠ABE＝∠A′BE，∠DBC＝∠DBC′，再根据平角的度数是180°，∠ABE＝34°，继而即可求出答案．【解答】解：根据翻折的性质可知，∠ABE＝∠A′BE，∠DBC＝∠DBC′，又∵∠ABE+∠A′BE+∠DBC+∠DBC′＝180°，∴∠ABE+∠DBC＝90°，又∵∠ABE＝34°，∴∠DBC＝56°．故答案为：56【点评】此题考查了角的计算，根据翻折变换的性质，得出三角形折叠以后的图形和原图形全等，对应的角相等，得出∠ABE＝∠A′BE，∠DBC＝∠DBC′是解题的关键．30．已知∠AOB＝80°，∠BOC＝50°，OD是∠AOB的角平分线，OE是∠BOC 的角平分线，则∠DOE＝65°或15°．【分析】需要分类讨论：射线OC在∠AOB的内部和射线OC在∠AOB的外部两种情况．由题意可得∠BOD＝×80°＝40°，∠EOB＝×50°＝25°，则由∠DOE、∠BOD与∠EOB的关系可求得∠DOE的度数．【解答】解：∵∠AOB＝80°，∠BOC＝50°，且OD，OE分别为∠AOB，∠BOC的角平分线，∴∠BOD＝∠AOB＝40°，∠EOB＝∠BOC＝25°，①当OC在∠AOB内时，如图1，∴∠DOE＝∠DOB﹣∠EOB＝40°﹣25°＝15°．②当OC在∠AOB外时，如图2，∠DOE＝∠DOB+∠EOB＝40°+25°＝65°．综上所述，∠DOE的度数为65°或15°．故答案是：65°或15°．【点评】本题考查了角的计算以及角平分线线的定义的运用．解题时注意结合图形求得角与角间的和差关系：∠DOE＝∠BOD﹣∠EOB或∠DOE＝∠BOD+∠EOB．31．将一副三角板如图摆放，若∠BAE＝135°17′，则∠CAD的度数是44°43′．【分析】利用三角形的各角度数和图中角与角的关系计算．【解答】解：∠BAE＝∠BAD+∠CAE﹣∠CAD则∠CAD＝∠BAD+∠CAE﹣∠BAE＝90+90﹣∠BAE＝44°43′．故填44°43′．【点评】对∠BAE＝∠BAD+∠CAE﹣∠CAD这一关系的认识是解题的关键．32．如图所示，点C，O，D在同一条直线上，∠AOC＝40°，∠BOD＝50°，OM，ON分别是∠AOC，∠BOD的平分线，则∠MON＝135°．【分析】根据角平分线的定义得到∠MOA＝∠AOC＝20°，∠NOB＝∠BOD ＝25°，结合图形计算即可．【解答】解：∵∠AOC＝40°，∠BOD＝50°，∴∠AOB＝90°，∵OM，ON分别是∠AOC，∠BOD的平分线，∴∠MOA＝∠AOC＝20°，∠NOB＝∠BOD＝25°，∴∠MON＝∠MOA+∠AOB+∠NOB＝135°，故答案为：135°．【点评】本题考查的是角的计算，掌握角的和差计算、正确认识图形是解题的关键．33．如图，直线AB、CD相交于点O，∠DOE＝∠BOE，OF平分∠AOD，若∠BOE＝28°，则∠EOF的度数为90°．【分析】根据已知条件“∠DOE＝∠BOE，OF平分∠AOD，若∠BOE＝28°”和平角的定义可以求得∠AOF＝∠DOF＝∠AOD＝62°，∠DOE＝∠BOE ＝28°；然后根据图形求得∠EOF＝∠DOF+∠DOE＝62°+28°＝90°．【解答】解：∵∠DOE＝∠BOE，∠BOE＝28°，∴∠DOB＝2∠BOE＝56°；又∵∠AOD+∠BOD＝180°，∴∠AOD＝124°；∵OF平分∠AOD，∴∠AOF＝∠DOF＝∠AOD＝62°，∴∠EOF＝∠DOF+∠DOE＝62°+28°＝90°．故答案是：90°．【点评】本题考查了角的计算．解题时，注意利用隐含在题干中的已知条件“∠AOB＝180°”．三．解答题（共17小题）34．如图，∠AOB＝120°，点C为∠AOB内部一点，OD平分∠BOC，OE平分∠AOD（1）如果∠AOC＝30°，依题意补全图形；（2）在（1）的条件下，求∠EOC的度数；（3）如果∠AOC＝α（0°＜α＜120°），直接用含α的代数式表示∠EOC的度数．【分析】（1）根据题意画出图形即可；（2）首先求出∠COB的度数，然后根据角平分线的定义求得∠DOB＝∠DOC＝45°，那么∠DOA＝75°，再根据角平分线的定义求得∠DOE，然后根据∠EOC＝∠DOC﹣∠DOE求解；（3）与（2）解法相同．【解答】解：（1）如图1所示：（2）∵∠AOB＝120°，∠AOC＝30°，∴∠COB＝90°；∵OD平分∠BOC，∴∠DOB＝∠DOC＝45°；∵∠AOB＝120°，∠DOB＝45°，∴∠DOA＝75°；∵OE平分∠AOD，∴∠DOE＝∠AOE＝37.5°；∴∠EOC＝∠DOC﹣∠DOE＝45°﹣37.5°＝7.5°；（3）∵∠AOB＝120°，∠AOC＝α，∴∠COB＝120°﹣α；∵OD平分∠BOC，∴∠DOB＝∠DOC＝60°﹣α；∵∠AOB＝120°，∠DOB＝60°﹣α，∴∠DOA＝60°+α；∵OE平分∠AOD，∴∠DOE＝∠AOE＝30°+α；∴∠EOC＝|∠DOE﹣∠DOC|＝|30°+α﹣（60°﹣α）|＝|α﹣30°|．【点评】本题考查了角度的计算，理解角平分线的定义是关键．35．如图OC是∠AOB内部的一条射线，∠BOC＝2∠AOC，OD平分∠AOC．（1）若∠AOB＝120°，求∠BOC和∠BOD的度数；（2）画出∠BOC的平分线OE，说明∠DOE＝∠AOB．【分析】（1）设∠AOC＝x，根据题意列出方程，解方程求出x，计算即可；（2）根据角平分线的定义证明．【解答】解：（1）设∠AOC＝x，则∠BOC＝2x，所以x+2x＝120°，则x＝40°，即∠AOC＝40°，∠BOC＝80°，因为OD平分∠AOC，∴∠DOC＝20°，所以∠DOB＝∠DOC+∠BOC＝20°+80°＝100°；（2）∠BOC的平分线OE如图所示：因为OD平分∠AOC，∴∠DOC＝∠AOC，因为OE平分∠BOC，∴∠EOC＝∠BOC，∠DOE＝∠DOC+∠EOC＝∠AOC+∠BOC＝∠AOB．【点评】本题考查的是角的计算、角平分线的定义，掌握角平分线的定义以及角平分线的画法是解题的关键．36．如图1所示：已知，∠AOB＝90°，∠BOC＝30°，OM平分∠AOC，ON 平分∠BOC．（1）∠MON═45°；（2）如图2，∠AOB＝90°，∠BOC＝x°，仍然分别作∠AOC、∠BOC的平分线OM、ON，能否求出∠MON的度数若能，求出其值；若不能，说明理由．（3）如图3，若∠AOB＝α，∠BOC＝β（α、β均为锐角，且α＞β），仍然分别作∠AOC、∠BOC的平分线OM、ON，能否求出∠MON的度数．若能，求∠MON的度数．（4）从（1）、（2）、（3）的结果中，你发现了什么规律？【分析】（1）根据题意可知，∠AOC＝120°，由OM平分∠AOC，ON平分∠BOC；推出∠MOC＝∠AOC＝60°，∠CON＝∠BOC＝15°，由图形可知，∠MON＝∠MOC﹣∠CON，即∠MON＝45°；（2）根据（1）的求解思路，先利用角平分线的定义表示出∠MOC与∠NOC的度数，然后相减即可得到∠MON的度数；（3）用α、β表示∠MOC，∠NOC，根据∠MON＝∠MOC﹣∠NOC得到．（4）由（1）、（2）、（3）的结果中，∠MON的度数与∠BCO无关，∠MON＝．【解答】解：（1）∵∠AOB＝90°，∠BOC＝30°，∴∠AOC＝∠AOB+∠BOC＝90°+30°＝120°，∵OM平分∠AOC，ON平分∠BOC，∴∠MOC＝∠AOC＝60°，∠CON＝∠BOC＝15°，∴∠MON＝∠MOC﹣∠CON＝60°﹣15°＝45°；故答案为：45；（2）能．∵∠AOB＝90°，∠BOC＝x°，∴∠AOC＝90°+x°∵OM、ON分别平分∠AOC，∠BOC，∴∠MOC＝∠AOC＝（90°+x°）＝45°+x，∴∠CON＝∠BOC＝x，∴∠MON＝∠MOC﹣∠CON＝45°+x﹣x＝45°．（3）∵∠AOB＝α，∠BOC＝β，∴∠AOC＝∠AOB+∠BOC＝α+β，∵OM平分∠AOC，∴∠MOC＝∠AOC＝（α+β），∵ON平分∠BOC，∴∠NOC＝∠BOC＝，∴∠MON＝∠MOC﹣∠NOC＝（α+β）﹣＝．（4）规律：∠MON的度数与∠BCO无关，∠MON＝．理由：∵∠AOB＝α，∠BOC＝β，∴∠AOC＝∠AOB+∠BOC＝α+β，∵OM平分∠AOC，∴∠MOC＝∠AOC＝（α+β），∵ON平分∠BOC，∴∠NOC＝∠BOC＝，∴∠MON＝∠MOC﹣∠NOC＝（α+β）﹣＝．【点评】本题考查角的和差定义、角平分线的定义，利用∠MON＝∠MOC﹣∠NOC是解决问题的关键．37．如图1，O为直线AB上一点，过点O作射线OC，∠AOC＝30°，将一直角三角板的直角顶点放在点O处，一边ON在射线OA上，另一边OM与OC 都在直线AB的上方．现将图25﹣1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周．（1）如图2，若经过t秒后，线段OM恰好平分∠BOC，此时∠COM＝75°；∠AON＝15°；t＝5秒；（2）在（1）的条件下，线段ON是否平分∠AOC？请说明理由；（3）如图3，若三角板在转动的同时，射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周，那么经过多长时间OC平分∠MON？【分析】（1）根据角平分线的定义计算即可；（2）求出∠AON，∠CON的值即可判断；（3）设∠AON＝3t，∠AOC＝30+6t，根据∠AOC﹣∠AON＝∠CON，构建方程即可解决问题；【解答】解：（1）如图2中，∵∠AOC＝30°，∴∠BOC＝180°﹣∠AOC＝150°，∵OM平分∠BOC，∴∠COM＝∠BOM＝∠BOC＝75°，∠AON＝180°﹣90°﹣75°＝15°，∴t＝＝5s，故答案为75，15，5；（2）结论：ON平分∠AOC．理由：∵∠AOC＝30°，∠AON＝15°，∴∠CON＝∠AOC﹣∠AON＝15°，∴∠AON＝∠CON．∴ON平分∠AOC．（3）∵OC平分∠MON，∠MON＝90°，∴∠CON＝∠COM＝45°，∵三角板绕点O以每秒3°的速度，射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周，∴设∠AON＝3t，∠AOC＝30+6t，∵∠AOC﹣∠AON＝∠CON，∴30+6t﹣3t＝45，解得t＝5，∴经过5秒OC平分∠MON．【点评】本题考查角的计算、角平分线的定义、旋转变换等知识，解题的关键是理解题意，学会利用参数解决问题，属于中考常考题型．38．如图，已知∠AOB＝90°，∠EOF＝60°，OE平分∠AOB，OF平分∠BOC，求∠COB和∠AOC的度数．【分析】直接利用角平分线的定义结合已知角度得出∠BOF的度数，进而分析得出答案．【解答】解：∵∠AOB＝90°，OE平分∠AOB，∴∠BOE＝∠AOB＝45°，∵∠EOF＝60°，∴∠BOF＝∠EOF﹣∠BOE＝15°，∵OF平分∠BOC，∴∠BOC＝2∠BOF＝30°，∴∠AOC＝∠AOB+∠BOC＝120°．【点评】此题主要考查了角的计算以及角平分线的定义，正确应用角平分线的定义是解题关键．39．如图，已知∠AOB＝90°，射线OC绕点O从OA位置开始，以每秒4°的速度顺时针方向旋转；同时，射线OD绕点O从OB位置开始，以每秒1°的速度逆时针方向旋转．当OC与OA成180°时，OC与OD同时停止旋转．（1）当OC旋转10秒时，∠COD＝40°．（2）当OC与OD的夹角是30°时，求旋转的时间．（3）当OB平分∠COD时，求旋转的时间．【分析】（1）根据已通知以及即可得到结论；（2）设转动t秒，OC与OD的夹角是30度，①如图1，列方程即可得到结论；②如图2，列方程即可得到结论；（3）如图3，设转动m秒时，根据角平分线的定义列方程即可得到结论．【解答】解：（1）∵射线OC绕点O从OA位置开始，以每秒4°的速度顺时针方向旋转，∴当OC旋转10秒时，∠COD＝×10＝40°，故答案为：40；（2）设转动t秒，OC与OD的夹角是30度，①如图1，4t+t＝90﹣30，t＝12，②如图2，4t+t＝90+30，t＝24，∴旋转的时间是12秒或24秒；（3）如图3，设转动m秒时，OB平分∠COD，则4m﹣90＝m，解得，m＝30，∴旋转的时间是30秒．【点评】本题考查了角的有关计算和角平分线定义的应用，熟记角平分线的定义是解题的关键．40．如图所示，已知∠AOB＝90°，∠BOC＝30°，OM平分∠AOC，ON平分∠BOC；（1）求∠MON；（2）∠AOB＝α，∠BOC＝β，求∠MON的度数．【分析】（1）根据角平分线的定义得到∠MOC＝∠AOC，∠NOC＝∠BOC，则∠MON＝∠MOC﹣∠NOC＝（∠AOC﹣∠BOC）＝∠AOB，然后把∠AOB的度数代入计算即可；（2）同理可得，∠MOC＝，∠CON＝，所以∠MON＝∠MOC ﹣∠CON＝＝．【解答】解：（1）∵OM平分∠AOC，ON平分∠BOC，∴∠MOC＝∠AOC，∠NOC＝∠BOC，∵∠AOC＝∠AOB+∠BOC，∴∠MON＝∠MOC﹣∠NOC＝（∠AOB+∠BOC﹣∠BOC）＝∠AOB，∵∠AOB＝90°，∴∠MON＝×90°＝45°．（2）同理可得，∠MOC＝，∠CON＝，∴∠MON＝∠MOC﹣∠CON＝＝．【点评】本题考查了角平分线的定义，属于基础题，解决本题的关键是熟记平分线的定义．41．如图，已知∠AOC＝60°，∠BOD＝90°，∠AOB是∠DOC的3倍，求∠AOB的度数．【分析】设∠COD＝x，则∠AOD可表示为60°﹣x，于是∠AOB＝90°+60°﹣x＝150°﹣x，再根据∠AOB是∠DOC的3倍得到150°﹣x＝3x，解得x＝37.5°，然后计算3x即可．【解答】解：设∠COD＝x，∵∠AOC＝60°，∠BOD＝90°，∴∠AOD＝60°﹣x，∴∠AOB＝90°+60°﹣x＝150°﹣x，。

初中数学浙教版七年级上册6.7角的和差同步练习一、单选题（共10题；共20分）1.如图，OC为内一条直线，下列条件中不能确定OC平分的是A. B.C. D.2.如图，OC在∠AOB的内部，∠BOC：∠AOC＝1：2．∠AOB＝63°，则∠AOC＝（）A. 52°B. 42°C. 39°D. 21°3.如图，∠AOC＝∠BOD＝90°，∠AOD＝140°，则∠BOC的度数为（）A. 30°B. 45°C. 50°D. 40°4.∠AOB的大小可由量角器测得(如右图所示)，则180°-∠AOB的大小为( )A. 0°B. 70°C. 110°D. 180°5.如图，是直角顶点重合的一副三角尺，若∠BCD=30°，下列结论错误的是（）A. ∠ACD=120°B. ∠ACD=∠BCEC. ∠ACE=120°D. ∠ACE-∠BCD=120°6.如图，射线OA的端点O在直线CD上，若∠COA＝40°，则∠AOD的度数是（）A. 170°B. 160°C. 150°D. 140°7.借助常用的直角三角尺，能画出一些度数的角，下列选项中不能画出的角是（）A. 15°B. 100°C. 165°D. 135°8.在同一平面内，若∠BOA＝50.3°，∠BOC＝10°30′，则∠AOC的度数是( )A. 60.6°B. 40°C. 60.8°或39.8D. 60.6°或40°9.如图，∠AOB是直角，∠AOC=38°，OD平分∠BOC，则∠AOD的度数为（）A. 52°B. 38°C. 64°D. 26°10.如图，∠AOB=130°，射线OC是∠AOB内部任意一条射线，OD、OE分别是∠AOC、∠BOC的平分线，下列叙述正确的是（）A. ∠DOE的度数不能确定B. ∠AOD+∠BOE=∠EOC+∠COD=∠DOE=65°C. ∠BOE=2∠CODD. ∠AOD=二、填空题（共4题；共7分）11.如图，OB是________的平分线；OC是________的平分线，∠AOD＝________，∠BOD＝________．12.，，________13.将两个三角尺的直角顶点重合为如图所示的位置，若，则________．14.如图，∠AOC=90°，∠BOC=60°，OM平分∠AOB，ON平分∠BOC．∠MON的度数为________．三、解答题（共3题；共25分）15.用三角尺或量角器，画出三角形AC 边上的高，BC 边上的中线，∠ACB 的角平分线．不写作法，写好结论．16.已知一条射线OA，若从点O再引两条射线OB和OC，使∠AOB=60°，∠BOC=20°，求∠AOC的度数．17.将一副三角板放在同一平面内，使直角顶点重合于点O（1）如图①，若∠AOB=155°，求∠AOD、∠BOC、∠DOC的度数.（2）如图①，你发现∠AOD与∠BOC的大小有何关系？∠AOB与∠DOC有何关系？直接写出你发现的结论.（3）如图②，当△AOC与△BOD没有重合部分时，（2）中你发现的结论是否还仍然成立，请说明理由.答案解析部分一、单选题1.【答案】C【解析】【解答】解：A、能确定OC平分∠AOB，故不符合题意；B、能确定OC平分∠AOB，故不符合题意；C、∠AOC+∠COB=∠AOB，不能确定OC平分∠AOB，故符合题意；D、能确定OC平分∠AOB，故不符合题意。

D O C B A 《角的和差》习题
一、填空题
1、如图，∠1＝∠2，∠3＝∠4，∠5＝130度，那么∠A ＝( )度
.
2、如图5，点0为直线AB 上的一点，∠BOC 是直角，∠BOD ：∠COD =4：1.则∠AOD 是( )度
.
3、如图，∠AOB 的顶点0在直线l 上，已知图中所有小于平角的角之和是400度，则∠AOB ＝________度
.
二、解答题
如图，已知∠AOB 是∠AOC 的余角，∠AOD 是∠AOC 的补角，且BOD BOC ∠=
∠21求∠B OD 、∠AOC 的度数
一条射线OA ，若从点O 再引两条
射线OB 、OC ，使∠AOB =60°，∠BOC
=20°，求∠AOC 的度数.
已知，如图∠BOC 为∠AOC 内的一个锐角，射线OM 、ON 分别平分∠AOC 、∠BOC .
(1)若∠AOB =90°，∠BOC =30°，求∠MON 的度数；
(2)若∠AOB =α，∠BOC =30°，求∠MON 的度数；
(3)若∠AOB =90°，∠BOC =β，还能否求出∠MON 的度数？若能，求出其值，若不能，说明理由.
从前三问的结果你发现了什么规律？
N。

浙教版初中数学
重点知识精选
掌握知识点，多做练习题，基础知识很重要！浙教版初中数学和你一起共同进步学业有成！
,( ,( AOC＝∠BOD＝90°，下列结论中正确的个数是(C) COD　②∠AOD＝3∠
BOC＝∠AOC＋∠BOD
(
(
折叠，使点D落在
AOB和∠COD都是直角，则∠
,( ,(
是直线AB上一点，已知∠BOD＝30°，OE平分∠
平分∠AOB，OD平分∠OE平分∠BOC，则图中与∠个，与∠AOC相等的角有
,( ,(
OB是∠AOC的平分线，COE的平分线．
AOC＝80°，那么∠BOC
AOC＝80°，∠COE＝50°＝__65°__．
(第11题)
点O，OB平分∠DOE
交于点O，
(第12题)
90°＋α，
,( ,(
．如图，将书页斜折过去，使顶角处，BC为折痕，然后把边重合，折痕为BD，那么两折痕，BD间的夹角度数为
由题意，可得BC，BD，∠EBE′的平分线，∠ABA′，∠E′
(第15题)
＝40°，∠BOD＝50°
(第16题) ＝30°，
，
相信自己，就能走向成功的第一步
教师不光要传授知识，还要告诉学生学会生活。

数学思维
可以让他们更理性地看待人生。

初中数学浙教版七年级上册6.7 角的和差基础巩固训练新版姓名:________ 班级:________ 成绩:________一、单选题 (共8题；共16分)1. （2分）在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB的大小为（）A .B .C .D .2. （2分）利用三角板工具画角很方便，但是只能画出一些特殊的角，下列角度不能用一副三角板(不再用其他工具)画出的是（）A . 15°B . 20°C . 75°D . 105°3. （2分）如图，小刚将一副三角板摆成如图形状，如果∠DOC=120°，则∠AOB=（）A .B .C .D .4. （2分）如图，己知l1∥AB，AC为角平分线，下列说法错误的是（）A . ∠1=∠4B . ∠1=∠5C . ∠2=∠3D . ∠1=∠35. （2分）如图，在△ABC中，AD是∠BAC的平分线，E为AD上一点，且EF⊥BC于点F．若∠C=35°，∠DEF=15°，则∠B的度数为（）A . 65°B . 70°C . 75°D . 85°6. （2分）如图，△ABC中，AH⊥BC，BF平分∠ABC，BE⊥BF，EF∥BC，以下四个结论：①AH⊥EF，②∠ABF=∠EFB，③AC∥BE，④∠E=∠ABE．正确的是（）A . ①②③④B . ①②C . ①③④D . ①②④7. （2分）如图，∠AOB=∠COD，则∠AOC与∠DOB的大小关系是（）A . ∠AOC＞∠DOBB . ∠AOC＜∠DOBC . ∠AOC=∠DOBD . ∠AOC与∠DOB无法比较大小8. （2分）如图，将矩形纸片ABCD沿EF折叠（E、F分别是AD、BC上的点），使点B 与四边形CDEF内一点B′重合，若∠B′FC=50°，则∠AEF等于（）A . 110°B . 115°C . 120°D . 130°二、填空题 (共4题；共4分)9. （1分）如图，点O在直线AB上，射线OC平分∠DOB，若∠COB＝35°，则∠AOD＝________°．10. （1分）如图，将一副三角板叠在一起，使它们的直角顶点重合于O点，且∠AOB ＝155°，则∠COD＝________°．11. （1分）如图,在▱ABCD中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为________.12. （1分）如图，将直角三角形AOB绕点0旋转得到直角三角形COD，若∠AOB=90°，∠BOC=130°，则∠AOD的度数为________.三、解答题 (共2题；共15分)13. （5分）如图，已知直线AB、CD、EF相交于点O，∠2＝2∠1，∠3＝3∠2，求∠DOE 的度数．14. （10分）如图，∠AOC与∠BOC互余，OD平分∠BOC ，∠EOC＝2∠AOE ．（1）若∠AOD＝75°，求∠AOE的度数．（2）若∠DOE＝54°，求∠EOC的度数．参考答案一、单选题 (共8题；共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、二、填空题 (共4题；共4分)9-1、10-1、11-1、12-1、三、解答题 (共2题；共15分)13-1、14-1、14-2、。

6。

7 角的和差随堂检测1、如图，∠AOC和∠BOD都是直角,如果∠AOB=1400，则∠DOC的度数是（）A、300B、400C、500D、6002、一副三角尺可拼成很多角，如下图是由一副三角尺拼成的2个图形，请你计算：在第一个图中：∠ACD=°，∠ABD=°;在第二个图中：∠BAG=°，∠AGC=°。

图1 图23、将一副直角三角板（如图）叠在一起，使直角顶点重合于点O,则∠AOB+∠DOC=。

4、计算：102°43′32″+77°16′28″＝____________;87 o2′36″—36o37′24″＝______________。

5、如图，已知∠AOB=50º，OD平分∠BOC，OE平分∠AOC。

求∠EOD的度数。

拓展提高1、平面内两个角∠AOB=60°，∠AOC=20°，OA 为两角的公共边,则∠BOC 为（ ） A 、40° B 、80° C、40°或80° D、无法确定2、下面一些角中，可以只用一副三角尺（不用量角器)画出来的角是（ ） （1）150的角 (2)650的角 （3）750的角 （4）1350的角 （5）1450的角 A 、（1）（3）(4） B 、(1）（3）（5） C 、（1）（2）（4) D 、（2）（4）（5)3、已知：∠A=50º24’，∠B=50.24º，∠C =50º14’24”，那么下列各式正确的是（ ）A 、∠A>∠B〉∠C B、∠A〉∠B=∠C C 、∠B〉∠C>∠A D、∠B=∠C>∠A4、如图，BO 、CO 分别平分∠ABC 和∠ACB ，已知任意三角形的3个内角的和都是180°，若∠A ＝80°，你能求出∠BOC 的度数吗？试试看。

5、如图，∠AOC=90°，ON 是锐角∠COD 的平分线，OM 是∠AOD的平分线, 求∠MON 的度数。

章节测试题1.【题文】如图，OB是∠AOC的平分线，∠BOC＝30°，∠COD＝40°，求∠AOD的度数．【答案】100°.【分析】由OB是∠AOC的平分线，∠BOC=30°，可求∠AOC=2∠BOC=60°，由∠AOD=∠AOC+∠COD，将∠AOC与∠COD的度数代入即可．【解答】解：因为OB是∠AOC的平分线，∠BOC＝30°，所以∠AOC＝2∠BOC＝60°．因为∠AOD＝∠AOC＋∠COD，∠COD＝40°，所以∠AOD＝60°＋40°＝100°．2.【题文】如图，两直线AB，CD相交于点O，OE平分∠BOD，∠AOC∶∠AOD ＝7∶11．（1）求∠COE的度数；（2）若OF⊥OE，求∠COF的度数．【答案】（1）145°；（2）125°．【分析】（1）首先依据∠AOC：∠AOD=7：11，∠AOC+∠AOD=180°可求得∠AOC、∠AOD的度数，然后可求得∠BOD的度数，依据角平分线的定义可求得∠DOE的度数，最后可求得∠COE的度数；（2）先求得∠FOD的度数，然后依据邻补角的定义求解即可．【解答】解：（1）∵∠AOC：∠AOD=7：11，∠AOC+∠AOD=180°，∴∠AOC=70°，∠AOD=110°，∴∠BOD=70°．∵OE平分∠BOD，∴∠DOE=35°，∴∠COE=180°﹣35°=145°．（2）∵∠DOE=35°，OF⊥OE，∴∠FOD=55°，∴∠FOC=180°﹣55°=125°．3.【题文】如图，点O是直线AB上的一点，OD是∠AOC的平分线，OE是∠COB的平分线，若∠AOD＝14°，求∠DOE，∠BOE的度数．【答案】90° 76°【分析】利用角平分线和图中角与角的关系计算．【解答】解：因为OD是∠AOC的平分线，∠AOD＝14°，所以∠AOC＝2∠AOD＝2×14°＝28°.因为∠AOB＝180°，OE是∠COB的平分线，所以∠BOE＝∠BOC＝×(180°－∠AOC)＝76°，∠DOE＝∠BOC＋∠AOC＝76°＋14°＝90°.4.【题文】如图，已知OE、OD分别平分∠AOB和∠BOC，若∠AOB=90°，∠EOD=70°，求∠BOC的数。