纹理的灰度共生矩阵计算问题的分析
- 格式:pdf
- 大小:608.40 KB
- 文档页数:7

opencvpython灰度共生矩阵纹理特征-回复在这篇文章中,我将介绍OpenCV-Python 中的灰度共生矩阵(Gray-Level Co-occurrence Matrix,简称GLCM)以及如何利用它来提取纹理特征。
通过本文,你将了解GLCM 的基本概念、计算方法和使用实例,以及在图像分析、模式识别等领域中的应用。
一、引言近年来,图像处理和计算机视觉领域发展迅速,但图像中的特征提取仍然是一个重要的挑战。
纹理特征是图像中常用的特征之一,它可以用来描述图像的细节、纹理和结构。
而GLCM 在图像处理中被广泛应用,能够提取出图像中的纹理信息,从而帮助我们理解图像中的结构和特征。
二、灰度共生矩阵(GLCM)的基本概念灰度共生矩阵(GLCM)是一种用于描述图像纹理特征的统计工具。
它通过计算图像中相邻像素的灰度值出现频率和空间关系,生成一个对称矩阵。
GLCM 的每个元素表示了在特定方向和距离上,两个像素灰度值之间的出现频率。
通过分析这个矩阵,我们可以获得图像的纹理特征。
三、计算灰度共生矩阵(GLCM)要计算灰度共生矩阵,首先需要将图像转换为灰度图像。
然后,选择一个距离和方向,对图像进行扫描,计算相邻像素的灰度值出现频率。
通过累计相邻像素的灰度值对的个数,我们可以得到一个对称的GLCM。
在计算GLCM 时,我们还需要设置一个灰度级别的参数,用于指定像素的灰度值范围。
在OpenCV-Python 中,我们可以使用`cv2.glcm` 函数来计算灰度共生矩阵。
首先,我们需要导入OpenCV 和NumPy 库,并加载图像。
然后,我们可以使用`cv2.cvtColor` 函数将图像转换为灰度图像。
接下来,使用`cv2.glcm` 函数计算灰度共生矩阵。
pythonimport cv2import numpy as np# 加载图像img = cv2.imread('image.jpg')# 将图像转换为灰度图像gray_img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)# 计算灰度共生矩阵glcm = cv2.glcm(gray_img, distances=[1], angles=[0], levels=256)在上述代码中,我们选择了距离为1,方向为水平的参数。
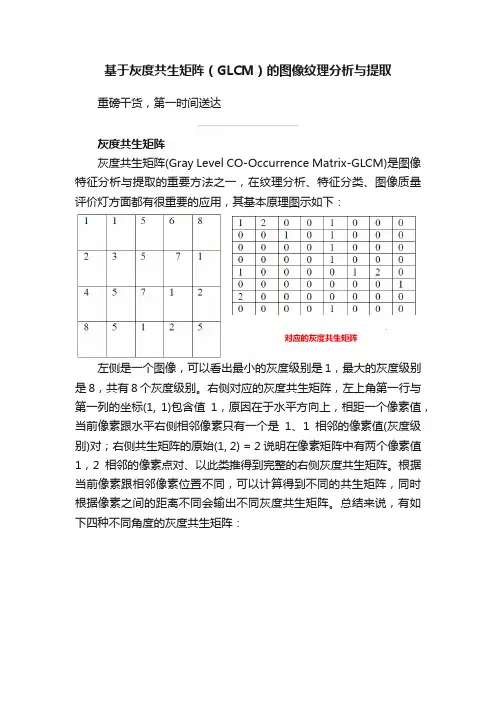
基于灰度共生矩阵(GLCM)的图像纹理分析与提取重磅干货,第一时间送达灰度共生矩阵灰度共生矩阵(Gray Level CO-Occurrence Matrix-GLCM)是图像特征分析与提取的重要方法之一,在纹理分析、特征分类、图像质量评价灯方面都有很重要的应用,其基本原理图示如下:左侧是一个图像,可以看出最小的灰度级别是1,最大的灰度级别是8,共有8个灰度级别。
右侧对应的灰度共生矩阵,左上角第一行与第一列的坐标(1, 1)包含值1,原因在于水平方向上,相距一个像素值,当前像素跟水平右侧相邻像素只有一个是1、1相邻的像素值(灰度级别)对;右侧共生矩阵的原始(1, 2) = 2 说明在像素矩阵中有两个像素值1,2相邻的像素点对、以此类推得到完整的右侧灰度共生矩阵。
根据当前像素跟相邻像素位置不同,可以计算得到不同的共生矩阵,同时根据像素之间的距离不同会输出不同灰度共生矩阵。
总结来说,有如下四种不同角度的灰度共生矩阵:•0度水平方向GLCM•45度方向GLCM•90度垂直方向GLCM•135度方向GLCM根据相邻像素点之间距离参数D不同可以得到不同距离的GLCM。
此外对正常的灰度图像来说,最小灰度值为0,最大的灰度值为255,共计256个灰度级别,所以GLCM的大小为256x256,但是我们可以对灰度级别进行降维操作,比如可以每8个灰度值表示一个level这样,这样原来256x256大小的共生矩阵就可以改成256/8 * 256 /8 = 32x32的共生矩阵。
所以最终影响灰度共生矩阵生成有三个关键参数:•角度 (支持0、45、90、135)•距离(大于等于1个像素单位)•灰度级别(最大GLCM=256 x 56)GLCM实现纹理特征计算灰度共生矩阵支持如下纹理特征计算,它们是:•能量•熵值•对比度•相关性•逆分差这些纹理特征计算公式如下:上述5个是常见的GLCM的纹理特征,GLCM总计由14个特征值输出,这里就不再赘述了!感兴趣的可以自己搜索关键字GLCM。

灰度共生矩阵法灰度共生矩阵法是一种常用的图像纹理特征分析方法,它通过统计图像中不同灰度值之间出现的空间关系来描述图像的纹理特征。
本文将从以下几个方面详细介绍灰度共生矩阵法。
一、灰度共生矩阵法的基本原理灰度共生矩阵法是一种基于灰度级别的统计方法,它通过计算同一图像区域内不同位置处两个像素之间的灰度值关系,得出各种方向上不同距离处两个像素之间某些特定关系的概率分布。
具体而言,对于给定的图像I(x,y),以及距离d和角度θ,可以定义一个二元组(x,y)和另一个二元组(x+d*cosθ,y+d*sinθ)之间的关系,通常称为共生对。
然后可以通过统计所有这些共生对在整个图像中出现的频率来生成一个称为灰度共生矩阵(GLCM)的矩阵。
二、灰度共生矩阵法的主要步骤1. 灰度化:将彩色图像转换为灰度图像。
2. 分块:将整幅图像分割成若干个小块,每个小块的大小可以根据实际需求来确定。
3. 计算灰度共生矩阵:对于每个小块,计算其灰度共生矩阵。
具体而言,对于每个像素点,统计它周围距离为d、方向为θ的所有像素点的灰度值,并将这些灰度值作为共生对出现的频率填入GLCM中。
4. 特征提取:从GLCM中提取出各种特征参数。
常用的特征参数包括能量、熵、对比度、相关性等。
5. 分类识别:将提取出来的特征参数输入到分类器中进行分类识别。
三、灰度共生矩阵法的常用特征参数1. 能量(Energy):能量是指GLCM中所有元素平方和的开方,它反映了图像纹理的粗细程度。
能量越大,表示图像纹理越粗糙。
2. 熵(Entropy):熵是指GLCM中所有元素对数之和的相反数,它反映了图像纹理的复杂程度。
熵越大,表示图像纹理越复杂。
3. 对比度(Contrast):对比度是指GLCM中元素值之差与元素位置之间距离的加权和,它反映了图像纹理的明暗程度。
对比度越大,表示图像纹理越明暗分明。
4. 相关性(Correlation):相关性是指GLCM中元素值之间的线性关系程度,它反映了图像纹理的方向性。


纹理特征分析的灰度共生矩阵(GLCM)灰度共生矩阵(GLCM)是一种用于纹理特征分析的图像处理技术。
它广泛应用于各种领域,例如图像识别、图像分类、医学图像分析等。
GLCM通过统计图像中不同灰度级别的像素对出现的频次来描述图像的纹理特征。
GLCM是一个二维矩阵,它以图像中的像素值为输入,生成一个矩阵。
矩阵中的每个元素表示了两个像素具有一定距离(通常为1个像素)时,它们具有其中一种特定的灰度相对关系(如相等、相邻或对称等)的频次统计。
这个频次统计是通过扫描整个图像来进行计算的。
为了计算GLCM,我们需要遍历图像中的每个像素,对于每个像素,我们将与其距离为d的像素对应的GLCM矩阵元素+1、距离d是一个参数,用于确定计算GLCM时考虑的像素对的距离。
通常,我们将距离d设置为1,以考虑邻近像素之间的关系。
GLCM矩阵的大小与图像的灰度级数有关。
如果图像有N个灰度级别,则GLCM矩阵的大小为N×N。
矩阵中的每个元素(i,j)表示在图像中,像素值为i的像素和像素值为j的像素成对出现的频次。
这个频次可以用于计算一些统计特征,这些特征可以用来描述图像的纹理特征。
常用的灰度共生矩阵特征包括:1. 对比度(Contrast):对比度是通过计算矩阵中不同灰度级别像素对的频次差异来描述图像的纹理对比度。
2. 逆差矩(Inverse Difference Moment):逆差矩用于衡量图像的纹理细节程度,即描述图像中相邻不同灰度级别像素对的频次。
3. 相关度(Correlation):相关度用于衡量图像的纹理的线性依赖性,即描述图像中相邻像素的线性相关性。
4. 能量(Energy):能量用于衡量图像的纹理的均匀性,即描述图像中不同灰度级别像素对的频次的平方和。
5. 熵(Entropy):熵用于衡量图像的纹理的复杂性,即描述图像中不同灰度级别像素对的频次的信息熵。
这些特征可以用来描述图像的纹理特征,从而可以用于图像分类、识别等应用中。

灰度共生矩阵八个纹理特征灰度共生矩阵是图像处理领域中常用的一种特征提取方法,其八个纹理特征可以快速、准确地描述图像的纹理特征。
下面我们就来详细介绍一下灰度共生矩阵八个纹理特征。
第一步,灰度共生矩阵的计算。
灰度共生矩阵是一种二维矩阵,用来描述图像中每种灰度值像素与其相邻像素的空间位置关系。
灰度共生矩阵的特征值,直接与图像的纹理特征相关。
第二步,各向同性的方差特征。
通过计算灰度共生矩阵中各向同性方差的平均值,可以简单地描述被分析图像的纹理特征,在统计分析时常常被使用。
第三步,方向性差异特征。
使用灰度共生矩阵构建方向性纹理特征,可以通过计算每个方向的概率分布,描述图像中不同方向纹理的差异。
第四步,灰度分布均匀度特征。
用来描述图像的灰度差异程度,一般是计算灰度值的标准差,标准差越小,灰度分布越均匀,图像质量越好。
第五步,灰度共生矩阵的能量特征。
计算灰度共生矩阵的能量值,有助于描述图像中出现频次较高的灰度值。
第六步,灰度共生矩阵的相关度特征。
描述灰度级之间纹理依赖关系的特征,计算灰度值之间的相关性。
第七步,灰度共生矩阵的对比度特征。
计算灰度共生矩阵的对比度,描述图像纹理的明暗变化程度。
第八步,灰度共生矩阵的熵特征。
描述灰度共生矩阵中信息的随机性,熵越高,灰度分布越杂乱,图像质量越低。
综上所述,灰度共生矩阵八个纹理特征可以有效地描述图像的纹理特征,应用广泛。
在实际应用中,可以根据实际需求选取不同的特征进行分析,以更准确地得出结论,提升数据分析的准确性和有效性。

Matlab中的灰度共生矩阵与纹理分析方法详解纹理分析是图像处理和计算机视觉中的一个重要领域,它用于描述和提取图像中的纹理信息。
而在Matlab中,灰度共生矩阵(Gray Level Co-occurrence Matrix, GLCM)是一种常用的纹理分析方法。
本文将详细介绍GLCM的基本原理和应用,并探讨在Matlab中如何使用GLCM进行纹理分析。
第一部分:GLCM的基本原理1.1 GLCM的定义灰度共生矩阵是一种用于描述图像纹理特征的统计矩阵。
它基于图像中像素灰度值之间的统计关系,并计算出像素对之间的灰度值共生概率分布。
GLCM通常使用一个邻域半径来定义像素对,而这个半径可以控制计算纹理特征的尺度。
1.2 GLCM参数与特征在计算GLCM时,有几个常用的参数需要设定,包括像素对的邻域距离、邻域角度、灰度级数目等。
根据这些参数,可以得到一系列的GLCM,并从中提取出各种纹理特征。
常见的GLCM特征包括对比度、相关性、能量和熵等。
第二部分:在Matlab中使用GLCM进行纹理分析2.1 GLCM的计算在Matlab中,可以利用函数graycomatrix来计算图像的GLCM。
该函数需要指定输入图像、邻域距离、邻域角度和灰度级数目等参数。
通过调用该函数,可以得到一个GLCM矩阵。
2.2 GLCM特征的提取利用GLCM矩阵,可以进一步提取各种纹理特征。
在Matlab中,可以使用函数graycoprops来计算GLCM特征。
该函数需要指定GLCM矩阵以及要计算的特征类型。
例如,调用graycoprops(GLCM, 'Contrast')可以计算出GLCM的对比度特征。
2.3 GLCM的应用GLCM在图像处理和计算机视觉中有着广泛的应用。
例如,在医学图像中,可以利用GLCM来分析肿瘤组织的纹理特征,为肿瘤诊断提供依据。
另外,GLCM还可以用于图像分类和识别等领域。
第三部分:GLCM在实际应用中的案例分析3.1 肿瘤组织分析以医学图像中的肿瘤组织分析为例,假设我们有一组CT图像,其中包含正常组织和恶性肿瘤组织。

灰度共生矩阵提取纹理特征Novel non-invasive distribution measurement of texture profile analysis (TPA) in salmon fillet byusing visible and near infrared hyperspectral imagingDi Wu and Da-Wen Sun论文中提到:Five spectral features (mean, standard deviation, skew, energy, and entropy) and twentytwo image texture features obtained from graylevel co-occurrence matrix (GLCM) were extracted fromhyperspectral images in this study.灰度共生矩阵提取纹理特征的实验结果分析在图像检索中, 常用的纹理特征主要有Tamura 纹理特征[ 1] 、自回归纹理模型[ 2] 、方向性特征、小波变换[ 3- 4] 和共生矩阵等形式。
这些纹理分析方法的共同点是提取了那些在特定纹理描述中最重要的特征, 突出纹理的不同方面。
其中, 灰度共生矩阵GLCM是由文献[5] 提出的一种用来分析图像纹理特征的重要方法。
目前, 基于共生矩阵的纹理检索算法被广泛应用[ 6- 9] 。
( 1) 角二阶矩ASM=i ! j !P(i,j)2;角二阶矩是灰度共生矩阵各元素的平方和,又称能量。
它是影像纹理灰度变化均一的度量, 反映了影像灰度分布均匀程度和纹理粗细度。
( 2) 对比度CON=i ! j !(i- j)2P(i,j);对比度是灰度共生矩阵主对角线附近的惯性矩, 它度量矩阵的值是如何分布和影像中局部变化的多少, 反映了影像的清晰度和纹理的沟纹深浅。
( 3) 相关CORRLN=i ! j !((ij)p(i,j))-μx μy " #/σxσy; 它度量空间灰度共生矩阵元素在行或列方向上的相似程度, 因此, 相关值大小反映了影像中局部灰度相关性。

灰度共生矩阵解题思路
一、确定灰度级
在进行灰度共生矩阵分析之前,需要先确定图像的灰度级。
灰度级决定了图像的亮度范围,通常取值范围在0-255之间。
在确定灰度级时,可以根据图像的实际情况进行调整,以保证图像的细节和对比度。
二、计算距离
在灰度共生矩阵中,距离是一个重要的参数。
它表示两个像素点之间的距离,通常取值范围在0-1之间。
在计算距离时,可以根据实际情况进行调整,以保证灰度共生矩阵的准确性和可靠性。
三、生成矩阵
生成灰度共生矩阵是解题的关键步骤之一。
根据灰度级和距离参数,可以计算出所有像素点之间的距离,并构建一个二维矩阵。
矩阵中的每个元素表示两个像素点之间的距离出现的次数或概率。
四、计算特征值
特征值是灰度共生矩阵中的一个重要概念,它可以反映图像的纹理特征。
常见的特征值包括能量、熵、对比度和相关性等。
通过计算这些特征值,可以对图像的纹理进行定量描述和分析。
五、判断纹理
判断纹理是灰度共生矩阵解题的最终目的。
根据计算出的特征值,可以对图像的纹理进行分类、识别和比较。
例如,可以利用灰度共生矩阵分析图像中的边缘、纹理和噪声等特征,为图像处理和计算机视觉等领域提供有力的支持。
总之,灰度共生矩阵是一种有效的图像处理和分析方法,它可以用于描述和比较图像中的纹理特征。
通过掌握灰度共生矩阵的解题思路和方法,可以为相关领域的研究和应用提供有力的帮助。

基于灰度共生矩阵的纹理特征提取概述及解释说明1. 引言1.1 概述纹理特征是一种用于描述图像或物体表面细节的重要特征。
在许多领域中,如计算机视觉、图像处理和模式识别等,纹理特征的提取对于实现自动分析和识别具有重要作用。
然而,由于图像数据量庞大且复杂多样,如何从中提取出有效的纹理特征一直是一个具有挑战性的问题。
1.2 文章结构本文将着重介绍一种基于灰度共生矩阵(Gray Level Co-occurrence Matrix, GLCM)的纹理特征提取方法。
为了更好地说明该方法的原理和优势,文章将依次介绍灰度共生矩阵概念、纹理特征提取方法、应用案例与实验结果分析,并最后对整个研究工作进行总结和展望。
1.3 目的本文旨在通过对基于灰度共生矩阵的纹理特征提取方法进行概述及解释说明,帮助读者深入了解该方法的原理和应用领域。
同时,通过应用案例与实验结果分析部分的介绍,使读者更好地理解该方法在模式识别中的应用价值。
最后,本文将对研究工作进行总结和展望,为未来的应用和发展提供参考。
2. 灰度共生矩阵概念2.1 灰度共生矩阵定义灰度共生矩阵(Gray-Level Co-occurrence Matrix,简称GLCM)是一种常用的纹理分析方法,用于描述图像中像素间的灰度值关系。
其基本思想是统计图像中不同位置像素对之间的灰度值相关特征,从而表征图像纹理的统计信息。
2.2 灰度共生矩阵计算方法灰度共生矩阵的计算主要包括以下步骤:首先,选择一个特定的灰度距离和方向,根据距离和方向确定相邻像素对;然后,统计这些相邻像素对在指定灰度级别上出现次数,并构建灰度级别之间的共生矩阵;最后,根据所得到的共生矩阵可以计算出一系列反映图像纹理特征的统计量。
2.3 灰度共生矩阵特性分析通过分析灰度共生矩阵可以得到多项有关图像纹理特征的统计参数。
常见的参数包括:(1) 对比度(Contrast):反映了不同灰度级别对之间强度变化的对比程度;(2) 同质性(Homogeneity):反映了不同灰度级别对之间相邻像素对灰度值接近程度的均匀性;(3) 能量(Energy):反映了图像中不同灰度级别出现的频率或概率,即图像的复杂程度;(4) 相关性(Correlation):反映了图像中不同灰度级别对之间线性相关关系的强弱;(5) 熵(Entropy):反映了图像中不确定性和复杂性,越大表示纹理越复杂。

基于灰度共生矩阵提取地震纹理属性的研究及影响因素分析地层由于受到构造作用,地下流体作用的影响,会产生断层和裂缝等一系列地质构造特征,这些构造特征会在三维地震资料中呈现出强弱不同的振幅,振幅在垂向地震剖面和横向地层切片上的变化就形成了一种特殊的地震纹理特征,这些纹理特征所形成的不同区域代表了不同的地质构造。
文章将利用灰度共生矩阵方法对地震资料中的纹理属性进行提取,并对其影响因素进行分析。
标签:纹理;纹理属性;灰度共生矩阵;灰度级数;提取窗口1 概述纹理作为图形图像的一项基本特征,通常指呈现在物体表面的凹凸不平的沟纹,它反映了物体表面的粗糙度,光滑度和起伏程度。
对于纹理的定义不尽相同,普遍认为它是像素灰度按一定规律变化形成的,只有把图像分割成若干区域才能对其纹理进行研究。
同时由于自然界中的任何物体表面都会产生不尽相同的纹理,即具有不同的纹理特征,利用纹理的独有性,我们可以通过不同物体所具有的不同的纹理特征来区分不同的图像,从而将其应用于数字图像处理、计算机图形学、遥感影像、生物医学,地球物理勘探等领域。
2 地震纹理属性概述地震数据中像元的反射振幅与波形在特定方向上会发生变化,地震资料中纹理的粗细直接或间接反映了不同地质构造所形成的反射振幅的强弱。
随着几十年来油田勘探开发的深入,勘探对象已经从构造油气藏转向复杂油气藏,传统地震属性对于断距较小的小断层、裂缝以及薄储层的响应不明显,而纹理属性所具有的直观性则可以为小型地质体的识别以及薄砂体储层的预测提供一定的指导依据。
3 灰度共生矩阵原理为了弄清不同的纹理集合所揭示的地质构造特征和地震相,我们需要对地震图像进行纹理分割和纹理基元的合成。
纹理属性的提取是图像分析中一项很重要也很具有难度的工作,不少中外学者对纹理属性的提取方法进行了研究,目前,最广为人们接受的是1993年Jain提出的四大类方法:统计分析方法、模型分析方法、结构分析方法、信号处理方法[1]。
提取图像纹理特征——灰度共生矩阵摘要图像的特征提取是图像的识别和分类、基于内容的图像检索、图像数据挖掘等研究内容的基础性工作,其中图像的纹理特征对描述图像内容具有重要意义,纹理特征提取己成为目前图像领域研究的热点。
文中深入研究了基于灰度共生矩阵(GLCM)的纹理特征提取方法,给出了基于Matlab的简便实现代码,分析了共生矩阵各个构造参数对构造共生矩阵的影响。
分析结果对优化灰度共生矩阵的构造、实现基于灰度共生矩阵( GLCM)的特定图像的纹理特征提取等都具有重要参考意义。
本文分析了图像纹理的特征提取—灰度共生矩阵,是物体表而最本质的属性。
纹理特征提取是作为纹理分析的首要任务,纹理提出了用灰度共生矩阵的方法提取纹理特征,通过MA丁LAB仿真实现,结果由灰度共生矩阵产生的四个纹理特征能具有较好的鉴别能力。
关键词: 特征提取;灰度共生矩阵;纹理特征;Matlab目录1 设计目的 (1)2相关知识 (1)2.1 MATLAB简介 (1)2.2 MATLAB应用 (1)2.3 MATLAB特点 (2)3 设计方案 (3)3.1 二阶距(能量) (3)3.2 惯性矩 (4)3.3 相关 (4)3.4 熵 (4)4 程序设计 (4)5 仿真结果与分析 (10)5.1 仿真图 (10)5.2 结果分析 (17)6结论 (18)参考文献 (19)提取图像纹理特征——灰度共生矩阵1 设计目的由于纹理是由灰度分布在空间位置上反复出现而形成的,因而在图像空间中相隔某距离的两象素之间会存在一定的灰度关系,即图像中灰度的空间相关特性。
灰度共生矩阵就是一种通过研究灰度的空间相关特性来描述纹理的常用方法。
直觉上来说,如果图像的是由具有相似灰度值的像素块构成,则灰度共生矩阵的对角元素会有比较大的值;如果图像像素灰度值在局部有变化,那么偏离对角线的元素会有比较大的值。
灰度直方图是对图像上单个象素具有某个灰度进行统计的结果,而灰度共生矩阵是对图像上保持某距离的两象素分别具有某灰度的状况进行统计得到的[5]。
纹理特征分析的灰度共⽣矩阵(GLCM)纹理分析是对图像灰度(浓淡)空间分布模式的提取和分析。
纹理分析在遥感图像、X射线照⽚、细胞图像判读和处理⽅⾯有⼴泛的应⽤。
关于纹理,还没有⼀个统⼀的数学模型。
它起源于表征纺织品表⾯性质的纹理概念,可以⽤来描述任何物质组成成分的排列情况,例如医学上X 射线照⽚中的肺纹理、⾎管纹理、航天(或航空)地形照⽚中的岩性纹理等。
图像处理中的视觉纹理通常理解为某种基本模式(⾊调基元)的重复排列。
因此描述⼀种纹理包括确定组成纹理的⾊调基元和确定⾊调基元间的相互关系。
纹理是⼀种区域特性,因此与区域的⼤⼩和形状有关。
两种纹理模式之间的边界,可以通过观察纹理度量是否发⽣显著改变来确定。
纹理是物体结构的反映,分析纹理可以得到图像中物体的重要信息,是、和分类识别的重要⼿段。
对于空间域图像或变换域图像(见),可以⽤统计和结构两种⽅法进⾏纹理分析。
统计纹理分析寻找刻划纹理的数字特征,⽤这些特征或同时结合其他⾮纹理特征对图像中的区域(⽽不是单个像素)进⾏分类。
图像局部区域的⾃相关函数、灰度共⽣矩阵、灰度游程以及灰度分布的各种统计量,是常⽤的数字纹理特征。
如灰度共⽣矩阵⽤灰度的空间分布表征纹理。
由于粗纹理的灰度分布随距离的变化⽐细纹理缓慢得多,因此⼆者有完全不同的灰度共⽣矩阵。
结构纹理分析研究组成纹理的基元和它们的排列规则。
基元可以是⼀个像素的灰度、也可以是具有特定性质的连通的像素集合。
基元的排列规则常⽤来描述。
英⽂名称 Texture Analysis;学术解释 指通过⼀定的图像处理技术提取出纹理特征参数,从⽽获得纹理的定量或定性描述的处理过程.纹理分析⽅法按其性质⽽⾔,可分为两⼤类:统计分析⽅法和结构分析⽅法学术定义 纹理是⼀种普遍存在的视觉现象,⽬前对于纹理的精确定义还未形成统⼀认识,多根据应⽤需要做出不同定义. 定义1 按⼀定规则对元素(elements)或基元(primitives)进⾏排列所形成的重复模式. 定义2 如果图像函数的⼀组局部属性是恒定的,或者是缓变的,或者是近似周期性的,则图象中的对应区域具有恒定的纹理.作⽤分析 对这种表⾯纹理的研究称为纹理分析.它在计算机视觉领域有着重要的应⽤. 在机械⼯程中对机械零件加⼯表⾯的这种凹凸不平性开展研究同样具有重要的实践意义。
基于灰度共生矩阵的图像纹理特征提取算法研究图像纹理特征提取技术是图像处理领域中的一个重要分支,其有助于提高图像识别、分类等任务的准确性。
基于灰度共生矩阵的图像纹理特征提取算法则是其中一种重要方法,本文将围绕该技术展开探讨。
一、灰度共生矩阵概述灰度共生矩阵(Gray-Level Co-Occurrence Matrix,GLCM)是一个将像素间灰度差分布统计出来的矩阵,用于表征图像的纹理、对比度等特征。
在灰度共生矩阵中,每个元素G(i,j)表示距离为d、角度为θ时,灰度级i和灰度级j在图像中出现的概率,即GLCM(i,j)。
灰度共生矩阵中,角度θ用于控制图像锐利度。
通常情况下,我们会选择0、45、90、135度四个角度进行分析。
而距离d决定了一组像素中含有几个像素。
在进行矩阵计算时,需要选择一个合适的距离和角度值,以便提取出描述图像特征的重要信息。
二、灰度共生矩阵的计算灰度共生矩阵的计算过程,可简单归纳为以下几步:1. 将原始图像转为灰度图像;2. 根据所选的距离和角度,将灰度图像分为若干个方向的块;3. 对于每个块,计算该块内像素的灰度值及其空间关系。
在空间相同的情况下,统计不同灰度值出现的次数;4. 统计出每个灰度对出现的概率,构建灰度共生矩阵。
三、基于灰度共生矩阵的图像纹理特征提取算法基于灰度共生矩阵的图像纹理特征提取算法,主要是通过对灰度共生矩阵的处理,实现对图像纹理特征的提取。
常见的图像纹理特征包括熵、能量、对比度、均值、方差等,这些特征能够对不同的物体或背景进行区分和分类。
1. 熵熵(Entropy)是用于度量信源不确定性的一项指标。
在基于灰度共生矩阵的图像纹理特征中,熵是用于描述图像纹理复杂度的重要参数之一。
在计算熵时,根据灰度共生矩阵的式子,先统计每个灰度级出现的概率pi,再将pi带入以下式子进行计算:H=-Σ(pi*log2(pi))2. 能量能量(Energy)是描述图像统计规律性的一个参数。
基于灰度共生矩阵的图像纹理分析摘要图像纹理分析作为数字图像处理的重要内容之一,可以用于实现图像分类、目标检测和识别等多种应用。
灰度共生矩阵是一种最常用的图像纹理特征表达方法,通过统计灰度级领域像素之间的关系,可以提取出图像中各种纹理特征。
本文首先介绍了灰度共生矩阵的概念、计算方法和常用特征参数,然后通过实验结果分析表明,灰度共生矩阵可以有效地捕捉到图像中的纹理特征,并且具有很好的分类和识别能力。
最后结合具体应用案例,对灰度共生矩阵的优缺点以及未来发展方向进行了探讨。
关键词:灰度共生矩阵、图像纹理分析、特征提取、分类和识别AbstractTexture analysis of images is an important component of digital image processing, and can be used for various applications such as image classification, object detection and recognition. Gray-level co-occurrence matrix is the most commonly used method to describe texture features of an image by calculating the relationship between neighboring pixels in the gray-level domain. This paper firstly introduces the concept, calculation method, and commonly used feature parameters of gray-level co-occurrence matrix. Then, experimental results show that this method can effectively capture the texture features of an image and has good classification and recognition ability. Finally, combined with specific application cases, we discuss the advantages and disadvantages of gray-level co-occurrence matrix and its future development directions.Keywords: gray-level co-occurrence matrix, image texture analysis, feature extraction, classification and recognition一、引言图像纹理分析是数字图像处理领域中的一个重要研究方向,其应用范围广泛,例如纹理分类、纹理识别和目标检测等领域。