中考数学压轴题专题十动态几何问题

中考数学专题复习之十：动态几何型题
动态几何问题是近年来中考数学试题的热点题型之一，常以压轴题型出现。

这类问题主要是集中代数、几何、三角、函数知识于一体，综合性较强。

常用到的解题工具有方程的有关理论，三角函数的知识和几何的有关定理。

【范例讲析】
例：如图，长方形ABCD 中，AD=8cm,CD=4cm.
⑴假设点P 是边AD 上的一个动点,当P 在什么位置时PA=PC?
⑵在⑴中,当点P 在点P ＇时，有C P A P ''=，Q 是AB 边上的一个动点,假设4
15AQ =时, QP' 与C P '垂直吗？为什么？
D C
A
【闯关夺冠】：
如图，平面直角坐标系中，四边形OABC 为矩形，点A B ，的坐标分别为(40)43()，，，，动点M N ，分别从O B ，同时出发．以每秒1个的速度运动．其中，点M 沿OA 向终点A 运动，点N 沿BC 向终点C 运动．过点M 作MP OA ⊥，交AC 于P ，连结NP ，动点运动了x 秒．
〔1〕P 点的坐标为〔 ， 〕〔用含x 的代数式表示〕；
〔2〕试求NPC △面积S 的表达式，并求出面积S 的最大值及相应的x 值；
〔3〕当x 为何值时，NPC △是一个等腰三角形？简要说明理由．
y。

动态几何证明及实验题所谓动态几何是指题设图形中存在一个或多个动点，它们在线段、射线或弧线上运动的一类开放性题目．解决这类问题的关键是动中求静，灵活运用有关数学知识解决问题．此类题目注重对几何图形运动变化能力的考查．动态几何问题是近几年各地试题中常见的压轴试题，它能考查学生的多种能力，有较强的选拔功能。

解这类题目要“以静制动”，即把动态问题，变为静态问题来解。

解动态几何题一般方法是针对这些点在运动变化的过程中相伴随着的数量关系（如等量关系、变量关系）、图形位置关系（如图形的特殊状态、图形间的特殊关系）等进行研究考察．抓住变化中的“不变量”，以不变应万变．实验操作【要点导航】通过实验操作——观察猜想——科学论证，使我们体验和学到了发现、获得知识的过程和方法. 实验操作探索——理解题意、实验操作是基本保证，观察猜想、探索结论是关键，论证猜想的结论是落实.【典例精析】例1 取一张矩形纸片进行折叠，具体操作过程如下：第一步：先把矩形ABCD 对折，折痕为MN ，如图1；第二步：再把B 点叠在折痕线MN 上，折痕为AE ，点B 在MN 上的对应点为B '，得R t △AB 'E ，如图2；第三步：沿EB '线折叠得折痕EF ，使A 点落在EC 的延长线上，如图3．利用展开图4探究： （1）△AEF 是什么三角形？证明你的结论；（2）对于任一矩形，按照上述方法能否折出这种三角形？请说明你的理由．【思路分析】1．图形翻折后能重叠部分的图形全等，所以∠BEA =∠AEB '=∠FEC ，它们都是60°角，所以△AEF 是等边三角形． 2．由操作可知AF >AD 时，不能完整折出这种三角形．当图3中的点F 、D 重合时，便可求得矩形的长与宽的比例为2︰3．解（1）△AEF 是等边三角形．由折叠过程可得：60BEA AEF FEC ∠=∠=∠=︒．因为BC ∥AD ，所以60AFE FEC ∠=∠=︒．所以△AEF 是等边三角形．（2）不一定．当矩形的长恰好等于等边△AEF 的边AF 时，即矩形的宽∶长＝AB ∶AF ＝2:3时正好能折出．如果设矩形的长为A ，宽为B ，可知当a b 23≤时，按此种方法一定能折叠出等边三角形；当图1 图2图3图4a b a ＜＜23时，按此法无法折出完整的等边三角形． 〖方法点睛〗要从操作实验题中抽象出数学模型来，并借助图形运动的基本性质求解．例2 已知：在△ABC 中，∠BAC =90°，M 为BC 中点．操作：将三角板的90°角的顶点与点M 重合，并绕着点M 旋转，角的两边分别与边AB 、AC 相交于点E 、F ．（1）探究1：线段BE 、EF 、FC 是否能构成三角形？如果可以构成三角形，那么是什么形状的三角形？请证明你的猜想．（2）探究2：若改变为：“角的两边分别与边AB 、直线AC 相交于点E 、F ．”其它条件都不变的情况下，那么结论是否还存在？请画出对应的图形并请证明你的猜想． 〖思路分析〗1．由点M 是BC 中点，所以构造绕点M 旋转180°重合的全等三角形，将线段BE 、EF 、FC 移到同一个三角形中．2．当角的两边分别与边AB 、直线AC 相交于点E 、F 时，构造和证明的方法不变．证明（1）线段BE 、EF 、FC 可以构成直角三角形．如图1，延长EM 到G ，使得EM =M G ，联结GC 、FG ．因为M 为BC 中点，所以BM =CM ，又因为∠EMB =∠GMC ，EM =M G ，所以△EMB ≌△GMC ，所以BE =GC ，EM =MG ，∠B =∠MCG ．因为FM 垂直平分EG ，所以FE =FG ．又因为∠BAC =90°，所以∠B +∠ACB =90°，所以∠MCG +∠ACB FCG =90°，所以222FG FC GC =+，所以22FC BE =+（2）如图2，当点F 在CA 的延长线上时，延长EM 到G ，联结GC 、FG ．因为M 为BC 中点，所以BM =CM ，又因为∠EM =EG ，所以△EMB ≌△GMC ，所以BE =GC ，EM =MG ，∠B 为FM 垂直平分EG ，所以FE =FG ．又因为∠BAC =90°B +∠ACB =90°，所以∠MCG +∠ACB =90°，即∠FCG =90所以222FG FC GC =+，所以222EF FC BE =+．如图3，当点F 在AC 的延长线上时，同理可证222EF FC BE =+．M〖方法点睛〗线段之间常见的关系是和差关系或者满足勾股定理．若能将所要求线段移动到同一条直线上，则线段之间是和差关系的可能性较大，若能将所要求线段移动后能构成三角形，则线段之间满足勾股定理的可能性较大．【星级训练】第 天 ，年 月 日1. ★★★如图，在正方形ABCD 中，点E 在边AB 上（点E 与点A 、B 不重合），过点E 作FG ⊥DE ，FG 与边BC 相交于点F ，与边DA 的延长线相交于点G ．（1）操作：由几个不同的位置，分别测量BF 、AG 、AE 的长，从中你能发现BF 、AG 、AE 的数量之间具有怎样的关系？并证明你所得到的结论；（2）连结DF ，如果正方形的边长为2，设AE=x ，△DFG 的面积为y ，求y 与x 之间的函数解析式，并写出函数的定义域；（3）如果正方形的边长为2，FG 的长为25，求点C 到直线DE 的距离．2. ★★★操作：将一把三角尺放在边长为1的正方形ABCD 上，并使它的直角顶点P 在对角线AC 上滑动，直角的一边始终经过点B ，另一边与射线DC 相交于点Q ．探究：设A 、P 两点间的距离为x ．（1）当点Q 在边CD 上时，线段PQ 与线段PB 之间有怎样的大小关系？试证明你观察得到结论；（2）当点Q 在边CD 上时，设四边形PBCQ 的面积为y ，求y 与x 之间的函数解析式，并写出函数的定义域；（3）当点P 在线段AC 上滑动时，△PCQ 是否可能成为等腰三角形？如果可能，指出所有能使△PCQ 成为等腰三角形的点Q 的位置，并求出相应的x 的值；如果不可能，试说明理由．（图5、图6、图7的形状大小相同，图5供操作、实验用，图6和图7备用）GFD ACBD ACB供试验操作用DCB图5DC B图6DCB图73. ★★★在△ABC 中，AB =AC ，CG ⊥BA 交BA 的延长线于点G ．一等腰直角三角尺按如图1所示的位置摆放，该三角尺的直角顶点为F ，一条直角边与AC 边在一条直线上，另一条直角边恰好经过点B ．（1）在图1中请你通过观察、测量BF 与CG 的长度，猜想并写出BF 与CG 满足的数量关系，然后证明你的猜想；（2）当三角尺沿AC 方向平移到图2所示的位置时，一条直角边仍与AC 边在同一直线上，另一条直角边交BC 边于点D ，过点D 作DE ⊥BA 于点E ．此时请你通过观察、测量DE 、DF 与CG 的长度，猜想并写出DE ＋DF 与CG 之间满足的数量关系，然后证明你的猜想；（3）当三角尺在（2）的基础上沿AC 方向继续平移到图3所示的位置（点F 在线段AC 上，且点F 与点C 不重合）时，（2）中的猜想是否仍然成立？（不用说明理由），2B (5,3) 、C (-2,5) 关于直线l 的对称点B '、B ' 、 C ' ；归纳与发现：（2）结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P (a ,b )关于第一、三象限的角平分线l 的对称点P '的坐标为 （不必证明）； 运用与拓广：（3）已知两点D (1,-3)、E (-1,-4)，试在直线l 上确定一点Q ，使点Q 到D 、E 两点的距离之和最小，并求出Q 点坐标．探索性问题探索性问题是指命题中缺少一定的条件或无明确的结论，需要经过推断，补充并加以证明的题型．探索性问题一般有三种类型：（1）条件探索型问题；（2）结论探索型问题；（3）探索存在型问题．条件探索型问题是指所给问题中结论明确，需要完备条件的题目；结论探索型问题是指题目中结论不确定，不唯一，或题目结论需要类比，引申推广，或题目给出特例，要通过归纳总结出一般结论；探索存在型问题是指在一定的前提下，需探索发现某种数学关系是否存在的题目．条件探索【要点导航】图1“探索”是人类认识客观世界过程中最生动、最活跃的思维活动，探索性问题存在于一切学科领域之中，数学中的“条件探索”题型，是指命题中缺少一定的题设，需经过推断、补充并加以证明的命题，因而必须利用题设大胆猜想、分析、比较、归纳、推理，由结论去探索未给予的条件。

2024年九年级数学中考复习——反比例函数-动态几何问题1．如图，在矩形ABCD 中，已知点A （2，1），且AB ＝4，AD ＝3，把矩形ABCD 的内部及边上，横、纵坐标均为整数的点称为靓点，反比例函数y＝（x ＞0）的图象为曲线L ．（1）若曲线L 过AB 的中点．①求k 的值．②求该曲线L 下方（包括边界）的靓点坐标．（2）若分布在曲线L 上方与下方的靓点个数相同，求k 的取值范围．2．如图，在平面直角坐标系中，一次函数 与反比例函数 相交于点 ，与 轴相交于点 ，点 的横坐标为-2.（1）求 的值；（2）直接写出当 且 时， 的取值范围；（3）设点 是直线AB 上的一点，过点 作 轴，交反比例函数 的图象于点 .若以A ，O ，M ，N 为顶点的四边形为平行四边形，求点 的坐标.k x12y x =-+2(0)k y x x=<B x A B k 0x <12y y <x M M //MN x 2(0)k y x x=<N M3．如图，在平面直角坐标系中，OA ⊥OB ，AB ⊥x 轴于点C ，点A （，1）在反比例函数y ＝ 的图象上．（1）求反比例函数y ＝ 的表达式； （2）在x 轴上是否存在一点P ，使得S △AOP ＝S △AOB ，若存在，求所有符合条件点P 的坐标；若不存在，简述你的理由．4．如图，点 ， 在 轴上，以 为边的正方形 在 轴上方，点 的坐标为 ，反比例函数 的图象经过 的中点 ， 是 上的一个动点，将 沿 所在直线折叠得到 .（1）求反比例函数 的表达式； （2）若点 落在 轴上，求线段 的长及点 的坐标.k x k x12A B x AB ABCD x C (14)，(0)k y k x=≠CD E F AD DEF EF GEF (0)k y k x=≠G y OG F5．如图，已知反比例函数y＝（x ＞0）的图象经过点A （4，2），过A 作AC ⊥y 轴于点C ．点B 为反比例函数图象上的一动点，过点B 作BD ⊥x 轴于点D ，连接AD ．直线BC 与x 轴的负半轴交于点E ．（1）求k 的值；（2）连接CD ，求△ACD 的面积；（3）若BD ＝3OC ，求四边形ACED 的面积．6．已知：如图1，点是反比例函数图象上的一点．（1）求的值和直线的解析式；（2）如图2，将反比例函数的图象绕原点逆时针旋转后，与轴交于点，求线段的长度；（3）如图3，将直线绕原点逆时针旋转，与反比例函数的图象交于点，求点的坐标．k x(4)A n ，8(0)y x x=>n OA 8(0)y x x =>O 45︒y M OM OA O 45︒8(0)y x x=>B B7．已知：反比例函数的图像过点A （ ， ），B （ ， ）且 （1）求m 的值；（2）点C 在x 轴上，且 ，求C 点的坐标；（3）点Q 是第一象限内反比例函数图象上的动点，且在直线AB 的右侧，设直线QA ，QB 与y 轴分别交于点E 、D ，试判断DE 的长度是否变化，若变化请说明理由，若不变，请求出长度.8．规定：在平面直角坐标系中，横坐标与纵坐标均为整数的点，叫做整点，点，在反比例函数的图象上；（1）m= ；（2）已知，过点、D 点作直线交双曲线于E 点，连接OB ，若阴影区域（不包括边界）内有4个整点，求b 的取值范围．m y x =1x 121m --2x 45m-120x x +=16ABC s ∆=()22A ，()1B m ，()0k y x x=>0b >()40C b -，()0b ，()0k y x x=>9．已知，矩形OCBA 在平面直角坐标系中的位置如图所示，点C 在x 轴的正半轴上，点A 在y 轴的正半轴上，已知点B 坐标为（3，6），反比例函数的图象经过AB 的中点D ，且与BC 交于点E ，顺次连接O ，D ，E ．（1）求m 的值及点E 的坐标；（2）点M 为y 轴正半轴上一点，若△MBO 的面积等于△ODE 的面积，求点M 的坐标；（3）平面直角坐标系中是否存在一点N ，使得O ，D ，E ，N 四点顺次连接构成平行四边形？若存在，请直接写出N 的坐标；若不存在，请说明理由．10．如图，点P 为函数与函数图象的交点，点P 的纵坐标为4，轴，垂足为点B ．（1）求m 的值；（2）点M 是函数图象上一动点，过点M 作于点D ，若，求点M的坐标．m y x=1y x =+()0m y x x=>PB x ⊥()0m y x x =>MD BP ⊥12tan PMD ∠=11．如图，在平面直角坐标系中，直线与轴、轴分别交于点、，与双曲线交于点，直线分别与直线和双曲线交于点、．（1）求和的值；（2）当点在线段上时，如果，求的值；（3）点是轴上一点，如果四边形是菱形，求点的坐标．12．如图，等边和等边的一边都在x 轴上，双曲线经过的中点C 和的中点D ．已知等边的边长为4．（1）求k 的值；（2）求等边的边长；（3）将等边绕点A 任意旋转，得到等边，P 是的中点（如图2所示），连结，直接写出的最大值．xOy 34l y x b =+：x y A B x k H y =：922P ⎛⎫ ⎪⎝⎭，x m =H E D k b E AB ED BO =m C y BCDE C OAB AEF ()0k y k x=>OB AE OAB AEF AEF AE F '' E F ''BP BP13．如图，点A 、B 是反比例函数y ＝ 的图象上的两个动点，过A 、B 分别作AC ⊥x 轴、BD ⊥x 轴，分别交反比例函数y ＝－ 的图象于点C 、D ，四边形ACBD 是平行四边形. （1）若点A 的横坐标为－4.①直接写出线段AC 的长度；②求出点B 的坐标；（2）当点A 、B 不断运动时，下列关于□ACBD 的结论：①□ACBD 可能是矩形；②□ACBD 可能是菱形；③□ACBD 可能是正方形；④□ACBD 的周长始终不变；⑤□ACBD 的面积始终不变.其中所有正确结论的序号是 .8x2x14．在平面直角坐标系 中，正比例函数 与反比例函数 的图象相交于点 与点Q ． （1）求点Q 的坐标；（2）若存在点 ，使得 ，求c 的值； （3）过点 平行于x 轴的直线，分别与第一象限内的正比例函数 、反比例函数数 的图象相交于点 、点 ，当 时，请直接写出a 的取值范围．15．在平面直角坐标系中，直线y=x+2与x 轴交于点A ，与y 轴交于点B ，并与反比例函数y=（k≠0）的图象在第一象限相交于点C ，且点B 是AC 的中点xOy ()1110y k x k =≠()2220k y k x=≠(11)P ，(0)C c ，2PQC S = (0)M a ，()1110y k x k =≠()2220k y k x =≠()11A x y ，()22B x y ，1252x x +≤kx（1）如图1，求反比例函数y=（k≠0）的解析式；（2）如图2，若矩形FEHG 的顶点E 在直线AB 上，顶点F 在点C 右侧的反比例函数y=（k≠0）图象上，顶点H ，G 在x 轴上，且EF=4．①求点F 的坐标；②若点M 是反比例函数的图象第一象限上的动点，且在点F 的左侧，连结MG ，并在MG 左侧作正方形GMNP ．当顶点N 或顶点P 恰好落在直线AB 上，直接写出对应的点M 的横坐标．16．如图，动点P 在函数y （x ＞0）的图象上，过点P 分别作x 轴和y 轴的平行线，交函数y 的图象于点A 、B ，连接AB 、OA 、OB ．设点P 横坐标为a ．（1）直接写出点P 、A 、B 的坐标（用a 的代数式表示）；（2）点P 在运动的过程中，△AOB 的面积是否为定值？若是，求出此定值；若不是，请说明理由；（3）在平面内有一点Q （，1），且点Q 始终在△PAB 的内部（不包含边），求a 的取值范围．k xk x 3x =1x =-1317．如图1，一次函数y ＝kx ﹣3（k≠0）的图象与y 轴交于点B ，与反比例函数y＝（x ＞0）的图象交于点A （8，1）．（1）求出一次函数与反比例函数的解析式；（2）点C 是线段AB 上一点（不与A ，B 重合），过点C 作y 轴的平行线与该反比例函数的图象交于点D ，连接OC ，OD ，AD ，当CD 等于6时，求点C 的坐标和△ACD 的面积；（3）在（2）的前提下，将△OCD 沿射线BA 方向平移一定的距离后，得到△O'CD'，若点O 的对应点O'恰好落在该反比例函数图象上（如图2），求出点O'，D'的坐标．18．如图1所示，已知 图象上一点 轴于点 ，点 ，动点 是 轴正半轴点 上方的点，动点 在射线AP 上，过点 作AB 的垂线，交射线AP 于点 ，交直线MN 于点 ，连结AQ ，取AQ 的中点 . m x6(0)y x x=>P PA x ⊥，(0)A a ，(0)(0)B b b >，M y B N B D Q C（1）如图2，连结BP ，求 的面积；（2）当点 在线段BD 上时，若四边形BQNC 是菱形，面积为 .①求此时点Q ，P 的坐标；②此时在y 轴上找到一点E ，求使|EQ-EP|最大时的点E 的坐标.19．已知反比例函数y=的图象经过点A （6，1）．（1）求该反比例函数的表达式；（2）如图，在反比例函数y=在第一象限的图象上点A 的左侧取点C ，过点A 作x 轴的垂线交x 轴于点H ，过点C 作y 轴的垂线CE ，垂足为点E ，交直线AH 于点D ．①过点A 、点C 分别作y 轴、x 轴的垂线，两条垂线相交于点B ，求证：O 、B 、D 三点共线；②若AC=2CO ，求证：∠OCE=3∠CDO ．PAB Q k xk x20．如图，一次函数与反比例函数的图象交于点和，与y 轴交于点C ．（1） ， ；（2）过点A 作轴于点D ，点P 是反比例函数在第一象限的图象上一点，设直线与线段交于点E ，当时，求点P 的坐标．（3）点M 是坐标轴上的一个动点，点N 是平面内的任意一点，当四边形是矩形时，求出点M 的坐标．21．如图1，将函数的图象T 1向左平移4个单位得到函数的图象T 2，T 2与y 轴交于点．（1）若，求k 的值（2）如图2，B 为x 轴正半轴上一点，以AB 为边，向上作正方形ABCD ，若D 、C 恰好落在T 1上，线段BC 与T 2相交于点E①求正方形ABCD 的面积；②直接写出点E 的坐标．114y k x =+22k y x=()2A m ，()62B --，1k =2k =AD x ⊥OP AD Δ41ODE ODAC S S =四边形：：ABMN ()0k y x x =>()44k y x x =>-+()0A a ，3a =22．如图1，直线的图像与x 轴、y 轴分别交于A 、B 两点，点D 是线段AB 上一点，过D 点分别作OA 、OB 的垂线，垂足分别是C 、E ，矩形OCDE 的面积为4，且．（1）求D 点坐标；（2）将矩形OCDE 以1个单位/秒的速度向右平移，平移后记为矩形MNPQ ，记平移时间为t 秒．①如图2，当矩形MNPQ 的面积被直线AB 平分时，求t 的值；②如图3，当矩形MNPQ 的边与反比例函数的图像有两个交点，记为T 、K ，若直线TK 把矩形面积分成1：7两部分，请直接写出t 的值．23．如图1，在平面直角坐标系中，点，点，直线与反比例函数的图象在第一象限相交于点，26y x =-+CD DE >12y x=()40A -，()04B ，AB ()0k y k x=≠()6C a ，（1）求反比例函数的解析式；（2）如图2，点是反比例函数图象上一点，连接，试问在x 轴上是否存在一点D ，使的面积与的面积相等，若存在，请求点D 的坐标；若不存在，请说明理由；（3）新定义：如图3，在平面内，如果三角形的一边等于另一边的3倍，这两条边中较长的边称为“麒麟边”，两条边所夹的角称为“麒麟角”，则称该三角形为“麒麟三角形”，如图所示，在平面直角坐标系中，为“麒麟三角形”， 为“麒麟边”， 为“麒麟角”，其中A ，B 两点在反比例函数 图象上，且A 点横坐标为，点C 坐标为，当为直角三角形时，求n 的值．24．如图1，已知点A （a ，0），B （0，b ），且a 、b 满足 +（a +b +3）2＝0，平等四边形ABCD的边AD 与y 轴交于点E ，且E 为AD 中点，双曲线y ＝经过C 、D 两点． （1）a ＝ ，b ＝ ；（2）求D 点的坐标；（3）点P 在双曲线y ＝ 上，点Q 在y 轴上，若以点A 、B 、P 、Q 为顶点的四边形是平行四边形，试求满足要求的所有点Q 的坐标；（4）以线段AB 为对角线作正方形AFBH （如图3），点T 是边AF 上一动点，M 是HT 的中点，MN ⊥HT ，交AB 于N ，当T 在AF 上运动时， 的值是否发生改变？若改变，求出其变化范围；若()6E m ，()0k y k x=≠CE AE ，ACD ACE ABC AB BAC ∠n y x=1-()02，ABC k x k xMN HT不改变，请求出其值，并给出你的证明．25．在平面直角坐标系中，已知点，点.（1）若将沿轴向右平移个单位，此时点恰好落在反比例函数的图象上，求的值；（2）若绕点按逆时针方向旋转度.①当时，点恰好落在反比例函数图象上，求的值；②问点能否同时落在(1)中的反比例函数的图象上?若能，直接写出的值；若不能，请说明理由.26．如图，已知直线与双曲线交第一象限于点．（1）求点的坐标和反比例函数的解析式；（2）将点绕点逆时针旋转至点，求直线的函数解析式；（3）在（2）的条件下，若点C 是射线上的一个动点，过点作轴的平行线，交双曲线xOy ()A -()60B -，OAB x m A y =m OAB O α()0α180<<α30= B k y x=k A B ，α2y x =(0)k y k x=≠(4)A m ，A O A 90︒B OB OB C y的图像于点，交轴于点，且，求点的坐标．27．如图，一次函数的图象与反比例函数的图象交于点，与y 轴交于点B ．（1）求a ，k 的值；（2）直线CD 过点A ，与反比例函数图象交于点C ，与x 轴交于点D ，AC ＝AD ，连接CB ．①求△ABC 的面积；②点P 在反比例函数的图象上，点Q 在x 轴上，若以点A ，B ，P ，Q 为顶点的四边形是平行四边形，请求出所有符合条件的点P 坐标．28．如图1，反比例函数与一次函数的图象交于两点，已知．（1）求反比例函数和一次函数的表达式；（2）一次函数的图象与轴交于点，点（未在图中画出）是反比例函数图象上的一个动点，若，求点的坐标：(0)k y k x=≠D x E 23DCO DEO S S = ：：C 112y x =+()0k y x x =>()3A a ，k y x=y x b =+A B ，()23B ，y x b =+x C D 3OCD S = D（3）若点是坐标轴上一点，点是平面内一点，是否存在点，使得四边形是矩形？若存在，请求出所有符合条件的点的坐标；若不存在，请说明理由．29．如图，已知直线y=-2x 与双曲线y=（k<0）上交于A 、B 两点，且点A 的纵坐标为-2 （1）求k 的值；（2）若双曲线y= （k<0）上一点C 的纵坐标为 ，求△BOC 的面积；（3）若A 、B 、P 、Q 为顶点组成的四边形为正方形，直接写出过点P 的反比例函数解析式。

中考数学压轴题专题十动态几何问题试题特点用运动的观点来探究几何图形变化规律的问题称为动态几何问题，此类问题的显著特点是图形中的某个元素（如点、线段、三角形等）或整个图形按照某种规律运动，图形的各个元素在运动变化过程中互相依存、和谐统一，体现了数学中“变”与“不变”、“一般”与“特殊”的辩证思想．其主要类型有：1．点的运动（单点运动、多点运动）；2．线段（直线）的运动；3．图形的运动（三角形运动、四边形运动、圆运动等）．方式趋势动态几何题已成为中考试题的一大热点题型．在近几年各地的中考试卷中，以动点问题、平面图形的平移、翻折、旋转、剪拼问题等为代表的动态几何题频频出现在填空、选择、解答等各种题型中，总体呈现源于教材、高于教材，入口宽、难易适度、梯度分明，考查同学们对图形的直觉能力以及从变化中看到不变实质的数学洞察力．热点解析一、点的运动【题1】（2011盐城）如图1，已知一次函数y＝－x＋7与正比例函数y＝43x的图象交于点A，且与x轴交于点B．(1)求点A和点B的坐标；(2)过点A作AC⊥y轴于点C，过点B作直线l∥y轴，动点P从点O出发，以每秒1个单位长的速度，沿O－C－A的路线向点A运动；同时直线l从点B出发，以相同速度向左平移，在平移过程中，直线l交x轴于点R，交线段BA或线段AO于点Q．当点P到达点A时，点P和直线l都停止运动．在运动过程中，设动点P运动的时间为t秒．①当t为何值时，以A、P、R为顶点的三角形的面积为8?②是否存在以A、P、Q为顶点的三角形是等腰三角形？若存在，求t的值；若不存在，请说明理由．【思路】(1)联立方程y＝－x＋7和y＝43x即可求出点A的坐标，令－x＋7＝0即可得点B的坐标．(2)①只要把三角形的面积用t表示，求出即可．应注意分P在OC上运动和P在CA上运动两种情况．（D只要把有关线段用t表示，找出满足AP＝AQ，AP＝PQ，AQ＝PQ的条件时t的值即可，应注意分别讨论P在OC上运动（此时直线∠与AB相交）和P在CA上运动（此时直线∠与AO相交）时AP＝AQ，AP＝PQ，AQ＝PQ的条件．【失分点】以A、P、Q为顶点的三角形是等腰三角形有多种可能，容易考虑不周．【反思】涉及的主要知识点有：一次函数的图象和性质，解二元一次方程组，勾股定理，锐角三角函数，解一元二次方程，等腰三角形的判定．【牛刀小试】1．（2010湖北咸宁）如图6，直角梯形ABCD中，AB∥DC，∠DAB＝90°，AD＝2DC＝4，AB＝6．动点M以每秒1个单位长的速度，从点A沿线段AB向点B运动；同时点P以相同的速度，从点C沿折线C－D－A向点A运动，当点M到达点B 时，两点同时停止运动．过点M作直线∠∥AD，与线段CD的交点为E，与折线A－C －B的交点为Q．点M运动的时间为t（秒）．(1)当t＝时，求线段QM的长．(2)当0<t<2时，如果以C，P，Q为顶点的三角形为直角三角形，求t的值．(3)当t>2时，连接PQ交线段AC于点R，请探究CQRQ是否为定值．若是，试求这个定值；若不是，请说明理由．2．（2010湖南娄底）如图7，在梯形ABCD中，AB∥CD，AB＝2，DC＝10，AD＝BC＝5，点M，N分别在边AD，BC上运动，并保持MN∥AB，ME⊥DC，NF⊥DC，垂足分别为E，F．(1)求梯形ABCD的面积．(2)探究一：四边形MNFE的面积有无最大值？若有，请求出这个最大值；若无，请说明理由．(3)探究二：四边形MNFF能否为正方形？若能，请求出正方形的面积；若不能，请说明理由．3．(2010广西钦州)如图8，将OA＝6，AB＝4的矩形OABC放置在平面直角坐标系中，动点M，N以每秒1个单位的速度分别从点A，C同时出发，其中点M沿AO向终点0运动，点N沿CB向终点B运动，当两个动点运动了ts时，过点N作NP⊥BC，交OB 于点P，连接MP．(1)点B的坐标为_______；用含￡的式子表示点P的坐标为_______．(2)记△OMP的面积为S，求S与t的函数关系式(0<t<6)．并求t为何值时，S有最大值．(3)试探究：当S有最大值时，在y轴上是否存在点T，使直线MT把△ONC分割成三角形和四边形两部分，且三角形的面积是△ONC面积的13？若存在，求出点T的坐标；若不存在，请说明理由．二、线的运动【题2】（2010云南昭通）如图，已知直线l的解析式为y＝－x＋6，它与x轴，y 轴分别相交于A，B两点．平行于直线l的直线n从原点出发，沿x轴正方向以每秒1个单位长度的速度运动，运动时间为t秒，运动过程中始终保持n∥l．直线n与x轴，y轴分别相交于C，D两点．线段CD的中点为P，以P为圆心，以CD为直径在CD上方作半圆，半圆面积为S．当直线n与直线l重合时，运动结束．(1)求A，B两点的坐标．(2)求S与t的函数关系式及自变量t的取值范围．(3)直线n在运动过程中，①当t为何值时，半圆与直线l相切？②是否存在这样的T值，使得半圆面积S＝12S梯形ABCD？若存在，求出t值；若不存在，说明理由。

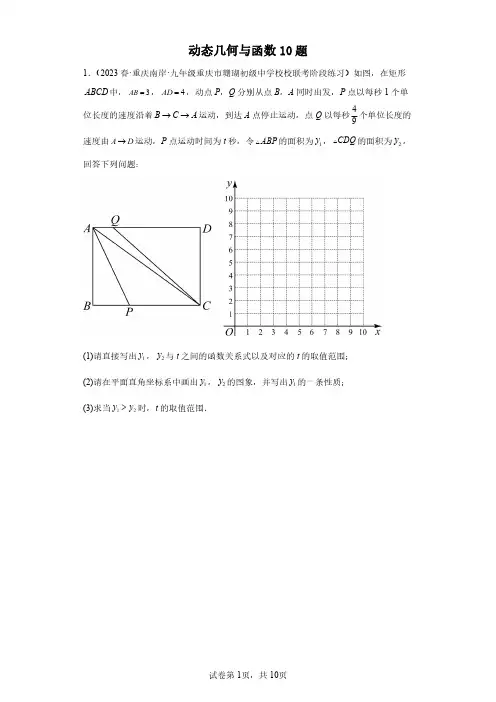
动态几何与函数10题(1)请直接写出1y ，2y 与t 之间的函数关系式以及对应的t 的取值范围；
(2)请在平面直角坐标系中画出1y ，2y 的图象，并写出1y 的一条性质；
(3)求当12y y >时，t 的取值范围．
(1)求出12,y y与x的函数关系式，并注明
(2)先补全表格中1y的值，再画出
x123456
y12632
1
(3)在直角坐标系内直接画出2y的函数图像，结合1y和2y的函数图像，x的取值范围．(结果取精确值)
(1)请求出1y 和2y 关于x 的函数解析式，并说明x 的取值范围；
(2)在图2中画出1y 关于x 的函数图象，并写出一条这一函数的性质：(3)若12103
y y -≥，请结合函数图像直接写出x 的取值范围（近似值保留一位小数，误差不超过0.2）
4．
（2023春·重庆江津·九年级校联考期中）如图，在矩形ABCD 中，3AB =，4BC =，点P 从点A 出发，以每秒2个单位的速度沿折线A B C D →→→运动，当它到达D 点时停止运动；同时，点Q 从点A 出发，以每秒1个单位的速度沿射线AD 运动，过Q 点做直线l 平行于AB ，点M 为直线l 上的一点，满足AMQ △的面积为2，设点P 点Q 的运动时间为t （0t >），ADP △的面积为1y ，QM 的长度为2y ．
(1)分别求出1y ，2y 与t 的函数关系，并注明t 的取值范围；
(2)在坐标系中画出1y ，2y 的函数图象；
(3)结合函数图象，请直接写出当12y y <时t 的取值范围．。

最新中考数学总复习几何动态压轴题专题分类讲练考情分析几何动态综合一般以特殊平行四边形或三角形为背景，考查线段长度、角度、点的坐标、菱形或平行四边形的判定、直角或等腰三角形的存在性、与面积有关的函数关系式及最值，涉及解直角三角形、三角形的面积公式、勾股定理、二次函数的性质及最值等．题目一般有3～4问，第一问较为简单，熟练运用基础知识即可；后几问综合性较强，经常用到分类讨论、数形结合思想．类型点动型综合题例1　如图1，正方形ABCD中，点A，B的坐标分别为(0,10)，(8,4)，点C在第一象限．动点P在正方形ABCD的边上，从点A出发沿A→B→C→D→A以每秒1个单位长度的速度匀速运动，同时动点Q以相同的速度从(1,0)出发在x轴正半轴上运动，当点P第一次回到A点时，两点同时停止运动，设运动的时间为t秒．(1)求正方形边长及顶点C的坐标；(2)当点P在AB上时，设△O PQ的面积为S，求S与t的函数关系式，并写出当t为何值时S最大；(3)如果点P，Q保持原速度不变，当点P沿A→B→C→D匀速运动时，O P与PQ能否相等？若能，写出所有符合条件的t的值；若不能，请说明理由．图1思路点拨　解决几何动态问题的关键是“化动为静”，找出几何图形中的自变量与时间t或线段长x的关系，并用函数关系式表示出来，再结合已知条件和图象性质求解．训练　1.如图2，Rt△ABC中，∠C＝90°，BC＝8 cm，AC＝6 cm.点P从B出发沿BA 向A运动，速度为每秒1 cm，点E是点B以P为对称中心的对称点，点P运动的同时，点Q从A出发沿AC向C运动，速度为每秒2 cm，当点Q到达顶点C时，P，Q同时停止运动，设P，Q两点运动时间为t秒．图2(1)当t为何值时，PQ∥BC?(2)设四边形PQCB的面积为y，求y关于t的函数关系式；(3)当t为何值时，△AEQ为等腰三角形？2. 正方形ABCD的边长为1，点O是BC边上的一个动点(与B，C不重合)，以O为顶点在BC所在直线的上方作∠MON＝90°.(1)当OM经过点A时，①请直接填空：ON__________(可能，不可能)过D点；(图3仅供分析)②如图4，在ON上截取O E＝O A，过E点作EF垂直于直线BC，垂足为点F，EH⊥CD于H，求证：四边形EFCH为正方形．(2)当OM不过点A时，设OM交边AB于G，且O G＝1.在ON上存在点P，过P点作PK垂直于直线BC，垂足为点K，使得S△PK O＝4S△O BG，连接GP，求四边形PKBG的最大面积．图3 图4 备用图类型线动型综合题例2　如图5，在△ABC中，AB＝AC＝10 cm，BD⊥AC于点D，BD＝8 cm.点M从点A出发，在AC上以每秒2 cm的速度匀速向点C运动，同时直线PQ从点B出发，沿BA 的方向以每秒1 cm的速度匀速运动，运动过程中始终保持PQ∥AC，直线PQ交AB于点P、交BC于点Q、交BD于点F.连接P M，设运动时间为t秒(0＜t≤5)．图5(1)当t为何值时，四边形PQC M是平行四边形？(2)设四边形PQC M的面积为y cm2，求y与t之间的函数关系式；(3)连接PC，是否存在某一时刻t，使点M在线段PC的垂直平分线上？若存在，求出此时t的值；若不存在，说明理由．训练　3.如图6，在△ABC中，∠C＝90°，∠A＝60°，AC＝2 cm.长为1 cm的线段MN 在△ABC的边AB上沿AB方向以1 cm/s的速度向点B运动(运动前点M与点A重合)．过M，N分别作AB的垂线交直角边于P，Q两点，线段MN运动的时间为t s.图6(1)若△A M P的面积为y，写出y与t的函数关系式；(写出自变量t的取值范围)(2)线段MN运动过程中，四边形MN QP有可能成为矩形吗？若有可能，求出此时t的值；若不可能，说明理由；(3)t为何值时，以C，P，Q为顶点的三角形与△ABC相似？4.如图7，在△ABC中，AB＝AC，∠BAC＝90°，AD⊥BC于点D，BC＝20 cm，AD＝10 cm.点P从点B出发，在线段BC上以每秒2 cm的速度向点C匀速运动，与此同时，垂直于AD的直线l从点A沿AD出发，以每秒1 cm的速度沿AD方向匀速平移，分别交AB，AC，AD于M，N，E.当点P到达点C时，点P与直线l同时停止运动，设运动时间为t 秒(t ＞0)．(1)在运动过程中(点P 不与B ，C 重合)，连接P N ，求证：四边形M BP N 为平行四边形；(2)如图8，以MN 为边向下作正方形M FG N ，FG 交AD 于点H ，连接PF ，PG ，当0＜t ＜时，求△PFG 的面积最大值；103(3)在整个运动过程中，观察图8,9，是否存在某一时刻t ，使△PFG 为等腰三角形？若存在，直接写出t 的值；若不存在，请说明理由． 图7 图8 图9类型形动型综合题例3　已知：把Rt △ABC 和Rt △DEF 按如图10摆放(点C 与点E 重合)，点B ，C (E )，F 在同一条直线上．∠ACB ＝∠EDF ＝90°，∠DEF ＝45°，AC ＝8 cm ，BC ＝6 cm ，EF ＝9 cm.如图11，△DEF 从图10的位置出发，以1 cm/s 的速度沿CB 向△ABC 匀速移动，在△DEF 移动的同时，点P 从△ABC 的顶点B 出发，以2 cm/s 的速度沿BA 向点A 匀速移动．当△DEF 的顶点D 移动到AC 边上时，△DEF 停止移动，点P 也随之停止移动．DE 与AC 相交于点Q ，连接PQ ，设移动时间为t (s)(0＜t ＜4.5)．解答下列问题：(1)当t 为何值时，点A 在线段PQ 的垂直平分线上？(2)连接PE ，设四边形APEC 的面积为y (cm 2)，求y 与t 之间的函数关系式；是否存在某一时刻t ，使面积y 最小？若存在，求出y 的最小值；若不存在，说明理由．(3)是否存在某一时刻t ，使P ，Q ，F 三点在同一条直线上？若存在，求出此时t 的值；若不存在，说明理由．图10 图11　训练　5.如图12所示，在▱ABCD中，AB＝3 cm，BC＝5 cm，AC⊥AB，△ACD沿射线AC的方向匀速平移得到△P NM，速度为1 cm/s，同时，点Q从点C出发，沿射线CB 方向匀速运动，速度为1 cm/s，当△P NM停止平移时，点Q也停止运动，如图13所示，设运动时间为t(s)(0＜t＜4)．(1)当t＝__________时，PQ∥MN；(2)设△Q M C的面积为y(cm2)，求y与t之间的函数关系式；(3)是否存在某一时刻t，使得PQ＝Q M，若存在，求出t的值；若不存在，请说明理由．图12 图136.已知矩形O ABC的顶点O(0,0)，A(4,0)，B(4，－3)．动点P从O出发，以每秒1个单位的速度，沿射线O B方向运动．设运动时间为t秒．(1)求P点的坐标；(用含t的代数式表示)(2)如图14，以P为一顶点的正方形PQ MN的边长为2，且边PQ⊥y轴．设正方形PQ MN与矩形O ABC的公共部分面积为S，当正方形PQ MN与矩形O ABC无公共部分时，运动停止．①当t＜4时，求S与t之间的函数关系式；②当t＞4时，设直线M Q，MN分别交矩形O ABC的边BC，AB于D，E，是否存在这样的t，使得△PDE为直角三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．图14参考答案例1　解：(1)如图1，过点B 作BF ⊥y 轴于F ，BE ⊥x 轴于E ，过点C 作CG ⊥x 轴于点G ，与FB 的延长线交于点H ，图1∵A (0,10)，∴OA ＝10.∵B (8,4)，∴BF ＝8，OF ＝4.∴AF ＝10－4＝6.∴AB ＝＝10.AF 2＋BF 2∵∠ABC ＝90°，∴∠ABF ＋∠CBH ＝90°.∵∠BAF ＋∠ABF ＝90°，∴∠BAF ＝∠CBH .又AB ＝BC ，∠AFB ＝∠BHC ＝90°，∴△ABF ≌△BCH .∴BH ＝AF ＝6，CH ＝BF ＝8.∴OG ＝FH ＝8＋6＝14，CG ＝8＋4＝12.∴点C 的坐标为(14,12)．(2)如图1，过点P 作PM ⊥y 轴于点M ，PN ⊥x 轴于点N ，∴PM ∥BF .则△APM ∽△ABF ，∴＝＝.AP AB AM AF PM BF∴＝＝.∴AM ＝t ，PM ＝t .t 10AM 6PM 83545∴PN ＝OM ＝10－t ，ON ＝PM ＝t .3545∴S ＝PN ·OQ ＝×(1＋t )＝－t 2＋t ＋5＝－2＋(0≤t ≤10)．1212(10－35t )3104710310(t －476)8 407360∴当t ＝时，S 取到最大值．476(3)OP 与PQ 可以相等，根据等腰三角形的相关性质可知，相等时P 点的横坐标等于Q 点的横坐标的一半．①当P 在AB 上时，如图1，t ＝(t ＋1)，t ＝；451253②当P 在BC 上时，如图2，图2则PB ＝t －10，sin ∠ABF ＝sin ∠BPM ＝＝，AF AB BM PB∴＝.∴BM ＝(t －10)．610BM t －1035∴ON ＝BF ＋BM ＝8＋(t －10)＝(t ＋1)．解得t ＝－15(舍去)；3512③当P 在CD 上时，如图3，过点C 作CR ⊥PN 于R ，则PC ＝t －20，图3cos ∠PCR ＝cos ∠BCH ＝＝，CH BC CR PC∴＝.810CR t －20∴CR ＝NG ＝(t －20)．45∴ON ＝OG －NG ＝14－(t －20)＝(t ＋1)，4512解得t ＝.29513综上所述，当t ＝或时，OP 与PQ 相等．2951353训练　1.解：(1)∵∠C ＝90°，BC ＝8 cm ，AC ＝6 cm ，∴AB ＝10 cm.∵BP ＝t ，AQ ＝2t ，∴AP ＝AB －BP ＝10－t .∵PQ ∥BC ，∴＝.AP AB AQ AC∴＝，解得t ＝.10－t 102t 63013即当t ＝时，PQ ∥BC .3013(2)∵S 四边形PQCB ＝S △ACB －S △APQ ＝AC ·BC －AP ·AQ ·sin A ，1212∴y ＝×6×8－×(10－t )·2t ·＝24－t (10－t )＝t 2－8t ＋24.12128104545即y 关于t 的函数关系式为y ＝t 2－8t ＋24.45(3)△AEQ 为等腰三角形分三种情况讨论：①如果AE ＝AQ ，那么10－2t ＝2t ，解得t ＝；52②如果AE ＝QE ，如图4，过点E 作EF ⊥AQ 于F，图4则F 为AQ 的中点，∴AF ＝AQ ＝t .12又AC ⊥BC ，∴EF ∥BC .∴sin ∠AEF ＝sin B ＝＝＝.AF AE AC AB 610即＝，解得t ＝；t 10－2t 6103011③如果AQ ＝QE ，可作QM ⊥AE 于M ，同理可得cos A ＝＝，即＝，解得t ＝.AM AQ AC AB 10－2t 22t 6102511故当t 为秒或秒或秒时，△AEQ 为等腰三角形．52301125112．(1)①解：不可能．【提示】若ON 过点D ，则OA ＞AB ，OD ＞CD ，∴OA 2＞AD 2，OD 2＞AD 2.∴OA 2＋OD 2＞2AD 2≠AD 2.∴∠AOD ≠90°，这与∠MON ＝90°矛盾，∴ON 不可能过D 点．②证明：∵EH ⊥CD ，EF ⊥BC ，∴∠EHC ＝∠EFC ＝90°，且∠HCF ＝90°.∴四边形EFCH 为矩形．∵∠MON ＝90°，∴∠EOF ＝90°－∠AOB .在正方形ABCD 中，∠BAO ＝90°－∠AOB ，∴∠EOF ＝∠BAO .∵∠EFO ＝∠B ，OE ＝OA ，∴△OFE ≌△ABO .∴EF ＝OB ，OF ＝AB .又OF ＝CF ＋OC ＝AB ＝BC ＝OB ＋OC ＝EF ＋OC ，∴CF ＝EF .∴四边形EFCH 为正方形．(2)解：如图5，∵∠POK ＋∠BOG ＝∠OGB ＋∠BOG ＝90°，图5∴∠POK ＝∠OGB .∵∠PKO ＝∠OBG ，∴△PKO ∽△OBG .∵S △PKO ＝4S △OBG ，∴＝2＝4.∴OP ＝2.S △PKO S △OBG (OP OG )∴S △POG ＝OG ·OP ＝×1×2＝1.1212∵S 四边形PKBG ＝S △POG ＋S △PKO ＋S △OBG ＝1＋5S △OBG ，∴只需求出S △OBG 的最大值．设OB ＝a ，BG ＝b ，则a 2＋b 2＝OG 2＝1，∴b ＝.1－a 2∴S △OBG ＝ab ＝a ＝12121－a 212－a 4＋a 2＝.12－(a 2－12)2＋14∴当a 2＝时，△OBG 有最大值为，此时S △PKO ＝4S △OBG ＝1.1214∴四边形PKBG 的最大面积为1＋1＋＝.1494例2　解：(1)若四边形PQCM 是平行四边形，则PM ∥QC ，∴AP ∶AB ＝AM ∶AC .∵AB ＝AC ，∴AP ＝AM ，即10－t ＝2t ，解得t ＝.103∴当t ＝时，四边形PQCM 是平行四边形．103(2)∵PQ ∥AC ，∴△PBQ ∽△ABC .∴△PBQ 为等腰三角形，PQ ＝PB ＝t .∴＝，即＝，解得BF ＝t .BF BD PB AB BF 8t 1045∴FD ＝BD －BF ＝8－t .45∴y ＝S △ABC －S △APM －S △BPQ ＝×10×8－×2t ×－×t ×t ＝t 2－8t ＋40.1212(8－45t )124525(3)假设存在某一时刻t ，使点M 在线段PC 的垂直平分线上，则MP ＝MC ，图6过M 作MH ⊥AB ，交AB 于H ，如图6所示，∵∠A ＝∠A ，∠AHM ＝∠ADB ＝90°，∴△AHM ∽△ADB .∴＝＝.HM BD AH AD AM AB又AD ＝6，∴＝＝.HM 8AH 62t 10∴HM ＝t ，AH ＝t .8565∴HP ＝10－t －t ＝10－t .65115在Rt △HMP 中，MP 2＝2＋2＝t 2－44t ＋100，(85t )(10－115t )375又MC 2＝(10－2t )2＝100－40t ＋4t 2，MP 2＝MC 2，∴t 2－44t ＋100＝100－40t ＋4t 2.375解得t 1＝，t 2＝0(舍去)．2017∴t ＝秒时，点M 在线段PC 的垂直平分线上．2017训练　3.解：(1)当点P 在AC 上时，∵AM ＝t ，∴PM ＝AM ·tan 60°＝t .3∴y ＝t ·t ＝t 2(0<t ≤1)．12332当点P 在BC 上时，PM ＝BM ·tan 30°＝(4－t )，33∴y ＝t ·(4－t )＝－t 2＋t (1≤t <3)．123336 2 33(2)∵AC ＝2，∴AB ＝4.∴BN ＝AB －AM －MN ＝4－t －1＝3－t .∴QN ＝BN ·tan 30°＝(333－t )．若要四边形MNQP 为矩形，需PM ＝QN ，且P ，Q 分别在AC ，BC 上．即t ＝(3－t )，∴t ＝.33334∴当t ＝ s 时，四边形MNQP 为矩形．34(3)由(2)知，当t ＝ s 时，34四边形MNQP 为矩形，此时PQ ∥AB ，∴△PQC ∽△ABC .除此之外，当∠CPQ ＝∠B ＝30°时，△QPC ∽△ABC ，此时＝tan 30°＝.CQ CP 33∵＝cos 60°＝，∴AP ＝2AM ＝2t .∴CP ＝2－2t .AM AP 12∵＝cos 30°＝，∴BQ ＝＝(3－t )．BN BQ 32BN 32 2 33又BC ＝2 ，∴CQ ＝2 －(3－t )＝.33 2 33 2 3t 3∴＝，解得t ＝.2 3t32－2t 3312∴当t ＝ s 或 s 时，以C ，P ，Q 为顶点的三角形与△ABC 相似．12344．(1)证明：∵l ⊥AD ，BC ⊥AD ，∴l ∥BC .∴＝.AM AB AN AC ∵AB ＝AC ，∴AM ＝AN .∵∠BAC ＝90°，∴ME ＝NE .∴MN ＝2AE ＝2t .∵BP ＝2t ，∴MN ＝BP .∴四边形MBPN 为平行四边形．(2)解：∵四边形MFGN 是正方形，∴FG ＝MN ＝MF ＝2AE ＝2t .∵EH ＝MF ＝2t ，∴DH ＝AD －AH ＝10－3t .∴S △PFG ＝FG ·DH ＝×2t ×(10－3t )＝－32＋.1212(t －53)253∵－3＜0,0＜t ＜，103∴当t ＝时，S △PFG 最大为.53253(3)解：存在，t ＝或.30±10 27103【提示】如图7，过点F 作FK ⊥BC 于K ，过点G 作GL ⊥BC 于L ，图7则FK ＝GL ＝DH ＝10－3t ，PK ＝BD －BP －KD ＝10－3t ，PL ＝PD ＋DL ＝10－2t ＋t ＝10－t .利用勾股定理得：PF 2＝2(10－3t )2，PG 2＝(10－3t )2＋(10－t )2，FG 2＝(2t )2.当PF ＝FG 时，2(10－3t )2＝(2t )2，解得t ＝；30±10 27当PF ＝PG 时，2(10－3t )2＝(10－3t )2＋(10－t )2，解得t ＝5，或t ＝0(舍去)；当t ＝5时，点P 为BC 中点，而F ，P ，G 三点共线，舍去．当FG ＝PG 时，(2t )2＝(10－3t )2＋(10－t )2，解得t ＝，或t ＝10(舍去)；103综上所述，t ＝或时，△PFG 为等腰三角形．30±10 27103例3　解：(1)∵点A 在线段PQ 的垂直平分线上，∴AP ＝AQ .∵∠DEF ＝45°，∠ACB ＝90°，∠DEF ＋∠ACB ＋∠EQC ＝180°，∴∠EQC ＝45°.∴∠DEF ＝∠EQC .∴CE ＝CQ .由题意知CE ＝t ，BP ＝2t ，∴CQ ＝t .∴AQ ＝8－t .在Rt △ABC 中，由勾股定理得AB ＝10 cm ，则AP ＝10－2t .∴10－2t ＝8－t ，解得t ＝2.(2)如图8，过点P 作PM ⊥BE 于M ，图8∴∠BMP ＝90°.∴sin B ＝＝，即＝.AC AB PM PB PM 2t 810解得PM ＝t .85∵BC ＝6 cm ，CE ＝t ，∴BE ＝6－t .∴y ＝S △ABC －S △BPE ＝×BC ×AC －×BE ×PM ＝×6×8－×(6－t )×t ＝t 2－t ＋24＝(t －121212128545245453)2＋.845∵＞0，∴抛物线开口向上．45∴当t ＝3时，y 最小＝.845(3)假设存在某一时刻t ，使点P ，Q ，F 三点在同一条直线上，如图9，过点P 作PN ⊥AC 于N，图9∴∠ANP ＝∠ACB ＝∠PNQ ＝90°.∵∠PAN ＝∠BAC ，∴△PAN ∽△BAC .∴＝＝，即＝＝.PN BC AP AB AN AC PN 610－2t 10AN 8解得PN ＝6－t ，AN ＝8－t .6585∵NQ ＝AQ －AN ，∴NQ ＝8－t －＝t .(8－85t )35∵∠ACB ＝90°，B ，C (E )，F 在同一条直线上，∴∠QCF ＝90°，∠QCF ＝∠PNQ .∵∠FQC ＝∠PQN ，∴△QCF ∽△QNP .∴＝，即＝，解得t ＝1.PN FC NQ CQ 6－65t 9－t 35t t训练　5.解：(1)；209【提示】如图10，由题意得，CQ ＝AP ＝t，图10∵AB ＝3，BC ＝5，∴AC ＝4.∴CP ＝4－t .由平移的性质可得MN ∥AB ，∵PQ ∥MN ，∴PQ ∥AB .∴＝，即＝，解得t ＝.CP AC CQ BC 4－t 4t 5209(2)如图11，过点P 作PF ⊥BC 于点F ，过点A 作AE ⊥BC 于点E，图11由S △ABC ＝AB ×AC ＝AE ×BC ，1212即×3×4＝×5AE ，可得AE ＝.1212125∴CE ＝＝＝.AC 2－AE 242－(125)2165∵PF ⊥BC ，AE ⊥BC ，∴AE ∥PF .∴△CPF ∽△CAE .∴＝＝，即＝＝.CP AC CF CE PF AE 4－t 4CF 165PF 125∴PF ＝，CF ＝.12－3t 516－4t 5∵PM ∥BC ，∴点M 到QC 的距离h ＝PF ＝.12－3t 5∴y ＝CQ ×h ＝×t ×＝－t 2＋t (0＜t ＜4)．121212－3t 531065(3)如图12，过点Q 作QK ⊥PM 于点D ，QE 交AC 于点H .图12∵PQ ＝MQ ，∴PK ＝KM ＝，且KQ ⊥BC .52∵∠A ＝∠HQC ，∠ACB ＝∠QCH ，∴△CQH ∽△CAB ，∴＝，即＝.CQ AC CH BC t 4CH 5∴CH ＝t .∴PH ＝AC －AP －CH ＝4－t －t ＝4－t .545494易证△PHK ∽△CBA ，∴＝，即＝，解得t ＝.PH BC PK AC 4－94t 5524718∴当t ＝时，PQ ＝QM .7186．解：(1)设设PN 与x 轴交于点G ，∵OA ＝4，AB ＝3，∠OAB ＝90°，∴OB ＝5.∵PG ∥AB ，∴△OPG ∽△OBA .∴＝＝.∴＝＝.OG OA PG AB OP OB OG 4PG 3t 5∴OG ＝t ，PG ＝.453t 5∴P 点的坐标为.(45t ，－35t )(2)①当0＜t ≤时，S ＝t ×t ＝t 2；5245351225当＜t ≤时，S ＝2×t ＝t ；521033565当＜t ＜4时，S ＝4.103②当QM 运动到AB 位置时，恰好无公共部分，t ＜4＋2，45即t ＜.152(ⅰ)当4＜t ＜5时，∠DPE ＞∠DBE ＝90°，△PDE 不可能为直角三角形；(ⅱ)当t ＝5时，∠DPE ＝∠DBE ＝90°，此时△PDE 是直角三角形；(ⅲ)当5＜t ＜时，如图13，ME ＝MN －NE ＝2－＝6－t ，DM ＝MQ －QD ＝2152(45t －4)45－＝5－t .(35t －3)35此时∠DPE ＜90°，有∠PDE ＝90°或∠PED ＝90°两种可能．若∠PDE ＝90°，则＝，PQ QD DM ME图13可得＝，235t －35－35t 6－45t 整理得9t 2－160t ＋675＝0，解得t ＝，应取t ＝；80±5 13980－5 139若∠PED ＝90°，则＝，PN NE ME DM可得＝，245t －46－45t 5－35t 整理得8t 2－115t ＋425＝0，注意到Δ＜0，该方程无实数解．综上所述，符合条件的t 的值有两个，t ＝5或t ＝.80－5 139。

（中考数学专题3） 动态几何问题【例1】如图，在梯形ABCD 中，AD BC ∥，3AD =，5DC =，10BC =，梯形的高为4．动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动；动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动．设运动的时间为t （秒）．D NCM B A（1）当MN AB ∥时，求t 的值；（2）试探究：t 为何值时，MNC △为等腰三角形．【例3】在△ABC 中，∠ACB=45º．点D （与点B 、C 不重合）为射线BC 上一动点，连接AD ，以AD 为一边且在AD 的右侧作正方形ADEF ．（1）如果AB=AC ．如图①，且点D 在线段BC 上运动．试判断线段CF 与BD 之间的位置关系，并证明你的结论．（2）如果AB ≠AC ，如图②，且点D 在线段BC 上运动．（1）中结论是否成立，为什么？（3）若正方形ADEF 的边DE 所在直线与线段CF 所在直线相交于点P ，设AC ＝42，3=BC ，CD=x ，求线段CP 的长．（用含x 的式子表示）【例4】已知如图，在梯形ABCD 中，24AD BC AD BC ==∥，，，点M 是AD 的中点，MBC △是等边三角形．（1）求证：梯形ABCD 是等腰梯形；（2）动点P 、Q 分别在线段BC 和MC 上运动，且60MPQ =︒∠保持不变．设PC x MQ y ==，，求y与x 的函数关系式； （3）在（2）中，当y 取最小值时，判断PQC △的形状，并说明理由．【例5】已知正方形ABCD 中，E 为对角线BD 上一点，过E 点作EF BD ⊥交BC 于F ，连接DF ，G 为DF 中点，连接EG CG ，． （1）直接写出线段EG 与CG 的数量关系；（2）将图1中BEF ∆绕B 点逆时针旋转45︒，如图2所示，取DF 中点G ，连接EG CG ，，． 你在（1）中得到的结论是否发生变化？写出你的猜想并加以证明．（3）将图1中BEF ∆绕B 点旋转任意角度，如图3所示，再连接相应的线段，问（1）中的结论是否仍然成立？（不要求证明）A DC B P M Q 60图3图2图1FEABCDABC DEFGGFED C BA【总结】 通过以上五道例题，我们研究了动态几何问题当中点动，线动，乃至整体图形动这么几种可能的方式。

2022年中考数学复习：动态几何问题压轴题专项训练1．已知AD是等边△ABC的高，AC=2，点O为直线AD上的动点(不与点A重合)，连接BO，将线段BO 绕点O顺时针旋转60°，得到线段OE，连接CE、BE．(1)问题发现：如图1，当点O在线段AD上时，线段AO与CE的数量关系为，△ACE的度数是．(2)问题探究：如图2，当点O在线段AD的延长线上时，(1)中结论是否还成立？请说明理由．(3)问题解决：当△AEC=30°时，求出线段BO的长2．如图1，在平面直角坐标系中，已知△ABC中，△ABC＝90°，B(4，0)，C(8，0)，tan△ACB＝2，抛物线y＝ax2+bx经过A，C两点．(1)求点A的坐标及抛物线的解析式；(2)如图2，过点A作AD△AB交BC的垂线于点D，动点P从点A出发，沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD向终点D运动，速度均为每秒1个单位长度，运动时间为t秒，过点P作PE△AB交AC于点E．△过点E作EF△AD于点F，交抛物线于点G．当t为何值时，线段EG取得最大值？最大值是多少？△连接EQ，在点P，Q运动过程中，t为何值时，使得△CEQ与△ABC相似？3．如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋1的对称轴为直线x32＝，其图象与x轴交于点A和点B（4，0），与y轴交于点C．(1)直接写出抛物线的解析式和△CAO的度数；(2)动点M，N同时从A点出发，点M以每秒3个单位的速度在线段AB上运动，点N速度在线段AC上运动，当其中一个点到达终点时，另一个点也随之停止运动．设运动的时间为t（t＞0）秒，连接MN，再将线段MN绕点M顺时针旋转90°，设点N落在点D的位置，若点D恰好落在抛物线上，求t的值及此时点D的坐标；(3)在（2）的条件下，设P为抛物线上一动点，Q为y轴上一动点，当以点C，P，Q为顶点的三角形与△MDB相似时，请直接写出点P及其对应的点Q的坐标．4．如图，在□ABCD 中，△ABD ＝90°，AD =，BD ＝8cm ．点P 从点A 出发，沿折线AB —BC 向终点C 运动，点P 在AB 边、BC 边上的运动速度分别为1cm /s /s ．在点P 的运动过程中，过点P 作AB 所在直线的垂线，交边AD 或边CD 于点Q ，以PQ 为一边作矩形PQMN ，且QM =2PQ ，MN 与BD 在PQ 的同侧．设点P 的运动时间为t （秒），矩形PQMN 与□ABCD 重叠部分的面积为S （cm 2）．(1)求边AB 的长；(2)当0＜t ＜4时，PQ ＝ ，当4＜t ＜8时，PQ ＝ （用含t 的代数式表示）；(3)当点M 落在BD 上时，求t 的值；(4)当矩形PQMN 与□ABCD 重叠部分图形为四边形时，求S 与t 的函数关系式．5．如图，四边形ABCD 是菱形，其中60B ∠=︒，点E 在对角线AC 上，点F 在射线CB 上运动，连接EF ，作60FEG ∠=︒，交DC 延长线于点G ．(1)试判断EFG 的形状，并说明理由；(2)图中7AB =，1AE =．△当CF 10=时，以点B 为原点，射线BC 为正半轴建立平面直角坐标系．平面内是否存在一点M ，使得以点M、E、F、G为顶点的四边形与菱形ABCD相似？若存在，求出点M的坐标，若不存在，说明理由；△记点F关于直线AB的轴对称点为点N．若点N落在EDC的内部（不含边界），求CF的取值范围．6．如图，在平面直角坐标系中，△AOB的边OA在x轴上，OA＝AB，且线段OA的长是方程x2﹣4x﹣5＝0的根，过点B作BE⊥x轴，垂足为E，tan∠BAE＝43，动点M以每秒1个单位长度的速度，从点A出发，沿线段AB向点B运动，到达点B停止．过点M作x轴的垂线，垂足为D，以MD为边作正方形MDCF，点C在线段OA上，设正方形MDCF与△AOB重叠部分的面积为S，点M的运动时间为t（t＞0）秒．(1)求点B的坐标；(2)求S关于t的函数关系式，并写出自变量t的取值范围；7．小明在学过圆之后，对该题进行重新探究，请你和他一起完成问题探究．【问题探究】小明把原问题转化为动点问题，如图1，在边长为6cm 的正方形ABCD 中，点E 从点A 出发，沿边AD 向点D 运动，同时，点F 从点B 出发，沿边BA 向点A 运动，它们的运动速度都是2cm/s ，当点E 运动到点D 时，两点同时停止运动，连接CF 、BE 交于点M ，设点E ， F 运动时问为t 秒．(1)【问题提出】如图1，点E ，F 分别在方形ABCD 中的边AD 、AB 上，且BE CF =，连接BE 、CF 交于点M ，求证：BE CF ⊥．请你先帮小明加以证明．(2)如图1，在点E 、F 的运动过程中，点M 也随之运动，请直接写出点M 的运动路径长 cm ．(3)如图2，连接CE ，在点E 、F 的运动过程中．△试说明点D 在△CME 的外接圆O 上； △若△中的O 与正方形的各边共有6个交点，请直接写出t 的取值范围．8．如图，菱形ABCD ，120ABC ∠=︒，点E 为平面内一点，连接AE ．(1)如图1，点E 在BC 的延长线上，将AE 绕点A 顺时针旋转60°得AF ，交EB 延长线于点G ，连接EF 交AB 延长线于点H ，若15AEB ∠=︒，4HF =，求AE 的长；(2)如图2，点E 在AC 的延长线上，将AE 绕点A 逆时针旋转60°得AF ，连接EF ，点M 为CE 的中点，连接BM ，FM ，证明：FM =；(3)如图3，将AB 沿AS 翻折得()120AE BAE ∠<︒，连DE 交AS 于点S ，点T 为平面内一点，当DS 取得最大值时，连接TD ，TE ，若3AT =，AD =6，求TD TE -的最大值．9．已知抛物线()()12y x x m m=+-与x 轴负半轴交于点A ，与x 轴正半轴交于点B ，与y 轴交于点C ，点P 为抛物线上一动点（点P 不与点C 重合）．(1)当ABC 为直角三角形时，求ABC 的面积(2)如图，当AP BC ∥时，过点P 作PQ x ⊥轴于点Q ，求BQ 的长．(3)当以点A ，B ，P 为顶点的三角形和ABC 相似时（不包括两个三角形全等），求m 的值．10．已知：如图，在△ABC 纸片中，AC ＝3，BC ＝4，AB ＝5，按图所示的方法将△ACD 沿AD 折叠，使点C恰好落在边AB上的点C′处，点P是射线AB上的一个动点．(1)求折痕AD长．(2)点P在线段AB上运动时，设AP＝x，DP＝y．求y关于x的函数解析式，并写出此函数的定义域．(3)当△APD是等腰三角形时，求AP的长．11．如图，抛物线y＝ax2＋bx﹣3经过A、B、C三点，点A（﹣3，0）、C（1，0），点B在y轴上．点P 是直线AB下方的抛物线上一动点（不与A、B重合）．(1)求此抛物线的解析式；(2)过点P作x轴的垂线，垂足为D，交直线AB于点E，动点P在什么位置时，PE最大，求出此时P点的坐标；(3)点Q是抛物线对称轴上一动点，是否存在点Q，使以点A、B、Q为顶点的三角形为直角三角形？若存在，请求出点Q坐标；若不存在，请说明理由．A-和点B，与y轴交于点C，顶点D 12．在平面直角坐标系中，抛物线2y ax bx c=++与x轴交于点(1,0)-．的坐标为(1,4)(1)直接写出抛物线的解析式；∠=∠，求点P的坐标；(2)如图1，若点P在抛物线上且满足PCB CBD⊥轴交抛物线于点N，Q是直线AC上一个动点，当(3)如图2，M是直线BC上一个动点，过点M作MN x∆为等腰直角三角形时，直接写出此时点M及其对应点Q的坐标QMNB-，与y轴交于点C，且13．如图，已知抛物线2(0)=++≠与x轴交于点(1,0)y ax bx c aA和点(3,0)=．OC OB（1）求此抛物线的解析式；（2）若点E为第二象限抛物线上一动点，连接BE，CE，BC，求BCE面积的最大值；（3）点P在抛物线的对称轴上，若线段P A绕点P逆时针旋转90︒后，点A的对应点'A恰好也落在此抛物线上，求点P 的坐标．14．综合与探究如图，已知抛物线228y x x =--与x 轴相交于点A ，B （点B 在点A 的右侧），与y 轴相交于点C ，其顶点为点D ，连接AC ，BC ．（1）求点A ，B ，D 的坐标；（2）设抛物线的对称轴DE 交线段BC 于点E ，P 为第四象限内抛物线上一点，过点P 作x 轴的垂线，交线段BC 于点F ．若四边形DEFP 为平行四边形，求点P 的坐标；（3）设点M 是线段BC 上的一个动点，过点M 作MN AB ，交AC 于点N ．点Q 从点B 出发，以每秒1个单位长度的速度沿线段BA 向点A 运动，运动时间为t （6t <）秒，直接写出当t 为何值时，QMN 为等腰直角三角形．15．如图△，在平面直角坐标系中，点A 、B 的坐标分别为A （4，0）、B （0，3），连结AB ．抛物线234y x bx c =++经过点B ，且对称轴是直线52x =-．（1）求抛物线的函数关系式．（2）将图△中的△ABO 沿x 轴向左平移得到△DCE （如图△），当四边形ABCD 是菱形时，说明点C 和点D 都在该抛物线上．（3）在（2）中，若点M 是抛物线上的一个动点（点M 不与点C 、D 重合），过点M 作MN △y 轴交直线CD 于点N ．设点M 的横坐标为m ，线段MN 的长为l ．求l 与m 之间的函数关系式．（4）在（3）的条件下，直接写出m 为何值时，以M 、N 、C 、E 为顶点的四边形是平行四边形．16．如图，抛物线y ＝－212x ＋32x ＋2与x 轴负半轴交于点A ，与y 轴交于点B ． （1）求A ，B 两点的坐标；（2）如图1，点C 在y 轴右侧的抛物线上，且AC ＝BC ，求点C 的坐标；（3）如图2，将△ABO 绕平面内点P 顺时针旋转90°后，得到△DEF （点A ，B ，O 的对应点分别是点D ，E ，F ），D ，E 两点刚好在抛物线上．△求点F 的坐标；△直接写出点P 的坐标．17．如图1，直线AB 与x 轴，y 轴分别交于A ，B 两点，点C 在x 轴负半轴上，这三个点的坐标分别为A(4，0)，B(0，4)，C(−1，0) ．（1）请求出直线AB的解析式；（2）连接BC，若点E是线段AC上的一个动点（不与A，C重合），过点E作EF//BC交AB于点F，当△BEF的面积是52时，求点E的坐标；（3）如图2，将点B向右平移1个单位长度得到点D，在x轴上存在动点P，若△DCO+△DPO=△α，当tan△α=4时，请直接写出点P的坐标．18．将矩形ABCD绕着点C按顺时针方向旋转得到矩形FECG，其中点E与点B，点G与点D分别是对应点，连接BG．(1)如图，若点A，E，D第一次在同一直线上，BG与CE交于点H，连接BE．△求证：BE平分△AEC．△取BC的中点P，连接PH，求证：PH∥CG．△若BC＝2AB＝2，求BG的长．(2)若点A，E，D第二次在同一直线上，BC＝2AB＝4，直接写出点D到BG的距离．19．如图，△ABC是等边三角形，AB＝4cm，动点P从A出发，以2cm/s的速度沿AB向点B匀速运动，过点P作PQ△AB，交折线AC﹣CB于点Q，以PQ为边作等边三角形PQD，使A，D在PQ异侧，设点P 的运动时间是x（s）（0＜x＜2）．（1）AP的长为cm（用含x的代数式表示）；（2）当Q与C重合时，则x＝s；（3）△PQD的周长为y（cm），求y关于x的函数解析式，并写出自变量的取值范围．20．如图1，在平面直角坐标系中，抛物线y＝ax2+154x+c与x轴负半轴相交于点A（﹣20，0），与y轴相交于点B（0，﹣15）．（1）求抛物线的函数表达式及直线AB的函数表达式；（2）如图2，点C是第三象限内抛物线上的一个动点，连接AC、BC，直线OC与直线AB相交于点D，当△ABC的面积最大时，求此时△ABC面积的最大值及点C的坐标；（3）在（2）的条件下，点E为线段OD上的一个动点，点E从点O开始沿OD速度向点D运动（运动到点D时停止），以OE为边，在OD的左侧做正方形OEFG，设正方形OEFG与△OAD重叠的面积为S，运动时间为t秒．当t＞3时，请直接写出S与t之间的函数关系式为（不必写出t的取值范围）．参考答案：1．解：AO =CE ，△ACE =90°，理由如下：△线段BO 绕点O 顺时针旋转60°，得到线段OE ，△BO =OE ，△BOE =60°，△△BOE 为等边三角形，△△OBE =60°，BE =BO ，△△OBE =60°=△OBD +△DBE ，△△ABC 为等边三角形，△△ABC =60°=△ABO +△OBD ，AB=AC ，△△ABO =△CBE ，在△ABO 和△CBE 中，AB AC ABO CBE BO BE =⎧⎪∠=∠⎨⎪=⎩，△△ABO △△CBE (SAS)，△AO =CE ，△BAO =△BCE ，△AD 是等边三角形ABC 的高，△△ACB =60°，AD 也是△BAC 的平分线，△△BAO =30°=△BCE ，△△ACE =△BCE +△ACB =30°+60°=90°，故答案为：AO =CE ，△ACE =90°；(2)解：成立，理由如下：如图：连接BE ．△线段BO 绕点O 顺时针旋转了60°得EO ，△BO =EO ，△BOE =60°，△△BOE 是等边三角形，△BO =BE ，△OBE =60°，△△ABC 是等边三角形，△BA =BC ，△ABC =60°，△△ABC +△OBC =△OBE +△OBC ，即△ABO =△CBE ，在△ABO 和△CBE 中，AB AC ABO CBE BO BE =⎧⎪∠=∠⎨⎪=⎩△△ABO △△CBE (SAS)，△AO =CE ，△BAO =△BCE ，△AD 是等边△ABC 的高，△△BCE =△BAO =30°，△BCA =60°，△△ACE =△BCE +△ACB =30°+60°=90°，△AO =CE ，△ACE =90°；(3)解：△当点O 1在线段AD 的延长线上时，由(1)和(2)知：△BO 1E 1是等边三角形，△ACE 1=90°，△△ACE 1=90°，△AE 1C =30°，△△E 1AC =60°，△△BAC =60°，△点A 、B 、E 1在一条直线上，△在Rt △ACE 1中，AC =2，△AE 1C =30°，△A E 1=4，△BO 1=BE 1=2；△当点O 2在线段DA 的延长线上时，△△ACE 2=90°，△AE 2C =30°，AC =2，△AE 2=4，2CE△△ABO 2△△CBE 2(SAS)，△22AO CE ==△AD 是等边△ABC 的高，AB =AC =2，△BD =1，AD ==在Rt △O 2DB 中，BD =1，而22O D AO AD ==+△2BO ===综上，BO =2或2．解：△B （4，0），C （8，0），△BC ＝4，△△ABC ＝90°，tan△ACB ＝2，△AB ＝BC •tan△ACB ＝8，△A 的坐标为（4，8），将A （4，8），C （8，0）代入y ＝ax ²+bx ，得：16486480+=⎧⎨+=⎩a b a b ， 解得：124⎧=-⎪⎨⎪=⎩a b ， △抛物线得解析式为：2142y x x =-+； (2)解：△由题得：AP ＝t ，△APE ＝△ABC ＝90°，△EAP ＝△CAB ，△tan△EAP ＝tan△CAB ＝=EP BC AP AB ， △4=8PE t ，即PE ＝2t ， △PB ＝AB ﹣AP ＝8﹣t ，△E 的坐标为（4+2t ，8﹣t ）， 将x ＝4+2t 代入2142y x x =-+， 得：2188=-+y t ， △G 的纵的坐标为2188-+t ， △EG ＝218(8)8-+--t t ＝21+8-t t ＝21(4)+28--t ，△0≤t ≤8， △t ＝4时，线段EG 有最大值且为2；△△CQ ＝t ，PE ＝2t ，AP ＝t ，BC ＝4，AB ＝8， △AE=，AC= △CE ＝AC ﹣AE＝，当△CEQ △△ACB 时，=CE CQ AC AB ，代入数据：8=t ，解得：t ＝4，当△CEQ △△ABC 时，=CE CQ AB AC ，代入数据：△28=解得t ＝409， △综上，t ＝4或409． 3． 解：由题意：32216410b a a b ⎧-=⎪⎨⎪++=⎩， 解得1434a b ⎧=-⎪⎪⎨⎪=⎪⎩， △抛物线的解析式为y 14=-x 234+x +1， 令y ＝0，可得x 2﹣3x ﹣4＝0，解得x ＝﹣1或4，△A （﹣1，0），令y ＝0，得到x ＝1，△C （0，1），△OA ＝OC ＝1，△△CAO ＝45°．(2)解：如图1中，过点C 作CE △OA 于E ，过点D 作DF △AB 于F ．△△NEM＝△DFM＝△NMD＝90°，△△NME + △DMF＝90°，△DMF+△MDF＝90°，△△NME＝△MDF，△NM＝DM，△MEN DFM AAS≌（）△NE＝MF，EM＝DF，△△CAO＝45°，AN=，AM＝3t，△AE＝EN＝t，△EM＝AM﹣AE＝2t，△DF＝2t，MF＝t，OF＝4t﹣1，△D（4t﹣1，2t），△14-（4t﹣1）234+（4t﹣1）+1＝2t，△t＞0，故可以解得t34 =，经检验，t34=时，M，N均没有达到终点，符合题意，△D（2，32）．(3)解：如图3﹣1中，当点Q在点C的下方，点P在y的右侧，△QCP＝△MDB时，取E （12，0），连接EC ，过点E 作EG △EC 交PC 于G ， △M （54，0），D （2，32），B （4，0） △53244FM =-=，DM =，BM 114=，BD 52=， △DF ＝2MF ，△OC ＝2OE ，△tan△OCE ＝tan△MDF 12=， △△OCE ＝△MDF ，△△OCP ＝△MDB ，△△ECG ＝△FDB ，△tan△ECG ＝tan△FDB 43=， △EC =， △EG =G （116，23）， △直线CP 的解析式为y 211=-x +1， 由2211113144y x y x x ⎧=-+⎪⎪⎨⎪=-++⎪⎩，解得01x y =⎧⎨=⎩或411139121x y ⎧=⎪⎪⎨⎪=⎪⎩， △4139(,)11121P ，(0,1)C ，△PC =当MD BD CQ CP =或时MD BD PC CQ =，△QCP 与△MDB 相似，可得615242CQ =或2050363，△373(0,)242Q -或1687(0,)363-． 如图3﹣2中，当点Q 在点C 的下方，点P 在y 的右侧，△QCP ＝△DMB 时，设PC 交x 轴于K ．△tan△OCK ＝tan△DMB ＝2，△OK ＝2OC ＝2，△点K 与F 重合，△直线PC 的解析式为112y x =-+， 由211213144y x y x x ⎧=-+⎪⎪⎨⎪=-++⎪⎩，解得01x y =⎧⎨=⎩或532x y =⎧⎪⎨=-⎪⎩， △3(5,)2P -，△PC =当DM BM PC CQ =或DM BM CQ PC =时，△QCP 与△MDB 相似，可得556CQ =或7522， △49(0,)6Q -或53(0,)22-． 当点Q 在点C 的下方，点P 在y 的右侧，△QCP ＝△DBM 时，同法可得2591257(,)(0,)3918P Q --，或1151(0,)99， 当点Q 在点C 上方，△QCP ＝△DMB 时，同法可得P （1，32），Q （0，176）或（0，3722）， 当点Q 在点C 上方，△QCP ＝△MDB 时，同法可得25171617(,)(0,)11121242P Q ，或1613(0,).363，当点Q 在点C 下方，点P 在y 轴的左侧时，△QCP ＝△DBM 时，同法可得71959(,)(0,)3918P Q ---，或251(0,)99-． 4(1)解：△△ABD ＝90°，AD =，BD ＝8cm ．△4cm AB = ；(2)解：当0＜t ＜4时，点P 在AB 边上，cm AP t = ，如图，△PQ △AB ，△ABD ＝90°，△PQ △BD ，△△APQ △△ABD ，△AP PQ AB BD = ， △4182AP AB PQ BD === ， 即12t PQ = ， △2cm PQ t = ；当4＜t ＜8时，点P 在BC 边上，)4cm BP t =- ，如图，△四边形ABCD 是平行四边形，△BC AD == ，AB △CD ，△BDC =△ABD =90°，△)()4cm CP BC BP t =-=-= ，△PQ △AB ，△PQ △CD ，△PQ △BD ，△△CPQ △△CBD ， △CP PQ BC BD= ，△CP BC PQ BD === ， △()162cm PQ t =- ；(3)解：如图，当点P 在AB 上时，cm AP t = ，则()4cm BP t =- ，在矩形PQMN 中， BP =QM ，△QM =2PQ ，△BP =2PQ ，△2cm PQ t =，△224t t ⨯=- ，解得：45t = ；如图，当点P 在BC 边上时，点M 与点D 重合，由（2）得：此时4182CQ CD PQ BD === ， △()162cm PQ t =-，△()18cm 2CQ PQ t ==- ， △()4cm MQ CD CQ t =-=- ，△QM =2PQ ，△()42162t t -=- ，解得：365t = ； 综上所述，当点M 落在BD 上时， t 的值为45或365； (4) 解：如图，当405t ≤≤ 时，△2cm PQ t =，QM =2PQ ，△4cm QM t =，△矩形PQMN 与□ABCD 重叠部分的面积为22248cm S PQ QM t t t =⋅=⨯= ； 如图，当445t << 时，设MQ 交BC 于点T ，根据题意得：AQ △BT ，QT △AB ，△四边形ABTQ 是平行四边形，△4cm QT = ，△()4cm BP AB AP t =-=- ，2cm PQ t =，△矩形PQMN 与□ABCD 重叠部分的面积为()()()2114428cm 22S PB QT PQ t t t t =+⨯=-+⨯=-+； 如图，当点N 落在AD 边上时，四边形ABPN 是平行四边形，△4cm PN AB == ，△4cm MQ PN == ，△QM =2PQ ，()162cm PQ t =-，△()21624t -= ，解得：7t = ，如图，当47t <≤ 时，设PN 交AD 于点K ，此时四边形ABPK 是平行四边形，△4cm PK AB == ，△()162cm PQ t =-，4182CQ CD PQ BD ===， △()18cm 2CQ PQ t ==- ， △()()484cm DQ t t =--=- ，△矩形PQMN 与□ABCD 重叠部分的面积为()()()()211441628cm 22S PK DQ PQ t t t t =+⨯=-+⨯-=-+； 如图，当3685t ≤< 时，△()162cm PQ t =-，QM =2PQ ，△()324cm MQ t =- ，△矩形PQMN 与□ABCD 重叠部分的面积为()()()221623248128512cm S PQ MQ t t t t =⨯=-⨯-=-+ ，综上所述，S 与t 的函数关系式为222248(0)548(4)58(47)368128512(8)5t t t t t S t t t t t t ⎧≤≤⎪⎪⎪-+<<⎪=⎨⎪-+<≤⎪⎪-+≤<⎪⎩．5．(1) EFG 是等边三角形，理由如下：如图，过点E 作EM AB ∥，交FC 于M ，△四边形ABCD 是菱形，△AB CB =，△60ACB ABC ∠=∠=︒，△60ACD ACB ∠=∠=︒，△120ACG ∠=︒,△EM AB ∥，△60ABC EMC ∠∠==︒，△120EMF ∠=︒，△60EMC ECM ∠=∠=︒，△EMC △是等边三角形，△EM EC =，60MEC ∠=︒,△60FEG MEC ∠=∠=︒，△FEM GEC ∠=∠，在FEM △和GEC 中，FGM GEC EM ECEMF ECG ∠=∠⎧⎪=⎨⎪∠=∠⎩， △()FEM GEC ASA ≅，△EF EG =，△EFG 是等腰三角形，△60FEG ∠=︒，△EFG 是等边三角形；(2)△如图所示，过点A 作AT y ⊥轴交于点T ，△60ABC ∠=︒，△30TBA ∠=︒， △1722AT AB ==，BT == 过点E 作EH y ⊥轴交于点H ，交AB 于点K ，△EH CF ∥，△AKE 是等边三角形，△1AK KE AE ===，△6BK =，△sin 6sin 606BH BK BKH =⋅∠=⨯︒==132HK BK ==，△E ，△4HE HK KE =+=，△四边形ABCD 是菱形，△7BC AB ==，△(7,0)C ，21(2D ， △CD 的解析式为373yx ，设(G x -， △EFG 是等边三角形，△22EG EF =，即2222(4)(34)x -+-=--+，解得：15=x 或212x =（舍去），当5x =时，y =-△(5,G -，当是菱形EFMG 时，(2,M --，当是菱形EFGM 时，M ，当是菱形FGEM 时，(M -，综上所述，(2,M --或(或(-；△如图，当N 在CD 上时，作CP AB ⊥于P ，点F '关于AB 的对称点N 在CD 上，△OF ON CP '==，CP BC ==△OF '=， 在Rt BOF '中，7sin 60OF OBF ''∠==︒， △14CF '=，如图，当N 在DE 上时，N 与F '关于AB 对称，AB 与DN 交于点Q ， △60ABN ABC ∠=∠=︒，△60BAC ∠=︒，△60ABN BAC ∠=∠=︒，△BN AE ∥， △AE AQ BN QB=， △AD BC ∥，△ADE CME ，AQD BQM ， △16AD AE MC CE ==，AQ AD QB MB =， △716MC =， △42MC =，△42735MB =-=， △71355AQ QB ==， △115BN =， △5BN =，△5BF BN '==，△752CF BC BF ''=-=-=，△214CF<<．6．解：由x2﹣4x﹣5＝0，解得x＝5或﹣1，∵OA是方程的根，∴OA＝5，∴AB＝OA＝5，在Rt△ABE中，tan∠BAE=BEAE＝43，AB＝5，∴BE＝4，AE＝3，∴OE＝OA+AE＝5+3＝8，∴B（8，4）；(2)解：如图1中，当点F落在OB上时，AM＝t，DM＝45t，AD＝35t，∵FM OA∥，∴FM MB OA BA=，∴45555tt-=，∴t＝259，如图2中，当0＜t≤259时，重叠部分是四边形ACFM，S＝12•（AC+FM）•DM＝14434 25555t t t t ⎛⎫⋅+-⋅ ⎪⎝⎭＝25t2，如图3中，259＜t ≤5时，重叠部分是五边形ACHGM ， S ＝S 梯形ACFM ﹣S △FGH ＝()22211455225t t t ⎡⎤-⨯⨯--⎢⎥⎣⎦＝﹣41100t 2+92t ﹣254；综上所述，S ＝25t 2（0＜t ≤259）或S ＝﹣41100t 2+92t ﹣254（259＜t ≤5）． 7．(1)四边形ABCD 是正方形，AB BC ∴=，BAE CBF ∠=∠又,E F 的运动速度都是2cm/s ，2AE BF t ∴==BAE CBF ∴≌BCF ABE ∴∠=∠90ABE EBC ABC ∠+∠=∠=︒90BCF EBC ∴∠+∠=︒90MBC ∴∠=︒(2)△90CMB ∠=．△点M 在以CB 为直径的圆上，如图1，当t ＝0时，点M 与点B 重合；如图2，当t ＝3时，点M 为正方形对角线的交点．点M 的运动路径为14圆，其路径长13642ππ⨯=． 故答案为：32π (3)△如图3．由前面结论可知：90CME ∠=△△CME 的外接圆的圆心O 是斜边CE 的中点， 则12OM OC OE CE === 在Rt △CDE 中，90D ∠=，O 是CE 的中点． △12OD CE =， △OM OC OE OD ===△点D 、C 、M 、E 在同一个圆（O ）上，即点D 在△CME 的外接圆O 上；． △304t <<． 如图4，当O 与AB 相切时，O 与正方形的各边共有5个交点，如图5则有6个交点，所以“当O 与AB 相切时”是临界情况．如图4，当O 与AB 相切（切点为G ），连接OG ，并延长GO 交CD 于点H ． △AB 与O 相切，△OG AB ⊥，又△AB CD ∥，132CH DC ∴== 设O 的半径为R ．由题意得：在Rt △CHO 中，2223(6)R R +-=，解得154R =△159,22CE DE =△32AE =，即3t 4= △如图5，当304t <<时，O 与正方形的各边共有6个交点．8．(1)解：过点H 作HL △EF ，交AF 于L ，△菱形ABCD ，120ABC ∠=︒△△DAB =180°-18012060ABC ∠=-=︒︒︒，AD∥BC ，△△DAE =△AEB ，△15AEB ∠=︒，△△DAE =15°，△AE 绕点A 顺时针旋转60°得AF ，△△AEF为等边三角形，△△F=60°，△HL△EF，△△HLF=90°-△F=30°，△LF=2HF=2×4=8，根据勾股定理LH△△DAE+△EAH=△EAH+△HAF=60°△△DAE=△HAF=15°，△△HLF为△AHL的外角，△△AHL=△HLF-△HAF=30°-15°=15°，△△AHL=△HAF，△AL=LH=△AE=AF=AL+LF=；(2)证明：过B作BL△AC于L，过F作FK△AE于K，设AE=m，AC=n，△将AE绕点A逆时针旋转60°得AF，△AE=AF=m，△EAF=60°，△△AEF为等边三角形，△AF=EF，△FK△AE，△△AFK=△EFK=30°，AK=EK=12 m，在Rt△AKF中，FK==，△菱形ABCD ，120ABC ∠=︒，BL △AC ，△AL =CL =12n ,△CBL =△ABL =60°，△△LCB =90°-△CBL =30°，△BC =2BL ，在Rt △BCL 中，根据勾股定理222+BC BL CL =，即2224+BL BL CL =，解得2n BL ==， △点M 为CE 中点，△CM =EM =()1122EC m n =+， △MK =ME -KE =()111222m n m n +-=，M L=MC -CL =()111222m n n m +-=，在Rt △MKF 中，根据勾股定理FM =在Rt △MLB 中，根据勾股定理BM ，△BM =，△FM =；(3)解：连结SB ，过E 作TL △DE ，，过G 作GI △AD 于I ，过T 作TJ △AB 于J ，在TD 上截取TE ′=TE ，△将AB 沿AS 翻折得()120AE BAE ∠<︒，△△BAS =△EAS ，AB =AE ，在△ABS 和△AES 中，AB AE BAS EAS AS AS =⎧⎪∠=∠⎨⎪=⎩，△△ABS △△AES （SAS ），△△ABS =△AES ，△四边形ABCD 为菱形，△AD =AB =AE =6，△ABC =120°，△△ADE =△AED =△ABS ，△DAB =180°-△ABC =60°，△A 、S 、B 、D 四点共圆，△点S 在△ABD 的外接圆劣弧AB 上运动，△当AS △AB 时，AS 长最大，△△ADH =90°-△DAH =30°，△AH =3，DH=△点T 在以点A 为圆3为半径的圆上运动，当点A 关于TJ 直线的对称点在△ADH 的角平分线DT 上时，TD TE -的值最大，设点A 的对称点为G ，△△ADG =△HDG =1152ADH ∠=︒，GI △AD ，GH △DH ， △GI =GH =m ,AG =AH –GH =3-m ，AI =AD -DI -DH=6-在Rt △AIG 中，根据勾股定理222+AG AI IG =即()(22236+m m -=-，解得9m =，在Rt △DGH 中，根据勾股定理DG△DT=DG +TG =3，△AG =12-△AJ =JG =6-△JH =AH -AJ =3-（6-=，△TJ △AB ，DE △AB ，TL △DE ，△△TJH =△JHL =△TLH =90°，△四边形JTLH 为矩形，△JH =TL =，在DL 上截取DN =TN ，△△NDT =△NTD =15°，△△FNL =△NDT +△NTD =30°，△DN =TN =2TL =6，在Rt △TNL 中，根据勾股定理，NL9=-△DL =DN +NL =6+93-=，在Rt △AHE 中，△EAH =60°，△DE =sin60°×AE△DE△LE =DE -DL ()3=TL ，△TE=△GT -TE 最大=3-．9．(1) 解：由抛物线()()12y x x m m=+-开口向上，则m ＞0令x =0，则y =-2，即C 点坐标为（0，-2），OC =2令y =0，则()()102x x m m=+-，解得x =-2或x =m ，即点A （-2，0），点B （m ，0） △OA =2,OB =m△AB =m +2由勾股定理可得AC 2=(-2-0)2+[0-（-2）]2=8, BC 2=(m -0)2+[0-（-2）]2=m 2+4 △当ABC 为直角三角形时，仅有△ACB =90°△AB 2= AC 2+BC 2,即(m +2)2=8+m 2+4,解得m =2△AB =m +2=4△ABC 的面积为：12·AB ·OC =12×4×2=4．(2)解：设BC 所在直线的解析式为：y =kx +b则02mk b b =+⎧⎨-=⎩ ，解得22k m b ⎧=⎪⎨⎪=-⎩ △BC 所在直线的解析式为y =2m x -2 设直线AP 的解析式为y =2m x +c 则有：0=2m×（-2）+c ，即c =4m △线AP 的解析式为y =2m x +4m 联立()()1224y x x m m y x m m⎧=+-⎪⎪⎨⎪=+⎪⎩ 解得x =-2（A 点横坐标）,x =m +2（P 点横坐标） △点P 的纵坐标为：()24822+m m m m⨯++= △点P 的坐标为（m +2，28m m +） △OQ =m +2△BQ =OQ -OB = m +2-m =2．(3)解：△点P 为抛物线()()12y x x m m=+-上一动点（点P 不与点C 重合）．△设P （x ，()()12x x m m+-） △在△ABC 中，△BAC =45°△当以点A ，B ，P 为顶点的三角形和ABC 相似时，有三种情况：△a .若△ABC △△BAP △BP AC AB AB= 又△BP =AC△△ABC △△BAP 不符合题意；b . 若△ABP △△BAC △BP AB AB AC= 过P 作PQ △x 轴于点Q ，则△PQB =90°△△BPQ =90°-△PBQ =45°△PQ =BQ =m -x由于PQ =()()12x x m m +- △1(2)()m x x x m m-=+- △1()(2)10x m x m ⎡⎤-++=⎢⎥⎣⎦△x -m =0或1(2)10x m++= △x =m （舍去），x =-m -2△BQ =m -（-m -2）=2m +2△1)PB m ==+=△m 2-4m -4=0，解得：m =2-m =△m =2-△当△P AB =△BAC =45°时，分两种情况讨论：a . 若△ABP △△ABC ,则AP AC AB AB = ,点C 与点P 重合，不合题意； b . 若△ABP △△BAC ,则PB AB AB AC= , 过P 作PQ △x 轴于点Q ，则△PQA =90°△△APQ =90°-△P AB =45°△PQ =AQ =x +2由于PQ =()()12x x m m +- △12(2)()x x x m m+=+- △1(2)(2)10x x m ⎡⎤+++=⎢⎥⎣⎦△x +2=0或1()10x m m--= △x =-2（舍去），x =2m△AQ = =2m +2△1)AP m ==+=△m 2-4m -4=0，解得：m =2-m =△m =△当△APB=△BAC=45°时，分两种情况讨论：a.过点A作PM//BC交抛物线于点M，则△MAB=△ABC，△△MAB≠△P AB，△△P AB≠△ABC，△△P AB与△BAC不相似；b. 取点C关于x轴的对称点C'，连接并延长BC'交抛物线于点N，则△NBA=△CBA，△△PBA≠△NBA，△△PBA≠△CBA，△△P AB与△BAC不相似；综上，m的值为m=2-m=10．解：如图1中，由翻折可知：CD=DC′，AC=AC′=3，设CD=DC′=x，在Rt△BDC中，△BD2=C′D2+C′B2，△（4-x）2=x2+22，解得：x=32，△AD==(2)如图2中，当点P在C'D左侧，AC=AC'=3，则PC'=3-x，△DP△10)y x =≤≤．当点P 在C 'D 右侧，同理可得10)y x =≤≤．△y 关于x 的函数解析式为10)y x =≤≤． (3) 如图3中，△当P A =PD 时，设P A =PD =m ， 在Rt △PCD 中，△PD 2=DC ′2+C ′P 2，△2223((3))2m m =+-，解得：158=m ， △P A =158．△当AD =AP P 在P′时，△ADP 是等腰三角形， △当PD =AD 时，点P 在AB 的延长线上．如图4，AP =2AC '=6．综上所述，满足条件的P A 的值为1586． 11． (1)解：把A （﹣3，0）和C （1，0）代入y ＝ax 2+bx ﹣3，得，093303a b a b =--⎧⎨=+-⎩，解得，12a b =⎧⎨=⎩，△抛物线解析式为y ＝x 2+2x ﹣3； (2)解：设P （x ，x 2+2x ﹣3），直线AB 的解析式为y ＝kx +b ， 由抛物线解析式y ＝x 2+2x ﹣3， 令x ＝0，则y ＝﹣3， △B （0，﹣3），把A （﹣3，0）和B （0，﹣3）代入y ＝kx +b ，得，033k b b=-+⎧⎨-=⎩，解得，13k b =-⎧⎨=-⎩，△直线AB 的解析式为y ＝﹣x ﹣3， △PE △x 轴， △E （x ，﹣x ﹣3），△P在直线AB下方，△PE＝﹣x﹣3﹣（x2+2x﹣3）＝﹣x2﹣3x＝﹣（x+32）2+94，当x＝﹣32时，y＝x2+2x﹣3＝154-，△当PE最大时，P点坐标为（﹣32，154-）；(3)存在，理由如下，△x＝﹣221⨯＝-1，△抛物线的对称轴为直线x＝-1，设Q（-1，a），△B（0，-3），A（-3，0），△当△QAB＝90°时，AQ2+AB2＝BQ2，△22+a2+32+32＝12+（3+a）2，解得：a＝2，△Q1（-1，2），△当△QBA＝90°时，BQ2+AB2＝AQ2，△12+（3+a）2+32+32＝22+a2，解得：a＝﹣4，△Q2（-1，﹣4），△当△AQB＝90°时，BQ2+AQ2＝AB2，△12+（3+a）2+22+a2＝32+32，解得：a1a1△Q3（-1，Q4（-1，综上所述：点Q的坐标是（-1，2）或（-1，﹣4）或（-1-1，．12．解：∵顶点D的坐标为（1，﹣4），∴设抛物线的解析式为y＝a（x﹣1）2﹣4，将点A（﹣1，0）代入，得0＝a（﹣1﹣1）2﹣4，解得：a＝1，∴y＝（x﹣1）2﹣4＝x2﹣2x﹣3，∴该抛物线的解析式为y＝x2﹣2x﹣3；(2)解：∵抛物线对称轴为直线x＝1，A（﹣1，0），∴B（3，0），设直线BD解析式为y＝kx+e，∵B（3，0），D（1，﹣4），∴304k ek e+=⎧⎨+=-⎩，解得：26ke=⎧⎨=-⎩，∴直线BD解析式为y＝2x﹣6，过点C作CP1∥BD，交抛物线于点P1，设直线CP1的解析式为y＝2x+d，将C（0，﹣3）代入，得﹣3＝2×0+d，解得：d＝﹣3，∴直线CP1的解析式为y＝2x﹣3，结合抛物线y＝x2﹣2x﹣3，可得x2﹣2x﹣3＝2x﹣3，解得：x1＝0（舍），x2＝4，故P1（4，5），过点B作y轴平行线，过点C作x轴平行线交于点G，∵OB＝OC，∠BOC＝∠OBG＝∠OCG＝90°，∴四边形OBGC是正方形，设CP1与x轴交于点E，则2x﹣3＝0，解得：x＝32，∴E（32，0），在x轴下方作∠BCF＝∠BCE交BG于点F，∵四边形OBGC 是正方形，∴OC ＝CG ＝BG ＝3，∠COE ＝∠G ＝90°，∠OCB ＝∠GCB ＝45°， ∴∠OCB ﹣∠BCE ＝∠GCB ﹣∠BCF ， 即∠OCE ＝∠GCF ， ∴△OCE ≌△GCF （ASA ），∴FG ＝OE ＝32，∴BF ＝BG ﹣FG ＝3﹣32＝32，∴F （3，﹣32），设直线CF 解析式为y ＝k 1x +e 1，∵C （0，﹣3），F （3，﹣32），∴1113332e k e =-⎧⎪⎨+=-⎪⎩，解得：11123k e ⎧=⎪⎨⎪=-⎩， ∴直线CF 解析式为y ＝12x ﹣3，结合抛物线y ＝x 2﹣2x ﹣3，可得x 2﹣2x ﹣3＝12x ﹣3， 解得：x 1＝0（舍），x 2＝52，∴P 2（52，﹣74），综上所述，符合条件的P 点坐标为：（4，5）或（52，﹣74）；(3)解：（3）设直线AC 解析式为y ＝m 1x +n 1，直线BC 解析式为y ＝m 2x +n 2， ∵A （﹣1，0），C （0，﹣3），∴11103m n n -+=⎧⎨=-⎩，解得：1133m n =-⎧⎨=-⎩，∴直线AC 解析式为y ＝﹣3x ﹣3， ∵B （3，0），C （0，﹣3），∴222303m n n +=⎧⎨=-⎩， 解得：2213m n =⎧⎨=-⎩，∴直线BC 解析式为y ＝x ﹣3， 设M （t ，t ﹣3），则N （t ，t 2﹣2t ﹣3）， ∴MN ＝|t 2﹣2t ﹣3﹣（t ﹣3）|＝|t 2﹣3t |，①当△QMN 是以NQ 为斜边的等腰直角三角形时，此时∠NMQ ＝90°，MN ＝MQ ，如图2，∵MQ ∥x 轴， ∴Q （﹣13t ，t ﹣3），∴|t2﹣3t|＝|t﹣（﹣13t）|，∴t2﹣3t＝±43 t，解得：t＝0（舍）或t＝53或t＝133，∴154 (,) 33M-，154 (,)93Q--；2134 (,) 33M，2134 (,)93Q-；②当△QMN是以MQ为斜边的等腰直角三角形时，此时∠MNQ＝90°，MN＝NQ，如图3，∵NQ∥x轴，∴Q（223t t-+，t2﹣2t﹣3），∴NQ＝|t﹣223t t-+|＝13|t2+t|，∴|t2﹣3t|＝13|t2+t|，解得：t＝0（舍）或t＝5或t＝2，∴M3（5，2），Q3（﹣5，12）；M4（2，﹣1），Q4（0，﹣3）；③当△QMN是以MN为斜边的等腰直角三角形时，此时∠MQN＝90°，MQ＝NQ，如图4，过点Q作QH⊥MN于H，则MH＝HN，∴H（t，262t t--），∴Q（26t t-+，262t t--），∴QH＝|t﹣26t t-+|＝16|t2+5t|，∵MQ＝NQ，∴MN＝2QH，∴|t2﹣3t|＝2×16|t2+5t|，解得：t＝7或1，∴M5（7，4），Q5（﹣7，18）；M6（1，﹣2），Q6（0，﹣3）；综上所述，点M及其对应点Q的坐标为：154 (,) 33M-，154 (,)93Q--；2134 (,) 33M，2134 (,)93Q-；M3（5，2），Q3（﹣5，12）；M4（2，﹣1），Q4（0，﹣3）；M5（7，4），Q5（﹣7，18）；M6（1，﹣2），Q6（0，﹣3）．13．解：（1）△抛物线y=ax2+bx+c（a≠0）与x轴交于点A（1，0）和点B（-3，0），△OB=3，△OC=OB，△OC=3，△c=3，△30 9330a ba b++=⎧⎨-+=⎩，解得：12ab=-⎧⎨=-⎩，△所求抛物线解析式为：223y x x=--+；（2）如图2，连接BC，过点E作EF△x轴于点F，设E（a，-a2-2a+3）（-3＜a＜0），△EF=-a2-2a+3，BF=a+3，OF=-a，△S△BEC=S四边形BOCE-S△BOC=12BF•EF+12（OC+EF）•OF-12•OB•OC=1 2（a+3）•（-a2-2a+3）+12（-a2-2a+6）•（-a）-92=-32a2-92a=-32（a+32）2+278，△当a=-32时，S△BEC最大，且最大值为278．。