大气稳定度课件

第七章 大氣的不穩定度（Atmospheric Instabilities ）● 7.1前言大氣中的水氣來自地表，而後經由平流輸送至相關地區，因而上升運動是形成天氣現象的先決條件之一。

而上升運動則取決於作用在單位氣塊上的力，以及環境大氣的不穩定程度。

至於大氣是否穩定則取決於它的熱力結構，動力結構或兩者組合後的條件，以及運動氣塊（air parcel ）與環境大氣之上述條件的對比。

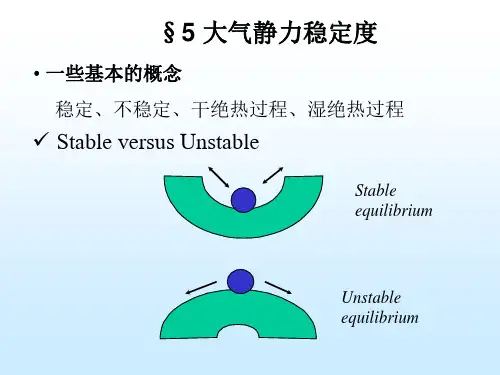
簡單的說，運動後的氣塊是否會到原位是判斷大氣穩定與否的指標。

下圖中附箭頭的小球代表氣塊，半圓或平面則代表大氣。

由而見大氣的三種穩定狀態。

圖7-1 大氣穩定與否之示意圖本章即對此方面問題做進一步的討論。

● 7.2氣象學中的不穩定度在氣象學中，大氣是否穩定有兩種參考標準， 1. 靜力不穩定度（static instability ）或流體靜力不穩定度（hydrostatic instability ），又稱重力（gravitational ）不穩定或浮力（buoyant ）不穩定。

它是以氣塊上升後的溫度為參考標準；如高於新環境的氣溫就是不穩定，反之為穩定。

2. 動力不穩定度（dynamic instability ）或流體動力不穩定度（hydrodynamic instability ）。

它是以氣塊在環境流中，亦即在大氣波中的狀態為依據；如氣塊進入新環境後不能與該處的大氣波動相契合就是不穩定，反之就是穩定。

第一部份：靜力或流體靜力不穩定度兩者均可用氣塊法（parcel method ）測定之。

● 7.3靜力或流體靜力不穩定度 1. 由)(P M M g F -=)(P g ρρ-= 單位容積i.e.，)(22P P g dtzd ρρρ-=…….（7.1）環境（enviroment ） （enviroment ）氣塊 （air parcel ）圖7-2 氣塊法示意圖之一在絕熱（等熵）運動中，如果氣塊運動中其p P 始終與環境之P 相等，即P P P =，則θθρρP P P T T ==，所以)()(22θθθ-=-=P P g T T T g dtzd ……………………….（7.2） i.e.，氣塊垂直加速度22dt z d 0⎪⎩⎪⎨⎧<=>，取決於⎪⎩⎪⎨⎧<=>-0θθP 。

而由於開始時0θθ=P ，在等熵運動中，氣塊0.θθ==const P ，但在新位置上，θθθ∆+=0e ，00θθθδθθ=<=>⇒<=>∂∂=∆P e z z 取決於不穩定中性穩定0<=>∂∂zθ2. 而由pC R PT )1000(=θ可得 0)(1)(1)(11<=>-Γ=+∂∂=∂∂-∂∂=∂∂γθθd p p TC g z T T z P P C R z T T z ………………..（7.3） 式中d Γ為乾絕熱降溫率，γ則是實際觀測到的降溫率。

如果一尚未飽和的氣塊向高空移動，其降溫率就是d Γ，即每升100公尺，溫度約降1℃；此時如果環境大氣之降溫率d Γ<γ，則0>∂∂z θ，即022<dtz d ，穩定，反之為不穩定。

∴大氣是否穩定可由d Γ與γ的相對大小決定，即不穩定中性穩定γ<=>Γd這是乾空氣的狀況。

7.4條件性不穩定如果大氣中有水氣但尚未飽和，則其中一氣塊上升時，是乾絕熱運動；一旦達到飽和，就成了濕絕熱運動。

所以如果，m d γγ>>Γ，則（7.3）式就有二種狀況，即 飽和前0)(11>-Γ=∂∂γθθd Tz ，穩定 飽和後由於()0<-γγm ，此時上升氣塊的溫度會高於周圍（環境）空氣之溫度，致022>dtzd ，不穩定此間分際可由垂直運動的變率獲得dtdw dt dz dt dw w w dt d E K dt d ===)2(.).(2 i.e.，dz dtdwwdw =，此表示， 氣塊之動能變率，來自它以加速度•w 位移z δ。

式中圖7-3 氣塊法示意圖之二)ln ()(1**P d g T R T R P dPg g dP dz d d -=-=-=ρ∴)ln ()())ln ()((******P d T T R P d G T R TT T g dz dt dw wdw P d d P --=--== i.e.，])ln ()ln ([)(212121**2122⎰⎰---=-P d T P d T R w w P d))(ln(**21T T P P R P d -=…………………………………….（7.4）式中**&P T T 為1至2之平均值。

這就是說，只要上升空氣之虛溫>*P T 環境空氣之虛溫*T ，則02122>-w w ，即氣塊之垂直動能就會增加，亦即上升有正的加速度，是為不穩定。

反之則為穩定。

又知，在斜溫圖上，的面積成正比。

能量，其大小與斜溫圖=-⎰21*)ln (P d T∴如果**T T P >，即Z T Z T γδδγ->-*00*0 i.e. 在上升氣塊未飽和前γγ>=d P T ，穩定但在飽和後γγγ<=m P ，不穩定圖7-4 氣塊法示意圖之三LFC 的高度對此影響很大。

如正區面積>負區面積（代表推舉氣塊至LFC 所需的能量）即為條件性不穩定，其不穩定度可由正負面積比定之。

7.5對流或位勢不穩定度（convective & potential instability ）由以上狀況可知，乾絕熱運動之穩定度由0<=>∂∂z θ，即0<=>-Γγd 決定；，z，0z濕空氣的絕熱運動之穩定度，則由0)3(<=>+∂∂≅∂∂r zz θθ，即0<=>-γγm 決定。

i.e.，當0<∂∂zEθ時為，對流亦即位勢不穩定。

由於()z r z r z z E ∂∂+∂∂=+∂∂≅∂∂33θθθ，所以，如果0<∂∂zr，且z r z ∂∂<∂∂3θ時z E ∂∂θ會小於0，濕絕熱對流不穩定。

即「下濕上乾之空氣柱具位勢不穩（定）度」。

在斜溫圖上此種不穩定度可由m γγ<=>判定，即「當一層空氣之特徵曲線（characteristic curve ）之斜率隨高度偏向假絕熱線右（左）邊時，該氣層為位勢穩定（不穩定）。

」〝A layer is potentially stable or potentially unstable according as its characteristic curve slopes upward to the right or to the left of the pseccdoadiabats on the thermodynamic diagram.〞此處的〝特徵曲線〞原為Rossby diagram （以d θlog 為縱軸，混合比為橫軸之熱力圖）上d θ與r 交點之連線，在現用之斜溫圖上，可以各層空氣LCL （又稱等熵凝結面，isentropic condensation level ）連線替代之（LCL 處之氣壓、溫度通常稱之為凝結氣溫與凝結溫度；而相對應之點則稱為特徵點characteristic point 、絕熱飽和點或絕熱凝結點（adiabatic saturation （condensation ）point ）。

各特性點即LCL 高度可以下述近似式求得：)(220)(120&&321321ftF d mC d T T T T h ︒︒-=-=Convective parameters ： 1.Stability indicesSI （The Showalter index ）={*500500P e T T -*由850T 沿d Γ上升至LCL ，而後沿m T 至500hPa 時之TLI （The lifted index ）=500500P e T T - 〈LI 與SI 0<時不穩定，SI LI ≥〉 K （K index ）={)(***700700**850*5008504342143421d d T T T T T --+-*potential instability 低層降溫率 **available moisture in the boundary layer ***reduction of buoyancy through entrainment of dry air near 700hPa〈K 與TT 0>時不穩定；35>K ，40>TT 可視為臨界值〉 TT （The totals-totals ）=85050085050085085022d d T T T T T T +-=-+如700hPa 之)(d T T -，即溫度露點差（dew point depression ）為C ︒5，則K=35 ex.：如850T ，850d T 及500T 分別為15，10及-15C ︒，則TT=55。

2.對流可用位能（CAPE ）=斜溫圖上正面積所代表之能量。

⎥⎦⎤⎢⎣⎡--=-⎰⎰2121**2122ln ln )(21P d T P d T R w w e P d ∴CAPE dz z T z T z T g ELLFC e e P ⎰-≡)()()(***，or ⎰⎥⎦⎤⎢⎣⎡-≡EL LFE e eP kg J dz z z z g )()()(θθθ3.對流整體李察遜數（convective bulk Richardson number ）（1）李察遜數慣性力浮力垂直風切靜力穩定度∝∝=∂∂∂∂=22)()(ln zV z gRi θ（2）整體對流李察遜數2SCAPE Ric ≡，250060002)(21u u S -= 式中5006000&u u 為高度6km 與0.5km 處之氣壓權重平均風向量7.6氣層穩定度（layer stability ）大氣並非只有「氣塊（air parcel ）」會作垂直運動；整層空氣升降常有發生，因而氣層的垂直運動與所導致之穩定度改變亦需討論。

設S 代表氣層之穩定度，則氣層在1z 與2z 時的穩定度，分別為又由質量守恆知：0)(=ρδz A dt d，式中A 為氣層底面積，z δ為厚度，ρ則為密度。

i.e.，ρρδδ•••--=A A z z ，而在乾絕熱運動中z w ∂∂Γ-=Γ•，即zzδδ••-=ΓΓ. 21122211ln ln z z S S z gS z gS δδδθδδθδ=⇒⎪⎪⎭⎪⎪⎬⎫==……（7.5） 乾絕熱垂直運動中，氣層之穩定度僅隨厚度變，即2112z z S S δδ=，亦即氣層穩定度比與其厚度比成反比。