第2章 动力响应理论
2.1引言
机柜结构动力响应的计算机仿真分析是以设备动力响应理论为基础的，是进行设备结构动力响应研究的一种有效手段。论文中主要研究设备动力响应两个方面的内容：设备结构固有特性分析和结构在地震波作用下的响应分析。固有特性分析可以得到结构的固有频率和固有振型，是进行响应分析的基础；地震波响应分析将得到设备响应的时间历程变化。在使用有限元工具对结构进行建模、分析之前必须掌握结构动力响应的理论和相关的有限元基本原理。因此，本章重点叙述了与设备结构动力响应相关的机械振动学理论及其有限元仿真技术。
2.2结构动力响应分析相关理论
2.2.1结构固有特性分析理论
机柜设备结构的固有特性包括固有频率和振型，是响应分析的基础。通过进行结构的固有特性分析可以使设计有效地避开结构的共振频率。机柜设备是一个复杂振动系统，在理论分析过程中，常常可以把机柜设备简化为多自由度集中参数系统。
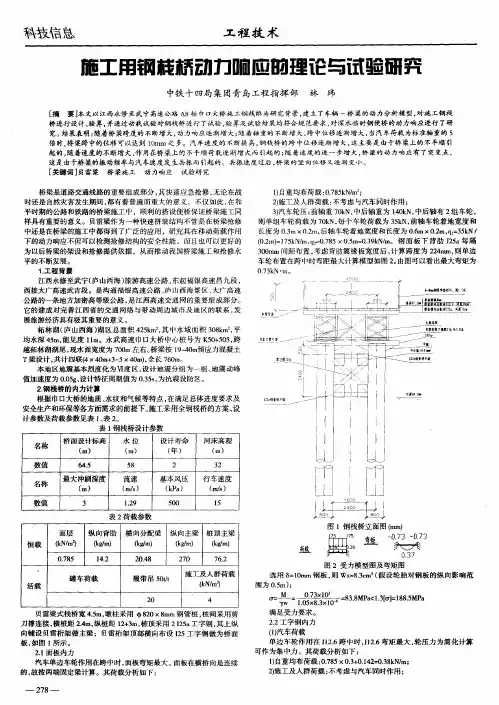
一般，多自由度系统的自由振动方程可以写成如下形式：
{}...
[]()[]{()}[]{()}{0}M x t C x t K x t ++= (21)a -
式中：[]M ， []C 和[]K 分别为系统的质量矩阵、阻尼矩阵和刚度矩阵;()x t 、
.()x t 、..
()x t 分别为系统的位移列向量、速度列向量和加速度列向量。而多自由系统的无阻尼自由振动方程可以写成如下形式:
{}..
[]()[]{()}{0}M x t K x t += (21)b -
通常系统的自由振动是简谐振动，所以可以假设式 (21)b -的解为： {()}{}sin x t X pt = (22)- 式中：{}X 为系统的振幅列向量;p 为系统的自由振动频率。将(22)-代入(21)b -，就可以得到系统的振型方程，其具体形式如下：
2[][]{}{0}K M X p -= (23)- 可以看到，式(23)-是一个齐次线性方程组，根据线性代数知识，它具有非零解的充分必要条件为系数矩阵的行列式为零，亦即有下式成立。
2[][]0K M p -= (24)- 式 (24)-称为系统的特征方程或频率方程，他是关于
2p 的n 次代数方程。解之，
我们可以得到n 个解。具体如下： 2222123n p p p p ≤≤≤≤ (25)-
若系统为正定系统，则有 20(1,2,3,
,)i p i n ≥= (26)- 式中：i p 为系统的第i 阶固有圆频率。将i p 分别代入系统的振型方程（2-3）中，可以解得与之对应的振幅列向量{}i X ，也称为系统的主模态或主振型。 注意：
（1）系统固有频率和模态的数目与系统拥有的自由度数相同，n 自由度系统必有n 阶固有频率和模态（主振型）。
（2）系统的固有频率仅与系统的质量矩阵和刚度矩阵有关，而与外界干扰力无关，它们是系统本身的固有性质。
（3）系统的主振型{}(1,2,3,,)i X i n =表示系统以频率i p 作自由振动时系统的各 个自由度的振幅的相对比值。
2.2.2结构冲击响应分析理论
通过系统的自由振动方程，可以解得系统得固有频率和主振型。在冲击激励作用下，多自由度系统振动将作受迫振动。利用激励响应理论可以解得系统受迫振动过程中系统的响应。
2.2.2.1 多自由度系统的受迫振动方程
多自由度系统的受迫振动方程可以写成如下形式：
...
[]{()}[]{()}[]{()}{()}M x t C x t K x t f t ++= (27)- 式中：{()}f t 为系统受到的激励力向量，如果系统受到基础加速度激励则激励力向量就是该加速度系统的等效惯性力；其他符号的意义同式（2-1）。通常情况下，系统的各个自由度之间存在耦合，方程（2-7）中的[]M 、[]C 和[]K 不是对角阵，方程难以求解。为了得到系统的响应必须选择适当的坐标系将（2-7）式解耦。
2.2.2.2振动方程的解耦
（1）正则振型与正则振型矩阵
在对振动方程解耦之前先介绍系统的正则振型与正则振型矩阵的概念。通过式（2-3）与式（2-4）已经求得系统的各阶固有频率(1,2,3,
,)i p i n =和相应的主振型{}(1,2,3,,)i X i n =。令
1{}{}(1,2,3,,)i i i x X i n μ== (28)-
使得 {}[]{}1(1,2,3,,)T
i i i M X M X i n === (29)- 式中：{}i X 为第i 阶正则振型；i μ为待定系数。将（2-8）带入（2-9），可以得到
(1,2,3,,)
i i M i n μ== (210)-
将（2-10）带入（2-8）可得到各阶正则振型，进而可以写出正则振型矩阵，具体如下：
~123[]{{}{}{}{}}n P X X X X = (211)- （2）振动方程解耦
由于各阶主振型关于[]M 、[]K 是正交的，各阶正则振型也是关于[]M 、[]K 正交的，可以利用正则振型矩阵来对振动方程进行解耦。选取一组广义坐标()q t 又称为主坐标，令
{()}[]{()}x t P q t = (212)-
将（2-12）代入（2-7）中，并且将方程两端左乘[]T P ，则可以得到解耦后的振
动方程：
..~.~
[]{()}[]{()}[]{()}{()}I q t C q t q t f t ++Λ= (213)a - 式中，[]I 为单位阵；[]Λ伪对角阵，其对角限元素为各阶固有频率的平方；~[]C 为对角化的阻尼阵，采用比例阻尼假设，其对角线上的第i 个元素为： ~
2i i c p αβ=+ (213)b - ~{()}f t 为外力对角阵，可进一步表示为：
~~{()}[]{()}T f t P f t = (213)c - 式（2-13a ）是一个非齐次线性方程组，其中第i 个方程可以写成：
..~2()()()()i i i i i q t c q t p q t f t ++= (214)- 式中，()i q t 为第i 个主坐标。
2.2.2.3单自由度系统对任意激励的响应
式（2-14）在形式上与单自由度系统的振动方程一致，可以将上式看作单自由系统的受迫振动方程。求解方程（2-14）即计算单自由度系统对任意激励的响应。单自由度系统对任意激励的响应，可以看作系统对一连串单位脉冲响应的叠加。
单自由度系统对单位脉冲的响应可以用下式表述：
1sin()0()00
pt id id i e p t t mp h t t ξ-?≥?=??
式（2-15）表示的是单自由度系统对发生在t=0时刻的单位脉冲的响应，单自由度系统对发生在任意时刻t τ=的单位脉冲的响应可以写成如下形式： ()1sin(())()0i p t id id i e p t t mp h t t ξτττττ--?-≥?-=??
(216)-
则方程（2-14）所示的单自由度系统对任意激励的响应可用杜哈美积分表示为： ~0()()()t i i i q t f h t d τττ=-? (217)-
式（2-15）、（2-16）、（2-17）中，~
2i i c p ξ=
为式（2-14）表示的单自由度系统的阻尼比；21id i p p ξ=-为考虑阻尼时系统的第i 阶固有频率。式（2-15），（2-16）称为单自由度系统的脉冲响应函数。至此，第i 个自由度的响应己经求得。式（2-17）表述的()i q t 为振动方程的全解，包含了瞬态解和稳态解两部分。
2.2.2.4多自由度系统任意激励的响应
上节求得了第i 个自由度的响应解。同理可以解得其他自由度的响应解，全部自由度的解可以写成向量{()}q t ，具体形式如下：
~0{()}[()]{()}t q t h t f d τττ=-? (218)-
式中，~{()}f t 由式~
~{()}[]{()}T f t P f t =确定。 上式表示的响应为系统在主坐标下的响应。要得到原物理坐标下的响应{()}x t 只要将式（2-18）代入式（2-13）。具体如下：
~~~0{()}[]{()}[][()][]{()}t T x t P q t P h t P f d τττ==-? (219)- 也可以写成和的形式：
~{()}{}()
(1,2,3,,)n i i i x t X q t i n ==∑ (220)-
式中，
~
{}
i
X为第i阶正则振型，可由式（2-8）确定，()
i
q t为杜哈美积分，可由
式（2-17）确定。
2.3 结构动力响应的有限元仿真技术
2.3.1有限元分析的一般步骤
有限元方法是求解微分方程的一种非常有效的数值方法，其基本思想是用分片函数（单元形状函数）来逼近原函数，也就把无限自由度问题转化为有限自由度问题求解，通过求解一个线性方程组，得到原问题的近似解。有限元方法的名称是Clough在处理平面弹性问题时，第一次提出使用的。有两种通常与有限元方法相关的方法。一种是力法或称作柔度法，它使用内力作为问题的基本未知量;另一种是位移法或称作刚度法，它使用节点位移为问题的基本未知量。这两种方法在分析中得出不同的未知量（力或位移），并得出与其公式相关的不同的矩阵（柔度矩阵或刚度矩阵）。目前绝大多数的通用有限元程序，如ANSYS，HYPERMESH，ABAQUS等，采用的都是位移法(或刚度法)。有限元方法涉及用相互连接的、称作有限单元的小单元来模拟连续结构。使用有限元工具进行分析计算通常有三个步骤：第一，把对象进行合理的简化建立其有限元模型；第二，按照实际的工况对模
型施加约束和激励并进行必要的求解设置，然后开始求解；第三，待求解结束后，综合运用理论、经验或实验结果对计算结果进行分析、论证。
2.3.1.1有限元分析模型的建立
在有限元分析过程中，从结构对象的实际模型到计算模型的简化和物理特征提取的过程称为结构对象的特征建模。特征建模的过程也就是对结构实际模型进行简化的过程。实际工程中的结构对象可以分为两种：一种是离散体结构，另一种是连续体结构。杆梁结构体系是最常见的离散体结构，由于其本身存在有自然的连接关系即自然节点，一般可以直接基于这些节点进行单元划分和离散。而连续体离散化过程需要人为地在连续体内部和边界上划分节点，以分片（单元）连续的形式来逼近原来复杂的几何形状。一般情况下，连续体的有限元分析特征模型和结构对象的实际模型不是直接对应的，需要更好地进行问题的特征建模。它需要分析人员具有相应的数学和力学基础、工程分析经验，以及对软件的熟练操作，以便做出准确合理的简化，得到既能反映实际结构对象的特征，又具有合理离散方案的有限元计算
模型。
在机柜设备结构有限元分析中，一个重要的问题就是如何建立逼真的有限元模型。近40年来实体造型理论和技术的成熟以及大批实用实体造型软件的出现，现在可以很轻松的建立分析对象的几何模型。这样，有限元模型的逼真程度主要取决于物理特征建模，即选定单元类型、设定材料特性、确定边界条件、约束和载荷。
2.3.1.2有限元模型的求解
有限元动力响应分析的求解阶段，程序根据前处理阶段建立的网络模型、模型的材料数据、约束和激励的信息，通过单元位移插值函数和材料的本构关系计算模型中各个单元的质量矩阵、阻尼矩阵和刚度矩阵，然后将各个单元的单元矩阵组装成模型的整体矩阵，再求解模型的固有频率及振型、位移响应、应力响应等结果数据。
在将建立的有限元模型提交给计算机计算之前，需要指定一些分析计算的控制信息，如采用何种数值算法、需要提取那些分析结果以及模型的动力参数等等。进行合理的求解设置有助于减少计算需要的时间、提高计算效率，在一定程度上还可能影响得到的分析结果。
2.3.1.3有限元分析结果的处理
由于有限元方法的近似性，分析结果不可避免的存在误差。有限元模型的网格密度会影响有限元分析结果的精度。在一定范围内，适当加大网格的密度，有限元分析的精度会有所提高。但是，网格精度对有限元分析结果精度的影响不是绝对的，当结果的精度提高到一定程度后，再加大网格的密度，计算结果的精度不仅不会提高反而会降低。正由于有限元法是一种工程近似求解的方法，存在误差，所以在用有限元软件进行工程分析计算时，必须对结果进行分析评估。通常以下方式来判定有限元分析结果正确与否：
（1）将分析结果与理论计算结果进行比较。
（2）将分析结果与实验结果进行比较。例如，模态实验可以作为判别有限元模型正确与否的标准。
（3）根据己有的经验判断分析结果。
了解有限元分析结果的特点和产生误差的原因对理解和解释有限元分析结果具有重要的意义。只有经过检验为正确的分析结果才是真正对工程应用有意义的。
2.3.2 ANSYS用于机柜设备结构动力响应分析的可行性
ANSYS软件是结构、热、流体、电磁、声学于一体的大型CAE通用有限元分析软件，可以广泛应用于核工业、铁道、石油化工、航空航天、机械制造、能源、汽车交通、电子、造船、轻工等一般工业及科学研究。ANSYS软件具有丰富和完善的单元库、材料模型库和求解器，从而保证了其出色的分析计算能力。ANSYS 的结构分析计算功能非常强大。它可以完成结构静力分析、结构动力学分析和结构非线性分。其中，ANSYS可以进行的结构动力学分析类型包括:模态分析、瞬态动力学分析、谐波响应分析及随机振动响应分析。本论文涉及到ANSYS软件的动力学分析功能的模态分析、瞬态动力学分析和随机振动分析三种分析类型。
2.4 本章小结
本章对设备结构动力响应的相关理论做了介绍，明确了论文中涉及的设备动力响应的两个方面的内容:结构固有特性分析和结构在瞬态冲击激励作用下的响应分析。随后，对结构动力响应的有限元仿真技术进行了叙述，并在说明有限元仿真的一般步骤的基础上探讨了有限元仿真过程中应注意的问题和计算结果解释的常用方法。本章不但为后续章节的复杂结构分析工作提供了理论保证，而且还奠定了软件使用基础。
1.3.2风对高层建筑的作用 高层建筑，特别是超高层建筑大都具有柔性大、阻尼小的特点，这样使得风荷载成为其 结构设计时的主要控制荷载。风荷载作用于高层建筑，会产生明显的三维荷载效应，即顺风向风荷载、横风向风荷载和扭转风荷载。在三维动力风荷载的作用下，高层建筑在顺风向、横风向和扭转方向产生振动。 第1章绪论 1.3. 2.1顺风向风效应 我国荷载规范[80】中给出了高层建筑顺风向平均风荷载的计算公式: 矶=刀:户:拜，叽(l一10) 式中:哄为高层建筑:高度处的平均风压;叽为10米高度处的基本风压(我国规范Is0】中 给出的基本风压是基于B类地貌条件的，其它地貌条件下要进行相应的转化);户:和户，分 别为风压高度系数和体型系数;几为考虑脉动放大效应的风振系数。 一般认为顺风向脉动风荷载符合准定常假定，即顺风向风荷载的脉动主要由顺风向风速 脉动引起。Davenportl吕’l和几mural82]等提出利用脉动风速功率谱转化得到顺风向风荷载功率 谱的方法，许多学者还通过风洞试验的方法得到高层建筑顺风向风荷载谱的经验公式183.851。 高层建筑顺风向振动以一阶模态振动为主，一般假定高层建筑一阶振型为线性，但近年 来部分学者对线性假定提出异议，并给出了振型修正的计算方法186-87]，顺风向风振的计算中 必须考虑风荷载的水平和竖向空间相关性188】。 1.3. 2.2横风向风效应 横风向风荷载由尾流激励、来流紊流和结构横向位移及其对时间的各阶导数引起的激励 等因素构成，但主要是由结构尾流中的漩涡脱落引起建筑物两侧气压交替变化所致189】。当 建筑物高度较低或高宽比不大时，结构的顺风向风致响应大于横风向响应;而近年来大量的风洞试验和现场实测证明，当高层建筑的高宽比大于4时，其横风向风振响应往往会超过顺风向响应，成为结构设计的控制性因素190]。 由于横风向风荷载机理复杂以及横风向振动的重要性，使得这方面的研究一直是风工程 界的热点问题。横风向风荷载不符合准定常假定，因此横风向风荷载谱不能根据脉动风速谱得到1841，风洞试验是研究高层建筑横风特性的主要手段。国外的ohkuma[01]、H.choil92)以及 国内的梁枢果[93]、顾明194]、徐安【84]等都相继提出了横风向风荷载功率谱的数学模型。横风向风振应通过随机振动理论计算，vicke夕95】、Kareem[9e]和Kwoklgv]等对高层建筑横 风向振动的计算方法进行了详细的阐述和探讨;梁枢果等给出了矩形高层建筑横风向风振响应的简化计算方法[98]。 1.3. 2.3扭转风效应 扭转风荷载则是顺风向紊流、横风向紊流和漩涡脱落共同作用的结果l”]。高层建筑的 浙江大学博士学位论文2008 风致扭转力矩与结构的平面形状有很大关系，往往平面形状不规则的高层建筑会引起较大的风致扭矩，从而导致较大的扭转响应。xIEJi而ng等199]在研究多幢高层建筑风扭矩的基础上， 提出了结构“等效偏心”的概念。
第八届全国振动理论及应用学术会议论文集，上海，2003年11月 移动载荷作用下连续梁的动力响应分析 钟卫洲1, 2，罗景润1，高芳清3，徐友钜1 （1.中国工程物理研究院结构力学研究所，绵阳 621900；2.中国工程物理研究院研究生部，绵阳 621900; 3.西南交通大学振动与强度实验室，成都 610031） 摘要： 本文以磁悬浮交通轮轨接触车桥动力行为研究为背景，把车辆对桥梁的动力作用简化为一个稳态力和一个低频扰动力，把连续钢桥梁简化为伯努力—欧拉梁，建立了车辆过桥的力学模型和振动微分方程，运用模态分析法得到了该微分方程的解析解，分析了连续桥梁频率方程、模态表达式以及低阶模态。援引德国TR06和连续钢梁的参数对不同速度的移动荷载下连续钢梁的动力响应进行计算分析，给出了相应条件下连续梁的动挠度曲线（w-t图和w-x图），并分析了桥梁的动力响应特征。本文的研究为评定桥梁在高速车辆作用下的稳定性和安全性提供了参考。 关键词： 连续梁；模态分析；动力响应；动挠度 Dynamic Response Analysis of Continuous Beam Under Moving Load ZHONG Wei-zhou 1, 2, LUO Jing-run 1, GAO Fang-qing3, XU You-ju 1 (1.Institute of Structural Mechanics of CAEP, Mianyang 621900; 2.Graduated School of CAEP, Mianyang 621900; https://www.doczj.com/doc/5b1059042.html,boratory of Vibration and Intensity of SWJTU, Chengdu 610031) Abstract: This paper is based on the background of the study of the dynamic behavior between maglev vehicle and guideway. The moving force exerting on the bridge is simplified as a steady force and a pulsating force with low frequency. The continuous steel beam is taken as Bernoulli-Euler beam, then the corresponding force model and vibrating equation of the bridge is established. The modal analysis method is applied to solve the equation of vibration. Frequency equation, analytical solution of mode of the beam and the lower modes are analysed. By quoting the data of TR06 of German, the dynamic response of continuous beam is obtained under moving vehicle at several typical speeds. The results of this paper can be taken as reference to assess security and stability of a bridge under moving load.
用有限元方法进行摩托车动力响应分析 文>>月辉史春涛骞郝志勇 摘要本文采用有限元方法对某125型骑式摩托车进行了动力响应分析。文章首先建立了摩托车整车的有限元模型，并利用该模型进行摩托车整车的动态特性计算，取得了和实验模态分析一致的结果。而后分析了摩托车在发动机激励和路面不平度激励下的整车动力学响应特性，得出了具有工程参考价值的结论。 关键词摩托车应力有限元法 本文采用有限元方法研究了摩托车整车结构的动态特性，并进行了在各种激励作用下的动力响应分析，得到了发动机车架的应力场，可用于进一步的摩托车强度分析。 1、摩托车有限元模型的建立 摩托车有限元模型如图1所示。 摩托车的车架结构大多是由各种截面形状的梁组合而成的空间框架结构，而且其截面尺寸，包括直径、壁厚，与构件长度相比很小，因此选用空间的直梁或者曲梁单元来离散车架结构，而车架的一些板件和加强盘可以采用空间板元模拟，各种梁单元的截面力学特性可用有限元程序的前处理模块或CAD软件计算。 摩托车的发动机具有较大质量，同时也具有很大刚度。考虑到发动机在车体结构中所起的作用及变形小的特点，将发动机简化为若干个板单元，这些板的总质量应与发动机的质量相同。然后，根据发动机与车架的实际连接方式，将由这些板单元模拟的发动机与车架组装到一起。 摩托车的减振器主要作用是支撑车体并缓和振动与冲击。考虑到减振器的结构与作用，简化后减振器的模型在受到载荷时应具有较大的轴向位移，同时又要有较大抗弯刚度。本文把减振器简化为一种梁单元和弹簧阻尼单元的综合体——轴向刚度由弹簧阻尼单元提供，而抗弯刚度由梁单元提供。 摩托车车轮主要由轮胎和轮辋组成，其中轮胎直接与路面接触，与摩托车悬挂共同缓和摩托车行驶时所受到的冲击，并协助减振，轮辋是固定轮胎的骨架，它与轮胎共同承受作用在车轮上的负荷。轮辋可以采用若干个梁单元模拟，轮胎
弹性联轴器运动与动力特性 1.1 弹性联轴器的刚度和阻尼 弹性联轴器由于具有能产生较大弹性变形和阻尼作用的弹性元件，因此除能补偿两轴相对位移外，还能起缓冲和吸振的作用。弹性联轴器能适应载荷的波动，所以其应用较广，类型也较多。这种联轴器的缓冲和吸振性能主要与其刚度和阻尼有关。 联轴器的刚度可分为径向刚度、周向刚度和扭转刚度。由于载荷变化多数以扭矩波动形式出现，由此引起的振动也是以扭转振动为主，所以联轴器最主要的刚度是扭转刚度。扭转刚度易产生单位扭转变形所需的扭矩表示。通常，由于传动轴系中其它零件的刚度都比弹性联轴器的刚度大得多。所以为了简化起见，其它零件的弹性可以略去不计。仅考虑联轴器弹性，并根据这一情况以联轴器的刚度作为传动轴系的刚度。 刚度可用下式表示： C=T/（3-1） 式中 T——联轴器传递的扭矩； ——在扭矩作用下两半联轴器的相对扭转角。 当轴系接近发生共振时，刚度随扭矩增大而增大，改变传动轴系的固有频率与振动频率之间的关系，就能避开共振。 弹性联轴器在传递不稳定扭矩的过程中，弹性元件的弹性变形随扭矩的改变而增减。由于变形的不稳定，在弹性元件相对运动的接触表面上产生外摩擦，同时在弹性元件内部还存在内摩擦。这些摩擦将吸收一部分动能转化为热能，使温度升高。这就是联轴器的阻尼作用。阻尼作用能实现缓冲和衰减振动。联轴器的阻尼性能可以用阻尼系数表示。它是每一次载荷循环中产生的阻尼能和储存在扭转弹性元件中的变形能之比，即ф=W d/W e。在振动运动微分方程中，粘滞阻力系数用γ来表示，它与阻尼系 数之间的关系为γ=，ω为振动频率或绕动力矩变化频率。阻尼系数大，由于摩擦而消耗的能量就多，反之，阻尼系数小，由于摩擦而消耗的能量就少。 弹性联轴器一般都有缓冲和吸振功能，但是具有某一定值弹性的联轴器，并不是在任意的变扭矩作用下都能产生减振的效果，有时反而会引起更强烈的振动。其原因不在于此联轴器的刚度大小。可见，只有刚度和整个传动轴系的其他参数和载荷协调时，才能产生减振效果。因此，必须根据课题条件，通过计算来定出联轴器的刚度。 1.2 周期性载荷作用下的动力特性计算 对于某一已定的传动轴系，转动惯量和固有频率可由计算求得，如果已知所传扭矩的变化规律，如振幅和频率等，就能建立起轴系在扭转振动式的运动微分方程，对该方程求解，即可得到所需的联轴器的刚度。 为了便于求解运动微分方程，需要对传动轴系中联轴器的主动和从动两侧的转动惯量和刚度作力学模型的简化。根据具体结构情况，可以将轴系简化为若干个等效转动惯量圆盘，以具有某一刚度的周联系起来。通常比较典型的是简化为两个等效的圆
基于 MATLAB 实现对结构动力响应的几种算法的验证 1. 算例 首先，本文给出一算例， 结构在外力谐振荷载 P (t ) = P 0 sin θt 作用下，分别利用理论解法，杜哈梅积分， Wilson-θ 法求出该结构的位移时程反应。其中： m = 3.5×103 kg ， P 0 = 1.0×104 N ， k =1.3584515×107 ，ξ=0.05 ，θ=52.3s ?1 ，ω=62.3s ?1 ， ? D ω= ω 1-ξ2 =62.222 ，初始位移、速度v (0) = 0 ，v (0) = 0 ； 2. 算法验证 2.1 理论解法 运动方程为： mv+cv+kv=0P sin t ?由线性代数解出其理论解为: ]cos 2)sin -[(] 4)-[(t] sin ) -(2cos [2] 4)-[(t] sin ) 0()0(cos )0([2 2222222022222 2 2 2 22 t t m P t m P e v v t v e v D D D t D D D t θξωθθθωθωξθωωωθωωξωξωθωξθωθωωξωωξωξω-++-+ ?++++=-- 由于初始位移v(0) =0 ，v(0) =0 ；则： ]cos 2)sin -[(] 4)-[(t] sin ) -(2cos [2] 4)-[(222 222220 22222222220 t t m P t m P e v D D D t θξωθθθωθωξθωωωθωωξωξωθωξθωθξω-++ -+ ?+=- v(t ) =-3.115t e ? 1.05269898×410-?[6.230cos62.222t ?18.106sin 62.222t] +2.012808757 6 10-??[1146sin 52.3t ?325.829cos52.3t] 可以用 MA TLAB 进行编程分析，画图位移时程图，详细程序见附录。 2.2Wilson-θ法 Wilson-θ法是Wilson 于1966年基于线性加速度法的基础上提出一种无条件收敛的计算方法。该方法假定在θt ?时程步长内，体系的加速度反应按线性变化。对于地震持续时间内
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 振!动!与!冲!击 第"#卷第$期 %&’()*+&,-./(*0.&)*)123&45 -678"#)68$"99:! 膜结构风荷载和风致响应研究进展( (国家自然科学基金优秀创新群体基金##9$"=99$%和教育部/高等学校骨干教师资助计划0项目收稿日期!"99#;9";=# 第一作者顾!明男"教授"=<#>年@月生 顾!明!陆海峰 #同济大学!土木工程防灾国家重点实验室"上海!"999<"% !!摘!要!膜结构是近年来在大跨度空间结构中广泛采用的结构形式&由于膜材料柔软)质轻的特点"膜结构对风 的作用却十分敏感"风荷载是该类结构设计中的主要控制荷载"在响应分析中必须考虑气动弹性效应"但至今仍没有行之有效的分析方法&从风洞试验研究)响应分析方法和数值模拟等方面详细评述了膜结构风致振动的研究进展"并给出了今后研究的建议& !!关键词!膜结构"风致振动"气动弹性 中图分类号!0’$<$8$!!!文献标识码!* !"引"言 膜结构是以建筑织物...膜作为覆面材料和受力 构件的一种空间结构形式&通过高强度)柔性的薄膜材料与支撑体系的结合"形成具有一定刚度的稳定曲面来承受外荷载"在大跨度空间结构中得到日益广泛应用和蓬勃发展#/I W JF U e 1D Z ‘U 6J ""999’=($/W I ]U TI g F G I =8 ""99"’?(%&建于=<N "由=>个连成一排的双锥膜单元覆盖"充分体现了膜结构造型自由轻巧)制作简易)安装快捷)节能等优点"已成为当地的标志性建筑#/F W K F W "=<<<’"(%$新千年 到来之际"建于伦敦的千年顶#0TFC D 77F JJD HN 16N F "图"%则集中体现了"9世纪建筑技术的精华#/I W JF U e 1D Z ‘U 6J ""999%& 图=!丹佛国际新机场 图"!伦敦千年顶 由于膜材料柔软)质量轻的特点"膜结构对地震荷 载有良好的适应性"对风的作用却十分敏感"风荷载是该类结构设计中的主要控制荷载&合理估计膜结构的风致动力响应并采取有效措施保证结构的强度和耐久性"是膜结构设计中的重要环节&佐治亚穹顶建成$年后的=<<#年"即在一次强风大雨袭击下有四片薄膜被撕裂"撕裂长度达=9余米&佐治亚穹顶的原设计风速是="@‘N h T "而事故发生当天的最大风速记录只有@9‘N h T #杨庆山""99"’$>(%&韩国为"99"世界杯建造 的济州岛体育馆#4TF f H d 6W 7]4H\2G I ]D HN %的膜屋盖 曾先后两次在台风袭击下出现膜材撕裂的现象&国内亦有一些膜结构被风撕毁的报道&尽管如找形)静力荷载分析)裁剪等一系列膜结构设计的问题都已经取得长足的进展#3I EF We *EF 7"=<@"$’F G I JD F G I 78" "999$/7F G P D JK F We (I N N E ""99=$C I HW D J e C 6G W 6 "=<<@$2TD N I ]I e0I ]I "=<<=%"但和高层)高耸)桥梁结构相比较"膜结构至今仍没有一套令人满意的风致振动分析方法"不能满足设计和使用的需要&这种状况近几年来正逐步受到了工程界的关注& 本文从风洞试验)风振响应计算和风荷载数值模拟这三个主要方面总结了膜结构抗风研究的研究状况"指出了存在的问题"并讨论了值得研究的方向& #"膜结构风振的特点 !!膜结构的应用始于=<>9年代"最早出现的是充气膜结构"早期的研究也主要针对充气膜结构"后来随着张拉膜结构的广泛应用"研究重点也向此方向转移& 膜结构多为复杂的三维空间曲面"建筑造型鲜有雷同"这就导致结构表面风压分布的个体差异显著&由于膜结构的水平跨度往往大于垂直高度"结构表面 万方数据
车辆动力学概述 回顾车辆动力学的发展历史，揭示车辆动力学研究内容及未来发展趋势，对车辆特性和设计方法也作了简要介绍。 1.历史发展 车辆动力学是近代发展起来的一门新兴学科。其发展历史可追溯到100多年前[1]，直到20世纪30年代初人们才开始注意车轮摆振问题等；而后一直到1952年间，人们通过不断研究，定义了不足转向和过度转向，建立了简单的两自由度操纵动力学方程，开始进行有关行驶平顺性研究并建立了K2试验台，提出了“平稳行驶”概念，引入前独立悬架等；1952年以后，人们扩展了操纵动力学分析，开始采用随机振动理论对行驶平顺性进行性能预测，理论和试验两方面对动力学的发展也起了很大作用。然而，在新车型的设计开发中，汽车制造商仍然需要依赖于具有丰富测试经验与高超主观评价技能的工程师队伍，实际测试和主观评价在车辆开发中还有不可替代的作用。 2.研究内容 严格地说，车辆动力学是研究所有与车辆系统运动有关的学科。它涉及范围很广，除了影响车辆纵向运动及其子系统的动力学响应（纵向动力学）外，还有行驶动力学和操纵动力学。人们长期以来习惯按纵向、垂向和横向分别独立研究车辆动力学问题，而实际情况是车辆同时受到三个方向的输入激励且各个方向运动响应特性相互作用、相互耦合。随着功能强大的计算机技术和动力学分析软件的发展，我们已经有能力将三个方向的动力学问题结合起来进行研究。 纵向动力学研究车辆直线运动及其控制的问题，主要是车辆沿前进方向的受力与其运动的关系，按工况不同分为驱动动力学和制动动力学两大部分。与行驶动力学有关的主要性能及参数包括悬架工作行程、乘坐舒适性、车体的姿态控制及轮胎动载荷的控制等；而行驶动力学研究的首要问题是建立考虑悬架特性在内的车辆动力学模型。操纵动力学内容相当丰富，轮胎在其中起着相当重要的作用；通常操纵动力学研究范围分为三个区域，即线性域、非线性域和非线性联合工况。 3.车辆特性和设计方法
７０ ＩｎｄｕｓｔｒｉａｌＣｏｎｓｔｒｕｃｔｉｏｎＶｏｌ畅４５，Ｎｏ畅５，２０１５工业建筑 ２０１５年第４５卷第５期石油化工框架式高塔结构动力响应分析 何国富 姜颜宁 杨 青 金 微 （中国石化集团上海工程有限公司，上海 ２００１２０） 摘 要：以某石油化工工程中的大长径比框架式高塔为对象，采用时程分析法，分析地震作用下设置限位导向支架的框架式高塔的结构响应，并与采用组合结构模型的框架塔进行对比分析。分析表明，设置限位导向支架的框架式高塔，塔体水平位移幅值变化具有时段性增大特征，最大塔顶位移比组合结构模型的框架塔增大约５０％；地震作用将导致框架与塔之间产生振荡接触，接触产生的压力以脉冲方式作用到塔体上，并在塔体局部区域产生应力集中和应力幅值极速变化；框架塔的结构模型对塔体底部的应力变化和框架支座反力变化的稳定性影响不大。分析同时认为，设置限位导向支架的框架塔属于多体系结构，采用单一组合结构模型进行工程设计存在一定的安全隐患，建议在目前缺乏设计标准明确规定的条件下，地震作用分析宜采用时程分析法。 关键词：框架式高塔；地震响应；时程分析；非线性接触 ＤＯＩ：１０畅１３２０４／ｊ．ｇｙｊｚ２０１５０５０１６ ＳＴＲＵＣＴＵＲＥＤＹＮＡＭＩＣＲＥＳＰＯＮＳＥＡＮＡＬＹＳＩＳＯＦＴＡＬＬＦＲＡＭＥＤＴＯＷＥＲＦＯＲＰＥＴＲＯ－ＣＨＥＭＩＣＡＬＰＲＯＪＥＣＴＳ ＨｅＧｕｏｆｕ ＪｉａｎｇＹａｎｎｉｎｇ ＹａｎｇＱｉｎｇ ＪｉｎＷｅｉ（ＳＩＮＯＰＥＣＳｈａｎｇｈａｉＥｎｇｉｎｅｅｒｉｎｇＣｏ．Ｌｔｄ，Ｓｈａｎｇｈａｉ２００１２０，Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｔａｋｉｎｇａｐｒａｃｔｉｃａｌｈｉｇｈｆｒａｍｅｄ－ｔｏｗｅｒｗｉｔｈｌａｒｇｅｌｏｎｇ－ｄｉａｍｅｔｅｒｒａｔｉｏｆｏｒｐｅｔｒｏ－ｃｈｅｍｉｃａｌｐｒｏｊｅｃｔａｓｔｈｅｏｂｊｅｃｔ，ｔｈｅｓｔｒｕｃｔｕｒｅｒｅｓｐｏｎｓｅｏｆｈｉｇｈｆｒａｍｅｄ－ｔｏｗｅｒｗｉｔｈｇａｐｌｉｍｉｔｉｎｇｓｕｐｐｏｒｔｕｎｄｅｒｔｈｅｓｅｉｓｍｉｃｅｆｆｅｃｔｗａｓａｎａｌｙｚｅｄｗｉｔｈｔｉｍｅ－ ｈｉｓｔｏｒｙａｎａｌｙｓｉｓ，ｗｈｏｓｅｒｅｓｕｌｔｓｗｅｒｅｃｏｍｐａｒｅｄｗｉｔｈａｃｏｍｂｉｎｅｄｓｔｒｕｃｔｕｒｅｍｏｄｅｌ．Ｔｈｅａｎａｌｙｓｉｓｉｎｄｉｃａｔｅｄｔｈａｔｔｈｅｃｈａｎｇｅｉｎｈｏｒｉｚｏｎｔａｌｄｉｓｐｌａｃｅｍｅｎｔｏｆｔｈｅｈｉｇｈｆｒａｍｅｄ－ｔｏｗｅｒｗｉｔｈｇａｐｌｉｍｉｔｉｎｇｓｕｐｐｏｒｔｈａｄｔｈｅｃｈａｒａｃｔｅｒｉｓｔｉｃｓｏｆｉｎｃｒｅａｓｅｉｎｔｉｍｅｓｔｅｐ，ｍａｘｔｏｐｄｉｓｐｌａｃｅｍｅｎｔｏｆｔｏｗｅｒｗａｓ５０％ｇｒｅａｔｅｒｔｈａｎｔｈａｔｏｆｔｈｅｈｉｇｈｆｒａｍｅｄ－ｔｏｗｅｒｏｆｔｈｅｃｏｍｂｉｎｅｄｓｔｒｕｃｔｕｒｅｍｏｄｅｌ；ａｎｄｔｈｅｓｅｉｓｍｉｃｅｆｆｅｃｔｗｏｕｌｄａｌｓｏｃａｕｓｅｏｓｃｉｌｌａｔｉｏｎｃｏｎｔａｃｔｂｅｔｗｅｅｎｔｏｗｅｒａｎｄｆｒａｍｅ，ａｎｄｔｈｅｐｒｅｓｓｕｒｅｇｅｎｅｒａｔｅｄｂｙｔｈｅｃｏｎｔａｃｔａｃｔｅｄｏｎｔｈｅｔｏｗｅｒｓｈｅｌｌｉｎｍｏｄｅｏｆｐｕｌｓｅｆｏｒｃｅ，ｗｈｉｃｈｃａｕｓｅｄｓｔｒｅｓｓｃｏｎｃｅｎｔｒａｔｉｏｎｉｎｌｏｃａｌａｒｅａａｎｄａｒａｐｉｄｃｈａｎｇｅｉｎｓｔｒｅｓｓａｍｐｌｉｔｕｄｅ．Ｔｈｅｔｙｐｅｏｆｓｔｒｕｃｔｕｒｅｍｏｄｅｌｈａｄｌｏｗｉｎｆｌｕｅｎｃｅｏｎｓｔａｂｉｌｉｔｙｏｆｔｈｅｓｔｒｅｓｓｖａｒｉａｔｉｏｎｏｆｔｏｗｅｒｂｏｔｔｏｍａｎｄｒｅａｃｔｉｏｎｖａｒｉａｔｉｏｎｏｆｆｒａｍｅｓｕｐｐｏｒｔ．Ｂａｓｅｄｏｎｔｈｅａｎａｌｙｓｉｓ，ｉｔｃｏｕｌｄａｌｓｏｂｅｃｏｎｓｉｄｅｒｅｄｔｈａｔｔｈｅｈｉｇｈｆｒａｍｅｄ－ｔｏｗｅｒｗｉｔｈｇａｐｌｉｍｉｔｉｎｇｓｕｐｐｏｒｔｗａｓａｍｕｌｔｉ－ｓｙｓｔｅｍｓｔｒｕｃｔｕｒｅ．Ｔｈｅｒｅｗｏｕｌｄｂｅｓｏｍｅｒｉｓｋｓｉｆｔａｋｉｎｇｓｉｎｇｌｅｃｏｍｂｉｎｅｄｓｔｒｕｃｔｕｒｅｍｏｄｅｌｔｏｐｅｒｆｏｒｍｅｎｇｉｎｅｅｒｉｎｇｄｅｓｉｇｎｆｏｒａｈｉｇｈｆｒａｍｅｄ－ｔｏｗｅｒ．Ｕｎｄｅｒｔｈｅｃａｓｅｏｆｎｏｄｅｔｅｒｍｉｎｅｄｓｔｉｐｕｌａｔｉｏｎｏｆｃｕｒｒｅｎｔｄｅｓｉｇｎｃｏｄｅｓ，ｕｓｅｏｆｔｉｍｅｈｉｓｔｏｒｙａｎａｌｙｓｉｓｍｅｔｈｏｄｗａｓｓｕｇｇｅｓｔｅｄｆｏｒｓｅｉｓｍｉｃｅｆｆｅｃｔ．Ｋｅｙｗｏｒｄｓ：ｈｉｇｈｆｒａｍｅｄ－ｔｏｗｅｒ；ｓｅｉｓｍｉｃｒｅｓｐｏｎｓｅ；ｔｉｍｅ－ｈｉｓｔｏｒｙａｎａｌｙｓｉｓ；ｎｏｎｌｉｎｅａｒｃｏｎｔａｃｔ第一作者：何国富，男，１９６１年出生，教授级高级工程师。电子信箱：ｈｅｇｕｏｆｕ．ｓｓｅｃ＠ｓｉｎｏｐｅｃ．ｃｏｍ收稿日期：２０１４－１１－０６ 与火炬塔架不同，自承式大长径比高塔依靠自 身强度和刚度承受外载荷，是石油化工装置中常见 的一种设备形式。当风荷载或地震作用较大时，完 全依靠塔体自身来承受载荷将显得不尽合理，采用 框架辅助结构作为高塔塔体的侧向支撑，形成塔体 和框架的整体协同工作是一种常见的做法，此类形 式一般称为框架式高塔（以下简称“框架式高塔”）。 “框架式高塔”的协同工作有两种基本模式，一种是 塔与框架两个子结构通过连接约束，在运动过程中 结构响应始终耦合为一个整体结构；另一种是两个子结构始终独立，仅在运动过程中的某个瞬时段内存在由于变形不同步而发生相互接触和作用。从结构体系特征来看，前者属于组合结构，后者则属于多体系结构。
道路在交通荷载作用下的动力响应 摘要：随着我国高速公路里程数逐年增长，交通超载超限现象也越发严重。由于动态荷载的存在，我国现行设计规范在交通荷载设置方面的一些问题也日益突出。通过对比国内外学者在道路动态响应方面的研究，我们可以总结出一种较符合工程实际的数值模拟实现途径，即采用半正弦不均匀移动荷载作用下的荷载-路面-路基接触模型。 关键词：交通荷载；沥青路面；动力响应；有限元模拟 Dynamic response of road under traffic load Abstract: as China's highway mileage increases year by year, traffic overload and overrun phenomenon is also becoming more and more serious. Due to the dynamic load, the current problem of design specification in the traffic load setting also becomes increasingly prominent. By comparising the research of domestic and foreign scholars in road dynamic response ,we can sum up a more practical way in engineering numerical simulation ,that is the load and pavement subgrade contact model under the action of the semi sinusoidal inhomogeneous moving load. Key words: Traffic load; Asphalt pavement; Dynamic response; Finite element simulation 0引言 随着国民经济和公路交通运输业的快速发展，我国高等级公路建设进入了个黄金时期。自1988年第一条高速公路—18.5公里的沪嘉高速公路建成通车以来,我国的高速公路建设每年几乎以成倍数的增长。由新修编的《湖南省高速公路网规划》可知，湖南省“7纵9横”高速交通总布局将有望在近几年实现，届时其总里程也突破8890km。 在高速公路及道路运输事业大发展的背景下，我国道路设计的现行规范在一定程度上已经与公路运输的实际情况不相适应，其中存在的一些问题也将日益突出。表1为我国及其他一些主要国家和地区对道路上行驶车辆的最大车辆总重和轴重的许可值。[1]我国现行《公路沥青路面设计规范(JTG D50-2006)规定公路沥青路面设计是以双轮组单轴载100kN为标准轴载，而在当量轴次换算时，被换算的各级轴载一般采用该车额定载重的轴载。[2]
第2章 动力响应理论 2.1引言 机柜结构动力响应的计算机仿真分析是以设备动力响应理论为基础的，是进行设备结构动力响应研究的一种有效手段。论文中主要研究设备动力响应两个方面的内容：设备结构固有特性分析和结构在地震波作用下的响应分析。固有特性分析可以得到结构的固有频率和固有振型，是进行响应分析的基础；地震波响应分析将得到设备响应的时间历程变化。在使用有限元工具对结构进行建模、分析之前必须掌握结构动力响应的理论和相关的有限元基本原理。因此，本章重点叙述了与设备结构动力响应相关的机械振动学理论及其有限元仿真技术。 2.2结构动力响应分析相关理论 2.2.1结构固有特性分析理论 机柜设备结构的固有特性包括固有频率和振型，是响应分析的基础。通过进行结构的固有特性分析可以使设计有效地避开结构的共振频率。机柜设备是一个复杂振动系统，在理论分析过程中，常常可以把机柜设备简化为多自由度集中参数系统。 一般，多自由度系统的自由振动方程可以写成如下形式： {}... []()[]{()}[]{()}{0}M x t C x t K x t ++= (21)a - 式中：[]M ， []C 和[]K 分别为系统的质量矩阵、阻尼矩阵和刚度矩阵;()x t 、 .()x t 、.. ()x t 分别为系统的位移列向量、速度列向量和加速度列向量。而多自由系统的无阻尼自由振动方程可以写成如下形式: {}.. []()[]{()}{0}M x t K x t += (21)b - 通常系统的自由振动是简谐振动，所以可以假设式 (21)b -的解为： {()}{}sin x t X pt = (22)- 式中：{}X 为系统的振幅列向量;p 为系统的自由振动频率。将(22)-代入(21)b -，就可以得到系统的振型方程，其具体形式如下： 2[][]{}{0}K M X p -= (23)- 可以看到，式(23)-是一个齐次线性方程组，根据线性代数知识，它具有非零解的充分必要条件为系数矩阵的行列式为零，亦即有下式成立。
曲柄连杆机构运动及动力特性分析 学生姓名： 学号： 专业： 院（系）： 完成时间： 摘要 本文针对柴油机曲柄连杆机构运动和动力特性分析，运用自己在理论力学、高等数学、线性代数、工程力学等科目的知识，深入的分析了曲柄连杆机构在运动过程中的运动规律，并且用代数的方法精确地了得出了机构在运动过程中机构中主要零件的运动规律和所承爱的力及力矩变化关系式，并且以 EA1113柴油机为例，进行了精确的计算。从而为设计曲柄连杆机构和减小发动机震动提供了理论支持。 关键词：曲柄连杆机构；运动分析；力学分析特性
目录 第1章柴油机介绍.......................... .. (4) 1.1柴油机概述 (4) 1.2柴油机系统的机构及工作原理 (4) 第2章柴油机的运动和力析 (5) 2.1曲柄连杆机构的类型 (5) 2.2曲柄连杆机构运动分析 (6) 2.2.1活塞位移 (7) 2.2.2活塞的速度 (8) 2.2.3活塞的加速度 (9) 2.3曲柄连杆机构中的作用力 (9) 2.3.1气缸内工作物质的作用力 (9) 2.3.2机构的惯性力 (11) 2.4本章小结 (17) 第3章国内外柴油机的发展现状 (17)
前言 人们想起柴油车，总会想起浓烟滚滚、噪音大等等问题，其实随着2003年第三代电控高压共轨喷射系统的发展，噪音问题和柴油机震动问题都有了改善，新一代的柴油发动机在保障噪音低和震动小的前提下，还拥有经济性好，动力大等优点。这吸引了国际上有关大公司对柴油发动机的热情，也大大促进了柴油车在国外的销售，如今欧洲柴油车已经抢夺了汽油车的半壁江山，而部分车型，比如路虎在欧洲90％都是柴油版本。 柴油车的优点如此突出，然而振动问题和噪声问题却日益突出，致使其零部件磨损加重、噪声升高、寿命降低、工作条件恶化。柴油机的曲轴是整个发动机中最重要的零件之一。它的受损及破坏可能引起柴油机其它零件的损坏，特别是随着发动机的强化与技术发展，使曲轴的工作条件愈发苛刻。曲轴是柴油机最重要的零部件之一，它的任务是将活塞的往复运动转换为旋转运动，并向外输出功率。柴油机的可靠性和寿命很大程度取决与曲轴的可靠性。在周期性变化的动载荷的作用下，柴油机的主要零部件在柴油机工作转速范围内发生强烈共振，严重影响柴油机工作的可靠性，在深入研究柴油机曲柄连杆机构工作过程与原理基础上，分析其运动过程于受力情况。本文针对柴油机曲柄连杆机构运动和动力特性分析，运用自己在理论力学、高等数学、线性代数、工程力学等科目的知识，深入的分析了曲柄连杆机构在运动过程中的运动规律，并且用代数的方法精确地了得出了机构在运动过程中机构中主要零件的运动规律和所承爱的力及力矩变化关系式，并且以EA1113柴油机为例，进行了精确的计算。在本文的末尾还将最近几年在柴油机领域的发展现状做了一个大致的概括和总结，让我们可以更好地了解柴油机的发展趋势，从而为设计曲柄连杆机构和减小发动机震动提供了理论支持。
在动载荷作用下的结构动力响应分析 一、问题的突出 1.求钢结构的动力学响应 2.结构及载荷数据 立柱间距长180，宽120；顶距 地面180 E=200GPa,v=0.3,p=7800kg/m3 A=100kg, w=20π 二、有限单元模型建立 1.单元类型选择以及截面性质定义 FINISH /CLE /PREP7 ET,1,BEAM188 mp,ex,1,200e9 mp,nuxy,1,0.3 mp,dens,1,7800 !截面1 sectype,1,beam,I secoffset,cent secdata,0.12,0.12,0.1212,0.00605, 0.00605,0.0039 !截面2 sectype,2,beam,I secoffset,cent secdata,0.06535,0.06535,0.0805,0.00465,0.00465,0.00285 !截面3 sectype,3,beam, HREC secoffset,cent secdata,0.06,0.06,0.0025,0.0025,0.0025,0.0025
选择Y方向为立柱方向，通过由下向上建模即由关键点到线。k,1, k,2,1.8 k,3,1.8,,1.2 k,4,,,1.2 k,5,,1.5 k,6,1.8,1.5 k,7,1.8,1.5,1.2 k,8,,1.5,1.2 l,1,5 l,2,6 l,3,7 l,4,8 k,9,1.8/2,1.8,1.2/2 l,9,5 l,9,6 l,9,7 l,9,8 l,5,8 l,8,7 l,7,6 l,6,5 3.对于不同的杆赋予不同的截面性质，并进行网格划分 lsel,s,,,1,4,1 lplot lesize,all,0.04 secnum,1 lmesh,all lsel,s,,,9,12 lplot lesize,all,0.04 secnum,2 lmesh,all lsel,s,,,5,8,1 lplot lesize,all,0.04 secnum,3 lmesh,all
第27卷 第1期2010年3月 建筑科学与工程学报 Journal of Architecture and Civil Engineering Vol.27 No.1Mar.2010 文章编号:167322049(2010)0120102206 收稿日期:2009209213 作者简介:王松帆(19692),男,江西黎川人,高级工程师,工学硕士,E 2mail :wangsfan @https://www.doczj.com/doc/5b1059042.html, 。 超高层建筑的风振响应及等效静风荷载研究 王松帆,汤 华 (广州市设计院,广东广州 510620) 摘要:为避免中国现行《建筑结构荷载规范》(G B 50009—2001)中所采用的风振系数仅考虑结构的 1阶振型,而不考虑周围环境影响对体型不规则超高层建筑结构抗风设计造成的不合理性,采用风 洞试验与风振动力响应计算分析相结合的方法,考虑结构不规则的影响以及相邻建筑的气动干扰和横风效应来获得超高层建筑结构抗风设计所需的顺风向和横风向的等效静风荷载和风致动力响应。结果表明:由于周围建筑的干扰,顺风向、横风向的风荷载规律与一般超高层建筑不同,其不利角度也与规范存在差异;所得结论为超高层建筑结构的抗风设计提供了依据和参考。关键词:超高层建筑;风振响应;风洞试验;等效风荷载;抗风设计中图分类号:TU312.1 文献标志码:A R esearch on Wind Vibration R esponse and Equivalent Static Wind Loads of Super High 2rise Buildings WAN G Song 2fan ,TAN G Hua (Guangzhou Design Institute ,Guangzhou 510620,Guangdong ,China ) Abstract :The wind vibration factor in current L oad Code f or Desi gn of B uil di ng S t ruct ures (G B 50009—2001)in China was advanced only considering t he first vibration shape of t he struct ure ,but for super high 2rise building st ruct ures wit h complex shape ,t he above calculation met hod was incompletely reasonable. Considering t he influence of irregular st ruct ure ,aerodynamic interference of adjacent buildings and cross 2wind effect ,aut hors obtained t he along 2wind and cross 2wind equivalent static wind loads and wind 2induced dynamic response needed for wind resistant design of super high 2rise building st ruct ures by using t he met hod of combining wind t unnel test wit h wind vibratio n response calculation ,and achieved good effect s in p roject practices.The result s show t hat because of interference of surrounding buildings ,along 2wind and cross 2wind equivalent static wind loads differ from normal super high 2rise buildings and t he disadvantageous wind directions are inconsistent from t ho se shown in code.The conclusions also provide evidence and reference for wind resistant design of super high 2rise building st ruct ures.K ey w ords :super high 2rise building ;wind vibration response ;wind t unnel test ;equivalent static wind load ;wind resistant design 0引 言 风荷载是超高层建筑结构的主要水平荷载之 一。位于台风多发地区的超高层建筑的风致振动已 成为其结构设计需要考虑的首要因素。中国现行 《建筑结构荷载规范》(G B 50009—2001)[1]中采用
SIMPACK车辆动力学习仿真系统 SIMPACK软件是德国INTEC Gmbh公司(于2009年正式更名为SIMPACK AG)开发的针对机械/机电系统运动学/动力学仿真分析的多体动力学分析软件包。它以多体系统计算动力学（Computational Dynamics of Multibody Systems）为基础，包含多个专业模块和专业领域的虚拟样机开发系统软件。SIMPACK软件的主要应用领域包括：汽车工业、铁路、航空/航天、国防工业、船舶、通用机械、发动机、生物运动与仿生等。 SIMPACK是机械系统运动学/动力学仿真分析软件。SIMPACK软件可以分析如：系统振动特性、受力、加速度，描述并预测复杂多体系统的运动学/动力学性能等。 SIMPACK的基本原理就是通过搭建CAD风格的模型（包括铰、力元素等）来建立机械系统的动力学方程，并通过先进的解算器来获取系统的动力学响应。 SIMPACK软件可以用来仿真任何虚拟的机械/机电系统，从仅仅只有几个自由度的简单系统到诸如一个庞大的火车。SIMPACK软件可以应用在我们产品设计、研发或优化的任何阶段。 SIMPACK软件独具有的全代码输出功能可以将我们的模型输出成Fortran或C代码，从而可以实现与任意仿真软件的联合。 车辆动力学仿真carsim CarSim是专门针对车辆动力学的仿真软件，CarSim模型在计算机上运行的速度比实时快3-6倍，可以仿真车辆对驾驶员，路面及空气动力学输入的响应，主要用来预测和仿真汽车整车的操纵稳定性、制动性、平顺性、动力性和经济性，同时被广泛地应用于现代汽车控制系统的开发。CarSim可以方便灵活的定义试验环境和试验过程，详细的定义整车各系统的特性参数和特性文件。 CarSim软件的主要功能如下: 适用于以下车型的建模仿真:轿车、轻型货车、轻型多用途运输车及SUV; 可分析车辆的动力性、燃油经济性、操纵稳定性、制动性及平顺性; 可以通过软件如MATLAB，Excel等进行绘图和分析; 可以图形曲线及三维动画形式观察仿真的结果;包括图形化数据管理界面，车辆模型求解器，绘图工具，三维动画回放工具，功率谱分析模块;程序稳定可靠; CarSim软件可以扩展为CarSim RT, CarSim RT 是实时车辆模型，提供与一些硬件实时系统的接口，可联合进行HIL仿真;
大系统动力响应分析平台 2011/1/14
大系统动力仿真分析平台分析对象示意图特点：有多个子系统部分结构用超单元 分析类型：模态分析谐波响应随机振动冲击响应传递函数
平台功能概述 软件环境： CAD软件：Pro/E … CAE前处理软件：I-DEAS… CAE求解器：NASTRAN… 功能概述： 1.CAE工作小组的人员能够平行开展子装配CAE模型的处理 2.子装配CAE模型可以方便快速地汇总成总体模型，各人的修改可以快速地在总 体模型中反映 3.部件之间连接形式：一般连接，滑移，弹性（阻尼）连接 4.根据需要引入超单元，自动处理超单元之间的连接，自动生成超单元刚度、质 量、阻尼矩阵的NASTRAN计算input文件，并调用NASTRAN进行计算 5.可以方便地定义计算系统（整个系统或分系统） 6.可以方便地对计算系统进行模态分析、谐波响应、随机振动、冲击、传递函数 等设置和计算，自动生成NASTRAN计算input文件，并调用NASTRAN进行计算 7.能够自动生成计算报告的主要内容 特点：按规范流程，使用大系统动力响应分析平台软件，一般的CAE分析工程师都能正确快速完成大型复杂系统动力响应分析
按照使用平台进行分析的总体流程，简要说明各个功能模块的实现原理。 1.UNV子装配（部件）模型读取 平台与分析起点的接口。读入内容包括节点、单元、坐标系、材料、物理属性、符合命名规则的组、R类型单元主节点系数、截面定义参数、位移约束等。 可以读入多个UNV模型，并按次序对所有节点、单元、坐标系、材料、物理属性进行编号，保证在分析各子系统和整机系统时节点、单元号的统一。 2.子装配（部件）连接关系生成 可以生成普通连接（RBE3单元）、滑移（变化RBE3单元从节点自由度）、弹簧阻尼连接（RBE3单元、新生成节点、弹簧阻尼单元）。 选择连接节点组、单元节点组、连接属性生成连接关系。组的定义在起点UNV模型中定义完整，可以选择手工连接和自动连接。其中新生成节点号、单元号、物理属性号在平台现有基础上递增。