应用高等数学5-319页PPT
- 格式：ppt
- 大小：681.50 KB
- 文档页数：19
下载文档原格式
合集下载
应用高等数学PPT(经管类)高职完整全套教学课件
第1章 函数
1.1.4 基本初等函数
第1章 函数
1.1.4 基本初等函数
第1章 函数
1.1.4 基本初等函数
第1章 函数
1.1.4 基本初等函数
第1章 函数
1.1.4 基本初等函数 三角函数
第1章 函数
1.1.4 基本初等函数 三角函数
第1章 函数
1.1.4 基本初等函数 三角函数
第1章 函数
的函数
函数概念的定义经过三百多年的锤炼、变革，形成了函数的现代 定义形式，随着以数学为基础的其他学科的发展，函数的概念还会继 续扩展.
第1章 函数
1．函数的定义
1.1.2 函数的概念
在某一过程中始终保持固定数值的 量称为常量,常用a、b、c 等符号表示;而 在过程进行中可以取不同数值的量称为 变量,常用x、y、z 等符号表示.
对复合函数进行分解,通常采 取由外层到内层分解的办法,将 y=f[φ(x)]拆分成若干个基本初等 函数或基本初等函数的四则运算 为止.
第1章 函数
2.初等函数
1.1.5 复合函数、初等函数
定义1-8 由基本初等函数经过有限次四则运算及有限次复 合步骤所构成,且可用一个解析式表示的函数,称为初等函数,否 则为非初等函数.
第1章 函数
1.1.3 反函数
【例1-2】 求函数y=3x+4的反函数.
第1章 函数
1.1.3 反函数
函数y=f(x)与其反函数y=f-1(x) 的图像关于直线y=x 对称,如图1-9 所示.常见函数中互为反函数的函 数 有 指 数 函 数 y=ax 与 对 数 函 数 y=logax,三角函数y=sinx 与反三角 函数y=arcsinx 等等.
了解商品的需求量和供给量随价格变化的规律,可以帮助生产和 销售双方及时掌握市场动向,并作出相应合理的决策.
《高等数学》课件第5章
因为图5-1所示的图形不是规则图形，所以它的面积不能 用学过的规则图形的面积公式直接求解. 该图形的三条边是 直线，其中有两条边垂直于第三条底边，而第四条边是曲线 段，这样的图形我们称为曲边梯形.
观察图5-2所示的图形发现：阴影部分的面积是两个曲 边梯形面积之差. 计算任意曲线所围成的平面图形面积的关 键在于计算曲边梯形的面积. 下面将研究曲边梯形的面积.
的近似值为
n
A f (i )xi
i1
(4) 取极限.当分割无限加细，即小区间的最大长度
max{ x1, x2 ,, xn}
趋近于零(λ→0)时，小矩形的面积之和趋近于曲边梯形面
积，即
n
A lim 0
i 1
f (i )xi
2. 引例5-2 已知物体直线运动的速度v=v(t)是时间t的连续 函数，且v(t)≥0，计算物体在时间段［T1，T2］内所经过的路 程s. 由于速度v=v(t)连续， 在解题思路上与求曲边梯形的面积 类似：
差一个常数，所以
x
f (t)dt F(x) C (a≤x≤b) a
在上式中，令x=a，解得C=－F(a)， 再代入上式得
x
a f (t)dt F(x) F(a)
再令x=b，并把积分变量t换成x，便得到
b
a f (x)dx F(b) F(a)
为方便表示，通常记 F(b)－F(a) [F(x)]ba
第5章 定积分及其应用
5.1 定积分的概念与性质 5.2 微积分基本定理 5.3 定积分的计算方法 5.4 广义积分 5.5 定积分的几何应用 5.6 定积分的物理应用 本章小结
5.1 定积分的概念与性质
5.1.1
引例5-1(校园草坪面积问题) 某学校校园草坪平面图形尺 寸如图5-1所示(单位：m)，其中曲线段部分是抛物线型，试 计算草坪的面积.
观察图5-2所示的图形发现：阴影部分的面积是两个曲 边梯形面积之差. 计算任意曲线所围成的平面图形面积的关 键在于计算曲边梯形的面积. 下面将研究曲边梯形的面积.
的近似值为
n
A f (i )xi
i1
(4) 取极限.当分割无限加细，即小区间的最大长度
max{ x1, x2 ,, xn}
趋近于零(λ→0)时，小矩形的面积之和趋近于曲边梯形面
积，即
n
A lim 0
i 1
f (i )xi
2. 引例5-2 已知物体直线运动的速度v=v(t)是时间t的连续 函数，且v(t)≥0，计算物体在时间段［T1，T2］内所经过的路 程s. 由于速度v=v(t)连续， 在解题思路上与求曲边梯形的面积 类似：
差一个常数，所以
x
f (t)dt F(x) C (a≤x≤b) a
在上式中，令x=a，解得C=－F(a)， 再代入上式得
x
a f (t)dt F(x) F(a)
再令x=b，并把积分变量t换成x，便得到
b
a f (x)dx F(b) F(a)
为方便表示，通常记 F(b)－F(a) [F(x)]ba
第5章 定积分及其应用
5.1 定积分的概念与性质 5.2 微积分基本定理 5.3 定积分的计算方法 5.4 广义积分 5.5 定积分的几何应用 5.6 定积分的物理应用 本章小结
5.1 定积分的概念与性质
5.1.1
引例5-1(校园草坪面积问题) 某学校校园草坪平面图形尺 寸如图5-1所示(单位：m)，其中曲线段部分是抛物线型，试 计算草坪的面积.
高等数学的幻灯片-5
k 1 ij3k.
1 1 0
故所求平面方程为
1（x1） 1(yo)3(z1)0 即 xy3z40
7
2019/10/9
天津商学院《高等数学课程组》
二.平面的一般方程
n={ A,B,C}
z
任意平面都可以用三元一次
方程Ax+By+Cz+D=0来表示；
任一三元一次方程 Ax+By+Cz+D=0的图形总是
由cos θ=|cos(n1,^n2)| 则两平面的夹角θ可由两个
向量夹角公式来确定.
四.两平面的夹角
co s |A A B B C C |
A B C A B C
θ n1
n2
Π2
θ
Π1
其中
平面Π1的法向量为 n1={A1,B1,C1} 平面Π2的法向量为 n2={A2,B2,C2}
天津商学院《高等数学课程组》
思考.练习.讨论
3.依条件求平面方程：
(1)平行于xOz面且经过点（2，-5，3）；
(2)通过z轴和点(-3,1,-2)；
(3)平行于x轴且经过两点(4,0,-2)和
（5,1,7) .
(1).y+ 5=0;
(2).x+ 3y=0;
(3).9y- z- 2=0.
27
2019/10/9
六.点到平面的距离
已知:平面Π1的法向量为 n1={A,B,C} 平面Π1外一点 P0={x0,y0,z0} 证明： P0到平面Π1的距离为
n1
P0
P1
N
Π1
证明思路：:平面Π1上取点 P1={x1,y1,z1}则所求距离等于向量 在法向量上n1的投影.即 P P
《高等数学课件PPT》-完整详细版
1
微积分基本定理
微积分基本定理的概念和推导，描述定积分和不定积分之间的关系。
2
带变限积分
带变限积分的计算方法和几何解释，通过例题演示如何求解带变限积分。
极限和连续
深入介绍极限和连续的概念、性质和运算法则，帮助学生理解和掌握这两个重要概念。
极限
数列极限和函数极限的定义和性质，常见的极限计 算方法和极限存在准则。
连续
函数连续的定义和判定条件，连续函数的性质和运 算法则。
函数及其图像
介绍函数的概念和性质，以及如何通过绘制函数图像来更好地理解函数。
函数
函数的定义、定义域、值域和性质，常见函数类型 和函数之间的关系。
图像
绘制函数图像的方法和技巧，通过观察图像认识函 数的特点和变化趋势。
导数和微分
介绍导数和微分的概念、性质和计算方法，以及它们在几何和物理中的应用。
1 导数
导数的定义和性质，导数的计算方法和常见 函数的导数公式。
2 微分
微分的概念和计算方法，微分在几何和物理 中的应用。
《高等数学课件PPT》-完整详 细版
一份完整详细的高等数学课件PPT，深入介绍高等数学的各个知识点，帮助 学生更好地理解和掌握这门重要学科。
课程目标和重要性
通过介绍高等数学课程的学习目标和重要性，帮助学生明确学习目标，激发学习兴趣，并认识到 高等数学在现实生活和学科发展中的广泛应用。
学习目标
深入理解高等数学的各个概念和方法，提高解决数学问题的能力。
不定积分与牛顿-莱布尼茨公式
深入研究不定积分的概念、性质和计算方法，以及牛顿-莱布尼茨公式的推导和应用。
1 不定积分
不定积分的定义和计算方法，常见函数的不 定积分公式。
高等数学完整详细PPT课件
所得曲线a, b两端点的函数值相等.
第7页/共175页
作辅助函数
F ( x) f ( x) [ f (a) f (b) f (a) ( x a)]. ba
F( x) 满足罗尔定理的条件,
则在(a, b)内至少存在一点,使得 F () 0.
即 f () f (b) f (a) 0 ba
第14页/共175页
例4 设函数f ( x)在[0,1]上连续, 在(0,1)内可导, 证明:
至少存在一点 (0,1),使 f ( ) 2[ f (1) f (0)].
证 分析: 结论可变形为
f (1) f (0) 10
f () 2
f ( x) ( x 2 )
x .
设 g( x) x2 ,
xa ,
xa
在 U 0(a, )内任取一点x, 在以 a 与 x 为端点的区间上,
f1( x), F1( x)满足柯西中值定理的条件, 则有
f ( x) f ( x) f (a) f ( ) F ( x) F ( x) F (a) F ( )
(在x与a之间)
当x a时, a,
lim f ( x) A, xa F ( x)
x0 1
第19页/共175页
二、试证明对函数 y px 2 qx r 应用拉氏中值定理 时所求得的点 总是位于区间的正中间 .
三、证明等式arcsin 1 x2 arctan x 1 x2 2
( x (0,1) ) . 四、设a b 0 ，n 1 ，证明
nbn1 (a b) a n bn na n1 (a b) .
第6页/共175页
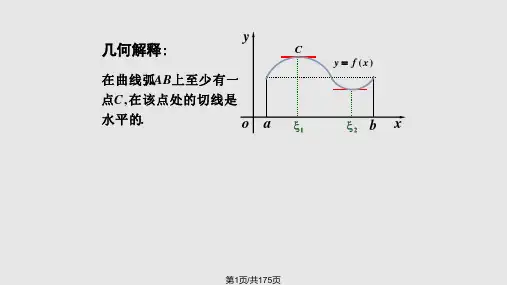
几何解释:
y
C
在曲线弧 AB 上至少有
一点 C ,在该点处的切
高等数学第三章 数的应用
– 第四级
f ( »x 2 第) 五f 级( x 1 ) f '() x 2 ( x 1 ) ( x 1 , x 2 )
如 果 在 ( a ,b ) 内 f ( x ) 0 ， 则 f () 0 ； 又 由 假 设 知 x 1 x 2
f( x 2 ) f( x 1 ) f'()x 2 ( x 1 ) 0
– 第二级 第一节 中值定理 • 第三级第二节 洛比达法则
– 第四级
»第第三五级节 函数的单调性
第四节 函数的极值
第五节 最大值、最小值问题
第六节 曲线的凹凸性与拐点
第七节 函数图像的描绘
10.20042.210-0241-10
25 25
单击函此数处编极辑值母的版定标义题样式
• 单击此处编辑母版文本样式
至少存 (0 ,1 )在 使 , f'(一 得 ) 0 ,即 点 5 4-4 1 0
10.20042.210-0241-10
66
单击拉此格处朗编日辑中母版值标定题理样式
• 单击此处编辑母版文本样式
– 第二级
若 • 函 第数 三级f ( x ) 满 足 下 列 条 件 ：
– 第四级
»在 第闭 五区 级间 [ a , b ] 上 连 续 ；
通 常 把 这 种 极 限 叫 做 未 定 式 ， 并 分 别 简 称 为 0型 或 型 . 0
在一定条件下通过分子分母分别求导再求极限来确定
未定式的极限值的方法称为洛必达（L′Hospital）法则
10.20042.210-0241-10
12 12
单击此处00 编型辑未母定版式标题样式
• 单击此处编辑母版文本样式
5
55
单击此处示编辑母版例标题样式
f ( »x 2 第) 五f 级( x 1 ) f '() x 2 ( x 1 ) ( x 1 , x 2 )
如 果 在 ( a ,b ) 内 f ( x ) 0 ， 则 f () 0 ； 又 由 假 设 知 x 1 x 2
f( x 2 ) f( x 1 ) f'()x 2 ( x 1 ) 0
– 第二级 第一节 中值定理 • 第三级第二节 洛比达法则
– 第四级
»第第三五级节 函数的单调性
第四节 函数的极值
第五节 最大值、最小值问题
第六节 曲线的凹凸性与拐点
第七节 函数图像的描绘
10.20042.210-0241-10
25 25
单击函此数处编极辑值母的版定标义题样式
• 单击此处编辑母版文本样式
至少存 (0 ,1 )在 使 , f'(一 得 ) 0 ,即 点 5 4-4 1 0
10.20042.210-0241-10
66
单击拉此格处朗编日辑中母版值标定题理样式
• 单击此处编辑母版文本样式
– 第二级
若 • 函 第数 三级f ( x ) 满 足 下 列 条 件 ：
– 第四级
»在 第闭 五区 级间 [ a , b ] 上 连 续 ；
通 常 把 这 种 极 限 叫 做 未 定 式 ， 并 分 别 简 称 为 0型 或 型 . 0
在一定条件下通过分子分母分别求导再求极限来确定
未定式的极限值的方法称为洛必达（L′Hospital）法则
10.20042.210-0241-10
12 12
单击此处00 编型辑未母定版式标题样式
• 单击此处编辑母版文本样式
5
55
单击此处示编辑母版例标题样式
应用高等数学课件 第五章 导数的应用
1 x
特别地 ，取 x 1 得
1 ( 1 x)
x
c f (1) arctan1 arctan1
x
4
2
4
，
2
因此当 x 0 时， arctan x arctan 1 ．
Page 14
补充知识： 拉格朗日中值定理的应用——证明不等式成立 复习：中学时期证明不等式的常用方法 若要证明 f ( x) g ( x) ,有如下两个方法： (1)若能说明 f ( x) g ( x) 0 恒成立，则：
于是
f ( x) = f ( x) f (1) f ( )( x 1) 0 x x 即 e xe>0 ．由此推出，当 x 1 时，恒有 e >xe ．
补充：洛必达法则
预备知识：
七种未定型极限：
0 0 0 " "， " " , "0 " , " " , "1 " , "0 " , " " 0
一、罗尔定理 定理3.1（罗尔 Rolle 定理） 如果函数 y f ( x) 满足条件： （1）在 [a, b] 上连续；
（2）在 ( a, b) 内可导； （3） f (a ) f (b) ， 则在区间 ( a, b)内至少存在 一点 ，使 f ( ) 0．
复习： 初等函数 f ( x) 的定义域若 为 [ a, b] ,则函数必定在 [ a, b] 上 连续， 并在 [ a, b] 内部， 即 ( a, b) 上可导。
Page 11
推论1 如果函数 y f ( x) 在区间 ( a, b) 内 任一点的导数 f ( x ) 都等于零，则在 ( a, b) 内 f ( x) 是一个常数.
特别地 ，取 x 1 得
1 ( 1 x)
x
c f (1) arctan1 arctan1
x
4
2
4
，
2
因此当 x 0 时， arctan x arctan 1 ．
Page 14
补充知识： 拉格朗日中值定理的应用——证明不等式成立 复习：中学时期证明不等式的常用方法 若要证明 f ( x) g ( x) ,有如下两个方法： (1)若能说明 f ( x) g ( x) 0 恒成立，则：
于是
f ( x) = f ( x) f (1) f ( )( x 1) 0 x x 即 e xe>0 ．由此推出，当 x 1 时，恒有 e >xe ．
补充：洛必达法则
预备知识：
七种未定型极限：
0 0 0 " "， " " , "0 " , " " , "1 " , "0 " , " " 0
一、罗尔定理 定理3.1（罗尔 Rolle 定理） 如果函数 y f ( x) 满足条件： （1）在 [a, b] 上连续；
（2）在 ( a, b) 内可导； （3） f (a ) f (b) ， 则在区间 ( a, b)内至少存在 一点 ，使 f ( ) 0．
复习： 初等函数 f ( x) 的定义域若 为 [ a, b] ,则函数必定在 [ a, b] 上 连续， 并在 [ a, b] 内部， 即 ( a, b) 上可导。
Page 11
推论1 如果函数 y f ( x) 在区间 ( a, b) 内 任一点的导数 f ( x ) 都等于零，则在 ( a, b) 内 f ( x) 是一个常数.
高等数学数学PPT课件精选全文完整版
归转化思想。
做
学生进行练习训练，个人独立思考与分组讨论相结合。
训
学生上黑板演示解题过程，其他学生点评，教师分析总结。
01
课程尚处于建设阶段，教学资源有待于进 一步完善，现有教学资源还没有得到充分 利用。
进一步开拓更多的学习资源，团队教师增 进针对教学方法和教学资源建设与利用方 面的交流。
பைடு நூலகம்
02
教学内容和教学设计在不断变化的社会需 求、学生思想，以及不断产生的新技术面 前有些滞后。
教学问题
转变传统的教学理念和改变旧的教学模式 探索、建立了新的教学模式和教学方法。
教学对象
教学对象为一年级学生，对大学学习环境、学习 方式需要有一定的适应期 。 教师向学生介绍大学学习的特点与方法，帮助学 生尽快度过适应期。
教学特色
通过不同形式的自主学习 、探究活动，让 学生体验
数学发现和创造的历程，发展他们的创 新意识 。
课程内容及授课学时数（1学期，共64课时）
序号 1 2 3 4 5 6
课程内容 第一章 函数的极限与连续 第二章 导数与微分 第三章 导数应用 第四章 不定积分 第五章 定积分 第六章 空间解析几何
授课学时 12 12 6 16 16 2
导向
依据
度
专业
满足 专业培养目
标
必需 够用
理论知识以“必需、够用”为原则,教学内 容体现“专业性”
教学内容的针对性
专业理论知识需求
后续课程学习要求
教学内容的适用性
高等数学基本要求 教学内容的针对性
淡化严格论证 强化数学应用 注重数学软件
符合课程目标
教学内容选择 辅助多媒体教学 自主学习能力
在高数中的应用PPT课件
x1 x2 3x3 x4 0
例1.2：求方程组 3x1 x2 3x3 4x4 0 的通解。
x1
5x2
9 x3
8x4
0
A=[1 1 -3 -1;3 -1 -3 4;1 5 -9 -8], z=null(A,'r'),%求有理基
第5页/共23页
1.3 非齐次线性方程通解的解法
求解步骤： 1. 判断方程AX=b的是否有解，如有则进行下一步计算； 2. 求方程AX=0的通解。 3. 求方程AX=b的特解。 4. AX=b的通解＝
第15页/共23页
§4 Matlab求积分
第16页/共23页
4.1 求积分
[调用格式] g1=inf(f,x,) g2=inf(f,x,a,b) g1和g2为结果表达式，g1是函数f对x的不定 积分，g2是函数f对x在[a,b]上的定积分。
第17页/共23页
例4.1：求
x 1 z2
dz和
1 x ln(1 x)dx。
A=[5 6 0 0;1 5 6 0;0 1 5 6; 0 0 1 5 ];
b=[1 0 0 0]';
rank(A),
X=A\b,
inv(A)*b,
[a,b]=eig(A)求特征值和特征向量
第4页/共23页
1.2 齐次线性方程通解的解法
[调用格式] z=null(A ,'r') Z的列向量为方程AX=0的有理基。
齐次方程的通解＋非齐次方程的特解
第2页/共23页
1.1 线性方程唯一解或者特解的解法
[调用格式] X＝A\b; X=inv(A)*b X为方程AX=b的解。
第3页/共23页
5x1 6x2 1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
案例5.3.1 放射物的泄漏：环保局近日对一起放射 性碘物质泄漏事件进行调查，检测结果显示，当事当日， 大气中辐射水平是可接受的最大限度的四倍，于是环保 局下令当地居民立即撤离这一地区. 已知碘物质放射源 的辐射水平是按
R(t)R0e0.004t 的速度衰减的，其中R是t时刻的辐射水平（单位：mR/h）， R 0 是初始（t=0）时的辐射水平，t是时间（单位：h）.
fttdtFt
FFFbFa.
所以
a bfx d x f t td t.
4 x2
例1
计算 0
d x. 1 2x
解
令
12xt,
则
x
t
2
2
1
,
dxtdt,
且
当 x0时，t 1; 当 x4时，t3.于是
4
x2
dx
t2 12 3 2 tdt
0 12x
1t
13
= 21
t23dt1 21 3t33t1 3
6 0 01 e 0 .0 0 4 5 0 0 ln 2
450. 答：已经泄漏出去的放射物的总量是450毫伦琴.
定积分的分部积分法 设函数 uux与 vvx
在区间 a,b 上有连续的导数，则
a b u ( x ) v ( x ) d x u ( x ) v ( x )b a a b v ( x ) u ( x ) d x .
总量.
分析 设开始3年内生产的石油总量为W，则有
W 0 3(10.02tsin(2t))dt.
上述两个案例中的定积分没有直接可用的公式，需 要通过换元积分法或分部积分法求解.
抽象归纳
定积分的换元积分法 设函数 f x 在 a,b 上连
续，令 xt, 且满足： （1）a, b; （2） 当 t从 变化到 时，t单调地从 a变化到 b;
1 223791 33232.
例2 计算 a a2x2dx(a0). 0
解 令 xasit,n则 dxacostdt,且当 x0
时，t 0; xa时，t . 于是 2
aa 2 x 2 d x 2a 2 a 2 s in 2 ta c o s td t
0
0
a2 2cos2tdta2 21cos2 tdt
小结：
1．换元积分法：
a bfxd x f t td t
2．分部积分法：
budvuvbbvdu
a
aa
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
或简写成
budvuvbbvdu.
a
aa
上列公式称为定积分的分部积分公式.
证 因为
(u)v u v u v.
两边分别求在区间[a，b]上的定积分，得
b
b
b
a(u v )dx av u dx au v dx ,
即 移项，得
uvbbvudxbuvdx.
aa
a
buvdxuvbbvudx.
a
aa
e1
例4 计算 0 ln(1x)dx.
e1
解 0 ln(1x)dx
xln (1x)e 1e 1xd [ln (1x)] 00
e1
[(e1)lne0]
x dx
0 1x
(e 1 ) [x ln (1 x)]e 1 0
(e 1 ) (e 2 ) 1 .
案例5.3.2的解 W 3(10.02tsin(2t))dt 0
31dt0.023tsin(2 t)dt
0
0
t 3 002.0 203td(cos2t)
3 0 .0 2 tc o s2t3 0 .0 23 c o s2td2sin2t3
2 42
0
30.033.0095.
答：该油井开始3年内生产的石油总量约为3.0095.
（2）因为可接受辐射水平的最大限度为0.6毫伦琴/h， 所以在 t 0 时的辐射水平为2.4毫伦琴/h，即R0 2.4. 设泄露出去的放射物总量为W，则有
W 500ln22.4e0.004t dt. 0
案例5.3.2 石油总产量：经济学家研究一口新井的 原油生产速度时，建立了下列数学模型
R ( t) 1 0 .0 2 ts in ( 2 t) ,求该油井开始3年内生产的石油
0
02
a2 2
t12sin2t02
1a2.
4
f[( t) ]( t)d t f[( t) ]d [( t) ]
(t)u bf(u)du. a
1 t2
例3 求定积分 t e 2 d t . 0
解
1tet22dt1et22(1t2)dt
0
0
2
1 t2
e2
d(1t2).
0
2
01 2eudueu0 1 2 ut2 2
（1）该地降低到可接受的辐射水平需要多长时间？
（2）如果可接受的辐射水平的最大限度为0.6毫伦琴 /h，那么降低到这一水平时已经泄漏出去的放射物的总 量是多少？
分析 （1）设降低到辐射水平需要t 1 小时，此时辐
射水平为R 0
的四分之一. 于是，得
1 4
R0
R0e0.004t1.
解得
t1500ln2(h).
e0e1 2
1
1e2.
1tet22dt1et22d(1t2)
0
0
2
t2
e2
1e0e1 21e1 2.
0
讨论：为什么后面的解法不需要换限？
案例5.3.1的解 W500ln22.4e0.004tdt 0
2.4 500ln2e 0.004td( 0.004t)
0.0040
600e0.004t 500ln2 0
（3） t 在 , 上连续，
则有定积分的换元公式
a bfx d x f t td t.
证 设 Fx是 f x 的一个原函数，则
a bfxdxFaFb.
根据复合函数的求导法则，有
d F [( t) ] d F d x f( x )( t) f[( t) ]( t)
d t
d xd t
因此，有
R(t)R0e0.004t 的速度衰减的，其中R是t时刻的辐射水平（单位：mR/h）， R 0 是初始（t=0）时的辐射水平，t是时间（单位：h）.
fttdtFt
FFFbFa.
所以
a bfx d x f t td t.
4 x2
例1
计算 0
d x. 1 2x
解
令
12xt,
则
x
t
2
2
1
,
dxtdt,
且
当 x0时，t 1; 当 x4时，t3.于是
4
x2
dx
t2 12 3 2 tdt
0 12x
1t
13
= 21
t23dt1 21 3t33t1 3
6 0 01 e 0 .0 0 4 5 0 0 ln 2
450. 答：已经泄漏出去的放射物的总量是450毫伦琴.
定积分的分部积分法 设函数 uux与 vvx
在区间 a,b 上有连续的导数，则
a b u ( x ) v ( x ) d x u ( x ) v ( x )b a a b v ( x ) u ( x ) d x .
总量.
分析 设开始3年内生产的石油总量为W，则有
W 0 3(10.02tsin(2t))dt.
上述两个案例中的定积分没有直接可用的公式，需 要通过换元积分法或分部积分法求解.
抽象归纳
定积分的换元积分法 设函数 f x 在 a,b 上连
续，令 xt, 且满足： （1）a, b; （2） 当 t从 变化到 时，t单调地从 a变化到 b;
1 223791 33232.
例2 计算 a a2x2dx(a0). 0
解 令 xasit,n则 dxacostdt,且当 x0
时，t 0; xa时，t . 于是 2
aa 2 x 2 d x 2a 2 a 2 s in 2 ta c o s td t
0
0
a2 2cos2tdta2 21cos2 tdt
小结：
1．换元积分法：
a bfxd x f t td t
2．分部积分法：
budvuvbbvdu
a
aa
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
或简写成
budvuvbbvdu.
a
aa
上列公式称为定积分的分部积分公式.
证 因为
(u)v u v u v.
两边分别求在区间[a，b]上的定积分，得
b
b
b
a(u v )dx av u dx au v dx ,
即 移项，得
uvbbvudxbuvdx.
aa
a
buvdxuvbbvudx.
a
aa
e1
例4 计算 0 ln(1x)dx.
e1
解 0 ln(1x)dx
xln (1x)e 1e 1xd [ln (1x)] 00
e1
[(e1)lne0]
x dx
0 1x
(e 1 ) [x ln (1 x)]e 1 0
(e 1 ) (e 2 ) 1 .
案例5.3.2的解 W 3(10.02tsin(2t))dt 0
31dt0.023tsin(2 t)dt
0
0
t 3 002.0 203td(cos2t)
3 0 .0 2 tc o s2t3 0 .0 23 c o s2td2sin2t3
2 42
0
30.033.0095.
答：该油井开始3年内生产的石油总量约为3.0095.
（2）因为可接受辐射水平的最大限度为0.6毫伦琴/h， 所以在 t 0 时的辐射水平为2.4毫伦琴/h，即R0 2.4. 设泄露出去的放射物总量为W，则有
W 500ln22.4e0.004t dt. 0
案例5.3.2 石油总产量：经济学家研究一口新井的 原油生产速度时，建立了下列数学模型
R ( t) 1 0 .0 2 ts in ( 2 t) ,求该油井开始3年内生产的石油
0
02
a2 2
t12sin2t02
1a2.
4
f[( t) ]( t)d t f[( t) ]d [( t) ]
(t)u bf(u)du. a
1 t2
例3 求定积分 t e 2 d t . 0
解
1tet22dt1et22(1t2)dt
0
0
2
1 t2
e2
d(1t2).
0
2
01 2eudueu0 1 2 ut2 2
（1）该地降低到可接受的辐射水平需要多长时间？
（2）如果可接受的辐射水平的最大限度为0.6毫伦琴 /h，那么降低到这一水平时已经泄漏出去的放射物的总 量是多少？
分析 （1）设降低到辐射水平需要t 1 小时，此时辐
射水平为R 0
的四分之一. 于是，得
1 4
R0
R0e0.004t1.
解得
t1500ln2(h).
e0e1 2
1
1e2.
1tet22dt1et22d(1t2)
0
0
2
t2
e2
1e0e1 21e1 2.
0
讨论：为什么后面的解法不需要换限？
案例5.3.1的解 W500ln22.4e0.004tdt 0
2.4 500ln2e 0.004td( 0.004t)
0.0040
600e0.004t 500ln2 0
（3） t 在 , 上连续，
则有定积分的换元公式
a bfx d x f t td t.
证 设 Fx是 f x 的一个原函数，则
a bfxdxFaFb.
根据复合函数的求导法则，有
d F [( t) ] d F d x f( x )( t) f[( t) ]( t)
d t
d xd t
因此，有