奥数讲座搭配问题

三下奥数思维训练搭配教案奥数思维训练搭配教案。

一、教学目标。

1.通过奥数思维训练，培养学生的逻辑思维能力和数学解决问题的能力。

2.激发学生对数学的兴趣，提高学生学习数学的积极性。

3.通过搭配教案，引导学生在解决问题时灵活运用奥数思维方法。

二、教学重点。

1.培养学生的逻辑思维能力。

2.引导学生在解决问题时灵活运用奥数思维方法。

三、教学难点。

1.如何引导学生在解决问题时灵活运用奥数思维方法。

2.如何激发学生对数学的兴趣。

四、教学方法。

1.启发式教学法，通过引导学生解决实际问题，激发学生的思维能力。

2.案例教学法，通过具体案例分析，引导学生灵活运用奥数思维方法。

五、教学过程。

1.导入，通过一个生活中的实际问题引入奥数思维训练的教学内容，激发学生的兴趣。

2.讲解，向学生介绍奥数思维训练的方法和技巧，引导学生理解奥数思维的重要性和应用。

3.案例分析，通过具体案例分析，引导学生灵活运用奥数思维方法，解决问题。

4.练习，设计一些练习题，让学生在课堂上进行练习，巩固所学的奥数思维方法。

5.讨论，组织学生进行讨论，分享他们在解决问题时的思路和方法，互相学习，互相提高。

6.总结，对本节课的内容进行总结，强调奥数思维训练的重要性，鼓励学生在日常学习中多多运用奥数思维方法。

六、教学反思。

通过奥数思维训练搭配教案的教学实践，我发现学生在解决数学问题时能够更加灵活运用奥数思维方法，提高了他们的解决问题的能力。

同时，学生对数学的兴趣也得到了激发，积极性也有所提高。

但是在教学中也发现，有些学生在灵活运用奥数思维方法时还存在一定的困难，需要我们在后续的教学中加强引导和训练。

希望通过我们的努力，能够培养出更多数学思维敏捷、解决问题能力强的学生。

二年级奥数间隔问题例1 丽丽住的这幢楼共七层，每层楼梯20级，她家在五楼，你知道丽丽走多少级楼梯才能到自己的家吗?例2 把一根粗细均匀的木头锯成5段，每锯一次要5分钟，一共要多少分钟？例3 少先队员在操场的一旁每隔5米栽一棵树，起点和终点都栽了，一共栽了21棵树，操场长多少米?例4 学校门前一条路长56米，为迎接国庆节，从头到尾都要插彩旗，每隔7米插一面，一共要插彩旗多少面？例5 圆形花圃的周长是27米，现在每隔3米栽一棵树，一共要栽多少棵树？例6 时钟两点钟敲2下，2秒敲完。

五点钟敲5下，几秒钟敲完？例7 校门口的一条路长20米，路的两边从头到尾都栽树，每隔2米栽一棵，一共要栽多少棵？课后练习：1、小红家住七楼，她从一楼到三楼要用2分钟，那么他从一楼到七楼要用几分钟？2、王师傅家住六楼，他从一楼到三楼要走40级台阶，那么他从一楼到六楼要走多少级台阶？3、把一根粗细均匀的木料锯成5段，每锯一次要5分钟，一共要多少分钟？4、一根铁丝长25厘米，把它剪成5厘米长的小段，要剪几次？5、一条河堤长40米，每隔4米栽一棵树，从头到尾一共要栽多少棵？6、校门口的一条路长10米，路的两边从头到尾都要插彩旗，每隔一米插一面，一共要插多少面？7、一个圆形花坛的周长是24米，在它的边上每隔4米放一盆月季花，一共要花多少盆月季花？8、时钟三点钟敲3下，需要4秒钟，那么十一点钟敲11下，需要几秒钟？9、一条路长25米，少先队员在路的两旁栽树，起点终点都栽，一共栽了12棵树，那么每两棵树之间相隔多少米？10、两栋楼之间相距12米，每隔两米栽一棵树，一共栽了几棵树？二年级奥数搭配方法例1 芳芳有三件衬衣，两条裙子，一共有几种穿法？例2 四个男同学和两个女同学进行乒乓球单打比赛，如果每个男同学和女同学都打一盘，那么一共要打几盘？例3 用数字1，2，3可以组成多少个没有重复数字的三位数？例4 从上海到南京要停9个站（包括上海和南京）。

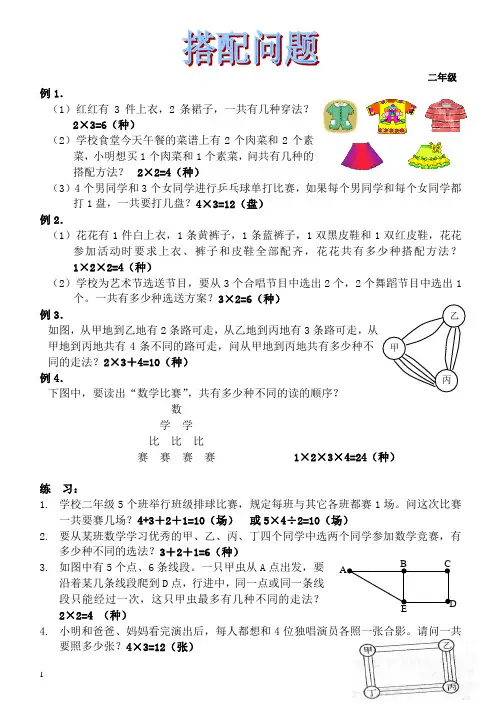
二年级例1．（1）红红有3件上衣，2条裙子，一共有几种穿法？2×3=6（种）（2）学校食堂今天午餐的菜谱上有2个肉菜和2个素菜，小明想买1个肉菜和1个素菜，问共有几种的搭配方法？ 2×2=4（种）（3）4个男同学和3个女同学进行乒乓球单打比赛，如果每个男同学和每个女同学都打1盘，一共要打几盘？4×3=12（盘）例2．（1）花花有1件白上衣，1条黄裤子，1条蓝裤子，1双黑皮鞋和1双红皮鞋，花花参加活动时要求上衣、裤子和皮鞋全部配齐，花花共有多少种搭配方法？ 1×2×2=4（种）（2）学校为艺术节选送节目，要从3个合唱节目中选出2个，2个舞蹈节目中选出1个。

一共有多少种选送方案？3×2=6（种）例3． 如图，从甲地到乙地有2条路可走，从乙地到丙地有3条路可走，从甲地到丙地共有4条不同的路可走，问从甲地到丙地共有多少种不同的走法？2×3＋4=10（种）例4． 下图中，要读出“数学比赛”，共有多少种不同的读的顺序？数学 学比 比 比赛 赛 赛 赛 1×2×3×4=24（种）练 习：1. 学校二年级5个班举行班级排球比赛，规定每班与其它各班都赛1场。

问这次比赛一共要赛几场？4+3＋2＋1=10（场） 或5×4÷2=10（场）2. 要从某班数学学习优秀的甲、乙、丙、丁四个同学中选两个同学参加数学竞赛，有多少种不同的选法？3＋2＋1=6（种）3. 如图中有5个点、6条线段。

一只甲虫从A 点出发，要沿着某几条线段爬到D 点，行进中，同一点或同一条线段只能经过一次，这只甲虫最多有几种不同的走法？ 2×2=4 （种）4. 小明和爸爸、妈妈看完演出后，每人都想和4位独唱演员各照一张合影。

请问一共要照多少张？4×3=12（张）5.如下图，从甲地到乙地有2条路，从乙地到丙地有4条路，从甲地到丁地有3条路，从丁地到丙地也有3条路，问：从甲地到丙地共有多少种不同的走法？2×4＋3×3=17（种）。

三年级奥数搭配问题及解析
在三年级的奥数学习中，搭配问题是一个重要的考点。

下面将介绍一些搭配问题及其解法。

1. 现在有5个红球、4个蓝球和3个绿球，请问从中任选两个球，有多少种不同的组合方式？
解析：总共有12个球，从中任选2个球的组合方式共有C(12,2) = 66种。

2. 小明有7本不同的书，他想从中选出3本，问有多少种不同的选法？
解析：小明从7本书中选出3本的选法共有C(7,3) = 35种。

3. 班级里有10个男生和8个女生，从中任选3个同学组成一个小组，请问有多少种不同的组合方式？
解析：首先从10个男生中选出1个同学，再从8个女生中选出2个同学，共有C(10,1) × C(8,2) = 280种组合方式。

4. 现在有4个小球，每个小球上写着一个不同的数字，从1到4。

请问从中任选2个小球，有多少种不同的组合方式？
解析：从4个小球中任选2个小球的组合方式共有C(4,2) = 6种。

5. 有5个小球，每个小球上写着一个不同的数字，从1到5。

请问从中任选3个小球，有多少种不同的组合方式？
解析：从5个小球中任选3个小球的组合方式共有C(5,3) = 10种。

以上是一些三年级奥数搭配问题及其解法，希望能对同学们的奥数学习有所帮助。

本讲我们将探索简单事物组合、排列的规律，培养有顺序地、全面地思考问题的意识．来看看最简单的搭衣服吧．上下装搭配的每种穿法需要两步来确定,一步是上装的选择,一步是下装的选择,一件上装搭配一件下装就是一种穿法．知识分类一：生活中的搭配小熊要穿衣服，它共有3件不同的上衣和4条不同的裤子．那么，小熊共有多少种不同的穿法？【提示】红色上衣可以和哪几条裤子搭配成一身衣服呢？用笔连一连．【解答】：3×4=12（种）答：小熊一共有12种穿法。

淘淘去餐厅点餐，看到菜单上写着，饮料有：可乐、橙汁；点心有：玉米、汉堡、薯条．如果饮料和点心只能各选一种，搭配成一份套餐，一共有多少种不同的搭配方法？【解答】：2×3=6（种）答：一共有6种不同的搭配方案。

知识分类二：路线问题小狗要去小猪家，必须经过小兔家，它一共有多少种不同的走法？【解答】：3×4=12（种）答：它一共有12种不同的走法。

丫丫从家到学校有3条路，从学校到少年宫有2条路，丫丫从家要到少年宫，中途必须经过学校，一共有多少种不同的走法？家少年宫学校【解答】：2×2=4（种）答：一共有4种不同的走法。

知识分类三：比赛和握手问题小明、小平、小丽、小花四个小朋友进行乒乓球单打比赛，要求每两个同学比赛一场，这次比赛一共要进行多少场？【解答】：3+2+1=6（种）答：这场比赛一共要进行6场。

白雪公主和7个小矮人在一起玩，每两个人都要握一次手，一共握了多少次手？【解答】：7+6+5+4+3+2+1=28（次）答：一共握了28次手。

体育课上，老师让小华去体育室拿3个球．体育室中有一个足球、一个篮球、一个排球和一个橄榄球．请问，小华共有多少种不同的拿法？【提示】当选好3个球之后，体育室中还剩余几个球？【解答】：4种。

跳跳的家里共有A、B、C、D、E这5盏吊灯．妈妈让跳跳关掉其中的4盏，请问，跳跳共有多少种不同的关灯方法？【解答】：5种。

知识分类四：搭配问题中的倒推法有一些游客去海边游玩，海边共停靠着7艘不同的快艇．如果这些游客要从中选出5艘快艇去游玩，那么共有多少种不同的选法？【提示】先把这7艘快艇编上序号吧！从7艘中选出5艘，那么会剩下几艘呢？【解答】：6+5+4+3+2+1=21（种）答：共有21种不同的选法熊老师有8个不同的礼物要奖励给6个优秀的学生（每人一个礼物），请问熊老师一共有多少种选法？【解答】：7+6+5+4+3+2+1=28（种）答：熊老师一共有28种选法。

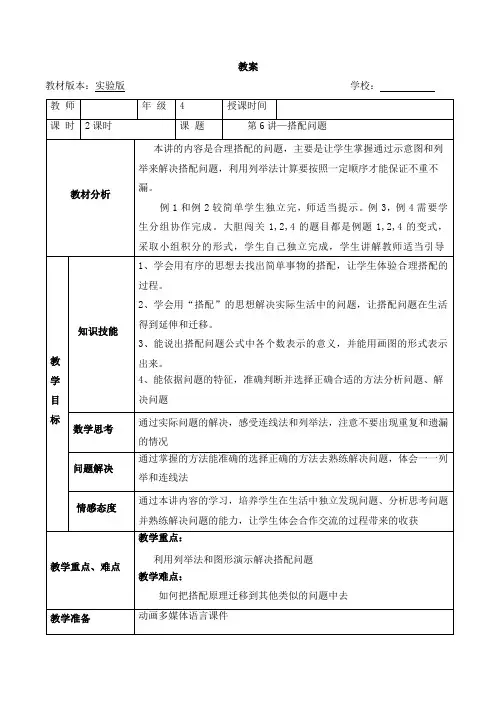
搭 配学校 姓名【例题讲解】开动脑筋和老师一起学吧！【例1】佳佳最喜欢玩给娃娃搭配服装的游戏。

一顶帽子搭配一条裙子，一共有几种不同的搭配？【例2】强强给妈妈买生日礼物。

用一枝鲜花搭配一块蛋糕，一共有几种不同的搭配呢？想一想，生活中，也有这样的搭配问题吗？和小朋友分享！【例3】学校举行乒乓球比赛。

二（3）班运动员名单如下——（1）配成混双选手，有几种不同的情况？（2）配成男双选手，有几种不同的情况？【让我们做一做】★４位学生和２位老师进行乒乓球单打比赛，如果每位学生和每位老师都打一局，一共打几局？★食品店有奶糖３种，水果糖５种，现在从奶糖、水果糖中各拿１种混合成什锦糖出售。

有多少种配糖的方法？★5个小朋友，每两个人通一次电话，一共要通多少次电话？★一组有4人，每2人握手1次，一共要握几次手？★一组有5人，每2人握手1次，一共要握几次手？★一组有6人，每2人握手1次，一共要握几次手？★★图书室新买了4本不同的故事书，5本不同的画册。

强强想借2本回去看。

（1）如果都借故事书，有几种不同的借法？（2）如果借1本故事书、1本画册，有几种不同的借法？搭配学校姓名【回家作业】★于老师有5件不同颜色的上衣，3条颜色不同的裤子，他想穿衣服去上课，可有多少种不同的搭配方法？★从小明家到电影院有5条路可走，从电影院到文化宫有4条路可走。

小明从家先去电影院，再到文化宫，一共有几种不同的走法？★用数字3、5、7可以组成多少个没有重复数字的三位数？★用1元、2元和5元的邮票各一张，可以组成多少种不同的邮资？★★从1个5分，4个2分，9个1分硬币中拿出9分钱，可以有多少种不同的拿法？★★★从A地到B地（包括A站与B站）共有9个车站。

各个火车站售票处要为这条线路准备几种不同的火车票？。

三年级数学奥赛起跑线
第9讲配对求和
1、计算：1+2+3+4+…+18+19
2、计算：2+4+6+8+…+98+100
3、计算：40+41+42+…+61
4、计算：100-99+98-97+…+2-1
5、有20个数，第一个数是9，以后每个数都比前一个数大3。

这20个数连加，和是多少？
6、有一串数，第一个数是5，以后每个数都比前一个数大5，最后一个数是90。

这串数连加，和是多少？
7、一堆圆木共15层，第1层有8根，下面每层多1根。

这堆圆木共有多少根？
8、胜利小学会议室有20排座位，呈梯形。

第1排有10个座位，第2排有11个座位，第3排有12个座位……这个会议室共有多少个座位？
9、时钟在每个整点时敲该钟点数，每半点时敲1下，问：一昼夜该时钟总共敲了多少下？
10、50把钥匙搞乱了，为了使每把锁都配上自己的钥匙，至少要试多少次？。

第6讲 组合问题【知识梳理】一、组合问题日常生活中有很多“分组”问题．如在体育比赛中，把参赛队分为几个组，从全班同学中选出几人参加某项活动等等．这种“分组”问题，就是我们将要讨论的组合问题，这里，我们将着重研究有多少种分组方法的问题．一般地，从n 个不同元素中取出m 个(m n ≤)元素组成一组不计较组内各元素的次序，叫做从n 个不同元素中取出m 个元素的一个组合．从排列和组合的定义可以知道，排列与元素的顺序有关，而组合与顺序无关．如果两个组合中的元素完全相同，那么不管元素的顺序如何，都是相同的组合，只有当两个组合中的元素不完全相同时，才是不同的组合．从n 个不同元素中取出m 个元素(m n ≤)的所有组合的个数，叫做从n 个不同元素中取出m 个不同元素的组合数．记作m n C ．一般地，求从n 个不同元素中取出的m 个元素的排列数n m P 可分成以下两步：第一步：从n 个不同元素中取出m 个元素组成一组，共有m n C 种方法；第二步：将每一个组合中的m 个元素进行全排列，共有m m P 种排法．根据乘法原理，得到m m m n n m P C P =⋅． 因此，组合数12)112321⋅-⋅-⋅⋅-+==⋅-⋅-⋅⋅⋅⋅m mn nm m P n n n n m C P m m m （）（（）（）（）． 这个公式就是组合数公式．二、组合数的重要性质一般地，组合数有下面的重要性质：m n m n n C C -=(m n ≤)这个公式的直观意义是：m n C 表示从n 个元素中取出m 个元素组成一组的所有分组方法．n m n C -表示从n 个元素中取出(n m -)个元素组成一组的所有分组方法．显然，从n 个元素中选出m 个元素的分组方法恰是从n 个元素中选m 个元素剩下的(n m -)个元素的分组方法．例如，从5人中选3人开会的方法和从5人中选出2人不去开会的方法是一样多的，即3255C C =．规定1n n C =，01nC =．三、插板法插板法一般用来解决求分解一定数量的无差别物体的方法的总数，使用插板法一般有三个要求：①所要分解的物体一般是相同的：②所要分解的物体必须全部分完：③参与分物体的组至少都分到1个物体，不能有没分到物体的组出现．在有些题目中，已知条件与上面的三个要求并不一定完全相符，对此应当对已知条件进行适当的变形，使得它与一般的要求相符，再适用插板法．使用插板法一般有如下三种类型：（1） m 个人分n 个东西，要求每个人至少有一个．这个时候我们只需要把所有的东西排成一排，在其中的(1)n -个空隙中放上(1)m -个插板，所以分法的数目为11m n C --．（2） 个人分个东西，要求每个人至少有个．这个时候，我们先发给每个人个，还剩下个东西，这个时候，我们把剩下的东西按照类型⑴来处理就可以了．所以分法的数目为．（3） m 个人分n 个东西，允许有人没有分到．这个时候，我们不妨先借来m 个东西，每个人多发1个，这样就和类型⑴一样了，不过这时候物品总数变成了()n m +个，因此分法的数目为11m n m C -+-．四、排除法对于某些有特殊要求的计数，当限制条件较多时，可以先计算所有可能的情况，再从中排除掉那些不符合要求的情况．【典例精讲】计算：（1）26C ； （2） 46C计算：（1）27C ； （2）57C ．m n a (1)a -[(1)]n m a --1(1)1m n m a C ----某校举行排球单循环赛，有12个队参加．问：共需要进行多少场比赛？芳草地小学举行足球单循环赛，有24个队参加．问：共需要进行多少场比赛？从分别写有1、3、5、7、9的五张卡片中任取两张，做成一道两个一位数的乘法题，问：⑴有多少个不同的乘积？（2）有多少个不同的乘法算式？9、8、7、6、5、4、3、2、1、0这10个数字中划去7个数字，一共有多少种方法？有10粒糖，分三天吃完，每天至少吃一粒，共有多少种不同的吃法？小红有10块糖，每天至少吃1块，7天吃完，她共有多少种不同的吃法？【能力提升】三所学校组织一次联欢晚会，共演出14个节目，如果每校至少演出3个节目，那么这三所学校演出节目数的不同情况共有多少种？【课后巩固】1.计算 ：（1）198200C ⑵ 5556C2.计算：⑴ 312C ； ⑵ 9981000C3.在一个圆周上有10个点，以这些点为端点或顶点，可以画出多少不同的直线段？4.在一个圆周上有10个点，以这些点为端点或顶点，可以画出多少不同的三角形？5.在一个圆周上有10个点，以这些点为端点或顶点，可以画出多少不同的四边形？6.从分别写有1、2、3、4、5、6、7、8的八张卡片中任取两张，做成一道两个一位数的加法题，有多少种不同的和？7.如图，问：图中，共有多少条线段？8.有12块糖，小光要6天吃完，每天至少要吃一块，问共有 种吃法。

《数学思维训练教程》教案教材版本：实验版学校：第一课时复备内容及讨教学过程论记录一、导入师：如果我们的小伙伴小豆丁，罗拉，卡卡来到我们身边，同学们，你们最想问他们什么问题呢？生自由答复。

师：生活在海底的小豆丁，罗拉，卡卡也对我们的生活感兴趣，这不他们也游到岸边看我们的暑期生活是什么样的。

课件播放导入二、呈现问题例1 两家早餐店早点菜单如下：小女孩想从两家早餐店任选一种早餐组合〔面点和米粥各选一种或面包和饮品各选一种〕，一共有多少种不同的搭配？1.学生读题，并尝试寻找看看有多少种搭配的方案。

2.师生共同分析：师：小女孩可以在哪里吃早餐呢？生：可以去安心包子铺吃中式早餐，也可以去英式早点吃西餐。

师：题目对小女孩吃的早餐有什么要求吗？生：面点和米粥各有一种，或面包和饮品各有一种。

师：去安心包子铺吃早餐，有多少种搭配方法呢？3.学生分组合作完成，然后指定学生汇报：生:：去安心包子铺吃早餐，有12种。

京共有多少种不同的走法呢？1.学生读题，分析解题思路：2.师引导学生分析：师：怎么从海南到南京呢？生：可以直接从海南到南京，还可以从海南到武汉，然后再从武汉到南京。

师：从海南直接到南京有几种走法？生：2种，可以乘飞机，也可以坐高铁有2种。

师：从海南到武汉，然后再从武汉到南京有几种方式呢？同学们赶紧数一数，看看谁数的又快又准？3.学生自己数，然后指定学生说说自己答案，其他同学指出错误，并更正。

生：从海南先乘船到武汉，然后可以乘船，高铁，飞机到南京，共有3种；从海南先乘高铁到武汉，然后可以乘船，高铁，飞机到南京，共有3种；所以共有2×3=6种走法。

师：那么从海南到南京共有多少种不同的走法呢？生： 6+2=8答案：2×3=6〔种〕6+2=8〔种〕答：欢欢一家从海南到南京共有8种不同的走法。

例3 沙滩上的小朋友们两两一组，正好分成5组。

每两组对战一次，他们一共要对战多少次？1.学生读题，寻找解题思路：2.师生合作，教师适当的引导：师：读完题，发现这道题的题意是什么？生：从5组中选2组进行对战第二课时闯关4是例4的变式，学生独立完成，然后采取小组积分的形式，学生讲解，答复正确的给所在小组积分，目的是增加学生的学习积极性和小组的荣誉感。

3升4奥数拓展：复杂搭配问题-数学四年级上册人教版一、选择题1．A、B、C、D、E五名同学进行象棋比赛，每两个都要比赛1场，到现在为止，A已赛了2场，B已赛了4场，C已赛了3场，D已赛1场，那么E赛了（）场。

A．2 B．3 C．4 D．52．用1元2元5元的人民币各一张，选其中一张或几张，不能得到的面值是（）。

A．4元B．5元C．6元D．7元3．学校组织春游活动因故提前了，张老师要尽快通知到每一位学生，如果用打电话的方式，每分钟通知1人，每人接到电话后立即通知其他不知道这一信息的同学，全班40位同学，最快（）分钟才能通知到全班同学。

A．4 B．5 C．6 D．74．参观比赛的两队选手，在比赛结束后互相握手，所有的人握了10次手，有（）人互相握手。

A．4 B．10 C．5 D．95．将7个点连成线段，任意三点不在同一条直线上，最多可以连成（）。

A．7条B．12条C．21条D．28条码时，每位数字均不能超过5，那么，可供每支球队选择的号码共（）个。

A．34 B．35 C．40 D．56二、填空题7．2022年卡塔尔世界杯，一共32支球队参加比赛，分成8个小组，每小组4支球队进行第一轮的单循环赛，请问每个小组要比赛( )场。

8．玲玲、丽丽、明明、陈红和嘉豪5名同学互相握手，每两人握一次，一共握手( )次。

9．开学时4位好朋友每2人拥抱一次，共要拥抱( )次；他们还要站成一排合影，小明站在最左边，其他人的位置可自由安排，共有( )种站法。

10．A、B、C、D、E五人进行乒乓球比赛，每两个人都要赛一场。

现在A、D赛了4场，B、C各自赛了3场，E至少赛( )场。

11．李老师要把语文、数学、英语、科学4本书（各1本）分给丽丽、阳阳、聪聪三个同学，每个同学至少分其中的一本，一共有( )种不同的分法。

12．有2名男生和2名女生如图站成一排拍照，那么他们一共有( )种不同的站法。

13．5名象棋爱好者进行比赛，规定每两人比赛一局，经过一段时间后统计，甲已赛了4局，乙已赛了3局，丙已赛了2局，丁已赛了1局，则此时戊已赛了( )局。

生：4种。

师：最后,可以用第三件上衣分别搭配4条不同的裤子,有几种方法？生：4种。

师：那大家观察一下,你们发现了什么？生：发现了有3个4种。

师：所以我们算有多少种不同的装束可以用什么方法计算？生：用乘法,即：4×3=12〈种〉。

师：非常好,那大家还可以怎么搭配呢？〈分小组讨论,然后汇报结果〉生1：可以用第一条裤子搭配上衣,有3种方法。

生2：可以用第二条裤子搭配上衣,有3种方法。

生3：可以用第三条裤子搭配上衣,有3种方法。

生4：可以用第四条裤子搭配上衣,有3种方法。

师：大家观察一下发现了什么？生：有4个3种方法。

师：所以我们可以用什么方法计算？生：用乘法,即：3×4=12〈种〉。

师：刚才我们是用列举的方法,那你还能用什么方法呢？大家互相讨论。

汇报结果。

生1：连线的方法。

生2：可以根据列举的方法总结出列算式计算的方法。

师：看来大家非常喜欢动脑。

那大家自己完成。

板书：4×3=12〈种〉答：最多可以搭配12种不同的装束。

练习1：〈6分〉芭啦啦书店有4种不同的语文书,5种不同的数学书出售,米德想买一种语文书和一种数学书,共有多少种不同的买法？分析：已知“4种不同的语文书,5种不同的数学书出售,”米德想买一种语文书和一种数学书。

可以先用第一种语文书与5种不同的数学书搭配,有5种搭配方法；还可以用第二种语文书与5种不同的数学书搭配,有5种搭配方法；还可以用第三种语文书与5种不同的数学书搭配,有5种搭配方法；最后用第四种语文书与5种不同的数学书搭配,有5种搭配方法,总共有4个5种搭配方法,用乘法计算：5×4=20〈种〉。

还有一种方法就是用5种不同的数学书与4种不同的语文书搭配,有5个4种搭配方法。

板书：5×4=20〈种〉答：共有20种不同的买法。

生1: 相当于每个人都与其他三个人通了一次电话。

生2：卡尔给米德打了电话,米德就不用给卡尔再打一次电话了。

师：大家想一下如果有人跟你打了电话,你还要再跟那个人打电话吗？生：不要。