下载文档原格式
第四章数控铣宏程序实例§4.1 椭圆加工（编程思路:以一小段直线代替曲线）例1 整椭圆轨迹线加工（假定加工深度为2mm)方法一:已知椭圆的参数方X=acosθ Y=bsinθ变量数学表达式设定θ= #1（0°～ 360°）那么 X= #2 = acos［#1］Y= #3= bsin［#1］程序O0001;S1000 M03;G90 G54 G00 Z100;G00 Xa Y0;G00 Z3;G01 Z-2 F100;#1=0;N99 #2=a*cos［#1］；#3=b*sin［#1］；G01 X#2 Y#3 F300;#1=#1+1;IF［#1LE360］GOTO99；GOO Z50；M30；例2 斜椭圆且椭心不在原点的轨迹线加工（假设加工深度为2mm ）椭圆心不在原点的参数方程X=a*C ＯS ［#1］+ MY=b*SIN ［#1］+ N变量数学表达式设定θ=#1; (0°～360°)那么X=#2=a*C ＯS ［#1］+ MY=#3=b*SIN ［#1］+ N因为此椭圆绕（M ,N ）旋转角度为A 可运用坐标旋转指令G68格式 G68 X - Y - R - X,Y ：旋转中心坐标; R: 旋转角度程序Ｏ0002;S1000 M03;G90 G54 G00 Z100;GOO X0 Y0;GOO Z3;G68 XM YN R45;#1=0;N99 #2=a*COS ［#1］+M;#3=b*SIN ［#1］+N;GO1 X#2 Y#3 F300;G01 Z-2 F100;#1=#1+1;IF［#1LE360］GOTO99;G69 GOO Z100;M30;例3:椭圆轮廓加工（深度2mm）采用椭圆的等距加工方法使椭圆的长半轴和短半轴同时减少一个行距的方法直到短半轴小于刀具的半径R根据椭圆的参数方程可设变量表达式θ=#1(0°～360°)a=#2b=#3(b-R～R)X=#2*COS［#1］=#4Y=#3*SIN［#1］=#5程序Ｏ0003;S1000 M03;G90 G54 G00 Z100;G00 XO YO;GOO Z3;G01 Z-2 F100;#2=a-R;#3=b-R;N99 #1=0;#4=#2*COS ［#1］;#5=#3*SIN ［#1］;G01 X#4 Y#5 F300;#1=#1+1；IF ［#1LE360］GOTO99;#2=#2-R;#3=#3-R;IF ［#3LER ］GOTO99;GOO Z100;M30;例4 非整椭圆轨迹线加工；（加工深度2mm ）已知椭圆的长半轴a 短半轴为b 且与X 轴正向夹角为A 1,A 2。
加工中心宏程序编程实例一、引言加工中心是一种高效率、高精度的数控机床，广泛应用于航空航天、汽车制造、模具加工等领域。
宏程序编程是加工中心的重要功能之一，它可以实现复杂加工过程的自动化控制。
本文将通过一个实例，介绍加工中心宏程序的编程方法和应用场景。
二、实例背景假设我们需要加工一个汽车发动机的曲轴。
曲轴具有复杂的几何形状，需要进行多道工序的加工，包括车削、铣削、钻孔等。
为了提高生产效率和减少人为误差，我们决定使用加工中心进行自动化加工，并编写宏程序来控制加工过程。
三、编程步骤1. 参数设置：首先，我们需要设置加工中心的相关参数，包括进给速度、切削速度、刀具半径等。
这些参数将直接影响加工效果和加工时间。
2. 坐标系设置：根据实际加工需求，确定加工中心的坐标系，以便后续编程中准确描述加工零件的位置和运动轨迹。
3. 刀具路径规划：根据曲轴的几何形状和加工要求，设计刀具路径。
刀具路径应尽量简洁、合理，以减少加工时间和提高加工质量。
4. 加工过程编写：根据刀具路径，编写加工过程的宏程序。
宏程序可以包括多个子程序，每个子程序实现一个具体的加工工序。
在编写过程中，需要考虑刀具的选择、进给速度、切削深度等因素。
5. 调试和优化：完成宏程序编写后，需要进行调试和优化。
通过模拟加工过程、检查刀具路径和加工结果，找出潜在的问题并进行修正，以确保加工质量和效率。
四、宏程序应用场景宏程序编程在加工中心中有广泛的应用场景，以下列举几个常见的实例：1. 多孔板加工：多孔板常用于过滤器、喷嘴等领域。
通过编写宏程序，可以实现自动化的孔加工，提高生产效率和加工精度。
2. 多工序加工：某些零件需要经过多个工序才能完成。
通过编写宏程序，可以实现多工序的自动化加工，减少人工操作和加工误差。
3. 复杂曲面加工：某些零件的曲面形状复杂，难以通过传统的编程方法进行描述和加工。
通过编写宏程序，可以实现复杂曲面的自动化加工，提高加工质量和效率。
4. 零件组合加工：某些零件需要进行组合加工，以实现整体的功能。
论文：数控机床宏程序编程的技巧和实例西北工业集团有限公司白锋刚2011年8月11日前言随着工业技术的飞速发展，产品形状越来越复杂，精度要求越来越高，产品更新换代越来越快，传统的设备已不能适应新要求。
现在我国的制造业中已广泛地应用了数控车床、数控铣床、加工中心机床、数控磨床等数控机床。
这些先进设备的加工过程都需要由程序来控制，需要由拥有高技能的人来操作。
要发挥数控机床的高精度、高效率和高柔性，就要求操作人员具有优秀的编程能力。
常用的编程方法有手工编程和计算机编程。
计算机编程的应用已非常广泛。
与手工编程比较，在复杂曲面和型腔零件编程时效率高、质量好。
因此，许多人认为手工编程已不再重要，特别是比较难的宏程序编程也不再需要。
只须了解一些基本的编程规则就可以了。
这样的想法并不能全面。
因为，计算机编程也有许多不足：1、程序数据量大，传输费时。
2、修改或调整刀具补偿需要重新后置输出。
3、打刀或其他原因造成的断点时，很难及时复位。
手工编程是基础能力，是数控机床操作编程人员必须掌握的一种编程方法。
手工编程能力是计算机编程的基础，是刀具轨迹设计，轨迹修改，以及进行后置处理设计的依据。
实践证明，手工编程能力强的人在计算机编程中才能速度快，程序质量高。
在程序中使用变量，通过对变量进行赋值及处理使程序具有特殊功能，这种有变量的程序叫宏程序。
宏程序是数控系统厂家面向客户提供的的二次开发工具，是数控机床编程的最高级手工方式。
合理有效的利用这个工具将极大地提升机床的加工能力。
作为一名从事数控车床、数控铣床、加工中心机床操作编程二十多年的技师，在平时的工作中，常常用宏程序来解决生产中的难题，因此对宏程序的编程使用积累了一些经验。
在传授指导徒弟和与同事探讨中，总结了许多学习编制宏程序应注意的要点。
有关宏编程的基础知识在许多书籍中讲过，我们在这里主要通过实例从编制技巧、要点上和大家讨论。
一、非圆曲面类的宏程序的编程技巧1、非圆曲面可以分为两类；（1）、方程曲面，是可以用方程描述其零件轮廓的曲面的。
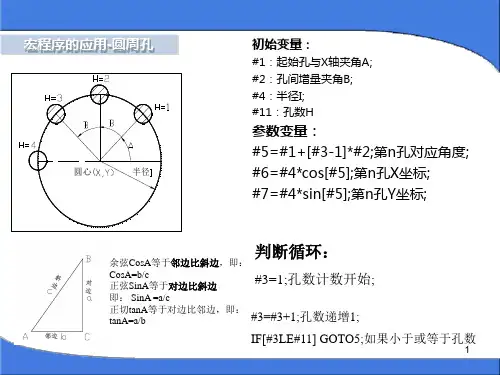
三、计算题1、如图工件原点在工件上表面圆心，设平底立铣刀直径φ10，由下而上周铣孔口倒圆角，试编写的宏程序部分。
G00 X0 Y0 Z10 起刀点定位在Z10Z–8G01 X15 F1000 加上刀具半径5，就是X20.半径补偿功能没有使用。
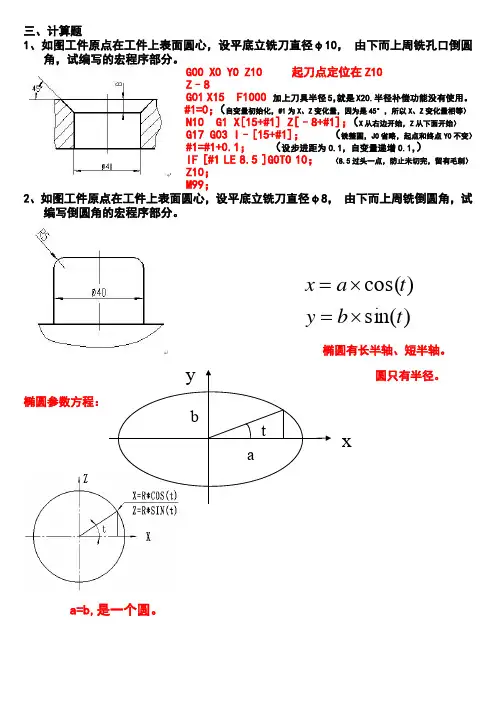
#1=0；（自变量初始化，#1为X、Z变化量，因为是45°，所以X、Z变化量相等）N10 G1 X[15+#1] Z[–8+#1]；（X从右边开始，Z从下面开始）G17 G03 I–[15+#1]；（铣整圆，J0省略，起点和终点Y0不变）#1=#1+0.1；（设步进距为0.1，自变量递增0.1，）IF [#1 LE 8.5 ]GOTO 10；（8.5过头一点，防止未切完，留有毛刺）Z10；M99；2、如图工件原点在工件上表面圆心，设平底立铣刀直径φ8，由下而上周铣倒圆角，试编写倒圆角的宏程序部分。
椭圆有长半轴、短半轴。
圆只有半径。
椭圆参数方程：a=b,是一个圆。
)sin()cos(tbytax⨯=⨯=tabxy立铣刀直径φ8，由下而上周铣倒圆角初始化，G00 X30 Y0 Z10；从右面下来Z -5；G01 X24 F300；从右面靠上工件。
#3=0；角度α赋初值，以角度作为自变量N10 #1=5*COS[#3]；X值计算COS[0]=1，COS[90]=0#2=5*SIN[#3]；Z值计算SIN[0]=0，SIN[90]=1G01 X[19+#1] Z[#2-5] F1000；刀具移动一个偏移量G17 G3 I-[19+#1]；XY平面加工整圆，起点、终点不变，J0省略。
#3=#3+1；设角度步进距为1°ºIF [#3 LE 90] GOTO 10；（第一象限，条件为圆的四分之一）Z10；M99；3、如图工件原点在工件上表面，设加工深度为5mm，试用变量编程编写该曲线轮廓A的宏程序部分。
渐开线函数为sin(t))*t-*(sin(t)y，t的取值范围是[0，3.14159]。
一变量普通加工程序直接用数值指定G代码和移动距离；例如，GO1和X100.0。
使用用户宏程序时，数值可以直接指定或用变量指定。
当用变量时，变量值可用程序或用MDI面板上的操作改变。
#1＝#2＋100G01 X#1 F300说明：变量的表示计算机允许使用变量名，用户宏程序不行。
变量用变量符号（#）和后面的变量号指定。
例如：#1表达式可以用于指定变量号。
此时，表达式必须封闭在括号中。
例如：#[#1+#2-12]变量的类型变量根据变量号可以分成四种类型#0 空变量该变量总是空,没有值能赋给该变量.#1-#33 局部变量局部变量只能用在宏程序中存储数据,例如,运算结果.当断电时,局部变量被初始化为空.调用宏程序时,自变量对局部变量赋值,#100-#199 #500-#999 公共变量公共变量在不同的宏程序中的意义相同.当断电时,变量#100-#199初始化为空.变量#500-#999的数据保存,即使断电也不丢失.#1000 系统变量系统变量用于读和写CNC运行时各种数据的变化,例如,刀具的当前位置和补偿值.变量值的范围局部变量和公共变量可以有0值或下面范围中的值:-1047到-10-29或-10-2到-1047如果计算结果超出有效范围,则发出P/S报警NO.111.小数点的省略当在程序中定义变量值时，小数点可以省略。
例：当定义#1＝123；变量#1的实际值是123.000。
变量的引用为在程序中使用变量值，指定后跟变量号的地址。
当用表达式指定变量时，要把表达式放在括号中。
例如：G01X[#1+#2]F#3;被引用变量的值根据地址的最小设定单位自动地舍入。
例如：当G00X#/;以1/1000mm的单位执行时，CNC把123456赋值给变量#1,实际指令值为G00X12346.改变引用变量的值的符号，要把负号（－）放在#的前面。
例如：G00X－#1当引用未定义的变量时，变量及地址都被忽略。
例如：当变量#1的值是0，并且变量#2的值是空时，G00X#1 Y#2的执行结果为G00X0。
第四章数控铣宏程序实例§4.1 椭圆加工（编程思路:以一小段直线代替曲线）例1 整椭圆轨迹线加工（假定加工深度为2mm)方法一:已知椭圆的参数方X=acosθ Y=bsinθ变量数学表达式设定θ= #1（0°～ 360°）那么 X= #2 = acos［#1］Y= #3= bsin［#1］程序O0001;S1000 M03;G90 G54 G00 Z100;G00 Xa Y0;G00 Z3;G01 Z-2 F100;#1=0;N99 #2=a*cos［#1］；#3=b*sin［#1］；G01 X#2 Y#3 F300;#1=#1+1;IF［#1LE360］GOTO99；GOO Z50；M30；例2 斜椭圆且椭心不在原点的轨迹线加工（假设加工深度为2mm）椭圆心不在原点的参数方程X=a*CＯS［#1］+ MY=b*SIN［#1］+ N变量数学表达式设定θ=#1; (0°～360°)那么X=#2=a*CＯS［#1］+ MY=#3=b*SIN［#1］+ N因为此椭圆绕（M ,N）旋转角度为A 可运用坐标旋转指令G68格式 G68 X- Y-R-X,Y：旋转中心坐标; R: 旋转角度程序Ｏ0002;S1000 M03;G90 G54 G00 Z100; GOO X0 Y0;GOO Z3;G68 XM YN R45;#1=0;N99 #2=a*COS［#1］+M; #3=b*SIN［#1］+N;GO1 X#2 Y#3 F300;G01 Z-2 F100;#1=#1+1;IF［#1LE360］GOTO99;G69 GOO Z100;M30;例3:椭圆轮廓加工（深度2mm）采用椭圆的等距加工方法使椭圆的长半轴和短半轴同时减少一个行距的方法直到短半轴小于刀具的半径R根据椭圆的参数方程可设变量表达式θ=#1(0°～360°)a=#2b=#3(b-R～R)X=#2*COS［#1］=#4Y=#3*SIN［#1］=#5程序Ｏ0003;S1000 M03;G90 G54 G00 Z100;G00 XO YO;GOO Z3;G01 Z-2 F100;#2=a-R;#3=b-R;N99 #1=0;#4=#2*COS［#1］;#5=#3*SIN［#1］;G01 X#4 Y#5 F300;#1=#1+1；IF［#1LE360］GOTO99;#2=#2-R;#3=#3-R;IF［#3LER］GOTO99;GOO Z100;M30;例4 非整椭圆轨迹线加工；（加工深度2mm）已知椭圆的长半轴a 短半轴为b 且与X轴正向夹角为A1,A2。
首先根据椭圆的参数方程求出θ1，θ2和P1(x1,y2) P2(x1,y2)此时要注意 A1≠θ1,A2≠θ2如图示ON=b , OM=aNP=P1Q, NP1=PQX 1=OQ, Y1=P1Q由上可列出方程OQ=OM*COSθ=a*COSθ=X (1) PQ=NP=ON*SINθ=b*SINθ=Y (2) TANa=PQ/OQ=Y/X (3)根据（1）（2）（3）可解出θ1，X1,Y1同理可解出θ2,X2,Y2编程方法一：根据参数方程 X=a*COSθ Y=b*SINθ设定变量表达式#1=0 (角度从θ1～θ2变化)#2=a*COS［#1］#3=b*SIN［#1］程序O0001;S1000 M03;G90 G54 G00 Z100;G00 Xa Y0;G00 Z3;G01 Z-2 F100;#1=0;N99 #2=a*cos［#1］；#3=b*sin［#1］；G01 X#2 Y#3F300;#1=#1+1;IF［#1LE360］GOTO99；GOO Z50；M30；编程方法二：根据椭圆标准方程 X2/a2+Y2/b2=1 设定变量表达式#1=X （X值由X～-X变化）#2=Y=b/a*SQRT［［a*a］-［#1*#1］］程序Ｏ0002;S1000 M03;G90 G54 G00 Z100;GOO X1 Y1;GOO Z3;G01 Z-2 F100;#1=X1;N99 #2=b/a*SQRT［a*a-#1*#1］;G01 X#1 Y#2 F300;#1=#1-0.2;IF［#1LE-a］GOTO99;G00 Z100;M30;4.2 球面加工（编程思想：以若干个不等半径的整圆代替曲面）例1 平刀加工凸半球已知凸半球的半径R，刀具半径r建立几何模型如图数学变量表达式#1=θ=0 (00～900,设定初始值#1=0)#2=X=R*SIN［#1］+r(刀具中心坐标)#3=Z=R-R*COS［#1］编程时以圆球的顶面为Z向O平面程序Ｏ0001;S1000 M03;G90 G54 GOO Z100;G00 X0 Y0;G00 Z3;#1=0;WHILE［#1LE90］DO1;#2=R*SIN［#1］+r;#3=R-R*COS［#1］;G01 X#2 Y0 F300;G01 Z-#3 F100;G02 X#2 Y0 I-#2 J0 F300;#1=#1+1;END1;G00 Z100;M30;当加工的球形的角度为非半球时可以通过调整#1也就是θ角变化范围来改变程序例2 球刀加工凸半球已知凸半球的半径R，刀具半径r建立几何模型如图设定变量表达式#1=θ=0 (0°～90°,设定初始值#1=0)#2=X=［R+r］*SIN［#1］(刀具中心坐标)#3=Z=R-［R+r］*COS［#1］+r=［R+r］*［1-COS［#1］］编程时以圆球的顶面为Z向O平面程序Ｏ0001;S1000 M03;G90 G54 GOO Z100;G00 X0 Y0;Z3;#1=0;WHILE［#1LE90］DO1;#2=［R+r］*SIN［#1］;#3=［R+r］*［1-COS［#1］］;G01 X#2 Y0 F300;G01 Z-#3 F100;G02 X#2 Y0 I-#2 J0 F300;#1=#1+1;END1;G00 Z100;M30;例3 球刀加工凹半球已知凸半球的半径R，刀具半径r建立几何模型如图设定变量表达式#1=θ=0 (0°～90°,设定初始值#1=0)#2=X=［R-r］*COS［#1］(刀具中心坐标) #3=Z=［R-r］*SIN［#1］+r程序Ｏ0003S1000 M03;G90 G54 GOO Z100;G00 X0 Y0;G00 Z3;#1=0;WHILE［#1LE90］DO1;#2=［R-r］*SIN［#1］;#3=［R-r］*COS［#1］+r;G01 X#2 Y0F300;G01Z-#3F100;G03 X#2 Y0 I-#2 J0F300;#1=#1+1;END1;G00Z100;M30;当加工凹半球的一部分时，可以通过改变#1即θ角来实现。
如果凹半球底部不加工可以利用平刀加工，方法相似。
4.3 孔口倒圆角编程思路：以若干不等半径整圆代替环形曲面例1 平刀倒凸圆角已知孔口直径φ，孔口圆角半径R,平刀半径r建立几何模型设定变量表达式#1=θ=0 （θ从0°～90°，设定初始值#1=0）#2=X=φ/2+R-r-R*SIN［#1］#3=Z=R-R*COS［#1］程序Ｏ0001;S1000 M03;G90 G54 GOO Z100;G00 X0 Y0;GOO Z3;#1=0N99#2 =φ/2+R-r-R*SIN［#1］#3 =R-R*COS［#1］G01 X#2 Y0 F300;G01Z-#3 F100;G03 X#2 Y0 I-#2 J0 F300;#1=#1+1;IF［#1LE90］GOTO99;G00 Z100;M30;例2 平刀加工凹圆角已知孔口直径φ，孔口圆角半径R,平刀半径r 建立几何模型设定变量表达式#1=θ=0（θ从0°～90°，设定初始值#1=0）#2=X=φ/2 +R*SIN［#1］–r#3=Z=R*SIN［#1］程序Ｏ0001;S1000 M03;G90 G54 GOO Z100;G00 X0 Y0;G00 Z3;#1=0N99#2 =φ/2+R*SIN［#1］-r#3 = R*SIN［#1］G01 X#2 Y0 F300;G01 Z-#3 F100;G03 X#2 Y0 I-#2 J0 F300;#1=#1+1;IF［#1LE90］GOTO99;G00 Z100;M30;例3 球刀倒凸圆角已知孔口直径φ，孔口圆角半径R,球刀半径r 建立几何模型设定变量表达式#1=θ=0（θ从0°～90°，设定初始值#1=0）#2=X=φ/2 +R-［R+r］*SIN［#1］#3=Z=R-［R+r］*COS［#1］+r=［R+r］*［1-COS［#1］］程序Ｏ0001;S1000 M03;G90 G54 GOO Z100;G00 X0 Y0;G00 Z3;#1=0N99#2 =φ/2 +R-［R+r］*SIN［#1］；#3=［R+r］*［1-COS［#1］］G01 X#2 Y0 F300;G01 Z-#3 F100;G03 X#2 Y0 I-#2 J0 F300;#1=#1+1;IF［#1LE90］GOTO99;G00 Z100;M30;例4 球刀倒凹圆角已知内口直径φ，孔口圆角半径R,球刀半径r 建立几何模型设定变量表达式#1=θ=0（θ从0°～90°，设定初始值#1=0）#2=X=φ/2 +R*COS［#1］-r#3=Z=R*SIN［#1］程序Ｏ0001;S1000 M03;G90 G54 GOO Z100;G00 X0 Y0;G00 Z3;#1=0N99#2 =φ/2 +R*COS［#1］-r；#3= R*SIN［#1］G01 X#2 Y0 F300;G01 Z-#3 F100;G03 X#2 Y0 I-#2 J0 F300;#1=#1+1;IF［#1LE90］GOTO99;G00 Z100;M30;4.4 孔口倒斜角（编程思路：以若干不等半径整圆代替环形斜面）例1 平刀倒孔口斜角已知内孔直径φ倒角角度θ倒角深度Ζ1建立几何模型设定变量表达式设定初始值#1=0）#1=θ=0（θ从0变化到Ζ1*COT［θ］-#1*COT［θ］-r#2=X=φ/2 +Ζ1程序Ｏ0001;S1000 M03;G90 G54 GOO Z100;G00 X0 Y0;G00 Z3;#1=0;］DO1;WHILE［#1LEΖ1*COT［θ］-#1*COT［θ］-r;#2=φ/2 +Ζ1G01 X#2 Y0 F300;G01Z-#1 F100;G03X#2 Y0 I-#2 J0 F300;#1=#1+O.1;END1;G00 Z100;M30;例2 球刀倒孔口斜角已知内孔直径φ倒角角度θ倒角深度Ζ1 建立几何模型首先求出 Z2=r-r*COS［θ］X2= r*SIN［θ］设定变量表达式#1=Z=Z2 (Z由Z2变化到Z1+Z2)#2=X=φ/2 +Ζ1*COT［θ］-［Z-Z2］*COT［θ］-X2=φ/2 +Ζ1*COT［θ］-r*SIN［θ］-［#1-r+r*COS［θ］*COT［θ］=φ/2+［Z-#1+r-r*COS［θ］*COT［θ］］-r*SIN［θ］程序Ｏ0001;S1000 M03;G90 G54 GOO Z100;G00 X0 Y0;G00 Z3;#1=Z2;WHILE［#1LE(Ζ1+Z2)］DO1;#2=φ/2+［Z-#1+r-r*COS［θ］*COT［θ］］-r*SIN［θ］; G01 X#2 Y0 F300;G01 Z-#1 F100;G03 X#2 Y0 I-#2 J0 F300;#1=#1+0.1;END1;G00 Z100;M30;4.3多元素倒角编程思路：通过改变半径补偿值改变加工轮廓的实际大小以若干个轮廓线代替轮廓曲面运用指令：G10 L12 P 半径补偿号 R 半径补偿值须知基本概念：刀具半径补偿值=刀具中心到加工轮廓的距离例1 平刀倒多元素圆角已知周边圆角半径R,刀具半径r建立几何模型如图所示设定变量表达式#1=θ=0（θ从0°～90°设定初始值#1=0）#2=D=R*SIN［#1］+r-R(D有可能是负值)#3=Z= R-R*COS［#1］程序Ｏ0001;S1000 M03;G90 G54 G40 G00 Z100;G00 XO Y-3O;GOO Z3;#1=0;N99#2= R*SIN［#1］+r-R;#3= R-R*COS［#1］;G01 Z-#3 F100;G10 L12 P1 R#2;D01 M98 P100 F3OO;#1=#1+1；IF［#1LE90］GOTO99;G00 Z100;M30;子程序Ｏ100;G41 G01 X0 Y-15G01 X-13;G02 X-13 Y15 R15;G01 X13;G02 X13 Y-15 R15;G01 X0 Y-15;G40 G01 X0 Y-30;M99;例2 球刀倒多元素圆角图同上例已知周边圆角半径R,刀具半径r建立几何模型如图所示设定变量表达式#1=θ=0（θ从0°～90°设定初始值#1=0）#2=D=［R+r］*SIN［#1］-R#3=Z= ［R+r］-［R+r］*COS［#1］主程序Ｏ0001;S1000 M03;G90 G54 G40 G00 Z100;G00 XO Y-3O;GOO Z3;#1=0;N99#2= ［R+r］*SIN［#1］-R;#3= ［R+r］-［R+r］*COS［#1］;G01 Z-#3 F100;G10 L12 P1 R#2;D01 M98 P100 F3OO;#1=#1+1；IF［#1LE90］GOTO99;G00 Z100;M30;子程序Ｏ100;G41 G01 X0 Y-15G01 X-13;G02 X-13 Y15 R15;G01 X13;G02 X13 Y-15 R15;G01 X0 Y-15;G40 G01 X0 Y-30;M99;例3 平刀倒多元素斜角已知倒角深度Z，角度θ，平刀半径r建立几何模型设定变量表达式#1=Z=0(Z由0变化到Z1,设定初始值#1=0)#2=D=Z*COT［θ］+r-Z1*COT［θ］= #1*COT［θ］+r-Z1*COT［θ］程序Ｏ0001;S1000 M03;G90 G54 G40 G00 Z100;G00 XO Y-3O;GOO Z3;#1=0;N99#2= #1*COT［θ］+r-Z1*COT［θ］；G01 Z-#1 F100;G10 L12 P1 R#2;D01M98P100F3OO;#1=#1+0.1；IF［#1LEZ1］GOTO99;G00Z100;M30;子程序Ｏ100;G41G01X0Y-15G01X-13;G02X-13Y15R15;G01X13;G02X13Y-15R15;G01X0Y-15;G40G01X0Y-30;M99;例4 球刀倒多元素斜角已知倒角深度Z，角度θ，平刀半径r建立几何模型设定变量表达式#1=Z=Z2(Z由Z2变化到Z1+Z2,设定初始值#1= Z2)#2=D=［Z- Z2］*COT［θ］+r*COT［θ］-Z1*COT［θ］=［#1-［r-r*COs［θ］］］*COT［θ］+r*COT［θ］- Z1*COT［θ］=#1+ r*COs［θ］*COT［θ］- Z1*COT［θ］程序Ｏ0001;S1000M03;G90 G54 G40 G00 Z100;G00 XO Y-3O;GOO Z3;#1= Z2;N99#2= #1+ r*COs［θ］*COT［θ］- Z1*COT［θ］；G01 Z-#1 F100; G10 L12 P1 R#2;D01 M98 P100 F3OO; #1=#1+0.1；IF［#1LE Z1+Z2］GOTO99;G00 Z100;M30;子程序Ｏ100;G41G01X0Y-15G01X-13;G02X-13Y15R15;G01X13;G02X13Y-15R15;G01X0Y-15;G40G01X0Y-30;M99;4.4特殊类型加工例1 运用个G10指令加工腔体或者凸台G10的格式 G10 L12 P 半径补偿号 R 半径补偿值编程思路：通过设定刀具半径补偿变量偏置轮廓加工腔体或凸台已知各尺寸如图刀具假定半径r=5每层加工2mm 加工行距8设定变量表达式#1=Z=2(Z从2变化到10 初始值Z=2)#2=D=5(刀具半径补偿初始值D=5)主程序Ｏ0001;S1000 M03;G90 G54 G40 G00 Z100;G00 XO Y0;GOO Z3;#1= 2;WHILE［#1LE10］DO1;WHILE［#2LE30］DO2;#2=5;G01 Z-#1 F100; G10 L12 P1 R#2; D01 M98 P100 F200; #2=#2+8；END2;#1=#1+2; END1; GOO Z100; M30;子程序Ｏ100;G41 G01 Y30;G01 X-26 Y30;G03 X-26 Y-30 R30;G01 X26 Y-30;G03 X26 Y30 R30;G01 X0 Y30;G40 G01 X0 Y0;M99;例2 螺纹加工螺纹加工方法有很多种，本例主要针对单齿螺纹刀运用G02G03指令加工螺旋括补代码 G02 G03格式 G02 X- Y- Z- I- J- F-;G03 X- Y- Z- I- J- F-;编程思路：运用G02 G03螺旋括补指令设定Z方向为变量以每一个螺距或导程为递增，加工螺纹加工M60×3的螺纹深度20设定变量 #1=Z=0(Z由3变化到-21 设定初始加工平面Z=3) (每加工一个齿下降一个螺距3)程序Ｏ0002;S1000 M03;G90 G54 G40 G00 Z100;G00 XO Y0;GOO Z3;#1=0;G42 G01 X30 Y0 D01 F100;WHILE［#1GE-21］DO1;G02 X30 Y0 Z#1 I-30;#1=#1-3;END1;G40 G01 X0 Y0;G00 Z100;M30;例3 阿基米德螺旋线的轨迹线加工(加工深度2mm)编程思路：以若干条小段直线代替曲线已知此曲线极坐标的方程为r=aθ（a：常数θ：弧度）起始角θ=0°=0弧度终止角θ=270°+360°=630°=630×3.14／180弧度=10.99弧度设定变量表达式 #1=θ=0°(θ由00变化到630°设定初始值#1=0) #2=θ（弧度=#1×3.14／180）#3=r=a*#2程序Ｏ0003;S1000 M03;G90 G54 G40 G00 Z100;G00 XO Y0;GOO Z3;G01 Z-2 F100;#1=0;WHILE［#1LE630］DO 1;#2=#1*3.14／180#3=a*#2G16 G01 X#3 Y#1 F300;#1=#1+1;END1;G15 G00 Z100;M30;例4 正弦曲线加工（深度2mm）设定变量表达式#1=t=0(t由0°变化到360°)#3=a*SIN［#1］=Y#2=b/360*#1=X程序Ｏ0003;S1000 M03;G90 G54 G40 G00 Z100;G00 XO Y0;GOO Z3;G01 Z-2 F100;#1=0;WHILE［#1LE360］DO 1;#2= b/360*#1;#3= a*SIN［#1］;G01 X#2 Y#3 F300;#1=#1+1;END1;G15 G00 Z100;M30;例5 正弦曲面四轴加工设定变量表达式#1=A=0(#1为第四轴A的角度由0°～360°) #2=X=a*SIN［3*#1］程序Ｏ0003;S1000 M03;G90 G54 G40 G00 Z100;G00 X-R Y0;GOO Z3;G01Z-m F100;G41 G01 XO YO D01 F200;#1=0;WHILE［#1LE360］DO 1;#2= a*SIN［3*#1］;G01 X#2 A#1;#1=#1+1;END1;G15 G00 Z100;M30;例5 椭球面加工已知椭球面的标准方程X2/a2+Y2/b2+Z2/c2=1和椭圆的参数方程X=a*COS［θ］ Y=b*SIN［θ］X,Y,Z方向三个半轴长度分别为 a,b,c刀半径r设定变量表达式#1=θ=0（Z向角度变量，θ由0°变化到90°设定初始值#1=0）#2=θ=0（平面内角度变量，θ由0°变化到360°设定初始值#2=0）#3=a=a*COS［#1］(X向半轴变量)1=c*SIN［#1］(Z向半轴变量)#4=c1#5=b/c*SQRT［c*c-#4*#4］(Y向半轴变量)#6=#3*COS［#2］+r(平面内X坐标变量)#7=#5*SIN［#2］+r(平面内Y坐标变量)程序Ｏ0003;S1000 M03;G90 G54 G40 G00 Z100;G00 X0 Y0;GOO Z3;#1=0;WHILE［#1LE90］DO 1;#3= a*COS［#1］;#4=c*SIN［#1］；#5=b/c*SQRT［c*c-#4*#4］；G01 X#3 Y#5 F300;G01 Z#4;#2=0;WHILE［#2LE360］DO 2;#6=#3*COS［#2］+r;#7=#5*SIN［#2］+rG01 X#6 Y#7;#2=#2+1;END2;#1=#1+1;END1;G00 Z100;M30;。
