2014虹口区中考数学一模试卷及答案

2014年上海市初中毕业生统一学业考试模拟测试数学试卷参考答案 （2014.6）说明：1．解答只列出试题的一种或几种解法．如果考生的解法与所列解法不同，可参照解答中评分标准相应评分；2．第一、二大题每题评分只有满分或零分；3．第三大题中各题右端所注分数，表示考生正确做到这一步可得到的分数； 4．评阅试卷，要坚持每题评阅到底，不能因考生解答中出现错误而中断对本题的评阅．如果考生的解答在某一步出现错误，影响后继部分而未改变本题的内容和难度，视影响的程度决定后继部分的给分，但原．则上不超过后继部分应得分数的一半．．．．．．．．．．．．．．．．． 一、填空题（本大题共6题，每题4分，满分24分）1. B ；2. A ；3. A ；4. B ；5. C ；6. C . 二、选择题（本大题共12题，每题4分，满分48分）7.⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛+23234x x ； 8.3->x ； 9.1-； 10.75； 11.︒1440； 12.1)2(22+-=x y ； 13.554或3148； 14.b a 6161+； 15.12； 16.213±； 17.如1-=k 等，不唯一； 18.()a 12±.三、解答题（本大题共7题，满分78分） 19.解：原式aba b a b a b b a +⋅-+-+=))((………………………………………………………（3分） ba -=1………………………………………………………………………（6分） 将2=a 、1=b 代入，上式12121+=-=……………………………（10分）20.解：1232322--=+-x x x x …………………………………………………………（2分） 0322=-+x x ……………………………………………………………………（3分） ()()0132=-+x x …………………………………………………………………（5分）解得：231-=x ，12=x …………………………………………………………（7分） 经检验，当1=x 时，方程无解，舍去……………………………………………（9分）故原方程的解为23-=x …………………………………………………………（10分） 21.解：(1)22……………………………………………………………………………（2分） (2) 过O 作AB OD ⊥、过C 作OB CE ⊥，D 、E 为垂足 由题意可知：︒=∠=∠45B A22)32(2222222=+⋅==∴AO OD ……………………………（3分）)32,2(A 3232tan ==∠AOC ︒=∠︒=∠∴30,60COB AOC设x EB CE ==，则x EO 3=，x OB )13(+=4)13(=+∴x 解得)13(2-=x ………………………………………（4分） )13(42-==∴x OC426sin +==∠OC OD OCA ………………………………………………（5分） (3) 过A 、B 分别作x 轴的垂线，D 、E 为垂足；过O 作AB OF ⊥，F 为垂足 ︒=90AOB ︒=∠+∠∴90COB AOC 又︒=∠+∠90OAD AOC OAD COB ∠=∠∴易证BOE OAD ∆≅∆，m BE OD ==、n OE AD ==),(m n B -∴ ……………………………………………………………………（6分）因而可求得直线AB 解析式为n m nm x n m n m y -+-⎪⎭⎫ ⎝⎛-+=22…………………（7分） 令0=y 则n m n m x ++=22 即nm n m OC ++=22……………………………… （8分）又由(2)同理可得2222n m OF +⋅=)(2)()(2sin 2222n m n m n m OC OFOCA ++⋅+==∠∴……………………………（10分）22.证明：连接GE ；过A 作BC AH ⊥，H 为垂足 47103422=+⋅=+=BC AD S AH ABCD ，3=-=AD BC BH ……………………（2分）522=+=∴BH AH AB ……………………………………………………（3分） F 为AE 中点xyOABC DExyOABC DE FEF AF =∴易证EBF AGF ∆≅∆，BE AG =……………………………………………（4分） E 为BC 中点， AB BE ==∴5ABEG ∴为菱形，GBC ABG ∠=∠，︒=∠90BFE ……………………（6分） 又CE AG //且CE AG =AECG ∴为平行四边形，GC AE //……（7分） D BFE BGC ∠=︒=∠=∠∴90……（8分） GCB DGC ∠=∠CBG GCD ∠=∠∴…………（9分） GCD ABC ∠=∠∴2………（10分） 23.解：(1) 当100≤≤x 时，设函数解析式为)0(2≠++=a c bx ax y将点)20,0(、)39,5(、)48,10(代入⎪⎩⎪⎨⎧=+=+=28101001952520b a b a c 解得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=2052451c b a20524512++-=∴x x y ……………………………………………………（1分） 当2010≤≤x 时，由于函数图像为平行于x 轴的线段，故函数解析式为48=y ………………………………………………………（2分）当20≥x 时，设函数解析式为)0(≠=k xky 将点)48,20(代入解得960=k xy 960=∴……………………………………………………………………（3分） 画图正确………………………………………………………………………（4分）(2) 将6=x 代入20524512++-=x x y ，解得5208=y ……………………（5分） 将25=x 代入x y 960=，解得5192=y ……………………………………（6分）51925208> 故第6分钟学生的听课注意力更集中………………………………………（8分）(3) 把36=y 代入20524512++-=x x y 解得41=x ，202=x (不符题意，舍去)……………………………………（9分）F ABCEGDH把36=y 代入x y 960= 解得380=x ……………………………………（10分） 243684380<=-∴…………………………………………………………（11分） 故老师无法经过适当的安排，从而能使学生在听这道题时的听课注意力指数都不 低于36.…………………………………………………………………………（12分）25.解：(1)ADEF的值保持不变，证明过程如下：………………………………………（1分） 【解法一】延长FO 、DB ，相交于点G BD AB = ，D A ∠=∠∴ 易证AFO RT ∆∽DFG RT ∆DGAODF AF =∴，G AOF ∠=∠……………………………………………（2分） 又BOG AOF ∠=∠，G BOG ∠=∠∴，5==BO BG ………………（3分）315105=+=+=∴BG DB AO DF AF 又由垂径定理可知EF AF =41=+=∴DF AF AF AD EF ，是定值…………………………………………（4分） 【解法二】连接OE 、BE OB OE AO ==AEO EAB ∠=∠∴、EBO OEB ∠=∠︒=∠+∠=∠∴90OEB AEO AEB …………………………………………（2分） 又BD AB =E ∴为AD 中点，ED AE =………………………………………………（3分） 由垂径定理可知EF AF =4142===∴EF EF AE EF AD EF ，是定值………………………………………（4分）. OA BCF E DG. OABCFE D(2) 连接AC 、CE ，并过E 作CD EG ⊥，G 为垂足 由(1)同理可证︒=∠90ACD 又由(1)可知E 为AD 中点【注：若上述结论在(1)中未证明，则需在(2)中给予证明】ED AD CE ==∴21…………………………………………………………（5分） y CD DG 2121==∴…………………（6分） 易证AFO RT ∆∽DGE RT ∆AODEAF DG =∴………………（7分） 5221x x y=∴ 整理得254x y =……………（9分）(3) 若圆F 与圆D 相切，这里只存在外切的可能……………………………（10分） 若两圆外切，则DE DC =易证DCE ∆为等边三角形，︒=∠60DABD ∆∴也为等边三角形，10==BD AD ………………………………（11分）521===∴AD AE BC ……………………………………………………（12分） 故当50<<BC 时，圆F 与圆D 相交；…………………………………（13分） 当5=BC 时，圆F 与圆D 相切；当105<<BC 时，圆F 与圆D 相离.…………………………………（14分）. OA BCF ED G。

2013-2014年上海市虹口区中考数学一模试卷参考答案与试题解析一、选择题（本大题共6小题，每小题4分，满分24分）[下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上]1．（4分）（2014•虹口区一模）下列函数中，属于二次函数的是（）A．y=B．y=2（x+1）（x﹣3）C．y=3x﹣2D．y=【考点】二次函数的定义．【分析】根据反比例函数的定义，二次函数的定义，一次函数的定义对各选项分析判断后利用排除法求解．【解答】解：A、y=是反比例函数，故本选项错误；B、y=2（x+1）（x﹣3）=2x2﹣4x﹣6，是二次函数，故本选项正确；C、y=3x﹣2是一次函数，故本选项错误；D、y==x+，不是二次函数，故本选项错误．故选B．【点评】本题考查了二次函数的定义，解题关键是掌握一次函数、二次函数、反比例函数的定义．2．（4分）（2014•虹口区一模）抛物线y=x2﹣3x+2与y轴交点的坐标是（）A．（0，0）B．（2，0）C．（0，2）D．（0，﹣1）【考点】二次函数图象上点的坐标特征．【分析】令x=0，求出y的值即可得解．【解答】解：x=0时，y=2，所以，抛物线与y轴的交点坐标为（0，2）．故选C．【点评】本题考查了二次函数图象上点的坐标特征，是基础题．3．（4分）（2014•孝感一模）在Rt△ABC中，∠C=90°，若a、b、c分别是∠A、∠B、∠C 的对边，则下列结论中，正确的是（）A．c•sinA=a B．b•cosB=c C．a•tanA=b D．c•tanB=b【考点】锐角三角函数的定义．【分析】根据锐角三角函数的定义就可以求解．【解答】解：∵由锐角三角函数的定义可知sinA=，cosB=，tanA=，tanB=，∴c•sinA=a．故选A．【点评】本题考查的是锐角三角函数的定义，比较简单，是基础题．4．（4分）（2014•虹口区一模）如图，若AB∥CD∥EF，则下列结论中，与相等的是（）A．B．C．D．【考点】平行线分线段成比例．【分析】根据AB∥CD∥EF，结合平行线分线段成比例定理可知BO：OC=AO：OD，AD：DF=BC：CE，由此可得出结论．【解答】解：根据AB∥CD∥EF得到：=．故选：D．【点评】本题考查了平行线分线段成比例定理，解题的关键是找准对应线段．5．（4分）（2014•虹口区一模）如图，在△ABC中，如果DE与BC不平行，那么下列条件中，不能判断△ADE∽△ABC的是（）A．∠ADE=∠C B．∠AED=∠B C．D．【考点】相似三角形的判定．【分析】根据相似三角形的判定方法：（1）三组对应边的比相等的两个三角形相似；（2）两组对应边的比相等且夹角对应相等的两个三角形相似；（3）有两组角对应相等的两个三角形相似，结合选项进行判断即可．【解答】解：A、∠ADE=∠C，∠A=∠A，则可判断△ADE∽△ACB，故本选项错误；B、∠B=∠AED，∠A=∠A，则可判断△ADE∽△ACB，故本选项错误；C、=，此时不等确定∠ADE=∠ACB，故不能确定△ADE∽△ACB，故本选项正确；D、=，∠A=∠A，则可判断△ADE∽△ACB，故本选项错误．故选C．【点评】此题考查了相似三角形的判定，属于基础题，关键是掌握相似三角形的几种判定定理．6．（4分）（2014•虹口区一模）如图，在四边形ABCD中，点E、F分别是边AB、AD的中点，若EF=2，BC=5，CD=3，则sinC的值为（）A．B．C．D．【考点】勾股定理的逆定理；三角形中位线定理；锐角三角函数的定义．【分析】根据中位线的性质得出EF∥BD，且等于BD，进而得出△BDC是直角三角形，求出即可．【解答】解：连接BD，则EF是△ABD的中位线，∴BD=4，在△BCD中，∵32+42=52，∴△BCD是以D点为直角顶点的直角三角形，∴sinC==．故选D．【点评】此题主要考查了锐角三角形的定义以及三角形中位线的性质以及勾股定理逆定理，根据已知得出△BDC是直角三角形是解题关键．二、填空题（本大题共12小题，每小题4分，满分48分）[请将结果直接填入答题纸的相应位置]7．（4分）（2014•虹口区一模）已知x：y=3：2，那么（x+y）：x=5：3．【考点】比例的性质．【分析】用x表示出y，然后代入比例式进行计算即可得解．【解答】解：∵x：y=3：2，∴y=x，∴（x+y）：x=（x+x）：x=5：3．故答案为：5：3．【点评】本题考查了比例的性质，用x表示出y是解题的关键．8．（4分）（2014•虹口区一模）计算：cos45°+sin260°=．【考点】特殊角的三角函数值．【分析】将cos45°=，sin60°=代入求解．【解答】解：原式=×+（）2=1+=．故答案为：．【点评】本题考查了特殊角的三角函数值，解答本题的关键是熟记几个特殊角的三角函数值．9．（4分）（2014•虹口区一模）在Rt△ABC中，∠C=90°，若AC=5，tanA=2，则BC=10．【考点】锐角三角函数的定义．【分析】根据正切函数的定义即可求解．【解答】解：∵tanA=，∴BC=AC•tanA=5×2=10．故答案是：10．【点评】本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边，余切为邻边比对边．10．（4分）（2014•虹口区一模）写出抛物线y=与抛物线y=﹣的一条共同特征是顶点坐标均为（0，0）（答案不唯一）．【考点】二次函数的性质．【分析】根据形如y=ax2的形式的二次函数的性质直接说出即可．【解答】解：∵抛物线y=与抛物线y=﹣的二次项系数互为相反数，∴两条抛物线关于x轴对称，∴抛物线y=与抛物线y=﹣的共同特征为：顶点坐标均为（0，0），对称轴均为y轴等，故答案为：顶点坐标均为（0，0）（答案不唯一）．【点评】本题考查了二次函数的性质，解题的关键是熟记形如y=ax2的形式的二次函数的性质．11．（4分）（2014•虹口区一模）已知抛物线y=﹣2（x﹣3）2+1，当x1＞x2＞3时，y1＜y2．（填“＞”或“＜”）【考点】二次函数图象上点的坐标特征．【分析】根据x＞3时，抛物线的y的值随x的增大而减小解答．【解答】解：∵﹣2＜0，对称轴为直线x=3，∴x＞3时，y的值随x的增大而减小，∵x1＞x2＞3，∴y1＜y2．故答案为：＜．【点评】本题考查了二次函数图象上点的坐标特征，熟练掌握二次函数的增减性是解题的关键．12．（4分）（2014•虹口区一模）将抛物线y=﹣3x2平移，使其顶点到点P（﹣2，1）的位置，则所得新抛物线的表达式是y=﹣3（x+2）2+1．【考点】二次函数图象与几何变换．【分析】根据平移只改变图形的位置不改变图形的形状与大小，利用顶点式解析式写出即可．【解答】解：∵抛物线y=﹣3x2平移后其顶点到点P（﹣2，1）的位置，∴所得新抛物线的表达式是y=﹣3（x+2）2+1．故答案为：y=﹣3（x+2）2+1．【点评】本题考查了二次函数图象与几何变换，此类题目利用顶点的平移解答更简便．13．（4分）（2014•虹口区一模）二次函数y=ax2+bx+c图象上部分点的坐标满足下表：x…﹣3﹣2﹣101…y…﹣3﹣2﹣3﹣6﹣11…则该函数图象的顶点坐标为（﹣2，﹣2）．【考点】二次函数图象上点的坐标特征．【分析】根据二次函数的对称性解答即可．【解答】解：∵x=﹣3、x=﹣1时的函数值都是﹣3，相等，∴函数图象的对称轴为直线x=﹣2，顶点坐标为（﹣2，﹣2）．故答案为：（﹣2，﹣2）．【点评】本题考查了二次函数图象上点的坐标特征，熟记二次函数的对称性是解题的关键．14．（4分）（2014•虹口区一模）如图，在△ABC中，EF∥BC，AD⊥BC交EF于点G，EF=4，BC=5，AD=3，则AG=．【考点】相似三角形的判定与性质．【分析】根据EF∥BC可以得到△AEF∽△ABC，然后根据相似三角形的对应高的比等于相似比，即可求得．【解答】解：∵EF∥BC，∴△AEF∽△ABC，∴=，即=，解得：AG=．故答案是：．【点评】本题考查了相似三角形的判定与性质，理解相似三角形的对应高的比等于相似比是关键．15．（4分）（2014•虹口区一模）如图，点G是△ABC的重心，GF∥BC，=，=，用、表示=﹣．【考点】*平面向量；三角形的重心．【分析】根据图示知=﹣．然后根据三角形重心的性质（重心到顶点的距离与重心到对边中点的距离之比为2：1），求得||与||的数量关系，然后再根据平面向量与的方向来确定它们之间的关系．【解答】解：如图，=﹣，即=﹣．∵GF∥BC，∴AG：AD=GF：BC；又∵点G是△ABC的重心，∴AG：AD=2：3，∴GF：DC=2：3；即：=2：3；∵=3，∴==﹣．故答案是：﹣．【点评】本题主要考查了三角形的重心、平面向量．在解答此题时要注意两点：①三角形的重心的性质：重心到顶点的距离与重心到对边中点的距离之比为2：1，即AG：GD=2：1，而不是AG：AD=2：1；②平面向量是有方向的．16．（4分）（2015•简阳市模拟）如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的正弦值为．【考点】锐角三角函数的定义；等腰直角三角形．【分析】首先利用勾股定理计算出AB2，BC2，AC2，再根据勾股定理逆定理可证明∠BCA=90°，然后得到∠ABC的度数，再利用特殊角的三角函数可得∠ABC的正弦值．【解答】解：AB2=32+12=10，BC2=22+12=5，AC2=22+12=5，∴AC=CB，BC2+AC2=AB2，∴∠BCA=90°，∴∠ABC=45°，∴∠ABC的正弦值为．故答案为：．【点评】此题主要考查了锐角三角函数，以及勾股定理逆定理，关键是掌握特殊角的三角函数．17．（4分）（2014•虹口区一模）如图，某公园入口处原有三级台阶，每级台阶高为20cm，深为30cm，为方便残疾人士，拟将台阶改为斜坡，设台阶的起点为A，斜坡的起始点为C，现设计斜坡的坡度i=1：5，则AC的长度是240cm．【考点】解直角三角形的应用-坡度坡角问题．【分析】如图所示：所有台阶高度和为BD的长，所有台阶深度和为AD的长，即BD=60m，AD=60m．然后根据坡度比解答即可．【解答】解：由题可知BD=60cm，AD=60cm．∵tan∠BCA==∴DC=300cm，∴AC=DC﹣AD=300﹣60=240（cm）．答：AC的长度是240cm，故答案为：240．【点评】本题考查了解直角三角形的应用﹣坡度坡角问题，运用所学的解直角三角形的知识解决实际生活中的问题，要求我们要具备数学建模能力（即将实际问题转化为数学问题）．18．（4分）（2014•虹口区一模）如图，Rt△ABC中，∠C=90°，AB=5，AC=3，在边AB上取一点D，作DE⊥AB交BC于点E，先将△BDE沿DE折叠，使点B落在线段DA上，对应点记为B1；BD的中点F的对应点记为F1．若△EFB∽△AF1E，则B1D=．【考点】相似三角形的判定与性质；翻折变换（折叠问题）．【分析】利用勾股定理列式求出BC，设BD=2x，得到BF=FD=DF1=B1F1=x，然后求出AF1，再利用相似三角形对应边成比例列式求出DE，然后利用勾股定理列式求出F1E，然后根据相似三角形对应边成比例列式求解得到x的值，从而可得B1D的值．【解答】解：如图，∵在Rt△ABC中，∠C=90°，AB=5，AC=3，∴BC===4，设BD=2x，∵点F为BD的中点，将△BDE沿DE折叠，点B对应点记为B1，点F的对应点为F1，∴BF=FD=DF1=B1F1=x，∵DE⊥AB，∠ACB=90°，∠B=∠B，∴△ABC∽△EBD，∴=，即=，解得DE=x，在Rt△DF1E中，E1F===，∴AF1=AB﹣BF1=5﹣3x根据题意知，EFB≌△EF1B1．∵△EFB∽△AF1E，∴△EF1B1∽△AF1E，∴=，∴EF12=AF1•B1F1，即（）2=x（5﹣3x），解得x=，∴B1D的长为2×=．故答案为：．【点评】本题考查了相似三角形的性质，主要利用了翻折变换的性质，勾股定理，相似三角形对应边成比例，综合题，熟记性质并准确识图是解题的关键．三、解答题（本大题共7小题，满分78分）19．（10分）（2014•虹口区一模）已知一个二次函数的图象经过（3，0）、（0，﹣3）、（1，﹣4）三点，求这个二次函数的解析式．【考点】待定系数法求二次函数解析式．【分析】设二次函数的解析式为y=ax2+bx+c，然后把三个点的坐标代入得到关于a、b、c 的方程组，再解方程组即可．【解答】解：设二次函数的解析式为y=ax2+bx+c，根据题意得，解得，所以二次函数的解析式为y=x2﹣2x﹣3．【点评】用待定系数法求二次函数的解析式．在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．20．（10分）（2014•虹口区一模）已知二次函数y=﹣﹣x+．（1）用配方法把该二次函数的解析式化为y=a（x+m）2+k的形式；（2）指出该二次函数图象的开口方向、顶点坐标和对称轴．【考点】二次函数的三种形式；二次函数的性质．【分析】（1）根据配方法的操作整理即可得解；（2）根据a小于0确定出抛物线开口向下，根据顶点式解析式写出顶点坐标和对称轴．【解答】解：（1）y=﹣x2﹣x+，=﹣（x2+2x+1）++，=﹣（x+1）2+4；（2）∵a=﹣＜0，∴二次函数图象的开口向下，顶点坐标为（﹣1，4），对称轴为直线x=﹣1．【点评】本题考查了二次函数的三种形式的转化，二次函数的性质，熟练掌握配方法的操作以及根据顶点式形式写出对称轴和顶点坐标的方法是解题的关键．21．（10分）（2014•虹口区一模）如图，在△ABC中，∠C=90°，AD是∠CAB的角平分线，BE⊥AE，垂足为点E．求证：BE2=DE•AE．【考点】相似三角形的判定与性质．【分析】若要证明BE2=DE•AE则问题可转化为证明比例线段所在的三角形相似即可，即△BDE∽△BAE．【解答】证明：∵AD是∠CAB的角平分线，∴∠CAD=∠BAD，∵∠C=90°，∴∠CAD+∠ADC=90°，∵BE⊥AE，∴∠E=90°，∴∠EBD+∠BDE=90°，∵∠ADC=∠BDE，∴∠BAD=∠DBE，∴△BDE∽△ABE，∴BE：AE=DE：BE，∴BE2=DE•AE．【点评】本题考查了比例式的证明，解题的一般思路是比例线段所在的三角形相似，同时也考查了对顶角相等这样性质，是一道不错的中考题．22．（10分）（2014•虹口区一模）我国南水北调中线工程的起点是某水库，按照工程计划，需对原水库大坝进行混凝土培厚加高，使坝高由原来的156米增加到173.2米，以抬高蓄水位．如图是某一段坝体加高工程的截面示意图，其中原坝体的高为BE，背水坡坡角∠BAE=69°，新坝体的高为DE，背水坡坡角∠DCE=60°．求工程完工后背水坡坡底端水平方向增加的宽度AC．（参考数据：sin69°≈0.93，cos69°≈0.36，tan69°≈2.60，≈1.732）【考点】解直角三角形的应用-坡度坡角问题．【分析】在直角△ABE中利用三角函数求得AE的长，然后再在直角△CDE中求得CE，根据AC=CE﹣AE即可求解．【解答】解：在直角△ABE中，tan∠BAE=，则AE=≈=60（米）；同理，CE===≈100（米），则AC=CE﹣AE=100﹣60=40（米）．答：求工程完工后背水坡坡底端水平方向增加的宽度AC是40米．【点评】本题考查了坡度坡角，正确理解三角函数的定义是关键．23．（12分）（2014•虹口区一模）在△ABC中，∠BAC=90°，∠EAF=90°，AB•AF=AC•AE．（1）求证：△AGC∽△DGB；（2）若点F为CG的中点，AB=3，AC=4，tan∠DBG=，求DF的长．【考点】相似三角形的判定与性质．【分析】（1）利用两边的比值相等并且它们的夹角相等的两个三角形相似即可先证明：△EAB∽△CAF，由此得到∠DBG=∠ACF，进而可证明△AGC∽△DGB；（2）由（1）可证明：△AGC∽△DGB，所以∠CAG=∠GDB=90°，所以△BDG是直角三角形，并且tan∠DBG=tan∠ACG=，由此DG可求，再根据已知条件求出GF的长即可得到DF的长．【解答】解：（1）∵∠BAC=90°，∠EAF=90°，∴∠EAF+∠GAF=∠CAF+GAF=90°，∴∠EAB=∠CAF，∵AB•AF=AC•AE，∴，∴∠DBG=∠ACF，∵∠DGB=∠AGC，∴△AGC∽△DGB；（2）∵△AGC∽△DGB；∴∠DBG=∠ACG，△DGB是直角三角形，∵tan∠DBG=，∴tan∠ACG=，∵AC=4，∴AG=2，∴CG==2，∵AB=3，∴BG=AB﹣AG=1，∵tan∠DBG=，∴DG=，∴DF=DG+GF=+=．【点评】本题考查了相似三角形的判定和性质、勾股定理的运用、解直角三角形的知识，题目的综合性很强，难度不小，对学生的解题能力要求很高，是一道不错的中考题．24．（12分）（2014•虹口区一模）如图，已知抛物线y=x2+bx+c经过点B（﹣4，0）与点C（8，0），且交y轴于点A．（1）求该抛物线的表达式，并写出其顶点坐标；（2）将该抛物线向上平移4个单位，再向右平移m个单位，得到新抛物线．若新抛物线的顶点为P，联接BP，直线BP将△ABC分割成面积相等的两个三角形，求m的值．【考点】二次函数综合题．【分析】（1）利用待定系数法求二次函数解析式即可，进而利用配方法求出顶点坐标；（2）利用三角形中线平分面积进而得出PP过AC中点，进而得出BP解析式，求出P点坐标即可得出答案．【解答】解：（1）将点B（﹣4，0）与点C（8，0），代入解析式得：，解得：，∴该抛物线的表达式为：y=x2﹣x﹣8，y=x2﹣x﹣8=（x2﹣4x）﹣8=（x﹣2）2﹣9，∴顶点坐标为：（2，﹣9）；（2）∵y=x2﹣x﹣8交y轴于点A，∴A（0，﹣8），根据题意得出：平移后解析式为：y=（x﹣2﹣m）2﹣5，∵直线BP将△ABC分割成面积相等的两个三角形，∴P为AC中点，∵A（0，﹣8），C（8，0），∴AC的中点坐标为：（4，﹣4），∴设BP的解析式为：y=ax+h，，解得：，∴BP的解析式为：y=﹣x﹣2，即直线过BP中点P（2+m，﹣5），﹣5=﹣（2+m）﹣2解得：m=4．【点评】此题主要考查了二次函数综合应用以及待定系数法求二次和一次函数解析式，利用三角形中线平分面积得出是解题关键．25．（14分）（2015•武汉模拟）已知：正方形ABCD的边长为4，点E为BC的中点，点P 为AB上一动点，沿PE翻折△BPE得到△FPE，直线PF交CD边于点Q，交直线AD于点G，联接EQ．（1）如图，当BP=1.5时，求CQ的长；（2）如图，当点G在射线AD上时，BP=x，DG=y，求y关于x的函数关系式，并写出x 的取值范围；（3）延长EF交直线AD于点H，若△CQE与△FHG相似，求BP的长．【考点】相似形综合题．【分析】（1）首先确定∠PEQ=90°，即PE⊥EQ，然后利用△PBE∽△ECQ，列出比例式求出CD的长度；（2）根据△PBE∽△ECQ，求出DQ的表达式；由QD∥AP，列出比例式求解；（3）本问分两种情形，需要分类讨论，避免漏解．【解答】解：（1）由翻折性质，可知PE为∠BPQ的角平分线，且BE=FE．∵点E为BC中点，∴EC=EB=EF，∴QE为∠CQP的角平分线．∵AB∥CD，∴∠BPQ+∠CQP=180°，即2∠EPQ+2∠EQP=180°，∴∠EPQ+∠EQP=90°，∴∠PEQ=90°，即PE⊥EQ．易证△PBE∽△ECQ，∴，即，解得：CQ=．（2）由（1）知△PBE∽△ECQ，∴，即，∴CQ=，∴DQ=4﹣．∵QD∥AP，∴，又AP=4﹣x，AG=4+y，∴，∴y=（1＜x＜2）．（3）由题意知：∠C=90°=∠GFH．①当点G在线段AD的延长线上时，如答图1所示．由题意知：∠G=∠CQE∵∠CQE=∠FQE，∴∠DQG=∠FQC=2∠CQE=2∠G．∵∠DQG+∠G=90°，∴∠G=30°，∴∠BEP=∠CQE=∠G=30°，∴BP=BE•tan30°=；②当点G在线段DA的延长线上时，如答图2所示．由题意知：∠FHG=∠CQE．同理可得：∠G=30°，∴∠BPE=∠G=30°，∴∠BEP=60°，∴BP=BE•tan60°=．综上所述，BP的长为或．【点评】本题是几何综合题型，主要考查了相似三角形、正方形、解直角三角形、角平分线等几何知识点．难点在于第（3）问，有两种情形，不要漏解．。

上海市虹口区中考数学一模试卷一、选择题（本大题共6题，每题4分，满分24分）下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上．1．已知α为锐角，如果sinα=，那么α等于( )A．30°B．45°C．60°D．不确定2．把二次函数y=x2﹣4x+1化成y=a（x+m）2+k的形式是( )A．y=（x﹣2）2+1B．y=（x﹣2）2﹣1C．y=（x﹣2）2+3D．y=（x﹣2）2﹣33．若将抛物线平移，得到新抛物线y=（x+3）2，则下列平移方法中，正确的是( ) A．向左平移3个单位B．向右平移3个单位C．向上平移3个单位D．向下平移3个单位4．若坡面与水平面的夹角为α，则坡度i与坡角α之间的关系是( )A．i=cosαB．i=sinαC．i=cotαD．i=tanα5．如图，▱ABCD对角线AC与BD相交于点O，如果=，=，那么下列选项中，与向量（+）相等的向量是( )A．B．C．D．6．如图，点A、B、C、D的坐标分别是（1，7）、（1，1）、（4，1）、（6，1），若▱CDE与▱ABC相似，则点E的坐标不可能是( )A．（4，2）B．（6，0）C．（6，4）D．（6，5）二、填空题（本大题共12题，每题4分，满分48分）[请将结果直接填入答题纸的相应位置]7．若x：y=5：2，则（x+y）：y的值是__________．8．计算：﹣3（﹣2）=__________．9．二次函数y=x2﹣2x的图象的对称轴是直线__________．10．如果抛物线y=﹣x2+3x﹣1+m经过原点，那么m=__________．11．已知点A（x1，y1）、B（x2，y2）为二次函数y=（x﹣1）2图象上的两点，若x1＜x2＜1，则y1__________y2．（填“＞”、“＜”或“=”）12．用“描点法”画二次函数y=ax2+bx+c的图象时，列出了下面的表格：x (2)101…y…﹣11﹣21﹣2…根据表格上的信息回答问题：当x=2时，y=__________．13．如果两个相似三角形的周长的比为1：4，那么周长较小的三角形与周长较大的三角形对应角平分线的比为__________．14．如图，在▱ABCD中，E是边BC上的点，分别联结AE、BD相交于点O，若AD=5，=，则EC=__________．15．如图，正方形DEFG的边EF在▱ABC的边BC上，顶点D、G分别在边AB、AC 上．若▱ABC的边BC长为40厘米，高AH为30厘米，则正方形DEFG的边长为__________厘米．16．如图，在▱ABC中，▱ACB=90°，若点G是▱ABC的重心，cos▱BCG=，BC=4，则CG=__________．17．如图，在四边形ABCD中，▱B=▱D=90°，AB=3，BC=2，tanA=，则CD=__________．18．如图，在矩形ABCD中，AB=6，AD=10，点E是边BC的中点，联结AE，若将▱ABE沿AE翻折，点B落在点F处，联结FC，则cos▱ECF=__________．三、解答题（本大题共7题，满分78分）19．计算：cos245°+tan60°•cos30°﹣3cot260°．20．已知一个二次函数的图象经过A（0，﹣3）、B（2，﹣3）、C（﹣1，0）三点．（1）求这个二次函数的解析式；（2）将这个二次函数图象平移，使顶点移到点P（0，﹣3）的位置，求所得新抛物线的表达式．21．如图，DC▱EF▱GH▱AB，AB=12，CD=6，DE：EG：GA=3：4：5．求EF和GH的长．22．如图，已知楼AB高36米，从楼顶A处测得旗杆顶C的俯角为60°，又从该楼离地面6米的一窗口E处测得旗杆顶C的仰角为45°，求该旗杆CD的高．（结果保留根号）23．如图，点E是四边形ABCD的对角线BD上的一点，▱BAE=▱CBD=▱DAC．（1）求证：DE•AB=BC•AE；（2）求证：▱AED+▱ADC=180°．24．在平面直角坐标系xOy中，抛物线与x轴分别交于点A（2，0）、点B（点B在点A 的右侧），与轴交于点C，tan▱CBA=．（1）求该抛物线的表达式；（2）设该抛物线的顶点为D，求四边形ACBD的面积；（3）设抛物线上的点E在第一象限，▱BCE是以BC为一条直角边的直角三角形，请直接写出点E的坐标．25．（14分）如图，在▱ABCD中，E为边BC的中点，F为线段AE上一点，联结BF并延长交边AD于点G，过点G作AE的平行线，交射线DC于点H．设==x．（1）当x=1时，求AG：AB的值；（2）设=y，求关于x的函数关系式，并写出x的取值范围；（3）当DH=3HC时，求x的值．上海市虹口区中考数学一模试卷一、选择题（本大题共6题，每题4分，满分24分）下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上．1．已知α为锐角，如果sinα=，那么α等于( )A．30°B．45°C．60°D．不确定【考点】特殊角的三角函数值．【分析】根据特殊角的三角函数值求解．【解答】解：▱α为锐角，sinα=，▱α=45°．故选B．【点评】本题考查了特殊角的三角函数值，解答本题的关键是掌握几个特殊角的三角函数值．2．把二次函数y=x2﹣4x+1化成y=a（x+m）2+k的形式是( )A．y=（x﹣2）2+1B．y=（x﹣2）2﹣1C．y=（x﹣2）2+3D．y=（x﹣2）2﹣3【考点】二次函数的三种形式．【分析】运用配方法把二次函数的一般式化为顶点式即可．【解答】解：y=x2﹣4x+1=x2﹣4x+4﹣3=（x﹣2）2﹣3，故选：D．【点评】本题考查的是二次函数的三种形式，正确运用配方法把二次函数的一般式化为顶点式是解题的关键．3．若将抛物线平移，得到新抛物线y=（x+3）2，则下列平移方法中，正确的是( ) A．向左平移3个单位B．向右平移3个单位C．向上平移3个单位D．向下平移3个单位【考点】二次函数图象与几何变换．【分析】先确定抛物线y=x2的顶点坐标为（0，0），抛物线y=（x+3）2的顶点坐标为（﹣3，0），然后利用顶点的平移情况确定抛物线的平移情况．【解答】解：抛物线y=x2的顶点坐标为（0，0），抛物线y=（x+3）2的顶点坐标为（﹣3，0），因为点（0，0）向左平移3个单位长度后得到（﹣3，0），所以把抛物线y=x2向左平移3个单位得到抛物线y=（x+3）2．故选A．【点评】本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．4．若坡面与水平面的夹角为α，则坡度i与坡角α之间的关系是( )A．i=cosαB．i=sinαC．i=cotαD．i=tanα【考点】解直角三角形的应用-坡度坡角问题．【分析】利用把坡面与水平面的夹角α叫做坡角，坡度i与坡角α之间的关系为：i==tanα．【解答】解：如图所示：i=tanα．故选：D．【点评】此题主要考查了解直角三角形的应用﹣坡度坡角的定义，正确把握坡角的定义是解题关键．5．如图，▱ABCD对角线AC与BD相交于点O，如果=，=，那么下列选项中，与向量（+）相等的向量是( )A．B．C．D．【考点】*平面向量．【分析】由四边形ABCD是平行四边形根据平行四边形法则，可求得==，然后由三角形法则，求得与，继而求得答案．【解答】解：▱四边形ABCD是平行四边形，▱==，▱=+=+，=﹣=﹣，▱=﹣=﹣（+），==（+），=﹣=﹣（﹣），==（﹣）．故选C．【点评】此题考查了平面向量的知识以及平行四边形的性质．注意掌握三角形法则与平行四边形法则的应用是解此题的关键．6．如图，点A、B、C、D的坐标分别是（1，7）、（1，1）、（4，1）、（6，1），若▱CDE与▱ABC相似，则点E的坐标不可能是( )A．（4，2）B．（6，0）C．（6，4）D．（6，5）【考点】相似三角形的判定；坐标与图形性质．【分析】根据相似三角形的判定：两边对应成比例且夹角相等的两三角形相似即可判断．【解答】解：▱ABC中，▱ABC=90°，AB=6，BC=3，AB：BC=2．A、当点E的坐标为（4，2）时，▱CDE=90°，CD=2，DE=1，则AB：BC=CD：DE，▱CDE▱▱ABC，故本选项不符合题意；B、当点E的坐标为（6，0）时，▱CDE=90°，CD=2，DE=1，则AB：BC=CD：DE，▱CDE▱▱ABC，故本选项不符合题意；C、当点E的坐标为（6，4）时，▱CDE=90°，CD=2，DE=3，则AB：BC≠DE：CD，▱EDC与▱ABC不相似，故本选项符合题意；D、当点E的坐标为（6，5）时，▱CDE=90°，CD=2，DE=4，则AB：BC=CD：DE，▱CDE▱▱ABC不相似，故本选项不符合题意；故选：C．【点评】本题考查了相似三角形的判定，难度中等．牢记相似三角形的判定定理是解题的关键．二、填空题（本大题共12题，每题4分，满分48分）[请将结果直接填入答题纸的相应位置]7．若x：y=5：2，则（x+y）：y的值是．【考点】比例的性质．【分析】根据合比性质：=⇒=，可得答案．【解答】解：由合比性质，得==，故答案为：．【点评】本题考查了比例的性质，利用合比性质是解题关键．8．计算：﹣3（﹣2）=﹣+6．【考点】*平面向量．【分析】直接利用平面向量的加减运算法则求解即可求得答案．【解答】解：﹣3（﹣2）=﹣3+6=﹣+6．故答案为：﹣+6．【点评】此题考查了平面向量的运算法则．注意掌握去括号时的符号变化是解此题的关键．9．二次函数y=x2﹣2x的图象的对称轴是直线x=1．【考点】二次函数的性质．【分析】先把二次函数y=x2﹣2x写成顶点坐标式y=（x﹣1）2﹣1，进而写出图象的对称轴方程．【解答】解：▱y=x2﹣2x，▱y=（x﹣1）2﹣1，▱二次函数的图象对称轴为x=1．故答案为x=1．【点评】本题主要考查了二次函数的性质，解答本题的关键是把二次函数写出顶点坐标式，此题难度不大．10．如果抛物线y=﹣x2+3x﹣1+m经过原点，那么m=1．【考点】二次函数图象上点的坐标特征．【专题】计算题．【分析】把原点坐标代入y=﹣x2+3x﹣1+m中得到关于m的一次方程，然后解一次方程即可．【解答】解：▱抛物线y=﹣x2+3x﹣1+m经过点（0，0），▱﹣1+m=0，▱m=1．故答案为1．【点评】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．11．已知点A（x1，y1）、B（x2，y2）为二次函数y=（x﹣1）2图象上的两点，若x1＜x2＜1，则y1＞y2．（填“＞”、“＜”或“=”）【考点】二次函数图象上点的坐标特征．【专题】计算题．【分析】先利用顶点式得到抛物线的对称轴为直线x=1，由于抛物线开口向上，在对称轴左侧，y随x的增大而减小，于是可判断y1与y2的大小．【解答】解：▱二次函数y=（x﹣1）2图象的对称轴为直线x=1，而x1＜x2＜1，▱y1＞y2．故答案为＞．【点评】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．解决本题的关键是运用二次函数的性质比较y1与y2的大小．12．用“描点法”画二次函数y=ax2+bx+c的图象时，列出了下面的表格：x (2)101…y…﹣11﹣21﹣2…根据表格上的信息回答问题：当x=2时，y=﹣11．【考点】二次函数的性质．【分析】首先根据表格数据得到二次函数图象的对称轴为x=0，然后求出当x=2时y的值．【解答】解：由表格数据可知：当x=﹣1，y=﹣2；x=1，y=﹣2，则二次函数的图象对称轴为x=0，又知x=﹣2和x=2关于x=0对称，当x=﹣2时，y=﹣11，即当x=2时，y=﹣11．故答案为﹣11．【点评】本题主要考查了二次函数的性质的知识，解答本题的关键是根据表格数据得到二次函数图象的对称轴为x=0，此题难度不大．13．如果两个相似三角形的周长的比为1：4，那么周长较小的三角形与周长较大的三角形对应角平分线的比为1：4．【考点】相似三角形的性质．【分析】根据相似三角形周长的比等于相似比、相似三角形对应角平分线的比等于相似比解答即可．【解答】解：▱两个相似三角形的周长的比为1：4，▱两个相似三角形的相似比为1：4，▱周长较小的三角形与周长较大的三角形对应角平分线的比为1：4，故答案为：1：4．【点评】本题考查的是相似三角形的性质，掌握相似三角形周长的比等于相似比、相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比是解题的关键．14．如图，在▱ABCD中，E是边BC上的点，分别联结AE、BD相交于点O，若AD=5，=，则EC=2．【考点】相似三角形的判定与性质；平行四边形的性质．【分析】根据平行四边形的性质得到AD▱BC，AD=BC，推出▱BE0▱▱DAO，根据相似三角形的性质得到，求得BE=3，即可得到结论．【解答】解：▱四边形ABCD是平行四边形，▱AD▱BC，AD=BC，▱▱BE0▱▱DAO，▱，▱AD=5，▱BE=3，▱CE=5﹣3=2，故答案为：2．【点评】此题考查了平行四边形的性质以及相似三角形的判定与性质．熟练掌握相似三角形的判定和性质是解题的关键．15．如图，正方形DEFG的边EF在▱ABC的边BC上，顶点D、G分别在边AB、AC 上．若▱ABC的边BC长为40厘米，高AH为30厘米，则正方形DEFG的边长为厘米．【考点】相似三角形的判定与性质；正方形的性质．【分析】由DG▱BC得▱ADG▱▱ABC，利用相似三角形对应边上高的比等于相似比，列方程求解．【解答】解：设正方形的边长为x．由正方形DEFG得，DG▱EF，即DG▱BC，▱AH▱BC，▱AP▱DG．由DG▱BC得▱ADG▱▱ABC▱=．▱PH▱BC，DE▱BC▱PH=ED，AP=AH﹣PH，即，由BC=40，AH=30，DE=DG=x，得，解得x=．故正方形DEFG的边长是．故答案为：．【点评】本题考查了相似三角形的判定与性质．关键是由平行线得到相似三角形，利用相似三角形的性质列方程．16．如图，在▱ABC中，▱ACB=90°，若点G是▱ABC的重心，cos▱BCG=，BC=4，则CG=2．【考点】三角形的重心．【分析】延长CG交AB于D，作DE▱BC于E，根据重心的概念得到点D为AB的中点，根据直角三角形的性质得到DC=DB，根据等腰三角形的三线合一得到CE=2，根据余弦的概念求出CD，根据三角形的重心的概念得到答案．【解答】解：延长CG交AB于D，作DE▱BC于E，▱点G是▱ABC的重心，▱点D为AB的中点，▱DC=DB，又DE▱BC，▱CE=BE=BC=2，又cos▱BCG=，▱CD=3，▱点G是▱ABC的重心，▱CG=CD=2，故答案为：2．【点评】本题考查的是三角形的重心的概念和性质以及锐角三角函数的定义，掌握三角形的重心是三角形三条中线的交点，且重心到顶点的距离是它到对边中点的距离的2倍是解题的关键．17．如图，在四边形ABCD中，▱B=▱D=90°，AB=3，BC=2，tanA=，则CD=．【考点】解直角三角形．【分析】延长AD和BC交于点E，在直角▱ABE中利用三角函数求得BE的长，则EC的长即可求得，然后在直角▱CDE中利用三角函数的定义求解．【解答】解：延长AD和BC交于点E．▱在直角▱ABE中，tanA==，AB=3，▱BE=4，▱EC=BE﹣BC=4﹣2=2，▱▱ABE和▱CDE中，▱B=▱EDC=90°，▱E=▱E，▱▱DCE=▱A，▱直角▱CDE中，tan▱DCE=tanA==，▱设DE=4x，则DC=3x，在直角▱CDE中，EC2=DE2+DC2，▱4=16x2+9x2，解得：x=，则CD=．故答案是：．【点评】此题考查了相似三角形的判定与性质，含30度直角三角形的性质，熟练掌握相似三角形的判定与性质是解本题的关键．18．如图，在矩形ABCD中，AB=6，AD=10，点E是边BC的中点，联结AE，若将▱ABE沿AE翻折，点B落在点F处，联结FC，则cos▱ECF=．【考点】翻折变换（折叠问题）；解直角三角形．【分析】由矩形的性质得出▱B=90°，BC=AD=10，由勾股定理求出AE，由翻折变换的性质得出▱AFE▱▱ABE，得出▱AEF=▱AEB，EF=BE=5，因此EF=CE，由等腰三角形的性质得出▱EFC=▱ECF，由三角形的外角性质得出▱AEB=▱ECF，cos▱ECF=cos▱AEB=，即可得出结果．【解答】解：如图所示：▱四边形ABCD是矩形，▱▱B=90°，BC=AD=10，▱E是BC的中点，▱BE=CE=BC=5，▱AE===，由翻折变换的性质得：▱AFE▱▱ABE，▱▱AEF=▱AEB，EF=BE=5，▱EF=CE，▱▱EFC=▱ECF，▱▱BEF=▱EFC+▱ECF，▱▱AEB=▱ECF，▱cos▱ECF=cos▱AEB===．故答案为：．【点评】本题考查了矩形的性质、勾股定理、翻折变换的性质、等腰三角形的判定与性质、三角形的外角性质、三角函数；熟练掌握矩形的性质和翻折变换的性质，证出▱AEB=▱ECF是解决问题的关键．三、解答题（本大题共7题，满分78分）19．计算：cos245°+tan60°•cos30°﹣3cot260°．【考点】特殊角的三角函数值．【分析】将特殊角的三角函数值代入求解．【解答】解：原式=（）2+×﹣3×（）2=1．【点评】本题考查了特殊角的三角函数值，解答本题的关键是掌握几个特殊角的三角函数值．20．已知一个二次函数的图象经过A（0，﹣3）、B（2，﹣3）、C（﹣1，0）三点．（1）求这个二次函数的解析式；（2）将这个二次函数图象平移，使顶点移到点P（0，﹣3）的位置，求所得新抛物线的表达式．【考点】二次函数图象与几何变换；待定系数法求二次函数解析式．【专题】计算题．【分析】（1）利用待定系数法求抛物线解析式；（2）利用顶点式写出所得新抛物线的表达式．【解答】解：（1）设所求二次函数的解析式为y=ax2+bx+c，由题意得，解得．所以这个二次函数的解析式为y=x2﹣2x﹣3；（2）因为新抛物线是由抛物线y=x2﹣2x﹣3平移得到，而新抛物线的顶点坐标是（0，﹣3），所以新抛物线的解析式为y=x2﹣3．【点评】本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．21．如图，DC▱EF▱GH▱AB，AB=12，CD=6，DE：EG：GA=3：4：5．求EF和GH的长．【考点】平行线分线段成比例．【专题】计算题．【分析】过C作CQ▱AD，交GH于N，交EF于M，交AB于Q，则可判断四边形AQCD 为平行四边形，所以AQ=CD=6，同理可得EM=EM=CD=6，则BQ=AB﹣AQ=6，再利用平行线分线段成比例定理得到DE：EG：GA=CF：HF：HB=3：4：5，然后根据平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例得到MF：BQ=CF：CB=3：（3+4+5），NH：BQ=CH：CB=（3+4）：（3+4+5），则可计算出MF和NH，从而得到GH和EF的长【解答】解：过C作CQ▱AD，交GH于N，交EF于M，交AB于Q，如图，▱CD▱AB，▱四边形AQCD为平行四边形，▱AQ=CD=6，同理可得GN=EM=CD=6，▱BQ=AB﹣AQ=6，▱DC▱EF▱GH▱AB，▱DE：EG：GA=CF：HF：HB=3：4：5，▱MF▱NH▱BQ，▱MF：BQ=CF：CB=3：（3+4+5），NH：BQ=CH：CB=（3+4）：（3+4+5），▱MF=×6=1.5，NH=×6=3.5，▱EM=EM+MF=6+1.5=7.5，HG=GN+NH=6+3.5=9.5．【点评】本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例．22．如图，已知楼AB高36米，从楼顶A处测得旗杆顶C的俯角为60°，又从该楼离地面6米的一窗口E处测得旗杆顶C的仰角为45°，求该旗杆CD的高．（结果保留根号）【考点】解直角三角形的应用-仰角俯角问题．【分析】过点C作CG▱AE，垂足为点G，由题意得▱CEF=45°=▱CEG，▱ACG=60°，设CG=x，在Rt▱ACG中，AG=CG•tan▱ACG=x，在Rt▱ECG中，EG=CG•cot▱CEG=x，根据AG+EG=AE，列方程=36﹣6，得到CF=EG=15﹣15，于是得到结论．【解答】解：过点C作CG▱AE，垂足为点G，由题意得▱CEF=45°=▱CEG，▱ACG=60°，设CG=x，在Rt▱ACG中，AG=CG•tan▱ACG=x，在Rt▱ECG中，EG=CG•cot▱CEG=x，▱AG+EG=AE，▱=36﹣6，解得：x=15﹣15，▱CF=EG=15﹣15，▱CD=15﹣15+6=15﹣9．答：该旗杆CD的高为（15﹣9）米．【点评】此题主要考查了仰角与俯角问题，正确应用锐角三角函数关系是解题关键．23．如图，点E是四边形ABCD的对角线BD上的一点，▱BAE=▱CBD=▱DAC．（1）求证：DE•AB=BC•AE；（2）求证：▱AED+▱ADC=180°．【考点】相似三角形的判定与性质．【专题】证明题．【分析】（1）根据已知条件得到▱BAC=▱EAD，根据三角形额外角的性质得到▱ABC=▱AED，推出▱ABC▱▱AED，根据三角形的外角的性质得到结论；（2）根据相似三角形的性质得到，推出▱ABE▱▱ACD，根据相似三角形的性质得到▱AEB=▱ADC，等量代换即可得到结论．【解答】证明：（1）▱▱BAE=▱DAC，▱▱BAE+▱EAC=▱DAC+▱EAC，即▱BAC=▱EAD，▱▱ABC=▱ABE+▱CBD，▱AED=▱ABE+▱BAE，▱▱CBD=▱BAE，▱▱ABC=▱AED，▱▱ABC▱▱AED，▱，▱DE•AB=BC•AE；（2）▱▱ABC▱▱AED，▱，即，▱▱BAE=▱DAC▱▱ABE▱▱ACD，▱▱AEB=▱ADC，▱▱AED+▱AEB=180°，▱▱AED+▱ADC=180°．【点评】本题考查了相似三角形的性质和判定，邻补角的定义，三角形外角的性质，熟练掌握相似三角形的判定和性质是解题的关键．24．在平面直角坐标系xOy中，抛物线与x轴分别交于点A（2，0）、点B（点B在点A 的右侧），与轴交于点C，tan▱CBA=．（1）求该抛物线的表达式；（2）设该抛物线的顶点为D，求四边形ACBD的面积；（3）设抛物线上的点E在第一象限，▱BCE是以BC为一条直角边的直角三角形，请直接写出点E的坐标．【考点】抛物线与x轴的交点；待定系数法求二次函数解析式．【分析】（1）由抛物线解析式和已知条件得出C和B的坐标，（0，3），OC=3，把A（2，0）、B（6，0）分别代入y=ax2+bx+3得出方程组，解方程即可；（2）把抛物线解析式化成顶点式得出顶点坐标，四边形ACBD的面积=▱ABC的面积+▱ABD的面积，即可得出结果；（3）设点E的坐标为（x，x2﹣2x+3），分两种情况：①当▱CBE=90°时；②当▱BCE=90°时；分别由三角函数得出方程，解方程即可．【解答】解：（1）▱当x=0时，▱C（0，3），OC=3，在Rt▱COB中，▱tan▱CBA=，▱=，▱OB=2OC=6，▱点B（6，0），把A（2，0）、B（6，0）分别代入y=ax2+bx+3，得：，解得：▱该抛物线表达式为y=x2﹣2x+3；（2）▱y=x2﹣2x+3=（x﹣4）2﹣1▱顶点D（4，﹣1），▱四边形ACBD的面积=▱ABC的面积+▱ABD的面积=×4×3+×4×1=8；（3）设点E的坐标为（x，x2﹣2x+3），分两种情况：①当▱CBE=90°时，作EM▱x轴于M，如图所示：则▱BEM=▱CBA，▱=tan▱BEM=tan▱CBA=，▱EM=2BM，即2（x﹣6）=x2﹣2x+3，解得：x=10，或x=6（不合题意，舍去），▱点E坐标为（10，8）；②当▱BCE=90°时，作EN▱y轴于N，如图2所示：则▱ECN=▱CBA，▱=tan▱ECN=tan▱CBA=，▱CN=2EN，即2x=x2﹣2x+3﹣3，解得：x=16，或x=0（不合题意，舍去），▱点E坐标为（16，35）；综上所述：点E坐标为（10，8）或（16，35）．【点评】本题考查了抛物线与x轴的交点、抛物线解析式的求法、三角函数的应用、解方程等知识；本题综合性强，有一定难度，求出抛物线解析式是解决问题的关键．25．（14分）如图，在▱ABCD中，E为边BC的中点，F为线段AE上一点，联结BF并延长交边AD于点G，过点G作AE的平行线，交射线DC于点H．设==x．（1）当x=1时，求AG：AB的值；（2）设=y，求关于x的函数关系式，并写出x的取值范围；（3）当DH=3HC时，求x的值．【考点】相似形综合题．【专题】综合题；图形的相似．【分析】（1）由平行四边形ABCD，得到AD与BC平行且相等，由两直线平行得到两对内错角相等，进而确定出三角形BEF与三角形AGF相似，由相似得比例，把x=1代入已知等式，结合比例式得到AG=BE，AD=AB，即可求出所求式子的值；（2）设AB=1，根据已知等式表示出AD与BE，由AD与BC平行，得到比例式，表示出AG与DG，利用两角相等的三角形相似得到三角形GDH与三角形ABE相似，利用相似三角形面积之比等于相似比的平方列出y与x的函数解析式，并求出x的范围即可；（3）分两种情况考虑：①当点H在边DC上时，如图1所示；②当H在DC的延长线上时，如图2所示，分别利用相似得比例列出关于x的方程，求出方程的解即可得到x的值．【解答】解：（1）在▱ABCD中，AD=BC，AD▱BC，▱▱BEF=▱GAF，▱EBF=▱AGF，▱▱BEF▱▱GAF，▱=，▱x=1，即==1，▱==1，▱AD=AB，AG=BE，▱E为BC的中点，▱BE=BC，▱AG=AB，则AG：AB=；（2）▱==x，▱不妨设AB=1，则AD=x，BE=x，▱AD▱BC，▱==x，▱AG=，DG=x﹣，▱GH▱AE，▱▱DGH=▱DAE，▱AD▱BC，▱▱DAE=▱AEB，▱▱DGH=▱AEB，在▱ABCD中，▱D=▱ABE，▱▱GDH▱▱EBA，▱=（）2，▱y=（）2=（x＞）；（3）分两种情况考虑：①当点H在边DC上时，如图1所示：▱DH=3HC，▱=，▱=，▱▱GDH▱▱EBA，▱==，即=，解得：x=；②当H在DC的延长线上时，如图2所示：▱DH=3HC，▱=，▱=，▱▱GDH▱▱EBA，▱==，即=，解得：x=2，综上所述，可知x的值为或2．【点评】此题属于相似型综合题，涉及的知识有：平行四边形的性质，相似三角形的判定与性质，以及平行线的性质，熟练掌握相似三角形的判定与性质是解本题的关键．。

2014年上海一模25题集锦1、（2014年一模宝山26题）、如图△ABC 中，；△DEF 0090305cm C A BC ∠=∠==，，中，，，. 现将△DEF 的直角边DF 与△AB C 的斜边AB 090D ∠=045E ∠=3cm DE =重合在一起，并将△DEF 沿AB 方向移动（如图）.在移动过程中，D 、F 两点始终在AB 边上（移动开始时点D 与点A 重合，一直移动至点F 与点B 重合为止）.（1）在△DEF 沿AB 方向移动的过程中，有人发现：E 、B 两点间的距离随AD 的变化而变化，现设，请你写出与之间的函数关系式及其定义域.,AD x BE y ==y x （2）请你进一步研究如下问题：问题①：当△DEF 移动至什么位置，即AD 的长为多少时，E 、B 的连线与AC 平行？ 问题②：在△DEF 的移动过程中，是否存在某个位置，使得 ？如果存在，022.5EBD ∠=求出AD 的长度；如果不存在，请说明理由.问题③：当△DEF 移动至什么位置，即AD 的长为多少时，以线段AD 、EB 、BC 的长度为三边长的三角形是直角三角形？ （本题6+8=14分）2、（2014年一模崇明25题）（本题满分14分，其中第1、2小题各5分，第3小题4分）如图，在△ABC 中，AB ＝8，BC ＝10，，，BD 平分∠ABC 交AC 边3cos 4C =2ABC C ∠=∠于点D ，点E 是BC 边上的一个动点（不与B 、C 重合），F 是AC 边上一点，且∠AEF ＝∠ABC ，AE 与BD 相交于点G 。

（1）求证：；AB BGCE CF=（2）设BE ＝x ，CF ＝y ，求y 与x 之间的函数关系式，并写出x 的取值范围；（3）当△AEF 是以AE 为腰的等腰三角形时，求BE 的长。

B25、（1）证明：∵BD 平分∴ABC ∠2ABC ABD ∠=∠∵∴2ABC C ∠=∠ABD C∠=∠∵ 即AEC ABC BAE ∠=∠+∠AEF FEC ABC BAE ∠+∠=∠+∠∵∴AEF ABC ∠=∠BAE FEC∠=∠∴△ABG ∽△ECF ∴AB BGCE CF=（2）过点A 作BC 的平行线交BD 的延长线于点M ∵AM ∥BC ∴∠M ＝∠DBC∵∠ABD ＝∠DBC ∴∠M ＝∠ABD ∴AM ＝AB ＝8过点A 作，垂足为NAN MB ⊥∵3,cos ,4ABD C C AB AC∠=∠==∴6,12BN MN BM ===∵AM ∥BC ∴∴∴AM MG BE BG =812BG x BG -=128xBG x =+∵∴AB BG CE CF =128810xx x y +=-∴()2303010216x x y x x -=<<+（3）当△AEF 是以AE 为腰的等腰三角形时存在以下两种情况：1°，则AE AF =AEF AFE∠=∠易证明， 又∵FE FC y ==3cos 4C =易得， 又∵32EC y =10EC x =-∴又∵2023x y -=2303216x x y x -=+解得()126.4,10x x ==舍去即BE 的长为6.42°EA EF=作线段CF 的垂直平分线交BC 于点H ，交FC 于点K ，联结HF 则易证△ABE ≌△EHF ，HF ＝HC ∴8,AB EH BE FH HC x=====∴2810x +=∴1x =即BE 的长为1综上所述，当△AEF 是以AE 为腰的等腰三角形时，BE 的长为6.4或1。

2014年上海市中考数学一模试卷一、选择题：（本大题共6题，每题4分，满分24分）1．在Rt△ABC中，∠C=90°，如果∠A=α，BC=a，那么AC等于（）．2．如果抛物线y=mx2+（m﹣3）x﹣m+2经过原点，那么m的值等于（）3．如图，已知平行四边形ABCD中，向量在，方向上的分量分别是（）．．、、4．（4分）抛物线y=﹣（x﹣2）2+1经过平移后与抛物线y=﹣（x+1）2﹣2重合，那么平移的方法可以是（）5．（4分）在△ABC，点D、E分别在边AB、AC上，如果AD=1，BD=2，那么由下列条件能够判定DE∥BC的是（）．．6．（4分）如图，已知AB、CD分别表示两幢相距30米的大楼，小明在大楼底部点B 处观察，当仰角增大到30度时，恰好能通过大楼CD的玻璃幕墙看到大楼AB的顶部点A的像，那么大楼AB的高度为（）米0二、填空题：（本大题12小题，每题4分，满分48分）7．函数y=（5+x）（2﹣x）图象的开口方向是_________．8．在Rt△ABC中，∠C=90°，如果∠A=45°，AB=12，那么BC=_________．9．已知线段a=3cm，b=4cm，那么线段a、b的比例中项等于_________cm．10．如果两个相似三角形周长的比是2：3，那么它们面积的比是_________．11．如图，在△ABC于△ADE中，，要使△ABC于△ADE相似，还需要添加一个条件，这个条件是_________．12．已知点G是△ABC的重心，AB=AC=5，BC=8，那么AG=_________．13．（4分）已知向量与单位向量方向相反，且，那么=_________（用向量的式子表示）14．如果在平面直角坐标系xOy中，点P的坐标为（3，4），射线OP与x的正半轴所夹的角为α，那么α的余弦值等于_________．15．（4分）已知一条斜坡的长度为10米，高为6米，那么坡角的度数约为_________（备用数据：tan31°=cot59°≈0.6，sin37°=cos53°≈0.6）16．如果二次函数y=x2+2kx+k﹣4图象的对称轴为x=3，那么k=_________．17．如图，小李推铅球，如果铅球运行时离地面的高度y（米）关于水平距离x（米）的函数解析式，那么铅球运动过程中最高点离地面的距离为_________米．18．（4分）（2014•静安区一模）如果将一个三角形绕着它一个角的顶点旋转后使这个角的一边与另一边重叠，再将旋转后的三角形相似缩放，使重叠的两边互相重合，我们称这样的图形为三角形转似，这个角的顶点称为转似中心，所得的三角形称为原三角形的转似三角形．如图，在△ABC中，AB=6，BC=7，AC=5，△A1B1C是△ABC 以点C为转似中心的其中一个转似三角形，那么以点C为转似中心的另一个转似三角形△A2B2C（点A2，B2分别与A、B对应）的边A2B2的长为_________．三、解答题：（本大题共7题，满分78分）19．（10分）如图，已知在直角坐标系中，点A在第二象限内，点B和点C在x轴上，原点O为边BC的中点，BC=4，AO=AB，tan∠AOB=3，求图象经过A、B、C三点的二次函数解析式．20．（10分）如图，已知在△ABC中，点D、E分别在边AB、AC上，DE∥BC，，如果，．（1）求（用向量的式子表示）（2）求作向量（不要求写作法，但要指出所作图表中表示结论的向量）21．（10分）（2014•静安区一模）已知：如图，在平行四边形ABCD中，E、F分别是边BC，CD上的点，且EF∥BD，AE、AF分别交BD与点G和点H，BD=12，EF=8．求：（1）的值；（2）线段GH的长．22．（10分）如图，已知某船向正东方向航行，在点A处测得某岛C在其北偏东60°方向上，前进8海里处到达点B处，测得岛C在其北偏东30°方向上．已知岛C周围6海里内有一暗礁，问：如果该船继续向东航行，有无触礁危险？请说明你的理由．23．（12分）（2014•静安区一模）已知，如图，在梯形ABCD中，AD∥BC，∠BCD=90°，对角线AC、BD相交于点E，且AC⊥BD．（1）求证：CD2=BC•AD；（2）点F是边BC上一点，联结AF，与BD相交于点G，如果∠BAF=∠DBF，求证：．24．（12分）已知在平面直角坐标系xOy中，二次函数y=﹣2x2+bx+c的图象经过点A （﹣3，0）和点B（0，6）．（1）求此二次函数的解析式；（2）将这个二次函数的图象向右平移5个单位后的顶点设为C，直线BC与x轴相交于点D，求∠ABD的正弦值；（3）在第（2）小题的条件下，联结OC，试探究直线AB与OC的位置关系，并说明理由．25．（14分）如图，已知在Rt△ABC中，∠ACB=90°，AB=10，tanA=，点D是斜边AB上的动点，联结CD，作DE⊥CD，交射线CB于点E，设AD=x．（1）当点D是边AB的中点时，求线段DE的长；（2）当△BED是等腰三角形时，求x的值；（3）如果y=，求y关于x的函数解析式，并写出它的定义域．2014年上海市中考数学一模试卷参考答案1. B2. C3. C4. A5. D6. B7. 向下8. 69. 2．10. 4:9 11. ∠B=∠E12. 213. ：﹣3．14.．15. 答案为：37°．16. K=-3 17. 2 18.答案为：．19. 解：∵原点O为边BC的中点，BC=4，∴B点坐标为（﹣2，0），C点坐标为（2，0），作AH⊥OB于H，如图，∵AO=AB，∴OH=BH=1，∵tan∠AOB==3，∴AH=3，∴A点坐标为（﹣1，3），设抛物线的解析式为y=a（x+2）（x﹣2），把A（﹣1，3）代入得a×1×（﹣3）=3，解得a=﹣1，∴经过A、B、C三点的二次函数解析式为y=﹣（x+2）（x﹣2）=﹣x2+4．20. 解：（1）∵DE∥BC，∴=，∵，，∴=+=+，∴==（+）=+；（2）如图，取点AB的中点M，作=，连接，则即为所求．21.解：（1）∵EF∥BD，∴=，∵BD=12，EF=8，∴=，∴=，∵四边形ABCD是平行四边形，∴AB=CD，∴=；（2）∵DF∥AB，∴==，∴=，∵EF∥BD，∴==，∴=，∴GH=6．22. 解：解：作CD⊥AB于点D，由题意可知，∠CAB=30°，∠CBD=60°，∴∠ACB=30°，在Rt△BCD中，∵∠BDC=90°，∠CBD=60°，∴∠BCD=30°，∴∠ACB=∠BCD．∴△CDB∽△ADC．∴=∵AB=CB=8∴BD=4，AD=12．∴=∴CD=3≈6.928＞6．∴船继续向东航行无触礁危险．23. 证明：（1）∵AD∥BC，∠BCD=90°，∴∠ADC=∠BCD=90°，又∵AC⊥BD，∴∠ACD+∠ACB=∠CBD+∠ACB=90°，∴∠ACD=∠CBD，∴△ACD∽△DBC，∴=，即CD2=BC×AD；（2）方法一：∵AD∥BC，∴∠ADB=∠DBF，∵∠BAF=∠DBF，∴∠ADB=∠BAF，∵∠ABG=∠DBA，∴△ABG∽△DBA，∴=，∴=，又∵△ABG∽△DBA，∴=，∴AB2=BG•BD，∴===，方法二：∵AD∥BC，∴∠ADB=∠DBF，∵∠BAF=∠DBF，∴∠ADB=∠BAF，∵∠ABG=∠DBA，∴△ABG∽△DBA，∴=（）2=，而=，∴=．24. 解：（1）由题意得，，解得，所以，此二次函数的解析式为y=﹣2x2﹣4x+6；（2）∵y=﹣2x2﹣4x+6=﹣2（x+1）2+8，∴函数y=2x2﹣4x+6的顶点坐标为（﹣1，8），∴向右平移5个单位的后的顶点C（4，8），设直线BC的解析式为y=kx+b（k≠0），则，解得，所以，直线BC 的解析式为y=x+6，令y=0，则x+6=0，解得x=﹣12，∴点D的坐标为（﹣12，0），过点A作AH⊥BD于H，OD=12，BD===6，AD=﹣3﹣（﹣12）=﹣3+12=9，∵∠ADH=∠BDO，∠AHD=∠BOD=90°，∴△ADH∽△BDO，∴=，即=，解得AH=，∵AB===3，∴sin∠ABD===；（3）AB∥OC．理由如下：方法一：∵BD=6，BC==2，AD=9，AO=3，∴==3，∴AB∥OC；方法二：过点C作CP⊥x轴于P，由题意得，CP=8，PO=4，AO=3，BO=6，∴tan∠COP===2，tan∠BAO===2，∴tan∠COP=tan∠BAO，∴∠BAO=∠COP，∴AB∥OC．25. 解：（1）在△ABC中，∵∠ACB=90°，AB=10，tanA=，∴BC=8，AC=6，∵点D为斜边AB的中点，∴CD=AD=BD=5，∴∠DCB=∠DBC，∵∠EDC=∠ACB=90°，∴△EDC∽△ACB，∴=，即=，则DE=；（2）分两种情况情况：（i）当E在BC边长时，∵△BED为等腰三角形，∠BED为钝角，∴EB=ED，∴∠EBD=∠EDB，∵∠EDC=∠ACB=90°，∴∠CDA=∠A，∴CD=AC，作CH⊥AB，垂足为H，那么AD=2AH，∴=，即AH=，∴AD=，即x=；（ii）当E在CB延长线上时，∵△BED为等腰三角形，∠DBE为钝角，∴BD=DE，∴∠BED=∠BDE，∵∠EDC=90°，∴∠BED+∠BCD=∠BDE+∠EDC=90°，∴∠BCD=∠BDC，∴BD=BC=8，∴AD=x=AB﹣BD=10﹣8=2；（3）作DM⊥BC，垂足为M，∵DM∥AC，∴==，∴DM=（10﹣x），BM=（10﹣x），∴CM=8﹣（10﹣x）=x，CD=，∵△DEM∽△CDM，∴=，即DE==，∴y==，整理得：y=（0＜x＜10）．。

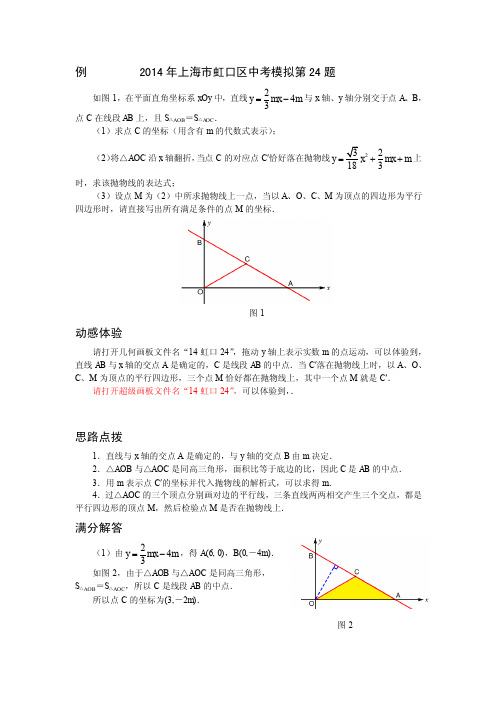
例 2014年上海市虹口区中考模拟第24题如图1，在平面直角坐标系xOy 中，直线243y mx m =-与x 轴、y 轴分别交于点A 、B ，点C 在线段AB 上，且S △AOB ＝S △AOC ．（1）求点C 的坐标（用含有m 的代数式表示）；（2）将△AOC 沿x 轴翻折，当点C 的对应点C ′恰好落在抛物线22183y x mx m =++上时，求该抛物线的表达式；（3）设点M 为（2）中所求抛物线上一点，当以A 、O 、C 、M 为顶点的四边形为平行四边形时，请直接写出所有满足条件的点M 的坐标．图1动感体验请打开几何画板文件名“14虹口24”，拖动y 轴上表示实数m 的点运动，可以体验到，直线AB 与x 轴的交点A 是确定的，C 是线段AB 的中点．当C ′落在抛物线上时，以A 、O 、C 、M 为顶点的平行四边形，三个点M 恰好都在抛物线上，其中一个点M 就是C ′． 请打开超级画板文件名“14虹口24”，可以体验到，．思路点拨1．直线与x 轴的交点A 是确定的，与y 轴的交点B 由m 决定．2．△AOB 与△AOC 是同高三角形，面积比等于底边的比，因此C 是AB 的中点．3．用m 表示点C ′的坐标并代入抛物线的解析式，可以求得m ．4．过△AOC 的三个顶点分别画对边的平行线，三条直线两两相交产生三个交点，都是平行四边形的顶点M ，然后检验点M 是否在抛物线上．满分解答（1）由243y mx m =-，得A (6, 0)，B (0,－4m )． 如图2，由于△AOB 与△AOC 是同高三角形，S △AOB ＝S △AOC ，所以C 是线段AB 的中点．所以点C 的坐标为(3,－2m )．图2（2）将C ′(3, 2m )代入223y x mx m =++，得22m m m =+．解得m =．所以抛物线的表达式为2y x x =．（3）满足条件的点M 的坐标是(3,、(-、，如图3所示． 考点伸展第（3）题的解题思路是这样的：如图3，因为A (6, 0)、O (0, 0)、C 是确定的，过△AOC 的三个顶点分别画对边的平行线，三条直线两两相交产生三个交点，都是平行四边形的顶点M ．①点O (0, 0)向右平移6个单位得到点 A (6, 0)，所以点C 向右平移6个单位得到点；②点A (6, 0)左平移6个单位得到点O (0, 0)，所以点C 向左平移6个单位得到点(-；③点C ′(3,也是平行四边形的一个顶点．经检验，、(-、(3,三个点都在抛物线2(69)18y x x =--上．图3。

虹口区2014学年度第一学期初三分层练习1数学学科（A ）卷参考答案及评分标准一、选择题（本大题共6题，每题4分，满分24分）1． B 2．C 3． A 4．D 5．C 6．B二、填空题（本大题共12题，每题4分，满分48分）7．32 8．4 9 10．203 11．10 12．19313．18 14．20 15．12 16．9 17．12 18．6或6三、解答题（本大题共7题，满分78分）19．解：根据题意，设3,4,5a k b k c k === …………………………………………………………（3分）∵212a b c +-=∴38512k k k +-= ……………………………………………………………………（2分） 解得： 2k = …………………………………………………………………（2分） ∴ 6 , 8 , 10a b c === ……………………………………………………………………（3分）20. 证明：∵AD //BC∴ ∠DAC =∠ACB ……………………………………………………………………（3分） ∵ ∠BAC=∠D∴△ABC ∽△DCA ……………………………………………………………………（2分）∴ A D A C A C B C= ……………………………………………………………………（3分） 即 2AC AD BC =⋅ ……………………………………………………………………（2分）21．解：设正方形DEFG 的边长为x cm . …………………………………………………………（1分）由题意得： DG //BC∴ △ADG ∽△ABC ……………………………………………………………………（1分） ∵ AH 是△ABC 的高∴ AH ⊥BC 又DG //BC∴ AP ⊥DG ………………………………………………………………………………………（1分） ∴ AP DG AH BC= ……………………………………………………………………………（2分） ∵ BC =30，AH =40，BE =5．DG =GF=x ∴ 202030x x -= …………………………………………………………………………（1分） 解得： x = 12 …………………………………………………………………………………（2分） 22144 cm DEFG S x ==正方形 ………………………………………………………………………（1分）答：正方形 DEFG 的面积是2144 cm . …………………………………………………………（1分）22．证明：（1） ∵ EG //BD ∴AE AG BE GD= …………………………………………………………………………（2分） 同理可证：AF AG FC GD =……………………………………………………………………………（1分）∴AE AF BE FC= ……………………………………………………………………………（1分） ∴ EG //BD ……………………………………………………………………………（1分）（2）∵ EG //BD∴AE EG AB BD= 同理可证：AF GF AC DC = AE AF EF AB AC BC== ∴ EG GF EF BD DC BC ==…………………………………………………………………………（2分） ∴ △GEF ∽△DBC ……………………………………………………………………（1分） ∴224()()25GEF DBC S EF AE S BC AB ===△△……………………………………………………………（2分）23．证明：（1）在□ABCD 中，AB ∥CD ，AB =CD ，AD ∥BC ， ………………………………………（1分）又∵E 是AB 的中点，∴12AF AE FC CD ==，…………………………………………………………（2分） ∵FG ∥AB ， ∴FG ∥CD ， ∴13FG AF CD AC ==，…………………………………………（2分） ∴13FG AB =， ∴AB =3FG ．………………………………………………………………………（1分） （2）∵FG ∥AB ， ∴GF DG AE DA=…………………………………………………………………（2分） ∵FG ∥CD ∴FG AG CD AD =…………………………………………………………………（2分） ∴1GF GF DG AG AE DC DA AD+=+=……………………………………………………………………（2分）24．证明：（1）∵∠DEB=∠A+∠ADE即∠DEC+∠CEB =∠A+∠ADE∵∠A =∠DEC∴∠CEB =∠ADE ……………………………………………………………………（2分）∵∠A=∠B∴△ADE ∽△BEC ……………………………………………………………………（1分）∴点E 是四边形ABCD 的边AB 上的相似点．……………………………………………（1分）（2）如图，E 点共2个，每个2分（3） 当AE =BE 时，点E 是四边形ABCM 的边AB 上的一个强相似点. ……………………（1分）证明如下：同上易证 △AME ∽△BEC∴AM ME EB EC= ……………………………………………………………………（1分） ∵ AE =BE ∴AM ME AE EC =……………………………………………………………………（1分） ∵∠A =∠MEC∴△AME ∽△MEC ………………………………………………………………（1分）∴△AME ∽△BEC ∽△MEC∴点E 是四边形ABCM 的边AB 上的一个强相似点.25．解：(1) 当△BPQ ∽△ABC 时，则：BP BQ BA BC = 或 BP BQ BC BA=………………………………………………………（2分） ∵BP =5t ，BQ =8-4t ，AB =10，BC =8，∴584108t t -= 或 584810t t -= ∴ 11t = ；23241t =…………………………………………（2分） ∴当t 为1或3241时，△BPQ ∽△ABC . (2) 如图1，过点P 作PM ⊥BC 于点M ………………………（1分）易证 △PBM ∽△ABC ∴ BP PM BA AC= ∴3PM t =……………………………（2分） ∵ABC PBQ ACQP S S S =-△△四边形 ………………………………………………………（1分） ∵BQ =8-4t ，AC =6，BC =8，∴y 关于t 的函数关系式是 261224y t t =-+ …………………………………………（2分）(3) 如图，过P 作PM ⊥BC 于点M ，AQ ，CP 交于点N ，则有PB =5t ，PM =3t ，MC =8﹣4t ，∵∠NAC +∠NCA =90°，∠PCM +∠NCA =90°，∴∠NAC =∠PCM 且∠ACQ =∠PMC =90°，∴△ACQ ∽△CMP ， ……………………………（1分）∴AC CQ CM MP =……………………………………（1分） ∴64843t t t=-………………………………………（1分） 解得：78t = ……………………………………（1分）第25题 图1QM。

2014年上海一模25题集锦1、（2014年一模宝山26题）、如图△ABC 中，；△DEF 0090305cm C A BC ∠=∠==，，中，，，. 现将△DEF 的直角边DF 与△AB C 的斜边AB 090D ∠=045E ∠=3cm DE =重合在一起，并将△DEF 沿AB 方向移动（如图）.在移动过程中，D 、F 两点始终在AB 边上（移动开始时点D 与点A 重合，一直移动至点F 与点B 重合为止）.（1）在△DEF 沿AB 方向移动的过程中，有人发现：E 、B 两点间的距离随AD 的变化而变化，现设，请你写出与之间的函数关系式及其定义域.,AD x BE y ==y x （2）请你进一步研究如下问题：问题①：当△DEF 移动至什么位置，即AD 的长为多少时，E 、B 的连线与AC 平行？ 问题②：在△DEF 的移动过程中，是否存在某个位置，使得 ？如果存在，022.5EBD ∠=求出AD 的长度；如果不存在，请说明理由.问题③：当△DEF 移动至什么位置，即AD 的长为多少时，以线段AD 、EB 、BC 的长度为三边长的三角形是直角三角形？ （本题6+8=14分）2、（2014年一模崇明25题）（本题满分14分，其中第1、2小题各5分，第3小题4分）如图，在△ABC 中，AB ＝8，BC ＝10，，，BD 平分∠ABC 交AC 边3cos 4C =2ABC C ∠=∠于点D ，点E 是BC 边上的一个动点（不与B 、C 重合），F 是AC 边上一点，且∠AEF ＝∠ABC ，AE 与BD 相交于点G 。

（1）求证：；AB BGCE CF=（2）设BE ＝x ，CF ＝y ，求y 与x 之间的函数关系式，并写出x 的取值范围；（3）当△AEF 是以AE 为腰的等腰三角形时，求BE 的长。

B25、（1）证明：∵BD 平分∴ABC ∠2ABC ABD ∠=∠∵∴2ABC C ∠=∠ABD C∠=∠∵ 即AEC ABC BAE ∠=∠+∠AEF FEC ABC BAE ∠+∠=∠+∠∵∴AEF ABC ∠=∠BAE FEC∠=∠∴△ABG ∽△ECF ∴AB BGCE CF=（2）过点A 作BC 的平行线交BD 的延长线于点M ∵AM ∥BC ∴∠M ＝∠DBC∵∠ABD ＝∠DBC ∴∠M ＝∠ABD ∴AM ＝AB ＝8过点A 作，垂足为NAN MB ⊥∵3,cos ,4ABD C C AB AC∠=∠==∴6,12BN MN BM ===∵AM ∥BC ∴∴∴AM MG BE BG =812BG x BG -=128xBG x =+∵∴AB BG CE CF =128810xx x y +=-∴()2303010216x x y x x -=<<+（3）当△AEF 是以AE 为腰的等腰三角形时存在以下两种情况：1°，则AE AF =AEF AFE∠=∠易证明， 又∵FE FC y ==3cos 4C =易得， 又∵32EC y =10EC x =-∴又∵2023x y -=2303216x x y x -=+解得()126.4,10x x ==舍去即BE 的长为6.42°EA EF=作线段CF 的垂直平分线交BC 于点H ，交FC 于点K ，联结HF 则易证△ABE ≌△EHF ，HF ＝HC ∴8,AB EH BE FH HC x=====∴2810x +=∴1x =即BE 的长为1综上所述，当△AEF 是以AE 为腰的等腰三角形时，BE 的长为6.4或1。

上海市虹口区2014年中考一模试卷数学试题（2014年1月）（考试时间：100分钟，满分：150分）一、 选择题（本大题共6题，每题4分，满分24分）1．下列函数中属于二次函数的是（ ▲ ）A ．2y x =；B ．2(1)(3)y x x =+-；C ．32y x =-；D ．21x y x +=． 2．抛物线232y x x =-+与y 轴交点的坐标是（ ▲ ）A ．512AC BC -=；B ．512AC AB -=； C ．512BC AB -=；D ．512CB AC +=． 3．在Rt △ABC 中，∠ C =90°，若a 、b 、c 分别∠A 、∠B 、∠C 的对边，则下列结论中，正确的是（ ▲ ）A ．sin c A a ⋅=；B ．cos b B c ⋅=；C ．tan a A b ⋅=；D ．tan c B b ⋅=．4．如图，若AB // CD // EF ，则下列结论中，与AD AF相等的是（ ▲ ） A ．AB EF ； B ．CD EF ； C ．BO OE ； D ．BC BE． 5．如图，在△ABC 中，如果DE 与BC 不平行，那么下列条件中，不能判断△ADE ∽△ABC 的是（ ▲ ） A ．∠ADE =∠C ； B ．∠AED =∠B ； C ．AD DE AB BC =； D ．AD AE AC AB=．6．如图，在四边形ABCD 中，点E 、F 分别是AB 、AD 的中点，若EF = 2，BC = 5，CD = 3，则sinC 的值为（ ▲ ）A ．34；B ． 43；C ．35；D ．45． 二、填空题（本大题共12题，每题4分，满分48分）7．已知:3:2x y =，则():x y x += ▲ ．82245sin 60︒+︒= ▲ ．9．在Rt △ABC 中，∠C = 90°，若AC =5，tan A = 2，则BC = ▲ ．10．写出抛物线212y x =与抛物线212y x =-的一条共同特征是 ▲ ． 11．已知抛物线22(3)1y x =--+，当123x x >>时，12____y y ．（填“>”或“<”）12．将抛物线23y x =-平移，使其顶点移到点P （– 2 , 1）的位置，则所得新抛物线的表达式是 ▲ ．13．二次函数2y ax bx c =++图像上部分点的坐标满足下表：x… – 3 – 2 – 1 0 1 … y … – 3 – 2 – 3 – 6 – 11 … 则该函数图像的顶点坐标为 ▲ ．14．在△ABC 中，EF // BC ，AD ⊥BC 交EF 于点G ，EF = 4，BC = 5，AD = 3，则AG = ▲ ．15．如图，点G 是△ABC 的重心，GF // BC ，,AB a AC b ==，用,a b 表示GF = ▲ ．16．如图，每个小正方形的边长为1，A 、B 、C 是小正方形的顶点，则∠ABC 的正弦值为 ▲ ．17．如图，某公园入口处原有三级台阶，每级台阶高为20cm ，深为30cm ，为方便残疾人士，拟将台阶改为斜坡，设台阶的起点为A ，斜坡的起始点为C ，现设计斜坡BC 的坡度1:5i =，则AC 的长度是 ▲ cm ．18．如图，Rt △ABC 中，∠C =90°，AB = 5，AC = 3，在边AB 上取一点D ，作DE ⊥AB 交BC 于点E ．现将△BDE 沿DE 折叠，使点B 落在线段DA 上，对应点记为B 1；BD 的中点F 的对应点记为F 1．若△EFB ∽△AF 1E ，则B 1D = ▲ ．三、解答题（本大题共7题，满分78分）19．（本题满分10分）已知：一个二次函数的图像经过（3，0）、（0，– 3）（1，– 4）三点，求这个二次函数解析式．20．（本题满分10分，第（1）小题满分4分，第（2）小题满分6分）已知二次函数21722y x x =--+ （1） 用配方法把该二次函数的解析式化为2()y a x m k =++的形式；（2） 指出该二次函数图像的开口方向、顶点坐标和对称轴．21．（本题满分10分）如图，在△ABC 中，∠C = 90°，AD 是∠CAB 的角平分线，BE ⊥AE ，垂足为点E ．求证：2BE DE AE =⋅22．（本题满分10分） 我国南水北调中线工程的起点是某水库，按照工程计划，需对原水库大（第18题图） F 1B 1F ED C B A EC坝进行混凝土培厚加高，使坝高由原来的156米增加到173.2米，以抬高蓄水位，如图是一段坝体加高工程的截面示意图，其中原坝体的高为BE ，背水坡坡角∠BAE = 69°，新坝体高为DE ，背水坡坡角∠DCE = 60°，求工程完工后背水坡底端水平方向增加的宽度AC ．23．（本题满分12分，第（1）小题满分6分，第（2）小题满分6分）在△ABC 中，∠BAC = 90°，∠EAF = 90°，AB AF AC AE ⋅=⋅．（1）求证：△AGC ∽△DGB ；（2）若点F 为CG 的中点，AB = 3，AC = 4，1tan 2DBG ∠=，求DF 的长．24．（本题满分12分，第（1）小题满分6分，第（2）小题满分6分）如图，已知抛物线214y x bx c =++经过点B （– 4 , 0）与点C （8 , 0），且交y 轴于点A ． （1）求该抛物线的表达式，并写出其顶点坐标；（2）将该抛物线向上平移4个单位，再向右平移m 个单位，得到新抛物线，若新抛物线的顶点为P ，联结BP ，直线BP 将△ABC 分割成面积相等的两个三角形，求m 的值．25．（本题满分14分，第（1）小题满分6分，第（2）小题满分4分，第（3）小题满分4分） 已知：正方形ABCD 的边长为4，点E 为BC 边的中点，点P 为AB 边上一动点长，沿PE 翻折△BPE 得到△FPE ，直线PF 交CD 边于点Q ，交直线AD 于点G ．（1）如图，当BP = 1.5时，求CQ 的长；（2）如图，当点G 在射线AD 上时，设BP =x ， DG = y ，求y 关于x 的函数关系式，并写出x的取值范围；（3）延长EF交直线AD于点H，若△CQE∽△FHG，求BP的长．B。