数据分析课后习题答案

数据分析：分析视角思维的培养课后测试•1、做市场预测的案例分析预测时，使用分类视角其实是一个（）的过程（10分）A由此及彼B由因索果C由部分推断总体D用波动推断风险正确答案:C•2、以下选项中，哪个选项不是分析视角应用时要遵循的原则？（10分）A对比对象要可比B描述角度要全面C分出各类有差异D相关即是因果正确答案:D•1、在市场预测分析中，以下哪几类视角可以固化下来帮助我们把预测应用到更多领域？（10分）A对比视角B相关视角C分类视角D描述视角E推演视角正确答案:ABCD•2、我们基于对比视角进行市场预测时，可以从以下哪几个维度展开（）（10分）A用已知推未知——空间维度B由过去推未来——时间维度C因索果的过程D从波动看风险正确答案:AB•3、我们还可以基于描述视角进行预测，这里的描述包含（）（10分）A中间趋势B集中趋势C离中趋势D平均趋势正确答案:BC•4、四分图模型主要是对满意度指标改进的优先级进行分析，它使用了哪类分析视角做了有机的组合？（10分）A对比视角B相关视角C分类视角D描述视角正确答案:AC•5、以下哪些分析方法解决的是分类视角的问题？（10分）A决策树分析B逻辑回归法C德尔斐法D构成关系法正确答案:ABD•6、分析视角原则中，以下说法正确的有（）（10分）A如果两个变量之间存在着因果关系，它一定具有相关性B两个相关事物，如果在数据上呈现出同向或者是反向的变化，它们相互之间其实是独立的C两个事物或者说两个变量相互之间是因果关系的话，也不一定先行的因就影响后行的果正确答案:AB•1、我们在使用描述视角进行分析时，其实是既要看集中趋势，也要看离中趋势的（10分）A正确B错误正确答案:正确•2、分析视角，一定要结合具体业务场景选择恰当的视角（10分）A正确B错误正确答案:正确。

Excel数据分析单选题•1、数据透视表被形象地形容为企业经营管理中的什么部分？（10 分）✔A血液✔B骨架✔C皮肤✔D肌肉正确答案:A•2、需要选择整张报表进行透视表计算时，可以怎样操作？（10 分）✔ACtrl+a快选整张表格✔B鼠标在最左行，变为黑色箭头时可以全选行✔C鼠标移动至报表内部可自动选择整张报表正确答案:C•3、在数据透视表中，需要对某一字段进行对比分析时，应将该数据放在哪类标签中更便利？（10 分）✔A报表筛选✔B列标签✔C行标签✔D西格玛数值（∑）正确答案:B•4、需要为单元格中的信息添加单位时，在设置单元格选项卡中，选择哪个功能项操作？（10 分）✔A常规✔B文本✔C特殊✔D自定义正确答案:D•5、需要为数据进行比重分析时，选择值字段设置中的哪个选项？（10 分）✔A值汇总方式✔B值显示方式正确答案:B•6、如何对汇总表中的单个数据进行核查操作？（10 分）✔A在原明细表中生成新的汇总数据✔B双击该单元格查看对应汇总数据✔C以上方法都可以正确答案:C•7、汇总表中的标题字段可以自定义吗？（10 分）✔A可以✔B不可以正确答案:A多选题•1、创建数据透视表的方式？（10 分）A创建一个新工作表，点击“数据透视表”，选择一个表或区域B创建一个新工作表，点击“数据透视表”，选择外部数据源C点选明细表中有效单元格，再点击“数据透视表”选项D点选明细表中任意单元格，再点击“数据透视表”选项正确答案:B C判断题•1、数据透视表是Excel中一种交互式的工作表，可以根据用户的需要按照不同关键字段来提取组织和分析数据。

（10 分）✔A正确✔B错误正确答案:正确•2、汇总表中的数据如果需要修正时，不可以直接更改，必须返回原明细表修改对应的原始数据。

（10分）✔A正确✔B错误正确答案:正确。

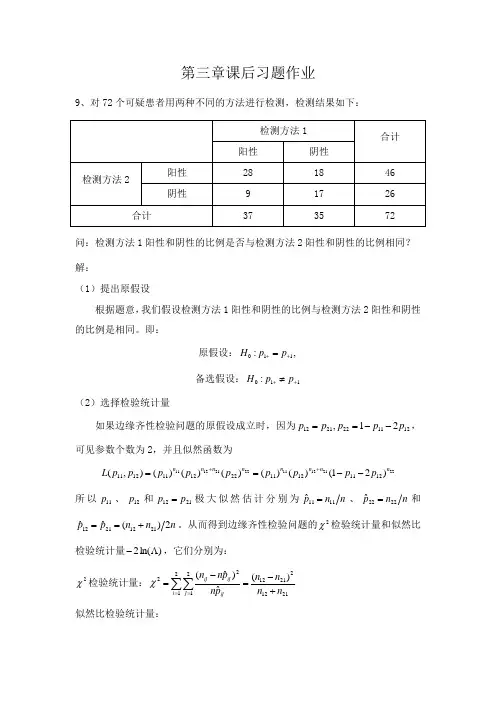
第三章课后习题作业9、对72个可疑患者用两种不同的方法进行检测，检测结果如下：问：检测方法1阳性和阴性的比例是否与检测方法2阳性和阴性的比例相同？ 解：（1）提出原假设根据题意，我们假设检测方法1阳性和阴性的比例与检测方法2阳性和阴性的比例是相同。

即：原假设：011:,H p p ++= 备选假设：011:H p p ++≠（2）选择检验统计量如果边缘齐性检验问题的原假设成立时，因为121122211221,p p p p p --==，可见参数个数为2，并且似然函数为2221121122211211)21()()()()()(),(121112112212111211n n n n n n n n p p p p p p p p p L --==++所以11p 、12p 和2112p p =极大似然估计分别为n n p1111ˆ=、n n p 2222ˆ=和n n n p p2)(ˆˆ21122112+==。

从而得到边缘齐性检验问题的2χ检验统计量和似然比检验统计量)ln(2Λ-，它们分别为：2χ检验统计量：211222112212122)(ˆ)ˆ(n n n n p n p n n i j ij ij ij +-=-=∑∑==χ似然比检验统计量：⎪⎪⎭⎫⎝⎛+++-=⎪⎪⎭⎫⎝⎛-=Λ-∑∑==212112211221121221212ln 2ln 2ˆln 2)ln(2n n n n n n n n n p n n i j ijijij它们都有渐近2χ分布，其自由度都是4-2-1=1。

（3）计算检验统计量和p 值，并作出决策则McNemar 2χ检验统计量和似然检验统计量)ln(2Λ-的值分别为：3918)918(22=+-=χ 05818.392918ln 9182918ln 182)ln(2=⎪⎭⎫ ⎝⎛⋅++⋅+-=Λ-我们在Excel 中分别输入“)1,3(chidist =”和“)1,05818.3(chidist =”，可得到2χ检验统计量和似然检验统计量)ln(2Λ-的p 值分别为：083264517.0)3)1((2=≥=χP p 080331601.0)05818.3)1((2=≥=χP p由于p 值都不小，我们不能拒绝原假设，从而认为检测方法1阳性和阴性的比例与检测方法2阳性和阴性的比例是相同。

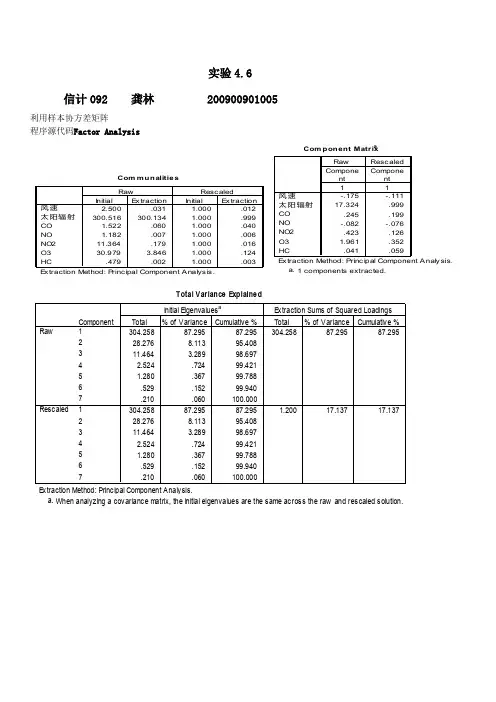
实验4.6信计092 龚林 200900901005利用样本协方差矩阵 程序源代码Factor AnalysisCom munalities 2.500.031 1.000.012300.516300.1341.000.9991.522.060 1.000.0401.182.007 1.000.00611.364.179 1.000.01630.9793.846 1.000.124.479.0021.000.003风速太阳辐射CO NO NO2O3HCInitialE xtractionInitialE xtractionRawRescaledE xtraction Method: P rincipal Com po nent Analysis.Com ponent Matrix a-.175-.11117.324.999.245.199-.082-.076.423.1261.961.352.041.059风速太阳辐射CO NO NO2O3HC1Component1ComponentRawRescal ed E xtraction Method: P rincipal Component Analysi s.1 components extracted.a.Total Variance Explained 304.25887.29587.295304.25887.29587.29528.2768.11395.40811.464 3.28998.6972.524.72499.4211.280.36799.788.529.15299.940.210.060100.000304.25887.29587.295 1.20017.13717.13728.2768.11395.40811.464 3.28998.6972.524.72499.4211.280.36799.788.529.15299.940.210.060100.000Component12345671234567RawRescaledTotal % of VarianceCumulative %Total % of VarianceCumulative %Initial Ei g envaluesaExtraction Sums of Squared Loadings Extraction Method: Principal Component Analysis.When analyzing a covariance matrix, the initial ei g envalues are the same across the raw and rescaled solution.a.利用样本相关矩阵 Factor AnalysisComponent Matrix a-.362.328.706.314-.620.246.842-.008-.125.577.512-.447.761.235.216.496-.667.175.488.362.594风速太阳辐射CO NO NO2O3HC123ComponentExtraction Method: Principal Component Analysis.3 components extracted.a.公因子方差（Communalities ）表如下Communalities1.000.7371.000.5441.000.7251.000.7951.000.6811.000.7221.000.722风速太阳辐射CO NO NO2O3HCInitialExtractionExtraction Method: P rincipal Component Analysi s .公因子方差变化于0.544～0.795之间，相差不是很大。

《Python数据分析、挖掘与可视化》课后题答案第⼆章课后题答案1.输⼊⼀个包含若⼲⾃然数的列表，输出这些⾃然数的平均值，结果保留3位⼩数。

ls=eval(input())ans=float(sum(ls)/len(ls))print('{:.3f}'.format(ans))2.输⼊⼀个包含若⼲⾃然数的列表，输出这些⾃然数降序排列后的新列表。

ls=eval(input())ls=sorted(ls,reverse=True)print(ls)3.输⼊⼀个包含若⼲⾃然数的列表，输出⼀个新列表，新列表中每个元素为原列表中每个⾃然数的位数。

ls=eval(input())ans=list()for i in ls:st=str(i)ans.append(len(st))print(ans)4.输⼊⼀个包含若⼲数字的列表，输出其中绝对值最⼤的数字。

ls=eval(input())m=ls[0]for i in ls:if abs(i)>m:m=iprint(m)5.输⼊⼀个包含若⼲整数的列表，输出这些整数的乘积。

ls=eval(input())ans=1for i in ls:ans*=iprint(ans)6.输⼊两个包含若⼲整数的等长列表，把这两个列表看作两个向量，输出这两个向量的内积。

ls1=eval(input())ls2=eval(input())ans=0for i in range(min(len(ls1),len(ls2))):ans+=ls1[i]*ls2[i]print(ans)第三章课后题答案1.输⼊⼀个字符串，输出其中每个字符的出现次数。

（⽤Counter类）2.输⼊⼀个字符串，输出其中只出现了⼀次的字符及其下标。

3.输⼊⼀个字符串，输出其中每个唯⼀字符最后⼀次出现的下标。

4.输⼊包含若⼲集合的列表，输出这些集合的并集。

（⽤reduce()函数和operator模块）5.输⼊⼀个字符串，输出加密后的结果字符串。

数据分析与商业智能课后习题参考答案题一: 数据分析基础1. 什么是数据分析？数据分析是一种通过收集、清洗、转换和分析数据来提取有价值信息的过程。

它的目标是帮助人们做出基于数据的决策，并揭示隐藏在数据背后的模式、趋势和关联性。

2. 数据分析的主要步骤有哪些？数据分析的主要步骤包括：- 收集数据：从各种来源获取数据，包括数据库、文本文件、传感器等。

- 清洗数据：对收集到的数据进行清洗，去除无效或错误的数据，并进行数据格式转换。

- 转换数据：将数据转换为适合分析的形式，如将文本数据转换为数值型数据。

- 分析数据：应用统计学和机器研究算法对数据进行分析，揭示数据背后的模式和关联性。

- 解释结果：对分析结果进行解释，并提供有关数据的见解和建议。

3. 数据分析的应用领域有哪些？数据分析在各个领域都有广泛的应用，包括但不限于：- 商业决策：帮助企业做出市场营销、供应链管理、产品定价等决策。

- 社交媒体分析：通过分析社交媒体数据了解用户偏好、社交趋势等。

- 金融风险分析：通过分析金融数据预测市场风险和投资回报。

- 医疗健康分析：分析医疗数据以支持疾病预防、诊断和治疗决策。

- 运输与物流优化：通过分析运输和物流数据提高效率和减少成本。

题二: 商业智能的概念和基本原理1. 什么是商业智能？商业智能（Business Intelligence，BI）是指通过收集、整理和分析企业内部和外部的数据，将其转化为有用信息，以支持企业决策和战略规划的过程。

2. 商业智能的基本原理是什么？商业智能的基本原理包括：- 数据仓库：将企业各个业务系统收集到的数据进行整合和存储，以便后续分析和查询。

- 数据清洗和转换：对数据进行清洗和转换，去除重复、无效或错误数据，并将其转换为适合分析的形式。

- 数据挖掘：应用数据挖掘技术，如聚类、分类、关联规则等，从大量的数据中挖掘有价值的信息。

- 可视化和报告：通过数据可视化和报告工具，以图表、表格等形式展示分析结果，以便用户理解和决策。

第五章习题解答1、给出数据点:013419156i i x y =⎧⎨=⎩(1)用012,,x x x 构造二次Lagrange 插值多项式2()L x ,并计算15.x =的近似值215(.)L 。

(2)用123,,x x x 构造二次Newton 插值多项式2()N x ,并计算15.x =的近似值215(.)N 。

(3)用事后误差估计方法估计215(.)L 、215(.)N 的误差。

解:(1)利用012013,,x x x ===,0121915,,y y y ===作Lagrange 插值函数2202130301191501031013303152933()()()()()()()()()()()()()()i i i x x x x x x L x l x y x x =------==⨯+⨯+⨯-------++=∑代入可得2151175(.).L =。

(2)利用123134,,x x x ===,1239156,,y y y ===构造如下差商表：于是可得插值多项式：229314134196()()()()()N x x x x x x =+-+---=-+-代入可得215135(.).N =。

(3)用事后误差估计的方法可得误差为1501511751350656304.(.)(..).R -=-=-◆ 2、设Lagrange 插值基函数是0012()(,,,,)nj i j i jj ix x l x i n x x =≠-==-∏试证明:①对x ∀,有1()ni i l x ==∑②00110001211()()(,,,)()()nk i i i n n k l x k n x x x k n =⎧=⎪==⎨⎪-=+⎩∑ 其中01,,,n x x x 为互异的插值节点。

证明：①由Lagrange 插值多项式的误差表达式101()()()()()!n ni i f R x x x n ξ+==-+∏知，对于函数1()f x =进行插值，其误差为0，亦即0()()ni ii f x l x f==∑精确成立，亦即1()ni i l x ==∑。

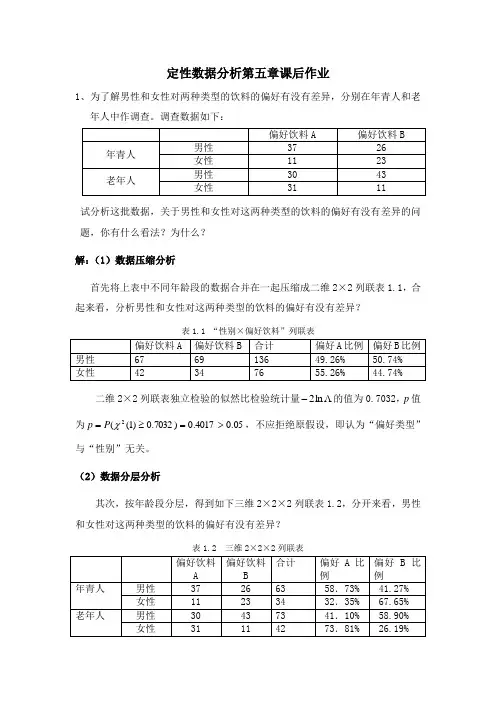
定性数据分析第五章课后作业1、为了解男性和女性对两种类型的饮料的偏好有没有差异，分别在年青人和老年人中作调查。

调查数据如下：试分析这批数据，关于男性和女性对这两种类型的饮料的偏好有没有差异的问题，你有什么看法？为什么？解：（1）数据压缩分析首先将上表中不同年龄段的数据合并在一起压缩成二维2×2列联表1.1，合起来看，分析男性和女性对这两种类型的饮料的偏好有没有差异？表1.1 “性别×偏好饮料”列联表二维2×2列联表独立检验的似然比检验统计量Λ2的值为0.7032，p值-ln为05≥==χp，不应拒绝原假设，即认为“偏好类型”(2>P4017.0)1().07032.0与“性别”无关。

（2）数据分层分析其次，按年龄段分层，得到如下三维2×2×2列联表1.2，分开来看，男性和女性对这两种类型的饮料的偏好有没有差异？表1.2 三维2×2×2列联表在上述数据中，分别对两个年龄段（即年青人和老年人）进行饮料偏好的调查，在“年青人”年龄段，男性中偏好饮料A 占58．73%，偏好饮料B 占41.27%；女性中偏好饮料A 占58．73%，偏好饮料B 占41.27%，我们可以得出在这个年龄段，男性和女性对这两种类型的饮料的偏好有一定的差异。

同理，在“老年人”年龄段，也有一定的差异。

（3）条件独立性检验为验证上述得出的结果是否可靠，我们可以做以下的条件独立性检验。

即由题意，可令C 表示年龄段，1C 表示年青人，2C 表示老年人；D 表示性别，1D 表示男性，2D 表示女性；E 表示偏好饮料的类型，1E 表示偏好饮料A ,2E 表示偏好饮料B 。

欲检验的原假设为：C 给定后D 和E 条件独立。

按年龄段分层后得到的两个四格表，以及它们的似然比检验统计量Λ-ln 2的值如下： 1C 层2C 层248.6ln 2=Λ- 822.11ln 2=Λ-条件独立性检验问题的似然比检验统计量是这两个似然比检验统计量的和，其值为07.18822.11248.6ln 2=+=Λ-由于2===t c r ，所以条件独立性检验的似然比检验统计量的渐近2χ分布的自由度为2)1)(1(=--t c r ，也就是上面这2个四格表的渐近2χ分布的自由度的和。

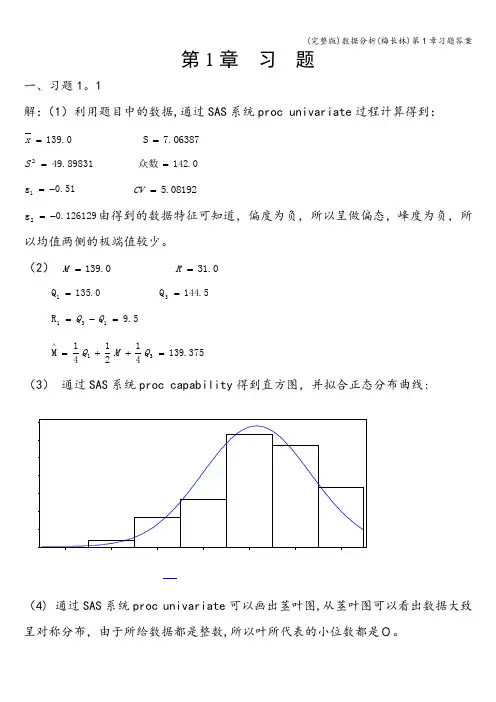
第1章 习 题一、习题1。

1解：（1）利用题目中的数据,通过SAS 系统proc univariate 过程计算得到：139.0=x 7.06387S =49.898312=S 0.142众数=51.0g 1-= 08192.5=CV126129.0g 2-=由得到的数据特征可知道，偏度为负，所以呈做偏态，峰度为负，所以均值两侧的极端值较少。

（2） 139.0=M31.0=R0.135Q 1= 5.144Q 3= 5.9R 131=-=Q Q375.139412141M 31=++=∧Q M Q （3） 通过SAS 系统proc capability 得到直方图，并拟合正态分布曲线:（4) 通过SAS 系统proc univariate 可以画出茎叶图,从茎叶图可以看出数据大致呈对称分布，由于所给数据都是整数,所以叶所代表的小位数都是０。

（5) 通过SAS 系统proc univariate 过程计算得到：0.971571W 0=00()H p P W W =≤= 0。

1741取0.05=α，因α>=0.1742p ，故不能拒绝0H ，认为样本来自正态总体分布。

通过画ＱＱ图和经验分布曲线和理论分布函数曲线，从图中可以看出ＱＱ图近似的在一条直线上，经验分布曲线的拟合程度也相当好，所以可以进一步说明此样本来自正态总体分布.Normal Line:Mu=139, Sigma=7.0639x 120125130135140145150155正态分位数-3-2-10123二、习题１.２7.8574027=x 1.62568785 S =2.642860982=S0.13721437g 1= 20.6898884=CV -1.4238025g 2=由得到的数据特征可知道，偏度为正，所以呈右偏态，峰度为负,所以均值两侧的极端值较少。

（2）7.636800=M 5.03650=R6.5859 Q 1= 9.3717Q 3= 2.78580R 131=-=Q Q809.7412141M 31=++=∧Q M Q （３）通过SAS 系统proc capability 得到直方图，SAS 系统自动将数据分为中值为4.5,5。