2012北京各区中考一模易错题之22题_几何变换

北京市海淀区区2012年初三一模试卷 数 学 2012. 5一、选择题8.下列图形中，能通过折叠围成一个三棱柱的是（ ）A.B. C. D.二、填空题12.在平面直角坐标系xOy 中，正方形111A B C O 、2221A B C B 、3332A B C B ，…，按图中所示的方式放置。

点1A 、2A 、3A ，…和1B 、2B 、3B ，…分别在直线y kx b =+和x 轴上。

已知1(1C ，1)-，27(2C ，3)2-，则点3A 的坐标是________；点n A 的坐标是___________________. . 22.小明遇到这样一个问题：如图1，ABO 和CDO BOC 的面积为1，试求以AD ，BC ，OC OD +的长度为三边长的三角形的面积.图1 图2小明是这样思考的，要解决这上问题，首先应想办法移动这些分散的线段，构造一个三角形，再计算其面积即可。

他利用图形变换解决了这个问题，其解题思路是延长CO 到E ，使OE CO =，连接BE ，可证OBE OAD≌，从而得到BCE即是以AD ，BC ，OC OD +的长度为三边长的三角形（如图2）.请你回答：图中BCE 的面积等于_______.请你尝试用平移，旋转，翻折的方法，解决下列问题：如图3，已知ABC，分别以AB ，AC ，BC 为边向外作正方形ABDE 、AGFC 、BCHI ，连接EG ，FH ，ID .（1）在图3中利用图形变换画出并指明以EG 、FH 、ID 的长度为三边长的一个三角形（保留画图痕迹）； （2）若ABC 的面积为1，则以EG ，FH ，ID 的长度为三边长的三角形面积等于_______.EOODBA DCBA HGFEDIC BA3图五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23.已知关于x 的方程2(31)30m mx x +++=.（1）求证：不论m 为任何实数，此方程总有实数根；（2）若抛物线2(31)3y m x mx +++=与x 轴交于两个不同的整数点，且m 为正整数，试确定此抛物线的解析式； （3）若点1(P x ，1)y 与点1(Q x n +，2)y 在（2）中抛物线上（点P 、Q 不重合），若12y y =，求代数式22114516812n x n x n ++++的值.24.在ABCD中，A DBC ∠=∠，过点D 作DE DF =，且EDF ABD =∠，连接EF ，EC ，N 、P 分别为EC ，BC 的中点，连接NP .（1）如图1，若点E 在DP 上，EF 与DC 交于点M ，试探究线段NP 与线段NM 的数量关系及ABD ∠与MNP ∠满足的等量关系，请直接写出你的结论；（2）如图2，若点M 在线段EF 上，当点M 在何位置时，你在（1）中得到的结论仍然成立，写出你确定的点M 的位置，并证明（1）中的结论.图1图2ABCDEFNPP NMFEDBA25.已知抛物线2y x bx c =++的顶点为P ，与y 轴交于点A ，与直线OP 交于点B . （1）如图1，若点P 的横坐标为1，点(3B ，6)，试确定抛物线的解析式；（2）在（1）的条件下，若点M 是直线AB 下方抛物线上的一点，且3ABM S = ，求点M 的坐标；（3）如图2，若P 在第一象限，且PA PO =，过点P 作PD x ⊥轴于点D ，将抛物线2y x bx c =++平移，平移后的抛物线经过点A 、D ，该抛物线与x 轴的另一个交点为C ，请探索四边形OABC 的形状，并说明理由.图1图2北京市西城区2012年初三一模试卷 数 学 2012. 5一、选择题（本题共32分，每小题4分）7．由n 个相同的小正方体堆成的几何体，其主视图、俯视图如下所示，则n 的最大值是A ．16B ．18C ．19D ．208．对于实数c 、d ，我们可用min{ c ，d }表示c 、d 两数中较小的数，如min{3，1-}=1-.若关于x 的函数y = min{22x ，2()a x t -}的图象关于直线3x =对称，则a 、t 的值可能是A ．3，6B ．2，6-C ．2，6D ．2-，6 二、填空题12．如图，直角三角形纸片ABC 中，∠ACB =90°，AC=8，BC =6．折叠该纸片使点B 与点C 重合，折痕与AB 、BC 的交点分别 为D 、E . (1) DE 的长为 ；(2) 将折叠后的图形沿直线AE 剪开，原纸片被剪成三块，其中最小一块的面积等于 ．22. 阅读下列材料：问题：如图1，在正方形ABCD 内有一点P ，PA =5，PB =2，PC =1，求∠BPC 的度数．小明同学的想法是：已知条件比较分散，可以通过旋转变换将分散的已知条件集中在一起，于是他将△BPC 绕点B 逆时针旋转90°，得到了△BP ′A （如图2），然后连结PP ′． 请你参考小明同学的思路，解决下列问题： (1) 图2中∠BPC 的度数为 ；(2) 如图3，若在正六边形ABCDEF 内有一点P ，且P A =132，PB =4，PC =2，则∠BPC 的度数为 ，正六边形ABCDEF 的边长为 ．五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23. 已知关于x 的一元二次方程210x px q +++=的一个实数根为 2． (1) 用含p 的代数式表示q ；(2) 求证：抛物线2y x px q =++与x 轴有两个交点；(3) 设抛物线21y x px q =++的顶点为M ，与 y 轴的交点为E ，抛物线221y x px q =+++ 顶点为N ，与y 轴的交点为F ，若四边形FEMN 的面积等于2，求p 的值．24．已知：在如图1所示的锐角三角形ABC 中，CH ⊥AB 于点H ，点B 关于直线CH 的对称点为D ，AC 边上一点E 满足∠EDA =∠A ，直线DE 交直线CH 于点F ． (1) 求证：BF ∥AC ；(2) 若AC 边的中点为M ，求证：2DF EM =；(3) 当AB =BC 时（如图2），在未添加辅助线和其它字母的条件下，找出图2中所有与BE 相等的线段，并证明你的结论．图25．平面直角坐标系xOy 中，抛物线244y ax ax a c =-++与x 轴交于点A 、点B ，与y 轴的正半轴交于点C ，点 A 的坐标为(1, 0)，OB =OC ，抛物线的顶点为D ． (1) 求此抛物线的解析式；(2) 若此抛物线的对称轴上的点P 满足∠APB =∠ACB ，求点P 的坐标；(3) Q 为线段BD 上一点，点A 关于∠AQB 的平分线的对称点为A '，若2=-QB QA ，求点Q 的坐标和此时△QAA '的面积．北京市东城区2011--2012学年第二学期初三综合练习（一）一、选择题（8. 如图，在正方形ABCD 中，AB =3cm ，动点M 自A 点出发沿AB 方向以每秒1cm 的速度向B 点运动，同时动点N 自A 点出发沿折线AD —DC —CB 以每秒3cm 的速度运动，到达B 点时运动同时停止.设△AMN 的面积为y （cm 2），运动时间为x （秒），则下列图象中能大致反映y 与x 之间的函数关系的是AB C D 二、填空题12. 如图，正方形ABCD 的边长为10，内部有6个全等的正方形，小正方形的顶点E 、F 、G 、H 分别落在边AD 、AB 、BC 、CD 上，则DE 的长为 ．22. 在ABC △中，AB 、BC 、AC小宝同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点ABC △（即ABC △三个顶点都在小正方形的顶点处），如图1所示．这样不需求ABC △的高，而借用网格就能计算出它的面积．（1）请你将ABC △的面积直接填写在横线上__________________； 思维拓展：（2）我们把上述求ABC △面积的方法叫做构图法．．．．若ABC △（0a >），请利用图2的正方形网格（每个小正方形的边长为a ）画出相应的ABC △，并求出它的面积填写在横线上__________________； 探索创新：（3）若ABC △（0a >），且ABC △的面积为22a ，试运用构图法．．．在图3的正方形网格（每个小正方形的边长为a ）中画出所有符合题意的ABC △(全等的三角形视为同一种情况)，并求出它的第三条边长填写在横线上__________________．五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23.已知关于x 的一元二次方程22(41)30x m x m m -+++=. （1）求证：无论m 取何实数时，原方程总有两个实数根；（2）若原方程的两个实数根一个大于2，另一个小于7，求m 的取值范围；（3）抛物线22(41)3y x m x m m =-+++与x 轴交于点A 、B ，与y 轴交于点C ，当m 取（2）中符合题意的最小整数时，将此抛物线向上平移n 个单位，使平移后得到的抛物线顶点落在△ABC 的内部（不包括△ABC 的边界），求n 的取值范围（直接写出答案即可）．24. 已知∠ABC =90°，点P 为射线BC 上任意一点（点P 与点B 不重合），分别以AB 、AP 为边在∠ABC 的内部作等边△ABE 和△APQ,连结QE 并延长交BP 于点F .（1）如图1，若AB =32，点A 、E 、P 恰好在一条直线上时，求此时EF 的长（直接写出结果）；（2）如图2，当点P 为射线BC 上任意一点时，猜想EF 与图中的哪条线段相等（不能添加辅助线产生新的线段），并加以证明；（3）若AB =32，设BP =x ，以QF 为边的等边三角形的面积y ，求y 关于x 的函数关系式．25. 如图，在平面直角坐标系xOy 中,二次函数2y bx c =++的图象与x 轴交于A （-1,0）、B （3,0）两点, 顶点为C .(1) 求此二次函数解析式；(2) 点D 为点C 关于x 轴的对称点，过点A 作直线l ：y x 交BD 于点E ，过点B 作直线BK ∥AD 交直线l 于K 点.问：在四边形ABKD 的内部是否存在点P ，使得它到四边形ABKD 四边的距离都相等，若存在，请求出点P 的坐标；若不存在，请说明理由；(3) 在（2）的条件下，若M 、N 分别为直线AD 和直线l 上的两个动点，连结DN 、NM 、MK ，求DN N M M K ++和的最小值.北京市朝阳区九年级综合练习（一）一、选择题 8．已知关于x 的一元二次方程02=++n mx x 的两个实数根分别为a x =1，b x =2（b a <），则二次函数n mx x y ++=2中，当0<y 时，x 的取值范围是A ．a x <B ．b x >C ．b x a <<D ．a x <或b x >二、填空题（第12题） 12．如图,在正方形ABCD 中，AB =1，E 、F 分别是BC 、CD 边上点，（1）若CE =12CB ，CF =12CD ，则图中阴影部分的面积是 ；（2）若CE =1n CB ，CF =1nCD ，则图中阴影部分的面积是 （用含n 的式子表示，n 是正整数）． 22. 根据对北京市相关的市场物价调研，预计进入夏季后的某一段时间，某批发市场内的甲种蔬菜的销售利润y 1（千元）与进货量x （吨）之间的函数kx y =1的图象如图①所示，乙种蔬菜的销售利润y 2（千元）与进货量x （吨）之间的函数bx ax y +=22的图象如图②所示. （1）分别求出y 1、y 2与x 之间的函数关系式；（2）如果该市场准备进甲、乙两种蔬菜共10吨，设乙种蔬菜的进货量为t 吨，写出这两种蔬菜所获得的销售利润之和W （千元）与t （吨）之间的函数关系式，并求出这两种蔬菜各进多少吨时获得的销售利润之和最大，最大利润是多少？图②五、解答题（本题共21分，第23题6分，第24题8分，第25题7分） 23. 阅读下面材料：问题：如图①，在△ABC 中， D 是BC 边上的一点，若∠BAD =∠C =2∠DAC =45°，DC =2．求BD 的长． 小明同学的解题思路是：利用轴对称，把△ADC 进行翻折，再经过推理、计算使问题 得到解决．（1）请你回答：图中BD 的长为 ；（2）参考小明的思路，探究并解答问题：如图②，在△ABC 中，D 是BC 边上的一点，若∠BAD =∠C =2∠DAC =30°，DC =2，求BD 和AB 的长．y （万元）（吨）O y （千元） A图① 图②24. 在平面直角坐标系xOy 中，抛物线23y ax bx =++经过点N （2,－5），过点N 作x 轴的平行线交此抛物线左侧于点M ，MN =6.（1）求此抛物线的解析式；（2）点P （x ,y ）为此抛物线上一动点，连接MP 交此抛物线的对称轴于点D ，当△DMN 为直角三角形时，求点P 的坐标； （3）设此抛物线与y 轴交于点C ，在此抛物线上是否存在点Q ，使∠QMN =∠CNM ？若存在，求出点Q 的坐标；若不存在，说明理由.25. 在矩形ABCD 中，点P 在AD 上，AB =2，AP =1，将三角板的直角顶点放在点P 处，三角板的两直角边分别能与AB 、BC 边相交于点E、F ，连接EF ．（1）如图，当点E 与点B 重合时，点F 恰好与点C 重合，求此时PC 的长；（2）将三角板从（1）中的位置开始，绕点P 顺时针旋转，当点E 与点A 重合时停止，在这个过程中，请你观察、探究并解答：① ∠PEF 的大小是否发生变化？请说明理由；② 直接写出从开始到停止，线段EF 的中点所经过的路线长．C B AD北京市丰台区2011-2012学年度第二学期初三综合练习（一）8．如图，矩形ABCD 中，AB =3，BC =5，点P 是BC 边上的一个动点 （点P 不与点B 、C 重合），现将△PCD 沿直线PD 折叠，使点C 落到点C’处；作∠BPC’的角平分线交AB 于点E ．设BP =x ，BE =y ，则下列图象中，能表示y 与x 的函数关系的图象大致是A ．B ．C ．D ．二、填空题（本题共16分，每小题4分）12．在数学校本活动课上，张老师设计了一个游戏，让电动娃娃在边长为1的正方形的四个顶点上依次跳动．规定：从顶点A 出发，每跳动一步的长均为1．第一次顺时针方向跳1步到达顶点D ，第二次逆时针方向跳2步到达顶点B ，第三次顺时针方向跳3步到达顶点C ，第四次逆时针方向跳4步到达顶点C ，… ，以此类推，跳动第10次到达的顶点是 ，跳动第2012次到达的顶点是 ．22．将矩形纸片分别沿两条不同的直线剪两刀，可以使剪得的三块纸片恰能拼成一个等腰三 角形（不能有重叠和缝隙）．小明的做法是：如图1所示，在矩形ABCD 中，分别取AD 、AB 、CD 的中点P 、E 、 F ，并沿直线PE 、PF 剪两刀，所得的三部分可拼成等腰三角形△PMN (如图2)． （1）在图3中画出另一种剪拼成等腰三角形的示意图；（2）以矩形ABCD 的顶点B 为原点，BC 所在直线为x 轴建立平面直角坐标系（如图4），矩形ABCD 剪拼后得到等腰三角形△PMN ，点P 在边AD 上（不与点A 、D 重合），点M 、N 在x 轴上（点M 在N 的左边）．如果点D 的坐标为(5,8)，直线PM 的解析式为=y kx b +，则所有满足条件的k 的值为 ．图一 图二 图三图四 备用五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23．已知：关于x 的一元二次方程：22240x mx m -+-=.EPC’A DBCP E FDA P E F DA B C（1）求证：这个方程有两个不相等的实数根；（2）当抛物线2224y x mx m =-+-与x 轴的交点位于原点的两侧，且到原点的距离相等时，求此抛物线的解析式；（3）将（2）中的抛物线在x 轴下方的部分沿x 轴翻折，其余部分保持能够不变，得到图形C 1,将图形C 1向右平移一个单位,得到图形C 2，当直线y=x b +(b <0)与图形C 2恰有两个公共点时，写出b 的取值范围.24．已知：△ABC 和△ADE 是两个不全等的等腰直角三角形，其中BA =BC ，DA =DE ，联结EC ，取EC 的中点M ，联结BM 和DM ．（1）如图1，如果点D 、E 分别在边AC 、AB 上，那么BM 、DM 的数量关系与位置关系是 ； （2）将图1中的△ADE 绕点A 旋转到图2的位置时，判断（1）中的结论是否仍然成立，并说明理由．CB AEMM EABC点A ，与x 轴相交于B 、C 两点（点B 在点C 的左边）． （1）求经过A 、B 、C 三点的抛物线的解析式；（2）在（1）中的抛物线上是否存在点M ，使△MBP 的面积是菱形ABCP 面积的21．如果 存在，请直接写出所有满足条件的M 点的坐标；如果若不存在，请说明理由；（3）如果一个动点D 自点P 出发，先到达y 轴上的某点，再到达x 轴上某点，最后运动到（1）中抛物线的顶点Q 处，求使点D 运动的总路径最短的路径的长．.（1）将两端剪掉则可以得到正五边形，若将展开，展开后的平面图形是 ；（2）若原长方形纸条（图①）宽为2cm ，求（1）中展开后平面图形的周长（可以用三角函数表示）． 五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23．已知：关于x 的方程()()01342=---+m x m x 有两个不相等的实数根．（1）求m 的取值范围；图① 图② 图③图②（2）抛物线C ：()()1342-+---=m x m x y 与x 轴交于A 、B 两点．若1-≤m 且直线1l :12--=x my 经过点A ,求抛物线C 的函数解析式；（3）在（2）的条件下，直线1l :12--=x my 绕着点A 旋转得到直线2l ：b kx y +=，设直线2l 与y 轴交于点D ，与抛物线C 交于点M （M 不与点A 重合），当23≤AD MA 时，求k 的取值范围．24．（1）如图1，在矩形ABCD 中，AB=2BC ，M 是AB 的中点．直接写出∠BMD 与∠ADM 的倍数关系；（2）如图2，若四边形ABCD 是平行四边形， AB=2BC ，M 是AB 的中点，过C 作CE ⊥AD 与AD 所在直线交于点E ．①若∠A 为锐角，则∠BME 与∠AEM 有怎样的倍数关系，并证明你的结论； ②当︒<∠<︒A 0时，上述结论成立；当︒<∠≤︒180A 时，上述结论不成立．M D BA CEADC25．已知二次函数)34()22(22-+++-=m m x m x y 中，m 为不小于0的整数，它的图像与x 轴交于点A 和点B ，点A 在原点左边，点B 在原点右边． （1）求这个二次函数的解析式；（2）点C 是抛物线与y 轴的交点，已知AD=AC （D 在线段AB 上），有一动点P 从点A 出发，沿线段AB 以每秒1个单位长度的速度移动，同时，另一动点Q 从点C 出发，以某一速度沿线段CB 移动，经过t 秒的移动，线段PQ 被CD 垂直平分，求t 的值；（3）在（2）的情况下，求四边形ACQD 的面积．顺义区2012届初三第一次统一练习一、选择题8．如图，在Rt△ABC中，90ACB∠=︒，60A∠=︒，AC=2，D是AB边上一个动点（不与点A、B重合），E是BC边上一点，且30CDE∠=︒．设AD=x，BE=y，则下列图象中，能表示y与x的函数关系的图象大致是二、填空题12．如图，菱形ABCD中，AB=2 ，∠C=60°,我们把菱形ABCD的对称中心称作菱形的中心．菱形ABCD在直线l上向右作无滑动的翻滚，每绕着一个顶点旋转60°叫一次操作，则经过1次这样的操作菱形中心O所经过的路径长为；经过18次这样的操作菱形中心O所经过的路径总长为；经过3n（n为正整数）次这样的操作菱形中心O所经过的路径总长为．(结果都保留π)22．问题背景（1）如图1，△ABC中，DE∥BC分别交AB，AC于D，E两点，过点D作DF∥AC交BC于点F．请按图示数据填空：四边形DFCE的面积S=，△DBF的面积1S=，△ADE的面积2S=．探究发现（2）在（1）中，若BF a=，FC b=，DＧ与BC间的距离为h．直接写出2S=（用含S、1S的代数式表示）．拓展迁移（3）如图2，□DEFG的四个顶点在△ABC的三边上，若△ADG、△DBE、△GFC的面积分别为4、8、1，试利用．．（2．）中的结论．．．．求□DEFG的面积，直接写出结果．五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）23．已知关于x的方程032)1(2=+++-kkxxk．（1）若方程有两个不相等的实数根，求k的取值范围；（2）当方程有两个相等的实数根时，求关于y的方程2(4)10y a k y a+-++=的整数根（a为正整数）．OABD24．如图，在平面直角坐标系xOy 中，抛物线y =mx 2+2mx +n 经过点A （-4，0）和点B （0，3）．（1）求抛物线的解析式；（2）向右平移上述抛物线，若平移后的抛物线仍经过点B ，求平移后抛物线的解析式；（3）在（2）的条件下，记平移后点A 的对应点为A’，点B 的对应点为B’，试问：在平移后的抛物线上是否存在一点P ，使'OA P △的面积与四边形AA ’B ’B 的面积相等，若存在，求出点P 的坐标；若不存在，说明理由．25．问题：如图1， 在Rt △ABC 中，90C ∠=︒，30ABC ∠=︒，点D 是射线CB 上任意一点，△ADE 是等边三角形，且点D 在ACB ∠的内部，连接BE ．探究线段BE 与DE 之间的数量关系．请你完成下列探究过程：先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明. （1） 当点D 与点C 重合时（如图2），请你补全图形．由BAC ∠的度数为 ，点E 落在 ，容易得出BE 与DE 之间的数量关系为 ；（2） 当点D 在如图3的位置时，请你画出图形，研究线段BE 与DE 之间的数量关系是否与（1）中的结论相同，写出你的猜想并加以证明．图1D EBCA。

顺义区2012届初三第一次统一练习 数学学科参考答案及评分细则二、填空题（本题共16分，每小题4分，）9．4；10．25()x x y -； 11．11.4； 12， 2)π+，π． 三、解答题（本题共30分，每小题5分） 13()12cos303-︒+--1213⎛⎫=+-- ⎪⎝⎭……………………………………………… 4分 113=+ 43= …………………………………………………………………… 5分 14．解： 221x y x y +=⎧⎨-=⎩①②①+②，得 33x =．1x =． …………………………………………………… 2分 把1x =代入①，得 12y +=．1y =． ………………………………………………………… 4分 ∴原方程组的解为 1,1.x y =⎧⎨=⎩ ………………………………………………… 5分15．证明：∵AB=AC ，∴B C ∠=∠． …………………………………………………………… 1分 在△ABD 和△ACE 中，,,,AB AC B C BD CE =⎧⎪∠=∠⎨⎪=⎩∴ △ABD ≌△ACE ．……………………………………………………… 3分 ∴ AD=AE ． ……………………………………………………………… 4分∴∠ADE =∠AED ． ……………………………………………………… 5分16．解：6931x x x x -⎛⎫⎛⎫-÷- ⎪ ⎪⎝⎭⎝⎭2693x x x x x -+-=÷ …………………………………………………… 2分 2(3)3x xx x -=-3x =- ……………………………………………………………………… 4分当2012x =时，原式=201232009-=．…………………………………… 5分17．解：（1）∵点(4,)A m 在反比例函数4y x=（0x >）的图象上， ∴414m ==． …………………………………………………………… 1分 ∴(4,1)A ．将(4,1)A 代入一次函数y x b =-+中，得 5b =．∴一次函数的解析式为5y x =-+． …………………………………… 2分（2）由题意，得 (0,5)B ， ∴5OB =．设P 点的横坐标为P x ．∵OBP △的面积为5， ∴1552p x ⨯=．…………………………………………………………… 3分 ∴2P x =±．∴点P 的坐标为（2，3）或（-2，7）． ………………………………… 5分 18．解：设A 户型的每户窗户改造费用为x 元，则B 户型的每户窗户改造费用为(500)x -元． ……………………………… 1分 根据题意，列方程得5400004800005x x =-． 解得 4500x =．经检验，4500x =是原方程的解，且符合题意．…………………………… 4分 ∴5004000x -=．答：A 户型的每户窗户改造费用为4500元，B 户型的每户窗户改造费用为4000 元．…………………………………… 5分MF EDCBAFE DCO BA四、解答题（本题共20分，每小题5分）19．解：（1）∵在□ABCD 中，∠B=60°，AB=4，∠ACB=45°，∴∠D=60°，CD=AB=4，AD ∥BC ． ……………………………… 1分 ∴∠DAC=45°． 过点C 作CM ⊥AD 于M ， 在Rt △CDM 中，sin 4sin 6023CM CD D ==︒=cos 4cos602DM CD D ==︒=．………………………………… 2分在Rt △ACM中，∵∠MAC=45°， ∴AM CM==∴2AD AM DM =+=．…………………………………… 3分∵EF ⊥AD ，CM ⊥AD ， ∴EF ∥CM ．∴12EF CM ==在Rt △AEF 中，AF EF ==4分∴22DF AD AF =-=-=．……………………… 5分20．（1）证明：连结OD ．∵AB 是⊙O 的直径，∴∠ADB=90°． ……………………………………………………… 1分 ∵∠A=30°， ∴∠ABD=60°．∴∠BDC =1302ABD ∠=︒． ∵OD=OB ，∴△ODB 是等边三角形． ∴∠ODB=60°．∴∠ODC=∠ODB+∠BDC =90°． 即OD ⊥DC ．∴CD 是⊙O 的切线．…………………………………………………… 2分（2）解：∵OF ∥AD ，∠ADB=90°，∴OF ⊥BD ，∠BOE=∠A =30°． ……………………………………… 3分∴112DE BE BD ===． 在Rt △OEB中，OB=2BE=2，OE ==．………… 4分 ∵OD=OB=2，∠C=∠ABD -∠BDC =30°，∠DOF=30°， ∴CD =tan 30DF OD =︒=∴CF CD DF =-== ……………………………5分21．解：（1）此次共调查了100名学生． …………………………………………………1分（2）填表：…………………………………………………3分（3）补全统计图如下：到校方式条形统计图 到校方式扇形统计图．…………………………………………………………………………5分22．解：（1）四边形DFCE 的面积S = 6 ，△DBF 的面积1S = 6 ，△ADE 的面积2S = 32 ． …………………………………… 3分（2）2S = 214S S （用含S 、1S 的代数式表示）． ………… 4分 （3）□DEFG 的面积为12． ………………………………………… 5分五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23．解：（1）△=244(1)(3)k k k --+=2244812k k k --+=812k -+ ……………………………………………………………… 1分∵方程有两个不相等的实数根， ∴10,0.k -≠⎧⎨∆>⎩ 即 10,8120.k k -≠⎧⎨-+>⎩∴k 的取值范围是32k <且1k ≠． …………………………………… 3分 （2）当方程有两个相等的实数根时，△=812k -+=0．∴32k =． ………………………………………………………………… 4分 ∴关于y 的方程为2(6)10y a y a +-++=．∴2'(6)4(1)a a ∆=--+2123644a a a =-+--21632a a =-+2(8)32a =--．由a 为正整数，当2(8)32a --是完全平方数时，方程才有可能有整数根． 设22(8)32a m --=（其中m 为整数），32p q =（p 、q 均为整数）， ∴22(8)32a m --=．即(8)(8)32a m a m -+--=．不妨设8,8.a m p a m q -+=⎧⎨--=⎩两式相加，得 162p q a ++=．∵(8)a m -+与(8)a m --的奇偶性相同，∴32可分解为216⨯，48⨯，(2)(16)-⨯-，(4)(8)-⨯-， ∴18p q +=或12或18-或12-．∴17a =或14或1-（不合题意，舍去）或2．当17a =时，方程的两根为1172y -±=，即12y =-，29y =-．…… 5分 当14a =时，方程的两根为822y -±=，即13y =-，25y =-．…… 6分当2a =时， 方程的两根为422y ±=，即13y =，21y =． ………… 7分24．解：（1）∵抛物线y =mx 2+2mx +n 经过点A （-4，0）和点B （0，3），∴1680,3.m m n n -+=⎧⎨=⎩ ∴3,83.m n ⎧=-⎪⎨⎪=⎩． ∴抛物线的解析式为：233384y x x =--+．………………………… 2分 （2）令3y =，得2333384x x --+=，得10x =，22x =-， ∵抛物线向右平移后仍经过点B ，∴抛物线向右平移2个单位．……… 3分∵233384y x x =--+ 233(21)388x x =-++++2327(1)88x =-++． ………… 4分∴平移后的抛物线解析式为2327(1)88y x =--+． …………………… 5分（3）由抛物线向右平移2个单位，得'(2,0)A -，'(2,3)B ．∴四边形AA ’B ’B 为平行四边形，其面积'236AA OB ==⨯=．设P 点的纵坐标为P y ，由'OA P △的面积=6， ∴1'62P OA y =，即1262P y ⨯= ∴6P y =， 6P y =±．………………………………………………… 6分当6P y =时，方程2327(1)688x --+=无实根， 当6P y =-时，方程2327(1)688x --+=-的解为16x =，24x =-．∴点P 的坐标为(6,6)-或(4,6)--．……………………………… 7分25．解：（1）完成画图如图2，由BAC ∠的度数为 60°，点E 落在 AB 的中点处 ，容易得出BE 与DE 之间的数量关系 为 BE=DE ；…………… 3分（2）完成画图如图3．猜想：BE DE =．证明：取AB 的中点F ，连结EF ．∵90ACB ∠=︒，30ABC ∠=︒，∴160∠=︒，12CF AF AB ==． ∴△ACF 是等边三角形．∴AC AF =． ① …… 4分∵△ADE 是等边三角形，∴260∠=︒， AD AE =． ②∴12∠=∠． ∴12BAD BAD ∠+∠=∠+∠．即CAD FAE ∠=∠．③ ………………………………………… 5分 由①②③得 △ACD ≌△AFE （SAS ）． …………………………… 6分 ∴90ACD AFE ∠=∠=︒． ∵F 是AB 的中点，∴EF 是AB 的垂直平分线．∴BE=AE . ……………………………………………………… 7分 ∵△ADE 是等边三角形， ∴DE=AE .∴BE DE =． …………………………………………………… 8分EAB C (D )图221F EDB C A图3。

北京市西城区2012年初三一模试卷数学答案及评分标准 2012. 5一、选择题（本题共32分，每小题4分） 题号 1 2 3 4 5 6 7 8 答案ACBCBDBC二、填空题（本题共16分，每小题4分）9101112x ≥-2()223b a -13 13+-或（各2分）4，4（各2分）三、解答题（本题共30分，每小题5分） 13．解：原式=32133321++⨯- …………………………………………………………4分=323+．…………………………………………………………………… 5分14．解：由①得2->x ．……………………………………………………………………1分由②得x ≤37． ……………………………………………………………………3分∴ 原不等式组的解集是-2< x ≤37．………………………………………………4分∴ 它的非负整数解为0，1，2．………………………………………………… 5分 15.（1）证明：如图1.∵ ∠ABC=90º，D 为AB 延长线上一点，∴ ∠A BE=∠CBD=90º . …………………………………………………1分 在△ABE 和△CBD 中,⎪⎩⎪⎨⎧=∠=∠=,,,BD BE CBD ABE CB AB∴ △ABE ≌△CBD. …………………… 2分（2）解：∵ AB=CB ，∠ABC=90º，∴ ∠CAB =45°. …….…………………… 3分 又∵ ∠CAE=30º，∴ ∠BAE =15°. ……………………………………………………………4分∵ △ABE ≌△CBD ，∴ ∠BCD =∠BAE =15°. ……………………………………………………5分16. 解：原式=()()()()2a ab a b a b ba ab ++-⋅- =()22b b a +. ..….….….….….……………………3分①② 图1⎪⎩⎪⎨⎧-+<-2115)1(3x x x ，≥2x -4，∵ 2a +b =0，∴ a b 2-=. ……………………………………………………………………… 4分 ∴ 原式=22224)2()(aaa a =--.∵ a 不为0，∴ 原式=41. (5)分17. 解：（1）∵ 反比例函数 的图象经过点),2(m A ，[来源:] ∴ 2m k =，且m ＞0.∵ AB ⊥x 轴于点B ，△AOB 的面积为1，∴ 1212m ⋅⋅=.解得 1=m . ........................................................................ 1分 ∴ 点A 的坐标为)1,2(. (2)分∴ 22km ==. (3)分（2）点C 的坐标为(0,3)或(0,-1). (5)分18．解：设甲工厂每天能加工x 件新产品，则乙工厂每天能加工1.5x 件新产品. 依题意得 105.112001200+=xx. ……………………………………………………2分解得40=x . …………………………………………………………………… 3分 经检验，40=x 是原方程的解，并且符合题意． …………………………… 4分[来源:学科网ZXXK]∴ 605.1=x .答: 甲工厂每天能加工40件新产品, 乙工厂每天能加工60件新产品. ……………5分四、解答题（本题共20分，每小题5分）19．解：（1）2，50；…………………………………2分 （2）5040%20⨯=，C 组的户数为20. … 3分补图见图2． …………………………4分 （3）∵ 500(28%8%)180⨯+=，∴ 根据以上信息估计，全社区捐款不少于300元的户数是180．[来源:学科网] ……………………………… 5分20．解：（1）∵ 梯形ABCD 中，AD ∥BC ，90A ∠=︒，60C ∠=︒，∴ 90ABC ∠=︒，180120AD C C ∠=︒-∠=︒． 在Rt △ABD 中，∵90A ∠=︒，15ABD ∠=︒，)0(>=k xk y 图2捐款户数分组统计图1∴ 75AD B ∠=︒．∴ 45BD C AD C AD B ∠=∠-∠=︒．…… 2分 （2）作BE C D ⊥于点E ，D F BC ⊥于点F ．（如图3）在Rt △BCE 中，∵ BC=2，60C ∠=︒，∴ sin 3BE BC C =⋅=，cos 1C E BC C =⋅=． ∵ 45BD C ∠=︒， ∴ 3DE BE ==．∴ 31CD DE CE =+=+． …………………………………………… 3分 ∵ BC D F C D BE ⋅=⋅， ∴ (31)33322C D B E D F B C⋅+⋅+===． …………………………… 4分∵ AD ∥BC ，90A ∠=︒，D F BC ⊥，∴ 332AB D F +==． …………………………………………………… 5分21．解：（1）作O F BD ⊥于点F ，连结OD ．（如图4） ∵ ∠BAD=60°，∴ ∠BOD=2∠BAD =120°．……………1分 又∵OB =OD ，∴ 30O BD∠=︒．……………………… 2分∵ AC 为⊙O 的直径，AC=4， ∴ OB= OD= 2．在Rt △BOF 中，∵∠OFB =90°， OB=2，︒=∠30OBF ， ∴ 130sin 2sin =︒=∠⋅=OBF OB OF ，即点O 到BD 的距离等于1. ………………………………………… 3分（2）∵ OB= OD ，O F BD ⊥于点F ，∴ BF=DF ．由DE=2BE ，设BE=2x ，则DE=4x ，BD=6x ，EF=x ，BF=3x ． ∵ cos 303BF OB =⋅︒=，∴ 33x =， EF=33．在Rt △OEF 中，90O FE ∠=︒， ∵ tan 3O F O ED EF∠==，∴ 60O ED ∠=︒，1cos 2O ED ∠=． …………………………………… 4分∴ 30BO E O ED O BD ∠=∠-∠=︒． ∴ 90D O C D O B BO E ∠=∠-∠=︒． ∴ 45C ∠=︒．∴ 222CD OC ==． ………………………………………………… 5分22．解：（1）135°；………………………………………………………………………… 2分图3FEA DBC图4FE DAOCB（2）120°；………………………………………………………………………… 3分27 ． ……………………………………………………………………… 5分五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23．解：（1）∵ 关于x 的一元二次方程2 10x px q +++=的一个实数根为 2，∴ 22 210p q +++=．…………………………………………………… 1分 整理，得 25q p =--． …………………………………………………… 2分 （2）∵ 222244(25)820(4)4p q p p p p p ∆=-=++=++=++， 无论p 取任何实数，都有2(4)p +≥0，∴ 无论p 取任何实数，都有 2(4)40p ++>．∴ 0∆>． ………………………………………………………………… 3分∴ 抛物线2y x px q =++与x 轴有两个交点．………………………… 4分（3）∵ 抛物线21y x px q =++与抛物线221y x px q =+++的对称轴相同，都为直线2p x =-，且开口大小相同，抛物线221y x px q =+++可由抛物线21y x px q =++沿y 轴方向向上平移一个单位得到，（如图5所示，省略了x 轴、y 轴） ∴ EF ∥MN ，EF =MN =1．∴ 四边形FEMN 是平行四边形． ………………5分 由题意得 22FEMN p S EF =⨯-=四边形．解得4p =±．………………………………………7分24．证明：（1）如图6．∵ 点B 关于直线CH 的对称点为D ，CH ⊥AB 于点H ，直线DE 交直线CH 于点F ， ∴ BF=DF ，DH=BH ．…………………1分 ∴ ∠1=∠2．又∵ ∠EDA =∠A ，∠EDA =∠1， ∴ ∠A ＝∠2．∴ BF ∥AC ．……………………………………………………………… 2分 （2）取FD 的中点N ，连结HM 、HN . ∵ H 是BD 的中点，N 是FD 的中点，∴ HN ∥BF ． 由（1）得BF ∥AC ， ∴ HN ∥AC ，即HN ∥EM ． ∵ 在Rt △ACH 中，∠AHC =90°，AC 边的中点为M ，图6图5y 2y 1FE N M∴ 12H MAC AM==．∴ ∠A ＝∠3． ∴ ∠EDA =∠3． ∴ NE ∥HM ．∴ 四边形ENHM 是平行四边形．……………………………………… 3分 ∴ HN=EM ．∵ 在Rt △DFH 中，∠DHF =90°，DF 的中点为N ， ∴ 12H ND F=，即2D F H N =．∴ 2DF EM =． ………………………………………………………… 4分 （3）当AB =BC 时，在未添加辅助线和其它字母的条件下，原题图2中所有与BE相等的线段是EF 和CE ． （只猜想结论不给分） 证明：连结CD ．（如图8）∵ 点B 关于直线CH 的对称点为D ，CH ⊥AB 于点H ，∴ BC=CD ，∠ABC ＝∠5． ∵ AB ＝BC ，∴ 1802ABC A ∠=︒-∠，AB ＝CD ．①∵ ∠EDA =∠A ，∴ 61802A ∠=︒-∠，AE =DE ．② ∴ ∠ABC ＝∠6=∠5． ∵ ∠BDE 是△ADE 的外角， ∴ 6BD E A ∠=∠+∠． ∵ 45BD E ∠=∠+∠， ∴ ∠A ＝∠4．③由①，②，③得 △ABE ≌△DCE ．………………………………………5分 ∴ BE = CE ． ……………………………………………………………… 6分由（1）中BF=DF 得 ∠CFE=∠BFC ．由（1）中所得BF ∥AC 可得 ∠BFC=∠ECF ． ∴ ∠CFE=∠ECF ． ∴ EF=CE ．∴ BE=EF ． ……………………………………………………………… 7分 ∴ BE =EF =CE ．（阅卷说明：在第3问中，若仅证出BE =EF 或BE =CE 只得2分）图825．解：（1）∵ 2244(2)y ax ax a c a x c =-++=-+，∴ 抛物线的对称轴为直线2x =．∵ 抛物线244y ax ax a c =-++与x 轴交于 点A 、点B ，点A 的坐标为(1,0)，∴ 点B 的坐标为(3,0)，OB ＝3．…………… 1分 可得该抛物线的解析式为(1)(3)y a x x =--． ∵ OB =OC ，抛物线与y 轴的正半轴交于点C ， ∴ OC =3，点C 的坐标为(0,3)．将点C 的坐标代入该解析式，解得a =1．……2分∴ 此抛物线的解析式为243y x x =-+．（如图9）…………………… 3分（2）作△ABC 的外接圆☉E ，设抛物线的对称轴与x 轴的交点为点F ，设☉E 与抛物线的对称轴位于x 轴上方的部分的交点为点1P ，点1P 关于x 轴的对称点为点2P ，点1P 、点2P 均为所求点.（如图10）可知圆心E 必在AB 边的垂直平分线即抛物线的对称轴直线2x =上．∵ 1AP B ∠、A C B ∠都是弧AB 所对的圆周角，∴ ACB B AP ∠=∠1，且射线FE 上的其它点P 都不满足ACB APB ∠=∠． 由（1）可知 ∠OBC=45°，AB=2，OF=2．可得圆心E 也在BC 边的垂直平分线即直线y x =上．∴ 点E 的坐标为(2,2)E ．………………………………………………… 4分∴ 由勾股定理得 5EA =．∴ 15EP EA ==．∴ 点1P 的坐标为1(2,25)P +．…………………………………………… 5分 由对称性得点2P 的坐标为2(2,25)P --． ……………………………… 6分 ∴符合题意的点P 的坐标为1(2,25)P +、2(2,25)P --. （3）∵ 点B 、D 的坐标分别为(3,0)B 、(2,1)D -，可得直线BD 的解析式为3y x =-，直线BD 与x 轴所夹的锐角为45°．[来源:学科网]∵ 点A 关于∠AQB 的平分线的对称点为A '，（如图11） 若设A A '与∠AQB 的平分线的交点为M ，则有 QA QA '=，AM A M '=，AA QM '⊥，Q ，B ，A '三点在一条直线上． ∵ 2Q A Q B -=，∴ .2''=-=-=QB QA QB QA BA作A N '⊥x 轴于点N ．∵ 点Q 在线段BD 上， Q ，B ，A '三点在一条直线上， ∴ sin 451A N B A ''=⋅︒=，cos 451B N B A '=⋅︒=． ∴ 点A '的坐标为(4,1)A '． ∵ 点Q 在线段BD 上，图9xyO 1DCBA∴ 设点Q 的坐标为(,3)Q x x -，其中23x <<． ∵ QA QA '=，∴ 由勾股定理得 2222(1)(3)(4)(31)x x x x -+-=-+--． 解得114x =．经检验，114x =在23x <<的范围内．∴ 点Q 的坐标为111(,)44Q -． …………………………………………… 7分 此时1115()2(1)2244Q AA A AB Q AB A Q S S S AB y y '''∆∆∆=+=⋅⋅+=⨯⨯+=．… 8分图10xy O 1FP 2EP 1DCBA图11xyO QMA'DB AN。

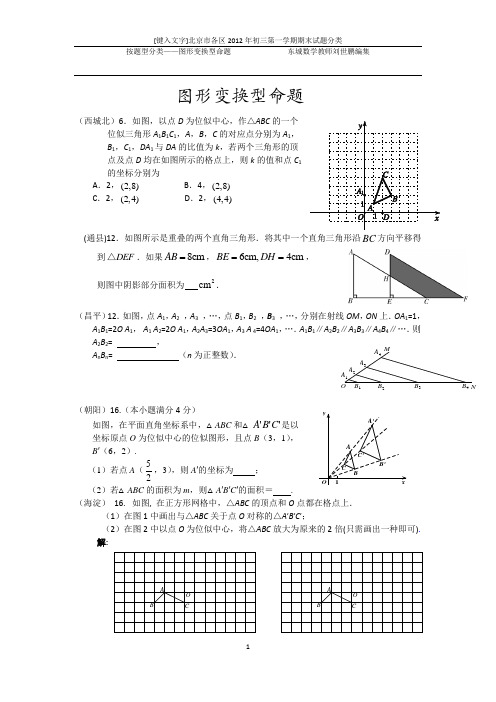
图形变换型命题（西城北）6．如图，以点D 为位似中心，作△ABC 的一个位似三角形A 1B 1C 1，A ，B ，C 的对应点分别为A 1，B 1，C 1，DA 1与DA 的比值为k ，若两个三角形的顶点及点D 均在如图所示的格点上，则k 的值和点C 1的坐标分别为A ．2，(2,8)B ．4，(2,8)C ．2，(2,4)D ．2，(4,4)(通县)12．如图所示是重叠的两个直角三角形．将其中一个直角三角形沿BC 方向平移得到DEF △．如果8cm AB =，6cm,4cm BE DH ==， 则图中阴影部分面积为 2cm ．（昌平）12．如图，点A 1，A 2 ，A 3 ，…，点B 1，B 2 ，B 3 ，…，分别在射线OM ，ON 上．OA 1=1，A 1B 1=2O A 1， A 1 A 2=2O A 1，A 2A 3=3OA 1，A 3 A 4=4OA 1，…．A 1B 1∥A 2B 2∥A 3B 3∥A 4B 4∥…．则A 2B 2= ，A nB n = （n 为正整数）．（朝阳）16.（本小题满分4分）如图，在平面直角坐标系中，△ABC 和△'''C B A 是以 坐标原点O 为位似中心的位似图形，且点B （3，1）， B ′（6，2）. （1）若点A （25，3），则A ′的坐标为 ； （2）若△ABC 的面积为m ，则△A ′B ′C ′的面积＝ .（海淀） 16. 如图, 在正方形网格中，△ABC 的顶点和O 点都在格点上．（1）在图1中画出与△ABC 关于点O 对称的△A ′B ′C ′；（2）在图2中以点O 为位似中心，将△ABC 放大为原来的2倍(只需画出一种即可). 解:4NMA 1A 2A 3A 4321QPNMOC BA(大兴)23. 已知：在ABC△中，AB AC=，点D为BC边的中点，点F在AB上，连结DF 并延长到点E,使BAE BDF∠=∠，点M在线段DF上，且ABE DBM∠=∠．（1）如图1，当45ABC∠=°时，求证：AE=；（2）如图2，当60ABC∠=°时，则线段AE MD、之间的数量关系为；（3）在（2）的条件下，延长BM到P，使MP BM=连接CP，若7AB AE==，tan EAB∠的值．（东城）12．如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，直角∠MON的顶点O在AB上，OM、ON分别交CA、CB于点P、Q，∠MON绕点O任意旋转．当12OAOB=时,OPOQ的值为；当1OAOB n=时，OPOQ的值为 .(用含n的式子表示)（朝阳）24. 已知，在△ABC中，∠BAC=90°，AB=AC，BC=22，点D、E在BC边上（均不与点B、C重合，点D始终在点E左侧），且∠DAE＝45°．（1）请在图①中找出两对相似但不全等的三角形，写在横线上，；（2）设BE＝m，CD＝n，求m与n的函数关系式，并写出自变量n的取值范围；（3）如图②，当BE＝CD时，求DE的长；（4）求证：无论BE与CD是否相等，都有DE2=BD2+CE2.FED CBA图① 图② 备用图（丰台）24．在Rt △ABC 中，∠ACB =90，AC =BC ，CD ⊥AB 于点D ，点E 为AC 边上一点，联结BE 交CD 于点F ，过点E 作EG ⊥BE 交AB 于点G ，（1） 如图1，当点E 为AC 中点时，线段EF 与EG 的数量关系是 ；（2） 如图2，当12CE AE =，探究线段EF 与EG 的数量关系并且证明； （3） 如图3，当nAE CE 1=，线段EF 与EG 的数量关系是．图1 图2 图3(大兴)12. 如图所示，长为4cm ，宽为3cm 的长方形木板在桌面上做 无滑动的翻滚（顺时针方向），木板上点A 位置变化为12A A A →→，由12A A 翻滚到时被桌面上一小木块挡住，此时长方形木板的边2A C 与桌面成30°角，则点A 翻滚到A 2位置时所经过的路径总长度为 cm.（延庆）7．如图，边长为1的菱形ABCD 绕点A 旋转，当B 、C 两点恰好落在扇形AEF 的弧EF 上时，弧BC 的长度等于 A ．π6 B ．π4 C ．π3 D. π2（西城北）19．如图所示，在平面直角坐标系xOy 中，正方形x轴的正方向连续滚动，即先以顶点A 为旋转中心将正方形PABC 顺时针旋转90°得到第二个正方形，再以顶点D 为旋转中心将第二个正方形顺时针旋转90°得到第三个正方形，依此方法继续滚动下去得到第四个正方形，…，第n 个正方形．设滚动过程中的点P 的坐标为(,)x y ．（1）画出第三个和第四个正方形的位置，并直接写出第三个正方形中的点P 的坐标；（2）画出点(,)P x y 运动的曲线（0≤x ≤4），并直接写出该曲线与x 轴所围成区域的面积．（平谷）22. 如图，Rt △OAB 中，∠OA B ＝90°，O 为坐标原点， 边OA 在x 轴上，OA ＝AB ＝1个单位长度．把Rt △OAB 沿x 轴正方向平移1个单位长度后得△11AA B ． （1）求以A 为顶点，且经过点1B 的抛物线的解析式； （2）若（1）中的抛物线与OB 交于点C ，与y 轴交于 点D ，求点D 、C 的坐标．（丰台）22．小明喜欢研究问题，他将一把三角板的直角顶点放在平面直角坐标系的原点O 处，两条直角边与抛物线2(0)y ax a =<交于A 、B 两点． （1）如图1，当2OA OB ==时，则a = ；（2）对同一条抛物线，当小明将三角板绕点O 旋转到如图2所示的位置时，过点B 作BC x ⊥轴于点C ，测得1OC =，求出此时点A 的坐标；（3）对于同一条抛物线，当小明将三角板绕点O 旋转任意角度时，他惊奇地发现，若三角板的两条直角边与抛物线有交点，则线段A B 总经过一个定点，请直接写出该定点的坐标．（丰台）25．在平面直角坐标系xOy 中，已知抛物线C 1：212.y x x =-+（1）将抛物线C 1先向右平移2个单位，再向上平移1个单位，得到抛物线C 2，求抛物线C 2的顶点P 的坐标及它的解析式．（2）如果x 轴上有一动点M ，那么在两条抛物线C 1、C 2上是否存在点N ，使得以点O 、P 、M 、N 为顶点的四边形是平行四边形（OP 为一边）？若存在，求出点N 的坐标；若不存在，请说明理由．(房山)25. 已知抛物线y=﹣x 2+bx+c 的对称轴为直线x=1,最小值为3，此抛物线与y 轴交于点A ，顶点为B ，对称轴BC 与x 轴交于点C ． （1）求抛物线的解析式.（2）如图1．求点A 的坐标及线段OC 的长； （3）点P 在抛物线上，直线PQ ∥BC 交x 轴于点Q ，连接BQ ． ①若含45°角的直角三角板如图2所示放置．其中，一个顶点与点C 重合，直角顶点D 在BQ 上，另一 个顶点E 在PQ 上．求直线BQ 的函数解析式； ②若含30°角的直角三角板一个顶点与点C 重合，直角顶点D 在直线BQ 上，另一个顶点E 在PQ 上，求点P 的坐标．（东城）25．在平面直角坐标系xOy 中，抛物线235y mx x m =+++与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C （0 , 4），D 为OC 的中点.（1）求m 的值；y x12345678–1–2123–1–2–3–4–5O（2）抛物线的对称轴与 x 轴交于点E ，在直线AD 上是否存在点F ，使得以点A 、B 、F 为顶点的三角形与ADE ∆ 相似？若存在，请求出点F 的坐标，若不存在，请说明理由；（3）在抛物线的对称轴上是否存在点G ，使△GBC 中BC求出点G 的坐标；若不存在，请说明理由．（燕山）25. 在直角坐标系xOy 中，已知某二次函数的图象经过A （－4，0）、B （0，－3），与x 轴的正半轴相交于点C ，若△AOB ∽△BOC （相似比不为1）． （1）求这个二次函数的解析式； （2）求△ABC 的外接圆半径r ；（3）在线段AC 上是否存在点M （m ，0），使得以线段BM 为直径的圆与线段AB 交于N 点，且以点O 、A 、N为顶点的三角形是等腰三角形？若存在，求出m 的值；若不存在，请说明理由． （海淀）23. 已知二次函数y =ax 2+bx +c 的图象与反比例函数xa y 4+=的图象交于点A (a , -3)，与 y 轴交于点B .（1）试确定反比例函数的解析式;（2）若∠ABO =135︒, 试确定二次函数的解析式;（3）在（2）的条件下,将二次函数y =ax 2 + bx + c 的图象先沿x 轴翻折, 再向右平移到与反比例函数xa y 4+=的图象交于点P (x 0, 6) . 当x 0 ≤x ≤3时, 求平移后的二 次函数y 的取值范围.(大兴)25.已知二次函数21342y x x =-+. （1）求它的对称轴与x 轴交点D 的坐标；（2）将该抛物线沿它的对称轴向上平移，如图所示，设平移后的抛物线的顶点为M ，与x 轴、y 轴的交点分别为A 、B 、C 三点，连结AC 、BC,若∠ACB =90°. ①求此时抛物线的解析式；②以AB 为直径作圆，试判断直线CM 与此圆的位置关系，并说明理由.（燕山）24. 已知：如图，正方形纸片ABCD 的边长是4，点M 、N 分别在两边AB 和CD 上（其中点N 不与点C 重合），沿直线MN 折叠该纸片，点B 恰好落在AD 边上点E 处． （1）设AE ＝x ，四边形AMND 的面积为 S ，求 S 关于x 的函数解析式，并指明该函数的定义域；（2）当AM 为何值时，四边形AMND 的面积最大？最大值是多少？ （3）点M 能是AB 边上任意一点吗？请求出AM 的取值范围．（东城）16．在平面直角坐标系xoy 中，已知ABC △三个顶点的坐标分别为 ()()()1,2,3,4,2,9.A B C --- ⑴ 画出ABC △；⑵ 画出ABC △绕点A 顺时针旋转90后得到的11AB C △，并求出1CC 的长.（朝阳）9. 如图，△ABC 为等边三角形，D 是△ABC 内一点，且AD ＝3，将△ABD 绕点A 旋转到△ACE 的位置，连接DE ，则DE 的长为 .θAA 'CBB '30︒B 'A 'CB A(石景山)23．如图1，在△ABC 中，∠ACB =90°，AC =3，BC =4，将△ABC 绕顶点C 顺时针旋转30°，得到△A ′B ′C ．联结A ′A 、B ′B ，设△ACA ′和△BCB ′的面积分别为S △ACA ′ 和S △BCB ′． （1）直接写出S △ACA ′ ︰S △BCB ′ 的值 ；（2）如图2，当旋转角为θ（0°＜θ＜180°）时，S △ACA ′ 与S △BCB ′ 的比值是否发生变化，若不变请证明；若改变，写出变化后的比值（可用含θ的代数式表示）．图1 图2（昌平）22.已知正方形纸片ABCD ．如图1，将正方形纸片折叠，使顶点A 落在边CD 上的点P 处（点P 与C 、D 不重合），折痕为EF ，折叠后AB 边落在PQ 的位置，PQ 与BC 交于点G ．（1）请你找到一个与EDP △相似的三角形，并证明你的结论；（2）当AB =2，点P 位于CD 中点时，请借助图2画出折叠后的示意图，并求CG 的长．（海淀）22. 已知△ABC 的面积为a ，O 、D 分别是边AC 、BC 的中点.（1）画图：在图1中将点D 绕点O 旋转180︒得到点E , 连接AE 、CE . 填空：四边形ADCE 的面积为 ；（2）在（1）的条件下，若F 1是AB 的中点，F 2是AF 1的中点, F 3是AF 2的中点,…,F n 是AF n -1的中点 (n 为大于1的整数), 则△F 2CE 的面积为 ; △F n CE 的面积为 .解: （1）画图:图1 备用图 填空：四边形ADCE 的面积为 .（2）△F 2CE 的面积为 ;P G QF E D C B A A B C D 图2图1图1FE DCBA图2ABCDE F图3ABCDEF△F n CE 的面积为 .（东城）24．已知△ABC 和△ADE 是等腰直角三角形，∠ACB =∠ADE =90°，点F 为BE 中点，连结DF 、CF .（1）如图1, 当点D 在AB 上，点E 在AC 上，请直接写出此时线段DF 、CF 的数量关系和位置关系（不用证明）；（2）如图2，在（1）的条件下将△ADE 绕点A 顺时针旋转45°时，请你判断此时（1）中的结论是否仍然成立，并证明你的判断；（3）如图3，在（1）的条件下将△ADE 绕点A 顺时针旋转90°时，若AD =1，AC=求此时线段CF 的长(直接写出结果).（海淀）24. 已知在□ABCD 中，AE ⊥BC 于E ，DF 平分∠ADC 交线段AE 于F .（1）如图1，若AE =AD ，∠ADC =60︒, 请直接写出线段CD 与AF +BE 之间所满足的等量关系;（2）如图2, 若AE =AD ，你在（1）中得到的结论是否仍然成立, 若成立,对你的结论 加以证明, 若不成立, 请说明理由；（3）如图3, 若AE : AD =a : b ，试探究线段CD 、AF 、BE 之间所满足的等量关系， 请直接写出你的结论.解: （1）线段CD 与AF +BE 之间所满足的等量关系为:.（2） 图1图2（3）线段CD 、AF 、BE 之间所满足的等量关系为: D A F C E B A B ECDFDAF.图3（怀柔）24. 把边长分别为4和6的矩形ABCO如图放在平面直角坐标系中，将它绕点C顺时针旋转α角，旋转后的矩形记为矩形EDCF．在旋转过程中，（1）如图①，当点E在射线CB上时，E点坐标为；∆是等边三角形时，旋转角α的度数是（α为锐角时）；（2）当CBD（3）如图②，设EF与BC交于点G，当EG=CG时，求点G的坐标．α= 时，请判断矩形EDCF的对称中心H是否在以C为顶点，(4) 如图③，当旋转角90且经过点A的抛物线上．图①图②图③。

(3) 设抛物线21y x px q =++的顶点为M ，与 y 轴的交点为E ，抛物线221y x px q =+++ 顶点为N ，与y 轴的交点为F ，若四边形FEMN 的面积等于2，求p 的值．（2012通州）23．已知二次函数2248y x ax a =-+-+（1）求证：无论a 为任何实数，二次函数的图象与x 轴总有两个交点. （2）当x ≥2时，函数值y 随x 的增大而减小，求a 的取值范围. （3）以二次函数2248y x ax a =-+-+图象的顶点A 为一个顶点作该二次函数图象的内接正三角形AMN （M ，N 两点在二次函数的图象上），请问：△AMN的面积是与a 无关的定值吗？若是，请求出这个定值；若不是，请说明理由. （2012房山）23． 已知：关于x 的方程()0322=-+-+k x k x ⑴求证：方程()0322=-+-+k x k x 总有实数根；⑵若方程()0322=-+-+k x k x 有一根大于5且小于7，求k 的整数值；⑶在⑵的条件下，对于一次函数b x y +=1和二次函数2y =()322-+-+k x k x ，当71<<-x 时，有21y y >，求b 的取值范围． 证明：⑴解：⑵ ⑶（2012密云）23．已知：1x 、2x 分别为关于x 的一元二次方程2220mx x m ++-=的两个实数根．（1） 设1x 、2x 均为两个不相等的非零整数根，求m 的整数值； （2）利用图象求关于m 的方程1210x x m ++-=的解． （2012丰台）23．已知：关于x 的一元二次方程：22240x mx m -+-=. （1）求证：这个方程有两个不相等的实数根；（2）当抛物线2224y x mx m =-+-与x 轴的交点位于原点的两侧，且到原点的距离相等时，求此抛物线的解析式；（3）将（2）中的抛物线在x 轴下方的部分沿x 轴翻折，其余部分保持能够不变，得到图形C 1,将图形C 1向右平移一个单位,得到图形C 2，当直线y=x b +(b <0)与图形C 2恰有两个公共点时，写出b 的取值范围. （2012石景山）23．已知：关于x 的方程()()01342=---+m x m x 有两个不相等的实数根．（1）求m 的取值范围；（2）抛物线C ：()()1342-+---=m x m x y 与x 轴交于A 、B 两点．若1-≤m 且直线1l :12--=x my 经过点A ,求抛物线C 的函数解析式； （3）在（2）的条件下，直线1l :12--=x my 绕着点A 旋转得到直线2l ：b kx y +=，设直线2l 与y 轴交于点D ，与抛物线C 交于点M （M 不与点A 重合），当23≤AD MA 时，求k 的取值范围．（2012海淀）23．已知关于x 的方程 03)13(2=+++x m mx . （1）求证: 不论m 为任何实数, 此方程总有实数根；（2）若抛物线()2313y mx m x =+++与x 轴交于两个不同的整数点，且m 为正整数，试确定此抛物线的解析式；（3）若点P ),(11y x 与Q ),(21y n x +在（2）中抛物线上 (点P 、Q 不重合), 且y 1=y 2, 求代数式81651242121++++n n n x x 的值.（2012平谷）23.已知关于x 的二次函数2212m y x mx +=-+与2222m y x mx +=--，这两个二次函数图象中的一条．．与x 轴交于A 、B 两个不同的点.（1）试判断哪个二次函数的图象经过A 、B 两点（写出判断过程）；（2）若A 点坐标为（1-,0），求点B 的坐标；（3）在（2）的条件下，设点C 是抛物线上的一点，且△ABC 的面积为10，直接写出点C 的坐标（2012门头沟）23.已知：关于x 的一元二次方程02)21(22=-++-k x k x 有两个实数根. （1）求k 的取值范围；（2）当k 为负整数时，抛物线2)21(22-++-=k x k x y 与x 轴的交点是整数点，求抛物线的解析式；（3）若（2）中的抛物线与y 轴交于点A ，过A 作x 轴的平行 线与抛物线交于点B ，连接OB ，将抛物线向上平移n 个单位， 使平移后得到的抛物线的顶点落在△OAB 的内部（不包括 △OAB 的边界），求n 的取值范围. （2012昌平）23．已知关于x 的方程（k +1）x 2+(3k -1)x +2k -2=0． （1）讨论此方程根的情况；（2）若方程有两个整数根，求正整数k 的值；（3）若抛物线y =（k +1）x 2+(3k -1)x +2k -2与x 轴的两个交点之间的距离为3，求k 的值．（2012燕山）23．已知：如图，在直角坐标系xOy 中，直线y=2x 与函数y=x2的图象在第一象限的交于A 点，AM ⊥x 轴，垂足是M ，把线段OA 的垂直平分线记作l ，线段AN 与OM 关于l 对称. （3）抛物线22(41)3y x m x m m =-+++与x 轴交于点A 、B ，与y 轴交于点C ，当m 取（2）中符合题意的最小整数时，将此抛物线向上平移n 个单位，使平移后得到的抛物线顶点落在△ABC 的内部（不包括△ABC 的边界），求n 的取值范围（直接写出答案即可）．（2012朝阳） 23. 阅读下面材料：问题：如图①，在△ABC 中， D 是BC 边上的一点，若∠BAD =∠C =2∠DAC =45°，DC =2．求BD 的长． 小明同学的解题思路是：利用轴对称，把△ADC 进行翻折，再经过推理、计算使问题 得到解决．（1）请你回答：图中BD 的长为 ；（2）参考小明的思路，探究并解答问题：如图②，在△ABC 中，D 是BC 边上的一点，若∠BAD =∠C =2∠DAC =30°，DC =2，求BD 和AB 的长．图① 图②（2012怀柔）23．已知：关于x 的方程2(1)(1)20a x a x --++=.（1）a 取何整数值时，关于x 的方程2(1)(1)20a x a x --++=的根都是整数；（2）若抛物线y=2(1)(1)20a x a x --++=的对称轴为x =－1，顶点为M ，当k 为何值时，一次函数13y kx k =+的图象必过点M.解：（2012大兴）23．在平面直角坐标系xOy 中，O 为坐标原点，已知抛物线221(2) 1.4y x k x k =-+++ （1）k 取什么值时，此抛物线与x 轴有两个交点？ （2）此抛物线221(2)14y x k x k =-+++与x 轴交于A ()12(,0),0x B x 、 两点（点A 在点B 左侧），且123x x +=，求k 的值.。

2012年北京市中考数学一模分类汇编——几何综合等边三角形、等腰三角形+旋转变换1. （燕山）已知：如图，点P是线段AB上的动点，分别以AP、BP为边向线段AB的同侧作正△APC和正△BPD，AD和BC交于点M.（1）当△APC和△BPD面积之和最小时，直接写出AP : PB的值和∠AMC 的度数；（2）将点P在线段AB上随意固定，再把△BPD按顺时针方向绕点P旋转一个角度α，当α<60°时，旋转过程中，∠AMC的度数是否发生变化？证明你的结论.（3）在第（2）小题给出的旋转过程中，若限定60°<α<120°，∠AMC 的大小是否会发生变化？若变化，请写出∠AMC的度数变化范围；若不变化，请写出∠AMC的度数2. （东城）已知∠ABC=90°，点P为射线BC上任意一点（点P与点B不重合），分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连结QE并延长交BP于点F.2，点A、E、P恰好在一条直线上时，求此时EF （1）如图1，若AB=3的长（直接写出结果）；（2）如图2，当点P为射线BC上任意一点时，猜想EF与图中的哪条线段相等（不能添加辅助线产生新的线段），并加以证明；2，设BP=x，以QF为边的等边三角形的面积y，求y关（3）若AB=3于x的函数关系式．3．（顺义）问题：如图1， 在Rt △ABC 中，90C ∠=︒，30ABC ∠=︒，点D 是射线CB 上任意一点，△ADE 是等边三角形，且点D 在ACB ∠的内部，连接BE ．探究线段BE 与DE 之间的数量关系．请你完成下列探究过程：先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明.（1） 当点D 与点C 重合时（如图2），请你补全图形．由BAC ∠的度数为 ，点E 落在 ，容易得出BE 与DE 之间的数量关系为 ；（2） 当点D 在如图3的位置时，请你画出图形，研究线段BE 与DE之间的数量关系是否与（1）中的结论相同，写出你的猜想并加以证明．DB CAABC (D )图3图2图1D EBCA4.（延庆）如图1，已知：已知：等边△ABC ，点D 是边BC 上一点（点D 不与点B 、点C 重合），求证：BD+DC > AD下面的证法供你参考：把ACD ∆绕点A 瞬时间针旋转60得到ABE ∆则有ABE ACD ∆≅∆,DC=EB ∵AD=AE,60=∠DAE∴ADE ∆是等边三角形∴AD=DE在DBE ∆中，BD+EB > DE 即：BD+DC>AD实践探索：（1）请你仿照上面的思路，探索解决下面的问题：如图2，点D 是等腰直角三角形△ABC 边上的点（点D 不与B 、C 重合），求证：BD+DC>2AD（2）如果点D 运动到等腰直角三角形△ABC 外或内时，BD 、DC 和AD 之间又存在怎样的数量关系？ 直接写出结论.B D 图2 CB 图1间接利用旋转变换添加辅助线5．（密云）已知：正方形ABCD 中，45MAN ∠=，绕点A 顺时针旋转，它的两边分别交CB 、DC （或它们的延长线）于点M 、N ． （1）如图1，当MAN ∠绕点A 旋转到BM DN =时，有BM DN MN +=．当MAN ∠ 绕点A 旋转到BM DN ≠时，如图2，请问图1中的结论还是否成立？如果成立，请给予证明，如果不成立，请说明理由； （2）当M A N∠绕点A 旋转到如图3的位置时，线段BM DN ，和MN 之间有怎样的等量关系？请写出你的猜想，并证明．6．（平谷）如图，已知四边形ABCD是正方形，对角线ACBD相交于O. （1）如图1，设E、F分别是AD、AB上的点，且∠EOF=90°，线段AF、BF和EF之间存在一定的数量关系．请你用等式直接写出这个数量关系；（2）如图2，设E、F分别是AB上不同的两个点，且∠EOF=45°，请你用等式表示线段AE、BF和EF之间的数量关系，并证明.图 1图 27．（怀柔）探究：（1）如图1，在正方形ABCD 中，E 、F 分别是BC 、CD 上的点，且∠EAF ＝45°，判断BE 、DF 与EF 三条线段之间的数量关系，直接写出判断结果：（2）如图2，若把(1)问中的条件变为“在四边形ABCD 中，AB ＝AD ，∠B ＋∠D ＝180°，E 、F 分别是边BC 、CD 上的点，且∠EAF =21∠BAD ”，则（1）问中结论是否仍然成立？若成立，请给出证明，若不成立，说明理由； （3）在（2）问中，若将△AEF 绕点A 逆时针旋转，当点分别E 、F 运动到BC 、CD 延长线上时，如图3所示，其它条件不变，则（1）问中的结论是否发生变化？若变化，请给出结论并予以证明..与中点有关的问题8．（丰台）已知：△ABC 和△ADE 是两个不全等的等腰直角三角形，其中BA =BC ，DA =DE ，联结EC ，取EC 的中点M ，联结BM 和DM ．（1）如图1，如果点D 、E 分别在边AC 、AB 上，那么BM 、DM 的数量关系与位置关系是 ；（2）将图1中的△ADE 绕点A 旋转到图2的位置时，判断（1）中的结论是否仍然成立，并说明理由．DCB AEMMEABC9．（石景山）（1）如图1，在矩形ABCD 中，AB=2BC ，M 是AB 的中点．直接写出∠BMD 与∠ADM 的倍数关系；（2）如图2，若四边形ABCD 是平行四边形， AB=2BC ，M 是AB 的中点，过C 作CE ⊥AD 与AD 所在直线交于点E ．①若∠A 为锐角，则∠BME 与∠AEM 有怎样的倍数关系，并证明你的结论； ②当︒<∠<︒A 0时，上述结论成立； 当︒<∠≤︒180A 时，上述结论不成立．MDBACEADC10．（海淀）在□ABCD 中，∠A =∠DBC , 过点D 作DE =DF , 且∠EDF=∠ABD ,连接EF 、 EC , N 、P 分别为EC 、BC 的中点，连接NP ． （1）如图1，若点E 在DP 上, EF 与DC 交于点M , 试探究线段NP 与线段NM 的数量关系及∠ABD 与∠MNP 满足的等量关系，请直接写出你的结论； （2）如图2，若点M 在线段EF 上, 当点M 在何位置时，你在（1）中得到的结论仍然成立，写出你确定的点M 的位置，并证明（1）中的结论.图1 图2MBDCEA NPPNAE FCDB轴对称+中点+旋转思想添辅助线11．（西城）已知：在如图1所示的锐角三角形ABC中，CH⊥AB于点H，点B关于直线CH的对称点为D，AC边上一点E满足∠EDA=∠A，直线DE 交直线CH于点F．(1) 求证：BF∥AC；(2) 若AC边的中点为M，求证：2；DF EM(3) 当AB=BC时（如图2），在未添加辅助线和其它字母的条件下，找出图2中所有与BE相等的线段，并证明你的结论．图1 图2轴对称思想添辅助线12.（门头沟）已知：在△ABC中，BC=2AC，∠DBC=∠ACB，BD=BC，CD交线段AB于点E．（1）如图l，当∠ACB=90°时，直接写出线段DE、CE之间的数量关系；（2）如图2，当∠ACB=120°时，求证：DE=3CE；（3）如图3，在（2）的条件下，点F是BC边的中点，连接DF，DF与AB 交于G，△DKG和△DBG关于直线DG对称（点B的对称点是点K），延长DK 交AB于点H．若BH=10，求CE的长.图 1EDAC B图 2EDACBFGKH图 3EDACB13．（昌平） 如图，在四边形ABCD 中，对角线AC 、BD 相交于点O ，直线MN 经过点O ，设锐角∠DOC =∠ ，将△DOC 以直线MN 为对称轴翻折得到△D ’OC ’，直线A D ’、B C ’相交于点P ．（1）当四边形ABCD 是矩形时，如图1，请猜想A D ’、B C ’的数量关系以及∠APB 与∠α的大小关系；（2）当四边形ABCD 是平行四边形时，如图2，（1）中的结论还成立吗？ （3）当四边形ABCD 是等腰梯形时，如图3，∠APB 与∠α有怎样的等量关系？请证明．图3图2图1D BANC'OMPD'D CBAN C'O MPD'D'PMOC'N A BCD14.（朝阳） 阅读下面材料：问题：如图①，在△ABC 中， D 是BC 边上的一点，若∠BAD =∠C =2∠DAC =45°，DC =2．求BD 的长．小明同学的解题思路是：利用轴对称，把△ADC 进行翻折，再经过推理、计算使问题得到解决．（1）请你回答：图中BD 的长为 ；（2）参考小明的思路，探究并解答问题：如图②，在△ABC 中，D 是BC边上的一点，若∠BAD =∠C =2∠DAC =30°，DC =2，求BD 和AB 的长．图①图②几何探究与函数关系式问题15．（通州）已知四边形ABCD，点E是射线BC上的一个动点（点E不与B、C两点重合），线段BE的垂直平分线交射线AC于点P，联结DP，PE. （1）若四边形ABCD是正方形，猜想PD与PE的关系，并证明你的结论.（2）若四边形ABCD是矩形，（1）中的PD与PE的关系还成立吗？（填：成立或不成立）.（3）若四边形ABCD是矩形，AB=6，cos∠ACD=35，设AP=x，△PCE的面积为y,当AP>12AC时，求y与x之间的函数关系式.图1C 图2C几何最值问题16．（房山）如图1，在△ABC 中，∠ACB =90°，AC =BC =5，以点B 为圆心，以2为半径作圆.⑴设点P 为☉B 上的一个动点，线段CP 绕着点C 顺时针旋转90°，得到线段CD ，联结DA ，DB ，PB ，如图2．求证：AD =BP ；⑵在⑴的条件下，若∠CPB =135°，则BD =___________； ⑶在⑴的条件下，当∠PBC =_______° 时，BD 有最大值，且最大值为_____； 当∠PBC =_________° 时，BD 有最小值，且最小值为_____．旋转变换中不变量+辅助圆的构造17.（朝阳） 在矩形ABCD 中，点P 在AD 上，AB =2，AP =1，将三角板的直角顶点放在点P 处，三角板的两直角边分别能与AB 、BC 边相交于点E 、F ，连接EF ．（1）如图，当点E 与点B 重合时，点F 恰好与点C 重合，求此时PC 的长； （2）将三角板从（1）中的位置开始，绕点P 顺时针旋转，当点E 与点A重合时停止，在这个过程中，请你观察、探究并解答： ① ∠PEF 的大小是否发生变化？请说明理由；② 直接写出从开始到停止，线段EF 的中点所经过的路线长．备用图相似列方程几何计算18.（大兴）已知：如图，N 、M 是以O 为圆心，1为半径的圆上的两点，B 是MN 上一动点（B 不与点M 、N 重合），∠MON =90°，BA ⊥OM 于点A ，BC ⊥ON 于点C ，点D 、E 、F 、G 分别是线段OA 、AB 、BC 、CO 的中点，GF 与CE 相交于点P ，DE 与AG 相交于点Q ．（1）四边形EPGQ （填“是”或者“不是”）平行四边形； （2）若四边形EPGQ 是矩形，求OA 的值； （3）连结PQ ，求223PQ OA 的值．2012年北京市中考数学一模分类汇编——几何综合等边三角形、等腰三角形+旋转变换1. （燕山）已知：如图，点P 是线段AB 上的动点，分别以AP 、BP 为边向线段AB 的同侧作正△APC 和正△BPD ，AD 和BC 交于点M .（1）当△APC 和△BPD 面积之和最小时，直接写出AP : PB 的值和∠AMC的度数；（2）将点P 在线段AB 上随意固定，再把△BPD 按顺时针方向绕点P 旋转一个角度α，当α<60°时，旋转过程中，∠AMC 的度数是否发生变化？证明你的结论.（3）在第（2）小题给出的旋转过程中，若限定60°<α<120°，∠AMC的大小是否会发生变化？若变化，请写出∠AMC 的度数变化范围；若不变化，请写出∠AMC 的度数24.⑴ 1，60° ………………………2分 ⑵ 不变化.证明：如图，点E 在AP 的延长线上，∠BPE=α<60°.（只要画出了符合题意的图形即可得分）………3分 ∵∠BPC=∠CPD+60°,∠DPA=∠CPD+60°∴∠BPC=∠DPA. 在△BPC 和△DPA 中，又∵BP=DP，PC=PA，∴△BPC≌△DPA. …………4分∴∠BCP=∠DAP.∴∠AMC=180°-∠MCP-∠PCA-∠MAC= 120°-∠BCP -∠MAC=120°-（∠DAP+∠MAC）-∠PCA=120°-∠PAC= 60°，且与α的大小无关.……………………6分⑶不变化，60°…………………………7分2. （东城）已知∠ABC=90°，点P为射线BC上任意一点（点P与点B不重合），分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连结QE并延长交BP于点F.2，点A、E、P恰好在一条直线上时，求此时EF （1）如图1，若AB=3的长（直接写出结果）；（2）如图2，当点P为射线BC上任意一点时，猜想EF与图中的哪条线段相等（不能添加辅助线产生新的线段），并加以证明；2，设BP=x，以QF为边的等边三角形的面积y，求y关（3）若AB=3于x的函数关系式．24. （本小题满分7分）解：（1）EF=2．……………1分（2）EF=BF．……………2分证明：∵∠BAP=∠BAE-∠EAP=60°-∠EAP，∠EAQ=∠QAP-∠EAP=60°-∠EAP，∴∠BAP=∠EAQ ．在△ABP 和△AEQ 中，AB=AE ，∠BAP=∠EAQ ， AP=AQ ，∴ △ABP ≌△AEQ ．∴ ∠AEQ=∠ABP=90°．∴ ∠BEF 180180906030AEQ AEB =︒-∠-∠=︒-︒-︒=︒． 又∵ ∠EBF =90°-60°=30°，∴EF =BF ．……4分 (3) 在图1中，过点F 作FD ⊥BE 于点D ． ∵ △ABE 是等边三角形, ∴ BE=AB=32．由（2）得 =∠EBF 30°，在Rt △BDF中，BD =．∴ BF=2cos30BG=︒．∴ EF =2 ． ∵ △ABP ≌△AEQ , ∴ QE=BP=x ． ∴ QF =QE ＋EF 2x =+．∴ 以QF 为边的等边三角形的面积222)x x +=+ 3．（顺义）问题：如图1， 在Rt △ABC 中，90C ∠=︒，30ABC ∠=︒，点D 是射线CB 上任意一点，△ADE 是等边三角形，且点D 在ACB ∠的内部，连接BE ．探究线段BE 与DE 之间的数量关系．请你完成下列探究过程：先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明.（1） 当点D 与点C 重合时（如图2），请你补全图形．由BAC ∠的度数为 ，点E 落在 ，容易得出BE 与DE 之间的数量关系为 ；（2） 当点D 在如图3的位置时，请你画出图形，研究线段BE 与DE图1D EBCA之间的数量关系是否与（1）中的结论相同，写出你的猜想并加以证明．DB CAABC (D )图3图2解：（1）完成画图如图2，由BAC ∠的度数为 60°，点E 落在 AB 的中点处 ，容易得出BE 与DE 之间的数量关系 为 BE=DE ；…………… 3分（2）完成画图如图3． 猜想：BE DE =． 证明：取AB 的中点F ，连结EF ．∵90ACB ∠=︒，30ABC ∠=︒，∴160∠=︒，12CF AF AB ==．∴△ACF 是等边三角形．∴AC AF =． ① …… 4分 ∵△ADE 是等边三角形，∴260∠=︒，AD AE =． ②∴12∠=∠．∴12BAD BAD ∠+∠=∠+∠．即CAD FAE ∠=∠．③ …………………… 5分 由①②③得 △ACD ≌△AFE （SAS ）．………… 6分 ∴90ACD AFE ∠=∠=︒．∵F 是AB 的中点，∴EF 是AB 的垂直平分线． ∴BE=AE . ………………………… 7分∵△ADE 是等边三角形，∴DE=AE .∴BE DE =．…………… 8分21FEDBCA 图3CB4.（延庆）如图1，已知：已知：等边△ABC ，点D 是边BC 上一点（点D 不与点B 、点C 重合），求证：BD+DC > AD下面的证法供你参考：把ACD ∆绕点A 瞬时间针旋转 60得到ABE ∆则有ABE ACD ∆≅∆,DC=EB ∵AD=AE, 60=∠DAE∴ADE ∆是等边三角形∴AD=DE在DBE ∆中，BD+EB > DE 即：BD+DC>AD实践探索：（1）请你仿照上面的思路，探索解决下面的问题：如图2，点D 是等腰直角三角形△ABC 边上的点（点D 不与B 、C 重合），求证：BD+DC>2AD（2）如果点D 运动到等腰直角三角形△ABC 外或内时，BD 、DC 和AD 之间又存在怎样的数量关系？ 直接写出结论.（1）证明：把ACD ∆绕点A 瞬时针旋转90得到∆连接ED ， ---1分则有ABE ACD ∆≅∆,DC=EBB D 图2 CB 图1∴AED 是等腰三角形由全等可得：∠CAD=∠BAE ∴∠EAD=α过A 作AF ⊥DE 于F 点则∠EAF=α2,DF=12DE=12BE+BD ()在Rt AFD 中，DF=AD •sin α2即：12BE+BD ()=AD •sinα2∵AD=AE, 90=∠DAE ∴ADE ∆是等腰直角三角形 ∴DE=2AD ------------------2分 在DBE ∆中，BD+EB > DE即：BD+DC>2AD ------------------- 3分 （2）BD+DC ≥2AD ---------4分 （3）猜想1：BD+DC 〈2AD证明：把ACD ∆绕点A 顺时针旋转α，得到ABE ∆则有ABE ACD ∆≅∆, DC=EB ，∠ACD=∠ABE ---------5分 ∵∠BAC+∠BDC=180 º∴∠ABD+∠ACD=180 º∴∠ABD+∠ABE=180 º即：E 、B 、D 三点共线---------6分∵AD=AE, 在ADE ∆中∵AE+AD>DE即BD+DC 〈2AD ---------------------7分或者猜想2：--------7分间接利用旋转变换添加辅助线5．（密云）已知：正方形ABCD 中，45MAN ∠=，绕点A 顺时针旋转，E C它的两边分别交CB 、DC （或它们的延长线）于点M 、N ． （1）如图1，当MAN ∠绕点A 旋转到BM DN =时，有BM DN MN +=．当MAN ∠ 绕点A 旋转到BM DN ≠时，如图2，请问图1中的结论还是否成立？如果成立，请给予证明，如果不成立，请说明理由； （2）当M A N∠绕点A 旋转到如图3的位置时，线段BM DN ，和MN 之间有怎样的等量关系？请写出你的猜想，并证明．解：（1）答：（1）中的结论仍然成立，即 BM DN MN +=．证明：如图2，在MB 的延长线上截取BE =DN ，连结AE ．易证 ABE ADN △≌△ （SAS ）． ∴ AE =AN ；∠EAB=∠NAD ．90,45,45.45.BAD NAM BAM NAD EAB BAM ∠=∠=∴∠+∠=∴∠+∠=∴EAM NAM ∠=∠．又AM 为公共边， ∴AEM ANM △≌△． ME MN ∴=．MN ME BE BM DN BM ∴==+=+图 1图 2A A 即 DN BM MN +=． ------------------4分（2）猜想：线段BM DN ，和MN 之间的等量关系为：DN BM MN -= ．证明：如图3，在DN 延长线上截取DE =MB ，连结A E ．易证 ABM ADE △≌△（SAS ）． ∴ AM =AE ；∠MAB =∠EAD ． 易证 AMN AEN △≌△（SAS ）．MN EN ∴= ．∵DN DE EN -=，∴DN BM MN -=． --------------7分6．（平谷）如图，已知四边形ABCD 是正方形，对角线ACBD 相交于O . （1） 如图1，设 E 、F 分别是AD 、AB 上的点，且∠EOF =90°，线段AF 、BF 和EF 之间存在一定的数量关系． 请你用等式直接写出这个数量关系；（2）如图2，设 E 、F 分别是AB 上不同的两个点，且∠EOF =45°，请你用等式表示线段AE 、BF 和EF 之间的数量关系，并证明.(1)222AE AF EF +=……….…...1分 (2) 线段AE 、BF 和EF 之间的数量关系：222EF BF AE =+.………….…...2分证明：过O 作OH ⊥OF ，交AD 于点H ，连结HE .….…..3分 ∵∠1=45°，∠AOB 90=︒， ∴∠2+∠3=∠2+∠4=45°.∴∠3=∠4.由正方形性质可知，OA =OB ，∠5=∠6=45°.∴△AOH ≌△BOF . ............................4分 ∴BF =AH，OF =OH . ………………5分H在△EOH 和△EOF 中,45,,OE OE EOH EOF HO FO =⎧⎪∠=∠=︒⎨⎪=⎩∴△EOH ≌△EOF .∴EF =EH ……………………………………6分 在Rt △AEH 中， ∵ 222AE AH EH +=∴222EF BF AE =+.………………………7分7．（怀柔）探究：（1）如图1，在正方形ABCD 中，E 、F 分别是BC 、CD 上的点，且∠EAF ＝45°，判断BE 、DF 与EF 三条线段之间的数量关系，直接写出判断结果：（2）如图2，若把(1)问中的条件变为“在四边形ABCD 中，AB ＝AD ，∠B ＋∠D ＝180°，E 、F 分别是边BC 、CD 上的点，且∠EAF =21∠BAD ”，则（1）问中结论是否仍然成立？若成立，请给出证明，若不成立，说明理由； （3）在（2）问中，若将△AEF 绕点A 逆时针旋转，当点分别E 、F 运动到BC 、CD 延长线上时，如图3所示，其它条件不变，则（1）问中的结论是否发生变化？若变化，请给出结论并予以证明..24．探究：（1）通过观察可知，EF= BE ＋DF.………………………1分（图3）（图2）（2）结论EF= BE ＋DF 仍然成立（如图2）.…………2分证明:将△ADF 绕点A 顺时针旋转，使AD 与AB 重合，得到'ABF ∆， ∴△ADF ≌'ABF ∆，∴∠1=∠2， A 'F =AF ，'BF =DF. ∠'ABF =∠D 又∵∠EAF=21∠BAD ，即∠4=∠2+∠3. ∴∠4=∠1+∠3.又∵∠ABC ＋∠D ＝180°，∴∠A 'BF ＋∠AB E=180°，即：'F 、B 、E 共线.在△AEF 与△AEF 1中， AF=A 'F ， ∠4=∠1+∠3， AE=AE∴△AEF ≌△AE 'F 中，………………………………………3分 ∴EF=E 'F ，又E 'F =BE ＋B 'F ,即：EF= BE ＋DF. …………………………………………4分 （3）发生变化. EF 、BE 、DF 之间的关系是EF= BE －DF. ……………………5分证明：将△ADF 绕点A 顺时针旋转，使AD 与AB 重合，点F 落在BC 上点'F 处，得到△AB 'F ，如图3所示. ∴△ADF ≌△AB 'F ，∴∠B A 'F =∠DAF ， A 'F =AF ，B 'F =DF. 又∵∠EAF=21∠BAD ，且∠B A 'F =∠DAF ∴∠'F AE=∠FA E.在△'F AE 与△FA E 中 AF=A 'F ，∠'F AE=∠FA E, AE=AE,∴△'F AE ≌△FA E.…………………………………6分 ∴EF=E 'F ，又∵BE= B 'F ＋E 'F ， ∴E 'F =BE －B 'F .即EF= BE －DF.…………………………………………7分与中点有关的问题8．（丰台）已知：△ABC 和△ADE 是两个不全等的等腰直角三角形，其中BA =BC ，DA =DE ，联结EC ，取EC 的中点M ，联结BM 和DM ．（1）如图1，如果点D 、E 分别在边AC 、AB 上，那么BM 、DM 的数量关系与位置关系是 ；（2）将图1中的△ADE 绕点A 旋转到图2的位置时，判断（1）中的结论是否仍然成立，并说明理由．解：（1）BM =DM 且BM ⊥DM ． ………2分（2）成立． ……………3分理由如下：延长DM 至点F ，使MF =MD ，联结CF 、BF 、BD ． 易证△EMD ≌△CMF ．………4分∴ED =CF ，∠DEM =∠1．∵AB =BC ，AD =DE ，且∠ADE =∠ABC =90°，∴∠2=∠3=45°, ∠4=∠5=45°． ∴∠BAD =∠2+∠4+∠6=90°+∠6．∵∠8=360°-∠5-∠7-∠1，∠7=180°-∠6-∠9，∴∠8=360°-45°-（180°-∠6-∠9）-（∠3+∠9）=360°-45°-180°+∠6+∠9- 45°-∠9 =90°+∠6 ． ∴∠8=∠BAD ．………5分 又AD =CF ． ∴△ABD ≌△CBF ．∴BD =BF ，∠ABD =∠CBF ．………6分 ∴∠DBF =∠ABC =90°．CB AEMME ABC∵MF =MD ，∴BM =DM 且BM ⊥DM ．.…………7分9．（石景山）（1）如图1，在矩形ABCD 中，AB=2BC ，M 是AB 的中点．直接写出∠BMD 与∠ADM 的倍数关系；（2）如图2，若四边形ABCD 是平行四边形， AB=2BC ，M 是AB 的中点，过C 作CE ⊥AD 与AD 所在直线交于点E ．①若∠A 为锐角，则∠BME 与∠AEM 有怎样的倍数关系，并证明你的结论； ②当︒<∠<︒A 0时，上述结论成立； 当︒<∠≤︒180A 时，上述结论不成立．（1）∠BMD= 3 ∠ADM ………… 2分（2）联结CM ，取CE 的中点F ，联结MF ，交DC 于N∵M 是AB 的中点，∴MF ∥AE ∥BC ，∴∠AEM=∠1，∠2=∠4， ……… 3分 ∵AB=2BC ，∴BM=BC ，∴∠3=∠4.∵CE ⊥AE ，∴MF ⊥EC ，又∵F 是EC 的中点，∴ME=MC ，∴∠1=∠2. ……….4分 ∴∠1=∠2=∠3. ∴∠BME =3∠AEM. ………. 5分（3）当0°<∠A<120°时，结论成立；当︒<∠≤︒180120 A 时，结论不成立. …………7分 10．（海淀）在□ABCD 中，∠A =∠DBC , 过点D 作DE =DF , 且∠EDF=∠ABD ,连接EF 、 EC , N 、P 分别为EC 、BC 的中点，连接NP ． （1）如图1，若点E 在DP 上, EF 与DC 交于点M , 试探究线段NP 与线段NM 的数量关系及∠ABD 与∠MNP 满足的等量关系，请直接写出你的结论； （2）如图2，若点M 在线段EF 上, 当点M 在何位置时，你在（1）中得到M D BA CEADCFA MBC ED 4321MBDCEANPPNA EFCDB的结论仍然成立，写出你确定的点M 的位置，并证明（1）中的结论.图1 图2 解:（1） NP =MN , ∠ABD +∠MNP =180︒ (或其它变式及文字叙述,各1分). ………2分（2）点M 是线段EF 的中点(或其它等价写法). 证明：如图, 分别连接BE 、CF .∵ 四边形ABCD 是平行四边形，∴ AD ∥BC ，AB ∥DC ，∠A =∠DCB ， ∴∠ABD =∠BDC .∵ ∠A =∠DBC ，∴ ∠DBC =∠DCB .∴ DB =DC . ① ……………3分∵∠EDF =∠ABD ,∴∠EDF =∠BDC .∴∠BDC-∠EDC =∠EDF-∠EDC . 即∠BDE =∠CDF . ② 又 DE =DF ， ③由①②③得△BDE ≌△CDF .……………4分 ∴ EB =FC , ∠1=∠2.∵ N 、P 分别为EC 、BC 的中点，∴NP ∥EB , NP =EB 21.同理可得 MN ∥FC ，MN =FC 21.∴ NP = NM . …………………………5分 ∵ NP ∥EB ,∴∠NPC =∠4.∴∠ENP =∠NCP +∠NPC =∠NCP +∠4.∵MN ∥FC ， ∴∠MNE =∠FCE =∠3+∠2=∠3+∠1.∴∠MNP =∠MNE +∠ENP =∠3+∠1+∠NCP +∠4=∠DBC +∠DCB =180︒-∠BDC =180︒-∠ABD .∴ ∠ABD +∠MNP =180︒. ……………7分轴对称+中点+旋转思想添辅助线11．（西城）已知：在如图1所示的锐角三角形ABC 中，CH ⊥AB 于点H ，点M1 32 4 PNA E FCDBB 关于直线CH 的对称点为D ，AC 边上一点E 满足∠EDA =∠A ，直线DE交直线CH 于点F ． (1) 求证：BF ∥AC ；(2) 若AC 边的中点为M ，求证：2DF EM =；(3) 当AB =BC 时（如图2），在未添加辅助线和其它字母的条件下，找出图2中所有与BE 相等的线段，并证明你的结论．图1 图224．证明：（1）如图6．∵ 点B 关于直线CH 的对称点为D ， CH ⊥AB 于点H ， 直线DE 交直线CH 于点F ，∴ BF=DF ，DH=BH ．…………………1分 ∴ ∠1=∠2．又∵ ∠EDA =∠A ，∠EDA =∠1，∴ ∠A ＝∠2．∴ BF ∥AC ．…………………………………… 2分 （2）取FD 的中点N ，连结HM 、HN .∵ H 是BD 的中点，N 是FD 的中点，∴ HN ∥BF ．由（1）得BF ∥AC ， ∴ HN ∥AC ，即HN ∥EM ． ∵ 在Rt △ACH 中，∠AHC =90°，AC 边的中点为M ，∴ 12HM AC AM ==．∴ ∠A ＝∠3．∴ ∠EDA =∠3． ∴ NE ∥HM ．∴ 四边形ENHM 是平行四边形．……………… 3分 ∴ HN=EM ．∵ 在Rt △DFH 中，∠DHF =90°，DF 的中点为N ， ∴ 12HN DF =，即2DF HN =．∴ 2DF EM =．…………………………… 4分（3）当AB =BC 时，在未添加辅助线和其它字母的条件下，原题图2中所有与BE 相等的线段是EF 和CE ． （只猜想结论不给分）证明：连结CD ．（如图8）∵ 点B 关于直线CH 的对称点为D ，CH ⊥AB 于点H ，∴ BC=CD ，∠ABC ＝∠5． ∵ AB ＝BC ，∴ 1802ABC A ∠=︒-∠，AB ＝CD ．①∵ ∠EDA =∠A ，∴ 61802A ∠=︒-∠，AE =DE ．② ∴ ∠ABC ＝∠6=∠5． ∵ ∠BDE 是△ADE 的外角， ∴ 6BDE A ∠=∠+∠． ∵ 45BDE ∠=∠+∠， ∴ ∠A ＝∠4．③由①，②，③得 △ABE ≌△DCE ．……………5分 ∴ BE = CE ．…………………………… 6分由（1）中BF=DF 得 ∠CFE=∠BFC ．由（1）中所得BF ∥AC 可得 ∠BFC=∠ECF ． ∴ ∠CFE=∠ECF ． ∴ EF=CE ．∴ BE=EF ．………………… 7分 ∴ BE =EF =CE ．（阅卷说明：在第3问中，若仅证出BE =EF 或BE =CE 只得2分）轴对称思想添辅助线12.（门头沟）已知：在△ABC 中，BC =2AC ，∠DBC =∠ACB ，BD =BC ，CD 交线段AB 于点E ．（1）如图l ，当∠ACB =90°时，直接写出线段DE 、CE 之间的数量关系；（2）如图2，当∠ACB =120°时，求证：DE =3CE ；（3）如图3，在（2）的条件下，点F 是BC 边的中点，连接DF ，DF 与AB 交于G ，△DKG 和△DBG 关于直线DG 对称（点B 的对称点是点K ），延长DK 交AB 于点H ．若BH =10，求CE 的长.24.(1)DE=2CE………………………1分 (2)证明：过点B 作BM ⊥DC 于M ∵BD=BC ，∴DM=CM, ………………………..2分∴∠DMB=∠CMB=90°,∠DBM=∠CBM=21∠DBC=60° ∴∠MCB=30° BM=21BC ∵BC=2AC ， ∴BM=AC.∵∠ACB=120°, ∴∠ACE=90°. ∴∠BME=∠ACE图 1EDACB 图 2EDACBF G K H图 3ED AC B图 2MEDACB∵∠MEB=∠AEC ∴△EMB ≌△ECA ∴ME=CE=21CM ………………………3分 ∴DE=3EC ………………………………4分(3) 过点B 作BM ⊥DC 于M ，过点F 作FN ⊥DB 交DB 的延长线于点N.∵∠DBF=120°, ∴∠FBN=60°. ∴FN=23BF,BN=21BF…5分 ∵DB=BC=2BF, DN=DB+BN=25BF ∴DF=7BF∵AC=21BC,BF=21BC ∴AC=BF∵∠DBC=∠ACB ∴△DBF ≌BCA∴∠BDF=∠CBA.∵∠BFG=∠DFB, FBG ∽△FDB ∴DBBGDF BF BF FG == ∴FD FG BF ⋅=2,∴77=FG BF ∴DG=776BF,BG=772BF ∵△DKG 和△DBG 关于直线DG 对称，∴∠GDH=∠BDF.∠ABC=∠GDH. ∵∠BGF=∠DGA,∴△BGF ∽△DGH. ∴GHGFDG BG =. ∴GH=773BF. ∵BH=BG+GH=775BF=10, ∴BF=72.………….6分NM图 3HK G F EDACB∴BC=2BF=47 ,CM=212 ∴CD=2CM=214. ∵DE=3EC ∴EC=41CD=21 ……………………………..7分 13．（昌平） 如图，在四边形ABCD 中，对角线AC 、BD 相交于点O ，直线MN 经过点O ，设锐角∠DOC =∠ ，将△DOC 以直线MN 为对称轴翻折得到△D ’OC ’，直线A D ’、B C ’相交于点P ．（1）当四边形ABCD 是矩形时，如图1，请猜想A D ’、B C ’的数量关系以及∠APB 与∠α的大小关系；（2）当四边形ABCD 是平行四边形时，如图2，（1）中的结论还成立吗？ （3）当四边形ABCD 是等腰梯形时，如图3，∠APB 与∠α有怎样的等量关系？请证明．图3图2图1D CBANC'OMPD'CBAN C'O MPD'D'PMOC'N A BCD25．解：图3图2图1D CBANC'OMPD'CBAN C'O MPD'D'PM OC'N A BCD（1） A D ’=B C ’，∠APB =∠α． …………………… 2分 （2） A D ’=B C ’ 仍然成立，∠APB =∠α不一定成立．………… 3分（3）∠APB =180°-∠α…………………… 4分 证明：如图3，设OC ’，PD ’交于点E ．E∵ 将△DOC 以直线MN 为对称轴翻折得到△D ’OC ’， ∴ △DOC ≌△D ’OC ’，∴ OD =OD ’， OC =OC ’，∠DOC =∠D ’OC ’． ∵ 四边形ABCD 是等腰梯形，∴ AC =BD ，AB =CD, ∠ABC = ∠DCB ． ∵ BC=CB ，∴ △ABC ≌△DCB ． ∴ ∠DBC =∠ACB ．∴ OB =OC ，OA =OD ．∵ ∠AOB = ∠COD =∠C ’O D ’， ∠BOC ’ = ∠D ’O A ． ∵ OD ’=OA ，OC ’=OB ，∴ △D ’OC ’≌△AOB ， ∴ ∠OD ’C ’= ∠OAB ．∵ OD ’=OA ，OC ’=OB ，∠BOC ’ = ∠D ’O A ， ∴ ∠OD ’A = ∠OAD ’=∠OBC ’=∠OC ’ B ．∵ ∠C ’EP = ∠D ’EO ，∴ ∠C ’PE = ∠C ’OD ’=∠COD =∠α．∵∠C ’PE +∠APB =180°，∴∠APB =180°-∠α．………… 8分 14.（朝阳） 阅读下面材料：问题：如图①，在△ABC 中， D 是BC 边上的一点，若∠BAD =∠C =2∠DAC =45°，DC =2．求BD 的长．小明同学的解题思路是：利用轴对称，把△ADC 进行翻折，再经过推理、计算使问题得到解决．（1）请你回答：图中BD 的长为 ；（2）参考小明的思路，探究并解答问题：如图②，在△ABC 中，D 是BC边上的一点，若∠BAD =∠C =2∠DAC =30°，DC =2，求BD 和AB 的长．图①图②23. 解：（1）22 BD . ………………………………2分（2）把△ADC 沿AC 翻折，得△AEC ，连接DE ，∴△ADC ≌△AEC .∴∠DAC =∠EAC ，∠DCA =∠ECA ， DC ＝EC .∵∠BAD =∠BCA =2∠DAC =30°，∴∠BAD =∠DAE =30°，∠DCE =60°. ∴△CDE 为等边三角形. ……………………3分 ∴DC ＝DE .在AE 上截取AF ＝AB ，连接DF ， ∴△ABD ≌△AFD .∴BD ＝DF .在△ABD 中，∠ADB =∠DAC ＋∠DCA =45°， ∴∠ADE =∠AED =75°，∠ABD =105°. ∴∠AFD =105°.∴∠DFE =75°.∴∠DFE =∠DEF .∴DF ＝DE .∴BD ＝DC ＝2. …………………4分 作BG ⊥AD 于点G ， ∴在Rt △BDG 中， 2=BG . ………………5分∴在Rt △ABG 中，22=AB .……………………6分几何探究与函数关系式问题15．（通州）已知四边形ABCD ，点E 是射线BC 上的一个动点（点E 不与B 、C 两点重合），线段BE 的垂直平分线交射线AC 于点P ，联结DP ，PE.（1）若四边形ABCD 是正方形，猜想PD 与PE 的关系，并证明你的结论.（2）若四边形ABCD 是矩形，（1）中的PD 与PE 的关系还成立吗？（填：成立或不成立）.（3）若四边形ABCD 是矩形，AB =6，cos ∠ACD =35，设AP=x ，△PCE 的面积为y ,当AP>12AC 时，求y 与x 之间的函数关系式.25 （1）PE ＝PD ，……………………………..(1分)PE ⊥PD ……………………………..(2分)①当点E 在射线BC 边上,且交点P 在对角线AC 上时,连结PBPE D CBA∵四边形ABCD 是正方形， ∴AB ＝AD ，∠BAP ＝∠DAP 。

专题7：几何三大变换相关问题.1. （2012北京市7分）在ABC △中，BA=BC BAC ∠=α，，M 是AC 的中点，P 是线段BM上的动点，将线段PA 绕点P 顺时针旋转2α得到线段PQ 。

（1） 若α=60︒且点P 与点M 重合（如图1），线段CQ 的延长线交射线BM 于点D ，请补全图形，并写出∠CDB 的度数；（2） 在图2中，点P 不与点B ，M 重合，线段CQ 的延长线与射线BM 交于点D ，猜想∠CDB 的大小（用含α的代数式表示），并加以证明；（3） 对于适当大小的α，当点P 在线段BM 上运动到某一位置（不与点B ，M 重合）时，能使得线段CQ 的延长线与射线BM 交于点D ，且PQ=QD ，请直接写出α的范围。

2. （2012海南省I11分）如图（1），在矩形ABCD 中，把∠B、∠D 分别翻折，使点B 、D 分别落在对角线BC 上的点E 、F 处，折痕分别为CM 、AN. （1）求证：△AND≌△CBM.（2）请连接MF 、NE ，证明四边形MFNE 是平行四边形，四边形MFNE 是菱形吗？请说明理由？ （3）P 、Q 是矩形的边CD 、AB 上的两点，连结PQ 、CQ 、MN ，如图（2）所示，若PQ=CQ ，PQ∥MN。

且AB=4，BC=3，求PC 的长度.3. （2012天津市10分）已知一个矩形纸片OACB，将该纸片放置在平面直角坐标系中，点A（11，0），点B（0，6），点P为BC边上的动点（点P不与点B、C重合），经过点O、P折叠该纸片，得点B′和折痕OP．设BP=t．（Ⅰ）如图①，当∠BOP=300时，求点P的坐标；（Ⅱ）如图②，经过点P再次折叠纸片，使点C落在直线PB′上，得点C′和折痕PQ，若AQ=m，试用含有t的式子表示m；（Ⅲ）在（Ⅱ）的条件下，当点C′恰好落在边OA上时，求点P的坐标（直接写出结果即可）．4. （2012福建南平12分）在平面直角坐标系中，矩形OABC如图所示放置，点A在x轴上，点B的坐标为（m，1）（m＞0），将此矩形绕O点逆时针旋转90°，得到矩形OA′B′C′．（1）写出点A、A′、C′的坐标；（2）设过点A、A′、C′的抛物线解析式为y=ax2+bx+c，求此抛物线的解析式；（a、b、c 可用含m的式子表示）（3）试探究：当m的值改变时，点B关于点O的对称点D是否可能落在（2）中的抛物线上？若能，求出此时m的值．5. （2012广东汕头12分）如图，在矩形纸片ABCD中，AB=6，BC=8．把△BCD沿对角线BD 折叠，使点C落在C′处，BC′交AD于点G；E、F分别是C′D和BD上的点，线段EF交AD 于点H，把△FDE沿EF折叠，使点D落在D′处，点D′恰好与点A重合．（1）求证：△ABG≌△C′DG；（2）求tan∠ABG的值；（3）求EF的长．6. （2012广东省9分）如图，在矩形纸片ABCD中，AB=6，BC=8．把△BCD沿对角线BD折叠，使点C落在C′处，BC′交AD于点G；E、F分别是C′D和BD上的点，线段EF交AD 于点H，把△FDE沿EF折叠，使点D落在D′处，点D′恰好与点A重合．（1）求证：△ABG≌△C′DG；（2）求tan∠ABG的值；（3）求EF的长．7. （2012广东珠海9分）已知，AB是⊙O的直径，点P在弧AB上（不含点A、B），把△AOP 沿OP对折，点A的对应点C恰好落在⊙O上．（1）当P、C都在AB上方时（如图1），判断PO与BC的位置关系（只回答结果）；（2）当P在AB上方而C在AB下方时（如图2），（1）中结论还成立吗？证明你的结论；（3）当P、C都在AB上方时（如图3），过C点作CD⊥直线AP于D，且CD是⊙O的切线，证明：AB=4PD．8. （2012广西南宁10分）如图，已知矩形纸片ABCD，AD=2，AB=4．将纸片折叠，使顶点A与边CD上的点E重合，折痕FG分别与AB，CD交于点G，F，AE与FG交于点O．（1）如图1，求证：A，G，E，F四点围成的四边形是菱形；（2）如图2，当△AED的外接圆与BC相切于点N时，求证：点N是线段BC的中点；（3）如图2，在（2）的条件下，求折痕FG的长．9. （2012湖北天门、仙桃、潜江、江汉油田10分）△ABC中，AB=AC，D为BC的中点，以D为顶点作∠MDN=∠B．（1）如图（1）当射线DN经过点A时，DM交AC边于点E，不添加辅助线，写出图中所有与△ADE相似的三角形．（2）如图（2），将∠MDN绕点D沿逆时针方向旋转，DM，DN分别交线段AC，AB于E，F点（点E与点A不重合），不添加辅助线，写出图中所有的相似三角形，并证明你的结论．（3）在图（2）中，若AB=AC=10，BC=12，当△DEF的面积等于△ABC的面积的14时，求线段EF的长．10. （2012湖北天门、仙桃、潜江、江汉油田12分）如图，抛物线y=ax 2+bx+2交x 轴于A （﹣1，0），B （4，0）两点，交y 轴于点C ，与过点C 且平行于x 轴的直线交于另一点D ，点P 是抛物线上一动点．（1）求抛物线解析式及点D 坐标；（2）点E 在x 轴上，若以A ，E ，D ，P 为顶点的四边形是平行四边形，求此时点P 的坐标； （3）过点P 作直线CD 的垂线，垂足为Q ，若将△CPQ 沿CP 翻折，点Q 的对应点为Q′．是否存在点P ，使Q′恰好落在x 轴上？若存在，求出此时点P 的坐标；若不存在，说明理由．11. （2012湖北武汉12分）如图1，点A 为抛物线C 1：21y=x 22的顶点，点B 的坐标为(1，0)，直线AB 交抛物线C 1于另一点C ．(1)求点C 的坐标；(2)如图1，平行于y 轴的直线x ＝3交直线AB 于点D ，交抛物线C 1于点E ，平行于y 轴的直线x ＝a 交直线AB 于F ，交抛物线C 1于G ，若FG ：DE ＝4∶3，求a 的值； (3)如图2，将抛物线C 1向下平移m(m ＞0)个单位得到抛物线C 2，且抛物线C 2的顶点为点P ，交x 轴于点M ，交射线BC 于点N ，NQ⊥x 轴于点Q ，当NP 平分∠MNQ 时，求m 的值．图1 图212. （2012湖北宜昌11分）如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°．点E为底AD上一点，将△ABE沿直线BE折叠，点A落在梯形对角线BD上的G处，EG的延长线交直线BC于点F．（1）点E可以是AD的中点吗？为什么？（2）求证：△ABG∽△BFE；（3）设AD=a，AB=b，BC=c①当四边形EFCD为平行四边形时，求a，b，c应满足的关系；②在①的条件下，当b=2时，a的值是唯一的，求∠C的度数．13. （2012江西南昌12分）已知，纸片⊙O的半径为2，如图1，沿弦AB折叠操作．（1）①折叠后的 AB所在圆的圆心为O′时，求O′A的长度；②如图2，当折叠后的 AB经过圆心为O时，求 AOB的长度；③如图3，当弦AB=2时，求圆心O到弦AB的距离；（2）在图1中，再将纸片⊙O沿弦CD折叠操作．①如图4，当AB∥CD，折叠后的 AB与 CD所在圆外切于点P时，设点O到弦AB．CD的距离之和为d，求d的值；②如图5，当AB与CD不平行，折叠后的 AB与 CD所在圆外切于点P时，设点M为AB的中点，点N为CD的中点，试探究四边形OMPN的形状，并证明你的结论．14. （2012湖南益阳10分）已知：如图，抛物线y=a （x ﹣1）2+c 与x 轴交于点A ()10和点B ，将抛物线沿x 轴向上翻折，顶点P 落在点P'（1，3）处． （1）求原抛物线的解析式；（2）学校举行班徽设计比赛，九年级5班的小明在解答此题时顿生灵感：过点P'作x 轴的平行线交抛物线于C 、D 两点，将翻折后得到的新图象在直线CD 以上的部分去掉，设计成一个“W”型的班徽，“5”的拼音开头字母为W ，“W”图案似大鹏展翅，寓意深远；而且小明通过计算惊奇的发现这个“W”图案的高与宽（CD （约等于0.618）．请你计算这个“W”图案的高与宽的比到底是多少？（参考数据：2.236 2.449≈≈，结果可保留根号）15. （2012江苏南通14分）如图，经过点A(0，－4)的抛物线y ＝ 1 2x 2＋bx ＋c 与x 轴相交于点B(－0，0)和C ，O 为坐标原点．(1)求抛物线的解析式；(2)将抛物线y ＝ 1 2x 2＋bx ＋c 向上平移 72个单位长度、再向左平移m(m ＞0)个单位长度，得到新抛物线．若新抛物线的顶点P 在△ABC 内，求m 的取值范围； (3)设点M 在y 轴上，∠OMB＋∠OAB＝∠ACB，求AM 的长．16. （2012江苏淮安12分）如图，矩形OABC在平面直角坐标系中，O为坐标原点，点A （0，4），C（2，0），将矩形OABC绕点O按顺时针方向旋转1350，得到矩形EFGH（点E与O 重合）.（1）若GH交y轴于点M，则∠FOM＝，OM=（2）矩形EFGH沿y轴向上平移t个单位。

北京市西城区2012年初三一模错题汇总、单项选择题2 •图1所示的四种现象中，属于光的反射现象的是8 •关于电流、电压和电阻的关系，下列说法正确的是A •导体的电阻与电压成正比，与电流成反比B. 导体的电阻越大，这段导体两端的电压就越高C. 通过导体的电流越大，这段导体的电阻就越小D. 导体两端的电压越高，通过这段导体的电流就越大10 .将两个定值电阻串联接到电压为U的电源两端，R i消耗的功率为P i, R2消耗的功率为3P1。

将这两个定值电阻并联接在同一电源两端时，下列说法中正确的是A. 串联时R1与R?两端的电压之比为3 : 1 B•并联时R1消耗的功率为16P1C.并联时通过R1与R2的电流之比为1 : 3 D •并联时两电阻消耗的总功率为16 P1311 •将物体甲放在水平桌面上匀速向右推动时，所用水平推力为F1，地面对物体甲的摩擦力为右。

现将物体乙叠放在物体甲上，如图5所示，用水平拉力F2使物体甲向右匀速移动过程中，物体乙被左边墙上固定的细绳拉住且保持静止，地面对物体甲的摩擦力为f2物体乙对物体甲的摩擦力为f3,细绳对物体乙的水平拉力为T。

下列判断正确的是A • f1> F1, f1的方向水平向左B. f2>F1, f2的方向水平向左C. f2= F2, f2 和F 2是- -对平衡力D. f3= T, f3和T是一对相互作用力12 .有A、B两个密度分别为P A、P的实心正方体，它们所受的重力分别为G A和G B,它们的边长之比为2 : 1。

将它们如图6所示叠放在水平桌面上时，A对B的压强与B对桌面的压强之比为6 : 7。

水平桌面上有甲、乙两个圆柱形容器，将物体A和B分别放入甲、乙两容器的液体中，物体A漂浮，有1/4的体积露出水面。

液体静止时，物体A、B所受浮力分别为F A和F B。

已知酒精密度是水密度的0.8倍。

下列判断正确的是露珠下叶脉看起来变粗平面镜中形成小狗的像景物逆光形成“剪影”筷子好像在水面“折断”DA.F A :F B= 15:2,P A<PB.p A :p = 3:4,F A< F BC.G A::G B= 1:6,P A< P BD.F A :F B= 5 :2,G A>G B图5二、多项选择题（下列各小题均有四个选项，其中符合题意的选项均多于一个。