广东省职业高中历年数学考试试题

2020年广东省普通高等学校招收中等职业学校毕业生统一考试数 学本试卷共4页，满分150分。

考试时间120分钟 注意事项：一、选择题：本大题共15小题，每小题5分，满分75分，在每小题给出的4个选项中，只有一项是符合题目要求的。

1. 已知集合M={x|1<x<5}，N={-2<x<2}，则M ∩N=( ) A ．{x|-2<x<1} B. {x|-2<x<2} C. {x|-2<x<5} D. {x|1<x<2}2. 函数f(x)=log 2(3x −2)的定义域是( ) A. [ 23,+∞) B. ( 23,+∞)C. [2,+∞)D. (2,+∞)3. 已知函数f(x)=2x-1(x ∈R )的反函数是g(x)，则g(-3)=( ) A. -9 B. -1 C. 1 D. 94. 不等式x 2-x-6<0的解集是（ ）A. {x|-3<x<2}B. {x|x<-3或x>2}C. {x|-2<x<3}D. {x|x<-2或x>3}5. 已知角α的顶点与原点重合，始边与x 轴的非负半轴重合，终边经过点(-3,4)，则sin α=( ) A. -45B. -35C. 35D. 456. 已知向量a =(1，x)，向量b =(2，4)，若a ∥b ，则x=( ) A. -2 B. -12C. 12D. 27. “-2<x<1”是“2x<2”的( )A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 非充分非必要条件8. 双曲线x217−y28的右焦点坐标为( )A. (-5,0)B. (-3,0)C. (3,0)D. (5,0)9. 在平面直角坐标系xOy中，点(3, 2)到直线x-2y+2=0的距离为( )A. √55B. 2√55C. 3√55D. 4√5510. 某同学军训时第一次和第二次的打靶成绩（单位：环）分别为8，8，9，8，7和7，8，9，9，7，对这两次成绩的稳定性进行评判，其结论是( )A. 第一次比第二次稳定B. 第二次比第一次稳定C. 两次的稳定性相同D. 无法判断11. 抛物线y2=4x的准线方程为( )A. x=-1B. x=1C. y=-1D. y=112. 已知数列{a n}为递增的等数列,a1=2，若a1、a2、a4成等比数列，则数列{a n}的公差为( )A. 0B. 1C. 2D. 313. 已知tanα=3, 则sinα−cosαsinα+cosα= ( )A. 25B. 12C. 35D. 3414. 掷两枚质地均匀骰子，则向上的点数之和为5的概率为( ) A.118 B.112C. 19 D. 1615. 已知f(x)是定义在R 上的偶函数，且在[0,+∞)内单调递减，则满足f(x-1)>f(3)的x 的取值范围为( )A. (−12 ,14) B. (-2,4)C. (−∞,−12)∪(14,+∞) D. (−∞,−2)∪(4,+∞)二、填空题：本大题共5小题，每小题5分，满分25分。

广东职高高考数学练习题一、选择题（每题3分，共30分）1. 下列函数中，哪一个是奇函数？A. y = x^2B. y = |x|C. y = x^3D. y = sin(x)2. 已知函数f(x) = 2x - 1，求f(-1)的值。

A. 1B. -3C. -1D. 33. 计算下列极限：\[\lim_{x \to 0} \frac{\sin(x)}{x}\]A. 0B. 1C. 2D. ∞4. 以下哪个不等式是正确的？A. 2 < π < 3B. π < 3 < 4C. 3 < π < 4D. 4 < π < 55. 求下列二项式展开式中x^2的系数：\[(1 + x)^4\]A. 4B. 6C. 4D. 106. 已知向量a = (3, -1)和向量b = (1, 2)，求向量a和向量b的点积。

A. 5B. -1C. 1D. -57. 计算下列定积分：\[\int_0^1 x^2 dx\]A. 1/3B. 1/2C. 1D. 28. 已知圆的方程为x^2 + y^2 = 1，求圆心到直线y = x的距离。

A. √2/2B. 1C. √2D. 09. 计算下列三角函数值：\[\cos(\frac{\pi}{6})\]A. √3/2B. 1/2C. √2/2D. 110. 已知等比数列{an}的首项a1 = 2，公比q = 2，求第5项a5的值。

A. 16B. 32C. 64D. 128二、填空题（每题4分，共20分）11. 已知等差数列{bn}的首项b1 = 3，公差d = 2，求第10项b10的值。

12. 计算下列函数的导数：\[f(x) = x^2 - 4x + 3\]13. 已知双曲线方程为x^2/a^2 - y^2/b^2 = 1，求其渐近线方程。

14. 计算下列函数的不定积分：\[\int (2x + 1) dx\]15. 已知抛物线方程为y^2 = 4x，求其焦点坐标。

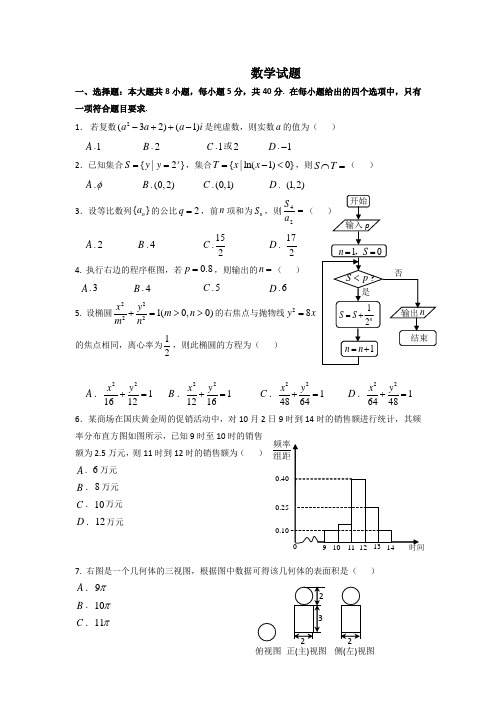
数学试题一、选择题：本大题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，只有一项符合题目要求.1． 若复数2(32)(1)a a a i -++-是纯虚数，则实数a 的值为（ ）A .1B .2C .1或2D .1-2．已知集合{|2}xS y y ==，集合{|ln(1)0}T x x =-<，则S T ⋂=（ ） A .φ B .(0,2)C .(0,1)D . (1,2)3．设等比数列{}n a 的公比2q =，前n 项和为n S ，则=24a S（A .2B .4C .152D .1724. 执行右边的程序框图，若0.8p =，则输出的n =（ ）A .3B .4C .5D .65. 设椭圆22221(0,0)x y m n m n+=>>的右焦点与抛物线28y x =的焦点相同，离心率为12，则此椭圆的方程为（ ）A ．2211612x y += B ．2211216x y += C ．2214864x y += D ．2216448x y +=6．某商场在国庆黄金周的促销活动中，对10月2日9时到14时的销售额进行统计，其频率分布直方图如图所示，已知9时至10时的销售额为2.5万元，则11时到12时的销售额为（ ）A . 6万元B ．8万元C ．10万元D ．12万元7. 右图是一个几何体的三视图，根据图中数据可得该几何体的表面积是（ ）A ．9πB ．10πC ．11π俯视图 正(主)视图 侧(左)视图FADBCD ．12π8．已知函数3()),f x x x =-则对于任意实数,(0)a b a b +≠, 则()()f a f b a b++的值为（ ）A ．恒正 B.恒等于0 C ．恒负 D. 不确定二、填空题（本大题共7小题，分为必做题和选做题两部分．每小题5分，满分30分） （一）必做题：第9至13题为必做题，每道试题考生都必须作答．9．设随机变量ξ服从正态分布(3,4)N ，若(23)(2)P a P a ξξ<-=>+，则a 的值为 ．10. 已知向量(0,1,1)a =-，(4,1,0)b =，||29a b λ+=且0λ>，则λ= ．11. 某班级要从4名男生、2名女生中选派4人参加社区服务，如果要求至少有1名女生，那么不同的选派方案种数为 ．（用数字作答）12. 若0,0a b ≥≥，且当001x y x y ≥⎧⎪≥⎨⎪+≤⎩，，时，恒有1ax by +≤，则以a ,b 为坐标点(,)P a b 所形成的平面区域的面积等于 ．13. 对于*n N ∈，将n 表示为1101102222k k k k n a a a a --=⨯+⨯+⋅⋅⋅+⨯+⨯，当i k =时，1i a =；当01i k ≤≤-时，i a 为0或1. 定义n b 如下：在n 的上述表示中，当012,,,,ka a a a ⋅⋅⋅中等于1的个数为奇数时，1nb =；否则0n b =.则3456b b b b +++= ． （二）选做题：第14、15题为选做题，考生只选做其中一题，两题全答的，只计前一题的得分。

2023广东省高等职业院校招收中等职业学校毕业生考试试卷数学试题本试卷共24小题，满分150分。

考试用时120分钟。

注意事项：1．答卷前，考生务必用黑色字迹旳钢笔将自己旳姓名和考生号、试室号、座位号填写在答题卡上。

用2B铅笔将试卷类型填涂在答题卡对应位置上。

将条形码横贴在答题上右上角“条形码粘贴处”。

2．选择题每题选出答案后，用2B铅笔把答题卡上对应题目选项旳答案信息点涂黑；如需改动，用橡皮擦洁净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹旳钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内对应位置上；如需改动，先画掉本来旳答案，然后再写上新旳答案；不准使用铅笔和涂改液。

不按以上规定作答旳答案无效。

4．考生必须保持答题卡旳整洁。

考试结束后，将试卷和答题卡一并交回。

一、选择题：本大题共15小题，每题5分，满分75分。

在每题给出旳四个选项中，只有一项是符合题目规定旳。

1.若集合A={2,3,a} ，B={1,4} ，且A∩B={4}，则a=A. 1B. 2C. 3D. 42.函数y=√2x+3旳定义域是,+∞）A. （-∞，+∞）B. [-32］ D. （0, +∞）C. （-∞，- -323.设a，b为实数，则“b=3”是“a（b-3）=0”旳A. 充足非必要条件B. 必要非充足条件C. 充足必要条件D. 非充足非必要条件4.不等式x2−5x−6≤0旳解集是A. {x|−2≤x≤3}B. {x|−1≤x≤6}C. {x|−6≤x≤1}D. {x|x≤−1或x≥6}5. 下列函数在其定义域内单调递增旳是 A. y= x 2B. y=（13）xC. y= 3x2x D. y= - log 3x6. 函数y=cos （π2−x ）在区间[π3，56π]上旳最大值是A. 12B. √22C. √32D. 17. 设向量a =（-3,1），b =（0,5），则|a -b |= A. 1 B. 3 C. 4 D. 58. 在等比数列{a n }中，已知a 3=7，a 6=56，则该等比数列旳通项公式是A. 2B. 3C. 4D. 89. 函数y=（sin 2x −cos 2x ）2旳最小正周期是 A. π2 B. πC. 2πD. 4π10. 已知f （x ）为偶函数，且y=f （x ）旳图像通过点（2，-5），则下列等式恒成立旳是A. f （-5）=2B. f （-5）=-2C. f （-2）=5D. f （-2）=-511. 抛物线x 2=4y 的准线方程是 A. y= -1 B. y=1 C. x= -1 D. X=112. 设三点A （1,2），B （-1,3）和C （x-1，5），若AB ⃗⃗⃗⃗⃗ 与BC ⃗⃗⃗⃗⃗⃗ 共线，则x = A. – 4 B. – 1 C. 1 D. 413. 已知直线l 旳倾斜角为 π4 ，在y 轴上旳截距为2，则l 旳方程是A. y +x -2=0B. y +x +2=0C. y -x -2=0D. y -x +2=014. 若样本数据3，2，x ，5旳均值为3，则改样本旳方差是A. 1B. 1.5C. 2.5D. 615. 同步抛三枚硬币，恰有两枚硬币正面朝上旳概率是 A. 18B. 14C. 38D. 58二、 填空题：本大题共5小题，每题5分，满分25分。

2018 年广东省普通高校高职考试数学试题一、 选择题（共15 小题，每题 5 分，共 75 分）1、（2018）已知集合 A 0,12,4,5， ， B 0,2 ，则 A I B （）A. 1B. 0,2C.3,4,5D.0,1,22.（2018）函数 f x3 4 x 的定义域是（）A 、 3,B 、 4,C 、,3D 、,4434 33.（2018）下列等式正确的是（）A 、 lg5 lg3lg 2B 、 lg5lg3lg8C 、 lg 5lg101 lg 5D 、 lg = 21004．（ 2018）指数函数 y a x 0a 1 的图像大致是（ ）AB C D5.（2018）“ x3 ”是 “ x 2 9 ”的（）A 、必要非充分条件B 、充分非必要条件C 、充分必要条件D 、非充分非必要条件6.（2018）抛物线 y 24x 的准线方程是（）A 、 x1B 、 x 1C 、 y 1D 、 y17. （ 2018）已知 ABC ， BC3, AC6, C90 ，则（ ）A 、 sin A2 B 、coA=62D 、 cos( A B)12C 、 tan A311 1 1L1（）8.（2018） 12223 24 2n 12A 、 2 ( 12 n ) B 、 2 ( 121 n )C 、 2 ( 12n 1 )D 、 2 ( 12n )uuuruuur 3,4uuur9.（2018）若向量 AB 1,2 , AC，则 BC （）A 、 4,6B 、 2, 2C 、 1,3D 、 2,210.（2018）现有 3000 棵树，其中 400 棵松树，现在提取 150 做样本，其中抽取松树 做样本的有（ ）棵A 、15B 、 20C 、25D 、 30 11.（2018） f xx3 , x 0，则 ff 2（）x 21, x 0A 、1B 、0C 、 1D 、 212. （2018）一个硬币抛两次，至少一次是正面的概率是（）A 、1B 、1C 、2D 、3323 413.（2018）已知点 A 1,4 , B 5,2 ，则 AB 的垂直平分线是（）A 、 3x y 3B 、 3xy 9 0C 、 3x y 100 D 、 3x y 8 0 14.（2018）已知数列 a n 为等比数列，前 n 项和 S n3n 1a ，则 a（）A 、 6B 、 3C 、0D 、315.（2018）设 f x 是定义在 R 上的奇函数，且对于任意实数 x ，有 fx 4f x ，若 f 1 3 ，则 f 4f 5（ ）A 、 3B 、3C 、 4D 、6二、二、填空题（共 5 小题，每题 5 分，共25 分）16、（2018）双曲线x2y21的离心率 e；432r r r r r17、（2018）已知向量 a，，，若 a b ，则 b；4 3 , b x 418、（2018）已知数据10, x,11, y,12, z的平均数为8，则 x, y, z 的平均数为；19、（2018）以两直线x y0 和 2x y 3 0 的交点为圆心，且与直线 2x y 2 0相切的圆的标准方程是；20 已知ABC对应边分别为的内角A B，C的对边分别为a, b, c ，已知 3b 4a, B 2 A，，则 cosA；三、解答题（ 50 分）21、（ 2018）矩形周长为10，面积为 A ，一边长为x。

图（1）侧视图正视图俯视图数学试题一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 在复平面内，复数(1)i i -对应的点位于A.第一象限B. 第二象限C.第三象限D. 第四象限 2. 已知集合{|lg(3)},{|2}A x y x B x x ==+=≥，则下列结论正确的是 A.3A -∈ B.3B ∉ C. AB B = D. A B B =3.“φπ=”是“函数sin(2)y x φ=+为奇函数的”A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件 4. 向量(1,2),(3,4),BA BC =-=则AC = .A.(4,2)B.(4,2)--C.(2,6)D.(4,2)-5. 若双曲线22221x y a b-=，则其渐近线的斜率为--.-A.2±B. C.12±D. 2±6. 已知约束条件1400x x y kx y ≥⎧⎪+-≤⎨⎪-≤⎩表示面积为1的直角三角形区域，则实数k 的值为A.1B. 1-C.0D.2- 7. 图（1）中的网格纸是边长为1的小正方形，在其上用粗线画 出了某多面体的三视图，则该多面体的体积为 A.4 B.8 C.16 D.20 8. 已知24()2,()f x x px q g x x x=++=+是定义在集合 5{|1}2M x x =≤≤上的两个函数．对任意的x M ∈,存在常数0x M ∈，使得0()()f x f x ≥，0()()g x g x ≥，且00()()f x g x =．则函数()f x 在集合M 上的最大值为A.92 B.4 C. 6 D. 892二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分． （一）必做题（9－13题）9. 10(1)x -的展开式中2x 的系数是 ．（用数字作答）10. 若命题：“对2,10x R kx kx ∀∈--<”是真命题，则k 的取值范围是 ．11. 设函数,0()0x x f x x x⎧≥⎪=⎨<-⎪⎩，若()(1)2f a f +-=，则实数a = ．12. 图（2）是甲、乙两人在5次综合测评中成绩的茎叶图，其中一个 数字被污损；则甲的平均成绩超过乙的平均成绩的概率为 ．131213141513+++++=．可得131415161+++++= ；进而还可以算出141516171+++++、151617181+++++的值，并可归纳猜11(1)1(2)1(3)1n n n n ++++++++= ．（*n N ∈）（二）选做题（14—15题，考生只能从中选做一题）14．（坐标系与参数方程选做题）在极坐标中，已知点P 为方程()cos sin 2ρθθ-=所表示的曲线上一动点，4,3Q π⎛⎫⎪⎝⎭，则PQ 的最小值为 ． 15．（几何证明选讲选做题）如图（3），已知AB 是圆O 的直径，C 是AB 延长线上一点，CD 切圆O 于D ，CD=4，AB=3BC ， 则圆O 的半径长是 ．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本小题满分12分）设数列{}n a 是公比为正数的等比数列，12a =，3212a a -=． （1）求数列{}n a 的通项公式；.--.-（2）若数列{}n b 满足：333log ()log 2nn n b a =+，求数列{}n n a b +的前n 项和n S ．17．（本小题满分12分）图（6）yxBOEFD图（4）六级五级四级三级二级一级空气质量级别2天数64810根据空气质量指数AQI （为整数）的不同，可将空气质量分级如下表:某市2013年10月1日—10月30日，对空气质量指数进行监测,获得数据后得到如图（4）的条形图:（1）估计该城市本月(按30天计)空气质量类别为中度污染的概率；（2）在上述30个监测数据中任取2个,设ξ为空气 质量类别颜色为紫色的天数,求ξ的分布列. 18. （本小题满分14分） 在△ABC 中，角A 、B 、C 所对应的边为c b a ,, （1）若cos()2cos ,3A A π-= 求A 的值；--.-（2）若1cos ,3A =且△ABC 的面积22S c =，求C sin 的值. 19．（本小题满分14分）如图（5），已知,,A B C 为不在同一直线上的三点，且111////AA BB CC ，111AA BB CC ==.(1)求证:平面ABC //平面111A B C ；(2)若1AA ⊥平面ABC ，且14AC AA ==,3,5BC AB ==, 求证：A 1C 丄平面AB 1C 1(3)在（2）的条件下，求二面角C 1-AB 1 -C 的余弦值.20.（本小题满分14分）如图（6），已知(,0)F c 是椭圆2222:1(0)x yC a b a b+=>>的右焦点； 222:()F x c y a -+=与x 轴交于,D E 两点，其中E 是椭圆C 的左焦点.(1)求椭圆C 的离心率； (2)设F 与y 轴的正半轴的交点为B ，点A 是点D 关于y 轴的对称点，试判断直线AB 与F 的位置关系；AQI （数值）050 51100 101150 151200 201300 300>空气质量级别 一级 二级 三级 四级 五级 六级 空气质量类别优 良 轻度污染 中度污染 重度污染 严重污染空气质量类别颜色 绿色 黄色 橙色 红色 紫色 褐红色(3)设直线AB 与椭圆C 交于另一点G ，若BGD ∆的面积为13c ，求椭圆C 的标准方程. 21．（本小题满分14分）已知0x >，函数()ln 1axf x x x =-+（1）当0a ≥时，讨论函数()f x 的单调性；（2）当()f x 有两个极值点（设为1x 和2x ）时，求证：121()()[()1]x f x f x f x x x++≥⋅-+．参考答案一．选择题CDAA BACC解析：8.依题意知，两个函数的图象有共同的最低点，由4()4g x x x =+≥=，当且仅当2x =“=”成立，故两函数图象的最低点为（2,4），由此得8,12p q =-=，所以2()2812f x x x =-+，()f x 在集合M 上的最大值为(1)6f =，选C.二．填空题：9.45；10.40k -<≤ ；11.1± 12.45；13.4、1n +；14.;15. 3. 解析：12.设被污损的数字为x （x N ∈），则由甲的平均成绩超过乙的平均成绩得，88899291908383879990x ++++>+++++，解得08x ≤<，即当x 取0,1，……，7时符合题意，故所求的概率84105P ==.13. +=x 3,=解得4x =，+=5，……，由此可猜测+=1n +.三.解答题：16.解：（1）设数列{}n a 的公比为q ，由12a =，3212a a -=，得222120q q --=，即260q q --=．-------------------------------------------------------------3分解得3q =或2q =-，--------------------------------------------------------------------------------------5分∵0q >∴2q =-不合舍去，∴123n n a -=⨯；---------------------------------------------------------6分（2）由333log ()log 2nn n b a =+得n b =121333log (23)log 3212n n n n --⨯⨯==-，----------------------------------------------------------8分∴数列{}n b 是首项11,b =公差2d =的等差数列，-----------------------------------------------------9分∴n S 1212()()n n a a a b b b =+++++++2(31)(121)312n n n -+-=+-231n n =-+．-----------------------------------------------------------12分17.解：（1）由条形统计图可知,空气质量类别为中度污染的天数为6, ---------------------------1分所以该城市本月空气质量类别为中度污染的概率 61305P ==.------------------------------------4分（2）随机变量ξ的可能取值为0,1,2,----------------------------------------------------------------------5分则()22623065087C P C ξ===,--------------------------------------------------------------------------------7分()114262301041435C C P C ξ===,--------------------------------------------------------------------------------9分 ()2423022145C P C ξ===-----------------------------------------------------------------------------------11分 所以ξ的分布列为:--------------------------------------------------------------------------------------------------------------------12分18.解：（1）由cos()2cos ,3A A π-=得cos cos sin sin 2cos ,33A A A ππ+=-------------------------------------------------------------------2分1cos sin 2cos ,22A A A ∴+= 3cos A A =,-----------------------------------------------4分∴tan A =6分 ∵0A π<< ∴3A π=；-----------------------------------------------------------------------------------7分（2）解法1：1cos ,A = ∴02A π<<∴sin A ==-----------------------------------------------------------------------------8分由21sin 23S bc A ===得3b c =，------------------------------------------------------10分由余弦定理得：22222222cos 928a b c bc A c c c c =+-=+-=，∴a =-----------12分由正弦定理得：sin sin a cA C=，即sin sin c A C = 1sin3C ∴==.------------------------------------------------------.----------------------------14分 【解法2：1cos ,3A = ∴02A π<<∴sin A ==-------------------------------------.----------------------8分由21sin 23S bc A ===得3b c =，------------------------------------------------------10分由余弦定理得：22222222cos 928a b c bc A c c c c =+-=+-=，∴a =-----------12分∵22222289a c c c c b +=+==，∴△ABC 是Rt △，角B 为直角，------------------------------13分1sin 3c C b ∴==．--------------------------------------------------------------------------------------------14分】【:解法3：1cos ,3A = ∴02A π<<∴sin ,3A ==------------------------------------------------------------------------------8分由21sin 23S bc A ===得3b c =，----------------------------------------------------------10分由余弦定理得：22222222cos 928a b c bc A c c c c =+-=+-=，∴a =----------------12分又21sin 2S ab C ==，得213sin 2c C ⋅⋅⋅=，∴1sin 3C =.-----------------------14分】【解法4：1cos ,3A = ∴02A π<<∴sin A ==-----------------------------------------------------------------------------8分由21sin 2S bc A ===得3b c =，------------------------------------------------------10分由正弦定理得：sin sin b cB C=，则3sin sin sin[()]C B A C π==-+sin()A C =+，--11分3sin sin()sin cos cos sin C A C A C A C =+=+,13sin sin 3C C C =+,整理得cos C C =,代入22sin cos 1C C +=,得21sin 9C =，-------------------------13分由c b <知02C π<<,1sin 3C ∴=．------------------------------------------------------------------------------------------------14分】 19.解：（1）证明：∵11//AA CC 且11AA CC = ∴四边形11ACC A 是平行四边形，-------------------------------------------------------------------------------------------1分 ∴//AC 11A C ,∵AC ⊄面111A B C ，11A C ⊂面111A B C ∴//AC 平面111A B C ，--------------------------------------------------------------------------------------------------------3分z yxA B CA 1B 1C 1同理可得//BC 平面111A B C ,又AC CB C =,∴平面ABC //平面111A B C ----------------------------------------------------------------------------------------------------4分(2)证法1： ∵1AA ⊥平面ABC ，1AA ⊂平面11ACC A ∴平面11ACC A ⊥平面ABC ，---------------------5分平面11ACC A 平面ABC =AC ，∵4AC=,3BC =,5AB = ∴222AC BC AB += ∴BC AC ⊥ --------------------------6分∴BC⊥平面11ACC A ,---------------------------------------------------------------------------------------7分∴1BCA C ⊥，∵11//BCBC ∴111B C AC ⊥ 又1AA AC ⊥,1AC AA =得11ACC A 为正方形，∴11A C AC ⊥-----------------------------------8分又1111AC B C C =,∴A 1C 丄平面AB 1C 1--------------------------------------------------------------------------------------------9分【证法2：∵4AC =,3BC =,5AB = ∴222AC BC AB += ∴BC AC ⊥，---------------5分∵1AA ⊥平面ABC ，11//AA CC ∴1CC ⊥平面ABC ----------------------------------------------6分以点C 为原点，分别以AC 、CB 、CC 1所在的直线为x 、y 、z 轴建立空间 直角坐标系如图示，由已知可1(4,0,0),(0,3,0),(0,0,0),(4,0,4)A B C A ,11(0,3,4),(0,0,4)B C ,则11(4,0,4),(4,0,4)AC C A =--=-,11(0,3,0)C B =------------------7分 ∵111110,0,AC C A AC C B ⋅=⋅= ∴11111,AC C A AC C B ⊥⊥ ---------8分 又1111,C A C B C =∴1A C ⊥平面11AB C .----------------------------------------------------------9分】(3)由（2）得1(4,0,0),(0,3,4)CA CB ==,------------------------------------------------------------10分设平面1AB C 的法向量(,,)n x y z =，则由1,CB n CA n ⊥⊥得34040y z x +=⎧⎨=⎩，------------------------------------------------------------------------------------11112,||||20n AC AC n AC ⋅>==---------------------------------------------------------------------14分20.解：(1)∵圆过椭圆的左焦点，把代入圆F 的方程，得224c a =，故椭圆C 的离心率12c e a ==；--------------------------------------------------------------3分(2) 在方程222()x c y a -+=中令0x =得2222y a c b =-=，可知点B 为椭圆的上顶点， 由(1)知，12c a =，故2,a c b ===，故B )，--------------------------4分在圆F 的方程中令y=0可得点D 坐标为(3,0)c ，则点A 为(3,0)c -，--------------------------5分于是可得直线AB的斜率AB k ==，----------------------------------------------------------6分而直线FB的斜率FB k ==，------------------------------------------------------------------7分∵1AB FD k k ⋅=-, ∴直线AB 与F 相切。

2019年广东省高等职业院校招收中等职业学校毕业生考试数 学班级 学号 姓名本试卷共4页，24小题，满分150分，考试用时120分钟一、选择题：(本大题共15小题，每小题5分，满分75分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1．已知集合{}{}0,2,1,0,1<=-=x x B A ，则A B =I （ ）A 、 {}2,1B 、 {}1-C 、{}1,1-D 、 {}0,1,22.函数)2lg(+=x y 的定义域是 （ ）A 、),2(+∞-B 、),2[+∞-C 、)2,(--∞D 、]2,(--∞3.不等式0)5)(1(>-+x x 的解集是 （ ）A 、]5,1(-B 、)5,1(-C 、[)+∞--∞,5]1,(YD 、),5(]1,(+∞--∞Y4．已知函数R x x f y ∈=是)(上的增函数，则下列关系正确的是 （ ） A 、)3()2(f f >- B 、)3()2(f f < C 、 )3()2(-<-f f D 、)0()1(f f >-5.某职业学习有两个班，一班有30人，二班有35人，从两个班选一个去参加技能大赛，则不同的选择方案有 （ ） A 、30 B 、35 C 、65 D 、10506.”“1>a 是 ”“1->a 的 （ ） A 、必要非充分条件 B 、充分非必要条件 C 、充分必要条件 D 、即非充分非必要条件7.已知向量,),1,3(),3,(b a b x a ρρρρ⊥=-=若则=x （ ）A 、9-B 、1-C 、1D 、98..双曲线1162522=-y x 的焦点坐标是（ ）A 、)0,3(),0,3(-B 、)0,41(),0,41(-C 、)3,0(),3,0(-D 、)41,0(),41,0(- 9.袋中有2个红球，2个白球，红球和白球除颜色外，外形，质量完全相同，现取出球，取得全是红球的概率是（ ）A 、61 B 、21 C 、31 D 、3210.若)(,13)(2R b bx x x f ∈-+=是偶函数，则)1(-f =（ ）A 、4B 、4-C 、2D 、2-11.若等差数列{}n a 的前n 项和)(2R a a n S n ∈+=，则=a （ ）A 、2B 、0C 、1-D 、2 12.已知=+∈=)cos(),,2(,21sin απππαα则（ ）A 、23-B 、21-C 、23D 、21 13.已知函数⎩⎨⎧≤>=0,100,lg )(13x x x x f x，若t f =)101(，则=)(t f （ ）A 、1B 、101 C 、1- D 、114.抛物线x y 42=上一点P 到其焦点F 的距离为3，则点P 到y 轴的距离（ ）A 、1B 、2C 、3D 、415.直线1C 的方程为033=--y x ，直线2C 的倾斜角是直线1C 的2的倍，且2C 经过坐标原点O ，则直线2C 的方程为（ ）A 、032=-y xB 、032=+y xC 、03=-y xD 、03=+y x二、填空题：(本大题共5个小题，每小题5分，满分25分。

2023广东高职高考数学试卷全文共四篇示例，供读者参考第一篇示例：2023年广东高职高考数学试卷一、选择题（共10小题，每小题2分，共20分）1. 下列各组数中，哪一组数中既有有理数又有无理数？A. 2，-3B. 1.5，3C. 3，√2D. 0.5，12. 若a+b=2，a-b=6，则a的值是A. -2B. 2C. 4D. 14. 在矩形ABCD中，AB=4，BC=3，若CD=√13，则AD的长度为A. 2B. 3C. 4D. 55. 已知正比例函数y=kx中，当x=3时y=9，则k=A. 1B. 3C. 4D. 27. 若函数y=ax²+bx+c的图像与x轴有两个交点，则A. a=0B. b=0C. c=0D. a,b,c都不能为08. 若a为正数，且对任意的实数x都有f(x)=ax²+2x+1≥0，则a 的取值范围是A. a≥1B. a<1C. a>0D. a≥09. 直角三角形斜边长为10，一个锐角为30°，则直角边长为A. 5B. 10√3C. 5√3D. 1011. 一次方程3x-5=7的解为_________12. 根号2的整数部分为_________13. 等差数列{an}的公差d=2，且a1=1，a4=7，则a7=_________14. 若正整数a、b满足a=2b，则a和b的最大公因数为_________15. 若三角形的三个内角分别为（2x-10)°、(3x-20)°、(4x-30)°，则x的取值范围为_________三、解答题（共4小题，共45分）16. 已知函数y=ax²+bx+c的图像过点(2,3)，(3,0)，(4,-1)，求a，b，c的值17. 若正比例函数y=kx中，当x=1时，y=3；当x=2时，y=6。

求k的值。

18. 已知△ABC中，AB=5，AC=3，BC=4，过点B作高BD，求BD的长度。

试卷类型：A2021年广东省高等职业院校招收中等职业学校毕业生考试数学本试卷共4页，24小题，总分值150分。

考试用时120分钟。

考前须知：1．答卷前，考生务必用黑色字迹钢笔或签字笔将自己姓名与考生号、试室号、座位号填写在答题卡上。

用2B铅笔将试卷类型(A)填涂在答题卡相应位置上。

将条形码横贴在答题卡右上角“条形码粘贴处〞。

2．选择题每题选出答案后，用2B铅笔把答题卡上对应题目选项答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上;如需改动，先划掉原来答案，然后再写上新答案;不准使用铅笔与涂改液。

不按以上要求作答答案无效。

4．考生必须保持答题卡整洁。

考试完毕后，将试卷与答题卡一并交回。

一、选择题：本大题共15小题，每题5分，总分值75分. 在每题给出四个选项中，只有一项为哪一项符合题目要求.1．设集合M＝｛2，3，4｝，N＝｛2，4，5｝，那么NM =A．｛2，3，4，5｝ B．｛2，4｝ C．｛3｝D．｛5｝2．a为实数，且a，2a，4成等比数列，那么a＝4A．0 B．2 C．1 D．3 3．函数是实数）(),0+=图像过点(1,7)与(0,4)，那么>(≠f x,1a且bxabaf解析式是(x)A．2xf D．5(+)=xfx3=x(+)24=x(+)5xf B．3x=x(+)f C．44．以下向量中与向量)3,2(-=a 平行是A ．〔-4，6〕B ．〔4，6〕C ．〔-3，2〕D ．〔3，2〕 5．函数)1lg()(2x x x f +=是A ．奇函数B ．既是奇函数又是偶函数C ．偶函数D ．既不是奇函数也不是偶函数 6．集合}032|{≥-+=xx x A ，那么A ＝A ．]2,(--∞B ．),3(+∞C ．)3,2[-D ．]3,2[- 7．设函数)(x f y =在区间),0(+∞内是减函数，那么)6(sin πf a =，)4(sin πf b =，)3(sin πf c =大小关系是A ．a b c >>B ．a c b >>C ．c a b >>D ．c b a >> 8．设c b a ，，均为实数，那么“b a >〞是“c b c a +>+〞 A ．充分非必要条件 B ．必要非充分条件 C ．充分必要条件 D ．既非充分也非必要条件9．直线x y =21：，直线0122=++x y ： ，那么1 与2 A ．相交不垂直 B ．相交且垂直 C ．平行不重合 D ．重合10．双曲线191622=-y x 焦距为A ．7B ．5C ．72D ．1011．函数为实数）b bx x x f (3)(2++=图像以1=x 为对称轴，那么)(x f 最小值为 A ．1 B ．2 C ．3 D ．4 12．设πθ20≤≤，如果0sin <θ，且0cos <θ，那么θ取值范围是A ．πθπ<<2B ．πθπ≤≤2C ．23πθπ<< D ．23πθπ≤≤13．直线2-=x y 与圆422=+y x 交于两点M 与N ，O 是坐标原点，那么=⋅ON OMA ．-1B ．0C ．1D ．2 14．设n S 为等差数列｛n a ｝前n 项与，且1073=+a a ，那么=9SA ．45B ．50C ．55D ．90 15．将函数x y sin =图像按向量)1,1(=a 平移得到图像对应一个函数解析式是 A ．)1sin(1++-=x y B ．)1sin(1++=x y C ．)1sin(1-+-=x y D ．)1sin(1-+=x y 二、填空题：本大题共5小题，每题5分，总分值25分.16．某服装专卖店今年5月推出一款新服装，上市第1天售出20件，以后每天售出件数都比前一天多5件，那么上市第7天售出这款服装件数是 . 17．向量)4,3(-=a ，那么向量a 模=||a . 18．不等式)13(log )5(log 22+<-x x 解是 .19．在ABC ∆中，如果C B A ∠∠∠，，对边分别为c b a ，，，且满足等式ac b c a =-+222，那么=∠B .20．m 为实数，椭圆1322=+my x 一个焦点为抛物线x y 42=焦点，那么m＝ .三、解答题：本大题共4小题，第21～23题各12分，第24题14分，总分值50分.解答须写出文字说明、证明过程与演算步骤. 21．〔本小题总分值12分〕 设41)2sin(=+πα，且α是锐角.〔1〕求αsin ; 〔2〕求)4tan(πα+.22．〔本小题总分值12分〕小王移动 按月结算话费，月话费元）(y 与通话时间分钟）(t 关系可表示为函数⎩⎨⎧>-+≤≤=360)360(683600,68t t a t y ，，其1月份通话时间为460分钟，月话费为86元.〔1〕求a 值;〔2〕假设小王2、3月份通话时间分别为300分钟、500分钟，求其2、3月份移动 话费总与. 23．〔本小题总分值12分〕在平面直角坐标系中，动点M 到两定点)01(1，-F 与)01(2，F 距离之与为22，且点M 轨迹与直线12:+=x y 交于A 、B 两点.〔1〕求动点M 轨迹方程;〔2〕求以线段AB 为直径圆方程. 24．〔本小题总分值14分〕数列｛n a ｝满足为常数）b b a (1=，)32(2211 ，，=-=--n a a n n n.〔1〕证明：数列}2{nna是等差数列; 〔2〕求数列｛n a ｝通项公式; 〔3〕求数列｛n a ｝前n 项与n S .2021年广东省高等职业院校招收中等职业学校毕业生考试数学试题一、 选择题：本大题共15小题，每题5分，总分值75分，在每题给出四个选项中，只有一项为哪一项符合题目要求. 1. 集合}1,1{-=M ,}3,1{-=N ,那么=N M A. }1,1{- B. }3,1{- C. }1{- D. }3,1,1{-2.函数xx y -+=21定义域是A. )2,(-∞B. ),2(+∞C. ),1()1,(+∞---∞D. ),2()2,(+∞-∞ 3.不等式1|1|<-x 解集是 A. }0|{<x xB. }20|{<<x xC. }2|{>x xD. }20|{><x x x 或 4.设函数00,2,log )(3≤>⎩⎨⎧=x x x x f x,那么=)]1([f fA. 0B. 2log 3C. 1D. 25.函数182)(++=x xx f 在区间),0(,+∞内最小值是A. 5B. 7C. 9D. 116.)2,1(-P 是叫α终边上一点,那么以下等式中,正确是 A. 51sin -=α B. 52sin =αC. 52cos -=αD. 51cos =α7.以下不等式中,正确是 A. ︒<︒45sin 20sin B. ︒<︒45cos 20cos C. ︒>︒45tan 20sin D. ︒>︒45tan 20cos8.函数xx x f cos sin )(=是 A. 最小正周期为π2偶函数 B. 最小正周期为π偶函数C. 最小正周期为π2奇函数D. 最小正周期为π奇函数9.假设函数)(x f y =满足:对区间],[b a 上任意两点1x ,2x ,当21x x <时，有)()(21x f x f >，且0)()(<b f a f ，那么)(x f y =在区间],[b a 上图像只可能是10. 将向量)2,1(-=n 按向量)1,1(-=a 平移得到向量m，那么m 模=||mA. 1B. 2C. 5D. 1311. 向量),2(k a -=,向量)1,(m b =,假设a 与b 平行,那么k 与m 应满足关系 A. 02=-m k B. 02=+m k C. 02=-km D. 02=+km12. 等比数列 ,3,3,12-前n 项与=n S A. 213-nB.231n-C.43)1(1nn -+D. 43)1(1nn --13. “22>>b a 且〞是“4>+b a 〞A. 必要非充分条件B. 充分非必要条件C. 充要条件D. 非充分非必要条件14. 双曲线161022=-y x 焦点坐标是A. )0,2(),0,2(-B. )2,0(),2,,0(-C. )4,0(),4,0(-D. )0,4(),0,4(-15. 假设直线0=++k y x 与圆0222=++y y x 相切,那么=k A. 21+-或21-- B. 21+或21- C. 2-或2 D. 1-或1BCDA二、 填空题,本大题共5小题,每题5分,总分值25分16. 假设4)2)(5lg 20(lg =+x ,那么=x ___________.17. 直线1+=ax y 倾斜角为3π,那么α=_________________. 18. 设321,,a a a 成等差数列,且22=a ,令)3,2,1(2==n b n a n ,那么=⋅31b b _______.19. 设向量,向量)1,2(=n ,且7=⋅AC n ,那么=⋅BC n _______. 20. 点)2,5(A 与)4,1(-B ,那么以AB 为直径圆方程是_________________.三、 解答题,本大题共4小题,第21～ 21. (本小题总分值12分)如图,有一直角墙角,两边长度足够长,在P 点处有一水龙头(不考虑水龙头粗细),与两墙距离分别为4米与a 米(12≤a ).现在要用16米长篱笆,借助原有墙角围成一个矩形花圃ABCD ,要求水龙头围在花圃内.设x AD =米.(1) 确定花圃ABCD 面积S 与x 之间函数关系式(要求给出x 取值范围);(2) 当3=a 时,求使花圃面积最大x 值. 22. (本小题总分值12分)中心在坐标原点，焦点1F 、2F 在x 轴上椭圆C 离心率为23,抛物线y x 42=焦点是椭圆C 一个顶点.(1) 求椭圆C 方程;(2) 过焦点2F 直线l 与椭圆C 两个交点为A 与B ,且3||=AB ,求||||21BF AF +.23. (本小题总分值12分)在△ABC 中,︒=∠45A ,1010cos =B .(1) 求C cos ;(2) 假设5=BC ,求AC 长.24. (本小题总分值14分) 数列}{n a 前n 项与n n S n-=23,11++=n n n a a b .(1) 求数列}{n a 通项公式; (2) 求数列}{n b 通项公式； (3) 证明：点),2,1)(1,( =-n nS a P nn n 在同一条直线上；并求出该直线方程.2021年广东省高等职业院校招收中等职业学校毕业生考试数学试题本试卷共4页，24小题，总分值为150分.考试用时120分钟.一、选择题：本大题共15小题，每题5分，总分值75分.在每题给出四个选项中，只有一项为哪一项符合题目要求. 1.设集合{}M x x =2=，N={-3，1}，那么=N M( )A.∅B.{-3,-2,1}C. {-3,1,2}D. {-3,-2,1,2}2.以下等式中,正确是 〔 〕 A. 322327()=-- B. 322327()=⎡⎤--⎣⎦C. 202lg lg 1-=D. 52lg lg 1⋅= 3.函数y = ( )A. []11,-B. (11),- C. ()1,-∞ D. ()1,-+∞4. 设α为任意角,以下等式中,正确是 ( )A. sin()cos 2παα-= B. cos()sin 2παα-=C. sin()sin απα+=D. cos()cos απα+=5. 在等差数列}{n a 中, 假设630a =, 那么39a +a = ( )A. 20B. 40C. 60D. 806. 三点O(0,0) , A(k, -2), B(3,4), 那么OB AB,k ⊥=则 ( )A. 173- B. 83C. 7D. 117. 函数()y f x =是函数x y a =反函数，假设(8)3f =, 那么a=( )A.2B.3C.4D. 8 8. 角θ终边上一点坐标为)(0)(x x <，那么tan cos θθ⋅=( )A.9. 向量14AB (,)=-,向量31BC (,)=,那么AC =( )D. 510. 函数2()(sin 2cos 2)f x x x =-最小正周期及最大值分别是( )A. 1,πB. ,2πC. 22,π D. 2,3π11. 不等式211x ≥+解集 ( ) A. {11}x x -<≤ B. {1}x x ≤C. {1}x x>-D. {11}x x x ≤>-或12. “7x =〞是 “7x ≤〞( )A. 充分非必要条件B. 必要非充分条件C. 充分必要条件D. 既非充分也非必要条件13. 函数12log ,1sin ,01,03x x f(x)x x x x ⎧>⎪⎪=≤≤⎨⎪⎪<⎩ ,那么以下结论中,正确是( )()()A. f x ,+∞在区间1上是增函数(]()1B. f x ,∞在区间-上是增函数 C. ()12f π= D. (2)1f = 14. 一个容量为n 样本分成假设干组,假设其中一组频数与频率分别是40与0.25,那么n=( )A. 10B. 40C. 100D.16015. 垂直于x 轴直线l 交抛物线42y x =于A 、B 两点,且AB =,那么该抛物线焦点到直线l 距离是 ( )A. 1B. 2C. 3D.4二、填空题：本大题共5小题，每题5分，总分值25分.16. 在边长为2等边ABC ∆中,AB BC ⋅= .17. 设l 是过点(0,及点直线, 那么点1(2到l 距离是 . 18. 袋中装有6只乒乓球, 其中4只是白球, 2只是黄球, 先后从袋中无放回地取出两球, 那么取到两球都是白球概率是 .19. 等比数列}{n a 满足1231a a a =++,456a a a =2++-,那么}{n a 公比q= .20. 经过点(01),-及点(10),, 且圆心在直线1y x =+上圆方程是 .三.解答题：本大题共4小题，第21题12分，第22题10分，第23题、第24题各14分，总分值50分.解答须写出文字说明、证明过程与推演步骤.21.(本小题总分值12分)ABC ∆锐角三角形,a 、b 、c 是ABC ∆中A ∠、B ∠、C ∠对边,S 是ABC ∆面积,假设a=2,b=4, ,求边长c.22.(本小题总分值12分)设函数()f x 既是R 上减函数, 也是R 上奇函数, 且(1)2f =.(1) 求(1)f -值;(2) 假设2(31)2f t t -+>-, 求t 取值范围.23.(本小题总分值12分) 椭圆22221x y a b +=左、右焦点1F 、2F 为双曲线22143x y -=顶点，且倍.(1) 求椭圆方程；(2) 过1F 直线l 与椭圆两个交点为11()A x ,y 与22()B x ,y , 且123y -y =, 假设圆C 周长与2ABF ∆周长相等,求圆C 面积及2ABF ∆面积.24.(本小题总分值14分) 数列}{n a 前n 项与为n S ,且满足11a =,11()n n a S n N ++=+∈.(1) 求}{n a 通项公式；(2) 设等差数列{}n b 前n 项与为n T , 假设330T =,0n b ≥()n N +∈,且11a b +,22a b +,33a b +成等比数列, 求n T ；(3) 证明: 9()n nT n N a +≤∈.。

广东中职生数学2024年高考试卷一、选择题（每小题3分，共15分）下列计算正确的是( )A. 3a+2b=5abB. a2⋅a3=a6C. a3÷a2=aD. (a+b)2=a2+b2已知x2−2x−1=0，则x−x1的值为( )A. −2B. 2C. ±2D. 不能确定直角坐标系中，点 P(x,y) 到 x 轴的距离为2，到 y 轴的距离为3，且 y<0，则点 P 的坐标为( )A. (2,−3)B. (−2,−3)C. (3,−2)D. (−3,−2)下列命题是真命题的是( )A. 相等的角是对顶角B. 互补的角一定是邻补角C. 平行于同一条直线的两条直线互相平行D. 同位角相等下列函数中，y 随 x 的增大而减小的是( )A. y=2xB. y=x2C. y=x2D. y=−x二、填空题（每小题3分，共12分）若关于 x 的一元二次方程x2−2x−k=0有两个相等的实数根，则 k= _______．计算：9−∣−2∣+(31)−1= _______．已知一个直角三角形的两条直角边分别为 6 和8，则这个直角三角形的斜边上的高为_______．在平面直角坐标系中，将点P(2,−3)向右平移4 个单位长度后得到点 Q，则点 Q 的坐标为(，)．三、解答题（共73分）（8分）解方程组：{3x−2y=72x+3y=8（8分）已知一次函数 y=kx+b（k=0）的图象经过点 A(2,1) 和点B(−1,−2)，求这个一次函数的解析式。

（10分）在△ABC 中，∠A=90∘，AB=AC，D 是 AC 上一点，AE⊥BD 于 E，交 BC 于 F，若 BD=3，求 DF 的长。

（10分）某商店经销一种品牌的空调，其中某一型号的空调每台进价为 x 元，商店将进价提高 25% 后作为零售价进行销售，一段时间后，商店又以 9 折优惠价促销，这时该型号空调的零售价为 2700 元/台，求该型号空调每台进价 x 的值。