06立体几何 练习5-6

立体几何练习题及答案在学习立体几何的过程中，练习题对于巩固知识、提高应用能力起着至关重要的作用。

本文将为大家提供一些立体几何的练习题，并给出详细的答案解析，以帮助读者更好地理解和掌握立体几何的知识。

一、球的表面积和体积1. 某个球的半径为3cm，求其表面积和体积。

解析：球的表面积公式为S = 4πr²，体积公式为V = (4/3)πr³。

将半径r代入公式进行计算即可。

表面积：S = 4π(3)² = 4π(9) ≈ 113.04cm²体积：V = (4/3)π(3)³ = (4/3)π(27)≈ 113.04cm³因此，该球的表面积约为113.04cm²，体积约为113.04cm³。

二、立方体的表面积和体积2. 一个立方体的边长为5cm，求其表面积和体积。

解析：立方体的表面积公式为S = 6a²，体积公式为V = a³。

将边长a代入公式进行计算即可。

表面积：S = 6(5)² = 6(25) = 150cm²体积：V = (5)³ = 5(5)(5) = 125cm³因此，该立方体的表面积为150cm²，体积为125cm³。

三、圆柱的表面积和体积3. 一个圆柱的底面半径为4cm，高度为10cm，求其表面积和体积。

解析：圆柱的表面积公式为S = 2πr² + 2πrh，体积公式为V = πr²h。

将底面半径r和高度h代入公式进行计算即可。

表面积：S = 2π(4)² + 2π(4)(10) = 2π(16) + 2π(40) ≈ 321.2cm²体积：V = π(4)²(10) = π(16)(10) ≈ 502.4cm³因此，该圆柱的表面积约为321.2cm²，体积约为502.4cm³。

立几测001试一、选择题：1．a 、b 是两条异面直线，以下结论正确的选项是〔 〕A ．过不在a 、b 上的任一点，可作一个平面与a 、b 都平行B ．过不在a 、b 上的任一点，可作一条直线与a 、b 都相交C ．过不在a 、b 上的任一点，可作一条直线与a 、b 都平行D ．过a 可以且只可以作一个平面与b 平行2．空间不共线的四点，可以确定平面的个数为 ( )Ａ．0 Ｂ．1 Ｃ．1或4 Ｄ．无法确定3．在正方体1111ABCD A B C D -中，M 、N 分别为棱1AA 、1BB 的中点，则异面直线CM 和1D N 所成角的正弦值为 ( ) Ａ．19 Ｂ．23Ｃ．459 Ｄ．2594．平面α⊥平面β，m 是α的一直线，n 是β的一直线，且m n ⊥，则：①m β⊥；②n α⊥；③m β⊥或n α⊥；④m β⊥且n α⊥。

这四个结论中，不正确．．．的三个是 ( )Ａ．①②③Ｂ．①②④Ｃ．①③④Ｄ．②③④5.一个简单多面体的各个面都是三角形，它有6个顶点，则这个简单多面体的面数是( ) A. 4 B.5 C. 6 D. 86. 在北纬45°的纬度圈上有甲、乙两地，两地经度差为90°，则甲、乙两地最短距离为〔设地球半径为R 〕( )A.R π42B.R 3πC.R 2πD.3R7. 直线l ⊥平面α，直线m ⊂平面β，有以下四个命题(1)m l ⊥⇒βα//(2)m l //⇒⊥βα(3)βα⊥⇒m l //(4)βα//⇒⊥m l 其中正确的命题是( )A. (1)与(2)B. (2)与(4)C. (1)与(3)D. (3)与(4)8. 正三棱锥的侧面均为直角三角形，侧面与底面所成角为α，则以下不等式成立的是( ) A.60πα<< B.46παπ<< C.34παπ<< D.23παπ<<9．ABC ∆中，9AB =，15AC =，120BAC ∠=︒，ABC ∆所在平面α外一点P 到点A 、B 、C 的距离都是14，则P 到平面α的距离为( )Ａ．7 Ｂ．9 Ｃ．11 Ｄ．1310．在一个45︒的二面角的一个平面有一条直线与二面角的棱成角45︒，则此直线与二面角的另一个平面所成角的大小为 ( )Ａ．30︒ Ｂ．45︒ Ｃ．60︒ Ｄ．90︒11. 如图,E, F 分别是正方形SD 1DD 2的边D 1D,DD 2的中点, 沿SE,SF,EF 将其折成一个几何体,使D 1,D,D 2重合,记作 D.给出以下位置关系:①SD ⊥面DEF; ②SE ⊥面DEF; ③DF ⊥SE; ④EF ⊥面SED,其中成立的有: ( )Ａ. ①与② B. ①与③ C. ②与③ D. ③与④12. *地球仪的北纬60度圈的周长为6πcm,则地球仪的外表积为( )A. 24πcm 2B. 48πcm 2C.144πcm 2D. 288πcm 2二、填空题〔本大题共4小题，每题4分，共16分〕13. 直二面角α—MN —β中，等腰直角三角形ABC 的斜边BC ⊂α，一直角边AC ⊂β，BC 与β所成角的正弦值是46，则AB 与β所成角大小为__________。

共面问题与异面直线的垂直问题异面直线的垂直问题:1.如图,在直三棱柱ABC-A 1B 1C 1中, ∠ACB=90。

,AC=BC=a, D 为棱AB 的中点.求证: A 1B 1⊥C 1D.2.如图,在三棱锥P-ABC 中,AC=BC=2, ∠ACB=90。

,AP=BP=AB,PC ⊥AC.求证:PC ⊥AB.3.如图,在直四棱柱ABCD-A 1B 1C 1D 1中,已知DC=DD 1=2AD=2AB,AD ⊥DC,AB ∥DC.求证:D 1C ⊥AC 1.4. 如图,平面PCBM ⊥平面ABC, ∠PCB=90。

,PM ∥BC,直线AM 与直线PC 所成的角为60。

,又AC=1,BC=2PM=2, ∠ACB=90。

.求证:AC ⊥BM.ABB 1CA 1C 1DPABBA CDA 1B 1C 1D 1PMABC5.四棱锥S-ABCD 中,底面ABCD 为平行四边形,侧面SBC ⊥底面ABCD.已知∠ABC=45。

，AB=2，BC=2√2，SA=SB=√3.求证:SA ⊥BC.6.如图,四棱锥A-BCDE 中,底面BCDE 为矩形,侧面ABC ⊥底面BCDE,BC=2,CD=√2,AB=AC.求证:AD ⊥CE.共面问题:1.如图,在正方体ABCD-A 1B 1C 1D 1中,点E 在AA 1上,点F 在CC 1上,且AE=FC 1.求证:E 、B 、F 、D 1 四点共面.2.如图,平面ABEF ⊥平面ABCD,四边形ABEF 与ABCD 都是直角梯形,∠BAD=∠FAB=90。

,BC 1/2 AD,BE 1/2 FA,G 、H 分别为FA 、FD 的中点.(1)证明:四边形BCHG 是平行四边形; (2)C 、E 、F 、D 四点是否共面?为什么?SABCDABCDABC D EFA CDFEHGBA CDE∥ ∥。

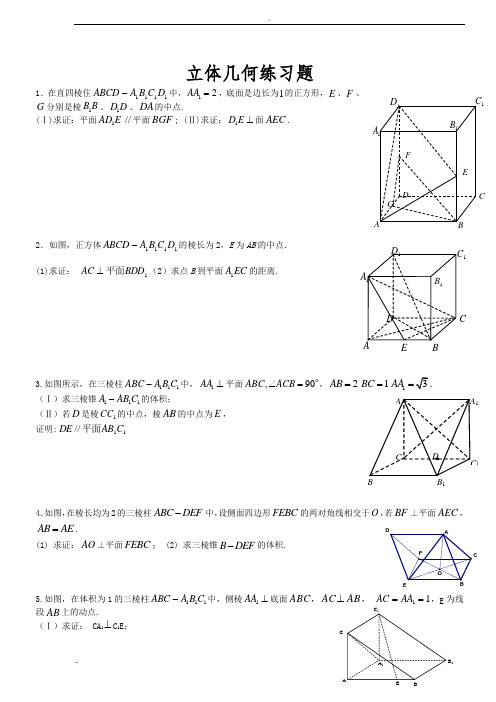
E O ACB FD立体几何练习题1．在直四棱住1111D C B A ABCD -中，12AA =，底面是边长为1的正方形，E 、F 、G 分别是棱B B 1、D D 1、DA 的中点.(Ⅰ)求证：平面E AD 1//平面BGF ; (Ⅱ)求证：1D E ⊥面AEC .2．如图，正方体1111D C B A ABCD -的棱长为2，E 为AB 的中点． (1)求证： 1BDD AC 平面⊥（2）求点B 到平面EC A 1的距离.3.如图所示，在三棱柱111ABC A B C -中，1AA ⊥平面,90ABC ACB ∠=，2AB =1BC =13AA =．（Ⅰ）求三棱锥111A AB C -的体积；（Ⅱ）若D 是棱1CC 的中点，棱AB 的中点为E ， 证明:11//C AB DE 平面4．如图，在棱长均为2的三棱柱ABC DEF -中，设侧面四边形FEBC 的两对角线相交于O ，若BF ⊥平面AEC ，AB AE =.(1) 求证：AO ⊥平面FEBC ； (2) 求三棱锥B DEF -的体积.5.如图，在体积为1的三棱柱111C B A ABC -中，侧棱⊥1AA 底面ABC ，AB AC ⊥， 11==AA AC ，E 为线段AB 上的动点.（Ⅰ）求证： CA 1C CA 11⊥C 1E ；FEABDC G 1C 1A1B 1D 1B 1C ED CBA1D 1A ABCA 1B 1C 1DC 1C（2）线段AB 上是否存在一点E ，使四面体E-AB 1C 1的体积为61？若存在，请确定点E 的位置；若不存在，请说明理由.6．已知三棱柱ABC —A 1B 1C 1的直观图和三视图如图所示，其主视图BB 1A 1A 和侧视图A 1ACC 1均为矩形，其中AA 1=4。

俯视图ΔA 1B 1C 1中，B 1C 1=4，A1C 1=3，A 1B 1=5，D 是AB 的中点。

（1）求证：AC ⊥BC 1；（2）求证：AC 1∥平面CDB 1；（3）求异面直线AC 1与B 1C 所成角的余弦值。

1、以下命题（其中a ，b 表示直线，α表示平面） 正确个数是 （ ） ①若a ∥b ，b ⊂α，则a ∥α ②若a ∥α，b ∥α，则a ∥b ③若a ∥b ，b ∥α，则a ∥α ④若a ∥α，b ⊂α，则a ∥b（A ）0个 （B ）1个 （C ）2个 （D ）3个2、已知m ，n 为异面直线，m ∥平面α，n ∥平面β，α∩β=l ，则l （ ）（A ）与m ，n 都相交 （B ）与m ，n 中至少一条相交 （C ）与m ，n 都不相交（D ）与m ，n 中一条相交3、已知a ，b 是两条相交直线，a ∥α，则b 与α的位置关系是 （ ） A 、b ∥α B 、b 与α相交 C 、b ⊂α D 、b ∥α或b 与α相交4、A 、B 是直线l 外的两点，过A 、B 且和l 平行的平面的个数是（ ）（A ）0个（B ）1个 （C ）无数个 （D ）以上都有可能5、直线a ∥平面α，点A ∈α，则过点A 且平行于直线a 的直线（ ） （A ）只有一条，但不一定在平面α内 （B ）只有一条，且在平面α内（C ）有无数条，但都不在平面α内 （D ）有无数条，且都在平面α内6、直线a ，b 异面直线， a 和平面α平行，则b 和平面α的位置关系是（ ）（A ）b ⊂α （B ）b ∥α （C ）b 与α相交 （D ）以上都有可能7、梯形ABCD 中AB//CD ，AB ⊂平面α，CD ⊄平面α，则直线CD 与平面α内的直线的位置关系只能是 （ ）（A ）平行 （B ）平行和异面 （C ）平行和相交 （D ）异面和相交 8、点P 在直线a 上，直线a 在平面ａ内可记为( )A 、P ∈a ，a ⊂ａB 、P ⊂a ，a ⊂ａC 、P ⊂a ，a ∈ａD 、P ∈a ，a ∈ａ 9、已知P 是平行四边形ABCD 所在平面外一点，E 、F分别为AB 、PD 的中点，求证：AF ∥平面PEC10、在正方体ABCD -A 1B 1C 1D 1中，E 、F 分别为棱BC 、C 1D 1的中点求证：EF ∥平面BB 1D 1D11、已知正方体ABCD-A`B`C`D`中，E ，F 分别是A`B`，B`C`的中点。

立体几何中的轨迹问题在立体几何中，某些点、线、面依一定的规则运动，构成各式各样的轨迹，探求空间轨迹与求平面轨迹类似，应注意几何条件，善于基本轨迹转化．对于较为复杂的轨迹，常常要分段考虑，注意特定情况下的动点的位置，然后对任意情形加以分析判定，也可转化为平面问题．对每一道轨迹命题必须特别注意轨迹的纯粹性与完备性．立体几何中的最值问题一般是指有关距离的最值、角的最值或面积的最值的问题．其一般方法有：1、几何法：通过证明或几何作图，确定图形中取得最值的特殊位置，再计算它的值；2、代数方法：分析给定图形中的数量关系，选取适当的自变量及目标函数，确定函数解析式，利用函数的单调性、有界性，以及不等式的均值定理等，求出最值．轨迹问题【例1】如图，在正四棱锥S－ABCD中，E是BC的中点，P点在侧面△SCD内及其边界上运动，并且总是保持PE AC．则动点P的轨迹与△SCD组⊥成的相关图形最有可能的是( )D DA．B．C．解析：如图，分别取CD、SC的中点F、G，连结EF、EG、FG、BD．设AC与BD的交点为O，连结SO，则动点P的轨迹是△SCD的中位线FG．由正四棱锥可得SB⊥AC，EF⊥AC．又∵EG∥SB ∴EG⊥AC∴AC⊥平面EFG，∵P∈FG，E∈平面EFG，∴AC⊥PE．另解：本题可用排除法快速求解．B中P在D点这个特殊位置，显然不满足PE AC；C中P点所在的轨⊥迹与CD平行，它与CF成角，显然不满足PE AC；D于中P点所在的轨迹与CD平行，它与CF所成的角π4⊥为锐角，显然也不满足PE AC．⊥评析：动点轨迹问题是较为新颖的一种创新命题形式，它重点体现了在解析几何与立体几何的知识交汇处设计图形．不但考查了立体几何点线面之间的位置关系，而且又能巧妙地考查求轨迹的基本方法，是表现最为活跃的一种创新题型．这类立体几何中的相关轨迹问题，如“线线垂直”问题，很在程度上是找与定直线垂直的平面，而平面间的交线往往就是动点轨迹．【例2】(1)如图，在正四棱柱ABCD —A1B1C1D1中，E、F、G、H分别是CC1、C1D1、DD1、DC的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M满足时，有MN∥平面B1BDD1．(2)正方体ABCD—A1B1C1D1中，P在侧面BCC1B1及其边界上运动，且总保持AP⊥BD1，则动点P的轨迹是线段B1C．(3)正方体ABCD —A1B1C1D1中，E、F分别是棱A1B1，BC上的动点，且A1E=BF，P为EF的中点，则点P的轨迹是线段MN(M、N分别为前右两面的中心)．(4)已知正方体ABCD—A1B1C1D1的棱长为1，在正方体的侧面BCC1B1上到点A距离为的点的集合形成一条曲线，那么这条曲线的形状是，它的长度是．1ACC1AE1AA1A1(1)(2)(3)(4)若将“在正方体的侧面BCC1B1上到点A距离为的点的集合”改为“在正方体表面上与点A距离为的点的集合”那么这条曲线的形状又是，它的长度又是．A【例3】(1)(04北京)在正方体ABCD -A 1B 1C 1D 1中，P 是侧面BB 1C 1C 内一动点，若P 到直线BC 与直线C 1D 1的距离相等，则动点P 的轨迹所在的曲线是 ( D )A ．A 直线B ．圆C ．双曲线D ．抛物线变式：若将“P 到直线BC 与直线C 1D 1的距离相等”改为“P 到直线BC 与直线C 1D 1的距离之比为1：2(或2：1)”， 则动点P 的轨迹所在的曲线是 椭圆 (双曲线)．(2)(06北京)平面α的斜线AB 交α于点B ，过定点A 的动直线l 与AB 垂直，且交α于点C ，则动点C 的轨迹是 (A )A ．一条直线B ．一个圆C ．一个椭圆D ．双曲线的一支解：设l 与l 是其中的两条任意的直线，则这两条直线确定一个平面，且斜线AB 垂直这个平面，由过平面外一点有且只有一个平面与已知直线垂直可知过定点A 与AB 垂直所有直线都在这个平面内，故动点C 都在这个平面与平面α的交线上，故选A ．(3)已知正方体ABCD —A 1B 1C 1D 1的棱长为1，M 在棱AB 上，且AM =，点P 到直13线A 1D 1的距离与点P 到点M 的距离的平方差为1，则点P 的轨迹为 抛物线 ．(4)已知正方体ABCD —A 1B 1C 1D 1的棱长为3，长为2的线段MN 点一个端点M 在DD 1上运动，另一个端点N 在底面ABCD 上运动，则MN 的中点P 的轨迹与正方体的面所围成的几何体的体积为 ．π6【例4】(04重庆)若三棱锥A -BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等，则动点P 的轨迹与△ABC 组成图形可能是：( D )BAB CD 【例5】四棱锥P -ABCD ，AD ⊥面PAB ，BC ⊥面PAB ，底面ABCD 为梯形，AD =4，BC =8，AB =6，∠APD =∠CPB ，满足上述条件的四棱锥的顶点P 的轨迹是()A ．圆B ．不完整的圆C ．抛物线D ．抛物线的一部分分析：∵AD ⊥面PAB ，BC ⊥平面PAB ∴AD ∥BC 且AD ⊥PA ，CB ⊥PB ∵∠APD =∠CPB ∴tanAPD =tanCPB∴=AD PA CBPB ∴PB =2PA在平面APB 内，以AB 的中点为原点，AB 所在直线为x 轴建立平面直角坐标系，则A (-3，0)、B (3，0)，设P (x ，y )(y ≠0)，则(x -3)2+y 2=4[(x +3)2+y 2](y ≠0)即(x +5)2+y 2=16(y ≠0)∴P 的轨迹是(B)1AA 3A立体几何中的轨迹问题（教师版）1．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 与到直线B 1C 1的距离相等，则动点P 所在曲线的形状为（D ）．A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分 简析本题主要考查点到直线距离的概念，线面垂直及抛物线的定义．因为B 1C 1面AB 1，所以⊥PB 1就是P 到直线B 1C 1的距离，故由抛物线的定义知：动点的轨迹为抛物线的一段，从而选D ．2．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为2：1，则动点P 所在曲线的形状为（B ）．A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分3．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为1：2，则动点P 所在曲线的形状为（C ）．A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分4．在正方体ABCD-A 1B 1C 1D 1中，E 为AA 1的中点，点P 在其对角面BB 1D 1D 内运动，若EP 总与直线AC 成等角，则点P 的轨迹有可能是（A ）．A ．圆或圆的一部分B ．抛物线或其一部分C ．双曲线或其一部分D ．椭圆或其一部分 简析由条件易知：AC 是平面BB 1D 1D 的法向量，所以EP 与直线AC 成等角，得到EP 与平面BB 1D 1D 所成的角都相等，故点P 的轨迹有可能是圆或圆的一部分．5．已知正方体的棱长为a ，定点M 在棱AB 上（但不在端点A ，B 上），点P 是平面ABCD A B C D -1111ABCD 内的动点，且点P 到直线的距离与点P 到点M 的距离的平方差为a 2，则点P 的轨迹所在曲线为A D 11（A ）．A ．抛物线B ．双曲线C ．直线D ．圆简析在正方体中，过P 作PF AD ，过F 作FE A 1D 1，垂足分别为F 、E ，ABCD A B C D -1111⊥⊥连结PE ．则PE 2=a 2+PF 2，又PE 2-PM 2=a 2，所以PM 2=PF 2，从而PM ＝PF ，故点P 到直线AD 与到点M 的距离相等，故点P 的轨迹是以M 为焦点，AD 为准线的抛物线．6．在正方体中，点P 在侧面BCC 1B 1及其边界上运动，总有AP BD 1，则动点P 的轨迹ABCD A B C D -1111⊥为__________． 简析在解题中，我们要找到运动变化中的不变因素，通常将动点聚焦到某一个平面．易证BD 1面ACB 1，所以满足BD 1AP 的所有点P 都在一个平面ACB 1上．而已知条件中的点P 是在侧面BCC 1B 1及⊥⊥其边界上运动，因此，符合条件的点P 在平面ACB 1与平面BCC 1B 1交线上，故所求的轨迹为线段B 1C ．本题的解题基本思路是：利用升维，化“动”为“静”，即先找出所有点的轨迹，然后缩小到符合条件的点的轨迹．7．在正四棱锥S-ABCD 中，E 是BC 的中点，点P 在侧面SCD 内及其边界上运动，总有PE AC ，则动点∆⊥P 的轨迹为_______________． 答案线段MN （M 、N 分别为SC 、CD 的中点）8．若A 、B 为平面的两个定点，点P 在外，PB ，动点C （不同于A 、B ）在内，且PC AC ，则αα⊥αα⊥动点C 在平面内的轨迹是________．（除去两点的圆）9．若三棱锥A —BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等，则动点P 的轨迹与ABC 组成的图形可能是：（D ）∆A A A AB C B C B C B C A B C D简析动点P 在侧面ABC 内，若点P 到AB 的距离等于到棱BC 的距离，则点P 在的内角∠ABC 平分线上．现在P 到平面BCD 的距离等于到棱AB 的距离，而P 到棱BC 的距离大于P 到底面BCD 的距离，于是，P 到棱AB 的距离小于P 到棱BC 的距离，故动点P 只能在的内角平分线与AB 之间的区域∠ABC 内．只能选D ．10．已知P 是正四面体S-ABC 的面SBC 上一点，P 到面ABC 的距离与到点S 的距离相等，则动点P 的轨迹所在的曲线是（B ）． A ．圆B ．椭圆 C ．双曲线D ．抛物线解题的要领就是化空间问题为平面问题，把一些重要元素集中在某一个平面内，利用相关的知识去解答，象平面几何知识、解析几何知识等．11．已知正方体的棱长为1，在正方体的侧面上到点A 距离为的点的轨迹形ABCD A B C D -1111BCC B 11233成一条曲线，那么这条曲线的形状是_________，它的长度为__________．12．已知长方体中，，在线段BD 、上各有一点P 、Q ，PQ 上有一点ABCD A B C D -1111AB BC ==63,A C 11M ，且，则M 点轨迹图形的面积是 ．PM MQ =2提示轨迹的图形是一个平行四边形．13．已知棱长为3的正方体中，长为2的线段MN 的一个端点在上运动，另一个端点ABCD A B C D -1111DD 1N 在底面ABCD 上运动，求MN 中点P 的轨迹与正方体的面所围成的几何体的体积．14．已知平面平面，直线，点，平面、间的距离为4，则在内到点P 的距离为5且到直//αβl α⊂l P ∈αββ线的距离为的点的轨迹是（ ）l 29A ．一个圆B ．两条平行直线C ．四个点D ．两个点简析：如图，设点P 在平面内的射影是O ，则OP 是、的公垂线，OP=4．在βαβ点的轨迹是四个点，故选C ．16．在四棱锥中，面PAB ，面PAB ，底面ABCD 为梯形，AD=4，BC=8，AB=6，ABCD P -⊥AD ⊥BC ，满足上述条件的四棱锥的顶点P 的轨迹是（ ）CPB APD ∠=∠A ．圆B ．不完整的圆C ．抛物线D ．抛物线的一部分简析：因为面PAB ，面PAB ，所以AD//BC ，且．⊥AD ⊥BC ︒=∠=∠90CBP DAP 又，8BC ,4AD ,CPB APD ==∠=∠由于点P 不在直线AB 上，故此轨迹为一个不完整的圆，选B ．17．如图，定点A 和B 都在平面内，定点P C 是内异于A 和B α,PB ,α⊥α∉α的动点．且，那么动点C 在平面内的轨迹是（ ）AC PC ⊥αA ．一条线段，但要去掉两个点B ．一个圆，但要去掉两个点C ．一个椭圆，但要去掉两个点D ．半圆，但要去掉两个点简析：因为，且PC 在内的射影为BC ，所以，即．所以点C 的轨迹是PC AC ⊥αBC AC ⊥︒=∠90ACB 以AB 为直径的圆且去掉A 、B 两点，故选B ．18．如图，在正方体中，P 是侧面内一动点，若P 到直线1111D C B A ABCD -1BC BC 与直线的距离相等，则动点P 的轨迹所在的曲线是（ ）11D C A ．直线B ．圆C ．双曲线D ．抛物线简析：因为P 到的距离即为P 到的距离，所以在面内，P 到定点11D C 1C 1BC 的距离与P 到定直线BC 的距离相等．由圆锥曲线的定义知动点P 的轨迹为抛物线，故选D ．1C 19．已知正方体的棱长为1，点P 是平面AC 内的动点，若点P 到直线的距离等于点1111D C B A ABCD -11D A P 到直线CD 的距离，则动点P 的轨迹所在的曲线是（ ）A ．抛物线B ．双曲线C ．椭圆D ．直线简析：如图4，以A 为原点，AB 为x 轴、AD 为y 轴，建立平面直角坐标系．设P （x ，y ），作于E 、于F ，连结EF ，易知AD PE ⊥11D A PF ⊥建议收藏下载本文，以便随时学习！1x |EF ||PE ||PF |2222+=+=又作于N ，则．依题意，CD PN ⊥|1y ||PN |-=|PN ||PF |=故动点P 的轨迹为双曲线，选B ．20．如图，AB 是平面的斜线段，A 为斜足，若点P 在平面内运动，使得△ABP a a 的面积为定值，则动点P 的轨迹是（ ）（A ）圆 （B ）椭圆 （C ）一条直线 （D ）两条平行直线分析：由于线段AB 是定长线段，而△ABP 的面积为定值，所以动点P 到线段AB 的距离也是定值．由此可知空间点P 在以AB 为轴的圆柱侧面上．又P 在平面内运动，所以这个问题相当于一个平面去斜切一个圆柱(AB 是平面的斜线段)，得到的切痕是椭圆．P 的轨迹就是圆柱侧面与平面的交线 ．a 21．如图，动点在正方体的对角线上．过点作垂直于平面的直线，与正P 1111ABCD A B C D -1BD P 11BB D D 方体表面相交于．设，，则函数的图象大致是（ ）M N ，BP x =MN y =()y f x=ABCD MN P A 1B 1C 1D 1分析：将线段MN 投影到平面ABCD 内，易得y 为x 一次函数．22．已知异面直线a ，b 成角，公垂线段MN 的长等于2，线段AB 两个端点A 、B 分别在a ，b 上移动，且︒60线段AB 长等于4，求线段AB 中点的轨迹方程．图5简析：如图5，易知线段AB 的中点P 在公垂线段MN 的中垂面上，直线、为平面内过MN 的中α'a 'b α点O 分别平行于a 、b 的直线，于，于，则，且P 也为的中点．'a 'AA ⊥'A 'b 'BB ⊥'B P 'B 'A AB =⋂'B 'A 由已知MN=2，AB=4，易知得．,2AP ,1'AA ==32'B 'A =则问题转化为求长等于的线段的两个端点、分别在、上移动时其中点P 的轨迹．现以32'B 'A 'A 'B 'a 'b 的角平分线为x 轴，O 为原点建立如图6所示的平面直角坐标系．'OB 'A ∠图6设，，)y ,x (P n |'OB |,m |'OA |==则)n 21,n 23('B ),m 21,m 23('A -)n m (41y ),n m (43x -=+=222)32()n m (41)n m (43=++-消去m 、n ，得线段AB 的中点P 的轨迹为椭圆，其方程为．1y 9x 22=+点评：例5和例6分别将立体几何与解析几何中的双曲线与椭圆巧妙地整合在一起，相互交汇和渗透，有利于培养运用多学科知识解决问题的能力．立体几何中的轨迹问题1．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 与到直线B 1C 1的距离相等，则动点P 所在曲线的形状为 （ ）A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分2．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为2：1，则动点P 所在曲线的形状为（ ） A ．线段 B ．一段椭圆弧 C ．双曲线的一部分 D ．抛物线的一部分3．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为1：2，则动点P 所在曲线的形状为（ ） A ．线段 B ．一段椭圆弧 C ．双曲线的一部分 D ．抛物线的一部分4．在正方体ABCD-A 1B 1C 1D 1中，E 为AA 1的中点，点P 在其对角面BB 1D 1D 内运动，若EP 总与直线AC 成等角，则点P 的轨迹有可能是（ ） A ．圆或圆的一部分 B ．抛物线或其一部分 C ．双曲线或其一部分 D ．椭圆或其一部分5．已知正方体的棱长为a ，定点M 在棱AB 上（但不在端点A ，B 上），点P 是平面ABCD A B C D -1111ABCD 内的动点，且点P 到直线的距离与点P 到点M 的距离的平方差为a 2，则点P 的轨迹所在曲线为（ A D 11）A ．抛物线B ．双曲线C ．直线D ．圆6．若三棱锥A —BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等，则动点P 的轨迹与ABC 组成的图形可能是（ ∆）A A AB C B C B C B CA B C D7．已知P 是正四面体S-ABC 的面SBC 上一点，P 到面ABC 的距离与到点S 的距离相等，则动点P 的轨迹所在的曲线是（ ） A ．圆B ．椭圆 C ．双曲线D ．抛物线8．已知平面平面，直线，点，平面、间的距离为4，则在内到点P 的距离为5且到直//αβl α⊂l P ∈αββ线的距离为的点的轨迹是（l 29）A ．一个圆B ．两条平行直线C ．四个点D ．两个点9．在四棱锥中，面PAB ，面PAB ，底面ABCD 为梯形，AD=4，BC=8，AB=6，ABCD P -⊥AD ⊥BC ，满足上述条件的四棱锥的顶点P 的轨迹是（ ）CPB APD ∠=∠A ．圆B ．不完整的圆C ．抛物线D ．抛物线的一部分10．如图，定点A 和B 都在平面内，定点P C 是内异于A 和B α,PB ,α⊥α∉α的动点．且，那么动点C 在平面内的轨迹是（ ）AC PC ⊥αA ．一条线段，但要去掉两个点B ．一个圆，但要去掉两个点C ．一个椭圆，但要去掉两个点D ．半圆，但要去掉两个点11．已知正方体的棱长为1，点P 是平面AC 内的动点，若点P 到直线的距离等于点1111D C B A ABCD -11D A P 到直线CD 的距离，则动点P 的轨迹所在的曲线是（）A ．抛物线B ．双曲线C ．椭圆D ．直线12．如图，AB 是平面的斜线段，A 为斜足，若点P 在平面内运动，使得△ABP a a 的面积为定值，则动点P 的轨迹是（ ）A ．圆B ．椭圆C ．一条直线D ．两条平行直线13．如图，动点在正方体的对角线上．过点作垂直于平面的直线，与正P 1111ABCD A B C D -1BD P 11BB D D 方体表面相交于．设，，则函数的图象大致是（ ）M N ，BP x =MN y =()y f x =ABCD MN P A 1B 1C 1D 114．在正方体中，点P 在侧面BCC 1B 1及其边界上运动，总有AP BD 1，则动点P 的轨迹ABCD A B C D -1111⊥为________．15．在正四棱锥S-ABCD 中，E 是BC 的中点，点P 在侧面SCD 内及其边界上运动，总有PE AC ，则动点∆⊥P 的轨迹为_______________．16．若A 、B 为平面的两个定点，点P 在外，PB ，动点C （不同于A 、B ）在内，且PC AC ，则αα⊥αα⊥动点C 在平面内的轨迹是________．17．已知正方体的棱长为1，在正方体的侧面上到点A 距离为的点的轨迹形ABCD AB C D -1111BCC B 11233成一条曲线，那么这条曲线的形状是_________，它的长度为__________．18．已知长方体中，，在线段BD 、上各有一点P 、Q ，PQ 上有一点ABCD A B C D -1111AB BC ==63,A C 11M ，且，则M 点轨迹图形的面积是．PM MQ =219．已知棱长为3的正方体中，长为2的线段MN 的一个端点在上运动，另一个端点ABCD A B C D -1111DD 1N 在底面ABCD 上运动，则MN 中点P 的轨迹与正方体的面所围成的几何体的体积是．20．已知异面直线a ，b 成角，公垂线段MN 的长等于2，线段AB 两个端点A 、B 分别在a ，b 上移动，且︒60线段AB 长等于4，求线段AB 中点的轨迹方程．。

立体几何初步第1课时棱柱、棱锥和棱台开始时间40min1棱柱的侧面是____________.形，棱锥的侧面是____________.形，棱台的侧面是形____________.，棱柱的面至少有____________.个。

2正方体可以看做是由____________.形向____________.或向____________.平移而得到的几何体，平移的距离等于____________.3一个正棱柱如图所示，这个棱柱的底面________________________.侧棱是___________________________侧面是___________________________4有一个简单几何体有六个面，两个面是平行且全等的正方形，另外四个面是正方形，这样的几何体是____________.（填“棱柱”、“棱锥”或“棱台’）.5给出命题：（1）用平行于底面的平面截棱锥所得的截面与底面相似；（2）两底面平行，各侧面都是梯形的几何体是棱台；（3）棱柱的侧面展开后是一个平行四边形或矩形。

其中为正确的命题个数为：____________.6棱锥的几何特征有____________;____________.7观察周围的物体，请举出几个棱柱、棱锥和棱台的实例（也可以几何体的一部分是棱柱、棱锥或棱台）：__________________________________________________.8画出一个五棱锥和五棱台。

9设计一个平面图形，使它能够折成一个侧面与底面都是等边三角形的三棱锥。

结束时间实际用时本节疑惑：第2课时圆柱、圆锥、圆台和球开始时间40min1矩形绕着它的一边旋转一周而形成的几何体叫做圆柱，这条边称为圆柱的_____________. 2橄榄球可以近似看成是由____________.旋转而成的。

3充满气的车轮胎可以由下面哪个图形绕图中所給轴线旋转而生成____________.(1) (2) (3) (4)4图中表示某单位公章，这个几何体是由简单几何体中____________.组成的(第4题) （第5题）5在图中指出母线、旋转轴、底面6观察周围的物体，请举出几个圆柱、圆锥和圆台的实例：_____________________________（也可以几何体的一部分是圆柱、圆锥和圆台）。

【课时训练】第39节直线、平面垂直的判定与性质一、选择题1．(银川模拟)如图,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF 的中点,现沿AE、AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,那么,在这个空间图形中必有()A．AH⊥平面EFH B．AG⊥平面EFHC．HF⊥平面AEF D．HG⊥平面AEF【答案】A【解析】由平面图形可得AH⊥HE,AH⊥HF,又HE∩HF＝H,∴AH⊥平面HEF.故选A.2．(惠州调研)设α,β,γ为不同的平面,m,n,l为不同的直线,则m⊥β的一个充分条件为()A．α⊥β,α∩β＝l,m⊥l B．α∩γ＝m,α⊥γ,β⊥γC．α⊥γ,β⊥γ,m⊥αD．n⊥α,n⊥β,m⊥α【答案】D【解析】若α⊥β,α∩β＝l,m⊥l,则m与β的位置不确定；若α∩γ＝m,α⊥γ,β⊥γ,则α,β可能平行,此时m∥β；若α⊥γ,β⊥γ,m⊥α,则α,β不一定平行,则m 不一定与β垂直；若n⊥α,n⊥β,则α∥β,则m⊥β.故选【答案】D.3．(黄冈质检)已知两个不同的平面α,β和两条不重合的直线m,n,有下列四个命题：①若m∥n,m⊥α,则n⊥α；②若m⊥α,m⊥β,则α∥β；③若m,n与α所成的角相等,则m∥n；④若m∥α,α∩β＝n,则m∥n.其中正确命题的个数是()A．1 B．2C．3 D．4【答案】B【解析】对于①,若m∥n,m⊥α,则n⊥α,故该命题为真命题；对于②,若m ⊥α,m⊥β,则α∥β,故该命题为真命题；对于③,若m,n与α所成的角相等,则m 与n可能平行、相交或异面,故该命题为假命题；对于④,若m∥α,α∩β＝n,则m 与n的位置关系不确定,故该命题为假命题．故选【答案】B.4．(宝鸡质检)对于四面体ABCD,给出下列四个命题：①若AB＝AC,BD＝CD,则BC⊥AD；②若AB＝CD,AC＝BD,则BC⊥AD；③若AB⊥AC,BD⊥CD,则BC⊥AD；④若AB⊥CD,AC⊥BD,则BC⊥AD.其中为真命题的是()A．①②B．②③C．②④D．①④【答案】D【解析】①如图,取BC的中点M,连接AM,DM,由AB＝AC⇒AM⊥BC,同理DM⊥BC⇒BC⊥平面AMD,而AD⊂平面AMD,故BC⊥AD.④设A在平面BCD内的射影为O,连接BO,CO,DO(图略),由AB⊥CD⇒BO⊥CD,由AC⊥BD⇒CO⊥BD⇒O为△BCD 的垂心⇒DO⊥BC⇒AD⊥BC.故选D.二、填空题5．(广西南宁一模)如图,∠BAC＝90°,PC⊥平面ABC,则在△ABC和△P AC 的边所在的直线中,与PC垂直的直线有________________；与AP垂直的直线有______________．【答案】AB,BC,AC AB【解析】∵PC⊥平面ABC,∴PC垂直于直线AB,BC,AC；∵AB⊥AC,AB⊥PC,AC∩PC＝C,∴AB⊥平面P AC.∴与AP垂直的直线是AB.6．(青岛模拟)如图所示,在四棱锥P－ABCD中,P A⊥底面ABCD,且底面各边都相等,M是PC上一动点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为正确的条件即可)【答案】DM⊥PC(或BM⊥PC等)(不唯一)【解析】如图,连接AC,∵四边形ABCD的各边都相等,∴四边形ABCD为菱形,∴AC⊥BD.又P A⊥平面ABCD,∴P A⊥BD.又AC∩P A＝A,∴BD⊥平面P AC.∴BD⊥PC.∴当DM⊥PC(或BM⊥PC等)时,有PC⊥平面MBD.而PC⊂平面PCD,∴平面MBD⊥平面PCD.7．(泰州模拟)若α,β是两个相交平面,m为一条直线,则下列命题中,所有真命题的序号为________．①若m⊥α,则在β内一定不存在与m平行的直线；②若m⊥α,则在β内一定存在无数条直线与m垂直；③若m⊂α,则在β内不一定存在与m垂直的直线；④若m⊂α,则在β内一定存在与m垂直的直线．【答案】②④【解析】对于①,若m⊥α,如果α,β互相垂直,则在平面β内存在与m平行的直线,故①错误；对于②,若m⊥α,则m垂直于平面α内的所有直线,故在平面β内一定存在无数条直线与m垂直,故②正确；对于③④,若m⊂α,则在平面β内一定存在与m垂直的直线,故③错误,④正确．三、解答题8．(广东七校联考)如图所示,M,N,K分别是正方体ABCD－A1B1C1D1的棱AB,CD,C1D1的中点．求证：(1)AN∥平面A1MK；(2)平面A1B1C⊥平面A1MK.【证明】(1)如图所示,连接NK.在正方体ABCD－A1B1C1D1中,∵四边形AA1D1D,DD1C1C都为正方形,∴AA1∥DD1,AA1＝DD1,C1D1∥CD,C1D1＝CD.∵N,K分别为CD,C1D1的中点,∴DN∥D1K,DN＝D1K.∴四边形DD1KN为平行四边形．∴KN∥DD1,KN＝DD1.∴AA1∥KN,AA1＝KN.∴四边形AA1KN为平行四边形．∴AN∥A1K.∵A1K⊂平面A1MK,AN⊄平面A1MK,∴AN∥平面A1MK.(2)如图所示,连接BC1.在正方体ABCD－A1B1C1D1中,AB∥C1D1,AB＝C1D1.∵M,K分别为AB,C1D1的中点,∴BM∥C1K,BM＝C1K.∴四边形BC1KM为平行四边形．∴MK∥BC1.在正方体ABCD－A1B1C1D1中,A1B1⊥平面BB1C1C,BC1⊂平面BB1C1C,∴A1B1⊥BC1.∵MK∥BC1,∴A1B1⊥MK.∵四边形BB1C1C为正方形,∴BC1⊥B1C.∴MK⊥B1C.∵A1B1⊂平面A1B1C,B1C⊂平面A1B1C,A1B1∩B1C＝B1,∴MK⊥平面A1B1C.又∵MK⊂平面A1MK,∴平面A1B1C⊥平面A1MK.9．(贵州贵阳第一中学月考)如图,在三棱锥K－ABC中,D,E,F分别是KA,KB,KC的中点,平面KBC⊥平面ABC,AC⊥BC,△KBC是边长为2的正三角形,AC＝3.(1)求证：BF⊥平面KAC；(2)求三棱锥F －BDE 的体积．(1)【证明】因为平面KBC ⊥平面ABC ,且AC ⊥BC ,所以AC ⊥平面KBC .又因为BF ⊂平面KBC ,所以BF ⊥AC . 又因为△KBC 是正三角形,且F 为CK 的中点, 所以BF ⊥KC .又AC ∩KC ＝C ,所以BF ⊥平面KAC .(2)【解】S △EFB ＝12×32×1＝34.又因为AC ⊥平面KBC ,DF ∥AC ,所以DF ⊥平面KBC .又因为DF ＝12AC ＝32,所以V F －BDE ＝V D －EFB ＝13S △EFB ·DF ＝13×34×32＝38.。

第6讲空间线段以及线段之和最值问题一、单选题1．（2024·湖北·校联考模拟预测）已知四棱锥P ABCD -的底面为矩形，AB =4BC =，侧面PAB 为正三角形且垂直于底面ABCD ，M 为四棱锥P ABCD -内切球表面上一点，则点M 到直线CD 距离的最小值为（）A 2B1C ．2D ．12．（2024上·江西萍乡·高二统考期末）以等腰直角三角形斜边BC 上的高AD 为折痕，把ABD △和ACD 折成60的二面角.若AB ，()1DM xDA yDB x y DC =++--，其中,x y ∈R ，则DM 的最小值为（）A B ．7C ．14D ．73．（2024上·四川成都·高三树德中学校考期末）如图，已知正方体1111ABCD A B C D -的棱长为2,P 为底面正方形ABCD 内（含边界）的一动点，则下列结论中:①若点Q 为1CC 的中点，则1PA PQ +②过点P 作与1AD 和1BA 都成π6的直线，可以作四条；③若点P 为BC 的中点时，过点C 作与直线1D P 垂直的平面α，则平面α截正方体1111ABCD A B C D -的截面周长为④若点P 到直线1BB 与到直线AD 的距离相等，CD 的中点为E ，则点P 到直线AE 的最短距离是3510.其中正确的命题有（）A ．4个B ．3个C ．2个D ．1个4．（2024·全国·高三专题练习）在空间直角坐标系O xyz -中，已知点()1,0,2A ，()0,2,1B ，点C ，D 分别在x 轴，y 轴上，且AD BC ⊥，那么CD的最小值是（）AB C D5．（2024上·黑龙江大庆·高三校考阶段练习）已知直四棱柱1111ABCD A B C D -的底面ABCD 为矩形，1AA =且该棱柱外接球O 的表面积为20π，E 为线段AB 上一点．则当该四棱柱的体积取最大值时，1D E CE +的最小值为（）A ．6BC ．2D ．二、多选题6．（2024下·山东·高三校联考开学考试）在长方体1111ABCD A B C D -中，12,1,AB AA AD E ===为11A B 的中点，点P 满足1(01)DP DB λλ=<<，则（）A ．若M 为1A D 的中点，则三棱锥P BEM -体积为定值B ．存在点P 使得AP BE ⊥C ．当23λ=时，平面PBC 截长方体1111ABCD A B C D -D ．若Q为长方体1111ABCD A B C D -外接球上一点，23λ=，则3QE QP +7．（2024·广西南宁·南宁三中校联考一模）在边长为2的正方体1111ABCD A B C D -中，动点M 满足1AM xAB y AD z AA =++，(,,R x y z ∈且0,0,0)x y z ≥≥≥，下列说法正确的是（）A ．当[]1,0,0,14x z y ==∈时，1B M MD +B ．当11,2x y z ===时，异面直线BM 与1CD 所成角的余弦值为5C ．当1x y z ++=，且AM =MD ．当1,0x y z +==时，AM 与平面11AB D 8．（2024下·江西·高三校联考开学考试）化学中经常碰到正八面体结构（正八面体是每个面都是正三角形的八面体），如六氟化硫（化学式6SF ）､金刚石等的分子结构.将正方体六个面的中心连线可得到一个正八面体（如图1），已知正八面体E ABCD F --的（如图2）棱长为2，则（）A ．正八面体E ABCD F --的内切球表面积为8π3B ．正八面体E ABCD F --的外接球体积为8π3C ．若点P 为棱EB 上的动点，则AP CP +的最小值为D ．若点Q 为棱AF 上的动点，则三棱锥E QBC -的体积为定值2239．（2024下·安徽·高三池州市第一中学校联考开学考试）已知棱长为2的正方体1111ABCD A B C D -中，动点M 在棱1DD 上，记平面1BC M 截正方体所得的截面图形为Ω，则（）A ．平面1A BC ⊥平面11BC DB ．不存在点M ，使得直线CM //平面11BA CC ．1B M CM +的最小值为D ．Ω的周长随着线段DM 长度的增大而增大10．（2024下·江西上饶·高二上饶市第一中学校考开学考试）在正方体1111ABCD A B C D -中，4AB E F =,,分别为1,BB CD 的中点，点P 满足1,[0,1]BP BC =∈λλ，则（）A ．1A F ⊥平面1AD EB ．三棱锥1P AD E -的体积与P 点的位置有关C ．1DP B P +的最小值为4+D ．当10,3λ⎛⎤∈ ⎥⎝⎦时，平面PEF 截正方体的截面形状为五边形11．（2024下·湖北·高二应城市第一高级中学校联考开学考试）棱长为1的正方体1111ABCD A B C D -中，点P满足1DP DD DA λμ=+，[]0,1λ∈，[]0,1u ∈，则下面结论正确的是：（）A ．当λμ=时，1BP AC ⊥B ．当12μ=时，三棱锥11C PB C -的体积为定值C ．当1λμ+=时，直线CP 与平面11BCC B 所成的角不可能为π3D ．当1λμ+=时，PC PB +12．（2024下·重庆·高三重庆八中校考开学考试）已知正四棱柱1111ABCD A B C D -的底面边长为1，12AA =，点P 在底面ABCD 内运动（含边界），点Q 满足[]1,0,1CQ mCC m =∈ ，则（）A ．当12m =时，1A P PQ +B ．当14m =时，存在点P ，使1A PQ ∠为直角C ．当78m =时，满足11D P A Q ⊥的点P 的轨迹平行平面1C BD D ．当116m =时，满足1A P PQ ⊥的点P 的轨迹围成的区域的面积为π413．（2023上·河北保定·高三校联考阶段练习）在三棱锥1A ABC -中，1A A ⊥平面ABC ，AB AC ⊥，13AA AB AC ===，P 为1A BC 内的一个动点（包括边界），AP 与平面1A BC 所成的角为45 ，则（）A ．1A P -B ．1A P C ．有且仅有一个点P ，使得1A P BC ⊥D ．所有满足条件的线段AP 形成的曲面面积为414．（2024上·江苏常州·高三统考期末）在棱长为2的正方体1111ABCD A B C D -中，P 在线段1BD 上运动（包括端点），下列说法正确的有（）A ．存在点P ，使得⊥CP 平面1A DBB ．不存在点P ，使得直线1C P 与平面1A DB 所成的角为30 C ．PC PD +的最小值为D ．以P 为球心，PA 为半径的球体积最小时，被正方形11ADD A 截得的弧长是π315．（2024上·安徽蚌埠·高二统考期末）如图，正方体1111ABCD A B C D -的棱长为2，点M ，N 分别是棱11A D ，CD 的中点，点P 在四边形ABCD 内，若PM =，则下列结论正确的有（）A ．MN BD⊥B ．MN //1A BC ．点P 的轨迹长度为πD ．PN 116．（2024上·江苏南京·高二南京市第九中学校考期末）已知正方体1111ABCD A B C D -的棱长为1，点E 满足()101,01BE BC BB λμλμ=+≤≤≤≤，则（）A ．若λμ=，则1BC AE⊥B ．若1λμ+=，则1B C 平面1A DEC ．若1λμ+=，则1AE D E +D ．若221λμ+=，则AE 与平面11BB C C 的所成角为定值π417．（2024上·湖南·高二湖南师大附中校考期末）下列有关正方体的说法，正确的有（）A ．正方体的内切球､棱切球､外接球的半径之比为B ．若正方体1111ABCD A BCD -的棱长为1,Q 为正方体侧面11BCC B 上的一个动点，,EF 为线段1AC 的两个三等分点，则QE QF +C ．若正方体8个顶点到某个平面的距离为公差为1的等差数列，则正方体的棱长为D ．若正方体ABCD A B C D -''''的棱长为3，点P 在棱CC '上，且2PC PC ='，则三棱锥B D AP '-'的外接球表面积为99π418．（2024上·山西太原·高三统考期末）在棱长为1的正方体1111ABCD A B C D -中，E 为线段1B C 的中点，点P 和Q 分别满足111D P D C λ=，11D Q D B μ=，其中λ，[0,1]μ∈，则下列结论正确的是（）A ．当12λ=时，三棱锥Q PDE -的体积为定值B ．当12μ=时，四棱锥Q ABCD -的外接球的表面积是9π4C ．当1λ=时，不存在μ使得11PQ BD ⊥D ．PQ EQ +的最小值为619．（2024上·湖南衡阳·高二统考期末）已知四棱台1111ABCD A B C D -的底面为正方形，棱1AA ⊥底面ABCD ，且11122AD AA A D ===，则下列说法正确的是（）A ．直线1CD 与平面1A BD 相交B ．若直线1AC 与平面11BDD B 交于点M ，则M 为线段1AC 的中点C ．平面1ACD 将该四棱台分成的大､小两部分体积之比为5:2D ．若点,P Q 分别在直线11,AA CD 上运动，则线段PQ 20．（2024上·宁夏固原·高二统考期末）如图，在长方体1111ABCD A B C D -中，14,2,3,AB BC CC M ===为11B C 的中点，,P Q 分别是直线1,CC AM 上的动点，则下列结论正确的是（）A ．三棱锥A BDM -的体积为4B ．1AC =C ．直线1,AC BDD ．PQ 21．（2023上·福建泉州·高三福建省泉州第一中学校考阶段练习）在正方体1111ABCD A B C D -中，4AB E F =，，分别为1,BB CD 的中点，，点P 满足1B B C P λ=，[]01λ∈，，则（）A ．1A F ⊥平面1AD EB ．三棱锥1P AD E -的体积与P 点的位置有关C ．1DP B P +的最小值为4+D ．当10,3λ⎛⎫∈ ⎪⎝⎭时，平面PEF 截正方体的截面形状为五边形22．（2023上·河北石家庄·高三石家庄市第二十七中学校考阶段练习）已知正方体1111ABCD A B C D -的棱长为1，点P 满足1CP CD CC λμ=+，其中[][],0,10,1λμ∈∈，以下结论正确的是（）A ．当1λ=时，1B P AC⊥B ．当λμ=时，DP AP +C ．当1B P PC ⊥时，BP 的最大值2D ．若1B P 与平面11CC D D 所成角为π4，则点P 的轨迹长度为π23．（2023上·山东·高三校联考阶段练习）如图，已知菱形ABCD 的边长为2，60ADC ∠=︒，将ACD 沿AC 翻折为三棱锥-P ABC ，点P 为翻折过程中点D 的位置，则下列结论正确的是（）A ．无论点P 在何位置，总有AC PD ⊥B ．点P 存在两个位置，使得1P ABC V -=成立C ．当PB =AD 旋转所形成的曲面的面积为2D ．当2PB =时，M 为PB 上一点，则AM CM +的最小值为24．（2023·山西临汾·校考模拟预测）如图，在正四棱柱1111ABCD A B C D -中，122AA AB ==，E ，F ，N 分别是棱1CC ，11C D ，1AA 的中点，P 是NC 上一点，Q 在平面ABCD 内，则（）A ．CN ⊥平面BDEB ．直线BE 与1A F 是异面直线C ．当BP 取得最小值时，BP PQ +61+D ．直线NC 与平面BDE 的交点是BDE △的外心25．（2023上·山东济南·高二山东省济南市莱芜第一中学校考阶段练习）已知正方体1111ABCD A B C D -的棱长为1，P 为线段11A C 上任意一点，下列说法正确的是（）A ．1PD BD ⊥B ．动点P 到线段BD 2C ．P 是11A C 中点时，直线PD 与平面1A BD 所成的角的正弦值是23D ．三棱锥1P A BD -体积最大时，若点M 满足1OM xOA yOB zOD =++，其中1x y z ++=，则PM 的2326．（2023上·黑龙江大庆·高三大庆实验中学校考期末）如图，已知正方体1111ABCD A B C D -的棱长为2,P 为底面正方形ABCD 内（含边界）的一动点，则下列结论正确的是（）A ．存在点P ，使得1C P ⊥平面11B CD B ．三棱锥111B A D P -的体积为定值C ．当点P 在棱CD 上时，1PA PB +的最小值为2+D ．若点P 到直线1BB 与到直线AD 的距离相等，CD 的中点为E ，则点P 到直线AE 27．（2024上·湖南长沙·高三长沙一中校考阶段练习）四棱锥P ABCD -的底面为正方形，PA 与底面垂直，2PA =，1=AB ，动点M 在线段PC 上，则（）A ．不存在点M ，使得AC BM ⊥B ．MB MD +C ．四棱锥P ABCD -的外接球表面积为6πD ．点M 到直线AB 28．（2024上·黑龙江哈尔滨·高三哈尔滨三中校考期末）在棱长为1的正方体1111ABCD A B C D -中，下列结论正确的有（）A ．11//AC 平面1B CDB ．点1C 到平面1B CD 的距离为22C ．当P 在线段11CD 上运动时，三棱锥11A B PC -的体积不变D ．若Q 为正方体侧面11BCC B 上的一个动点，,EF 为线段1AC 的两个三等分点，则QE QF +的最小值为3三、填空题29．（2024上·广东·高二统考期末）如图，正方形ABCD 和正方形ABEF 的边长都是1，且它们所在的平面所成的二面角D AB F --的大小是60︒，则直线AC 和BF 夹角的余弦值为．若,M N 分别是,AC BF 上的动点，且AM BN =，则MN 的最小值是．30．（2024上·江西九江·高二统考期末）如图，正三棱锥-P ABC 中，三条侧棱,,PA PB PC 两两垂直且相等，2,PA M =为PC 的中点，N 为平面ABC 内一动点，则NM NP +的最小值为.31．（2024上·浙江宁波·高三余姚中学校联考期末）在棱长为1的正方体1111ABCD A B C D -中，,,E F M 分别是棱1111,,B C C D AB 的中点，,G H 分别是线段1,AC EF 上的动点，则GH GM +的最小值为.32．（2024上·河北邯郸·高二统考期末）如图，正三棱柱111ABC A B C -的底面边长为2，侧棱长为3,D 为BC的中点，设()1111,01A P A B DQ DC λλλ==≤≤，则PQ 的最小值为.33．（2024上·四川成都·高三石室中学校考期末）如图，在三棱锥111A A B C -中，1AA ⊥平面111A B C ，11190A B C ∠=︒，11111222A B A A B C ===，P 为线段1AB 的中点，,M N 分别为线段1AC 和线段11B C 上任意一点，MN+的最小值为．34．（2024上·重庆·高二统考期末）一种糖果的包装纸由一个边长为3的正方形和两个等腰直角三角形组成（如图1），沿AD ，BC 将这两个三角形折起到与平面ABCD 垂直（如图2），连接EF ，AE ，CF ，AC ，若点G 满足DG xDA yDC zDF =++且1x y z ++=，则||EG 的最小值为．35．（2024上·上海·高二上海市复旦中学校考期末）已知在直三棱柱111ABC A B C -中，底面为直角三角形，90ACB ∠=︒，6AC =，1BC CC ==P 是1BC 上一动点，则1CP PA +的最小值为．36．（2023上·河北石家庄·高二石家庄一中校考阶段练习）正方体1111ABCD A B C D -的棱长为2，点M 在线段DC 上，且DM ，动点P 在正方形ABCD 内运动（含边界），若1D P =，则当1B P 取得最小值时，三棱锥1B MPB -外接球的表面积为37．（2024·河南·方城第一高级中学校联考模拟预测）在棱长为1的正方体1111ABCD A B C D -中，M ，N 分别为线段1A D 和11B D 上的动点，且12D N DM =，则MN 的最小值为.38．（2024·全国·模拟预测）如图，在长方体1111ABCD A B C D -中，3AB =，12BC CC ==，M ，N 分别为BC ，1CC 的中点，点P 在矩形11BCC B 内运动（包括边界），若1//A P 平面AMN ，则1A P 取最小值时，三棱锥1P MA B-的体积为．39．（2023上·上海·高二格致中学校考阶段练习）已知直三棱柱111ABC A B C -，底面三角形ABC 是等腰直角三角形，其中B 为直角顶点，且13,AB AA ==D 为棱1AA 的中点，点M 为平面BCD 的一动点，则11B M C M +的最小值是．第6讲空间线段以及线段之和最值问题一、单选题1．（2024·湖北·校联考模拟预测）已知四棱锥P ABCD -的底面为矩形，AB =4BC =，侧面PAB 为正三角形且垂直于底面ABCD ，M 为四棱锥P ABCD -内切球表面上一点，则点M 到直线CD 距离的最小值为（）A 2B1C ．2D ．1【答案】B【解析】如图，设四棱锥的内切球的半径为r ，取AB 的中点为H ，CD 的中点为N ，连接PH ，PN ，HN ，球O 为四棱锥P ABCD -的内切球，底面ABCD 为矩形，侧面PAB 为正三角形且垂直于底面ABCD ，则平面PHN 截四棱锥P ABCD -的内切球O 所得的截面为大圆，此圆为PHN 的内切圆，半径为r ，与HN ，PH 分别相切于点E ，F ，平面PAB ⊥平面ABCD ，交线为AB ，PH ⊂平面PAB ，PAB 为正三角形，有PH AB ⊥，PH ∴⊥平面ABCD ，HN ⊂平面ABCD ，PH HN ∴⊥，AB =4BC =，则有3PH =，4HN =，5PN =，则PHN 中，()113434522PHN S r =⨯⨯=++ ，解得1r =.所以，四棱锥P ABCD -内切球半径为1，连接ON .PH ⊥Q 平面ABCD ，CD ⊂平面ABCD ，CD PH ∴⊥，又CD HN ⊥，,PH HN Ì平面PHN ，PH HN H = ，CD \^平面PHN ，ON ⊂ 平面PHN ，可得ON CD ⊥，所以内切球表面上一点M 到直线CD 的距离的最小值即为线段ON 的长减去球的半径，又ON ==所以四棱锥P ABCD -内切球表面上的一点M 到直线CD 1.故选：B.2．（2024上·江西萍乡·高二统考期末）以等腰直角三角形斜边BC 上的高AD 为折痕，把ABD △和ACD 折成60的二面角.若AB ，()1DM xDA yDB x y DC =++--，其中,x y ∈R ，则DM 的最小值为（）A ．21B C ．14D ．7【答案】D【解析】由已知得,AD BD AD CD ⊥⊥，所以BDC ∠是ABD △和ACD 折成60 的二面角的平面角，所以60BDC ∠= ，又AB =，所以1AB AC AD BD CD =====，222+2cos 601BC AD CD AD CD =-⋅⋅= ，所以1BC =，因为()1DM xDA yDB x y DC =++-- ，其中,x y ∈R ，所以点M 在平面ABC 内，则DM的最小值为点D 到平面ABC 的距离，设点D 到平面ABC 的距离为h ，因为,AD BD AD CD ⊥⊥，BD CD D ⋂=，BD ⊂平面BDC ，CD ⊂平面BDC ，所以AD ⊥平面BDC ，所以AD 是点A 到平面BDC 的距离，所以111111sin 332A BDC BDC V AD S BDC -=⨯⨯=⨯⨯⨯⨯⨯∠=又ABC 中，1AB AC BC ===，所以2223cos 24AB AC BC BAC AB AC +-∠==⋅⋅，所以7sin 4BAC ∠=，则11sin 2244ABC S AB AC BAC =⋅⋅∠==，所以1133412D ABC ABC V h S h -=⨯⨯=⨯⨯ ，解得h DM 的最小值为7，故选：D.3．（2024上·四川成都·高三树德中学校考期末）如图，已知正方体1111ABCD A B C D -的棱长为2,P 为底面正方形ABCD 内（含边界）的一动点，则下列结论中:①若点Q 为1CC 的中点，则1PA PQ +②过点P 作与1AD 和1BA 都成π6的直线，可以作四条；③若点P 为BC 的中点时，过点C 作与直线1D P 垂直的平面α，则平面α截正方体1111ABCD A B C D -的截面周长为④若点P 到直线1BB 与到直线AD 的距离相等，CD 的中点为E ，则点P 到直线AE 的最短距离是10.其中正确的命题有（）A ．4个B ．3个C ．2个D ．1个【答案】C【解析】在棱长为2的正方体1111ABCD A B C D -中，延长QC 到Q '，使1CQ '=，由点Q 为1CC 的中点，得平面ABCD 是线段QQ '的中垂面，连接111,A Q A C '，则PQ PQ '=，111PA PQ PA PQ AQ ''+=+≥===,当且仅当点P 为直线1A Q '与平面ABCD 的交点时取等号，①正确；连接1BC ，四边形11ABC D 是正方体1AC 的对角面，则四边形11ABC D 是矩形，即11//BC AD ，显然1111A B BC AC ==，则11π3A BC ∠=，11A BC ∠的平分线与直线11,BA BC 都成π6的角，显然在空间过点B 作与直线11,BA AD 都成π6角的直线只有1条，则过空间任意点作与直线11,BA AD 都成π6角的直线只有1条，②错误；当点P 为BC 的中点时，取1,BB BA 的中点,F G ，连接1,,,CG CF GF C P ，显然Rt BCF ≌1Rt CC P ，则1BCF CC P ∠=∠，111π2CPC BCF CPC CC P ∠+∠=∠+∠=，即有1CF C P ⊥，而11D C ⊥平面11BCC B ，CF ⊂平面11BCC B ，则11CF D C ⊥，又1111111,,D C C P C D C C P =⊂ 平面11D C P ，于是CF ⊥平面11D C P ，而1D P ⊂平面11D C P ，因此1CF D P ⊥，同理1CG D P ⊥，显然,,CG CF C CG CF =⊂ 平面CGF ，所以CGF △是平面α截正方体1111ABCD A B C D -所得截面，其周长为25GF CG CF ++=，③错误；由于1BB ⊥平面ABCD ，则点P 到直线1BB 距离等于PB ，即点P 到点B 的距离等于它到直线AD 的距离，因此点P 轨迹是以点B 为焦点，直线AD 为准线的抛物线在正方形ABCD 及内部，以线段AB 中点O 为原点，建立如图所示的平面直角坐标系，点P 轨迹方程为24(02)y x y =≤≤，直线AE 的方程为22y x =+，令000(,21)P x x x ≤，因此点P 到直线AE ：220x y -+=的距离0020|222|213()25525x x d x -+=-+，于是当014x =，即点1(,1)4P 时，min 3510d =所以正确命题的个数为2.故选：C4．（2024·全国·高三专题练习）在空间直角坐标系O xyz -中，已知点()1,0,2A ，()0,2,1B ，点C ，D 分别在x 轴，y 轴上，且AD BC ⊥，那么CD的最小值是（）AB C ．2D 【答案】B【解析】设(),0,0C x ，()0,,0D y ，且()1,0,2A ，()0,2,1B ，∴()1,,2AD y =-- ，(),2,1BC x =-- ，又AD BC ⊥，∴220AD BC x y ⋅=--+=，即22x y +=．∵(),,0CD x y =-，∴CD =当且仅当45y =时等号成立.故选：B5．（2024上·黑龙江大庆·高三校考阶段练习）已知直四棱柱1111ABCD A B C D -的底面ABCD 为矩形，1AA =且该棱柱外接球O 的表面积为20π，E 为线段AB 上一点．则当该四棱柱的体积取最大值时，1D E CE +的最小值为（）A ．6BC ．2D ．【答案】D【解析】设外接球O 的半径为R ，则球O 的表面积24π20πS R ==，所以R设矩形ABCD 的长和宽分别为x 和y ，则((2222x y ++=，所以228x y+=，)111122ABCD A B C D V x y -=≤+=，当且仅当2x y ==时取等号，即底面为边长为2的正方形时，四棱柱的体积最大.则有14BC ===，将平面ABCD 沿AB 展开，与11ABC D 处于同一平面，则11D E EC D C +≥=即平面图形中1,,D E C 三点共线时，1D E CE +有最小值故选：D 二、多选题6．（2024下·山东·高三校联考开学考试）在长方体1111ABCD A B C D -中，12,1,AB AA AD E ===为11A B 的中点，点P 满足1(01)DP DB λλ=<<，则（）A ．若M 为1A D 的中点，则三棱锥P BEM -体积为定值B ．存在点P 使得AP BE ⊥C ．当23λ=时，平面PBC 截长方体1111ABCD A B C D -D ．若Q为长方体1111ABCD A B C D -外接球上一点，23λ=，则3QE QP +【答案】ACD【解析】对于A ：因为M 为1A D 的中点，E 为11A B 的中点，所以1//DB EM ，1DB ⊄面BEM ，EM ⊂面BEM ，所以1//DB 面BEM ，故A 正确；则P 到面BEM 的距离为定值，所以体积为定值．对于B ：AP 在平面11ABB A 的投影为1AB ，设P 在平面11ABB A 的投影为G ，则G 在直线1AB 上.则PG ⊥平面11ABB A ，BE ⊂平面11ABB A ，所以PG BE ⊥，若AP BE ⊥，PG AP P ⋂=，所以BE ⊥平面APG ，1AB ⊂平面APG ，则1AB BE ⊥，因为四边形11ABB A 为正方形，所以1AB 与BE 不垂直，所以B 错．对于C ：平面PCD 与平面1B CD 重合，平面1B CD 与平面11DCB A 重合，所以延长CP 会与11A B 有交点，因为123DP DB =，所以延长CP 与11A B 交于点E ，取11C D 中点F ，则平面PBC 截长方体1111ABCD A B C D -所得截面为矩形BCFE C 正确；对于D ：长方体1111ABCD A B C D -外接球球心为1B D 中点，半径为132,23DP DB =，由阿氏球得，在直线1B D 上必存在一点N ，使得3QP QN =，此时点N 在1DB 延长线上，且满足13B N =，以D 为原点，建系如图，13,6DB DN ==所以12DN DB =，则()4,2,4N ，因为()1,1,2E ，所以min min (3)()QE QP QE QN NE +=+==D 正确.故选：ACD.7．（2024·广西南宁·南宁三中校联考一模）在边长为2的正方体1111ABCD A B C D -中，动点M 满足1AM xAB y AD z AA =++，(,,R x y z ∈且0,0,0)x y z ≥≥≥，下列说法正确的是（）A ．当[]1,0,0,14x z y ==∈时，1B M MD +B ．当11,2x y z ===时，异面直线BM 与1CD 所成角的余弦值为105C ．当1x y z ++=，且3AM =时，则M 的轨迹长度为3D ．当1,0x y z +==时，AM 与平面11AB D 所成角的正弦值的最大值为3【答案】AD【解析】对于A ，在AB 上取点H ，使14AH AB = ，在DC 上取点K ，使14DK DC =，因为[]1,0,0,14x z y ==∈，即14AM AB y AD =+ ，故M 点在HK 上，将平面11B HKC 与平面AHKD 沿着HK 展开到同一平面内，如图：连接1B D 交HK 于P ，此时,,B P D 三点共线，1B M MD +取到最小值即1B D 的长，由于113,422AH AB BH ==∴= ，则152B H ==，故11513,22A B B D =+=∴即此时1B M MD +A 正确；对于B ，由于11,2x y z ===时，则111122AM AB AD AA AC CC =++=+ ，此时M 为1CC 的中点，取11C D 的中点为N ，连接,,BM MN BN，则1MN CD ∥,故BMN ∠即为异面直线BM 与1CD 所成角或其补角，又112MN CD BM ===3BN ===，故2222223cos 2BM MN BN BMN BM MN +-+-∠===⋅而异面直线所成角的范围为π(0,]2，故异面直线BM 与1CD B 错误；对于C ，当1x y z ++=时，可得点M 的轨迹在1A BD 内（包括边界），由于1CC ⊥平面ABCD ，BD ⊂平面ABCD ，故1CC BD ⊥，又BD AC ⊥，11,,AC CC C AC CC =⊂ 平面1ACC ，故BD ⊥平面1ACC ，1AC ⊂平面1ACC ，故1BD AC ⊥，同理可证11A B AC ⊥,11,,A B BD B A B BD =⊂ 平面1A BD ，故1AC ⊥平面1A BD ，设1AC 与平面1A BD 交于点P ，由于11113222324A A BD A ABD VV --=⨯⨯==⨯⨯，1A BD 为边长为A 到平面1A BD的距离为43AP =若AM =，则MP =，即M 点落在以P 为圆心，3为半径的圆上，P 点到1A BD 三遍的距离为31223<，即M 点轨迹是以P 为圆心，3为半径的圆的一部分，其轨迹长度小于圆的周长42π3，C 错误；对于D ，因为11,B D BD BD ⊄∥平面11AB D ，11B D ⊂平面11AB D ，故BD ∥平面11AB D ，因为当1,0x y z +==时，AM AB AD =+，即M 在BD 上，点M 到平面11AB D 的距离等于点B 到平面11AB D 的距离，设点B 到平面11AB D 的距离为d ，则111111111142223323B AB D ABB ABB D V V S A D --==⋅=⨯⨯⨯⨯= ，11AB D 为边长为(12114333A BD S d d ⋅=⨯= ，解得3d =，又M 在BD 上，当M 为BD 的中点时，AM ，设直线AM 与平面11AB D 所成角为π,[0,2θθ∈，则3sind AM AM θ==AM 与平面11AB D D 正确，故选：AD8．（2024下·江西·高三校联考开学考试）化学中经常碰到正八面体结构（正八面体是每个面都是正三角形的八面体），如六氟化硫（化学式6SF ）､金刚石等的分子结构.将正方体六个面的中心连线可得到一个正八面体（如图1），已知正八面体E ABCD F --的（如图2）棱长为2，则（）A ．正八面体E ABCD F --的内切球表面积为8π3B ．正八面体E ABCD F --的外接球体积为8π3C ．若点P 为棱EB 上的动点，则AP CP +的最小值为D ．若点Q 为棱AF 上的动点，则三棱锥E QBC -的体积为定值223【答案】ACD【解析】对于A 项，设该正八面体内切球的半径为r ，由内切球的性质可知正八面体的体积111822sin60222323V r =⨯⨯⨯⨯⨯⋅=⨯⨯⨯ ，解得3r =，故它的内切球表面积为28π4π3⨯=⎝⎭，故A 项正确；对于B 项，设该正八面体外接球的半径为R ，由图知，ABCD 是正方形，222OA OB OC OD ====,在Rt EOB △中，OE ==,利用对称性知OF =故点O 为正八面体外接球的球心，则R =，所以正八面体外接球的体积为3，故B 项错误；对于C 项，如图，因ABE 与BCE 是边长为2的全等的正三角形，可将BCE 翻折到BCE ' ，使其与ABE 共面，从而得到一个菱形ABC E '.连接AC 与BE 相交于点P ，此时,AP EB C P EB '⊥⊥,322AP C P '==⨯则AP CP +取得最小值为故C 项正确；对于D 项，易知AF //EC ，因为AF ⊄平面,EBC EC ⊂平面EBC ，所以AF //平面EBC ，所以1122323E QBC Q EBC A EBC E ABC V V V V ----====⨯⨯⨯=三棱锥三棱锥三棱锥三棱锥，故D 项正确.故选：ACD.9．（2024下·安徽·高三池州市第一中学校联考开学考试）已知棱长为2的正方体1111ABCD A B C D -中，动点M 在棱1DD 上，记平面1BC M 截正方体所得的截面图形为Ω，则（）A ．平面1A BC ⊥平面11BC DB ．不存在点M ，使得直线CM //平面11BA CC ．1B M CM +的最小值为D ．Ω的周长随着线段DM 长度的增大而增大【答案】ACD【解析】由于正方体的对角面相互垂直，故A 正确；当点M 与1D 重合时，直线CM //平面11BA C ，故B 错误；将四边形11DCC D 翻折至与四边形11BB D D 共面，则11B M CM B C +≥=C 正确；当0DM =时，Ω为1BC D ，且1BC D 的周长为当2DM =时，Ω为四边形11ABC D ，且四边形11ABC D 的周长为4+当02DM <<时，如图，过点M 作MN //1AD ，易得MN //1BC ，所以Ω为四边形1MNBC ，设DM x =，四边形1MNBC 的周长为l ，则()l x =，所以()l x '=()0l x '>，解得04x <<，所以()l x 在()0,2上单调递增，所以Ω的周长随着线段DM 长度的增大而增大，故D 正确．故选:ACD ．10．（2024下·江西上饶·高二上饶市第一中学校考开学考试）在正方体1111ABCD A B C D -中，4AB E F =,,分别为1,BB CD 的中点，点P 满足1,[0,1]BP BC =∈λλ，则（）A ．1A F ⊥平面1AD EB ．三棱锥1P AD E -的体积与P 点的位置有关C ．1DP B P +的最小值为4+D ．当10,3λ⎛⎤∈ ⎥⎝⎦时，平面PEF 截正方体的截面形状为五边形【答案】AD【解析】A 选项，以D 为坐标原点，以1,,DA DC DD 所在直线为,,x y z 轴建立空间直角坐标系，则11(4,0,0),(4,4,2),(0,0,4),(0,2,0),(4,0,4)A E D F A =则11(4,0,4),(4,2,4),(0,4,2)AD A F AE =-=--= ，11(4)(4)024(4)0,A F AD ⋅=-⨯-+⨯+⨯-=1(4)024(4)20,A F AE ⋅=-⨯+⨯+-⨯=所以111,A F AD A F AE ⊥⊥，又1,AE AD A AE ⋂=⊂平面11,AD E AD ⊂平面1AD E ，所以1A F ⊥平面1AD E ，故A 正确；B 选项，因为在正方体1111ABCD A BCD -中，11//AB C D 且11AB C D =，所以四边形11ABC D 为平行四边形，因此11//BC AD ，又1BC ⊂/平面11,AED AD ⊂平面1AED ，所以1//BC 平面1AED ，因此棱1BC 上的所有点到平面1AED 的距离都相等，又P 是棱1BC 上的动点，所以三棱锥1P AED -的体积始终为定值，故B 错；C 选项，11(4,4,0),(0,4,4),(4,4,4)B C B ，因为1,[0,1]BP BC =∈λλ，所以(44,4,4)P -λλ，所以1(44,4,4),(4,0,44)DP B P =-=-- λλλλ，2211323232323216DP B P DP B P λλλλ+=+=-+-+ 2211322432822λλ⎛⎫⎛⎫=-+-+ ⎪ ⎪⎝⎭⎝⎭[0,1]λ∈又，当12λ=时，1DP B P +有最小值，最小值为2622C 错误；D 选项，连接EC ，取1AA 中点为G ，当EC 与1BC 交点为点P 时，平面PEF 截正方体截面图形ECDG 为四边形，如下图1，此时11~,~,,PM MC PM BM PMC EBC PMB C CB EB BC CC BC == ，此时13λ=，当103λ<<时，如下图2，截面为五边形EBFKL ，故D 正确；故选∶AD11．（2024下·湖北·高二应城市第一高级中学校联考开学考试）棱长为1的正方体1111ABCD A B C D -中，点P满足1DP DD DA λμ=+，[]0,1λ∈，[]0,1u ∈，则下面结论正确的是：（）A ．当λμ=时，1BP AC ⊥B ．当12μ=时，三棱锥11C PB C -的体积为定值C ．当1λμ+=时，直线CP 与平面11BCC B 所成的角不可能为π3D ．当1λμ+=时，PC PB +【答案】ABC 【解析】根据正方体可建立如图所示的空间直角坐标系，则()()()()0,0,0,1,0,0,1,1,0,0,1,0,A B C D ()()()()11110,0,1,1,0,1,1,1,1,0,1,1A B C D .故()()10,0,1,0,1,0DD DA ==- ，因为1DP DD DA λμ=+，故()0,,DP μλ=- ，故()0,1,P μλ-对于A ，当λμ=时，()0,1,P λλ-，故()1,1,BP λλ=--，而()11,1,1AC = ，故1110BP AC λλ⋅=-+-+= ，故1BP AC ⊥，故A 成立.对于B ，因为()0,1,P μλ-，故P 在平面11ADD A ，故P 到平面11B C C 的距离为1，而11B C C △的面积为定值，故11P C B C V -为定值，故11C PB C V -为定值，故B 正确.对于C ，()0,,P λλ，故()1,1,CP λλ=-- ，而平面11BCC B 的法向量为()1,0,0AB =，设直线CP 与平面11BCC B 所成的角为θ，则sin AB CP AB CP θ⋅= 因为[]0,1λ∈，故23131424λ⎛⎫≤-+≤ ⎪⎝⎭，故sin 232θ≤，故θ不可能为π3，故C 错误.对于D ，由C 的分析可得()0,,P λλ且()1,1,CP λλ=-- ，()1,,BP λλ=-，故PC PB +==，设(),0M λ，1,2N S ⎛⎛⎝⎭⎝⎭，1,2N ⎛ ⎝⎭'，如下图，故))PC PB MN MS MNMS '+=+=+S'D 错误.12．（2024下·重庆·高三重庆八中校考开学考试）已知正四棱柱1111ABCD A B C D -的底面边长为1，12AA =，点P 在底面ABCD 内运动（含边界），点Q 满足[]1,0,1CQ mCC m =∈ ，则（）A ．当12m=时，1A P PQ +B ．当14m =时，存在点P ，使1A PQ ∠为直角C ．当78m =时，满足11D P A Q ⊥的点P 的轨迹平行平面1C BD D ．当116m =时，满足1A P PQ ⊥的点P 的轨迹围成的区域的面积为π4【答案】ACD【解析】以D 为坐标原点，1,,DA DC DD 所在直线分别为,,x y z 轴，建立空间直角坐标系，则()()11,0,2,0,1,1A Q ，则点Q 关于平面ABCD 的对称点为()0,1,1Q '-，连接1A Q '，与平面ABCD 的交点即为使得1A P PQ +取最小值的点P ，此时11A P PQ AQ +=='A 正确；B 选项，当14m =时，()111,0,2,0,1,2A Q ⎛⎫ ⎪⎝⎭，设(),,0P s t ，则()222114A P s t =-++，()222114PQ s t =+-+，22111711224A Q ⎛⎫=++-=⎪⎝⎭，令22211A P PQ A Q +=，即()()222211714144s t s t -++++-+=，故()()2222110s t s t -+++-=，则需满足10,0,0,10s s t t -===-=，不合要求，故不存在点P ，使1A PQ ∠为直角，B 错误；C 选项，当78m =时，()()1171,0,2,0,1,,0,0,24A Q D ⎛⎫ ⎪⎝⎭，设(),,0P s t ，则()()11710,1,1,0,21,1,,,,244A Q D P s t ⎛⎫⎛⎫=-=--=- ⎪ ⎪⎝⎭⎝⎭ ，()11111,1,,,2042A Q D P s t s t ⎛⎫⋅=--⋅-=-++= ⎪⎝⎭ ，在平面ABCD 中画出(),,0P s t 点的轨迹，如图所示，其轨迹为线段MN ，其中,M N 分别为,AD AB 的中点，其中//MN BD ，又BD ⊂平面1C BD ，MN ⊄平面1C BD ，故//MN 平面1C BD ，当78m =时，满足11D P A Q ⊥的点P 的轨迹平行平面1C BD ，C 正确；D 选项，当116m =时，()111,0,2,0,1,8A Q ⎛⎫ ⎪⎝⎭，设(),,0P s t ，则()111,,2,,1,8A P s t PQ s t ⎛⎫=--=-- ⎪⎝⎭ ，则()221111,,2,1,084A P PQ s t s t s s t t ⎛⎫⋅=--⋅--=-+-+-= ⎪⎝⎭ ，即22111224s t ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭，故点P 的轨迹为以11,22⎛⎫ ⎪⎝⎭为圆心，12为半径的圆，刚好与正方形ABCD 相切，故面积为211ππ24⎛⎫= ⎪⎝⎭，当116m =时，满足1A P PQ ⊥的点P 的轨迹围成的区域的面积为1π4，D 正确.故选：ACD13．（2023上·河北保定·高三校联考阶段练习）在三棱锥1A ABC -中，1A A ⊥平面ABC ，AB AC ⊥，13AA AB AC ===，P 为1A BC 内的一个动点（包括边界），AP 与平面1A BC 所成的角为45 ，则（）A ．1A P -B ．1A P C ．有且仅有一个点P ，使得1A P BC ⊥D ．所有满足条件的线段AP 【答案】ACD【解析】因为1A A ⊥平面ABC ，,AB AC ⊂平面ABC ，所以11,A A AB A A AC ⊥⊥，又1,3AB AC AA AB AC ⊥===，所以11A B AC BC ===取BC 的中点M ，则1,AM BC A M BC ⊥⊥，又11,,AM A M M AM A M =⊂ 平面1A AM ，所以BC ⊥平面1A AM ，过A 作1AH A M ⊥于H ，因为AH ⊂平面1A AM ，所以AH BC ⊥，又11,,A M BC M A M BC =⊂ 平面1A BC ，所以AH ⊥平面1A BC ，所以APH ∠为AP 与平面1A BC 所成的角的平面角，因为1A A ⊥平面ABC ，AM ⊂平面ABC ，则1A A AM ⊥，又在1Rt A AM V中，113,2A A AM BC ==1A M =所以11AA AM AH A M ⋅=因为45APH ∠=︒，所以AH HP =，AP =所以点P 轨迹是以H1A BC内部的一部分，如图，所以1A P的最小值为1A H HP -，故A 正确；由于轨迹圆部分在平面1A BC 外部，所以1A P的最大值不等于1A H HP +，故B 错误；因为BC ⊥平面1A AM ，1A M ⊂平面1A AM ，所以1BC A M ⊥，若1A P BC ⊥，则点P 在线段1A M 上，有且仅有一个点P 满足题意，故C 正确；动线段AP 形成的曲面为圆锥AH 侧面积的一部分，易知三棱锥1A A BC -是正三棱锥，AH ⊥平面1A BC ，故H 为等边1A BC 的中心，所以11133HM A M ==，因为11cos 2HM B HM HB ∠==，所以1π4B HM ∠=，因为π2π23142π4-⨯⨯=，所以曲面面积为圆锥侧面面积的14，圆锥AH侧面积为π=，所以所有满足条件的动线段AH形成的曲面面积为4，故D 正确.故选：ACD.14．（2024上·江苏常州·高三统考期末）在棱长为2的正方体1111ABCD A B C D -中，P 在线段1BD 上运动（包括端点），下列说法正确的有（）A ．存在点P ，使得⊥CP 平面1A DBB ．不存在点P ，使得直线1C P 与平面1A DB 所成的角为30 C ．PC PD +的最小值为D ．以P 为球心，PA 为半径的球体积最小时，被正方形11ADD A 截得的弧长是π3【答案】BCD 【解析】方法一：如图，以D 为原点，分别以1,,DA DC DD 为,,x y z 轴建立空间直角坐标系，()2,2,0B ，()10,0,2D ，()2,0,0A ，()10,2,2C ，()12,2,2BD =-- ，()12,2,2AC =-,1BP BD λ=，则()22,22,2P λλλ--，对于A ，因为1111ABCD A B C D -为正方体，所以11AB A B ⊥，11AD A D⊥由三垂线定理得11AC A B ⊥，11AC A D ⊥，因为111A B A D A = ，11,A B A D ⊂平面1A DB ，所以1AC ⊥平面1A DB ，()12,2,2AC =-是平面1A BD 一个法向量，假设⊥CP 面1A DB ，则()22,2,2CP λλλ=--与()2,2,2-共线矛盾，假设不成立，A 错．对于B ，若存在P ，1C P 与1A DB 所成角为30 ，则160AC P ∠= 或120︒，11,60C A C P 〈〉= 或120︒，111112C A C P C A C P ⋅∴=λ=假设不成立，B 对．对于C，PC PD +==．表示(),0P λ与2,33E ⎛⎝⎭，1,33F⎛- ⎝⎭距离之和，1PEPF EF +≥=，PC PD +≥C 对．对于D，PA =13λ=时PA 最小，442,,333P ⎛⎫⎪⎝⎭，PA =，设截面小圆的圆心为N ，半径为r ，则NP ⊥平面11ADD A ，所以42,0,33N ⎛⎫ ⎪⎝⎭，3r ==，因为3NA ==，所以球与面11ADD A N 因为190A AD ∠=︒，所以Q 在正方形11ADD A内轨迹为半圆，弧长12233=⋅⋅=ππ，选项D 正确；。

第七章立体几何初步【知识图解】【方法点拨】立体几何研究的是现实空间，认识空间图形，可以培养学生的空间想象能力、推理论证能力、运用图形语言进行交流的能力以及几何直观能力。

空间的元素是点、线、面、体，对于线线、线面、面面的位置关系着重研究它们之间的平行与垂直关系，几何体着重研究棱柱、棱锥和球。

在复习时我们要以下几点：1．注意提高空间想象能力。

在复习过程中要注意：将文字语言转化为图形，并明确已知元素之间的位置关系及度量关系；借助图形来反映并思考未知的空间形状与位置关系；能从复杂图形中逻辑的分析出基本图形和位置关系，并借助直观感觉展开联想与猜想，进行推理与计算。

2．归纳总结，分门别类。

从知识上可以分为：平面的基本性质、线线、线面、面面的平行与垂直、空间中角与距离的计算。

3．抓主线，攻重点。

针对一些重点内容加以训练，平行和垂直是位置关系的核心，而线面垂直又是核心的核心，角与距离的计算已经降低要求。

4．复习中要加强数学思想方法的总结与提炼。

立体几何中蕴含着丰富的思想方法，如：将空间问题转化成平面图形来解决、线线、线面与面面关系的相互转化、空间位置关系的判断及角与距离的求解转化成空间向量的运算。

补充知识：空间向量空间向量的许多知识可由平面向量的知识类比而得.下面对空间向量在立体几何中证明，求值的应用进行总结归纳.1、直线的方向向量和平面的法向量 ⑴．直线的方向向量：若A 、B 是直线l 上的任意两点，则AB 为直线l 的一个方向向量；与AB平行的任意非零向量也是直线l 的方向向量. ⑵．平面的法向量：若向量n 所在直线垂直于平面α，则称这个向量垂直于平面α，记作n α⊥ ，如果n α⊥，那么向量n叫做平面α的法向量.⑶．平面的法向量的求法（待定系数法）： ①建立适当的坐标系．②设平面α的法向量为(,,)n x y z =．③求出平面内两个不共线向量的坐标123123(,,),(,,)a a a a b b b b ==．④根据法向量定义建立方程组0n a n b ⎧⋅=⎪⎨⋅=⎪⎩ .⑤解方程组，取其中一组解，即得平面α的法向量.（如图）1、 用向量方法判定空间中的平行关系 ⑴线线平行设直线12,l l 的方向向量分别是a b 、，则要证明1l ∥2l ，只需证明a ∥b ，即()a kb k R =∈.即：两直线平行或重合两直线的方向向量共线。