工程力学习题集
- 格式:doc
- 大小:799.66 KB
- 文档页数:34

专业 学号 姓名 日期 成绩第一章 静力学基础一、是非判断题1.1 在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ) 1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( ) 1.3 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( ) 1.4 力的可传性只适用于刚体,不适用于变形体。
( ) 1.5 两点受力的构件都是二力杆。
( ) 1.6 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( ) 1.7 力的平行四边形法则只适用于刚体。
( ) 1.8 凡矢量都可以应用平行四边形法则合成。
( ) 1.9 只要物体平衡,都能应用加减平衡力系公理。
( ) 1.10 凡是平衡力系,它的作用效果都等于零。
( ) 1.11 合力总是比分力大。
( ) 1.12 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( ) 1.13 若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ) 1.14 当软绳受两个等值反向的压力时,可以平衡。
( ) 1.15 静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ) 1.16 静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( )1.17 凡是两端用铰链连接的直杆都是二力杆。
( ) 1.18 如图所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、 BC 构件都不是二力构件。
( )二、填空题2.1如图所示,F 1在x 轴上的投影为 ;F 1在y 轴上的投影为 ;F 2在x 轴上的投影为 ;F 2在y 轴上的投影为 ;F 3在x 轴上的投影为 ;F 3在y 轴上的投影为 ;F 4在x 轴上的投影为 ;F 4在y 轴上的投影为 。
轴上的投影为 。
2.2将力F 沿x , y 方向分解,已知F = 100 N, F 在x 轴上的投影为86.6 N, 而沿x 方向的分力的大小为115.47 N , 则F 的y 方向分量与x 轴的夹角β为 ,F 在y 轴上的投影为 。
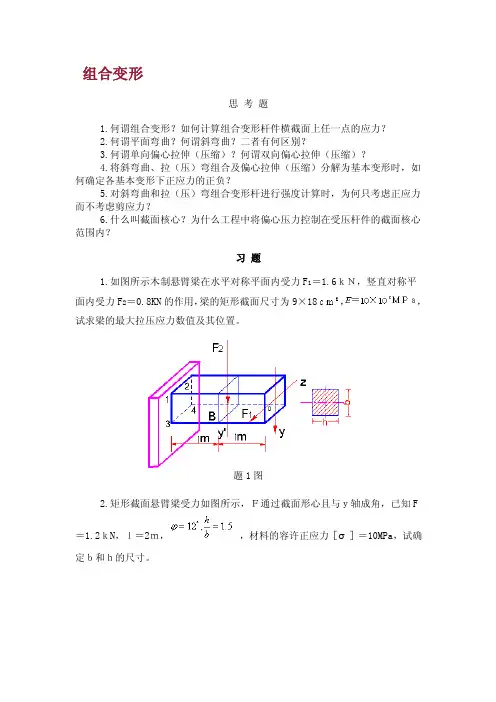
组合变形思考题1.何谓组合变形?如何计算组合变形杆件横截面上任一点的应力?2.何谓平面弯曲?何谓斜弯曲?二者有何区别?3.何谓单向偏心拉伸(压缩)?何谓双向偏心拉伸(压缩)?4.将斜弯曲、拉(压)弯组合及偏心拉伸(压缩)分解为基本变形时,如何确定各基本变形下正应力的正负?5.对斜弯曲和拉(压)弯组合变形杆进行强度计算时,为何只考虑正应力而不考虑剪应力?6.什么叫截面核心?为什么工程中将偏心压力控制在受压杆件的截面核心范围内?习题1.如图所示木制悬臂梁在水平对称平面内受力F1=1.6kN,竖直对称平面内受力F2=0.8KN的作用,梁的矩形截面尺寸为9×18,,试求梁的最大拉压应力数值及其位置。
题1图2.矩形截面悬臂梁受力如图所示,F通过截面形心且与y轴成角,已知F =1.2kN,l=2m,,材料的容许正应力[σ]=10MPa,试确定b和h的尺寸。
题2图3.承受均布荷载作用的矩形截面简支梁如图所示,q与y轴成角且通过形心,已知l=4m,b=10cm,h=15cm,材料的容许应力[σ]=10MPa,试求梁能承受的最大分布荷载。
题3图4.如图所示斜梁横截面为正方形,a=10cm,F=3kN作用在梁纵向对称平面内且为铅垂方向,试求斜梁最大拉压应力大小及其位置。
题4图5.柱截面为正方形,边长为a,顶端受轴向压力F作用,在右侧中部挖一个槽(如图),槽深。
求开槽前后柱内的最大压应力值。
题5图6.砖墙及其基础截面如图,设在1m长的墙上有偏心力F=40kN的作用,试求截面1-1和2-2上的应力分布图。
题6图7.矩形截面偏心受拉木杆,偏心力F=160kN,e=5cm,[σ]=10MPa,矩形截面宽度b=16cm,试确定木杆的截面高度h。
题7图8.一混凝土重力坝,坝高H=30m,底宽B=19m,受水压力和自重作用。
已知坝前水深H=30m,坝体材料容重,许用应力[]=10MPa,坝体底面不允许出现拉应力,试校核该截面正应力强度。

工程力学习题集2009年11月第一章习题1.1 画出图 1.1(a) ~ (f) 中各物体的受力图。
未画重力的物体 , 质量均不计 , 所有接触处均为光滑接触。
1.2 画出图 1.2 所示各物体系中各物体的受力图。
未画重力的物体 , 质量均不计 , 所有接触处均为光滑接触。
1.4 如图 1.4 所示矩形搁板ABCD 可绕轴线AB 转动,M 、K 均为圆柱铰链 , 搁板用DE 杆支撑于水平位置,撑杆DE 两端均为铰链连接,搁板重为W ,试画出搁板的受力图。
1.5 图 1.5 所示为一水轮机简图,巳知使水轮机转动的力偶矩M z ,在锥齿轮B 处的力分解为三个分力:圆周力F t 、轴向力F a 、径向力F r ,试画出水轮机的受力图。
第二章习题2.1 已知图 2.1 中,F 1 = 150N ,F 2 = 200N 及F 3 = l00N 。
试用图解法及解析法求这四个力的合力。
2.2 起重用的吊环如题图 2.2 所示,侧臂AB 及AC 均由两片组成,吊环自重可以不计,起吊重物P =1200KN ,试求每片侧臂所受的力。
2.3 图示梁在A 端为固定铰支座,B 端为活动铰支座,P =20KN 。
试求在图示两种情形下A 和B 处的约束反力。
2.4 图示电动机重 W=5KN ,放在水平梁AC 的中间,A 和B 为固定铰链,C 为中间铰链,试求A 处的约束反力及杆BC 所受的力。
2.5 简易起重机用钢绳吊起重量G =2000N 的重物。
各杆的自重、滑轮的自重和尺寸都忽略不计,试求杆AB 和AC 受到的力。
假定A 、B 、C 三处可简化为铰链连接。
2.6 重为G =2KN 的球搁在光滑的斜面上,用一绳把它拉住。
巳知绳子与铅直墙壁的夹角为30 0 ,斜面与水平面的夹角为15° ,试求绳子的拉力和斜面对球的约束反力。
2.7 压榨机构如图所示,杆AB 、BC 自重不计,A 、B 、C 都可看作为铰链连接,油泵压力P =3KN ,方向水平。

工程力学习题集(总34页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第9章 思考题在下面思考题中A 、B 、C 、D 的备选答案中选择正确的答案。
(选择题答案请参见附录)9.1 若用积分法计算图示梁的挠度,则边界条件和连续条件为。
(A) x=0: v=0; x=a+L: v=0; x=a: v 左=v 右,v /左=v /右。
(B) x=0: v=0; x=a+L: v /=0; x=a: v 左=v 右,v /左=v /右。
(C) x=0: v=0; x=a+L: v=0,v /=0; x=a: v 左=v 右。
(D) x=0: v=0; x=a+L: v=0,v /=0; x=a: v /左=v /右。
梁的受力情况如图所示。
该梁变形后的挠曲线为图示的四种曲线中的 (图中挠曲线的虚线部分表示直线,实线部分表示曲线)。
xxxx(A)(B)等截面梁如图所示。
若用积分法求解梁的转角和挠度,则以下结论中(A) 该梁应分为AB 和BC 两段进行积分。
(B) 挠度的积分表达式中,会出现4个积分常数。
(C) 积分常数由边界条件和连续条件来确定。
(D) 边界条件和连续条件的表达式为:x=0:y=0; x=L,v 左=v 右=0,v/=0。
结论中AxAx(A) AB杆的弯矩表达式为M(x)=q(Lx-x2)/2。
(B) 挠度的积分表达式为:y(x)=q{∫[∫-(Lx-x2)dx]dx+Cx+D}/2EI。
(C) 对应的边解条件为:x=0: y=0; x=L:y=∆L CB(∆L CB=qLa/2EA)。
(D) 在梁的跨度中央,转角为零(即x=L/2: y/=0)。
已知悬臂AB如图,自由端的挠度vB=-PL3/3EI –ML2/2EI,则截面CM(A) -P(2L/3)3/3EI –M(2L/3)2/2EI。
(B) -P(2L/3)3/3EI –1/3M(2L/3)2/2EI。

工程力学习题答案第一章静力学基础知识思考题:1. X ;2. V ;3. V ;4. V ;5. K 6. K 7. V ;8. V习题一1•根据三力汇交定理,画出下面各图中A 点的约束反力方向。
解:(a )杆AB 在 A B 、C 三处受力作用。
u由于力p和uuv R B 的作用线交于点Q 如图(a )所示,根据三力平衡汇交定理, 可以判断支座A 点的约束反力必沿 通过A 0两点的连线。
uP 3uvB 处受绳索作用的拉力uuv R B (b )同上。
由于力交于0点,根据三力平衡汇交定理, 可判断A 点的约束反力方向如 下图(b )所示。
的作用线 2.不计杆重,画出下列各图中 AB 杆的受力图。
uP 解:(a )取杆AB 和E 两处还受光滑接触面约束。
约束力UJVN E uuvuuN A 和 N E,在A的方向分别沿其接触表面的公法线, 外,在 并指向杆。
其中力uuvN A 与杆垂直,通过半圆槽的圆心 Q力 AB 杆受力图见下图(a )。
和C 对它作用的约束力 NBo------- r -------- —y —uuv N C铰销此两力的作用线必须通过(b )由于不计杆重,曲杆 BC 只在两端受 故曲杆BC 是二力构件或二力体,和 B 、C 两点的连线,且B O两点的连线。
见图(d).第二章力系的简化与平衡思考题:1. V ;2.>;3. X ;4. K 5. V ;6.$7.>;8. x ;9. V .1.平面力系由三个力和两个力偶组成, 它们的大小和作用位置如图示,长度单位为cm 求此力系向O 点简化的结果,并确定其合力位置。
uvR R 解:设该力系主矢为 R ,其在两坐标轴上的投影分别为Rx、y。
由合力投影定理有:。
4.梁AB 的支承和荷载如图, 小为多少?解:梁受力如图所示:2. 位置:d M o /R 25000.232 火箭沿与水平面成F ,100 0.6100 80 2000 0.5 580m 23.2cm,位于O 点的右侧。

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F BC AB 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交 NF N F F F FF F F C A GA yC A x 200020110/1tan sin ,0,cos ,0=======∑∑解得:ααα2-4 图示为一拔桩装置。
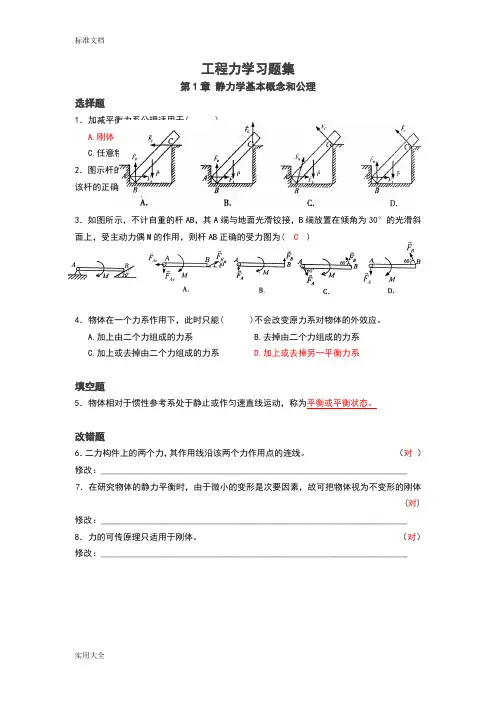

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)2 第一章静力学基础(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)第一章静力学基础 3(a)1—3 画出图中指定物体的受力图.所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)4 第一章静力学基础(b)(c)(d)第一章静力学基础 5 (e)6 第一章静力学基础(f)(g)第四章 材料力学基本概念 7第二章 平面力系2—1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力.题2—1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得:N P F F B A 5000===8 第一章 静力学基础2—2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起.设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接.当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2—2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得:PF P F BC AB 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。

1.力在平面上的投影(矢量)与力在坐标轴上的投影(代数量)均为代数量。
正确2.力对物体的作用是不会在产生外效应的同时产生内效应。
错误3.在静力学中,将受力物体视为刚体(D)A. 没有特别必要的理由B. 是因为物体本身就是刚体C. 是因为自然界中的物体都是刚体D. 是为了简化以便研究分析。
4.力在垂直坐标轴上的投影的绝对值与该力的正交分力大小一定相等。
正确5.轴力图、扭矩图是内力图,弯矩图是外力图。
错误6.胡克定律表明,在材料的弹性变形范围内,应力和应变(A)A .成正比B .相等C .互为倒数 D. 成反比7.材料力学的主要研究对象是(B)A.刚体B.等直杆C.静平衡物体D.弹性体8.通常工程中,不允许构件发生(A)变形A.塑性B.弹性C.任何D.小9.圆轴扭转时,同一圆周上的切应力大小(A)A.全相同B.全不同C.部分相同D.部分不同10.杆件两端受到等值、反向且共线的两个外力作用时,一定产生轴向拉伸或压缩变形。
正确1.材料力学的主要研究对象是(B)A.刚体B.等直杆C.静平衡物体D.弹性体2.构件的许用应力是保证构件安全工作的(B)A.最低工作应力B.最高工作应力C.平均工作应力D.极限工作应力3.低碳钢等塑性材料的极限应力是材料的(A)A.屈服极限B.许用应力C.强度极限D.比例极限4.一个力作平行移动后,新点的附加力偶矩一定(B)A.存在B.存在且与平移距离有关C.不存在D.存在且与平移距离无关5.力矩不为零的条件是(A)A.作用力和力臂均不为零B.作用力和力臂均为零C. 作用力不为零D.力臂不为零6.构件抵抗变形的能力称为(B)A.强度B.刚度C.稳定性D.弹性7.工程实际计算中,认为切应力在构件的剪切面上分布不均匀。
错误8.力在垂直坐标轴上的投影的绝对值与该力的正交分力大小一定相等。
正确9.圆轴扭转时,横截面上的正应力与截面直径成正比。
错误10.扭转时的内力是弯矩。
错误1.各力作用线互相平行的力系,都是平面平行力系。
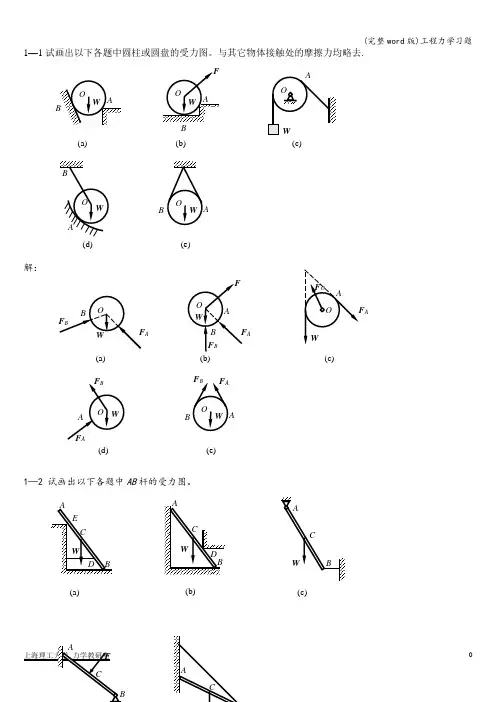
1—1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去.解:1—2 试画出以下各题中AB 杆的受力图。
(a)B(b)(c)(d)(e)A(a)(b) A(c)A(d)(e)(c)(a)(b)解:1—3 试画出以下各题中AB 梁的受力图。
解:(e)B B(a) B(b)(c)F B(a) (c)F (b)(d)(e)F WA1—4 试画出以下各题中指定物体的受力图.(a) 拱ABCD;(b)半拱AB部分;(c) 踏板AB;(d)杠杆AB;(e)方板ABCD;(f) 节点B。
解:(d)D(e)F Bx(a) (b) (c)(d) (e)W(f)(a)D(b) CB(c)BF DF CBFF BC1-5 试画出以下各题中指定物体的受力图。
(a)结点A,结点B;(b) 圆柱A和B及整体;(c) 半拱AB,半拱BC及整体;(d)杠杆AB,切刀CEF 及整体;(e) 秤杆AB,秤盘架BCD及整体.解:(a)(b)(c)(c) (d)ATF BAF(b)D(e)(d)(e)’CB2—2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2—3 水平力F 作用在刚架的B 点,如图所示.如不计刚架重量,试求支座A 和D 处的约束力。
解:(1) 取整体ABCD 为研究对象,受力分析如图,画封闭的力三角形:(2)F 1F FDF F AF D211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴===2—4 在简支梁AB 的中点C 作用一个倾斜45o的力F ,力的大小等于20KN ,如图所示。

《工程力学》课程习题集西南科技大学成人、网络教育学院版权所有习题【说明】:本课程《工程力学》(编号为14001)共有单选题,计算题等多种试题类型,其中,本习题集中有[单选题]等试题类型未进入。
一、计算题1.如图所示重力为W的钢管放置在刚性墙和平板之间,管子与平板中点D接触,管子与墙和平板均为光滑接触。
平板下端与墙铰接,上端与墙用缆绳连接,平板与墙的夹角为300。
试求铰链A的约束力和缆绳BC的拉力。
(18分)2.如图所示等直杆,直径为d,AB、BC段的长度均为L ,材料的弹性模量为E AB= 2E BC=E , 绘出杆件的轴力图,并求出杆的总变形△L (不计杆的自重)。
(18分)绘出如图所示梁的弯矩图和剪力图。
(18分)4. 如图所示悬臂梁(抗弯刚度为EI ),求A 、B 点的挠度和转角。
(18分)5. 如图微元为某平面受力构件中一点的受力状态,其应力σx =20 MPa ,σy =10 MPa ,τxy = 5 MPa 。
(1)求主应力和主方向;(2)在Mohr 应力圆上指出代表主平面和以x 、y 为法线的平面的点。
(18分)6. 如图为同时受扭矩m 和轴向力P 作用的实心圆轴。
(1)指出圆轴危险点的位置,并画出危险点的应力状态。
(2)已知P 、m = Pd/8、材料的许用应力为『σ』,试用第三强度理论(最大剪应力强度理论)设计该轴的直径d 。
(18分)7. 如图所示上下铰接,长为L,直径为D的圆形截面压杆,承受沿杆轴线方向的压力。
材料的弹性模量为E,许用(容许)应力为[σ]。
求压杆的临界荷载;并确定柔度小于何值时就不会首先出现稳定性失效?(18分)8. 两个直径为d ,重为P 的钢球,装在直径为D (d<D<2d )的桶内,不计桶的变形和钢球与桶、钢球与钢球的摩擦。
求钢球之间的作用力、钢球对桶壁的作用力、钢球对桶底的作用力。
(18分)xσ9.绘出图所示梁的剪力图和弯矩图。
(18分)10.如图所示圆截面轴AC,其直径为d,绘出轴AC的扭矩图,并求出最大扭转剪应力。
一、 单项选择题(本大题共5小题,每小题2分,共10分)1、用三种不同材料制成尺寸相同的试件, 在相同的试验条件下进行拉伸试验,得到的应力—应变曲线如图示。
比较三条曲线,可知拉伸强度最高、弹性模量最大、塑性最好的材料分别是( CA. a 、b 、c ;B. b 、c 、a ;C. b 、a 、cD. c 、b 、a2、在校核图示拉杆头部的剪切强度和挤压强度时,剪切面和挤压面的面积 分别为:( A ) A. dh π;(224D dπ-C.()224D d π-;π3所用的连续条件是(AA .3c c c c x w w θθ===左右左右时,;;B .3c c x θθ==左右时,;C .3c c x w w ==左右时,。
4、单元体上的应力如图所示,其第三强度理论的相当应力为:(B ) A. 60MPa B. 70MPa C. 10 MPa D.50MPa5、两端铰支的细长压杆,当其横截面直径增加时,则:( )A .其临界压力也增加,临界应力不变;B .其临界压力不变,临界应力增加;C .其临界压力和临界应力均增加;2h 2hy 2A E 1AE a aD .其临界压力和临界应力均降低。
二、 判断题(本大题共10小题,每小题1分,共10分)(F )1、力是滑移矢量,沿其作用线滑移不改变对物体的作用效果。
( T )2、一个力不可能分解为一个力偶,一个力偶也不可能合成为一个力。
( F )3、物体的形心总是与重心重合的。
( T )4、一般情况下,动摩擦系数小于静摩擦系数。
( )5、平面运动刚体的动能等于随质心移动的动能和相对于质心转动的 动能两者之和。
( T )6、点的速度合成定理指的是动点的绝对速度等于其牵连速度和 相对速度的矢量和。
( )7、平面图形随基点移动的规律与基点的选择无关。
( )8、当质点系的动量守恒时,其中各质点的动量也保持不变。
( )9、转动惯量是刚体转动时惯性的度量。
( )10、质点的惯性力并非质点本身所受的力,而是质点作用于 施力物体上的力。
——————————————工程力学习题——————————————第一章绪论思考题1) 现代力学有哪些重要的特征?2) 力是物体间的相互作用。
按其是否直接接触如何分类?试举例说明。
3) 工程静力学的基本研究内容和主线是什么?4) 试述工程力学研究问题的一般方法。
第二章刚体静力学基本概念与理论习题2-1 求图中作用在托架上的合力F R。
习题2-1图2-2 已知F 1=7kN ,F 2=5kN, 求图中作用在耳环上的合力F R 。
2-3 求图中汇交力系的合力F R 。
2-4 求图中力F 2的大小和其方向角α。
使 a )合力F R =1.5kN, 方向沿x 轴。
b)合力为零。
2习题2-2图(b)F 1F 1F 2习题2-3图(a )F 1习题2-4图2-5 二力作用如图,F 1=500N 。
为提起木桩,欲使垂直向上的合力为F R =750N ,且F 2力尽量小,试求力F 2的大小和α角。
2-6 画出图中各物体的受力图。
F 12习题2-5图(b)(a)(c)(d)AC2-7 画出图中各物体的受力图。
(f)(g) 习题2-6图(b)(a )DC2-8 试计算图中各种情况下F 力对o 点之矩。
(d)习题2-7图习题2-8图 P(d)(c)(a ) A2-9 求图中力系的合力F R 及其作用位置。
习题2-9图( a )1F 3 ( b )F 3F 2( c) 1F /m( d )F 32-10 求图中作用在梁上的分布载荷的合力F R 及其作用位置。
2-11 图示悬臂梁AB 上作用着分布载荷,q 1=400N/m ,q 2=900N/m, 若欲使作用在梁上的合力为零,求尺寸a 、b 的大小。
( a )q 1=600N/m2( b )q ( c )习题2-10图B习题2-11图第三章静力平衡问题习题3-1 图示液压夹紧装置中,油缸活塞直径D=120mm,压力p=6N/mm2,若α=30︒, 求工件D所受到的夹紧力F D。
For personal use only in study and research; not for commercial use工程力学习题集2009年11月第一章习题1.1 画出图 1.1(a) ~ (f) 中各物体的受力图。
未画重力的物体 , 质量均不计 , 所有接触处均为光滑接触。
?1.2 画出图 1.2 所示各物体系中各物体的受力图。
未画重力的物体 , 质量均不计 , 所有接触处均为光滑接触。
1.4 如图 1.4 所示矩形搁板ABCD 可绕轴线AB 转动,M 、K 均为圆柱铰链 , 搁板用DE 杆支撑于水平位置,撑杆DE 两端均为铰链连接,搁板重为W ,试画出搁板的受力图。
1.5 图 1.5 所示为一水轮机简图,巳知使水轮机转动的力偶矩M z ,在锥齿轮B 处的力分解为三个分力:圆周力F t 、轴向力F a 、径向力F r ,试画出水轮机的受力图。
第二章习题2.1 已知图 2.1 中,F 1 = 150N ,F 2 = 200N 及F 3 = l00N 。
试用图解法及解析法求这四个力的合力。
2.2 起重用的吊环如题图 2.2 所示,侧臂AB 及AC 均由两片组成,吊环自重可以不计,起吊重物P =1200KN ,试求每片侧臂所受的力。
2.3 图示梁在A 端为固定铰支座,B 端为活动铰支座,P =20KN 。
试求在图示两种情形下A 和B 处的约束反力。
2.4 图示电动机重 W=5KN ,放在水平梁AC 的中间,A 和B 为固定铰链,C 为中间铰链,试求A 处的约束反力及杆BC 所受的力。
2.5 简易起重机用钢绳吊起重量G =2000N 的重物。
各杆的自重、滑轮的自重和尺寸都忽略不计,试求杆AB 和AC 受到的力。
假定A 、B 、C 三处可简化为铰链连接。
2.6 重为G =2KN 的球搁在光滑的斜面上,用一绳把它拉住。
巳知绳子与铅直墙壁的夹角为30 0 ,斜面与水平面的夹角为15° ,试求绳子的拉力和斜面对球的约束反力。
工程力学(一)习题集及部分解答指导第一章静力学基础一、判断题1-1.如物体相对于地面保持静止或匀速运动状态,则物体处于平衡。
()1-2.作用在同一刚体上的两个力,使物体处于平衡的必要和充分条件是:这两个力大小相等、方向相反、沿同一条直线。
()1-3.静力学公理中,二力平衡公理和加减平衡力系公理仅适用于刚体。
()1-4.二力构件是指两端用铰链连接并且指受两个力作用的构件。
()1-5.对刚体而言,力是滑移矢量,可沿其作用线移动。
()1-6.对非自由体的约束反力的方向总是与约束所能阻止的物体的运动趋势的方向相反。
()1-7.作用在同一刚体的五个力构成的力多边形自行封闭,则此刚体一定处于平衡状态。
()1-8.只要两个力偶的力偶矩相等,则此两力偶就是等效力偶。
()二、单项选择题1-1.刚体受三力作用而处于平衡状态,则此三力的作用线()。
A、必汇交于一点B、必互相平行C、必都为零D、必位于同一平面内1-2.力的可传性()。
A、适用于同一刚体B、适用于刚体和变形体C、适用于刚体系统D、既适用于单个刚体,又适用于刚体系统1-3.如果力FR是F1、F2二力的合力,且F1、F2不同向,用矢量方程表示为FR=F1+F2,则三力大小之间的关系为()。
A、必有FR=F1+F2B、不可能有FR=F1+F2C、必有FR>F1,FR>F2D、必有FR<F1,FR<F21-4.作用在刚体上的一个力偶,若使其在作用面内转移,其结果是()。
A、使刚体转动B、使刚体平移C、不改变对刚体的作用效果D、将改变力偶矩的大小三、计算题1-1.已知:F1=2000N,F2=150N,F3=200N,F4=100N,各力的方向如图1-1所示。
试求各力在某、y轴上的投影。
解题提示F某=+FcoαFy=+Finα注意:力的投影为代数量;式中:F某、Fy的“+”的选取由力F的指向来确定;α为力F与某轴所夹的锐角。
图1-11-2.铆接薄钢板在孔A、B、C、D处受四个力作用,孔间尺寸如图1-2所示。
一、判断题1、力偶在任一轴上投影为零,故写投影平衡方程时不必考虑力偶。
()2、轴力的大小与杆件的横截面面积有关。
()3、轴力越大,杆件越容易被拉断,因此轴力的大小可以用来判断杆件的强度。
()4、平面图形对任一轴的惯性矩恒为正。
()5、弯曲应力有正应力和剪应力之分。
一般正应力由弯矩引起,剪应力由剪力引起。
()6、构件抵抗变形的能力称为刚度。
()7、作用力与反作用力是一组平衡力系。
()8、两个力在同一轴上的投影相等,此两力必相等。
()9、力偶对其作用面内任意点的力矩值恒等于此力偶的力偶矩,同时与力偶与矩心间的相对位置相关。
()10 、平面任意力系简化后,其主矢量与简化中心有关,主矩与简化中心无关。
()11、力系的合力一定比各分力大。
()12、平面汇交力系由多边形法则及的合力R,其作用点仍为各力的汇交点,其大小和方向与各力相加的次序无关。
()13、作用于物体上的力,均可平移到物体的任一点,但必须同时增加一个附加力偶。
()14、平面任意力系向任一点简化,其一般结果为一个主矢量和一个主矩。
()16、约束反力是被约束物体对其他物体的作用力。
()17、在拉(压)杆中,拉力最大的截面不一定是危险截面。
()18、平面弯曲梁的挠曲线必定是一条与外力作用面重合的平面曲线。
()19、两根材料、杆件长度和约束条件都相同的压杆,则其临界力也必定相同。
()20、主矢代表原力系对物体的平移作用。
()二、填空题1.工程实际中所使用的联接件其主要两种破坏形式为和。
2.实心圆杆扭转剪应力在横截面上的分布为,其中心应力为。
3.平面弯曲是。
4.内力图是指。
5.材料力学中变形固体的基本假设是,,和。
6.截面法的要点是(1);(2);(3)。
8.轴向拉伸(压缩)的强度条件是。
9. 强度是指的能力,刚度是指的能力,稳定性是指的能力。
10.力使物体产生的两种效应是效应和效应。
11.力偶对任意点之矩等于,力偶只能与平衡。
12.从拉压性能方面来说,低碳钢耐铸铁耐。
第9章 思考题在下面思考题中A 、B 、C 、D 的备选答案中选择正确的答案。
(选择题答案请参见附录)9.1 若用积分法计算图示梁的挠度,则边界条件和连续条件为。
(A) x=0: v=0; x=a+L: v=0; x=a: v 左=v 右,v /左=v /右。
(B) x=0: v=0; x=a+L: v /=0; x=a: v 左=v 右,v /左=v /右。
(C) x=0: v=0; x=a+L: v=0,v /=0; x=a: v 左=v 右。
(D) x=0: v=0; x=a+L: v=0,v /=0; x=a: v /左=v /右。
9.2梁的受力情况如图所示。
该梁变形后的挠曲线为图示的四种曲线中的(图中挠曲线的虚线部分表示直线,实线部分表示曲线)。
xxxx x(A)(B)(C)(D)9.3等截面梁如图所示。
若用积分法求解梁的转角和挠度,则以下结论中是错误的。
(A) 该梁应分为AB 和BC 两段进行积分。
(B) 挠度的积分表达式中,会出现4个积分常数。
(C) 积分常数由边界条件和连续条件来确定。
(D) 边界条件和连续条件的表达式为:x=0:y=0; x=L,v 左=v 右=0,v/=0。
9.4等截面梁左端为铰支座,右端与拉杆BC 相连,如图所示。
以下结论中是错误的。
(A) AB 杆的弯矩表达式为M(x)=q(Lx-x 2)/2。
(B) 挠度的积分表达式为:y(x)=q{∫[∫-(Lx-x 2)dx]dx+Cx+D} /2EI 。
(C) 对应的边解条件为:x=0: y=0; x=L: y=∆L CB (∆L CB =qLa/2EA)。
(D) 在梁的跨度中央,转角为零(即x=L/2: y /=0)。
9.5已知悬臂AB 如图,自由端的挠度vB=-PL 3/3EI –ML 2/2EI,则截面C 处的挠度应为。
(A) -P(2L/3)3/3EI –M(2L/3)2/2EI 。
(B) -P(2L/3)3/3EI –1/3M(2L/3)2/2EI 。
(C) -P(2L/3)3/3EI –(M+1/3 PL)(2L/3)2/2EI 。
(D) -P(2L/3)3/3EI –(M-1/3 PL)(2L/3)2/2EI 。
AxAxM9.6 图示结构中,杆AB 为刚性杆,设ΔL1,ΔL2, ΔL3分别表示杆(1),(2),(3(A) ΔL 3=21223ΔL 1。
(C) 2ΔL 2=ΔL 1+ΔL 3。
(D) ΔL 3=ΔL 1+2ΔL 2。
9.7 一悬臂梁及其所在坐标系如图所示。
其自由端的(A) 挠度为正,转角为负; (B) 挠度为负,转角为正; (C) 挠度和转角都为正; (D) 挠度和转角都为负。
9.8 图示悬臂梁AB ,一端固定在半径为R 的光滑刚性圆柱面上,另一端自由。
梁AB 变形后与圆柱面完全吻合,而无接触压力,则正确的加载方式是(A) 在全梁上加向下的均布载荷; (B) 在自由端B 加向下的集中力;(C) 在自由端B 加顺时针方向的集中力偶; (D) 在自由端B 加逆时针方向的集中力偶。
9.9 一铸铁简支梁,如图所示.当其横截面分别按图示两种情况放置时,梁的(A) 强度相同,刚度不同; (B) 强度不同,刚度相同; (C) 强度和刚度都相同; (D) 强度和刚度都不同。
A A v第9章 习题积分法9.1 图示各梁,弯曲刚度EI 均为常数。
(1) 试根据梁的弯矩图与支持条件画出挠曲轴的大致形状; (2) 利用积分法计算梁的最大挠度与最大转角。
习题9.1图解:(a )(1M A =M e(2)画剪力图和弯矩图(3)画挠曲轴的大致形状(4)列弯矩方程],0[)(a x M x M e∈=(5)挠曲线近似微分方程xF S xMq MeA MeM AM AEI M dx v d e=22 (6)直接积分两次C x EIM v e+='=θ D Cx x EI M v e ++=22(7)确定积分常数边界条件:0 ,0 :0===v x θ求解得积分常数0 , 0==D C转角和挠曲线方程是x EIM v e ='=θ, 22x EI M v e =(7)最大转角与最大挠度。
EIaM v e ='=max θ, EI M a v e 22max =(b )(1)求约束反力F A =F B =q a/2(2)画剪力图和弯矩图xxqB(3)画挠曲轴的大致形状(4)列弯矩方程],0[22)(2a x qx x qa x M ∈-=(5)挠曲线近似微分方程)22(1222qx x qa EI dxv d -= (6)直接积分两次C qx x qa EI v +-='=)64(132θD Cx qx x qa EI v ++-=)2412(143(7)确定积分常数边界条件:0 :0==v x 0 :==v a x求解得积分常数0 , 243=-=D EIqa C转角和挠曲线方程是24EIqa -)64(1332qx x qa EI v -='=θ xqx x qa EI v 24EI qa -)2412(1343-=(8)最大转角与最大挠度。
EIqa v 243='=θ,EI qa v 38454-=q9.2 图示各梁,弯曲刚度EI 均为常数。
(1) 试写出计算梁位移的边界条件与连续条件;(2) 试根据梁的弯矩图与支持条件画出挠曲轴的大致形状。
习题9.2图解:(a )(1)边界条件:0 :0==v x0 :==v l x(2)连续光滑条件:+-+-===θθ; :2v v lx (3)求约束反力F A =F B =M e /l(4)画剪力图和弯矩图(a)xF xM(a)(d)Bq(b)C(c)A q(5)画挠曲轴的大致形状(b )(1)边界条件:0 :0==v x0 :2==v lx(2)连续光滑条件:+-+-===θθ; :2v v lx (3)求约束反力F A =F, F B=2F(4)画剪力图和弯矩图(5)画挠曲轴的大致形状(a)CxM(b)CxF S(c )(1)边界条件:0 0,:0===v x θ (2)连续光滑条件:2121; :2θθ===v v lx (3)求约束反力F A =ql/2, M A =3ql 2/8 (4)画剪力图和弯矩图(5)画挠曲轴的大致形状(d )(1)边界条件:0 :0==v x 0 0, :===v l x θ(2)连续条件:21 :2v v lx ==F xM-3ql 2/8(c)C AF M A(c)Cq(3)求约束反力F A =ql/4 =F B , M B =ql 2/8(4)画剪力图和弯矩图(5)画挠曲轴的大致形状叠加法9.3 图示各梁,弯曲刚度EI 均为常数,试用叠加法计算截面B 的转角与截面C 的挠度。
习题9.3图(b)C(a)x(d)BqF S(d)B qM B F解:a )(1)F 单独作用时EI Fl v EI Fl FC FB 48163)2)-==θ(2)Me 单独作用时EI l M v EI l M e MeC e Me B 48332))-==θ(3)P 和Mo 共同作用时EIl M EI Flv v v EIl M EI Fl e Me C FC C eMe B FB B 4834831623))2))--=+=+=+=θθθ(b )EIFlEI Fl l EI Fl EI Fl l l EI lF v v v e C C C 4811325243)23(6)2(33232)2()1(=+-=+--=+=(1) +(2)(1)CA +(2)CEIFl EI lFl EI l M eB 42222===θ9.4 图示外伸梁,两端承受载荷F 作用,弯曲刚度EI 为常数,试问:(1) 当x/l 为何值时,梁跨度中点的挠度与自由端的挠度数值相等; (2) 当x/l 为何值时,梁跨度中点的挠度最大。
习题9.4图解:(2)C(2)C+(22)CA(21)CA (1+2)CD (1) + M B(1)自由端的挠度EIx l Fx EI Fx EI xx l M EI x x l M EI Fx v v v A A A 2)2(33)2(6)2(3233)2()1(---=-----=+= (2)中点的挠度EIx l Fx EI x l M v M8)2(16)2(222-=-=(3)中点的挠度与自由端的挠度数值相等时M A v v =EIx l Fx EI x l Fx EI Fx 8)2(2)2(3223-=-+ x (1)=0.705l (舍去), x (2)=0.152l(4)跨度中点的最大挠度0=dxdv M08)812(22=+-=EIl xl x F dx dv M x (1)= l/2(舍去), x (2)= l /69.5 试计算图示刚架截面A 的水平与铅垂位移。
设弯曲刚度EI 为常数。
习题9.5图F解:(1)水平位移δx分析CB 杆,由B 点水平位移引起EI Fah EI h M v B B x 2222===δEI Fah EI h M B B -=-=θ(2)铅垂位移δx分析AB 、CB 杆,由AB 杆A 点铅垂位移与CB 杆B 点转角引起A 点铅垂位移 EIh a Fa EI FahaEI Fa a v BAB A y 3)3(323)(+-=--=+=θδ9.6 试用叠加法计算图示各阶梯梁的最大挠度。
设惯性矩I 2=2I 1。
习题9.6图解:(a )13)1(3EI Fa v A -=(a)(b)M A =F a FB (1)A (2)A+131212)21(4323)2(3)22()2(3EI Fa a I E Faa aa I E a M v B A -=-=--=1312)22(125)23()2(6EI Fa a a I E Fa v A -=-⋅-=13131313)22()21()1(23125433EI Fa EI Fa EI Fa EI Fa v v v v A A A A -=---=++=∴(b )由梁的对称性,其右半端的变形与图中悬臂梁的变形相同。
由上题结论得:1313max 432)2(3EI Fa EI a F v v v B C -=-=-==∴F B =F/2 (22)A (21)A+9.7 一跨度l=4m 的简支梁如图所示,受集度q =10 kN/m 的均布载荷和P =20kN 的集中载荷作用。
梁由两槽钢组成。
设材料的许用应力[σ]=160MPa ,梁的许用挠度[ f ]=l/400。
试选定槽钢的型号,并校核其刚度。
梁的自重忽略不计。
习题9.7图解:(1)求约束反力30 2204102kN P ql F F B A =+⨯=+== (2)画出剪力图和弯矩图(3)[][]33463max max max 125 1025.110160210402 2cm m M W W M=⨯=⨯⨯⨯=≥∴≤=-σσσ查槽钢表,选用18号,其抗弯截面系数是W=152 cm 3,I =1370 cm 4; (4) 按刚度进行校核:用叠加法求梁的最大挠度m ql Pl EI EI ql EI Pl v v C 0109.0384410105484102010137021020013845481384548214333894343max =⎪⎪⎭⎫ ⎝⎛⨯⨯⨯+⨯⨯⨯⨯⨯⨯=⎪⎪⎭⎫⎝⎛+=--==-M Fs 30刚度校核∵[ f ]=l /400=4/400=0.01m ∴][m 0109.0max f v >= 轴的刚度不够。