对象特性和建模讲解
- 格式：ppt
- 大小：595.00 KB
- 文档页数：53
下载文档原格式
合集下载
化工仪表及自动化教案第8章
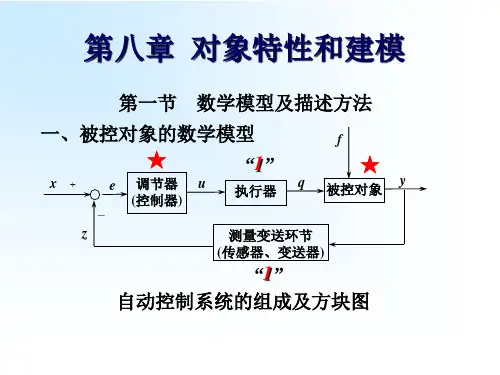
第八章 对象特性和建模内容提要:1.自动控制系统的组成2.自动控制系统的方块图3.过渡过程和品质指标1.数学模型及描述方法被控对象数学模型自动控制系统是由被控对象、测量变送装置、控制器和执行器组成。
系统的控制质量与被控对象的特性有密切的关系。
研究对象的特性，就是用数学的方法来描述出对象输入量与输出量之间的关系。
这种对象特性的数学描述就称为对象的数学模型。
干扰作用和控制作用都是引起被控变量变化的因素，如下图所示。
几个概念：输出变量；输入变量；通道 ；控制通道；干扰通道。
对象的数学模型分为静态数学模型和动态数学模型数学模型的表达形式分类非参量模型当数学模型是采用曲线或数据表格等来表示时，称为非参量模型。
非参量模型可以通过记录实验结果来得到，有时也可以通过计算来得到。
特点：形象、清晰，比较容易看出其定性的特征 。
缺点：直接利用它们来进行系统的分析和设计往往比较困难 。
表达形式：对象在一定形式输入作用下的输出曲线或数据来表示 。
参量模型当数学模型是采用数学方程式来描述时，称为参量模型。
对象的参量模型可以用描述对象输入、输出关系的微分方程式、偏微分方程式、状态方程、差分方程等形式来表示。
对于线性的集中参数对象通常可用常系数线性微分方程式来描述，如果以x （t ）表示输入量，y （t ）表示输出量，则对象特性可用下列微分方程式来描述()()()()()()()()()()()()t x b t x b t x b t x b t y a t y a t y a t y a m m m m n n n n 01110111+'+++=+'+++----在允许的范围内，多数化工对象动态特性可以忽略输入量的导数项可表示为()()()()()()()t x t y a t y a t y a t y a n n n n =+'+++--01112.机理建模 根据对象或生产过程的内部机理，列写出各种有关的平衡方程，如物料平衡方程、能量平衡方程、动量平衡方程、相平衡方程以及某些物性方程、设备的特性方程、化学反应定律、电路基本定律等，从而获取对象（或过程）的数学模型，这类模型通常称为机理模型。
简述建模的几点基本原理。
简述建模的几点基本原理。
建模是通过对现实问题或系统进行抽象和描述，建立相应的数学模型来研究和解决问题的过程。
建模的基本原理如下：
1. 确定研究对象：建模的第一步是确定研究对象，了解其特性、属性等，以便针对性地选择建模方法和建立数学模型。
2. 确定变量：变量是数学模型中的重要组成部分，建模需要确定哪些因素对研究对象产生影响，将其转化为数学变量，并进行量化和分析。
3. 建立模型：根据研究对象和变量，选择合适的数学模型，并进行建模。
模型的建立需要考虑模型的简洁性、可靠性、实用性等因素，以及模型的假设和局限性。
4. 模型求解：完成模型的建立后，需要对其进行求解，即通过数学方法求解模型的解析解或数值解，以获取研究对象的相关信息和预测结果。
5. 模型验证：建立的模型需要进行验证，检验其预测结果是否准确、可靠，并进行模型的修正和改进，以提高模型的精度和实用性。
总之，建模是一个复杂的过程，需要综合运用数学、物理、计算机等多学科知识，以及实践经验和创新思维。
建模的基本原理是建立在科学、严谨、实用和创新的基础上的。
- 1 -。
第一章 建立数学模型
分析：每天报纸的需求量随机，报童 每天的利润也是随机的．只能以长期 售报过程中每天的平均利润最大为目 标，确定最佳决策．
(3)每天的利润与哪些因素有关？ 设每天的利润为随机变量Q， Q＝ Q(n,r,a,b,c) 每天应购进多少份报纸n, 确定性变量 每天报纸的需求量r, 随机变量
每份报纸的购进价a, 参变量 每份报纸的零售价b,每份报纸的退回价c
0 n n
其中
，
1 ( x )2 p( x) exp( ) 2 2 2
可通过假设3计算
n
Max S (n) 0 [(b a) x (a c)(n x)] p( x)dx n (b a)n] p(x)dx
Max S (n) 0 [(b a) x (a c)(n x)] p( x)dx n (b a)n] p(x)dx
1)当 b a c 时，即购进价与退回价相同且零售价高于购进 价，报童不承担任何卖不出去的风险，他将从发行商处购 进尽可能多（无穷多）的报纸．这样必然造成发行商的损 失． 2)当b a c 时，即零售价与购进价相同且高于退回价， 报童无利润可得，他不从发行商处购进任何报纸 n 0 ( )． 这样发行商也无法获得任何利益．
• 作出简化假设（设降落伞所受空气阻力与速度成正比） 小提示：上述模型通过合理假设简化了现实的情况，一般， 模型只能近似表示实际的行为。一种非常强有力的简化关系是比例性。 (刻画了变量间的一种简单的线性关系)
• 用符号表示有关量（降落伞速度 V(t);重力P;阻力R;外力
F; 质量m;加速度a(t);重力加速度g）；
Max S(n)＝[(b a)r (a c)(n r )] f (r ) [(b a)n] f (r )
第二章过程特性及其数学模型(与“对象”有关文档共14张)
1）阶跃响应曲线法
2）矩行脉冲法
Q1
Q1
B
A
0
t
t
h
y
0 t1
t
t
图2-9 储槽的阶跃响应曲线
第7页，共14页。
矩形脉冲特性曲线
第三节 描述对象特性的参数
一、放大系数K
前面讨论了对象特性的描述方法，即水槽对象的输入 与输出的关系。得微分方程式。K称为放大系数，
T
dhh dt
KQ1
解微分方程得
说明当对象受到阶跃线
0
第13页，共14页。
纯滞后特性
滞后时间 示意图
第14页，共14页。
第5页，共14页。
h1 t1
Q2 Rs
t
t
h Q2 Rs
Rs—阀的阻力
代入上式
(Q1
h Rs
)dt
Adh
整理得 ARs ddhthRsQ1
令：T=ARs K=Rs
dh 所以 T dt hKQ1 一阶微分方程
第6页，共14页。
代入边界条件解微分方程
t
hKQ 1(1e T)
h
h1
0 t1
t
储槽的阶跃响应曲线
输出 h 是如何变化的。如图
t
hKQ 1(1e T)
Q1 B
t
hKB(1e T)
当t→∞时，
h(∞)=KB 或 K=h(∞)/B
放大系数，是对象的静态参数 第8页，共14页。
0
t
h
h(∞)
0
t
t1
储槽的阶跃响应曲线
意义：
1.放大系数的大小可以说明对象的灵敏度；
2.K大灵敏度高，稳定性下降；
第二章 过程特性及其数学模型-赵金才
为了进一步理解放大系数K与时间常数T的物理意义， 下面结合图2—2所示的水槽例子，来进一步加以说明。
由前面的推导可知,简单水槽的对象特性如下式所示。
假定Q1为阶跃作用，t＜0时Q1＝0；t≥0时Q1＝A，如图 2—16(a)所示。为了求得在Q1 作用下h的变化规律，可以对 上述微分方程式求解，得： −，当流人流量Q1有 一定的阶跃变化后，液位h也会有相应的变化，但最后会 稳定在某一数值上。为什么？ 如果我们将流量Q1的变化看作对象的输入、而液位h的 变化看作对象的输出，那么在稳定状态时，对象一定的输 入就对应着—定的输出，这种特性称为对象的静态特性。
其数学模型为：
(2) 一阶 电路 一阶RC电路
图2—3为RC电路，若取ei为输人参数，eo输出参数。
根据基尔霍夫定律可得：
ei = iR + e0
显然，i为中间变量，应消去，因为
de0 i=C dt
Q idt C= = U de0
联立两式，得
de0 RC + e0 = ei dt
或
de0 T + e0 = ei dt
h(∞) K= h(∞) = KA 或 A 这就是说，K是对象受到阶跃输入作用后，被控变量新 的稳定值与所加的输入量之比，故是对象的放大系数。它表 示对象受到输入作用后，重新达到平衡状态时的性能，是不 随时间而变的，所以是对象的静态性能。
1．阶跃反应曲线法 阶跃反应曲线法 所谓测取对象的阶跃反应曲线，就是用实验的方法测取对 象在阶跃输入作用下，输出量y随时间的变化规律。 例如要测取图2—7所示简单水槽的动态特性，这时，表征 水槽工作状况的物理量是液位h，我们要测取输入流量Q1 改变时，输出h的反应曲线。
优点：方法比较简单，不需要专用设备和仪器。 缺点：主要是对象在阶跃信号作用下，从不稳定到稳定 一般所需时间较长，在这样长的时间内，对象不可避免要 受到许多其他干扰因案的影响，因而测试精度受到限制。 为了提高精度，就必须加大所施加的输入作用幅值，可 是这样做就意味着对正常生产的影响增加，工艺上往往是 不允许的。 一般所加输入作用的大小是取额定值的5％~10％。因此， 阶跃反应曲线法是一种简易但精度较差的对象动态特性测试 方法。
第二章 过程特性及其数学模型
A—水槽截面积 将dV代入
0 h h2
t1
t
(Q1 Q2 )dt Adh
h1
t1
t
h Q2 Rs
Rs—阀的阻力
h )dt Adh 代入上式 (Q1 Rs
整理得
dh ARs h Rs Q1 dt
K=Rs
一阶常系数微分 方程
令：T=ARs 所以
dh T h KQ1 dt
t dh T h KQ1 解微分方程得 h KQ (1 e T ) 1 dt
当对象受到阶跃变化Q1=A 输出h是如何变化的。如图
Q1
A
0
h KA(1 e )
当t →∞时， h(∞)=KA 或 K=h(∞)/A
t T
t
h
h(∞) 0
t1
t
放大系数，是对象的静态参数
储槽的阶跃响应曲线
三、对象动态特性的研究方法 1.理论分析 根据系统工艺实际过程的数质量关系，分析计算 输入量与输出量之间的关系。
2.实验研究 需要在实际系统或实验系统中，通过一组输入 ,来 考察输出的跟随变化规律—反映输入与输出关系 的经验曲线和经验函数关系。
第二节 对象数学模型的建立
一、 机理建模法 机理法建摸就是根据生产过程的内在机理，写出各 种有关平衡方程式。如物料平衡方程式、能量平衡 1 方程式等。 1、一阶对象（单容对象） 举例 如图所示为一液体储槽对象 其静态方程
11．已知一个对象特性是具有纯滞后的一阶特性， 其时间常数为5，放大系数为10，纯滞后时间为2 ，试写出描述该对象特性的一阶微分方程式。
无滞后 有滞后 一阶微分方程式：
dy(t 2) 5 y(t 2) 10 x(t ) dt
0 h h2
t1
t
(Q1 Q2 )dt Adh
h1
t1
t
h Q2 Rs
Rs—阀的阻力
h )dt Adh 代入上式 (Q1 Rs
整理得
dh ARs h Rs Q1 dt
K=Rs
一阶常系数微分 方程
令：T=ARs 所以
dh T h KQ1 dt
t dh T h KQ1 解微分方程得 h KQ (1 e T ) 1 dt
当对象受到阶跃变化Q1=A 输出h是如何变化的。如图
Q1
A
0
h KA(1 e )
当t →∞时， h(∞)=KA 或 K=h(∞)/A
t T
t
h
h(∞) 0
t1
t
放大系数，是对象的静态参数
储槽的阶跃响应曲线
三、对象动态特性的研究方法 1.理论分析 根据系统工艺实际过程的数质量关系，分析计算 输入量与输出量之间的关系。
2.实验研究 需要在实际系统或实验系统中，通过一组输入 ,来 考察输出的跟随变化规律—反映输入与输出关系 的经验曲线和经验函数关系。
第二节 对象数学模型的建立
一、 机理建模法 机理法建摸就是根据生产过程的内在机理，写出各 种有关平衡方程式。如物料平衡方程式、能量平衡 1 方程式等。 1、一阶对象（单容对象） 举例 如图所示为一液体储槽对象 其静态方程
11．已知一个对象特性是具有纯滞后的一阶特性， 其时间常数为5，放大系数为10，纯滞后时间为2 ，试写出描述该对象特性的一阶微分方程式。
无滞后 有滞后 一阶微分方程式：
dy(t 2) 5 y(t 2) 10 x(t ) dt
03对象特性
➢ 1.阶跃反应曲线法 ➢ 2.矩形脉冲法 ➢ 3.矩形脉冲波法 ➢ 4.正弦信号法
➢ 1.阶跃反应曲线法:
➢ 突然开大进水阀，引进一阶跃 干扰作用。
➢ 特点:方法简单，但幅度不宜过 大，以免影响工艺参数，一般 取额定值的5-10%。
输 入 量
0 t0
时间 t
1.阶跃反应曲线法
➢ 2.矩形脉冲法:
Q12
)
Q2
h2 R2
⑤
dh2 dt
1 A
(Q12
Q2 )
⑥
Q12
A dh2 dt
Q2
⑦
Q2
将③④代入⑥并求导得：
④
d 2h2 dt 2
1 (1 AR
• dh1 dt
1 R2
•
dh2 ) dt
⑨
将⑧代入⑨并整Biblioteka 得：A R1 A R2d 2h2 dt 2
（AR1
AR2）ddht2
h2
R 2 Q1
1
Q1≠Q2
Q1
(Q1－Q2)dt＝Adh
Q2 不变
h
Q2
dh
1 A
Q1dt
1
h A Q1dt
1
二.机理建模
Q1
➢ 3.二阶对象：
h1
R1
Q12
物料平衡: h2→Q1（t）
(Q1－Q12)dt＝Adh1 ①
h2
R2
(Q12－Q2)dt＝Adh2 ②
Q12
h1 R1
dh1 1
dt A
③
(Q1
输 入 量
0 t0 t1
t2 时间 t
3.矩形脉冲波法
➢ 4.频率特性法(正弦信号):
➢ 1.阶跃反应曲线法:
➢ 突然开大进水阀，引进一阶跃 干扰作用。
➢ 特点:方法简单，但幅度不宜过 大，以免影响工艺参数，一般 取额定值的5-10%。
输 入 量
0 t0
时间 t
1.阶跃反应曲线法
➢ 2.矩形脉冲法:
Q12
)
Q2
h2 R2
⑤
dh2 dt
1 A
(Q12
Q2 )
⑥
Q12
A dh2 dt
Q2
⑦
Q2
将③④代入⑥并求导得：
④
d 2h2 dt 2
1 (1 AR
• dh1 dt
1 R2
•
dh2 ) dt
⑨
将⑧代入⑨并整Biblioteka 得：A R1 A R2d 2h2 dt 2
（AR1
AR2）ddht2
h2
R 2 Q1
1
Q1≠Q2
Q1
(Q1－Q2)dt＝Adh
Q2 不变
h
Q2
dh
1 A
Q1dt
1
h A Q1dt
1
二.机理建模
Q1
➢ 3.二阶对象：
h1
R1
Q12
物料平衡: h2→Q1（t）
(Q1－Q12)dt＝Adh1 ①
h2
R2
(Q12－Q2)dt＝Adh2 ②
Q12
h1 R1
dh1 1
dt A
③
(Q1
输 入 量
0 t0 t1
t2 时间 t
3.矩形脉冲波法
➢ 4.频率特性法(正弦信号):
面向对象的概念面向对象建模面向对象分析与模型化面向对象
打电话者拿起电话受话器 电话忙音开始 打电话者拨数字(8) 电话忙音结束 打电话者拨数字(2) ....... 打电话者拨数字(3) 接电话者的电话开始振铃 铃声在打电话者的电话上传出 接电话者回答 接电话者的电话停止振铃 铃声在打电话者的电话中消失 通电话 .........
状态图与事件追踪图的关系
揿下鼠标按钮(按钮、位置) 拿起电话受话器
数字拨号(数字)
事件追踪图
事件追踪图侧重于说明发生于系统 执行过程中的一个特定“场景”。
场景也叫做脚本，是完成系统某个 功能的一个事件序列。
场景通常起始于一个系统外部的输 入事件，结束于一个系统外部的输 出事件，它可以包括发生在这个期 间的系统所有的内部事件。
类是一组具有相同数据结构和相同 操作的对象的集合。
类的定义包括一组数据属性和在数 据上的一组合法操作。
类定义可以视为一个具有类似特性 与共同行为的对象的模板，可用来 产生对象。
在一个类中，每个对象都是类的实 例 (Instance)，它们都可使用类中 提供的函数。
继承 (Inheritance)
面向对象方法学的要点（2）
对象彼此之间仅能通过传递消息互相联系 面向对象的方法学可以用下列方程来概括：
OO=objects+classes+inheritance+ communication with messages
如果一个软件系统是使用这样 4 个概念设计和实现的，则我们认 为这个软件系统是面向对象的。
这个新的子集合可以认为是既存类 的一个特殊化。
面向对象建模
所谓模型，就是为了理解事物而对事物作出 的一种抽象，是对事物的一种无歧义的书面 描述。
第08章对象特性和建模.ppt
混合建模：将机理建模与实验建模结合起来，称为混合 建模。
混合建模是一种比较实用的方法，它先由机理分析的方 法提出数学模型的结构形式，把被研究的对象视为一个灰 箱子，然后对其中某些未知的或不确定的参数利用实验的 方法给予确定。这种在已知模型结构的基础上，通过实测 数据来确定数学表达式中某些参数的方法，称为参数估计。
对上式作拉氏变换： TsH (s) + H (s) = K Qi (s)
对象的传递函数：
H (s) = K Qi (s) Ts + 1 这是最典型的一阶对象的传递函数
该对象的阶跃响应：
如果qi为幅值为A的阶跃输入，则
H (s)
=
K Ts +1Qi
(s)
=
Ka s(Ts +1)
Qi (s)
=
a s
输入量——控制变量＋各种各样的干扰变量。 输出量——对象的被控变量。
被控对象
干扰变量
干扰通道
被控变量
控制变量
控制通道
根据线性叠加原理，对象输出为控制通道输出与各干扰 通道输出之和 。
2、建模的方法 机理建模、实验建模、混合建模
机理建模：根据物料、能量平衡、化学反应、传热传质等 基本方程，从理论上来推导建立数学模型。
h(t) = L-1[H (s)] = L-1[ Ka ]
一、一阶线性对象
qi Ah q0
解：该对象的输入量为qi 被控变量为液位h
根据物料平衡方程： 单位时间内水槽体积的改变＝输入流量 — 输出流量
dV
V = Ah
dt = qi - qo
A
dh dt
=
qi
-
qo
由于出口流量可以近似地表示为：
化工仪表及自动化第2章 第三节 描述对象特性的参数
化工仪表及自动化
第二章 过程特性及其数学模型
内容提要
化工过程的特点及其描述方法
对象数学模型的建立
建模目的 机理建模 实验建模
描述对象特性的参数
放大系数Κ 时间常数Τ 滞后时间τ
1
第三节 描述对象特性的参数
一、放大系数K
对于前面介绍的水槽对象，当流入流量Q1有一定的阶跃 变化后，液位h也会有相应的变化，但最后会稳定在某一 数值上。如果我们将流量Q1的变化ΔQ1看作对象的输入， 而液位h的变化Δh看作对象的输出，那么在稳定状态时， 对象一定的输入就对应着一定的输出，这种特性称为对象 的静态特性。
用初始条件y(0)=0， y(0)=0代入式（ 2-52 ）
可分别解得
ห้องสมุดไป่ตู้
C1
T1 T2 T1
KA
C2
T2 T2 T1
KA
（2-53） 图2-22 具有容量滞 后对象的反应曲线
（2-54）
42
第三节 描述对象特性的参数
将上述两式代入式（2-52），可得
y t
T1 T2
T1
et
T1
T2 T2 T1
图2-24 滞后时间τ示意图
结论
自动控制系统中，滞后的存在是不利于控制的。所以，在设 计和安装控制系统时，都应当尽量把滞后时间减到最小。
45
2. 容量滞后 一般是由于物料或能量的传递需要通过一定阻力而引起的。
举例 前面介绍过的两个水槽串联的二阶对象
将输出量h2用y表示，输入量Q1用x表示，则方程式可写为
T1T2
d2y dt 2
T1
T2
dy
dt
y
Kx
（2-46）
假定输入作用为阶跃函数，其幅值为A。已知，二阶常系 数微分方程式的解是
第二章 过程特性及其数学模型
内容提要
化工过程的特点及其描述方法
对象数学模型的建立
建模目的 机理建模 实验建模
描述对象特性的参数
放大系数Κ 时间常数Τ 滞后时间τ
1
第三节 描述对象特性的参数
一、放大系数K
对于前面介绍的水槽对象，当流入流量Q1有一定的阶跃 变化后，液位h也会有相应的变化，但最后会稳定在某一 数值上。如果我们将流量Q1的变化ΔQ1看作对象的输入， 而液位h的变化Δh看作对象的输出，那么在稳定状态时， 对象一定的输入就对应着一定的输出，这种特性称为对象 的静态特性。
用初始条件y(0)=0， y(0)=0代入式（ 2-52 ）
可分别解得
ห้องสมุดไป่ตู้
C1
T1 T2 T1
KA
C2
T2 T2 T1
KA
（2-53） 图2-22 具有容量滞 后对象的反应曲线
（2-54）
42
第三节 描述对象特性的参数
将上述两式代入式（2-52），可得
y t
T1 T2
T1
et
T1
T2 T2 T1
图2-24 滞后时间τ示意图
结论
自动控制系统中，滞后的存在是不利于控制的。所以，在设 计和安装控制系统时，都应当尽量把滞后时间减到最小。
45
2. 容量滞后 一般是由于物料或能量的传递需要通过一定阻力而引起的。
举例 前面介绍过的两个水槽串联的二阶对象
将输出量h2用y表示，输入量Q1用x表示，则方程式可写为
T1T2
d2y dt 2
T1
T2
dy
dt
y
Kx
（2-46）
假定输入作用为阶跃函数，其幅值为A。已知，二阶常系 数微分方程式的解是
第3章 被控对象特性与数学模型
干扰变量 工业过程的数学模型可分为动态 数学模型和静态数学模型。动态数学 模型是表示输出变量与输入变量之间 被控变量 随时间而变化的动态关系的数学描述 控制变量 。动态数学模型在对动态过程的分析 和控制中起着举足轻重的作用，可用 图3-1 对象的输入输出量示意图 于各类自动控制系统的设计和分析， 以及工艺设计和操作条件的分析和确 定。静态数学模型是描述输出变量与 输入变量之间不随时间而变化的数学 关系。
在建立对象数学模型（建模）时，一般将被控变量 看作对象的输出量，也叫输出变量，而将干扰作用和控 制作用看作对象的输入量，也叫输入变量。干扰作用和 控制作用都是引起被控变量变化的因素，从控制的角度 看，输入变量就是操纵变量（控制变量）和扰动变量， 输出变量就是被控变量，如图3-1所示。由对象的输入 变量至输出变量的信号联系称为通道，控制作用至被控 变量的信号联系称为控制通道；干扰作用至被控变量的 信号联系称为干扰通道。在研究对象特性时，应预先指 明对象的输入量是什么，输出量是什么，因为对于同一 个对象，不同通道的特性可能是不同的。
数学模型的表达形式主要有两大类：一类是非参量形式， 称为非参量模型；另一类是参量形式，称为参量模型。 1. 非参量模型 当数学模型是采用曲线或数据表格等来表示时，称为非 参量模型。
非参量模型可以通过记录实验结果来得到，有时也可以通 过计算来得到，它的特点是形象、清晰，比较容易看出其定 性的特征。但是，由于它们缺乏数学方程的解析性质，要直 接利用它们来进行系统的分析和设计往往比较困难，必要时 ，可以对它们进行一定的数学处理来得到参量模型的形式。
3.2 对象数学模型的建立
在工业控制过程中，建立被控对象的数学模型的目的 主要有以下几种。 （1）进行工业过程优化操作。 （2）控制系统方案的设计和仿真研究。 （3）控制系统的调试和控制器参数的整定。 （4）工业过程的故障检测与诊断。 （5）制订大型设备启动和停车操作方案。 （6）设计工业过程操作人员的培训系统。 （7）作为模型预测控制等先进控制方法的数学模型。
过程特性及数学模型
以简单水槽为例： K是对象受到阶跃作用后，被控参数的 稳 定值与所加的输入量之比。
当 t=T 时 h=Qk(1-e-1) e-1=0.368 ∵ h(∞)=KQ ∴ h=kQ(1-e-1)=0.632KQ=0.632h(∞) 即被控参数 达到新稳态值的63.2%所需 的时间就是时间常数 T
h(∞) 0.632h(∞)
二、时间常数T
T
T
时间常数 T 越大，表示对象受干扰作用后，被控参 数变化越慢，过度时间长；T 越小，表示对象受干扰 作用后，被控参数变化越快，过度时间短。
h(t) KQ1(1 et /T )
从理论上讲，只有当 T=∞,才有 h(∞)=KQ. 但是当t=3T 时， h(3T)=KQ(1-e-3)=0.95KQ=0.95h(∞) 可近似认为动态过程基本结束。
d 2h2 dt 2
(T1
T2 )
dh2 dt
h2
KQ1
一阶对象
Th h KQ1
h(t) KQ1(1 et /T )
2）串联RC电路 串联RC电路
三、对象特性的实验建模
常用的实验测取法 • 1、实验测取法：
人为加入干扰作用，用记录仪测取输 出的被控参数。
（阶跃反应曲线法、矩形脉冲法）
测量、变送环节一般由测量元件及变送器组成，其特性也可以表示程由K、T、τ三 个参数组成的一阶滞后环节，它对过渡过程的影响与被控对象相仿。通常要求，K在整 个测量范围内保持恒定，T、τ越小越好。
事实上，测量、变送环节本身的时间常数和纯滞后时间都很小，可以略去不计。所 以实际上它相当于一个放大环节。因此，放大倍数K在整个测量范围内保持恒定是最关 键的。
f
u
y
对象特性及其数学模型
第一节 对象特性及其描述方法
对象特性—是指对象输入量与输出量之间的关系（数学模型）
对象的输入量发生变化时，其输出量随时间的变化规律 —— 对象动态特性 （如何变化的、变化量为多少……） 而对象在静态时的输入量与输出量之间的关系 —— 对象静态特性
输出量？ 输入量？
被控变量 操纵变量（控制作用）＋各种各样的干扰作用
4
■ 一阶对象（对象动态特性可用一阶微分方程式来描述）
问题：简单水槽 Qi
解：该对象的输入量为Qi
根据物料平衡方程：
被控变量为液位h
h
A
开度不变
对象内物料贮存量的变化率＝ 单位时间内流入对象的物料 —单位时间内流出对象的物料 dh Qi Qo A 由于出口流量可以近似地表示为： Qo h R dt dh dh h T h K Qi T AR K R 式（1） A Qi dt dt R
Qo
dh0 h K Q , 0 由于 （h0、Qio为初始平衡状态的值） 0 i0 记 d t Qi Qi 0 Qi dh T h K Qi 式（2） dt 式 (1)是针对完全量的输入输出模型，式 (2)是针对变化量的输入输出模型，二者 结构形式完全相同。由于在控制领域中，对象特性的分析往往是针对变化量而言 的，所以广泛采用式(2)。但为了书写方便，在表达式中通常省略变化量符号 5
被控对象
干扰通道
通道：由对象的输入变量至输出变量的信号联系
控制通道：操纵变量至被控变量的信号联系 干扰变量 干扰通道：干扰作用至被控变量的信号联系 操纵变量 对象输出为控制通道输出与干扰通道输出之和
被控变量
控制通道
同一对象不同通道的特性一般是不同的！因此在研究对象特性时，应首 先指明研究哪个通道，即指明所研究的对象输入量和输出量各是什么
对象特性—是指对象输入量与输出量之间的关系（数学模型）
对象的输入量发生变化时，其输出量随时间的变化规律 —— 对象动态特性 （如何变化的、变化量为多少……） 而对象在静态时的输入量与输出量之间的关系 —— 对象静态特性
输出量？ 输入量？
被控变量 操纵变量（控制作用）＋各种各样的干扰作用
4
■ 一阶对象（对象动态特性可用一阶微分方程式来描述）
问题：简单水槽 Qi
解：该对象的输入量为Qi
根据物料平衡方程：
被控变量为液位h
h
A
开度不变
对象内物料贮存量的变化率＝ 单位时间内流入对象的物料 —单位时间内流出对象的物料 dh Qi Qo A 由于出口流量可以近似地表示为： Qo h R dt dh dh h T h K Qi T AR K R 式（1） A Qi dt dt R
Qo
dh0 h K Q , 0 由于 （h0、Qio为初始平衡状态的值） 0 i0 记 d t Qi Qi 0 Qi dh T h K Qi 式（2） dt 式 (1)是针对完全量的输入输出模型，式 (2)是针对变化量的输入输出模型，二者 结构形式完全相同。由于在控制领域中，对象特性的分析往往是针对变化量而言 的，所以广泛采用式(2)。但为了书写方便，在表达式中通常省略变化量符号 5
被控对象
干扰通道
通道：由对象的输入变量至输出变量的信号联系
控制通道：操纵变量至被控变量的信号联系 干扰变量 干扰通道：干扰作用至被控变量的信号联系 操纵变量 对象输出为控制通道输出与干扰通道输出之和
被控变量
控制通道
同一对象不同通道的特性一般是不同的！因此在研究对象特性时，应首 先指明研究哪个通道，即指明所研究的对象输入量和输出量各是什么
对象特性机理建模和试验建模
H1 qv 2 Rs 1
dH 2
22
dH 1 d 2 H 2 Rs1 dH 2 A2 Rs1 dt Rs 2 dt dt 2
H2 d 2 H 2 Rs1 dH 2 dH 2 qv1 A1 ( A2 Rs1 ) H 2 Rs 2 Rs 2 dt dt dt 2
d 2H2 dH 2 A1 A2 Rs1 Rs 2 ( A1 Rs1 A2 Rs 2 ) H 2 Rs 2 qv1 2 dt dt T1 A1 Rs1
设有时间函数 f(t)，当 t < 0 时，f(t)＝0；在 t≥0时定义函 数 f(t) 的拉普拉斯变换为：
F (s) L f (t ) f (t )est dt
0
象函数
拉氏变换符号
原函数
复变量
拉普拉斯变换：在一定条件下，把实数域中的实变函数 f(t) 变 换到复数域内与之等价的复变函数 F(s) 。
26
典型时间函数的拉普拉斯变换 (1) 单位阶跃函数பைடு நூலகம்
单位阶跃函数定义：
0, t 0 1(t ) 1, t 0
其拉普拉斯变换为：
L1(t ) 1(t )e dt
st 0
0
1 st e dt e s
st
0
1 st 1 0 1 lim e e t s s s
8
2.参量模型 当数学模型是采用数学方程式来描述时，称 为参量模型。对象的参量模型可以用描述对象输 入、输出关系的微分方程式、偏微分方程式、状 态方程、差分方程等形式来表示。
9
对于线性的集中参数对象
通常可用常系数线性微分方程式来描述，如果以x （ t ） 表示输入量，y（t）表示输出量，则对象特性可用下列微分 方程式来描述
数学建模简介及数学建模常用方法
数学模型是对于现实世界的一个特定对象，一个特定目的，根据特有的内在规律，做出一些必要的假设，运用适当的数学工具，得到一个数学结构。
简单地说：就是系统的某种特征的本质的数学表达式（或是用数学术语对部分现实世界的描述），即用数学式子（如函数、图形、代数方程、微分方程、积分方程、差分方程等）来描述（表述、模拟）所研究的客观对象或系统在某一方面的存在规律。
随着社会的发展，生物、医学、社会、经济……各学科、各行业都涌现现出大量的实际课题，亟待人们去研究、去解决。
但是，社会对数学的需求并不只是需要数学家和专门从事数学研究的人才，而更大量的是需要在各部门中从事实际工作的人善于运用数学知识及数学的思维方法来解决他们每天面临的大量的实际问题，取得经济效益和社会效益。
他们不是为了应用数学知识而寻找实际问题（就像在学校里做数学应用题），而是为了解决实际问题而需要用到数学。
而且不止是要用到数学，很可能还要用到别的学科、领域的知识，要用到工作经验和常识。
特别是在现代社会，要真正解决一个实际问题几乎都离不开计算机。
可以这样说，在实际工作中遇到的问题，完全纯粹的只用现成的数学知识就能解决的问题几乎是没有的。
你所能遇到的都是数学和其他东西混杂在一起的问题，不是“干净的”数学，而是“脏”的数学。
其中的数学奥妙不是明摆在那里等着你去解决，而是暗藏在深处等着你去发现。
也就是说，你要对复杂的实际问题进行分析，发现其中的可以用数学语言来描述的关系或规律，把这个实际问题化成一个数学问题，这就称为数学模型。
数学模型具有下列特征：数学模型的一个重要特征是高度的抽象性。
通过数学模型能够将形象思维转化为抽象思维，从而可以突破实际系统的约束，运用已有的数学研究成果对研究对象进行深入的研究。
数学模型的另一个特征是经济性。
用数学模型研究不需要过多的专用设备和工具，可以节省大量的设备运行和维护费用，用数学模型可以大大加快研究工作的进度，缩短研究周期，特别是在电子计算机得到广泛应用的今天，这个优越性就更为突出。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（8-27）
图8-4 积分对象
说明，所示贮槽具有积分特性。
21
第二节 机理建模
在初始条件为零时,根据拉氏变换的积分性质,对式 (8-27)进行拉氏变换,则有
H s
1 As
Q1
s
积分对象的传递函数G(s)为
Gs
H s Q1s
1 As
22
第二节 机理建模
三、时滞对象
7
第一节 数学模型及描述方法
二、数学模型的主要形式
非参量模型
当数学模型是采用曲线或数据表格等来表示时，称 为非参量模型。
特点 缺点
形象、清晰，比较容易看出其定性的特征
直接利用它们来进行系统的分析和设计往往 比较困难
8
第一节 数学模型及描述方法 参量模型
当数学模型是采用数学方程式来描述时，称为参 量模型。
（a）
研究的目 的是为了 使所设计 的控制系 统达到更 好的控制 效果。
（b）
在产品规格和产 量已确定的情况 下，通过模型计 算，确定设备的 结构、尺寸、工 艺流程和某些工 艺条件。
（c）
5
第一节 数学模型及描述方法 分类 数学模型建立的途径不同
机理建模 实测建模 混合模型
6
第一节 数学模型及描述方法
yt 1 xt Kxt
a0
11
（8-5）
第一节 数学模型及描述方法
2.传递函数
所谓一个环节 (或对象)的传递函数是在初始条件为
零时,这个环节输出变量的拉氏变换与输入变量的拉氏变
换之比,记为
Gs
Y s X s
（8-6）
拉氏变换是对函数的一种变换,定义为
F s f testdt 0 12
从大量的生产实践中发现，有的对象受到干扰后， 被控变量变化很快，较迅速地达到了稳定值；有的对象 在受到干扰后，惯性很大，被控变量要经过很长时间才 能达到新的稳态值。
图8-11 不同时间常数对象的反应曲线
32
第三节 描述对象特性的参数
如何定量地表示对象受 干扰后的这种特性呢？
在自动化领域中，往往用 时间常数T来表示。时间常 数越大，表示对象受到干 扰作用后，被控变量变化 得越慢，到达新的稳定值 所需的时间越长。
T yk 1 yk yk Kxk
t
或
T yk 1 1 T yk Kxk
t
t
16
第一节 数学模型及描述方法
写成一阶差分方程的一般形式,为
式中
a1yk 1 a0 yk b0xk
T
T
a1 t a0 1 t b0 K
对于二阶微分方程
a2 yk 2 a1yk 1 a0 yk b0xk
递推公式为 yk 1 a0 yk b0 xk
a1
a1
k 0时，y1 a0 y0 b0 x0
a1
a1
k 1时，y2 a0 y1 b0 x1
注意：安装成分分析仪器时，取样管线太长，取样点安装离设 备太远，都会引起较大的纯滞后时间，工作中要尽量避免。
25
第二节 机理建模
x为输入量
y
xt
0,
0
,
t t
0 0
（8-31）
将 y xt 0 在初始条件为零时进行拉
氏变换,得
Y s e0s X s
（8-7）
第一节 数学模型及描述方法
运用拉氏变换的线性性质与微分性质,对式 (8-1) 两端分别取拉氏变换,则得
ansnY s an1sn1Y s a1sY s a0Y s bmsm X s bm1sm1X s b1sX s b0 X s
10
第一节 数学模型及描述方法
举例 一个对象如果可以用一个一阶微分方程式来描 述其特性（通常称一阶对象），则可表示为
a1yt a0 yt xt
（8-3）
或表示成
Tyt yt Kxt
（8-4）
式中
T a1 , K 1
a0
a0
如果系统处于平衡状态 (静态) ,变量的导数项均为零
33
第三节 描述对象特性的参数
举例
简单水槽为例
由前面的推导可知
T
dh dt
h
KQ1
假定Q1为阶跃作用，t<0时Q1=0； t>0或t=0时Q1为一常数，如左图。
图8-12 反应曲线
则函数表达式为 ht KQ1 1 et T
（8-36）
34
第三节 描述对象特性的参数
从上页图反应曲线可以看出，对象受到阶跃作用后，被 控变量就发生变化，当t→∞时，被控变量不再变化而达到 了新的稳态值h（∞），这时上式可得：
因此,时滞对象的传递函数为
图8-7 时滞对象输入、 输出特性
Gs e0s
（8-32）
26
第二节 机理建模
对象可以用一阶微分方程式来描述, 但输入变量与 输出变量之间有一段时滞τ0
T
dyt
dt
yt
Kxt
0
（8-33）
在初始条件为零时,对上式进行拉氏变换,得
TsY s Y s Ke0s X s
28
第三节 描述对象特性的参数
hs KQ1 或
K hs Q1
图8-8 水槽液位的变化曲线
K在数值上等于对象重新稳定后的输 出变化量与输入变化量之比。K越大， 就表示对象的输入量有一定变化时， 对输出量的影响越大，即被控变量对 这个量的变化越灵敏。
29
第三节 描述对象特性的参数
举例
由此式可以方便地得到系统传递函数的一般形式
Gs
Y s X s
bm s m an s n
bm1sm1 b1s b0 an1sn1 a1s a0
（8-8）
13
第一节 数学模型及描述方法
对于一阶对象,由式 (8-4)两端取拉氏变换,得
式 (8-10)称为 n阶差分方程,当n= 1时称为一阶差 分方程。
15
第一节 数学模型及描述方法
对于一阶微分方程
T dyt yt Kxt
dt
（8-11）
如果将各个信号经过采样,采样间隔时间 (采样周期)为Δt
dyt yk关系代入式 (7-11) ,可得
a1
a1
17
（8-12） （8-13）
第二节 机理建模
一、一阶对象 1.水槽对象
依据
对象物料蓄存量的变化率 ＝单位时间流入对象的物料－单位时间流出对象的物料
18
第二节 机理建模
Q1 Q2 dt Adh
（8-14）
若变化量很微小，可以近似认为Q2与h 成正比
Q2
h Rs
图8-2 水槽对象
机理模型——从机理出发,即从对象内在的物理和化学
规律出发, 建立描述对象输入输出特性的数学模型。
经验模型——对于已经投产的生产过程,我们可以通过
实验测试或依据积累的操作数据,对系统的输入输出数 据,通过数学回归方法进行处理。
混合模型——通过机理分析,得出模型的结构或函数形
式，而对其中的部分参数通过实测得到。
由于
i C de0
dt
消去i
RC
de0 dt
e0
ei
图8-3 RC电路
或
T
de0 dt
e0
ei
T RC
20
第二节 机理建模
二、积分对象
当对象的输出参数与输入参数对时间的积分成比例关系时，
称为积分对象。
Q2为常数，变化量为0
1 dh A Q1dt
其中，A为贮槽横截面积
1
h A Q1dt
自动控制系统是由被控对象、测量变送装置、控
制器和执行器组成。
研究对象的特性，就是用数学的方法来描述出对象输 入量与输出量之间的关系。这种对象特性的数学描述就称 为对象的数学模型。干扰作用和控制作用都是引起被控变 量变化的因素，如下图所示。
几个概念
图8-1 对象的输入、输出量
3
通道
调节通道 ？
干扰通道
an ynt an1yn1t a1yt a0 yt bm xmt bm1xm1t b1xt b0xt
（8-1）
在允许的范围内，多数化工对象动态特性可以忽略输入 量的导数项可表示为
an ynt an1 yn1t a1 yt a0 yt xt
有的对象或过程,在受到输入作用后,输出变量要 隔上一段时间才有响应,这种对象称为具有时滞特性的
对象,而这段时间就称为时滞τ0 (或纯滞后)。
时滞的产生一般是由于介质的输送需要一段时间 而引起的。
23
第二节 机理建模
举例
溶解槽及其 反应曲线
纯滞后时间
显然，纯滞后时间τ0与皮带输送机的传送速度v和传送距
化工仪表及自动化
第八章 对象特性和建模
内容提要
数学模型及描述方法
被控对象数学模型 数学模型的主要形式
机理建模
一阶对象 积分对象 时滞对象
1
内容提要
描述对象特性的参数
放大系数Κ 时间常数Τ 滞后时间τ
实测建模
2
第一节 数学模型及描述方法
一、被控对象数学模型
第一节 数学模型及描述方法
对象的数学模型分为静态数学模型和动态数学模型
基础
静态数学模型
动态数学模型
特例
4
第一节 数学模型及描述方法