不规则图形面积的求法九年级中考复习

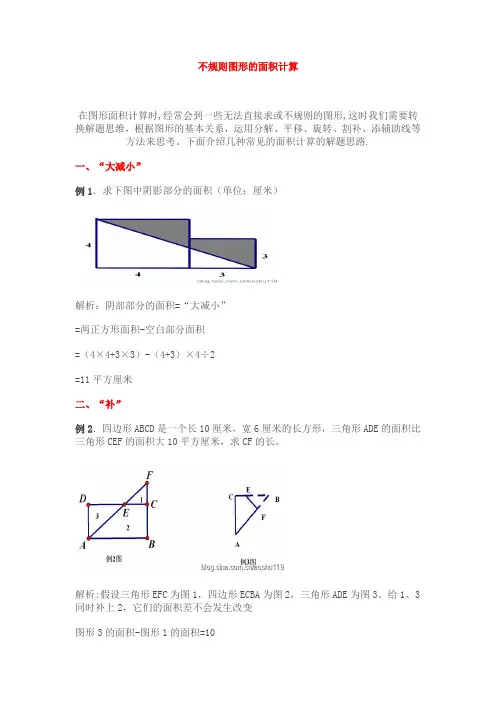
不规则图形的面积计算在图形面积计算时,经常会到一些无法直接求或不规则的图形,这时我们需要转换解题思维，根据图形的基本关系，运用分解、平移、旋转、割补、添辅助线等方法来思考。

下面介绍几种常见的面积计算的解题思路.一、“大减小”例1．求下图中阴影部分的面积（单位：厘米）解析：阴部部分的面积=“大减小”=两正方形面积-空白部分面积=（4×4+3×3）-（4+3）×4÷2=11平方厘米二、“补”例2．四边形ABCD是一个长10厘米，宽6厘米的长方形，三角形ADE的面积比三角形CEF的面积大10平方厘米，求CF的长。

解析:假设三角形EFC为图1，四边形ECBA为图2，三角形ADE为图3。

给1、3同时补上2，它们的面积差不会发生改变图形3的面积-图形1的面积=10（图形3+图形2）-（图形1+图形2）=即长方形ABCD的面积-三角形ABF的面积=10那么，三角形ABF的面积=60-10=50=AB×BF÷2可算出 BF=10厘米，所以CF=10-6=4厘米例3．如图，四边形ACEF中，角ACE=角EFA=90°，角CAF=45°，AC=8厘米，EF=2厘米，求四边形ACEF的面积解析：分别延长AF、CE，交于B点在三角形ABC中，很明显，它是个等腰直角三角形，面积=8×8÷2=32平方厘米在三角形EFB中，很明显，它也是一个等腰直角三角形，面积=2×2÷2=2平方厘米所以，S四边形ACEF=S△ABC-S△EFB=32-2=30平方厘米三、“移”例4．如图所示（1图），四边形ABCD是一个长方形草坪，长20米，宽14米，中间有一条宽2米的曲折小路，求路的面积。

解析：小路是曲折的，不规则图形，可用采用“移”的思路来解决把图1下面空白部分往上、往左移，使它与上面空白部分连接在一起，就成了图2中的空白部分，是一个长方形，长是20-2=18米，宽是14-2=12米，这个长方形的面积=18×12=216平方米，小路的面积=大长方形的面积-空白长方形的面积=20×14-216=64平方米例5．如图，AE=ED，AF=FC，已知三角形ABC的面积是100平方厘米，求阴影部分的面积解析：由于两阴影部分不在一起，我们可以考虑用“移”的思维把阴影变成一个整体。

不规则阴影部分面积的求解六法纵观历年全国各地的中考试卷中求阴影部分的面积试题的图形一般都是一些不规则的图形或没有公式可以直接套用的.因此，同学们在下笔时总感到左右为难，事实上，对于求解这类问题的关键只要能及时地将要求的阴影部分的图形转化为可求解的规则的图形的组合，从而使问题方便、快速、准确地解决.现举例说明一、面积的和差例1、如图所示，求阴影部分面积分析：阴影部分是一个不规则图形，可以转化为规则图形的面积和差来求即一个半圆减去一个直角三角形。

解：阴影部分面积=24825286252-=⨯-ππ 二、构造方程求解例2、如图所示，求阴影部分面积分析：本题虽可以转化为规则图形的面积和差计算阴影部分面积，但在作图中比较麻烦。

这儿的阴影部分和空白部分都有四部分组成，且形状大小一样。

因此可以根据图形中隐含的数量关系来构造方程求解。

解：设每一部阴影部分面积为x ，每一部分的空白部分面积为y ，根据图形得⎪⎩⎪⎨⎧=+=+364423y x 22y x π解得⎪⎩⎪⎨⎧-=-=2918929ππy x 所以阴影部分面积=361892944-=⎪⎭⎫ ⎝⎛-=ππx三、等积变形法 例3、 如图，A 是半径为1的⊙O 外的一点，OA=2，AB 是⊙O 的切线，B 是切点，弦BC ∥OA ，连结AC ，则阴影部分的面积等于_______．分析：一个图形的面积不易或难以求出时，可改求与其面积相等的图形面积，便可以使原来不规则的图形转化为规则图形。

解：连结OB 、OC ．∵BC ∥OA ，∴S △ABC=S △OBC ，∴S 阴影=S 扇形OBC ．∵AB 是⊙O 的切线，∴∠BOA=90°，∵OB=1，OA=2，∴∠OBC=∠B OA=60°，∴∠BOC= ， ∴扇形OBC 是圆的 ．∴S 阴影=S 扇形OBC=四、割补法 分析：从表面上看图形异常繁杂，由于两扇形是同一圆的五、整体思想例5、如图，⊙A 、⊙B 、⊙C 两两不相交，且半径都是0.5cm ，则图中的三个扇形的面积之和为（ ）（A ）212cm π（B ）28cm π（C ）26cm π（D ）24cm π分析：由于不知道每个块阴影部分的圆心角的度数，所以部分求和无法实现，而三个阴影部分他们半径相同，圆心角的和是︒180，将三个拼在一起用整体的方法求就很容易了。

Ｃ ＡＢ与 Ｒｔ △ＡＤＣ 个 规 则 图 形 面 积 的 差 ． 两
３ 特殊位置法 ．
例３ 如 图３Ａ ， 为大圆Ｄ 的直径 ， 大
圆的弦Ｃ Ｄ与 以Ａ Ｂ上 的 点 Ｏ为 圆 心 的 小 。
０
圈５
投 稿邮箱： ｊ ｖ ６． ｍ ｓｋ １３ ｏ ｘ＠ ｃ
解橱 连 结 Ｃ ｏ ｏ 由 Ｃ Ｄ为 羊 Ｄ， Ｃ． Ｄ． 、
＝
生 的思 维能力 ．是 中考 常见 的题 型． 文 本 将 较 全 面地 介 绍求 不规 则 图 形 面 积 的各
种 情况 ， 现举 例如 下 ， 供大 家参考 ． 求不 规 则 图形 面积 的基 本 思路 是 把 不 规则 图形 的 面积 转 化 为 规 则 图形 面 积 的和或 差 ． 后用 规 则 图形 的面积 公式 求 然
为直 径 ， 半 径 为２ 圆心 角 为 ９ 。 在 ， ０ 的扇 形 内作 半 圆 ， 曰 点 Ｄ， 结 ∞ ， 中 阴 交Ａ 于 连 图 影部 分 的面积 是 （ ）
Ａ．１一】 Ｔ Ｂ．丌一 ２
图 ２
． １ （
点评 位 置特 殊 化 法体 现 了从 特 殊
到一 般 的思 维方 法 ． 一种探 求 问题 规律 是 的有 效 思路． 解析 先补 形 ． 转化 ．补 出以 六个 再
一
２—×丌× ６ ／ 一 １ １ 、 — ２ｒ ６ ＿ ：
．
般 用 割 补 法 ． 先 分 割 ，再 补 形 ． 弓 形 把
ＣＤ 下 ． 证 出 弓形 ＣＤ的 面 积 ＝弓形 Ｄ的 割 可
面积．因此 ． 转移 弓形ｃＤ的位 置补 在 弓形 Ｂ Ｄ上 ，使 不规 则 的 阴影 图形 转化 成 扇形
割 成几 部 分 或 者进 一 步 把 分 割 下 的某 部

不规则面积计算公式和方法以下是 8 条关于不规则面积计算公式和方法的内容：1. 嘿，你知道吗？不规则图形的面积计算也有妙招呢！就像要给一块奇形怪状的拼图算面积。

比如说，咱可以把它分割成几个熟悉的图形，然后分别算出它们的面积，最后加起来不就得了嘛！就像那形状怪怪的花园，分成小块来算面积就轻松多了。

2. 哇塞，不规则面积的计算方法可多啦！其中有一种叫填补法，这就好比给不完整的东西补上缺失的那一块。

比如有个形状不规则的空洞，我们用一些规则的东西把它填满，填满部分的面积加上原来规则部分的面积，不就能算出整体面积了吗！多有意思呀！3. 嘿呀，要算不规则面积，还可以用称重法呢！这就好像通过称东西的重量来了解它的价值一样新奇。

像有块形状很怪的布料，我们可以通过称它和同样材质已知面积的布料的重量比例来算出它的面积，神奇吧！4. 哎呀呀，不规则面积还有这种计算方法咧！叫什么网格法哟。

就好像在一张大网上去数格子一样。

比如看那歪歪扭扭的池塘，我们在上面铺上网格，数数有多少个完整的和部分的格子，不就能大概知道它的面积了嘛，超好玩的！5. 哈哈，你晓得不，还有个估算不规则面积的办法呢！这就如同我们估算事情的难易程度一样。

好比有个不规则的岛屿，我们可以大致和一些熟悉的形状比较，给出个大概的面积范围哟，是不是挺简单粗暴但有用呀！6. 哇哦，对于一些不规则图形的面积计算，我们可以用相似图形法呀！就跟找相似的人一样。

比如说，有个不太规则的场地和另一个已知面积的相似场地，通过对比它们的相似之处就能算出我们要的面积啦，很妙吧！7. 咳咳，不规则面积的计算还有个投影法呢！这就好比把东西的影子投出来算大小。

像那个奇形怪状的雕塑，把它的投影画出来算面积，再根据角度推算真实面积，神奇不神奇？8. 哎哟喂，可别忘了还有蒙特卡罗法来算不规则面积哦！这就像是不断地尝试和猜测。

比如说在一个不规则的图形区域里随机扔很多点，统计在图形内的点的比例，就能算出面积啦，多酷啊！总之，计算不规则面积的方法多种多样，只要我们开动脑筋，总能找到合适的办法来搞定它们！。

专题复习三 运动路径及不规则图形面积的计算(1)运动路径一般由弧组成，计算时关键在于确定弧的度数与半径；与旋转变换有关的运动路径找到旋转中心最重要.(2)不规则图形的面积一般用“割”或“补”的方法转化为规则图形计算．1.如图所示的五个半圆，邻近的两半圆相切，两只小虫同时出发，以相同的速度从点A 到点B ，甲虫沿路线爬行，乙虫沿路线爬行，则下列结论正确的是(C ). A.甲先到点 B B.乙先到点B C.甲、乙同时到点BD.无法确定(第1题)(第2题)(第3题)2.如图所示，Rt△AB′C′是Rt△ABC 以点A 为中心逆时针旋转90°而得到的，其中AB=1，BC=2，则旋转过程中的长为(A ). A. 25π B. 25π C.5π D. 5π3.如图所示，已知∠ABC=90°，AB=πr，AB=2BC ，半径为r 的⊙O 从点A 出发，沿A→B→C 方向滚动到点C 时停止.则在此运动过程中，圆心O 运动的总路程为(A ).A.2πrB.3πrC. 23πrD. 25πr4.如图所示，已知正方形ABCD 的边长为22cm ，将正方形ABCD 在直线l 上顺时针连续翻转4次，则点A 所经过的路径长为(B ).A.4πcmB.(2+22)πcmC.22πcmD.(4+22)πcm (第4题)（第5题） 5.如图所示，分别以五边形ABCDE 的顶点为圆心、1为半径作圆，则图中阴影部分的面积之和为(C ). A. 23π B.3π C. 27π D.2π6.如图1所示为以AB 为直径的半圆形纸片，AB=6cm ，沿着垂直于AB 的半径OC 剪开，将扇形AOC 沿AB 方向平移至扇形A′O′C′，如图2所示.其中O′是OB 的中点，O′C′交于点F,则的长为 π cm ．（第6题）7.如图所示，正方形ABCD内接于⊙O，⊙O的半径为2，以圆心O为顶点作∠MON，使∠MON=90°，OM，ON分别与⊙O交于点E，F，与正方形ABCD的边交于点G，H，则阴影部分的面积S= π-2 ．(第7题) (第8题)8.如图所示，正方形ABCD边长为4，以BC为直径的半圆O交BD于点E.则阴影部分面积为6-π（结果保留π）．9.如图所示，线段AB的端点在边长为1的正方形网格的格点上，现将线段AB绕点A按逆时针方向旋转90°得到线段AC．(第9题)(1)请你用尺规在所给的网格中画出线段AC及点B经过的路径．(2)若将此网格放在一平面直角坐标系中，已知点A的坐标为(1，3)，点B的坐标为(-2，-1)，则点C的坐标为 (5，0) ．(3)在线段AB旋转到线段AC的过程中，线段AB扫过的区域的面积为25π ．4【答案】(1)图略(2)(5，0)25π(3)4（第10题）10.如图所示，在△ABC中，AB=AC，E在AC上，经过A，B，E三点的⊙O交BC于点D，且.(1)求证：AB为⊙O的直径.(2)若AB=8，∠BAC=45°，求阴影部分的面积.（第10题答图）【答案】(1)如答图所示，连结AD.∵，∴∠BAD=∠CAD.又AB=AC，∴AD⊥BC.∴∠ADB=90°.∴AB为⊙O的直径.(2)连结OE.∵∠BAC＝45°，∴∠BOE＝90°.∴∠AOE＝90°.∵AB为⊙O的直径，∴∠AEB ＝90°.∴AO ＝OE ＝OB ＝21AB ＝4.∴阴影部分的面积为21×4×4+3604902⨯π=8+4π.11.如图所示，在平面直角坐标系中放置一个边长为1的正方形ABCD ，将正方形ABCD 沿x 轴的正方向无滑动地在x 轴上滚动，当点A 离开原点后第一次落在x 轴上时，点A 运动的路径线与x 轴围成的图形面积为(C ).A.2π+21 B. 2π+1 C.π+1 D.π+21 (第11题)(第12题)12.如图所示，△ABC 为等边三角形，⊙O 的周长与等边三角形的边长相等，⊙O 在△ABC 的边上作无滑动滚动，从点P 出发沿顺时针方向滚动，又回到点P ，滚动的圈数是(D ).A.1B.2C.3D.413.如图1所示，有一张矩形纸片ABCD ，其中AD=8cm ，上面有一个以AD 为直径的半圆，正好与对边BC 相切，将它沿DE 折叠，使点A 落在BC 上，如图2所示.这时半圆还露在外面的部分(阴影部分)的面积是(B ).A.(π-23)cm 2B.（316π-43）cm 2 C.（21π+3）cm 2 D.（32π+3）cm 2 (第13题)(第14题)14.如图所示，两个半径相等的直角扇形的圆心分别在对方的圆弧上，半径AE ，CF 交于点G ，半径BE ，CD 交于点H ，且C 是的中点，若扇形的半径为2，则图中阴影部分的面积等于 2π-4 ． 15.如图所示，在半径为5，圆心角为45°的扇形AOB 内部作一个正方形CDEF ，使点C 在OA 上，点D ，E 在OB 上，点F 在上，则阴影部分的面积为 85 -23 (结果保留π)． (第15题)(第16题)16.已知一个圆心角为270°扇形工件，未搬动前如图所示，A ，B 两点触地放置，搬动时，先将扇形以点B 为圆心，作如图所示的无滑动翻转，再使它紧贴地面滚动，当A ，B 两点再次触地时停止.若扇形的半径为3m ，则圆心O 所经过的路线长是 6π m(结果保留π).(第17题)17.如图所示，在一个物体的横截面Rt△ABC中，∠ACB=90°，∠CAB=30°，BC=1m.工人师傅先将AB边放在地面(直线l)上．(1)请直接写出AB，AC的长．(2)工人师傅要把此物体搬到墙边，先按顺时针方向绕点B翻转到△A1BC1位置(BC1在l上)，最后沿BC1的方向平移到△A2B2C2的位置，其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).画出在搬动此物的整个过程中点A所经过的路径，并求出该路径的长度．(3)若没有墙，像(2)那样翻转，将△ABC按顺时针方向绕点B翻转到△A1BC1位置为第一次翻转，又将△A1BC1按顺时针方向绕点C1翻转到△A2B2C1(A2C1在l上)为第二次翻转，求两次翻转此物的整个过程中点A经过路径的长度．【答案】(1)AB=2m，AC=3m.（第17题答图）(2)如答图所示，点A经过的路径为.∵∠ABA1=180°-60°=120°，A1A2=AC=3 (m).∴点A 所经过的路径长为1802120⨯π+3=（34π+3）(m). (3)点A 经过的路径为.=1802120⨯π=34π(m), =180390⨯π=23π(m). ∴点A 经过的路径长度为34π+23π（m ）.18.【兰州】如图所示，⊙O 的半径为2，AB ，CD 是互相垂直的两条直径，点P 是⊙O 上任意一点(P 与点A ，B ，C ，D 不重合)，过点P 作PM⊥AB 于点M ，PN⊥CD 于点N ，Q 是MN 的中点，当点P 沿着圆周转过45°时，点Q 走过的路径长为(A ).A. 4πB. 2πC. 6πD. 3π （第18题）（第19题） （第19题答图） 19.【恩施州】如图所示，在Rt△ABC 中，∠BAC=30°，以直角边AB 为直径作半圆交AC 于点D ，以AD 为边作等边三角形ADE ，延长ED 交BC 于点F ，BC=23，则图中阴影部分的面积为 33-23π .(结果不取近似值)【解析】如答图所示，设半圆的圆心为O ，连结DO ，过点D 作DG⊥AB 于点G ，过点D 作DN⊥CB 于点N.在Rt△ABC 中，∠BAC=30°，∴∠ACB=60°，∠ABC=90°.∵△ADE 是等边三角形，∴∠EAD=∠E＝60°.易知△CDF 是等边三角形.在Rt△ABC 中，∠BAC=30°，BC=23，∴AC=43，AB=6，∠DOG=60°.∴AO＝BO ＝3.在Rt△DOG 中，∠DOG＝60°，OD ＝OB ＝3，∴DG=233.∴AD=33.∴DC=AC -AD=3.在Rt△DCN 中，∠C ＝60°，DC ＝3,∴CN＝23，DN=32.∴FC＝3.则S 阴影=S △ABC -S △AOD -S 扇形DOB -S △DCF =21×23×6-21×3×233-3603602⨯π-21×23×3=33-23π.20.如图所示，正方形ABCD 的边长为1，分别以正方形的四个顶点为圆心，边长为半径，在正方形内画圆弧，求图中阴影部分的面积．(第20题) （第20题答图）【答案】如答图所示，设正方形的各部分不规则图形的面积分别为x ，y ，z.S 正方形ABCD =x+4y+4z=1，S 扇形ABC =x+3y+2z=4π，S 曲边三角形BEC =x+2y+z=2S扇形BEC -S △BCE =2×3601602⨯π-43=3π-43，可解得x=3π+1-3.∴图中阴影部分的面积为3π+1-3.。

面积求解的九类方法一、相加法这种方法是将不规则图形转化成或割分成几个基本的规则图形，如三角形、四边形、扇形、半圆形或圆形，然后分别计算它们的面积，最后相加求出整个图形的面积。

例如求下图图形的面积。

解析：总面积=半圆的面积+正方形的面积二、相减法这种方法是将不规则图形看成是若干个基本规则图形的面积之差，然后分别计算它们的面积，最后相加减，得出所求图形的面积。

四、重新组合法这种方法是将不规则图形拆开并重组，根据具体情况和计算上的需要，重新组合成一个更容易求解的图形，这种思路可以理解为化零为整，如果在实际操作中，感觉拆分重组比较困难抽象，可以考虑单独求解每个独立的单元，然后利用相加法的思想求解。

例如求下图左侧图形阴影部分的面积。

解析：阴影部分面积=正方形的面积-圆形的面积五、辅助线法这种方法是根据图形的具体情况，在图形中添加一条或若干条辅助线，使不规则图形或一个动态图形通过平行、局部等面积转移，从而构造一个规则图形或一个面积固定的基本图形进行面积求解，通常这类题目涉及的知识点是等面积转化法，如同底等高，平行线转移顶点等，在中学阶段，这是一类难度相对较大的面积求解类问题。

例如求下图左侧图形阴影部分的面积。

解析：阴影部分面积=12ACxBH思路：连接BE，并过点B作BH⊥AC，交点为点H,因为AC、BE分别是两个正方形的对角线，所以AC∥BE，所以△ACE的面积与△ABC的面积相等。

六、割补法这种方法是将原图形的一部分切割下来补到图形中的另一部分使之成为基本规则图形，从而使问题得到解决。

这种方法的优点是构造完成后会很大程度上降低计算量，另外，割补法也是在初中阶段，计算二次函数图像或其它曲线围成的不规则图形进行求面积的唯一选择，但割补法对学生空间的想象能力有一定要求，在求解大多面积问题时，不要盲目强求通过割补，达到求解面积的目的，这样反而会在实际的考试中造成不必要的时间上浪费。

例如求下图图形阴影部分的面积。

2、现在要给小路铺上地砖，如果9块 地砖正好铺1m2，那么至少需要多少 块地砖？
复习旧知:
平行四边形的面积=底×高 用字母表示为S=a×h 三角形面积=底×高÷2 用字母表示为S=a×h÷2 梯形面积=（上底+下底）×高÷2 用字母表示为S=(a+b)h÷2 长方形面积=长×宽用字母表示为S=a×b 正方形面积=边长×边长用字母表示为
S=a×a= a 2
下面是某自然保护区一个湖泊的平面图 （每个小方格表示1公顷）。你能估计这 个湖泊的面积大约是多少公顷吗？
你准备怎样估计？
先数整格，再数不满整格， 不满整格作半格计算。
不规则图形面积的计算
你还记得吗？
长 方 形 的 面 积 = 长 ×宽
S=ab
正 方 形 的 面 积 = 边长×边长
S=a×a
平行四边形的面积= 底×高
S=ah
三 角 形 的 面 积 = 底×高÷2
S=ah÷2
梯 形 的 面 积 = (上底+下底）×高÷2 S=(a+b)h÷2
生活中有许多不规则的图形
法计算组合图形面积．
作业
课本23页练习四1到4题
学校开运动会要制作一 些锦旗，式样如右图。 一面锦旗需要多少平方 厘米面料？
(60＋45) ×(30÷2) ÷2×2 =105×15÷2×2 =1575(㎝²)
答：一面锦旗需要1575平方厘 米面料。
45cm 60cm
30cm
1、草坪的面积有多少平方米？
小 喷泉 湖
草坪
假山
游乐场
例如：华丰校园里有一块草坪（如图） 它的面积是多少平方米？
12m
4m 10m
方法一：分割法

求不规则面积的数学方法一、分割法。

1.1 原理阐述。

求不规则面积的时候啊，分割法是个挺不错的法子。

就是把那个不规则的图形啊，分割成咱们熟悉的图形，像三角形、长方形、正方形啥的。

这就好比把一个大难题啊，拆成一个个小问题，各个击破嘛。

就拿一块奇形怪状的地来说，咱们可以想象着用几条线把它切成几块规整的形状，就像切蛋糕似的。

1.2 实际例子。

比如说有个不规则的多边形，看着乱得很。

咱们仔细瞅瞅，从几个合适的点连线，把它分成了三个三角形和一个长方形。

三角形的面积公式咱都知道，底乘高除以二嘛，长方形面积就是长乘宽。

把这几个小图形的面积都算出来，然后一加，这个不规则多边形的面积就出来了。

这就像是把一群散兵游勇，按照不同的队伍编排好，再把每个队伍的人数一加，总数就清楚了。

二、填补法。

2.1 原理剖析。

填补法呢，和分割法有点相反。

要是遇到个不规则的图形，咱就想办法给它补上一块或者几块，让它变成一个咱们能轻松算面积的规则图形。

这就好比一个人衣服破了个洞，咱们补上一块布，让它完整起来。

等算出这个完整的规则图形的面积之后呢，再把咱们补上的那部分面积减掉，剩下的就是原来不规则图形的面积了。

2.2 举例说明。

就像有个图形，缺了一角，看着像个残缺不全的正方形。

咱们就给它补上那缺的一角，让它变成一个完整的正方形。

先算出这个正方形的面积，然后再算出补上的小三角形的面积。

正方形面积减去三角形面积，得嘞，原来那个不规则图形的面积就到手了。

这就像先把一个不完整的东西补全，再把多出来的部分去掉，就得到原本的东西了。

三、方格纸估算。

3.1 操作方法。

方格纸估算这个方法也很实用。

把这个不规则的图形画在方格纸上，每个方格的大小是一样的。

然后咱们就数这个图形占了多少个方格。

对于那些不满一格的，咱们就大概估算一下，是半格呢还是三分之一格之类的。

这就有点像咱们过日子，有时候大概估摸一下东西的数量。

3.2 实际操作。

比如说有个不规则的树叶形状的图形画在方格纸上。

不规则面积计算公式(二)不规则面积计算公式在数学和几何学中，计算不规则形状的面积是一项常见的任务。

不规则形状是指不符合常见几何图形的形状，例如梯形、矩形或圆形。

本文将介绍一些常见的不规则面积计算公式，并举例解释说明。

下面是一些常见的不规则面积计算公式：1. 多边形的面积计算公式对于任意一个简单闭合多边形，可以使用以下公式计算其面积：S = 1/2 * (x1y2 + x2y3 + ... + xn-1yn + xny1 - x2y1- x3y2 - ... - xnyn-1 - x1yn)其中，(x1, y1), (x2, y2), …, (xn, yn) 是多边形的各个顶点坐标。

该公式通过将多边形划分为多个三角形来计算面积，并累加这些三角形的面积。

例如，考虑一个三角形，其顶点坐标为 (0, 0), (4, 0), (0, 3)。

可以使用上述公式计算其面积：S = 1/2 * (0*4 + 4*3 + 0*0 - 0*0 - 4*3 - 0*4)= 1/2 * (0 + 12 + 0 - 0 - 12 - 0)= 1/2 * 0= 0因此，该三角形的面积为 0。

2. 圆形的面积计算公式圆形是一种常见的不规则形状，其面积可以使用以下公式计算：S = π * r^2其中，π 是一个数学常量，约等于，r 是圆的半径。

例如，考虑一个半径为 5 的圆，可以使用上述公式计算其面积：S = π * 5^2≈ * 25≈因此，该圆的面积约为。

3. 曲线围成的面积计算公式对于由曲线围成的不规则形状，可以使用积分来计算其面积。

具体而言，可以使用以下公式：S = ∫[a, b] y(x) dx其中，y(x) 是曲线的方程，[a, b] 是曲线在 x 轴上的投影区间。

例如，考虑由曲线 y = x^2 围成的形状，要计算其面积，可以使用上述公式：首先，找出曲线与 x 轴的交点，即解方程 x^2 = 0，得到 x = 0。

不规则图形的面积怎么算
面积计算方法：1、曲线拟合法，这个方法是大学学的一个比较高级的方法，用曲线拟合边界，然后用积分求面积；2、蒙特卡洛法，将物体放在规则图形上，随机撒点，计算落在目标物体上的概率，然后乘规则图形的已知面积；3、分割法，对于不规则的形状，我们可以把物体分割成若干规则图形，不规则区域用规则图形近似。

常见面积定理
1.一个图形的面积等于它的各部分面积的和；
2.两个全等图形的面积相等；
3.等底等高的三角形、平行四边形、梯形（梯形等底应理解为两底的和相等）的面积相等；
4.等底（或等高）的三角形、平行四边形、梯形的面积比等于其所对应的高（或底）的比；
5.相似三角形的面积比等于相似比的平方；
6.等角或补角的三角形面积的比，等于夹等角或补角的两边的乘积的比；等角的平行四边形面积比等于夹等角的两边乘积的比。

求不规则图形面积的三种方法方法一 用割补法求图形的面积1．如图1，已知⊙O 的半径是2，点A ，B ，C 在⊙O 上，若四边形OABC 为菱形，则图中阴影部分的面积为( )A .23π－2 3B .23π－ 3C .43π－2 3D .43π－ 3图1 图22．如图2，在△ABC 中，∠ACB ＝90°，AC ＝BC ＝2，将△ABC 绕AC 的中点D 逆时针旋转90°得到△A′B′C′，其中点B 的运动路径为BB′︵，则图中阴影部分的面积为________．3．如图3，△ABC 是等腰直角三角形，∠ACB ＝90°，AC ＝BC ＝2，把△ABC 绕点A 按顺时针方向旋转45°后得到△AB′C′，则线段BC 在上述旋转过程中所扫过部分(阴影部分)的面积是________．图34．如图4，在Rt △ABC 中，∠C ＝90°，AD 平分∠BAC ，交BC 于点D ，点O 在AB 上，⊙O 经过A ，D 两点，交AC 于点E ，交AB 于点F.(1)求证：BC 是⊙O 的切线；(2)若⊙O 的半径是2 cm ，E 是AD ︵的中点，求阴影部分的面积(结果保留π和根号)．图4方法二 用平移、旋转、对称转化求图形的面积5．如图5，正方形ABCD 内接于⊙O ，⊙O 的半径为2，以点A 为圆心，AC 长为半径画弧交AB的延长线于点E，交AD的延长线于点F，则图中阴影部分的面积为() A．4π－4 B．4π－8 C．8π－4 D．8π－8图5 图66．[如图6，CD为大半圆的直径，小半圆的圆心O1在线段CD上，大半圆O的弦AB 与小半圆O1交于点E，F，AB＝6 cm，EF＝2 cm，且AB∥CD，则阴影部分的面积为________cm2.7．当汽车在雨天行驶时，司机为了看清楚道路，要启动前方挡风玻璃上的雨刷．图7是某汽车的一个雨刷的转动示意图，雨刷杆AB与雨刷CD在B处固定连接(不能转动)，当杆AB绕点A转动90°时，雨刷CD扫过的面积是图中阴影部分的面积，现量得CD＝80 cm，∠DBA＝20°，AC＝115 cm，DA＝35 cm，试从以上信息中选择所需要的数据，求出雨刷扫过的面积．图78．如图8，在正方形ABCD中，AD＝2，E是AB的中点，将△BEC绕点B逆时针旋转90°后，点E落在CB的延长线上的点F处，点C落在点A处．再将线段AF绕点F顺时针旋转90°得线段FG，连接EF，CG.(1)求证：EF∥CG；(2)求点C ，A 在旋转过程中形成的AC ︵，AG ︵与线段CG 所围成的阴影部分的面积．图8方法三 用等积变形求图形的面积9．如图9，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，∠CDB ＝30°，CD ＝2 3，则图中阴影部分的面积为( )图9A ．4πB ．2πC ．πD .2π310．如图10，点A ，B ，C ，D 均在圆上，AD ∥BC ，BD 平分∠ABC ， ∠BAD ＝120°，四边形ABCD 的周长为15.(1)求此圆的半径； (2)求图中阴影部分的面积．图1011．如图11，AB 是半圆O 的直径，C 是半圆O 上的一点，AC 平分∠DAB ，AD ⊥CD ，垂足为D ，AD 交半圆O 于点E ，连接CE.(1)判断CD 与半圆O 的位置关系，并证明你的结论；(2)若E 是AC ︵的中点，半圆O 的半径为1，求图中阴影部分的面积．图11详解详析1．[解析]C如图所示，连接OB和AC交于点D.∵圆的半径为2，∴OB＝OA＝OC＝2.又∵四边形OABC 是菱形，∴OB ⊥AC ，OD ＝12OB ＝1.在Rt △COD 中，利用勾股定理可知CD ＝22－12＝3，∴AC ＝2CD ＝2 3， ∴∠COD ＝60°，∠AOC ＝2∠COD ＝120°， ∴S 菱形ABCO ＝12OB ·AC ＝12×2×2 3＝2 3，S 扇形AOC ＝120×π×22360＝4π3，∴图中阴影部分的面积为S 扇形AOC －S 菱形ABCO ＝43π－2 3.故选C.2．[答案]54π－32[解析] 连接DB ，DB ′，过点D 作DE ⊥A ′B ′.△ABC 绕AC 的中点D 逆时针旋转90°得到△A ′B ′C ′，此时点A ′在斜边AB 上，CA ′⊥AB ，DB ′＝12＋22＝5，A ′B ′＝22＋22＝2 2，DE ＝22，∴S 阴＝90π×5360－1×2÷2－(2 2－2)×22÷2＝54π－32. 3．[答案]12π[解析]∵△ABC 是等腰直角三角形，∴∠BAC ＝45°，AB ＝2AC ＝2 2.∵△ABC 绕点A 按顺时针方向旋转45°后得到△AB ′C ′，∴∠BAB ′＝∠CAC ′＝45°，∴点B ′，C ，A 共线，∴线段BC 在上述旋转过程中所扫过部分(阴影部分)的面积为S 扇形BAB ′＋S △AB ′C ′－S 扇形CAC ′－S △ABC ＝S 扇形BAB ′－S 扇形CAC ′＝45×π×（2 2）2360－45×π×22360＝12π.4．解：(1)证明：如图，连接OD . ∵OA ＝OD ，∴∠OAD ＝∠ODA . ∵AD 平分∠BAC ，∴∠OAD ＝∠DAC ， ∴∠ODA ＝∠DAC ，∴OD ∥AC ，∴∠ODB ＝∠C ＝90°，∴OD ⊥BC . ∵OD 是⊙O 的半径，∴BC 是⊙O 的切线．(2)连接OE ，OE 交AD 于点K .∵E 是AD ︵的中点，∴AE ︵＝DE ︵，∴OE ⊥AD .∵∠OAK ＝∠EAK ，AK ＝AK ，∠AKO ＝∠AKE ＝90°，∴△AKO ≌△AKE ，∴AO ＝AE ＝OE ，∴△AOE 是等边三角形， ∴∠AOE ＝60°，∴S 阴＝S 扇形OAE －S △AOE ＝60×π×22360－34×22＝2π3－ 3.5．[解析]A 利用对称性可知：阴影部分的面积＝扇形AEF 的面积－△ABD 的面积＝90×π×42360－12×4×2＝4π－4.故选A. 6．[答案] 4π[解析] 如图，将两个半圆变为同心半圆．过点O 作OM ⊥AB 于点M ，连接OB ，OF ，则MF ＝12EF ＝1，BM ＝12AB ＝3，∴S 阴影＝12πOB 2－12πOF 2＝12π(OB 2－OF 2)＝12π[OM 2＋32－(OM 2＋12)]＝4π(cm 2)．7．解：由题意可知△ACD ≌△AC ′D ′，所以可将△AC ′D ′旋转到△ACD 处，使阴影部分的面积成为一部分环形的面积，可通过两扇形面积之差求得，所以雨刷CD 扫过的面积S 阴影＝S 扇形ACC ′－S 扇形ADD ′＝90π×1152360－90π×352360＝π4×(115＋35)×(115－35)＝3000π(cm 2)．答：雨刷扫过的面积为3000π cm 2.8．解：(1)证明：∵四边形ABCD 是正方形， ∴AB ＝BC ＝AD ＝2，∠ABC ＝90°. ∵△BEC 绕点B 逆时针旋转90°得△BF A ，∴△BF A ≌△BEC ，∴∠F AB ＝∠ECB ，∠ABF ＝∠CBE ＝90°，AF ＝CE ，∴∠AFB ＋∠F AB ＝90°.∵线段AF 绕点F 顺时针旋转90°得线段FG ， ∴∠AFB ＋∠CFG ＝∠AFG ＝90°，AF ＝FG ， ∴∠CFG ＝∠F AB ＝∠ECB ，∴EC ∥FG . ∵AF ＝EC ，AF ＝FG ，∴EC ＝FG ， ∴四边形EFGC 是平行四边形，∴EF ∥CG .(2)∵△BF A ≌△BEC ，∴BF ＝BE ＝12AB ＝1，∴AF ＝AB 2＋BF 2＝ 5.由(1)知四边形EFGC 是平行四边形，FC 为其对角线， ∴点G 到FC 的距离等于点E 到FC 的距离，即BE ，∴S 阴影＝S 扇形BAC ＋S △ABF ＋S △FGC －S 扇形F AG ＝90π×22360＋12×2×1＋12×(1＋2)×1－90π×（5）2360＝52－π4(或10－π4)，∴阴影部分的面积为52－π4(或10－π4)．9．[解析]D 如图，连接OD .∵CD ⊥AB ，∴CE ＝DE ，∠CEO ＝∠DEO ＝90°.又∵OE ＝OE ，∴△COE ≌△DOE ，故S △COE ＝S △DOE ，即可得阴影部分的面积等于扇形OBD 的面积．∵∠CDB ＝30°， ∴∠COB ＝60°， ∴∠OCD ＝30°， ∴OE ＝12OC .由勾股定理可求得OC ＝2，故S 扇形OBD ＝60π×22360＝23π，即阴影部分的面积为2π3.故选D.10．解：(1)∵AD ∥BC ，∠BAD ＝120°， ∴∠ABC ＝60°. 又∵BD 平分∠ABC ，∴∠ABD ＝∠DBC ＝∠ADB ＝30°，∴AB ︵＝AD ︵＝DC ︵，∠BCD ＝60°， ∴AB ＝AD ＝DC ，∠BDC ＝90°， ∴BC 是圆的直径，BC ＝2DC ， ∴BC ＋32BC ＝15，解得BC ＝6，∴此圆的半径为3.(2)设BC 的中点为O ，由(1)可知点O 为圆心，连接OA ，OD . ∵∠ABD ＝30°，∴∠AOD ＝60°.根据同底等高的三角形面积相等可得S △ABD ＝S △AOD ， ∴S 阴影＝S 扇形OAD ＝60×π×32360＝32π.∴图中阴影部分的面积为32π.11．解：(1)CD 与半圆O 相切．证明：∵AC 平分∠DAB ，∴∠DAC ＝∠BAC . ∵OA ＝OC ，∴∠OAC ＝∠OCA ， ∴∠DAC ＝∠OCA ，∴OC ∥AD .∵AD ⊥CD ，∴OC ⊥CD .又∵OC 为半圆O 的半径，∴CD 与半圆O 相切． (2)连接OE .∵AC 平分∠DAB ，∴∠EAC ＝∠BAC ， ∴EC ︵＝BC ︵.又∵E 是AC ︵的中点，∴AE ︵＝EC ︵＝BC ︵， ∴S 弓形AE ＝S 弓形CE ，∠BOC ＝∠EOC ＝60°， ∴△OEC 是等边三角形， ∴∠ECO ＝60°，CE ＝1.由(1)得OC ⊥CD ，∴∠OCD ＝90°， ∴∠DCE ＝30°，∴DE ＝12，DC ＝32，∴S 阴影＝S △DEC ＝12×12×32＝38，3∴图中阴影部分的面积为8.。

不规则四边形万能公式
对于不规则四边形，没有通用的“万能”公式可以直接求出其面积。

不过，可以通过以下方法来计算其面积：
1. 分割法：将不规则四边形分割成两个或更多的三角形或规则图形，然后分别计算各部分的面积，最后相加得到总面积。

2. 海伦公式：适用于任意多边形，包括四边形。

公式为：假设有一个四边形ABCD，对角线AC=m，BD=n，对角线夹角为α，那么四边形的面积 = m n sin(α)。

3. 余弦定理：如果知道四边形的三个角的度数和第四条边的长度，可以使用余弦定理来计算面积。

4. 使用AutoCAD或类似的CAD软件：这些软件通常具有计算多边形面积的功能。

只需绘制出四边形，然后使用软件的测量工具即可得到面积。

请注意，以上方法都有一定的局限性，因此在实际应用中需要根据具体情况选择最合适的方法。

阴影面积求法阴影部分的图形一般是不规则图形或没有可直接利用的公式，因此，同学们常感到困难。

本文指出：求解这类问题的关键是将阴影部分图形转化为可求解的规则图形的组合。

如何转化呢?这里给出常用的9种转化方法。

1. 直接组合例1. 如下图，圆A 、圆B 、圆C 、圆D 、圆E 相互外离，它们的半径都是1，顺次连结五个圆心得到五边形ABCDE ，则图中五个扇形（阴影部分）的面积之和是（）A. B. 1.5 C. 2 D. 2.5ππππ（02年河南省中考）分析：由于每个扇形圆心角的具体角度未知，故无法直接进行计算。

因为五边形ABCDE 的内角和=540°=360°+180°，从而可知所求阴影部分的面积可以重新组合成一个圆和一个半圆的面积，即1.5个圆的面积：，选（B ）。

ππ5.1)1(5.12=⋅⨯ 2. 圆形分割例2. 如下图，ΔABC 中，∠C 是直角，AB=12cm ，∠ABC=60°，将ΔABC 以点B 为中心顺时针旋转，使点C 旋转到AB 边延长线上的点D 处，则AC 边扫过的图形（阴影部分）的面积是_________（=3.14159……，最后结果保留三个有效数字）。

2cm π（03年济南市中考）解：在中，ABC Rt ∆所以cm AB BC BAC ABC 6213060==︒=∠︒=∠又易证 ，EBD Rt ABC Rt ∆≅∆。

，，所以︒=∠=∠︒=∠=∠=∆∆12060CBD ABE EBD ABC S S EBD ABC 故所求阴影面积为整个图形的总面积减去空白图形的面积，即）。

（＝＝＝）（）＝（扇形扇形扇形扇形阴影22211336636012012360120cm S S S S S S S BCDBAE ABC BCD EBD BAE ≈⋅-⋅-+-+∆∆πππ3. 平移例3. 如下图，矩形内有两个相邻的正方形，面积分别为4和2，那么阴影部分的面积为________________。

例谈求阴影部分面积的几种常见方法【专题综述】在初中数学中，求阴影部分的面积问题是一个重要内容，在近年来的各地中考试题中屡见不鲜．这类试题大多数都是求不规则图形的面积，具有一定的难度，因此，正确把握求阴影部分面积问题的解题方法，显得尤为重要．本文举例介绍解决这类问题的常见方法．【方法解读】一、直接求解法例1 如图1，有一矩形纸片ABCD，AB＝10，AD＝6，将纸片折叠，使AD边落在AB边上，AD变到AD1位置，折痕为AE．再将△AED1以D1E为折痕，向右折叠，AE变到A1E位置，且A1E交BC于点F．求图中阴影部分的面积．分析因为阴影部分是一个规则的几何图形Rt△CEF，故根据已知条件可以直接计算阴影部分面积．解如图1，根据对称性可得AD＝AD1＝A1D1＝6．由已知条件易知：EC＝D1B＝4，BC＝6；Rt△FBA1∽Rt△FCE．设FC为x，则FB＝6－x．二、间接求解法例2 如图2，⊙O1与⊙O2外切于点C，且两圆分别和直线l相切于A、B两点，若⊙O1半径为3cm；⊙O2半径为1cm，求阴影部分面积．分析这是求一个不规则图形的面积，没有现成的面积公式，因此应采用间接的方法，设法转化为规则图形的面积的和或差去计算．三、整体合并法例3 如图3，⊙A、⊙B、⊙C两两不相交，且半径都是0.5cm，求三个阴影部分面积之和．分析所求的阴影部分面积是三个扇形面积之和，因为三个扇形圆心角度数不知道，所以无法单独求解，但仔细观察发现，三个扇形的圆心角分别是△ABC的三个内角，其和为180°，而扇形半径都相等，所以三个扇形能合并成一个半圆．于是问题获解．解如图3，因为三个圆的半径相等，三个扇形圆心角之和是180°，所以其面积就是半圆面积．四、等积变换法例4 如图4，A是半径为R的⊙O外一点，弦BC为3R，OA∥BC，求阴影部分面积．分析本题的阴影部分是不规则的图形，求其面积较困难，但灵活运用等积变换，就可以把它的面积转化为扇形OBC的面积，从而获解．解连接OC，OB，五、分割法例5 如图5，在Rt△ABC中，∠C＝90°，AC＝4，BC＝2，分别以AC、BC为直径画半圆，求阴影部分面积．分析阴影部分图形不规则，不能直接求面积，可以把它分割成几个部分求面积的和．解如图5，连接CD．∵AC、BC是直径，∴∠ADC＝∠BDC＝90°，∴A、D、B三点共线．设阴影部分面积被分割为S1、S2、S3、S4四部分．则六、转化法例6如图(1)，大半圆O与小半圆O1相切于点C，大半圆的弦AB与小半圆相切于点F，且AB∥CD，AB ＝4cm，求阴影部分面积．分析如果想直接求阴影部分面积，无法求解，因为它不是规则图形．但要采取转化思想，把小半圆平移到与大半圆的圆心重合的位置，作OE⊥AB于点E．连接OB，可知BE＝2cm，阴影部分面积等于大半圆面积减去小半圆的面积．解如图(2)，将小半圆O1移至与大半圆圆心重合，作O E⊥AB于点E，则BE＝12AB＝2cm．设大圆半径为R，小圆半径为x，在Rt△OEB中，有七、割补法例7 如图7，点P(3a，a)是反比例函数y＝12x与⊙O在第一象限内的一个交点，求阴影部分的面积．分析阴影部分分两部分，难于逐一求解，但考虑反比例函数的对称性，结合割补原理，问题变得特别简单．解如图7，把右上角的S1部分分割下来，移到左下方补在S3处，与S2就组成了一个扇形OAB．易知：∵P(3a，a)在反比例函数y＝12x的图象上，∴3a＝12a．解得：a1＝2，a2＝－2（舍去）．∴P坐标为(6，2)．连接OP，作PC⊥x轴于点C，得：八、方程建模法例8如图8，正方形边长为a，以每边为直径在正方形内画四个半圆，求阴影部分的面积．分析本题直接求阴影部分面积较复杂，但观察图形特点引入方程的思想，问题变得非常简单．解正方形由四个阴影花瓣和四个空白图形组成，如图8，设一个阴影花瓣面积为x，一个空白图形面积为y．根据题意得：因此阴影部分面积为．222aaπ-．【强化训练】1．（2017内蒙古包头市）如图，在△ABC中，AB=AC，∠ABC=45°，以AB为直径的⊙O交BC于点D，若BC=42，则图中阴影部分的面积为（）A．π+1B．π+2C．2π+2D．4π+12．（2017四川省凉山州）如图，一个半径为1的⊙O1经过一个半径为2的⊙O的圆心，则图中阴影部分的面积为（）A．1B．12C．2D．223．（2017四川省资阳市）如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=3，将Rt△ABC绕点A逆时针旋转30°后得到△ADE，则图中阴影部分的面积为（）A．1312πB．34πC．43πD．2512π4．（2017衢州）运用图形变化的方法研究下列问题：如图，AB是⊙O的直径，CD、EF是⊙O的弦，且AB∥CD∥EF，AB=10，CD=6，EF=8．则图中阴影部分的面积是（）A．252πB．10πC．24+4πD．24+5π5. （2017云南省）如图，边长为4的正方形ABCD外切于⊙O，切点分别为E、F、G、H．则图中阴影部分的面积为．6．（2017吉林省）如图，分别以正五边形ABCDE的顶点A，D为圆心，以AB长为半径画BE，CE．若AB=1，则阴影部分图形的周长为（结果保留π）．7. （2017四川省达州市）如图，矩形ABCD中，E是BC上一点，连接AE，将矩形沿AE翻折，使点B落在CD边F处，连接AF，在AF上取点O，以O为圆心，OF长为半径作⊙O与AD相切于点P．若AB=6，BC=33，则下列结论：①F是CD的中点；②⊙O的半径是2；③AE=92CE；④32S阴影．其中正确结论的序号是．8. （2017湖北省恩施州）如图，在Rt△ABC中，∠BAC=30°，以直角边AB为直径作半圆交AC于点D，以AD为边作等边△ADE，延长ED交BC于点F，BC=23，则图中阴影部分的面积为．（结果不取近似值）9. （2017内蒙古赤峰市）如图，点A是直线AM与⊙O的交点，点B在⊙O上，BD⊥AM垂足为D，BD 与⊙O交于点C，OC平分∠AOB，∠B=60°．（1）求证：A M是⊙O的切线；（2）若DC=2，求图中阴影部分的面积（结果保留π和根号）．10．（2017新疆）如图，AC为⊙O的直径，B为⊙O上一点，∠ACB=30°，延长CB至点D，使得CB=BD，过点D作DE⊥AC，垂足E在CA的延长线上，连接BE．（1）求证：B E是⊙O的切线；（2）当BE=3时，求图中阴影部分的面积．。

不规则图形计算的方法总结总结：对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合，分析整体与部分的和、差关系，问题便得到解决.常用的基本方法有：一、相加法：这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积.例如，右图中，要求整个图形的面积，只要先求出上面半圆的面积，再求出下面正方形的面积，然后把它们相加就可以了.二、相减法：这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如，右图，若求阴影部分的面积，只需先求出正方形面积再减去里面圆的面积即可.三、直接求法：这种方法是根据已知条件，从整体出发直接求出不规则图形面积.如下页右上图，欲求阴影部分的面积，通过分四、重新组合法：这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形面积即可.例如，欲求右图中阴影部分面积，可以把它拆开使阴影部分分布在正方形的4个角处，这时采用相减法就可求出其面积了.五、辅助线法：这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法解决即可.如右图，求两个正方形中阴影部分的面积.此题虽然可以用相减法解决，但不如添加一条辅助线后用直接法作更简便.六、割补法：这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形，从而使问题得到解决.例如，如右图，欲求阴影部分的面积，只需把右边弓形切割下来补在左边，这样整个阴影部分面积恰是正方形面积的一半.七、平移法：这种方法是将图形中某一部分切割下来平行移动到一恰当位置，使之组合成一个新的基本规则图形，便于求出面积.例如，如上页最后一图，欲求阴影部分面积，可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内，这样整个阴影部分恰是一个正方形。

八、旋转法：这种方法是将图形中某一部分切割下来之后，使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧，从而组合成一个新的基本规则的图形，便于求出面积.例如，欲求上图（1）中阴影部分的面积，可将左半图形绕B点逆时针方向旋转180°，使A与C重合，从而构成如右图（2）的样子，此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法：这种方法是作出原图形的对称图形，从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如，欲求右图中阴影部分的面积，沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。