4 网络最大流问题

最大流问题的求解方法及应用
最大流问题，是指在一个有向图中，从源点 s 到汇点 t 的最大
流量。

在实际应用中，最大流问题往往用于描述网络传输、油管输送等流量分配问题。

求解最大流问题的方法包括以下几种：
1. 网络流算法：这是一种基于图论和线性规划的算法。

通过构建网络流图，将最大流问题转化为最小割问题，再利用线性规划求解最小割问题的对偶问题来求解最大流问题。

2. 增广路算法：这是一种经典的最大流算法，其基本思想是不断找到增广路径，即从源点 s 到汇点 t 的一条路径，沿途边权
均有剩余容量，使得该路径上的边的剩余容量中的最小值最大化，最终得到最大流。

3. 矩阵树定理：这是一种基于图论和矩阵运算的算法，适用于有向图和无向图。

通过计算图的拉普拉斯矩阵的行列式等方法，求得图的生成树个数，从而计算最大流。

4. Dinic算法：是对增广路算法的改进。

在增广路算法中，每
次查找增广路径的过程需要遍历整个图，为了提高效率，
Dinic算法引入了分层图的概念，将图分层之后只在图的一层
中查找增广路径，最终求得最大流。

这些方法在实际应用中常常被用来解决路由选择、网络流量优化、模拟电路分析等问题。

例如，最大流可以被用来优化数据传输、流水线设计、流量管道的运营和管理，提高资源利用率和数据传输速度。

最大流问题解题步骤一、什么是最大流问题？最大流问题是指在一个有向图中，给定源点和汇点，每条边都有一个容量限制，求从源点到汇点的最大流量。

该问题可以用于网络传输、电力调度等实际应用中。

二、最大流问题的解法1. 增广路算法增广路算法是最基本的解决最大流问题的方法。

其基本思想是不断地寻找增广路，并将其上的流量加入到原来的流中，直到不存在增广路为止。

具体步骤如下：（1）初始化网络中各边上的流量均为0；（2）在残留网络中寻找增广路；（3）如果存在增广路，则将其上的最小剩余容量作为增量加入到原来的流中；（4）重复步骤2和步骤3，直到不存在增广路。

2. Dinic算法Dinic算法是一种改进型的增广路算法，其核心思想是通过层次分析和分层图来减少搜索次数，进而提高效率。

具体步骤如下：（1）构建分层图；（2）在分层图上进行BFS搜索寻找增广路径；（3）计算路径上可行流量并更新残留网络；（4）重复步骤2和步骤3，直到不存在增广路。

3. Ford-Fulkerson算法Ford-Fulkerson算法是一种基于增广路的算法，其核心思想是不断地寻找增广路，并将其上的流量加入到原来的流中，直到不存在增广路为止。

具体步骤如下：（1）初始化网络中各边上的流量均为0；（2）在残留网络中寻找增广路；（3）如果存在增广路，则将其上的最小剩余容量作为增量加入到原来的流中；（4）重复步骤2和步骤3，直到不存在增广路。

三、最大流问题解题步骤1. 确定源点和汇点首先需要确定问题中的源点和汇点，这是解决最大流问题的前提条件。

2. 构建残留网络在有向图中，每条边都有一个容量限制。

我们可以将这些边看作管道，容量看作管道的宽度。

在实际传输过程中，某些管道可能已经被占用了一部分宽度。

因此，在求解最大流问题时，需要构建一个残留网络来表示哪些管道还能够继续传输数据。

具体方法是：对于每条边(u,v)，分别构造两条边(u,v)和(v,u)，容量分别为c(u,v)-f(u,v)和f(u,v)，其中c(u,v)表示边的容量，f(u,v)表示当前流量。

图论中的网络与流问题在图论中，网络与流问题是一类重要且广泛应用的问题。

网络与流问题主要研究在图中如何有效地传递信息或者资源，其中最常见的问题是最大流问题和最小割问题。

一、最大流问题最大流问题是指在一个网络中找到从源点到汇点的最大流量。

在一个有向图中，每条边都有一个容量限制表示该边能够传输的最大流量。

通过网络中的流，我们可以将信息或者资源从源点流向汇点。

最大流问题的目标就是找到一种流量分配方案使得从源点到汇点的流量最大。

解决最大流问题的常用算法是Ford-Fulkerson算法和Edmonds-Karp算法。

这些算法通过不断寻找增广路径来更新流量，直到无法再找到增广路径为止，得到最大流量。

二、最小割问题最小割问题是指在一个网络中找到切割最小的边集。

切割是将网络分为两个不相交的部分，源点在一个部分中，汇点在另一个部分中。

割边是指源点部分和汇点部分之间的边。

最小割问题的目标是找到一种切割方式，使得切割的边集的容量之和最小。

解决最小割问题的常用算法是Ford-Fulkerson算法和边缘检测算法。

这些算法通过不断寻找割边来更新割集，直到无法再找到割边为止，得到最小割集。

三、应用领域网络与流问题具有广泛的应用领域，包括：1. 交通流量优化：通过建立网络模型，可以优化城市交通流量分配，提高交通效率；2. 电力传输优化：通过建立电力输电网络模型，可以实现电力资源的高效分配；3. 通信网络设计：通过建立通信网络模型，可以设计出高效的通信网络架构，提高网络传输速度和稳定性；4. 社交网络分析：通过建立社交网络模型，可以深入了解社交网络结构和信息传播规律。

总结：网络与流问题是图论中的重要问题，解决这类问题可以优化资源分配、提高效率，并在实际应用中发挥重要作用。

最大流问题和最小割问题是其中两个经典问题，通过不断寻找增广路径或割边来更新流量或割集，得到最大流量或最小割集。

网络与流问题在交通、电力、通信等领域有广泛的应用，帮助优化资源的利用和提高系统的性能。

四类基本模型1 优化模型1.1 数学规划模型线性规划、整数线性规划、非线性规划、多目标规划、动态规划。

1.2 微分方程组模型阻滞增长模型、SARS 传播模型。

1.3 图论与网络优化问题最短路径问题、网络最大流问题、最小费用最大流问题、最小生成树问题(MST)、旅行商问题(TSP)、图的着色问题。

1.4 概率模型决策模型、随机存储模型、随机人口模型、报童问题、Markov 链模型。

1.5 组合优化经典问题● 多维背包问题(MKP)背包问题：n 个物品，对物品i ，体积为i w ，背包容量为W 。

如何将尽可能多的物品装入背包。

多维背包问题：n 个物品，对物品i ，价值为i p ，体积为i w ，背包容量为W 。

如何选取物品装入背包，是背包中物品的总价值最大。

多维背包问题在实际中的应用有：资源分配、货物装载和存储分配等问题。

该问题属于NP 难问题。

● 二维指派问题(QAP)工作指派问题：n 个工作可以由n 个工人分别完成。

工人i 完成工作j 的时间为ij d 。

如何安排使总工作时间最小。

二维指派问题（常以机器布局问题为例）：n 台机器要布置在n 个地方，机器i 与k 之间的物流量为ik f ，位置j 与l 之间的距离为jl d ，如何布置使费用最小。

二维指派问题在实际中的应用有：校园建筑物的布局、医院科室的安排、成组技术中加工中心的组成问题等。

● 旅行商问题(TSP)旅行商问题：有n 个城市，城市i 与j 之间的距离为ij d ，找一条经过n 个城市的巡回（每个城市经过且只经过一次，最后回到出发点），使得总路程最小。

● 车辆路径问题(VRP)车辆路径问题（也称车辆计划）：已知n 个客户的位置坐标和货物需求，在可供使用车辆数量及运载能力条件的约束下，每辆车都从起点出发，完成若干客户点的运送任务后再回到起点，要求以最少的车辆数、最小的车辆总行程完成货物的派送任务。

TSP 问题是VRP 问题的特例。

● 车间作业调度问题(JSP)车间调度问题：存在j 个工作和m 台机器，每个工作由一系列操作组成，操作的执行次序遵循严格的串行顺序，在特定的时间每个操作需要一台特定的机器完成，每台机器在同一时刻不能同时完成不同的工作，同一时刻同一工作的各个操作不能并发执行。

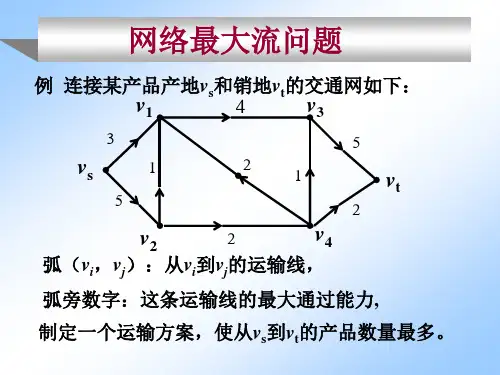
求解最大流问题的算法和模型最大流问题是图论中的一个基本问题，涉及到网络流的计算和优化。

在实际应用中，最大流问题的求解涉及到诸多算法和模型，如增广路径算法、Ford-Fulkerson算法、Dinic算法、最小割定理等。

本文将从这些方面进行论述。

1. 增广路径算法增广路径算法是求解最大流问题的经典算法，其基本思想是不断地寻找增广路径，通过增加路径上的流量来增加整个网络的流量。

具体来说，首先通过深度优先搜索或广度优先搜索找到一条从源点到汇点的增广路径，然后确定路径上的最小流量d，将当前流量增加d，将反向边的流量减少d，同时计算当前网络的流量。

2. Ford-Fulkerson算法Ford-Fulkerson算法是一种经典的增广路径算法，其基本理念与增广路径算法相同，但采用不同的策略来确定增广路径。

具体来说，Ford-Fulkerson算法采用贪心策略，在每次迭代中选择路径上的最小容量，从而确定增加的流量。

此外，Ford-Fulkerson算法还引入了残量图的概念，用于计算增广路径的容量。

3. Dinic算法Dinic算法是一种高效的增广路径算法，其主要优点是采用了分层图的策略来确定增广路径，使得每次迭代的搜索范围大为缩小。

具体来说，Dinic算法首先利用BFS算法确定每个节点的分层，然后在分层图上通过DFS算法查找增广路径，在路径上增加流量，更新分层图，重复此过程直至求解最大流。

4. 最小割定理最小割定理是求解最大流问题的重要定理，其核心思想是将网络分成两个不相交部分，并将其最小的割称为最小割。

最小割定理指出，在任意网络中，最大流等于最小割。

因此，求解最大流可以转化为求最小割问题，即在网络中寻找一组最小割，使得所有的割中容量最小的一组割。

总之，求解最大流问题是图论中的一个重要问题，其求解涉及到诸多算法和模型，如增广路径算法、Ford-Fulkerson算法、Dinic 算法、最小割定理等。

在实际应用中，不同情况下可能需要采用不同的算法和模型来求解，需要灵活应用。

网络流算法（NetworkFlow）网络流算法，是指寻找网络流问题的解的算法，它是一类重要的组合优化问题，被广泛应用于计算机科学及工程领域。

网络流是个有向图，它模拟了许多实际问题，如输电方案、货物运输、油管输送和信息传输等。

网络流算法的目的是在给定的网络流中，尽可能地将流量从源点流向汇点，同时满足各个节点的容量约束和流量平衡约束。

本文将介绍网络流模型的构建和基本算法。

一、网络流模型的构建网络流模型是一个有向图G=(V,E)，其中V表示节点集合，E表示边集合。

每条边都有一个容量c(e)表示其流量的最大值。

设源点为s，汇点为t，则网络流模型可以表示为一个三元组(N,s,t)，即：N=(V,E) s∈V t∈V s≠t在网络流模型中，源点始终是起点，汇点始终是终点。

我们在模型中引入一个源汇节点s'和汇源节点t'，并连接源点和汇点，得到源汇图G'=(V,E')，其中：E'=E∪{(s',s,c(s,t))}∪{(t,t',c(s,t))}即，在原图的基础上，加入两个新的虚拟节点s'和t'，并连接到源点和汇点。

这样构造的网络流模型中，所有的节点都满足容量和流量平衡约束。

在网络流问题中，我们需要求解最大流或最小割，以满足约束条件，并且尽可能地提高网络的利用率。

二、网络流的基本概念和算法1. 流量和容量网络流图中，首先需要确定每条边的容量和流量。

流量指的是通过该边的流量大小，容量指的是该边能够承受的最大流量。

在网络流模型中，每条边的容量是一个正实数，而流量可以是任意实数。

流量和容量通常表示为f(e)和c(e)。

2. 割在网络流模型中，割是一种对源汇图做出的划分，其中源点s和汇点t被分为两个集合S和T。

网络流通过割的概念来定义障碍物，即对流量的限制。

在网络流图中，割C(S,T)是指将源点s和汇点t割成两部分的划分，C(S,T)满足：s∈S t∈T S∩T=∅根据割的定义，可将所有割分为最小割和最大割。

图与网络分析试题及答案一、填空题1．图的最基本要素是点、点与点之间构成的边2．在图论中，通常用点表示，用边或有向边表示研究对象，以及研究对象之间具有特定关系。

3．在图论中，通常用点表示研究对象，用边或有向边表示研究对象之间具有某种特定的关系。

4．在图论中，图是反映研究对象_之间_特定关系的一种工具。

5．任一树中的边数必定是它的点数减1。

6．最小树问题就是在网络图中，找出若干条边，连接所有结点，而且连接的总长度最小。

7．最小树的算法关键是把最近的未接_结点连接到那些已接结点上去。

8．求最短路问题的计算方法是从0≤f ij≤c ij开始逐步推算的，在推算过程中需要不断标记平衡和最短路线。

二、单选题1、关于图论中图的概念，以下叙述(B)正确。

A图中的有向边表示研究对象，结点表示衔接关系。

B图中的点表示研究对象，边表示点与点之间的关系。

C图中任意两点之间必有边。

D图的边数必定等于点数减1。

2．关于树的概念，以下叙述(B)正确。

A树中的点数等于边数减1 B连通无圈的图必定是树C含n个点的树是唯一的D任一树中，去掉一条边仍为树。

3．一个连通图中的最小树(B)，其权(A)。

A是唯一确定的 B可能不唯一 C可能不存在 D一定有多个。

4．关于最大流量问题，以下叙述(D)正确。

A一个容量网络的最大流是唯一确定的B达到最大流的方案是唯一的C当用标号法求最大流时，可能得到不同的最大流方案D当最大流方案不唯一时，得到的最大流量亦可能不相同。

5．图论中的图，以下叙述(C)不正确。

A．图论中点表示研究对象，边或有向边表示研究对象之间的特定关系。

B．图论中的图，用点与点的相互位置，边的长短曲直来表示研究对象的相互关系。

C．图论中的边表示研究对象，点表示研究对象之间的特定关系。

D．图论中的图，可以改变点与点的相互位置。

只要不改变点与点的连接关系。

6．关于最小树，以下叙述(B)正确。

A．最小树是一个网络中连通所有点而边数最少的图B．最小树是一个网络中连通所有的点，而权数最少的图C．一个网络中的最大权边必不包含在其最小树内D．一个网络的最小树一般是不唯一的。