广东省东莞市2015届高三数学小综合专题练习 立体几何 文

2015年高考数学真题分类汇编 专题10 立体几何 文1.【2015高考浙江，文4】设α，β是两个不同的平面，l ，m 是两条不同的直线，且l α⊂，m β⊂（ ）A ．若l β⊥，则αβ⊥B ．若αβ⊥，则l m ⊥C ．若//l β，则//αβD ．若//αβ，则//l m【答案】A【解析】采用排除法，选项A 中，平面与平面垂直的判定，故正确；选项B 中，当αβ⊥时，,l m 可以垂直，也可以平行，也可以异面；选项C 中，//l β时，,αβ可以相交；选项D 中，//αβ时，,l m 也可以异面.故选A.【考点定位】直线、平面的位置关系.【名师点睛】本题主要考查空间直线、平面的位置关系.解答本题时要根据空间直线、平面的位置关系，从定理、公理以及排除法等角度，对个选项的结论进行确认真假.本题属于容易题，重点考查学生的空间想象能力以及排除错误结论的能力.2.【2015高考新课标1，文6】《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺，问：积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米有（ ）（A ）14斛 （B ）22斛 （C ）36斛 （D ）66斛【答案】B【解析】设圆锥底面半径为r ，则12384r ⨯⨯=，所以163r =，所以米堆的体积为211163()5433⨯⨯⨯⨯=3209，故堆放的米约为3209÷1.62≈22，故选B. 【考点定位】圆锥的性质与圆锥的体积公式【名师点睛】本题以《九章算术》中的问题为材料，试题背景新颖，解答本题的关键应想到米堆是14圆锥，底面周长是两个底面半径与14圆的和，根据题中的条件列出关于底面半径的方程，解出底面半径，是基础题.3.【2015高考浙江，文2】某几何体的三视图如图所示（单位：cm ），则该几何体的体积是（ ）A ．83cmB ．123cmC ．3233cm D ．4033cm【答案】C【解析】由三视图可知，该几何体是一个棱长为2的正方体与一个底面边长为2，高为2的正四棱锥的组合体，故其体积为32313222233V cm =+⨯⨯=.故选C. 【考点定位】1.三视图；2.空间几何体的体积.【名师点睛】本题主要考查空间几何体的体积.解答本题时要能够根据三视图确定该几何体的结构特征，并准确利用几何体的体积计算方法计算求得体积.本题属于中等题，重点考查空间想象能力和基本的运算能力.4.【2015高考重庆，文5】某几何体的三视图如图所示，则该几何体的体积为（ ）(A) 123π+ (B) 136π (C) 73π (D) 52π【答案】B【解析】由三视图可知该几何体是由一个底面半径为1，高为2的圆柱，再加上一个半圆锥：其底面半径为1，高也为1，构成的一个组合体，故其体积为61311612122πππ=⨯⨯⨯+⨯⨯，故选B.【考点定位】三视图及柱体与锥体的体积.【名师点睛】本题考查三视图的概念和组合体体积的计算，采用三视图还原成直观图，再利用简单几何体的体积公式进行求解.本题属于基础题，注意运算的准确性.5.【2015高考陕西，文5】一个几何体的三视图如图所示，则该几何体的表面积为（ ） A ．3π B ．4π C ．24π+ D ．34π+【答案】D 【解析】由几何体的三视图可知该几何体为圆柱的截去一半，所以该几何体的表面积为21121222342πππ⨯⨯+⨯⨯⨯+⨯=+，故答案选D【考点定位】1.空间几何体的三视图；2.空间几何体的表面积.【名师点睛】1.本题考查空间几何体的三视图及几何体的表面积，意在考查考生的识图能力、空间想象能力以及技术能力；2.先根据三视图判断几何体的结构特征，再计算出几何体各个面的面积即可；3.本题属于基础题，是高考常考题型.6.【2015高考广东，文6】若直线1l 和2l 是异面直线，1l 在平面α内，2l 在平面β内，l 是平面α与平面β的交线，则下列命题正确的是（ ）A ．l 至少与1l ，2l 中的一条相交B ．l 与1l ，2l 都相交C ．l 至多与1l ，2l 中的一条相交D ．l 与1l ，2l 都不相交【答案】A【解析】若直线1l 和2l 是异面直线，1l 在平面α内，2l 在平面β内，l 是平面α与平面β的交线，则l 至少与1l ，2l 中的一条相交，故选A ．【考点定位】空间点、线、面的位置关系．【名师点晴】本题主要考查的是空间点、线、面的位置关系，属于容易题．解题时一定要注意选项中的重要字眼“至少”、“至多”， 否则很容易出现错误．解决空间点、线、面的位置关系这类试题时一定要万分小心，除了作理论方面的推导论证外，利用特殊图形进行检验，也可作必要的合情推理．7.【2015高考浙江，文7】如图，斜线段AB 与平面α所成的角为60，B 为斜足，平面α上的动点P 满足30∠PAB =，则点P 的轨迹是（ ）A ．直线B ．抛物线C ．椭圆D ．双曲线的一支【答案】C【解析】由题可知，当P 点运动时，在空间中，满足条件的AP 绕AB 旋转形成一个圆锥，用一个与圆锥高成60角的平面截圆锥，所得图形为椭圆.故选C.【考点定位】1.圆锥曲线的定义；2.线面位置关系.【名师点睛】本题主要考查圆锥曲线的定义以及空间线面的位置关系.解答本题时要能够根据给出的线面位置关系，通过空间想象能力，得到一个无限延展的圆锥被一个与之成60角的平面截得的图形是椭圆的结论.本题属于中等题，重点考查学生的空间想象能力以及对圆锥曲线的定义的理解.8.【2015高考湖北，文5】12,l l 表示空间中的两条直线，若p ：12,l l 是异面直线；q ：12,l l 不相交，则（ ）A ．p 是q 的充分条件，但不是q 的必要条件B ．p 是q 的必要条件，但不是q 的充分条件C ．p 是q 的充分必要条件D ．p 既不是q 的充分条件，也不是q 的必要条件【答案】A .【解析】若p ：12,l l 是异面直线，由异面直线的定义知，12,l l 不相交，所以命题q ：12,l l 不相交成立，即p 是q 的充分条件；反过来，若q ：12,l l 不相交，则12,l l 可能平行，也可能异面，所以不能推出12,l l 是异面直线，即p 不是q 的必要条件，故应选A .【考点定位】本题考查充分条件与必要条件、异面直线，属基础题.【名师点睛】以命题与命题间的充分条件与必要条件为契机，重点考查空间中直线的位置关系，其解题的关键是弄清谁是谁的充分条件谁是谁的必要条件，正确理解异面直线的定义，注意考虑问题的全面性、准确性.9、【2015高考新课标1，文11】圆柱被一个平面截去一部分后与半球（半径为r ）组成一个几何体，该几何体的三视图中的正视图和俯视图如图所示，若该几何体的表面积为1620π+，则r =( )（A ）1 （B ）2（C ）4 （D ）8【答案】B【解析】由正视图和俯视图知，该几何体是半球与半个圆柱的组合体，圆柱的半径与球的半径都为r ，圆柱的高为2r ，其表面积为22142222r r r r r r πππ⨯+⨯++⨯=2254r r π+=16 + 20π，解得r=2，故选B.【考点定位】简单几何体的三视图；球的表面积公式；圆柱的测面积公式【名师点睛】本题考查简单组合体的三视图的识别，是常规提，对简单组合体三三视图问题，先看俯视图确定底面的形状，根据正视图和侧视图，确定组合体的形状，再根据“长对正，宽相等，高平齐”的法则组合体中的各个量.10.【2015高考福建，文9】某几何体的三视图如图所示，则该几何体的表面积等于（）A．8+ B．11+．14+．15【答案】B【解析】由三视图还原几何体，该几何体是底面为直角梯形，高为2的直四棱柱，且底面直角梯形的两底分别为12，，直角腰长为1，．底面积为12332⨯⨯=，侧面积为所以该几何体的表面积为11+B．【考点定位】三视图和表面积．【名师点睛】本题考查三视图和表面积计算，关键在于根据三视图还原体，要掌握常见几何体的三视图，比如三棱柱、三棱锥、圆锥、四棱柱、四棱锥、圆锥、球、圆台以及其组合体，并且要弄明白几何体的尺寸跟三视图尺寸的关系；有时候还可以利用外部补形法，将几何体补成长方体或者正方体等常见几何体，属于中档题．11.【2015高考山东，文9】已知等腰直角三角形的直角边的长为，将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )（A（B（）（）【答案】B【解析】由题意知，该等腰直角三角形的斜边长为，所得旋转体为同底等高的全等圆锥，所以，其体积为213π⨯⨯=，故选B.【考点定位】1.旋转体的几何特征；2.几何体的体积.【名师点睛】本题考查了旋转体的几何特征及几何体的体积计算，解答本题的关键，是理解所得旋转体的几何特征，确定得到计算体积所需要的几何量.本题属于基础题，在考查旋转体的几何特征及几何体的体积计算方法的同时，考查了考生的空间想象能力及运算能力，是“无图考图”的一道好题.12.【2015高考湖南，文10】某工作的三视图如图3所示，现将该工作通过切削，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工作的一个面内，则原工件材1112料的利用率为（材料利用率=新工件的体积/原工件的体积）（ ）A 、89πB 、827πC【答案】A【考点定位】三视图、基本不等式求最值、圆锥的内接长方体【名师点睛】运用基本不等式求最值要紧紧抓住“一正二定三相等”条件，本题“和为定”是解决问题的关键.空间想象能力是解决三视图的关键，可从长方体三个侧面进行想象几何体.求组合体的体积，关键是确定组合体的组成形式及各部分几何体的特征，再结合分割法、补体法、转化法等方法求体积.13.【2015高考北京，文7】某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为（）A．1 B C D．2【答案】C【解析】四棱锥的直观图如图所示：AB，S A是四棱锥最长的棱，由三视图可知，SC⊥平面CDSA===，故选C.【考点定位】三视图.【名师点晴】本题主要考查的是三视图，属于容易题．解题时一定要抓住三视图的特点，否则很容易出现错误．本题先根据三视图判断几何体的结构特征，再计算出几何体中最长棱的棱长即可．14【2015高考安徽，文9】一个四面体的三视图如图所示，则该四面体的表面积是（）（A ）1+（B ）1+（C ）2+ （D ）【答案】C【解析】由该几何体的三视图可知，该几何体的直观图，如下图所示：其中侧面PAC ⊥底面ABC ，且PAC ∆≌ABC ∆，由三视图中所给数据可知：2====BC AB PC PA ,取AC 中点,O 连接BO PO ,，则POB Rt ∆中，1==BO PO ⇒2=PB ∴3222212432+=⋅⋅+⋅⋅=S ，故选C . 【考点定位】本题主要考查空间几何体的三视图、锥体表面积公式.【名师点睛】在利用空间几何体的三视图求几何体的体积或者表面积时，一定要正确还原几何体的直观图，然后再利用体积或表面积公式求之；本题主要考查了考生的空间想象力和基本运算能力.【2015高考上海，文6】若正三棱柱的所有棱长均为a ，且其体积为316，则=a .【答案】4【解析】依题意，3162321=⨯⨯⨯⨯a a a ，解得4=a . 【考点定位】等边三角形的性质，正三棱柱的性质.【名师点睛】正三棱柱的底面是正三角形，侧棱垂直于底面.柱体的体积等于底面积乘以高.边长为a 的正三角形的面积为243a . 15.【2015高考天津，文10】一个几何体的三视图如图所示（单位:m ）,则该几何体的体积为 3m.【答案】8π3【解析】该几何体是由两个高为1的圆锥与一个高为2的圆柱组合而成,所以该几何体的体积为318π2π1π2(m )33⨯⨯⨯+⨯= . 【考点定位】本题主要考查三视图及几何体体积的计算.【名师点睛】由于三视图能有效的考查学生的空间想象能力,所以以三视图为载体的立体几何题基本上是高考每年必考内容,高考试题中三视图一般常与几何体的表面积与体积交汇.由三视图还原出原几何体,是解决此类问题的关键.16.【2015高考四川，文14】在三棱住ABC －A 1B 1C 1中，∠BAC ＝90°，其正视图和侧视图都是边长为1的正方形，俯视图是直角边长为1的等腰直角三角形，设点M ，N ，P 分别是AB ，BC ，B 1C 1的中点，则三棱锥P －A 1MN 的体积是______. 【答案】124【解析】由题意，三棱柱是底面为直角边长为1的A 1 C 1B 1 P等腰直角三角形，高为1的直三棱柱，底面积为12 如图，因为AA 1∥PN ，故AA 1∥面PMN ，故三棱锥P －A 1MN 与三棱锥P －AMN 体积相等，三棱锥P －AMN 的底面积是三棱锥底面积的14，高为1 故三棱锥P －A 1MN 的体积为111132424⨯⨯= 【考点定位】本题主要考查空间几何体的三视图、直观图及空间线面关系、三棱柱与三棱锥的体积等基础知识，考查空间想象能力、图形分割与转换的能力，考查基本运算能力.【名师点睛】解决本题，首先要正确画出三棱柱的直观图，包括各个点的对应字母所在位置，结合条件，三棱锥P －A 1MN 的体积可以直接计算，但转换为三棱锥P －AMN 的体积，使得计算更为简便，基本上可以根据条件直接得出结论.属于中档偏难题.17.【2015高考安徽，文19】如图，三棱锥P -ABC 中，PA ⊥平面ABC ，1,1,2,60PA AB AC BAC ===∠=o .（Ⅰ）求三棱锥P -ABC 的体积；（Ⅱ）证明：在线段PC 上存在点M ，使得AC ⊥BM ，并求PM MC的值.【答案】（Ⅱ）13PM MC = 【解析】A BC M N（Ⅰ）解：由题设AB ＝1,,2=AC 60=∠BAC可得ABC S ∆︒⋅⋅⋅=60sin 21AC AB 23=. 由⊥PA 面ABC可知PA 是三棱锥ABC P -的高,又1=PA所以三棱锥ABC P -的体积6331=⋅⋅∆PA S V ABC ＝ （Ⅱ）证：在平面ABC 内，过点B 作AC BN ⊥，垂足为N ，过N 作PA MN //交PC 于M ，连接BM .由⊥PA 面ABC 知AC PA ⊥，所以AC MN ⊥.由于N MN BN ＝⋂，故⊥AC 面MBN ，又⊂BM 面MBN ，所以BM AC ⊥.在直角BAN ∆中，21cos =∠⋅=BAC AB AN ，从而23=-=AN AC NC .由PA MN //，得31=NC AN MC PM ＝. 【考点定位】本题主要考查锥体的体积公式、线面垂直的判定定理和其性质定理.【名师点睛】本题将正弦定理求三角形的面积巧妙地结合到求锥体的体积之中，本题的第（Ⅱ）问需要学生构造出线面垂直，进而利用性质定理证明出面面垂直，本题考查了考生的空间想象能力、构造能力和运算能力.18.【2015高考北京，文18】（本小题满分14分）如图，在三棱锥V C -AB 中，平面V AB ⊥平面C AB ，V ∆AB 为等边三角形，C C A ⊥B 且C C A =B =，O ，M 分别为AB ，V A 的中点．（I ）求证：V //B 平面C MO ；（II ）求证：平面C MO ⊥平面V AB ；（III ）求三棱锥V C -AB 的体积．【答案】（I ）证明详见解析；（II ）证明详见解析；（III（Ⅱ）因为AC BC =，O 为AB 的中点，所以OC AB ⊥.又因为平面V AB ⊥平面C AB ，且OC ⊂平面C AB ，所以OC ⊥平面V AB .所以平面C MO ⊥平面V AB .（Ⅲ）在等腰直角三角形ACB 中，AC BC ==所以2,1AB OC ==.所以等边三角形V AB 的面积VAB S ∆=.又因为OC ⊥平面V AB ，所以三棱锥C V -AB 的体积等于13VAB OC S ∆⨯⨯=又因为三棱锥V C -AB 的体积与三棱锥C V -AB 的体积相等，所以三棱锥V C -AB 考点：线线平行、线面平行、面面平行、线线垂直、线面垂直、面面垂直、三棱锥的体积公式.【名师点晴】本题主要考查的是线面平行、面面垂直和几何体的体积，属于中档题．证明线面平行的关键是证明线线平行，证明线线平行常用的方法是三角形的中位线和构造平行四边形．证明面面垂直的关键是证明线面垂直，证明线面垂直可由面面垂直得到，但由面面垂直得到线面垂直一定要注意找两个面的交线，否则很容易出现错误．求几何体的体积的方法主要有公式法、割补法、等积法等，本题求三棱锥的体积，采用了等积法．19.【2015高考福建，文20】如图，AB 是圆O 的直径，点C 是圆O 上异于,A B 的点，PO 垂直于圆O 所在的平面，且1PO =OB =．（Ⅰ）若D 为线段AC 的中点，求证C A ⊥平面D P O ；（Ⅱ）求三棱锥P ABC -体积的最大值；（Ⅲ）若BC =E 在线段PB 上，求CE OE +的最小值．【答案】（Ⅰ）详见解析；（Ⅱ）13；【解析】解法一：（I ）在C ∆AO 中，因为C OA =O ，D 为C A 的中点，所以C D A ⊥O ．又PO 垂直于圆O 所在的平面，所以C PO ⊥A ．因为D O PO =O ，所以C A ⊥平面D P O ．（II ）因为点C 在圆O 上，所以当C O ⊥AB 时，C 到AB 的距离最大，且最大值为1．又2AB =，所以C ∆AB 面积的最大值为12112⨯⨯=． 又因为三棱锥C P -AB 的高1PO =，故三棱锥C P -AB 体积的最大值为111133⨯⨯=． （III ）在∆POB 中，1PO =OB =，90∠POB =，所以PB ==．同理C P =C C PB =P =B ．在三棱锥C P -AB 中，将侧面C B P 绕PB 旋转至平面C 'B P ，使之与平面ABP 共面，如图所示．当O ，E ，C '共线时，C E +OE 取得最小值．又因为OP =OB ，C C ''P =B ，所以C 'O 垂直平分PB ，即E 为PB中点．从而C C ''O =OE +E =+= 亦即C E +OE．O A BP解法二：（I ）、（II ）同解法一．（III ）在∆POB 中，1PO =OB =，90∠POB =，所以45∠OPB =，PB ==．同理C P =所以C C PB =P =B ，所以C 60∠PB =．在三棱锥C P -AB 中，将侧面C B P 绕PB 旋转至平面C 'B P ，使之与平面ABP 共面，如图所示．当O ，E ，C '共线时，C E +OE 取得最小值．所以在C '∆O P 中，由余弦定理得：()2C 1221cos 4560'O =+-⨯+1122=+--2=+从而C 'O ==所以C E +OE ． 【考点定位】1、直线和平面垂直的判定；2、三棱锥体积．【名师点睛】证明直线和平面垂直可以利用判定定理，即线线垂直到线面垂直；也可以利用面面垂直的性质定理，即面面垂直到线面垂直；决定棱锥体积的量有两个，即底面积和高，当研究其体积的最值问题时，若其中有一个量确定，则只需另一个量的最值；若两个量都不确定，可通过设变量法，将体积表示为变量的函数解析式，利用函数思想确定其最值；将空间问题转化为平面问题是转化思想的重要体现，通过旋转到一个平面内，利用两点之间距离最短求解．20.【2015高考广东，文18】（本小题满分14分）如图3，三角形DC P 所在的平面与长方形CD AB 所在的平面垂直，D C 4P =P =，6AB =，C 3B =．（1）证明：C//B 平面D P A ；（2）证明：C D B ⊥P ；（3）求点C 到平面D P A 的距离．【答案】（1）证明见解析；（2）证明见解析；（3 【解析】试题分析：（1）由四边形CD AB 是长方形可证C//D B A ，进而可证C//B 平面D P A ；（2）先证C CD B ⊥，再证C B ⊥平面DC P ，进而可证C D B ⊥P ；（3）取CD 的中点E ，连结AE 和PE ，先证PE ⊥平面CD AB ，再设点C 到平面D P A 的距离为h ，利用C D CD V V -P A P-A =三棱锥三棱锥可得h 的值，进而可得点C 到平面D P A 的距离．试题解析：（1）因为四边形CD AB 是长方形，所以C//D B A ，因为C B ⊄平面D P A ，D A ⊂平面D P A ，所以C//B 平面D P A（2）因为四边形CD AB 是长方形，所以C CD B ⊥，因为平面DC P ⊥平面CD AB ，平面DC P 平面CD CD AB =，C B ⊂平面CD AB ，所以C B ⊥平面DC P ，因为D P ⊂平面DC P ，所以C D B ⊥P（3）取CD 的中点E ，连结AE 和PE ，因为D C P =P ，所以CD PE ⊥，在Rt D ∆PE 中，PE ===，因为平面DC P ⊥平面CD AB ，平面DC P 平面CD CD AB =，PE ⊂平面DC P ，所以PE ⊥平面CD AB ，由（2）知：C B ⊥平面DC P ，由（1）知：C//D B A ，所以D A ⊥平面DC P ，因为D P ⊂平面DC P ，所以D D A ⊥P ，设点C 到平面D P A 的距离为h ，因为C D CD V V -P A P-A =三棱锥三棱锥，所以D CD 1133S h S ∆P A ∆A ⋅=⋅PE ，即CD D 2S h S ∆A ∆P A ⋅PE ===，所以点C 到平面D P A【考点定位】1、线面平行；2、线线垂直；3、点到平面的距离.【名师点晴】本题主要考查的是线面平行、线线垂直和点到平面的距离，属于中档题．证明线面平行的关键是证明线线平行，证明线线平行常用的方法是三角形的中位线和构造平行四边形．证明线线垂直的关键是证明线面垂直，证明线面垂直可由面面垂直得到，但由面面垂直得到线面垂直一定要注意找两个面的交线，否则很容易出现错误．点到平面的距离是转化为几何体的体积问题，借助等积法来解决．21.【2015高考湖北，文20】《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑. 在如图所示的阳马P ABCD -中，侧棱PD ⊥底面ABCD ，且PD CD =，点E 是PC 的中点，连接,,DE BD BE . （Ⅰ）证明：DE ⊥平面PBC . 试判断四面体EBCD 是否为鳖臑，若是，写出其每个面的直角（只需写出结论）；若不是，请说明理由； （Ⅱ）记阳马P ABCD -的体积为1V ，四面体EBCD 的体积为2V ，求12V V 的值． 【答案】（Ⅰ）因为PD ⊥底面ABCD ，所以PD BC ⊥. 由底面ABCD 为长方形，有BC CD ⊥，而PD CD D =，所以BC ⊥平面PCD . DE ⊂平面PCD ，所以BC DE ⊥. 又因为PD CD =，点E 是PC 的中点，所以DE PC ⊥. 而PCBC C =，所以DE ⊥平面PBC .四面体EBCD 是一个鳖臑；（Ⅱ）124.V V = 【解析】（Ⅰ）因为PD ⊥底面ABCD ，所以PD BC ⊥. 由底面ABCD 为长方形，有BC CD ⊥，而PD CD D =，所以BC ⊥平面PCD . DE ⊂平面PCD ，所以BC DE ⊥. 又因为PD CD =，点E 是PC 的中点，所以DE PC ⊥. 而PCBC C =，所以DE ⊥平面PBC . 由BC ⊥平面PCD ，DE ⊥平面PBC ，可知四面体EBCD 的四个面都是直角三角形，即四面体EBCD 是一个鳖臑，其四个面的直角分别是,,,.BCD BCE DEC DEB ∠∠∠∠（Ⅱ）由已知，PD 是阳马P ABCD -的高，所以11133ABCD V S PD BC CD PD =⋅=⋅⋅；由（Ⅰ）知，DE 是鳖臑D BCE -的高， BC CE ⊥，所以21136BCE V S DE BC CE DE ∆=⋅=⋅⋅.在Rt △PDC中，因为PD CD =，点E 是PC 的中点，所以DE CE ==，于是 12123 4.16BC CD PD V CD PD V CE DEBC CE DE ⋅⋅⋅===⋅⋅⋅ 【考点定位】本题考查直线与平面垂直的判定定理、直线与平面垂直的性质定理和简单几何体的体积，属中高档题.【名师点睛】以《九章算术》为背景，给予新定义，增添了试题的新颖性，但其实质仍然是考查线面垂直与简单几何体的体积计算，其解题思路：第一问通过线线、线面垂直相互之间的转化进行证明，第二问关键注意底面积和高之比，运用锥体的体积计算公式进行求解. 结合数学史料的给予新定义，不仅考查学生解题能力，也增强对数学的兴趣培养，为空间立体几何注入了新的活力.22.【2015高考湖南，文18】（本小题满分12分）如图4，直三棱柱111ABC A B C -的底面是边长为2的正三角形，,E F 分别是1,BC CC 的中点。

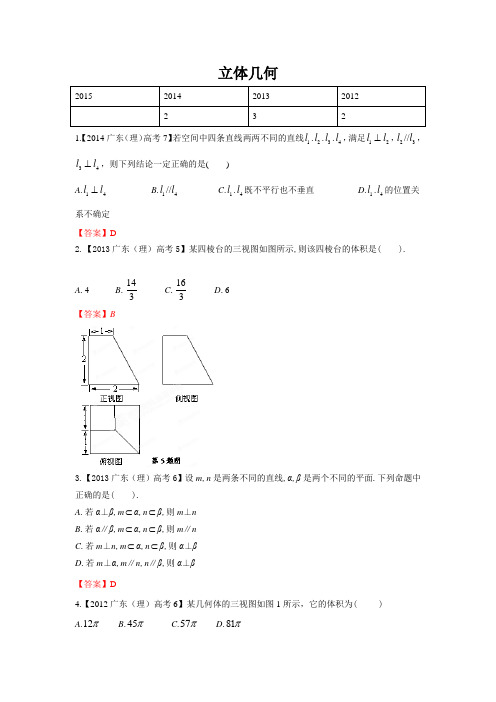
立体几何1.【2014广东（理）高考7】若空间中四条直线两两不同的直线1l .2l .3l .4l ，满足12l l ⊥，23//l l ，34l l ⊥，则下列结论一定正确的是( )A .14l l ⊥B .14//l lC .1l .4l 既不平行也不垂直D .1l .4l 的位置关系不确定 【答案】D2.【2013广东（理）高考5】某四棱台的三视图如图所示,则该四棱台的体积是( ).A .4B .143C .163D .6 【答案】B3.【2013广东（理）高考6】设m ,n 是两条不同的直线,α,β是两个不同的平面.下列命题中正确的是( ).A .若α⊥β,m ⊂α,n ⊂β,则m ⊥nB .若α∥β,m ⊂α,n ⊂β,则m ∥nC .若m ⊥n ,m ⊂α,n ⊂β,则α⊥βD .若m ⊥α,m ∥n ,n ∥β,则α⊥β 【答案】D4.【2012广东（理）高考6】某几何体的三视图如图1所示，它的体积为( ) A .12π B .45π C .π57 D .π81【答案】C5.【2014广东（理）高考18】 (本小题满分13分)如图4，四边形ABCD 为正方形，PD ⊥平面ABCD ，30DPC ∠=，AF PC ⊥于点F ，//FE CD ，交PD 于点E . (1)证明：CF ADF ⊥平面； (2)求二面角D AF E --的余弦值.【答案】(1)详见解析；(2)19. （１）PD ⊥平面ABCD ，PD AD ∴⊥，又CD AD ⊥，PD CD D =， AD ∴⊥平面PCD ，AD PC ∴⊥，又AF PC ⊥，PC ∴⊥平面ADF ，即CF ADF ⊥平面；（２）设1AB =，则Rt PDC ∆中，1CD =，又DPC ∠=2PC ∴=，PD =，由（１）知CF DF ⊥ DF ∴=AF ==12CF ∴==，又//FE CD ，14DE CF PD PC ∴==，DE ∴=，同理3344EF CD ==，如图所示，以D 为原点，建立空间直角坐标系，则(0,0,1)A ，E，3,0)4F，P ，(0,1,0)C ，设(,,)m x y z =是平面AEF 的法向量，则m AE m EF ⎧⊥⎨⊥⎩，又3(3(0,,0)4AE EF ⎧=⎪⎨=⎪⎩，所以304304m AE x z m EFy ⎧⋅=-=⎪⎨⋅==⎪⎩，令4x =，得z =，m =，由（１）知平面ADF 的一个法向量(,0)PC =， 设二面角D AF E --的平面角为θ，可知θ为锐角，||cos |cos ,|||||mPC m PC m PC ⋅=<>==⋅θ=，即所求．6.【2013广东（理）高考18】 (本小题满分14分)如图(1),在等腰直角三角形ABC 中,∠A ＝90°,BC ＝6,D ,E 分别是AC ,AB 上的点,CD ＝BEO为BC 的中点.将△ADE沿DE 折起,得到如图(2)所示的四棱锥A ′BCDE ,其中A ′O图(1)图(2)(1)证明：A ′O ⊥平面BCDE ；(2)求二面角A ′CDB的平面角的余弦值. 【答案】(1)详见解析 (2)5(Ⅰ) 在图1中,易得3,OC AC AD === 连结,OD OE ,在OCD ∆中,由余弦定理可得OD =由翻折不变性可知A D '=所以222A O OD A D ''+=,所以A O OD '⊥, 理可证A O OE '⊥, 又ODOE O =,所以A O '⊥平面BCDE .(Ⅱ) 传统法:过O 作OH CD ⊥交CD 的延长线于H ,连结A H ', 因为A O '⊥平面BCDE ,所以A H CD '⊥, 所以A HO '∠为二面角A CD B '--的平面角. 结合图1可知,H 为AC 中点,故2OH =,从而2A H '== 所以cos 5OH A HO A H '∠==',所以二面角A CD B '--.向量法:以O 点为原点,建立空间直角坐标系O xyz -则(A ',()0,3,0C -,()1,2,0D -所以(CA '=,(1,DA '=- 设(),,n x y z =为平面A CD '的法向量,则00n CA n DA ⎧'⋅=⎪⎨'⋅=⎪⎩,即3020y x y ⎧=⎪⎨-++=⎪⎩,解得y x z =-⎧⎪⎨=⎪⎩,令1x =,得(1,n =- 由(Ⅰ) 知,(OA '=为平面CDB 的一个法向量,所以cos ,3n OA n OA n OA '⋅'===',即二面角A CD B '--的平面角的余弦值为5.7.【2012广东（理）高考18】 (本小题满分13分)如图所示，在四棱锥P ABCD -中，底面ABCD 为矩形，PA ⊥平面ABCD ，点E 在线段PC 上，PC ⊥平面BDE . (1)证明：BD ⊥平面PAC ；(2)若1,2PA AD ==，求二面角B PC A --的正切值； 【答案】（1）证明：因为P A ⊥平面ABCD ，BD ⊂平面ABCD ，所以BD ⊥P A又因为PC⊥平面BDE，BD⊂平面BDE，BD⊥PC而P A∩PC=P，BD⊥平面P AC.（2）由（1）BD⊥平面P AC，得BD⊥AC，所以矩形ABCD为正方形设AC交BD于点O, 由PC⊥平面BDE,得PC垂直OE和BE所以∠BEO为二面角B－PC－A的平面角1,23PA AD AC BO OC PC==∴===∴==OE COOEPA PC===又所以在直角三角形BEO中，tan∠BEO33BOEO===，即二面角B-PC-A的正切值为3.8．（广东省湛江市湖光中学2014届高三上学期入学考试数学（理）试题）设三棱锥的三个侧面两两互相垂直,且侧棱长均为则其外接球的表面积为（）A．48πB．36πC．32πD．12π【答案】B9错误！未指定书签。

2015届高考理科数学立体几何一轮练习题-数学试题第1课时立体几何的结构及其三视图和直观图1．认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构．2．能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图，能识别上述三视图所表示的立体模型，会用斜二测画法画出它们的直观图．3．会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图，了解空间图形的不同表示形式．4．会画某些建筑物的三视图与直观图(在不影响图形特征的基础上，尺寸、线条等没有严格要求)．[对应学生用书P109]【梳理自测】一、空间几何体的结构特征1．(教材改编)下列说法正确的是()A．有两个面平行，其余各面都是四边形的几何体叫棱柱B．有两个面平行，其余各面都是平行四边形的几何体叫棱柱C．有一个面是多边形，其余各面都是三角形的几何体叫棱锥D．棱台各侧棱的延长线交于一点2．如图是一个正方体的展开图，将其折叠起来，变成正方体后的图形是()答案：1.D 2.B◆以上题目主要考查了以下内容：多面体棱柱棱柱的侧棱都平行且相等，上下底面是平行且全等的多边形．棱锥棱锥的底面是任意多边形，侧面是有一个公共顶点的三角形．棱台棱台可由平行于底面的平面截棱锥得到，其上下底面是平行且相似的多边形．旋转体圆柱圆柱可由矩形绕其任意一边所在直线旋转得到．圆锥圆锥可以由直角三角形绕其一条直角边所在直线旋转得到．圆台圆台可由直角梯形绕直角腰或等腰梯形绕上下底中点连线旋转得到，也可由平行于圆锥底面的平面截圆锥得到．球球可以由半圆或圆绕直径所在直线旋转得到.二、三视图1．有一个几何体的三视图如图所示，这个几何体应是一个()A．棱台B．棱锥C．棱柱D．都不对2．一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是()A．球B．三棱锥C．正方体D．圆柱答案：1.A 2.D◆以上题目主要考查了以下内容：名称几何体的三视图有：正视图、侧视图、俯视图画法1.画三视图时，重叠的线只画一条，挡住的线画成虚线. 2.三视图的正视图、侧视图、俯视图分别是从几何体的正前方、左方、正上方观察几何体得到的正投影图．规则1.画法规则：长对正、高平齐、宽相等. 2.摆放规则：侧视图在正视图的右侧，俯视图在正视图的下方.三、直观图及投影1．用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形，则原来的图形是()2．如图，过BC的平面截去长方体的一部分，所得的几何体________棱柱(填“是”或“不是”)．答案：1.A 2.是◆以上题目主要考查了以下内容：直观图空间几何体的直观图常用斜二测画法来画，其规则是：(1)原图形中x轴、y轴、z 轴两两垂直，直观图中，x′轴、y′轴的夹角为45°或135°，z′轴与x′轴和y′轴所在平面垂直. (2)原图形中平行于坐标轴的线段，直观图中仍平行于坐标轴，平行于x轴和z轴的线段长度在直观图中不变，平行于y轴的线段长度在直观图中等于原来的一半．投影1.平行投影：平行投影的投影线互相平行. 2.中心投影：中心投影的投影线相交于一点.【指点迷津】1．一个程序由三视图还原几何体按下面的程序进行定底面根据俯视图确定定棱及侧面根据正视图确定几何体的侧棱与侧面特征，调整实线、虚线对应棱的位置定形状确定几何体的形状2．三个“变”与“不变”斜二测画直观图时“三变”坐标轴的夹角改变，与y轴平行的线段的长度变为原来的一半，图形改变.“三不变”平行性不改变，与x、z轴平行的线段的长度不改变，相对位置不改变.[对应学生用书P110]考向一空间几何体的结构特征给出下列四个命题：①在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线；②底面为正多边形，且有相邻两个侧面与底面垂直的棱柱是正棱柱；③直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥；④棱台的上、下底面可以不相似，但侧棱长一定相等．其中正确命题的个数是()A．0B．1C．2 D．3【审题视点】根据柱、锥、台几何体的结构特征判定．【典例精讲】①不一定，只有这两点的连线平行于轴时才是母线；②正确；③错误．当以斜边所在直线为旋转轴时，其余两边旋转形成的面所围成的几何体不是圆锥．如图所示，它是由两个同底圆锥组成的几何体；④错误，棱台的上、下底面是相似且对应边平行的多边形，各侧棱延长线交于一点，但是侧棱长不一定相等．【答案】B【类题通法】(1)紧扣结构特征是判断的关键，熟悉空间几何体的结构特征，依据条件构建几何模型，在条件不变的情况下，变换模型中的线面关系或增加线、面等基本元素，然后再依据题意判定．(2)通过反例对结构特征进行辨析，即要说明一个命题是错误的，只要举出一个反例即可．1．给出下列四个命题：①有两个侧面是矩形的棱柱是直棱柱；②侧面都是等腰三角形的棱锥是正棱锥；③侧面都是矩形的直四棱柱是长方体；④若有两个侧面垂直于底面，则该四棱柱为直四棱柱．其中不正确的命题的个数是________个．解析：认识棱柱一般要从侧棱与底面的垂直与否和底面多边形的形状两方面去分析，故①③都不准确，②中对等腰三角形的腰是否为侧棱未作说明，故也不正确，④平行六面体的两个相对侧面也可能与底面垂直且互相平行，故④也不正确．答案：4考向二空间几何体的三视图(2014&#8226;陕西省高三质检)如图是由若干个相同的小立方体组成的几何体的俯视图，其中小立方体中的数字表示相应位置的小立方体的个数，则该几何体的左视图为()【审题视点】从左侧看这个几何体中小立方体组成的几何体的高度．【典例精讲】由俯视图知左视图从左到右最高的小立方体个数分别为2，3，1，选C.【答案】C【类题通法】(1)由实物图画三视图或判断选择三视图，此时需要注意“长对正、高平齐、宽相等”的原则；(2)由三视图还原实物图，这一题型综合性较强，解题时首先对柱、锥、台、球的三视图要熟悉，再复杂的几何体也是由这些简单的几何体组合而成的；其次，要遵循以下三步：①看视图，明关系；②分部分，想整体；③综合起来，定整体．2．(2014&#8226;山西高考训练)某几何体的三视图均为直角三角形，如图所示，则围成该几何体的各面中，直角三角形的个数为()A．1B．2C．3 D．4解析：选D.依题意得，该几何体是一个底面为直角三角形、一条侧棱垂直于底面的三棱锥，其四个面均为直角三角形，选D.考向三空间几何体的直观图已知正三角形ABC的边长为a，那么◆ABC的平面直观图◆A′B′C′的面积为()A.34a2B.38a2C.68a2D.616a2【审题视点】画出正三角形◆ABC的平面直观图◆A′B′C′，求◆A′B′C′的高即可．【典例精讲】先画出正三角形ABC，然后再画出它的水平放置的直观图，如图所示，由斜二测画法规则知B′C′＝a，O′A′＝34a.过A′作A′M◆x′轴，垂足为M，则A′M＝O′A′&#8226;sin 45°＝34a×22＝68a.◆S◆A′B′C′＝12B′C′&#8226;A′M＝12a×68a＝616a2.【答案】D【类题通法】对于直观图，除了了解斜二测画法的规则外，还要了解原图形面积S与其直观图面积S′之间的关系S′＝24S，能进行相关问题的计算．3．如图所示，四边形A′B′C′D′是一平面图形的水平放置的斜二测画法的直观图，在斜二测直观图中，四边形A′B′C′D′是一直角梯形，A′B′◆C′D′，A′D′◆C′D′，且B′C′与y′轴平行，若A′B′＝6，D′C′＝4，A′D′＝2.求这个平面图形的实际面积．解析：根据斜二测直观图画法规则可知该平面图形是直角梯形，且AB＝6，CD＝4保持不变．由于C′B′＝2A′D′＝22.所以CB＝42.故平面图形的实际面积为12×(6＋4)×42＝202.[对应学生用书P111]忽视几何体的放置与特征致误在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为()【正解】由正视图和俯视图可以推测几何体为半圆锥和三棱锥的组合体(如图所示)，且顶点在底面的射影恰是底面半圆的圆心，可知侧视图为等腰三角形，且轮廓线为实线，故选D.【答案】D【易错点】(1)根据正视图和俯视图确定原几何体的形状时出现错误，误把半圆锥看成半圆柱，不能准确判断出几何体的形状而误选A.(2)对实线与虚线的画法规则不明确而误选C.【警示】 1.首先确定几何体，面对读者是怎么放置的．2．要分清三视图中的虚线是被哪部分挡住的．3．要明确三视图中三角形的高度是不是几何体的高度．1．(2013&#8226;高考四川卷)一个几何体的三视图如图所示，则该几何体的直观图可以是()解析：选D.先观察俯视图，再结合主视图和侧视图还原为空间几何体．由俯视图是圆环可排除A，B，C，进一步将已知三视图还原为几何体，可得选项D. 2．(2013&#8226;高考湖南卷)已知正方体的棱长为1，其俯视图是一个面积为1的正方形，侧视图是一个面积为2的矩形，则该正方体的正视图的面积等于()A.32B．1C.2＋12D.2解析：选D.根据正方体的俯视图及侧视图特征想象出其正视图后求面积．由于该正方体的俯视图是面积为1的正方形，侧视图是一个面积为2的矩形，因此该几何体的正视图是一个长为2，宽为1的矩形，其面积为2.3．(2012&#8226;高考陕西卷)将正方体(如图(1)所示)截去两个三棱锥，得到如图(2)所示的几何体，则该几何体的左视图为()解析：选B.还原正方体后，将D1，D，A三点分别向正方体右侧面作垂线．D1A的射影为C1B，且为实线，B1C被遮挡应为虚线．4．(2012&#8226;高考湖南卷)某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能是()解析：选C.若为C选项，则主视图为：故不可能是C选项．。

2015届高三理科数学小综合专题练习——解析几何一、选择题1．已知两直线03:1=++my x l ，()0221:2=++-m my x m l ，若21//l l ，则m 的值为（ ）A ． 0B ． 1-或21C ．3D ．0或32．直线012=++y x 被圆25)1()2(22=-+-y x 所截得的弦长等于（ ） A.52 B.53 C.54 D.553．设P 是椭圆1162522=+y x 上的一点，21,F F 是焦点，若︒=∠3021PF F ，则21PF F ∆的面积为（ ）A.3316 B.)32(16- C. )32(16+ D.164．与曲线1492422=+y x 共焦点，且与曲线1643622=-y x 共渐近线的双曲线方程为（ ） A ．191622=-x y B ．191622=-y x C ．116922=-x y D ．116922=-y x5．设椭圆的两个焦点分别为1F 、2F ，过2F 作椭圆长轴的垂线交椭圆于点M ，若M F F 21∆为等腰直角三角形，则椭圆的离心率为（ ）A.22B.12-C.22-D.212-二、填空题6．直线210kx y k +++=必经过的点是 ．7．P 为圆122=+y x 上的动点，则点P 到直线01043=--y x 的距离的最小值为 ．8．已知抛物线)0(22>=p px y 的准线与直线03=-+y x 以及x 轴围成三角形面积为8，则p ＝__________________.9．若动圆M 与圆2)4(:221=++y x C 外切，且与圆2)4(:222=+-y x C 内切，则动圆圆心M 的轨迹方程________．10．已知双曲线)0,0(12222>>=-b a b y a x 和椭圆191622=+y x 有相同的焦点，且双曲线的离心率是椭圆离心率的两倍，则双曲线的方程为 _________ ．三、解答题11．已知椭圆)0,0(1:2222>>=+b a b y a x E 的离心率3 e =，并且经过定点1 (3,)2P （1）求椭圆 E 的方程；（2）问是否存在直线m x y +-=，使直线与椭圆交于B A , 两点，满足OA OB ⊥,若存在求 m 值，若不存在说明理由．12．椭圆2222:1(0)x y C a b a b +=>>过点3(1,)2A ，离心率为12，左、右焦点分别为12,F F ，过1F 的直线交椭圆于,A B 两点．（1）求椭圆C 的方程；（2）当2F AB∆的面积为27时，求直线的方程.13．无论m 为任何实数，直线m x y l +=:与双曲线)0(12:222>=-b b y x C 恒有公共点.（1）求双曲线C 的离心率e 的取值范围；（2）若直线l 过双曲线C 的右焦点F ，与双曲线交于Q P ,两点，并且满足→→=FQFP 51，求双曲线C 的方程.14．已知椭圆2222:1(0)x y C a b a b +=>>的两焦点与短轴的一个端点的连线构成等腰直角三角形，直线01=++y x 与以椭圆C 的右焦点为圆心，以b 2为半径的圆相切． （1）求椭圆的方程．（2）若过椭圆C 的右焦点F 作直线l 交椭圆C 于B A ,两点，交y 轴于M 点，且21,λλ==求证：21λλ+为定值15．已知抛物线y x C 4:2=的焦点为F ，过点F 作直线l 交抛物线C 于A 、B 两点；椭圆E 的中心在原点，焦点在x 轴上，点F 是它的一个顶点，且其离心率23=e ．（1）求椭圆E 的方程；（2）经过A 、B 两点分别作抛物线C 的切线1l 、2l ，切线1l 与2l 相交于点M ．证明：MF AB ⊥；（3） 椭圆E 上是否存在一点M '，经过点M '作抛物线C 的两条切线M A ''、M B ''（A '、B '为切点），使得直线A B ''过点F ？若存在，求出抛物线C 与切线M A ''、M B ''所围成图形的面积；若不存在，试说明理由．2015届高三理科数学小综合专题练习——解析几何参考答案 1．A【解析】由题，若0:1111=++C y B x A l ,0:2222=++C y B x A l ,当21//l l 时，有212121C C B B A A ≠=,故本题有m m m m 23211≠=-，即3≠m ，又因为当m=0，时，0:,3:21=-=x l x l ，因此，l1∥l2。

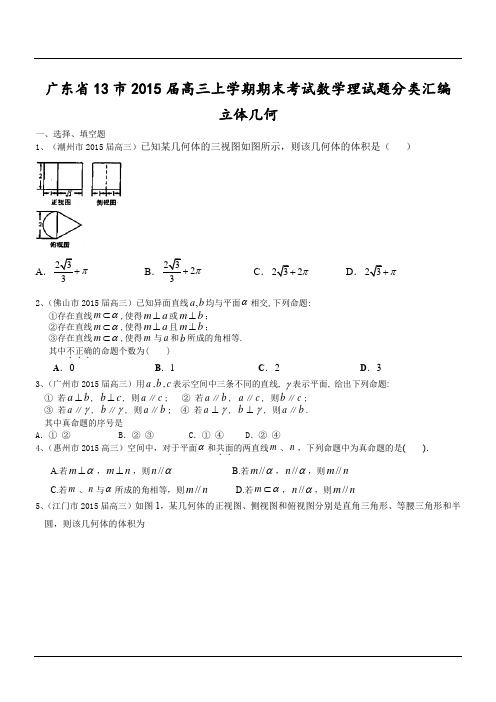
广东省13市2015届高三上学期期末考试数学理试题分类汇编立体几何一、选择、填空题1、（潮州市2015届高三）已知某几何体的三视图如图所示，则该几何体的体积是（ ）ABC ．D ． 2、（佛山市2015届高三）已知异面直线,a b 均与平面α相交,下列命题:①存在直线m α⊂,使得m a ⊥或m b ⊥； ②存在直线m α⊂,使得m a ⊥且m b ⊥；③存在直线m α⊂,使得m 与a 和b 所成的角相等. 其中不正确．．．的命题个数为( ) A ．0 B ．1 C ．2 D ．3 3、（广州市2015届高三）用a ,b ,c 表示空间中三条不同的直线, γ表示平面, 给出下列命题: ① 若a b ⊥, b c ⊥, 则a ∥c ; ② 若a ∥b , a ∥c , 则b ∥c ; ③ 若a ∥γ, b ∥γ, 则a ∥b ; ④ 若a ⊥γ, b ⊥γ, 则a ∥b . 其中真命题的序号是A ．① ②B ．② ③ C．① ④ D ．② ④4、（惠州市2015高三）空间中，对于平面和共面．．的两直线、，下列命题中为真命题的是( )． A.若，，则 B.若，，则 C.若、与所成的角相等，则 D.若，，则5、（江门市2015届高三）如图1，某几何体的正视图、侧视图和俯视图分别是直角三角形、等腰三角形和半圆，则该几何体的体积为π+2π+2ππαm n m α⊥m n ⊥//n α//m α//n α//m n m n α//m n m α⊂//n α//m nA ．4B ．8C ．π2D ．π46、（揭阳市2015届高三）一几何体的三视图如图3示, 则该几何体的体积为________7、（清远市2015届高三）某几何体的三视图如下图所示：其中正视图和侧视图都是上底为3，下底为9，高为4的等腰梯形，则该几何体的全面积为＿＿＿＿ 8、（汕头市2015届高三）给出下列命题，其中错误命题的个数为( ) （1）直线a 与平面不平行，则a 与平面内的所有直线都不平行； （2）直线a 与平面不垂直，则a 与平面内的所有直线都不垂直； （3）异面直线a 、b 不垂直，则过a 的任何平面与b 都不垂直； （4）若直线a 和b 共面，直线b 和c 共面，则a 和c 共面A ．1 B2 C3 D 4αααα9、（汕尾市2015届高三）已知直线l ⊥平面α，直线m ⊆平面β恒谦网，则下列四个结论：①若//αβ，则l m ⊥ ②若αβ⊥，则//l m③若//l m ，则αβ⊥④若l m ⊥，则//αβ。

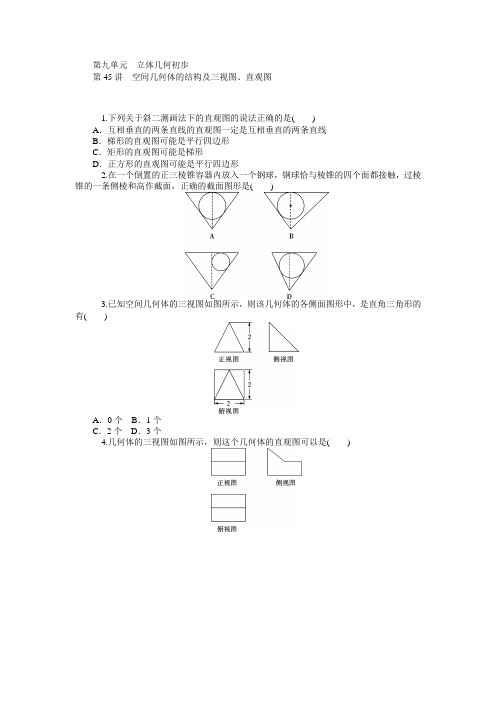
第九单元立体几何初步第45讲空间几何体的结构及三视图、直观图1.下列关于斜二测画法下的直观图的说法正确的是()A．互相垂直的两条直线的直观图一定是互相垂直的两条直线B．梯形的直观图可能是平行四边形C．矩形的直观图可能是梯形D．正方形的直观图可能是平行四边形2.在一个倒置的正三棱锥容器内放入一个钢球，钢球恰与棱锥的四个面都接触，过棱锥的一条侧棱和高作截面，正确的截面图形是()3.已知空间几何体的三视图如图所示，则该几何体的各侧面图形中，是直角三角形的有()A．0个B．1个C．2个D．3个4.几何体的三视图如图所示，则这个几何体的直观图可以是()5.如图，四边形ABCD在斜二测画法下的直观图是下底角为45°的等腰梯形，其下底长为5，一腰长为2，则原四边形的面积是________．6.一个三棱锥的正视图和侧视图及其尺寸如图所示，则该三棱锥俯视图的面积为______．7.一个简单几何体的正视图、侧视图如图所示，则其俯视图不可能为①长方形；②正方形；③圆；④椭圆．其中满足条件的序号是________．8.如图是一个几何体的正视图和俯视图．(1)试判断该几何体是什么几何体；(2)画出其侧视图，并求该平面图形的面积．9.某几何体的一条棱长为7，在该几何体的正视图中，这条棱的投影是长为6的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为a和b的线段，求a＋b的最大值．第46讲 空间几何体的表面积和体积1.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为( )A ．6B ．9C ．12D ．182.一个几何体的三视图如图所示，则该几何体的体积为( )A.a 32B.a 36 C.a 312 D.a 3183.如图为一个几何体的三视图，正视图和侧视图均为矩形，俯视图为正三角形，尺寸如图，则该几何体的表面积为( )A ．14 3B ．6＋ 3C ．12＋2 3D ．16＋2 34.设长方体的长、宽、高分别为2a 、a 、a ，其顶点都在一个球面上，则该球的表面积为( )A ．3πa 2B ．6πa 2C ．12πa 2D ．24πa 25.某圆锥的侧面展开图是半径为1 m 的半圆，则该圆锥的体积是__________m 3.6.矩形ABCD 中，AB ＝4，BC ＝3，沿AC 将矩形ABCD 折成一个直二面角B -AC -D ，则四面体ABCD的外接球的体积为________．7.已知H是球O的直径AB上一点，AH∶HB＝1∶2，AB⊥平面α，H为垂足，α截球O所得截面的面积为π，则球O的表面积为________．8.一几何体按比例绘制的三视图如图所示(单位：m)．(1)试画出它的直观图；(2)求它的表面积和体积．9.如图，正三棱锥O-ABC底面边长为2，高为1，求该三棱锥的体积及表面积．第47讲 空间点、线、面的位置关系1.已知a ，b ，c 为三条不重合的直线，下面有三个结论：①若a ⊥b ，a ⊥c ，则b ∥c ；②若a ⊥b ，a ⊥c ，则b ⊥c ；③若a ∥b ，b ⊥c ，则a ⊥c .其中正确的个数为( )A ．0个B ．1个C ．2个D ．3个2.若直线l 与平面α不平行，则下列结论正确的是( ) A ．α内的所有直线都与直线l 异面 B ．α内不存在与l 平行的直线 C ．α内的直线与l 都相交 D ．直线l 与平面α有公共点3.下列四个命题：①如果两条平行直线中的一条直线与一个平面平行，那么另一条直线也与这个平面平行；②若两个平面平行，则其中一个平面内的任何一条直线必平行于另一个平面； ③如果一个平面内的无数条直线平行于另一个平面，则这两个平面平行； ④如果一个平面内的任何一条直线都平行于另一平面，则这两个平面平行． 则真命题是( ) A ．①② B ．②④ C ．①③ D ．②③ 4.四棱锥P -ABCD 的所有侧棱长都为5，底面ABCD 是边长为2的正方形，则CD 与P A 所成角的余弦值为( )A.55B.255C.45D.355.在正方体ABCD -A 1B 1C 1D 1中，M ，N ，P ，Q 分别是AB ，AA 1，C 1D 1，CC 1的中点，给出以下四个结论：①AC 1⊥MN ；②AC 1∥平面MNPQ ；③AC 1与PM 相交；④NC 1与PM 异面．其中正确结论的序号是__________．6.下图是正方体的平面展开图，则在原正方体中：①BM 与DE 平行； ②CN 与BE 是异面直线； ③CN 与BM 成60°角； ④DM 与BN 垂直． 其中真命题的序号是________． 7.四棱锥P -ABCD 的顶点P 在底面ABCD 上的投影恰好是A ，其正视图与侧视图都是腰长为a 的等腰直角三角形，则在四棱锥P -ABCD 的任意两个顶点的连线中，互相垂直的异面直线共有 对．8.如图所示，在正方体ABCD-A1B1C1D1中，E，F分别为CC1，AA1的中点，画出平面BED1F与平面ABCD的交线．9.如图所示，在正方体ABCD-A1B1C1D1中，E为AB的中点，F为A1A的中点，求证：(1)E、C、D1、F四点共面；(2)CE、D1F、DA三线共点．第48讲 空间中的平行关系1.若直线a ⊥b ，且直线a ∥平面α，则直线b 与平面α的位置关系是( ) A ．b ⊂α B ．b ∥αC ．b ⊂α或b ∥αD ．b 与α相交或b ⊂α或b ∥α2.设m ，n 是平面α内的两条不同直线，l 1，l 2是平面β内的两条相交直线，则α∥β的一个充分而不必要条件是( )A ．m ∥β且l 1∥αB ．m ∥l 1且n ∥l 2C ．m ∥β且n ∥βD ．m ∥β且n ∥l 23.设α，β是两个平面，l ，m 是两条直线，下列命题中，可以判断α∥β的是( ) A ．l ⊂α，m ⊂α，且l ∥β，m ∥β B ．l ⊂α，m ⊂β，且m ∥α C ．l ∥α，m ∥β，且l ∥m D ．l ⊥α，m ⊥β，且l ∥m4.下列命题中正确的是________． ①若直线a 不在α内，则a ∥α；②若直线l 上有无数个点不在平面α内，则l ∥α；③若直线l 与平面α平行，则l 与α内的任意一条直线都平行；④如果两条平行线中的一条与一个平面平行，那么另一条也与这个平面平行； ⑤若l 与平面α平行，则l 与α内任何一条直线都没有公共点； ⑥平行于同一平面的两直线可以相交．5.如图所示，ABCD -A 1B 1C 1D 1是棱长为a 的正方体，M ，N 分别是下底面的棱A 1B 1，B 1C 1的中点，P 是上底面的棱AD 上的一点，AP ＝a3，过P ，M ，N 的平面交上底面于PQ ，Q 在CD 上，则PQ ＝____________.6.考察下列三个命题，请在“________”处添加一个条件，构成真命题(其中l ，m 为直线，α，β为平面)，则①⎭⎪⎬⎪⎫m ⊂αl ∥m ⇒l ∥α； ②⎭⎪⎬⎪⎫l ∥mm ∥α ⇒l ∥α； ③⎭⎪⎬⎪⎫a ⊂α，b ⊂αa ∥β，b ∥β ⇒α∥β. 7.空间四边形ABCD 的两条对棱AC 、BD 的长分别为5和4，则平行于两条对棱的截面四边形EFGH 在平移过程中，周长的取值范围是__________．8.求证：一条直线分别与两个相交平面平行，那么这条直线必与它们的交线平行．9.如图，在正方体ABCD-A1B1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，问：当点Q在什么位置时，平面D1BQ∥平面P AO?第49讲空间中的垂直关系1.直线l不垂直于平面α，则α内与l垂直的直线有()A．0条B．1条C．无数条D．α内的所有直线2.若三个平面α，β，γ之间有α⊥γ，β⊥γ，则α与β()A．垂直B．平行C．相交D．以上三种可能都有3.已知m是平面α的一条斜线，点A∉α，l为过点A的一条动直线，那么下列情形可能出现的是()A．l∥m，l⊥αB．l⊥m，l⊥αC．l⊥m，l∥αD．l∥m，l∥α4.已知直线l，m与平面α，β，γ满足β∩γ＝l，l∥α，m⊂α，m⊥γ，则有()A．α⊥γ且m∥βB．α⊥γ且l⊥mC．m∥β且l⊥m D．α∥β且α⊥γ5.如图所示，定点A和B都在平面α内，定点P∉α，PB⊥α，C是α内异于A和B的动点，且PC⊥AC，则BC与AC的位置关系是.6.已知a，b是两条不重合的直线，α，β，γ是三个两两不重合的平面，给出下列四个命题：①若a⊥α，a⊥β，则α∥β；②若α⊥γ，β⊥γ，则α∥β；③若α∥β，a⊂α，b⊂β，则a∥b；④若α∥β，α∩γ＝a，β∩γ＝b，则a∥b.其中正确命题的序号有________．7.在正方体ABCD-A1B1C1D1中，找一个平面与平面DA1C1垂直，则该平面是__________．(写出满足条件的一个平面即可)8.如图，在四面体ABCD中，CB＝CD，AD⊥BD，点E，F分别是AB，BD的中点，求证：(1)直线EF∥平面ACD；(2)平面EFC⊥平面BCD.9.如图，在四棱锥P-ABCD中，平面P AD⊥平面ABCD，AB＝AD，∠BAD＝60°，E，F分别是AP，AD的中点．求证：(1)直线EF∥平面PCD；(2)平面BEF⊥平面P AD.第50讲 空间角及计算1.平面α的斜线与α所成的角为30°，则此斜线和α内所有不过斜足的直线中所成的角的最大值为( )A ．30°B ．60°C ．90°D ．150°2.在边长为a 的正三角形ABC 中，AD ⊥BC 于D ，沿AD 折成二面角B －AD －C 后，BC ＝12a ，这时二面角B -AD -C 的大小为( )A ．30°B ．45°C ．60°D ．90° 3.三棱锥P -ABC 的两侧面P AB 、PBC 都是边长为2a 的正三角形，AC ＝3a ，则二面角A -PB -C 的大小为( ) A ．90° B ．30° C ．45° D ．60°4.已知三棱锥底面是边长为1的等边三角形，侧棱长均为2，则侧棱与底面所成角的余弦值为( )A.32B.12C.33D.365.已知三棱柱ABC -A 1B 1C 1的侧棱与底面垂直，体积为94，底面积是边长为3的正三角形，若P 为底面A 1B 1C 1的中心，则P A 与平面ABC 所成角的大小为( )A.5π12B.π3C.π4D.π66.二面角α-l -β的平面角为120°，A ，B ∈l ，AC ⊂α，BD ⊂β，AC ⊥l ，BD ⊥l ，若AB＝AC ＝BD ＝1，则CD 的长为 .7.已知∠AOB ＝90°，过O 点引∠AOB 所在平面的斜线OC ，与OA ，OB 分别成45°，60°，则以OC 为棱的二面角A -OC -B 的余弦值等于________．8.如图，在四棱锥P -ABCD 中，P A ⊥平面ABCD ，AB ＝BC ＝2，AD ＝CD ＝7，P A ＝3，∠ABC ＝120°，G 为线段PC 上的点． (1)证明：BD ⊥平面P AC;(2)若G 是PC 的中点，求DG 与P AC 所成的角的正切值．9.如图所示，AF，DE分别是⊙O，⊙O1的直径，AD与两圆所在的平面均垂直，AD ＝8，BC是⊙O的直径，AB＝AC＝6，OE∥AD.(1)求二面角B-AD-F的大小；(2)求直线BD与EF所成的角的余弦值．第51讲 空间距离及计算、展开与折叠问题1.将边长为a 的正方形ABCD 沿对角线AC 折起，使得BD ＝a ，则三棱锥D -ABC 的体积为( )A.a 26B.a 312C.312a 3D.212a 3 2.若长方体的三个面的对角线长分别是a ，b ，c ，则长方体体对角线长为( )A.a 2＋b 2＋c 2B.12a 2＋b 2＋c 2C.22a 2＋b 2＋c 2D.32a 2＋b 2＋c 2 3.若正四棱柱ABCD -A 1B 1C 1D 1的底面边长为1，AB 1与底面ABCD 成60°角，则直线A 1C 1到底面ABCD 的距离为( )A.33B ．1 C. 2 D. 34.A 、B 是直线l 上的两点，AB ＝4，AC ⊥l 于A ，BD ⊥l 于B ，AC ＝BD ＝3，又AC 与BD 成60°的角，则C ，D 两点间的距离是________．5.在等边△ABC 中，M ，N 分别为AB ，AC 上的点，满足AM ＝AN ＝2，沿MN 将△AMN 折起，使得平面AMN 与平面MNCB 所成的二面角为60°，则A 点到平面MNCB 的距离为________．6.设P A 垂直Rt △ABC 所在的平面α，∠BAC ＝90°，PB 、PC 分别与α成45°和30°角，P A ＝2，则P A 与BC 的距离是________；点P 到BC 的距离是________．7.如图，ABCD 与ABEF 均是边长为a 的正方形，如果二面角E -AB -C 的度数为30°，那么EF 与平面ABCD 的距离为________．8.如图所示，长方体ABCD -A 1B 1C 1D 1中，AB ＝a ，BC ＝b ，BB 1＝c ，并且a ＞b ＞c ＞0.求沿着长方体的表面自A 到C 1的最短线路的长．9.如图，在长方体ABCD -A 1B 1C 1D 1中，AB ＝2，AD ＝1，A 1A ＝1，证明直线BC 1平行于平面DA1C，并求直线BC1到平面D1AC的距离．第九单元 立体几何初步第45讲 空间几何体的结构及三视图、直观图 1．D 由斜二测画法的规则可知答案为D.2．B 由于球与侧棱不相交，因此截面图不可能存在截面圆与三角形都相切，排除A ，D ，又圆锥的高一定过球心，因此在截面图中三角形的高一定过截面圆的圆心，排除C ，故选B. 3.C 由三视图可知几何体是一个四棱锥，它的一个侧面与底面垂直，且此侧面的顶点在底面上的射影为对应底边的中点，易知其有两个侧面是直角三角形，故选C.4．B 由正视图可排除A ，C ；由侧视图可判断该几何体的直观图是B.5．82 作DE ⊥AB 于E ，CF ⊥AB 于F ， 则AE ＝BF ＝AD cos 45°＝1，所以CD ＝EF ＝3.将原图复原(如图)， 则原四边形应为直角梯形， ∠A ＝90°，AB ＝5，CD ＝3，AD ＝22，所以S 四边形ABCD ＝12×(5＋3)×22＝8 2.6．1 该三棱锥俯视图为直角三角形，两直角边分别为1,2，其面积为12×1×2＝1.7．②③ 由三视图的成图原则可知，正视图、侧视图的宽度不一样，故俯视图不可能为②正方形，③圆．8．解析：(1)由该几何体的正视图和俯视图可知该几何体是一个正六棱锥．(2)该几何体的侧视图如右图．其中AB ＝AC ，AD ⊥BC ，且BC 的长是俯视图正六边形对边的距离，即BC ＝3a . AD 是正六棱锥的高，即AD ＝3a ，所以该平面图形的面积S ＝12·3a ·3a ＝32a 2.9．解析：如图，P A ＝7，PC ⊥平面ABCD ，PD 为P A 的正视图，AC 为俯视图，PB 为侧视图，则AD ＝1.设PC ＝h ，AB ＝x .又⎩⎪⎨⎪⎧a 2＋x 2＝P A 2＝7b 2＋h 2＝P A 2＝7a 2－h 2＝BC 2＝1，得a 2＋b 2＝8.因为a 2＋b 22≥(a ＋b 2)2，所以a ＋b ≤2a 2＋b 22＝4.第46讲 空间几何体的表面积和体积1．B 由三视图可知，该几何体是三棱锥，其底面边长为6，高为3的等腰三角形，有一条长为3的侧棱垂直于底面，所以几何体的体积为V ＝13×12×6×3×3＝9，故选B.2．A 该几何体为底面是直角边为a 的等腰直角三角形，高为a 的直三棱柱，其体积为12×a ×a ×a ＝a 32，故选A. 3．C 据三视图可知几何体为一正三棱柱，其中侧棱长为2，底面三角形边上的高为3，即底面三角形边长为2，故其表面积S ＝3×2×2＋34×22×2＝12＋2 3.4．B 由题意，球的直径是长方体的体对角线， 所以2r ＝6a ，S ＝4πr 2＝6πa 2，故选B. 5.3π24设圆锥的底面圆的半径为r ，高为h ， 则由2πr ＝π，得r ＝12，h ＝12－(12)2＝32，所以该圆锥的体积V ＝13π×(12)2×32＝3π24(m 3)．6.125π6易知外接球球心O 即为AC 的中点， 故球半径r ＝12AC ＝52，所以V ＝4π3r 3＝4π3×(52)3＝125π6.7.9π2过H 的截面与球体上下分别交于M 、N 两点，三角形AMN 为直角三角形，因为MH ＝1，由射影定理可知，AH ＝22，BH ＝2，所以球体的半径为324，故表面积S ＝4×π×1816＝9π2. 8．解析：(1)直观图如图所示：(2)(方法一)由三视图可知该几何体是长方体被截去一个角，且该几何体的体积是以A 1A ，A 1D 1，A 1B 1为棱的长方体的体积的34，在直角梯形AA 1B 1B 中，作BE ⊥A 1B 1于E ，则AA 1EB 是正方形，所以AA 1＝BE ＝1. 在Rt △BEB 1中，BE ＝1，EB 1＝1，所以BB 1＝ 2. 所以几何体的表面积S ＝S 正方形AA 1D 1D ＋2S 梯形AA 1B 1B ＋S 矩形BB 1C 1C ＋S 正方形ABCD ＋S 矩形A 1B 1C 1D 1＝1＋2×12×(1＋2)×1＋1×2＋1＋1×2＝7＋2(m 2)．所以几何体的体积V ＝34×1×2×1＝32(m 3)，所以该几何体的表面积为(7＋2)m 2，体积为32m 3.(方法二)几何体也可以看作是以AA 1B 1B 为底面的直四棱柱，其表面积求法同方法一，V 直四棱柱D 1C 1CD -A 1B 1BA ＝Sh ＝12×(1＋2)×1×1＝32(m 3)．所以几何体的表面积为(7＋2)m 2，体积为32m 3.9．解析：三棱锥O -ABC 的体积V O -ABC ＝13·S △ABC ·1＝13×12×2×2×32＝33. 设O 在平面ABC 中的射影为Q ，BC 的中点为E ，则OQ ＝1，OE 2＝OQ 2＋EQ 2⇒12＋(33)2＝43⇒OE ＝23.三棱锥O -ABC 的表面积S O -ABC ＝3S △OBC ＋S △ABC ＝33，所以，三棱锥O -ABC 的体积V O -ABC ＝33，表面积S O -ABC ＝3 3. 第47讲 空间点、线、面的位置关系1．B ①b ，c 可能异面，也可能垂直；②b ，c 可能异面，也可能平行，故选B.2．D A 中过公共点的直线与直线l 相交，不异面，A 错误；B 、C 中l 在α内时，α内由无数多条直线与l 平行，B 、C 错误．直线l 与平面α不平行，则直线l 与α相交或在平面内，即l 与α有一个或无穷多个公共点，D 正确，故选D.3．B ①中满足条件的另一条直线也可能在平面中，不正确；③中满足条件的无数条直线如果互相平行，那么这两个平面也可能相交，不正确．排除①③，因此正确的命题是②④，故选B.4．A 因为CD 平行于AB ，则CD 与P A 所成角就是∠P AB ，由余弦定理可得cos ∠P AB ＝P A 2＋AB 2－PB 22P A ·AB ＝5＋4－52×5×2＝55，故选A.5．①③④ 由图形可以观察出AC 1与平面MNPQ 相交于正方体中心，易知①③④正确．6．③④ 还原正方体如图，可知：①BM 与ED 是异面直线；②CN 与BE 平行；③CN 与BM 成60°角；④DM 与BN 是异面直线，且DM 与BN 垂直．7．6 因为四棱锥P -ABCD 的顶点P 在底面ABCD 上的投影恰好是A ，其正视图与侧视图都是腰长为a 的等腰直角三角形，P A ⊥BC ，P A ⊥CD ，AB ⊥PD ，BD ⊥P A ，BD ⊥PC ，AD ⊥PB ，共6对．8．解析：在平面AA 1D 1D 内，延长D 1F . 因为D 1F 与DA 不平行，所以D 1F 与DA 必相交于一点，设为P ， 则P ∈FD 1，P ∈DA .又因为FD 1⊂平面BED 1F ，AD ⊂平面ABCD ， 所以P ∈平面BED 1F ，P ∈平面ABCD .又B 为平面ABCD 与平面BED 1F 的公共点，连接PB .所以PB 即为平面BED 1F 与平面ABCD 的交线，如图所示．9．证明：(1)分别连接EF 、A 1B 、D 1C .因为E 、F 分别是AB 和AA 1的中点，所以EF 綊12A 1B ，又A 1D 1綊B 1C 1綊BC ，所以四边形A 1D 1CB 为平行四边形．所以A 1B ∥CD 1，从而EF ∥CD 1， 所以EF 与CD 1确定一个平面． 所以E 、F 、D 1、C 四点共面．(2)因为EF 綊12CD 1，所以直线D 1F 和CE 必相交，设D 1F ∩CE ＝P ，因为P ∈D 1F 且D 1F ⊂平面AA 1D 1D ，所以P ∈平面AA 1D 1D ， 又P ∈EC 且CE ⊂平面ABCD ， 所以P ∈平面ABCD ，即P 是平面ABCD 与平面AA 1D 1D 的公共点， 而平面ABCD ∩平面AA 1D 1D ＝AD ，所以P ∈AD ，所以CE 、D 1F 、DA 三线共点． 第48讲 空间中的平行关系1．D b 与α相交或b ⊂α或b ∥α，都可以．2．B m ∥l 1且n ∥l 2，m ，n ⊂α，l 1，l 2为β内两条相交直线，则可得α∥β；若α∥β，l 1，l 2为β内两条相交直线，则不一定有m ∥l 1且n ∥l 2，故选B.3．D 条件A 中，增加l 与m 相交才能判断出α∥β，A 错．由条件B 、C 都有可能α与β相交，排除B 和C.而垂直于同一直线的两个平面平行，D 成立．4．⑤⑥ a ∩α＝A 时，a ⊄α，所以①错；直线l 与α相交时，l 上有无数个点不在α内，故②错； l ∥α时，α内的直线与l 平行或异面，故③错； a ∥b ，b ∥α时，a ∥α或a ⊂α，故④错；l ∥α，l 与α无公共点，所以l 与α内任一直线都无公共点，⑤正确； 长方体ABCD -A 1B 1C 1D 1中A 1C 1与B 1D 1都与平面ABCD 平行，所以⑥正确．故填⑤⑥. 5.223a 6．l ⊄α l ⊄α a 与b 相交解析：①②根据直线与平面平行的判定定理知均需要强调直线l 在平面外，均添加l ⊄α；③根据两个平面平行的判定定理知须强调两条直线相交，故添加a 与b 相交．7．(8,10) 设DH DA ＝GHAC＝k ，所以AH DA ＝EHBD＝1－k ，所以GH ＝5k ，EH ＝4(1－k )， 所以周长＝8＋2k .又因为0＜k ＜1，所以周长的取值范围为(8,10)． 8．证明：(方法一)借助于平行直线的传递性． 如图①所示，过a 作一平面γ交平面α于直线c .因为a ∥α，则c ∥a ，若c 、b 重合，命题成立；若c 与b 不重合， 又因为a ∥β，所以c ∥β，而α过c 且与β相交于b ， 所以c ∥b ，故a ∥b .(方法二)利用同一法，如图②所示，在平面α与β的交线b上任取一点A，过A作直线b′∥a.因为a∥α，所以b′在α内(一条直线与一个平面平行，那么过这个平面内一点而与这条直线平行的直线都在这个平面内)．同理，a∥β，所以b′也在平面β内．因为b′既在α内，又在β内，所以b′即为平面α与平面β的交线，即b′与b重合，所以a∥b.9．解析：当Q为CC1的中点时，平面D1BQ∥平面P AO.因为Q为CC1的中点，P为DD1的中点，所以QB∥P A.又QB⊄平面P AO，P A⊂平面P AO，所以QB∥平面P AO.连接DB.因为P，O分别为DD1，DB的中点，所以D1B∥PO.又D1B⊄平面P AO，PO⊂平面P AO，所以D1B∥平面P AO，又D1B∩QB＝B，所以平面D1BQ∥平面P AO.第49讲空间中的垂直关系1．C2．D垂直于同一个平面的两个平面的位置关系不确定，故选D.3．C对于A，由l∥m，l⊥α，则m⊥α，与已知矛盾；对于B，由l⊥m，l⊥α，可知m∥α或m⊂α，与已知矛盾；对于D，由l∥m，l∥α可知m∥α或m⊂α，与已知矛盾．由此排除A，B，D，故选C.4．B m⊂α，m⊥γ⇒α⊥γ，又l⊂γ⇒m⊥l，故选B.5．垂直因为PB⊥α，所以PB⊥AC.又因为PC⊥AC，且PC∩PB＝P，所以AC⊥平面PBC，所以AC⊥BC.6．①④垂直于同一直线的两平面平行，①正确；α⊥β也成立，②错；a、b也可异面，③错；由面面平行性质知，a∥b，④正确．7．平面ABD1连接AD1，在正方形ADD1A1中，AD1⊥A1D，又AB⊥平面ADD1A1，A1D⊂平面ADD1A1，所以AB⊥A1D.又AD1∩AB＝A，所以A1D⊥平面ABD1，又A1D⊂平面DA1C，故平面ABD1⊥平面DA1C1.8．证明：(1)在△ABD中，因为E，F分别是AB，BD的中点，所以EF∥AD.又AD⊂平面ACD，EF⊄平面ACD，所以直线EF∥平面ACD.(2)在△ABD 中，因为AD ⊥BD ，EF ∥AD ， 所以EF ⊥BD .在△BCD 中，因为CD ＝CB ，F 为BD 的中点， 所以CF ⊥BD .因为EF ⊂平面EFC ，CF ⊂平面EFC ， EF 与CF 交于点F ，所以BD ⊥平面EFC . 又因为BD ⊂平面BCD ， 所以平面EFC ⊥平面BCD .9．证明：(1)因为E ，F 分别是AP ，AD 的中点，所以EF ∥PD ，又因为PD ⊂平面PCD ，EF ⊄平面PCD ， 所以直线EF ∥平面PCD .(2)因为AB ＝AD ，∠BAD ＝60°，F 是AD 的中点，所以BF ⊥AD ，又平面P AD ⊥平面ABCD ，平面P AD ∩平面ABCD ＝AD ，所以BF ⊥平面P AD ，所以，平面BEF ⊥平面P AD . 第50讲 空间角及计算1．C 本题易误选D ，因斜线和α内所有不过斜足的直线为异面直线，故最大角为90°. 2．C3．D 取PB 的中点为M ，连接AM ，CM ，则AM ⊥PB ，CM ⊥PB ，所以∠AMC 为二面角A -PB -C 的平面角，在等边△P AB 与等边△PBC 中知AM ＝CM ＝3a ，即△AMC 为正三角形，所以∠AMC ＝60°，故选D.4．D 由于是三棱锥，故顶点在底面上的射影是底面正三角形的中心，底面的一个顶点到这个中心的距离是23×32＝33，所以据分析，所求的余弦值是332＝36，故选D.5．B 设三棱柱ABC -A 1B 1C 1的高为h ，所求的线面角为θ，由已知条件可得V ＝34×(3)2h ＝94，所以h ＝3，P A ＝3＋(32×3×23)＝2，所以sin θ＝h P A ＝32，所以θ＝π3.6．2 过B 作BE 綊AC ，连接CE ，DE .则∠DBE 即为二面角α-l -β的平面角．易证CE ⊥DE ，所以CD ＝CE 2＋DE 2＝AB 2＋BE 2＋BD 2－2BE ·BD ·cos ∠DBE ＝1＋1＋1－2×1×1·cos 120° ＝2.7．－33在OC 上取一点C ，使OC ＝1，过C 分别作CA ⊥OC 交OA 于A ，CB ⊥OC交OB 于B ，则AC ＝1，OA ＝2，BC ＝3，OB ＝2，Rt △AOB 中，AB 2＝6，△ABC 中，由余弦定理，得cos ∠ACB ＝－33.8．解析：(1)证明：设点O 为AC ，BC 的交点．由AB ＝BC ，AD ＝CD ，得BD 是线段AC 的中垂线． 所以O 为AC 的中点，BD ⊥AC .又因为P A ⊥平面ABCD ，BD ⊂平面ABCD ， 所以P A ⊥BD ，所以BD ⊥平面P AC . (2)连接OG .由(1)可知OD ⊥平面APC ，则DG 在平面APC 内的射影为OG ，所以∠OGD 是DG 与平面APC 所成的角．由题意得OG ＝12P A ＝32.在△ABC 中，AC ＝AB 2＋BC 2－2AB ·BC ·cos ∠ABC ＝23，所以OC ＝12AC ＝ 3.在直角△OCD 中，OD ＝CD 2－OC 2＝2，在直角△OGD 中，tan ∠OGD ＝OD OG ＝433.所以DG 与平面APC 所成的角的正切值为433.9．解析：(1)因为AD 与两圆所在的平面均垂直，所以AD ⊥AB ，AD ⊥AF ，故∠BAF 是二面角B -AD -F 的平面角．依题意可知，四边形ABFC 是正方形，所以∠BAF ＝45°， 即二面角B -AD -F 的大小为45°.(2)连接OD ，则OD ∥EF ，所以∠ODB 为异面直线BD 与EF 所成的角． 在Rt △ABD 中，BD ＝10，OA ＝OB ＝3 2. 因为四边形ABFC 是正方形，所以BO ⊥AF . 又AD ⊥平面ABFC ，所以AD ⊥BO ， 所以OB ⊥平面DAO ，所以OB ⊥OD ，故cos ∠ODB ＝DO BD ＝82＋(32)210＝8210.第51讲 空间距离及计算、展开与折叠问题 1．D2．C 设同一顶点的三条棱分别为x ，y ，z ，则x 2＋y 2＝a 2，y 2＋z 2＝b 2，x 2＋z 2＝c 2，得x 2＋y 2＋z 2＝12(a 2＋b 2＋c 2)，则对角线长为12(a 2＋b 2＋c 2)＝22a 2＋b 2＋c 2. 3.D 直线A 1C 1∥平面ABCD ，A 1C 1到底面ABCD 的距离即为正棱柱的高h ，tan 60°＝h1，所以h ＝3，故选D.4．5或43 CD ＝32＋32＋42±32＝5或43. 5.32在△ABC 中，过A 点作AF ⊥BC 交BC 于F 点，交MN 于E 点，由题意知折叠后∠AEF 即为平面AMN 与平面MNCB 所成二面角的平面角，故∠AEF ＝60°，过A 点作AH ⊥EF 于H 点，则AH 即为A 点到平面MNCB 的距离，因为AE ＝3，所以AH ＝AE ·sin 60°＝32.6.3 7 作AD ⊥BC 于点D ，因为P A ⊥面ABC ，所以P A ⊥AD .所以AD 是P A 与BC 的公垂线．易得AB ＝2，AC ＝23，BC ＝4，AD ＝3，连接PD ，则PD ⊥BC ，P 到BC 的距离PD ＝7.7.a2显然∠F AD 是二面角E -AB -C 的平面角，∠F AD ＝30°，过F 作FG ⊥平面ABCD 于G ，则G 必在AD 上，由EF ∥平面ABCD ，所以FG 为EF 与平面ABCD 的距离，即FG ＝a2.8．解析：将长方体相邻两个面展开有下列三种可能，如图所示．三个图形甲、乙、丙中AC 1的长分别为：(a ＋b )2＋c 2＝a 2＋b 2＋c 2＋2ab ， a 2＋(b ＋c )2＝a 2＋b 2＋c 2＋2bc ， (a ＋c )2＋b 2＝a 2＋b 2＋c 2＋2ac ， 因为a ＞b ＞c ＞0，所以ab ＞ac ＞bc ＞0. 故最短线路的长为a 2＋b 2＋c 2＋2bc . 9．解析：因为ABCD -A 1B 1C 1D 1为长方体，故AB ∥C 1D 1，AB ＝C 1D 1， 故ABC 1D 1为平行四边形， 故BC 1∥AD 1，显然B 不在平面D 1AC 上， 于是直线BC 1平行于平面DA 1C .直线BC 1到平面D 1AC 的距离即为点B 到平面D 1AC 的距离设为h ，考虑三棱锥A -BCD 1的体积，以ABC 为底面，可得V ＝13×(12×1×2)×1＝13.而△AD 1C 中，AC ＝D 1C ＝5，AD 1＝2，故S △AD 1C ＝32，所以，V ＝13×32×h ＝13⇒h ＝23，即直线BC 1到平面D 1AC 的距离为23.。

广东省13市2015届高三上学期期末考试数学文试题分类汇编立体几何一、选择题1、（潮州市2015届高三）已知某几何体的三视图如图所示，则该几何体的体积是（）A．B．C．D．2、（东莞市2015届高三）一个侧棱与底面垂直的四棱柱的正视图和俯视图如图所示，该四棱柱的体积为（）A．B．C．D．3、（佛山市2015届高三）在空间中，有如下四个命题：①平行于同一个平面的两条直线是平行直线；②垂直于同一条直线的两个平面是平行平面；③若平面内有不共线的三个点到平面距离相等，则∥；④过平面的一条斜线有且只有一个平面与平面垂直.其中正确的两个命题是( )A．①③B．②④C．①④D．②③4、（广州市2015届高三）用,,表示空间中三条不同的直线, 表示平面, 给出下列命题:①若, , 则∥; ②若∥, ∥, 则∥;③若∥, ∥, 则∥; ④若, , 则∥.其中真命题的序号是A．①②B．②③C．①④D．②④5、（惠州市2015届高三）下列命题正确的是（）A．若两条直线和同一个平面所成的角相等，则这两条直线平行B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面都垂直于第三个平面，则这两个平面平行6、（江门市2015届高三）某三棱锥的三视图如图1所示，这个三棱锥最长棱的棱长是A．B．C．D．7、（清远市2015届高三）一几何体三视图如图所示，则该几何体的体积是（）A、32－B、32－C、32－D、32－8、（汕头市2015届高三）如图是某几何体的三视图，其中正视图和侧视图是半径为的半圆，俯视图是个圆，则该几何体的全面积为（）A．B．C．D．9、（汕尾市2015届高三）某空间几何体的三视图如图（1）所示，则该几何体的体积为（）A．180 B．144 C．48 D．60www10、（韶关市2015届高三）已知两条直线，两个平面．给出下面四个命题：（）①；②；③；④．其中正确的命题序号为（）A．①②B．②③C．①④D．②④11、（深圳市2015届高三）如图2，三棱锥A－BCD中，AB平面BCD，BCCD，若AB＝BC ＝CD＝2，则该三棱锥的侧视图（投影线平行于BD）的面积为（）A、B、2 C、D、12、（肇庆市2015届高三）设l为直线，a，b是两个不同的平面，下列命题中正确的是A．若l//a，l//b，则a//b B．若a//b，l//a，则l//bC．若l^a，l//b，则a^b D．若a^b，l//a，则l^b13、（珠海市2015届高三）某几何体的三视图如图所示，则其体积为A、B、C、D、14、（惠州市2015届高三）右图是某个四面体的三视图，该四面体的体积为（）A．72 B．36 C．24 D．1215、（汕头市2015届高三）设，是两条不同直线，，是两个不同平面，则下列命题中正确的是（）A．若，，则B．若，，则C．若，，则D．若，，则16、（汕尾市2015届高三）已知直线平面，直线平面，则下列四个结论：①若，则②若，则③若，则④若，则其中正确的结论的序号是（）A.①④B.②④C.①③D.②③17、（肇庆市2015届高三）一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为A．B．C．D．二、解答题1、（潮州市2015届高三）如图，三棱柱中，，，．证明：；若，，求三棱锥的体积．2、（东莞市2015届高三）在如图所示的多面体中，四边形AB1B 1A 和ACC1 A1 都为矩形，AA1 ＝1，AC ＝，AB ＝2，设D ，E 分别是线段BC ，CC 1的中点.(1)若AC ⊥BC ，证明：直线BC ⊥平面ACC1A1；(2)设点M 为线段AB的中点，证明：直线DE // 平面A 1MC ；(3)在（1）条件下，求点D到平面A 1B1 E的距离.3、（佛山市2015届高三）如图,四棱锥,侧面是边长为的正三角形,且与底面垂直,底面是的菱形,为的中点.(Ⅰ) 求证:；(Ⅱ) 在棱上是否存在一点,使得四点共面?若存在,指出点的位置并证明；若不存在,请说明理由；(Ⅲ) 求点到平面的距离.4、（广州市2015届高三）如图3，在多面体中，平面，∥，平面平面，，，．（1）求证：∥；（2）求三棱锥的体积．5、（惠州市2015届高三）如图，在直三棱柱中，，、分别是，的中点．（1）求证：∥平面；（2）求证：平面平面；（3）若，，求三棱锥的体积．6、（江门市2015届高三）如图3，AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆周上不同于A、B的一点．⑴求证：平面PAC⊥平面PBC；⑵若PA=AB=2，∠ABC=30°，求三棱锥P-ABC的体积．7、（清远市2015届高三）在等腰直角△BCP中，BC=PC=4,∠BCP=90°,A是边BP的中点，现沿CA把△ACP折起，使PB=4，如图1所示.（1）在三棱锥P-ABC中，求证：直线PA⊥平面ABC；（2）在三棱锥P-ABC中，M、N、F分别是PC、BC、AC的中点,Q为MN上任取一点，求证：直线FQ∥平面PAB；8、（汕头市2015届高三）如图，已知平面，四边形为矩形，四边形为直角梯形，，，，．求证：平面；求证：平面；求三棱锥的体积．9、（汕尾市2015届高三）如图（4），在三棱柱中，侧面均为正方形，，点是棱的中点。

2015年全国各地高考数学试题及解答分类汇编大全（13立体几何）、选择题:1. （2015安徽文、理）一个四面体的三视图如图所示，则该四面体的表面积是V (9)題團(A) 1,3 ( B 1 2、2［解忻】由该几何悴■的三视图可知，该几何体的直观團+如下理所示,其中侧面岛匚丄底面且SPAC^ XkffG 由三视图中所给数据可知:FA = PC = .-L8 =BC =^/1一取3匚中点连接PO:BO.则RrAPOB中，PO = BO = PB - ^2~2+- D = 尽、故选C.［毛点定位】本题主要若查空囘几何郎阁三视圏、锥悴表面年只公式一【名0帀点睛】在眾J用空间几何悴的三视图求几何体的悴＜巳或者表瓯#貝时，一宦萝IE确还原几何郎的直观團,械后再利用你积或表面积公式求之I本題王套考査了考生的空间想象力和基本运算旨幻r2. （2015安徽理）已知m, n是两条不同直线，：•，一：是两个不同平面，则下列命题正确的是（）（A）若〉，'■垂直于同一平面，则:-与一：平行（B）若m , n平行于同一平面，则m与n平行（C）若〉，1不平行，则在:-内不存在与一：平行的直线(C) 2 3 (D) 2^ 2（D）若m , n不平行，则m与n不可能垂直于同一平面【答案】D【解析】由-長若住.0垂頁于同T 2面，则匸，尸可以相交、平行，故旦环正确；由衣，若用，苦平 行二同一平旨，则小•吒可」平行.重合、相交、异而,故E 不正确扌由（?，討 £下平行，但空平而 内会存在平行于0的直线，如理平面中平行于⑦0交线的直线；由D 项，耳逆否命題为“若阳与疋垂 直于同_平面,则饷打平行"是真命题,故D 项正晞，所以选H【考点定位】1•直建、平而的垂直、平行列定定理以及性质定理的应用.【名师点睛】空间直线、平面平行或垂直等位置关系命题的真假判断，常采用画图（尤其是画长方体h 现 实翊列断法（如墙角、桌面等h 瞬筛漑等；另外，若原命题不太容易判断真假，可以若虑它的逆否 命題，判断它的逆否兪题真假，原命题与逆否命题等价3、（2015北京文）某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为（A. 1 B . 、、2 C .,3£ <±> AS .由三视图可知，SC 丄平面ABCD SA 是四棱锥最长的棱,SA h ：'；sC 2 AC 2 = ：'；SC 2 AB 2 BC 2 = ：3.考点：三视图.zdi^4 ---- * t ■ HM < A > ftffi【答案】C【解析】试题分析：四棱锥的直观图如图所示:4. （2015北京理）某三棱锥的三视图如图所示，则该三棱锥的表面积是（A . 2+^5B • 4+^5C • 2+2J 5D . 5【答案】C 【解析】试题分析：根据三视图恢复成三棱锥P-ABC ，其中PC 丄平面ABC 取AB 棱的中点D,连接CDPD,有PD _ AB, CD _ AB ，底面ABC 为等腰三角形底边 AB 上的高CD 为2, AD=BD=1,PC=1, PD 二5, S ABC = *2 2=2,, S 呻=舟 2,5=5, AC二 BC = 5 ,S「AC = S PBC=㊁；"：；'51 -，三棱锥表面积 S表-2 5 2.考点：1.三视图；2.三棱锥的表面积.5. （2015福建文）某几何体的三视图如图所示，则该几何体的表面积等于（A. 8 22 B . 11 2 2 C . 14 2 2 D【答案】B【解析】学科网试题分析：由三视图还原几何体，该几何体是底面为直角梯形，高为)152的直四棱柱，且底面直角梯形的两底分别为1,2，直角腰长为1，斜腰为.2 •底面积为2 - 3 = 3，侧面积为则其表面积2为2+2+4+2 2=8+2 2，所以该几何体的表面积为11 2 2，故选B.考点：三视图和表面积.6. （2015广东文）若直线11和|2是异面直线，11在平面内，12在平面：内，I是平面〉与平面-的交线，则下列命题正确的是（）A . I至少与l1, l2中的一条相交B . I与l1, l2都相交C . l至多与l1, l2中的一条相交D . l与l1, l2都不相交【答案】A【解析】试题分析’若直线£和7：是异面直线，£在平面程内* 在平酝尸內，『是平面◎与平面戸的交线，则J至少与L L中的一条相交，故选亘考点：空间点、线、面的位置关系.7. （2015广东理）若空间中n个不同的点两两距离都相等，则正整数n的取值（）A .大于5 B. 等于5 C. 至多等于4 D. 至多等于3【答案】C .【解析】正四面悴的四个顶点是两两距离相等坯即空间中X个不同的点两两距离都相等，冋正整馥X的取值至多等于4,下面用反证法；假设空间中有5个……，故选C*【考点定位】本题考查空间想象能力、推理能力，属于中高档题.8. （2015湖南理）某工件的三视图如图3所示，现将该工件通过切割，加工成一个体积尽可能大的长方体新工件，并使新工件的一个面落在原工件的一个面内，=新工件的体积=原工件的体积【答案】A.则原工件材料的利用率为（材料利用率A•旦9 - B.16 C4（血-1）312（；2 -1）3D.。

一、选择题1．某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能．．．是2．一个空间几何体的三视图如图所示，则该几何体的表面积为A ．17848+ B ．17832+ C ．48 D ．80 3.下列命题正确的是（ ）A ．若两条直线和同一个平面所成的角相等,则这两条直线平行B ．若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C ．若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D ．若两个平面都垂直于第三个平面,则这两个平面平行4.下列命题中，n m 、表示两条不同的直线，γβα、、表示三个不同的平面． ①若αα//,n m ⊥，则n m ⊥； ②若γββα⊥⊥,，则γα//； ③若αα//,//n m ，则n m //； ④若αγββα⊥m ,//,//，则γ⊥m .正确的命题是( ) A ．①③ B ．①④ C ．②③ D ．②④ 5.如图是正方体平面展开图，在这个正方体中: ①BF 与ND 平行； ②CM 与BF 成60º角； ③CM 与BN 是异面直线； ④DF 与BM 垂直.以上四个命题中，正确命题的序号是( ) A.①②③ B.①③④ C.②④ D.③④二、填空题EB ANF CDM6. 如下图所示，直观图///BAO是有一个角为045的三角形，则其原平面图形的面积为________.第6题7．某几何体的三视图如图所示,它的体积为________．8．设zyx，，是空间中的不同直线或不同平面，下列条件中能保证“若zx⊥，且zy⊥，则yx//”为真命题的是________(填出所有正确条件的代号)．①x为直线，zy，为平面；②zyx，，为平面；③yx,为直线，z为平面；④yx,为平面，z为直线；⑤zyx，，为直线．9．如图，AB为圆O的直径，点C在圆周上(异于点BA，)，直线PA垂直于圆O所在的平面，点M为线段PB的中点．有以下四个命题：①//PA平面MOB；②//MO平面PAC；③⊥OC平面PAC；④平面PAC⊥平面PBC.其中正确的命题是________(填上所有正确命题的序号)．10．如图，在长方形ABCD中，2AB=，1BC=，E为DC的中点，F为线段EC（端点除外）上一动点．现将AFD∆沿AF折起，使平面ABD⊥平面ABC．在平面ABD内过点D作DK AB⊥，K为垂足．设AK t=，则t 的取值范围是．三、解答题11. 如图，长方体ABCD­A1B1C1D1中，AB＝1，AA1＝AD＝2.点E为AB中点．(1)求三棱锥A1­ADE的体积；(2)求证：A1D⊥平面ABC1D1；(3)求证：BD1∥平面A1DE.第7题第10题12. 如图，在圆锥PO 中，已知PO ＝2，⊙O 的直径AB ＝2，C 是弧AB 的中点，D 为AC 的中点．(1)证明：平面POD ⊥平面PAC ； (2)求二面角B -PA -C 的余弦值．13. 如图1，在Rt ABC ∆中，90C ∠=︒，36BC AC ==，．D 、E 分别是AC AB 、上的点，且//DE BC ，将ADE ∆沿DE 折起到1A DE ∆的位置，使1A D CD ⊥，如图2． （1）求证： BC ⊥平面1A DC ；（2）若2CD =，求BE 与平面1A BC 所成角的正弦值； （3）当D 点在何处时，1A B 的长度最小，并求出最小值．14. 如图，四棱锥ABCD P -中，底面ABCD 为正方形，PD PA =，⊥PA 平面PDC ，E 为棱PD 的中点．（1）求证：PB // 平面EAC ； （2）求证：平面PAD ⊥平面ABCD ； （3）求二面角B AC E --的余弦值．ACDE图1图2A 1BCDEEC 1B 1A 1CBA15. 如图，在直三棱柱111ABC A B C -中，90BAC ∠=︒， 12,AB AC AA ===E 是BC 中点.（1）求证：1//A B 平面1AEC ；（2）若棱1AA 上存在一点M ，满足11B M C E ⊥，求AM 的长； （3）求平面1AEC 与平面11ABB A 所成锐二面角的余弦值.16. 如图，在三棱锥P-ABC 中，PA=PB=AB=2，3BC =，90=∠ABC °,平面PAB ⊥平面ABC ，D 、E 分别为AB 、AC 中点.（1）求证：DE‖平面PBC ; （2）求证：AB ⊥PE ；（3）求二面角A-PB-E 的大小.17.直四棱柱ABCD A1B1C1D1中，底面ABCD为菱形，且∠BAD＝60°，A1A＝AB，E为BB1延长线上的一点，D1E⊥平面D1AC.(1)求二面角E AC D1的大小；(2)在D1E上是否存在一点P，使A1P∥平面EAC？若存在，求D1P∶PE的值，若不存在，说明理由．18. 如图5所示，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，点 E在线段PC上，PC⊥平面BDE。

一、选择题：1.（广东6）若直线1l 和2l 是异面直线，1l 在平面α内，2l 在平面β内，l 是平面α与平面β的交线，则下列命题正确的是（ ）A ．l 至少与1l ，2l 中的一条相交B ．l 与1l ，2l 都相交C ．l 至多与1l ，2l 中的一条相交D ．l 与1l ，2l 都不相交2.（新课标1，6）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺。

问：积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有（ ）A.14斛B.22斛C.36斛D.66斛3.（陕西5）一个几何体的三视图如图所示，则该几何体的表面积为（ ）A ．3πB ．4πC ．24π+D ．34π+4.（新课标2，6）一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为（ ）A ．81B ．71C ．61D ．51 5.（北京7）某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为（ ）A ．1B ．2C ．3D ．26.（安徽9）一个四面体的三视图如图所示，则该四面体的表面积是（ ）A ．13+B ．23+C ．122+D ．227.（福建9）某几何体的三视图如图所示，则该几何体的表面积等于（ ）A ．822+B ．1122+C ．1422+D ．158.（湖南10）某工件的三视图如图所示，现将该工件通过切割，加工成一个体积尽可能大的长方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率为（材料利用率=新工件的体积原工件的体积）（ ）A ．89πB ．169πC ．34(21)π-D ．312(21)π- 9.（新课标1，11）圆柱被一个平面截去一部分后与半球（半径为r ）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示。