函数的图像与相似三角形
- 格式:doc
- 大小:1.37 MB
- 文档页数:56

抛物线与相似三角形哎呀,说起抛物线和相似三角形,这可真是让不少同学头疼的知识点呢!但别担心,咱们一起来好好琢磨琢磨。
先来说说抛物线,你想象一下,就像一个调皮的孩子在玩扔球的游戏,球飞出去的轨迹,那就是抛物线。
它的形状弯弯的,有时候高,有时候低,可有意思啦!比如说,咱们去游乐场玩那种打水球的游戏,把水球用力一扔,它在空中划过的那道弧线,就是抛物线。
相似三角形呢,就像是一对对长得很像的“双胞胎”三角形。
它们的角是一样大的,边呢,成比例地放大或者缩小。
这就好比你有两个玩具积木搭成的三角形,一个大一点,一个小一点,但形状特别像,这就是相似三角形啦。
咱们来举个例子啊,有一天我在公园里散步,看到一个小朋友在放风筝。
那风筝线和地面形成的夹角,还有风筝的高度以及小朋友和风筝的距离,这不就构成了一个抛物线和相似三角形的问题嘛!小朋友想知道风筝到底飞多高,咱们就可以用抛物线的知识来算算。
假设风筝线和地面的夹角是 60 度,小朋友离风筝的水平距离是 10 米,而风筝线的长度是 15 米。
那咱们就能通过三角函数算出风筝的高度。
这时候,再想想相似三角形,假如在旁边还有另一个小朋友,他离风筝的距离和第一个小朋友不一样,但是角度相同,咱们就能通过相似三角形的比例关系,算出第二个小朋友看到的风筝高度和第一个小朋友看到的高度之间的关系。
在数学的世界里,抛物线和相似三角形经常会结伴出现。
比如说,一道数学题中,给了你一个抛物线的方程,然后在这个抛物线里面又藏着几个相似三角形。
这时候,咱们就得先把抛物线的图像在脑子里画出来,搞清楚它的对称轴、顶点这些关键的点。
然后再去找那些相似三角形,看看它们的边和角有什么关系。
做题的时候,咱们可以先从简单的入手。
比如说,先找出那些明显的相等的角,或者成比例的边。
就像拼图一样,一块一块地把这些线索拼凑起来,最后就能解开谜题啦!有时候,遇到难题别着急,多画画图,多想想咱们生活中的例子。
比如说,篮球场上投篮的轨迹,是不是也像抛物线?还有建筑工地上的塔吊,它的结构中是不是也能找到相似三角形?总之啊,抛物线和相似三角形虽然有点复杂,但只要咱们多观察,多练习,就一定能把它们拿下!相信自己,加油!。

15、八年级数学培佳班:相似判定和性质姓名一、知识梳理(1)本单元的知识结构数学的单元复习最重要就是梳理知识,穿线结网,形成清晰的知识链,就“相似三角形”这一单元而言,其知识网络大致如图所示:一、相似三角形判定的基本模型认识(一)A 字型、反A 字型(斜A 字型)(平行)B (不平行)(二)8字型、反8字型BCB C(蝴蝶型)(平行)(不平行) (三)母子型B(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景一线三等角的变形(五)一线三直角型:二、相似三角形判定的变化模型旋转型:由A字型旋转得到。
8字型拓展【典型例题】1.已知在平行四边形ABCD 中,AC =2AB ;求证:∠ABD =∠DAC2.已知:如图,在△ABC 中,∠ADE =∠B ,∠BAC =∠DAE .(1)求证:ACAEAB AD =; (2)当∠BAC =90°时,求证:EC ⊥BC .3、在Rt ABC ∆中, ∠ACB =90°, CD AB ⊥,垂足为D . E 、F 分别是AC 、BC 边上一点,且CE =13AC ,BF =13BC . (1 )求证∶AC BC =CDBD.(2 )求EDF ∠的度数.4、如图,在ABC △中,90BAC ∠=,AD 是BC 边上的高,点E 在线段DC 上,EF AB ⊥,EG AC ⊥,垂足分别为F G ,.求证:(1)EG CGAD CD =; (2)FD ⊥DG .EFEDC BA GF E D CBAC【三等角问题】(1)如图已知△ABC 中,AB=AC,∠APQ=∠B ,求证:△ABP ∽△PCQ变式:等边△ABC 的边长为6,点E 在AC 上,AE=2,BE 的中垂线交AB 于点P,交BC 于点F求 :BPBF的值.【重心问题】(重心问题)在∆ABC 中,矩形DEFG 的一边FG 在BC 上,点D 、E 分别在AB 、AC 上,AH 是BC 边上的高,BC=10,AH=6.(1)如图4,若DG=2DE ,求DE 的长;(2)如图5,对角线DF 与EG 的交点过∆ABC 的重心O ,求矩形DEFG 的面积.(面积问题)在平行四边形ABCD 中,AB=5,AD=3,平行四边形面积是10,点P 是AB 上一动点,(点P 不与点A 、点B 重合),过点P 作PQ ∥AD 交BD 于Q ,连结CQ ,设AP 的长为x ,四边形QPBC 的面积为y 。

专题12难点探究专题:相似三角形中动点问题压轴题六种模型全攻略【考点导航】目录【典型例题】 (1)【考点一相似三角形动点中求时间多解问题(利用分类讨论思想)】 (1)【考点二相似三角形动点中求线段长多解问题(利用分类讨论思想)】 (2)【考点三相似三角形动点中求线段及线段和最值问题】 (4)【考点四相似三角形中的动点问题与函数图像问题】 (5)【考点五相似三角形中的动点问题与几何综合问题】 (7)【考点六相似三角形中的动点探究应用问题】 (9)【典型例题】【考点一相似三角形动点中求时间多解问题(利用分类讨论思想)】【变式训练】1.(2023秋·安徽安庆·九年级统考期末)如图,在钝角A出发运动到点B停止,动点E运动的速度为2cm/s.如果两点同时运动,那么当以点2.(2023·上海·九年级假期作业)如图,米/秒的速度同时开始运动,其中点直移动到点A为止.经过多长时间后,3.(2022·辽宁·灯塔市第一初级中学九年级期中)如图,在平面直角坐标系内,已知点0),动点P从点A开始在线段段BA上以每秒2个单位长度的速度向点(1)当t为何值时,△APQ与△AOB相似?(2)当t为何值时,△APQ的面积为24 5【考点二相似三角形动点中求线段长多解问题(利用分类讨论思想)】【变式训练】2.(2023春·江苏无锡·八年级宜兴市实验中学校考阶段练习)如图,在矩形连接BD,点M,N分别是边BC,终落在BD上,当PBM为直角三角形时,线段3.(2023·江苏盐城·校考一模)如图,在动点,过点E作DE⊥为等腰三角形时,当BCF4.(2023·山东济宁·统考一模)如图,在矩形点P是直线BC上的一个动点.若【考点三相似三角形动点中求线段及线段和最值问题】【变式训练】1.(2023·江苏苏州AE翻折得AFE△连接PF,则PQ2.(2023·湖北襄阳·统考模拟预测)如图,矩形△M,连接EM、BM,将BEM为.3.(2023春·安徽·九年级专题练习)如图,在正方形,上的动点,且BEG是AB CD为.4.(2023·江苏南通·统考三模)点C 的坐标为()0,3上一点,且3AQ PQ =【考点四相似三角形中的动点问题与函数图像问题】例题:(2023春·河南安阳·九年级统考期末)如图,正方形ABCD 一边AB 在直线l 上,P 是直线l 上点A 左侧的一点,24AB PA ==,E 为边AD 上一动点,过点P ,E 的直线与正方形ABCD 的边交于点F ,连接BE BF ,,若设DE x =,BEF △的面积为S ,则能反映S 与x 之间函数关系的图象是()A .B ...2023·山西运城·统考二模)如图中,36B ∠=︒,动点P 速运动至点C 停止.点P 的运动速度为,设点P 的运动时间为t (函数图像如图2所示.当AP 时,BP 的长为()A .252+B .425-C .4+2.(2023·河南焦作·统考二模)如图,在Rt ABC △中,过点P 作直线l AB ⊥,交折线ACB 于点Q .设AP x =A ....2023·安徽合肥·校联考二模)如图,在正方形ABCD 中,1AB =,动点P 从A 点出发沿和BC 上匀速移动,连接DP 交BC 或BC 的延长线于Q ,记点移动的距离为x ,的函数图像大致是()A .B .C .D .4.(2023·黑龙江·模拟预测)如图,已知直线l 是线段AB 的中垂线,l 与AB 相交于点C ,D 是位于直线AB 下方的l 上的一动点(点D 不与点C 重合),连接AD BD ,,过点A 作AE BD ∥,过点B 作BE AE ⊥于点E ,若6AB =,设AD x =,AE y =,则y 关于x 的函数关系用图像可以大致表示为().A .B .C .D .【考点五相似三角形中的动点问题与几何综合问题】例题:(2023春·山东济宁·八年级统考期末)如图,在平面直角坐标系中,O 是坐标原点,矩形OABC 的两边分别在x 轴和y 轴上,点B 的坐标为()12,8,现有两动点P ,Q ,点P 以每秒3个单位的速度从点O 出发向终点A 运动,同时点Q 以每秒2个单位的速度从点A 出发向终点B 运动,连接PC ,PQ ,CQ .设运动时间为t 秒()0t >.(1)点P 的坐标为______,点Q 的坐标为______(用含t 的代数式表示);(2)请判断四边形APCQ 的面积是否会随时间t 的变化而变化,并说明理由;(3)若A ,P ,Q 为顶点的三角形与OCP △相似时,请求出t 的值.【变式训练】(1)BM =________;BN =__________.(2)若BMN 与ABC 相似,求t 的值;(3)连接AN CM ,,如图2,若AN CM ⊥BC=,点E是AD边上的一个动点,以CE为边在CE的右(2)如图2,四边形ABCD是矩形,2AB=,4CG CE=,连接DG,BE.判断线段DG与BE,有怎样的数量关系和位置关系,侧作矩形CEFG,且:1:2并说明理由;(3)如图3,在(2)的条件下,点E是从点A运动D点,则点G的运动路径长度为______;+的最小值为______.(4)如图3,在(2)的条件下,连接BG,则2BG BE【考点六相似三角形中的动点探究应用问题】【变式训练】【基础巩固】(1)参照小慧提供时思路,利用图(2)请证明上述结论;(2)A 、B 、C 、是同一直线l 上从左到右顺次的点,点P 是直线外一动点,【尝试应用】①若2AB =,1BC =,延长AB 至D ,使CD BC =【拓展提高】②拓展:若AB m =,BC n =,()m n ≠,P 点在长为___________(用含m 、n 的式子表示).。
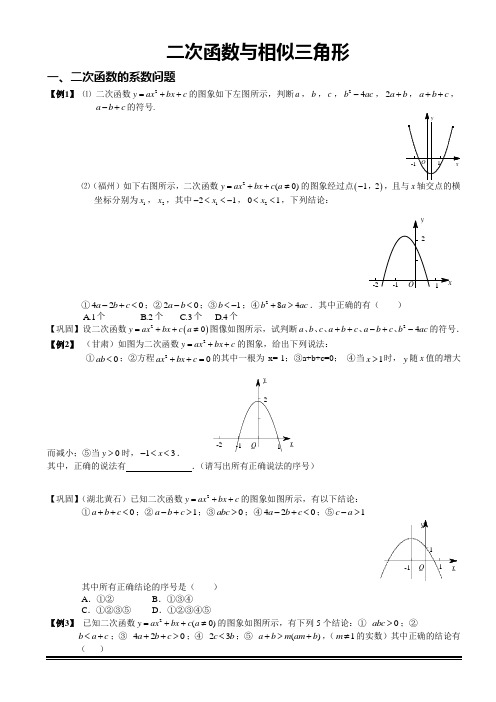
二次函数与相似三角形一、二次函数的系数问题【例1】 ⑴ 二次函数2y ax bx c =++的图象如下左图所示,判断a ,b ,c ,24b ac -,2a b +,a b c ++,a b c -+的符号.⑵(福州)如下右图所示,二次函数2(0)y ax bx c a =++≠的图象经过点()12-,坐标分别为1x ,2x ,其中121x -<<-,201x <<,下列结论:①420a b c -+<;②20a b -<;③1b <-;④284b a ac +>.其中正确的有( ) A.1个 B.2个 C .3个 D .4个【巩固】 设二次函数()20y ax bx c a =++≠图像如图所示,试判断24a b c a b c a b c b ac ++-+-、、、、、的符号. 【例2】 (甘肃)如图为二次函数2y ax bx c =++的图象,给出下列说法:①0ab <;②方程20ax bx c ++=的其中一根为x=-1;③a+b+c=0; ④当1x >时,y 随x 值的增大而减小;⑤当0y >时,13x -<<.其中,正确的说法有 _______.(请写出所有正确说法的序号)【巩固】(湖北黄石)已知二次函数2y ax bx c =++的图象如图所示,有以下结论:①0a b c ++<;②1a b c -+>;③0abc >;④420a b c -+<;⑤1c a ->其中所有正确结论的序号是( )A .①②B .①③④C .①②③⑤D .①②③④⑤【例3】 已知二次函数2(0)y ax bx c a =++≠的图象如图所示,有下列5个结论:① 0abc >;②b ac <+;③ 420a b c ++>;④ 23c b <;⑤ ()a b m am b +>+,(1m ≠的实数)其中正确的结论有( ) A. 2个 B. 3个 C. 4个 D. 5个【巩固】(08天门)已知二次函数()20y ax bx c a =++≠的图象如图所示,下列结论:①0abc >;②20a b +>;③0a b c -+<;④0a c +>,其中正确结论的个数为( )A. 4个B. 3个C. 2个D. 1个【例4】 已知函数2y ax bx c =++(0a≠)的图象,如图所示.求证:22()a c b +<【例5】 2y ax bx c =++的图象如图所示.并设|||||2||2|M a b c a b c ab a b =++--+++--则() A .0M > B .0M =C .0M <D .不能确定M 为正,为负或为0【例6】 二次函数2y ax bx c =++的图象的一部分如图所示,求a 的取值范围【巩固】 已知抛物线2y ax bx c =++的一段图象如图所示.⑴确定a 、b 、c 的符号;⑵求a b c ++的取值范围.【例7】 设二次函数2(0)y ax bx c a =++≠的图象如图所示,若OA OB =,求abc 的取值范围.二、二次函数图像特征【例8】 (09烟台)二次函数2y ax bx c =++的图象如图所示,则一次函数24y bx b ac =+-与反比例函数a b cy x++=在同一坐标系内的图象大致为( )【例9】 若二次函数c bx ax y ++=2的图象的开口向下,顶点在第一象限,抛物线交于y 轴的正半轴;则点⎪⎭⎫ ⎝⎛b c a P ,在( ).(A)第一象限 (B)第二象限限 (C) 第三象限 (D) 第四象限【例10】 ⑴(09湖北荆门)函数1y ax =+与()210y ax bx a =++≠的图象可能是( )(2) (09兰州)在同一直角坐标系中,函数y mx m =+和函数222y mx x =-++(m 是常数,且0m ≠)的图象可能..是【巩固】(09嘉兴)已知,在同一直角坐标系中,函数与的图象有可能是( )ABCDDCB A 0≠a ax y =2ax y =1. ⑴ 下左图所示为二次函数2y ax bx c =++的图象,则一次函数by ax c=-的图象不经过( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 ⑵ 二次函数2y ax bx c =++的图象的一部分如下右图所示,试求a b c ++的取值范围.⑶(2008天津)已知,如图所示为二次函数2y ax bx c =++的图象,则一次函数y ax bc =+的图象不经过( )A.第一象限B.第二象限C.第三象限D.第四象限2. (092()0y ax bx c a =++≠的图象如图所示,则下列结论:0ac >①;②方程20ax bx c++=的两根之和大于0;y ③随x 的增大而增大;④0a b c -+<,其中正确的个数( )A .4个 B .3个 C .2个 D .1个3. (1) 已知二次函数2y ax bx c =++(其中a 是正整数)的图象经过点()14A -,和()21B ,,且与x 轴 有两个不同的交点,求b c +的最大值.(2)二次函数2y ax bx c =++的图象一部分如下图,求a 的取值范围.4. ⑴ 函数22(1)1y x =---的图象可由函数22(2)3y x =-++的图象平移得到,那么平移的步骤是( )A. 右移三个单位,下移四个单位B. 右移三个单位,上移四个单位C. 左移三个单位,下移四个单位D. 左移四个单位,上移四个单位 ⑵ (07萧山)二次函数2241y x x =-++的图象如何移动就得到22y x =-的图象( )A习题精讲A.向左移动1个单位,向上移动3个单位.B.向右移动1个单位,向上移动3个单位.C.向左移动1个单位,向下移动3个单位.D.向右移动1个单位,向下移动3个单位.2.如图,抛物线y=12x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).(1)求抛物线的解析式及顶点D的坐标;(2)判断ABC△的形状,证明你的结论;(3)点(0)M m,是x轴上的一个动点,当MC+MD的值最小时,求m的值.三、相似三角形一、相似三角形的判定定理(1)有两个角对应相等的两个三角形相似;(2)两边对应成比例,且夹角相等的两个三角形相似;(3)三边对应成比例的两个三角形相似;(4)直角边和一条斜边对应成比例的两个直角三角形相似.二、相似三角形的性质(1)相似三角形对应的高线、中线、角平分线的比等于相似比;(2)相似三角形的周长之比等于相似比;(3)相似三角形的面积比等于相似比的平方.【例1】(2007年北师大附中期末试题)如图,D、E是ABC∆的边AC、AB上的点,且AD AC⋅=AE AB⋅,求证:ADE B∠=∠.巩固:如图,在ABC ∆中,AD BC ⊥于D ,CE AB ⊥于E ,∠ADE=∠ACE, ABC ∆的面积是BDE ∆面积的4倍,6AC =,求DE 的长.A ED CBA EDC。


一元二次函数一、一元二次函数的定义形如y=ax 2+bx+c(其中a ≠0)的函数称之为一元二次函数。
一般情况下,我们会把一元二次函数改写成:224()24b ac b y a x a a-=++写成这样的目的主要是:〔1〕可以看出对称轴方程及顶点坐标;抛物线的对称轴的方程为:x= -2b a 顶点坐标为〔-2b a ,244ac b a-)〔2〕可以得到最大、小值:当a >0,y 取最小值,y= 244ac b a-当a<0,y 取最大值,y= 244ac b a-由一元二次函数的对称轴,从而我们可以知道一元二次函数的单调性:当a>0时,〔-∞,-2b a ]为单调减区间;[-2b a ,+∞〕为单调增区间。
当a<0时,[-2b a ,+∞〕为单调减区间;〔-∞,-2ba]为单调增区间〔3〕解答平移问题方便。
平移的法那么遵循两条:左加右减,上加下减。
题型一:平移图像,求新的解析式 【例题1】:y=x 2-2x+3向左移动一个单位,向上移动两个单位,移动后的解析式是什么? 解答:y=(x-1)2+2根据“左加右减〞的原那么,向左移动一个单位,那么有:y=(x-1+1)2+2 根据“上加下减〞的原那么,向上移动两个单位,那么有y=(x-1+1)2+2+2 所以,最终的结果是:y=x 2+4题型二:三点求函数的解析式——方法:待定系数法【例题2】一元二次方程y=ax 2+bx+c 经过点A(1,3),B(2,4),C(3,11),求函数的解析式。
解答:根据题意有:a b c 34a 2b c 49a 3b c 11++=⎧⎪++=⎨⎪++=⎩解上面的方程组,得:388a b c =⎧⎪=-⎨⎪=⎩所以:y=3x 2-8x+8【例题3】函数y=ax 2+bx+c 与x 轴的交点为A(-3,0),B(1,0),并且经过点〔4,21〕,求函数的解析式。
一般情况下,如果告诉你一元二次方程的两个解x 1,x 2;这个时候我们设:y=a(x-x 1)(x-x 2)最为方便。
相似三角形的应用ppt课件contents •相似三角形基本概念与性质•相似三角形在几何问题中应用•相似三角形在三角函数中应用•相似三角形在物理问题中应用•相似三角形在建筑设计中应用•总结与展望目录01相似三角形基本概念与性质定义AAA 相似SAS 相似SSS 相似定义及判定方法01020304两个三角形如果它们的对应角相等,则称这两个三角形相似。
如果两个三角形的三组对应角分别相等,则这两个三角形相似。
如果两个三角形有两组对应边成比例且夹角相等,则这两个三角形相似。
如果两个三角形的三组对应边都成比例,则这两个三角形相似。
相似比与对应边长成比例关系相似比两个相似三角形的对应边之间的比值称为相似比。
对应边长成比例关系在相似三角形中,任意两边之间的比值等于其他两边之间的比值,即a/a'=b/b'=c/c',其中a、b、c和a'、b'、c'分别是两个相似三角形的对应边长。
相似三角形面积比关系面积比公式两个相似三角形的面积之比等于它们对应边长之比的平方,即(S1/S2)=(a/a')^2=(b/b')^2=(c/c')^2,其中S1和S2分别是两个相似三角形的面积,a、b、c和a'、b'、c'分别是它们的对应边长。
应用举例利用相似三角形的面积比关系可以解决一些实际问题,如测量高度、计算距离等。
02相似三角形在几何问题中应用利用相似三角形对应边成比例的性质,通过已知线段长度求解未知线段长度。
结合图形变换(如平移、旋转等)和相似三角形的性质,构造新的相似三角形,进而求解线段长度。
通过相似三角形的性质,建立比例关系,求解未知线段长度。
利用相似三角形求线段长度利用相似三角形证明角相等或互补通过相似三角形的性质,证明两个角相等或互补。
利用相似三角形对应角相等的性质,证明两个角相等。
结合图形变换和相似三角形的性质,构造新的相似三角形,证明两个角互补。
一次函数与相似三角形在数学中,一次函数是指具有形如y = mx + c的函数,其中m和c是常数,m为斜率,c为截距。
这篇文章将探讨一次函数与相似三角形之间的关系。
首先,我们需要了解什么是相似三角形。
相似三角形是指具有相同形状但大小不同的三角形。
我们可以使用比值来表示相似三角形之间的关系。
考虑一个线性函数y = mx + c,其中m为斜率,c为截距。
给定此一次函数图像上的两点A(x1, y1)和B(x2, y2),斜率m可以表示为:m=(y2-y1)/(x2-x1)这意味着我们可以通过斜率m来比较两个点之间的纵坐标和横坐标的变化。
此外,斜率也可以表示为相似三角形之间的比例。
接下来,我们考虑两个相似三角形ABC和DEF,其中AB与DE对应,BC与EF对应,AC与DF对应。
我们可以使用一次函数来表示这两个相似三角形之间的关系。
设A(x1,y1)和B(x2,y2)为第一个相似三角形ABC上的两个点,斜率为m1、同样地,设D(x3,y3)和E(x4,y4)为第二个相似三角形DEF上的两个点,斜率为m2考虑线段AB和DE之间的比例。
根据相似三角形的性质,比例应该等于两个相似三角形的边长之比:AB/DE=AC/DF我们可以用两点间的纵坐标差值除以横坐标差值来计算AB和DE之间的比例:AB/DE=(y2-y1)/(x2-x1)同样地,我们可以用两点间的纵坐标差值除以横坐标差值来计算AC和DF之间的比例:AC/DF=(y2-y1)/(x2-x1)由此可见,只要两个相似三角形上的两个点之间的纵坐标和横坐标的变化具有相同的比值,那么这两个相似三角形之间的比例就是相等的。
可以结论,一次函数的斜率等于两个相似三角形之间的比例。
换句话说,一次函数的斜率可以用来判断两个相似三角形之间的关系。
当两个线性函数的斜率相等时,它们所代表的线性函数之间的关系与两个相似三角形之间的关系相同。
此外,截距也是一次函数和相似三角形之间的另一个重要关系。
函数与相似三角形结合典型试题1、已知反比例函数y =m-2/x( x<0)的图象经过点A (-2,3),过点A 作直线AC 与函数y =m-2/x 的图象交于点B ,与x 轴交于点C ,且AB =2BC .(1)求m 的值及点B 的坐标:(2)求△AOB 的面积.2、如图,在△ABC 中,AB =AC =10,BC =12,AM ∥BC ,点P 在线段BC 上以每秒2个单位的速度由B 点向C 点运动,点Q 在线段BA 上以每秒1个单位的速度由B 点向A 点运动,在运动中,始终保持∠QPD =∠B ,且PD 交AC 于点E ,交AM 于点D ,当P 点运动到C 点时,Q 点随之停止运动.设运动时间为t (秒).(1)当t =4秒时,试证明:△BPQ ≌△CEP ; (2)设△BPQ 的面积为S ,求S 与t 之间的函数关系式;(3)当t 为何值时?使得S ∆ADE/S ∆CPE=1/4.3、如图,在直角梯形ABCD 中,∠D=90°,AB=10cm,BC=6cm ,AB ∥CD,AC ⊥BC, F 点以2cm/s 的速度在线段AB 上由A 向B 匀速运动,点E 同时以1cm/s 的速度在线段BC 上由B 向C 匀速运动,设运动的时间为t (0<t <5).(1)求证:⊿ACD ∽⊿BAC ;(2)求DC 的长(3)当t 为何值时,⊿FEB 与⊿ABC 相似?4、如图,已知△ABC 中,AB =AC =2,∠A =90°,O 为AB 边上移动,动点F 在AC 边上移动. (1)点E ,F 的移动过程中,△OEF 是否能成为∠EOF =45°的等腰三角形?若能,求BE 的长;若不能,请说明理由;(2)当∠EOF =45°时,设BE =x ,CF =y ,求y 与x 之间的函数解析式,并写出x 的取值范围.5、如图,在矩形ABCD 中,已知AB =2,BC =3,点E 为AD 边上一动点(不与A 、D 重合),连结CE ,作EF ⊥CE 交AB 边于F(1)求证:△AEF ∽△DCE ;(2)当△ECF ∽△AEF 时,求AF 的长;(3)在点E 的运动过程中,AD 边上是否存在异于点E 的点G ,使△AGF ∽△DCG 成立?若存在,请猜想点G 的位置,并给出证明;若不存在,请说明理由.6、如图1,已知,CE 是Rt △ABC 的斜边AB 上的高,点P 是CE 的延长线上任意一点,BG ⊥AP ,求证:(1)△AEP ∽△DEB ; (2) CE 2=ED·EP 。
函数的图像与相似三角形函数的图像与相似三角形一.选择题(共10小题)1.如图已知A1,A2,A3,…A n是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=A n﹣1A n=1,分别过点A1,A2,A3,…A n′作x轴的垂线交二次函数y=x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△P n﹣1B n﹣1P n(n>1)的面积为S n,则S n=().C D.2.如图,抛物线y=x2﹣x﹣与直线y=x﹣2交于A、B两点(点A在点B的左侧),动点P从A点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点B.若使点P运动的总路径最短,则点P运动的总路径的长为().C D.3.如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是﹣2,点B的横坐标是3,则以下结论:①抛物线y=ax2(a≠0)的图象的顶点一定是原点;②x>0时,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的函数值都随着x的增大而增大;③AB的长度可以等于5;④△OAB有可能成为等边三角形;⑤当﹣3<x<2时,ax2+kx<b,其中正确的结论是()4.已知抛物线y=﹣x2+1的顶点为P,点A是第一象限内该二次函数图象上一点,过点A作x轴的平行线交二次函数图象于点B,分别过点B、A作x轴的垂线,垂足分别为C、D,连结PA、PD,PD交AB于点E,△PAD与△PEA 相似吗?()5.如图,分别过点P i(i,0)(i=1、2、…、n)作x轴的垂线,交的图象于点A i,交直线于点B i.则的值为().D.6.(2012•武汉四月调考)在直角梯形ABCD中,AB∥CD,∠DAB=90°,G为AB中点,在线段DG上取点F,使FG=AG,过点F作FE⊥DG交AD于点E,连接EC交DG于点H.已知EC平分∠DEF.下列结论:①∠AFB=90°;②AF∥EC;③△EHD∽△BGF;④DH•FG=FH•DG.其中正确的是()7.(2011•和平区模拟)如图,正方形ABCD中,E是BC的中点,DF=3CF,下面得出六个结论中:①△ABE∽△AEF;②△ABE∽△ECF;③△ADF∽△ABE;④△AEF∽△ECF;⑤△AEF∽△ADF;⑥△ECF∽△ADF,其中正确的个数是()8.(2011•武汉五月调考)如图,等腰直角△ABC中,AC=BC,∠ACB=90°,AF为△ABC的角平分线,分别过点C、B作AF的垂线,垂足分别为E、D.以下结论:①CE=DE=BD;②AF=2BD;③CE+EF=AE;④=.其中结论正确的序号是()9.(2010•武汉五月调考)如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=4,CD=3.下列结论①∠AED=∠ADC;②=;③AC•BE=12;④3BF=4AC,其中结论正确的个数有()10.如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BC=CD,E为梯形内一点,∠BEC=90°,将△BEC绕C 点旋转90°,使BC与DC重合,得到△DCF,连接EF交CD于点M.给出以下5个命题:①DM:MC=MF:ME;②BE⊥DF;③若sin,则;④若tan,则点D到直线CE的距离为1;⑤若M为EF中点,则点B、E、D三点在同一直线上.则正确命题的个数()二.填空题(共10小题)11.(2014•武侯区一模)如图,n+1个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△B n+1D n C n的面积为S n,则S n=_________(用含n的式子表示).12.(2014•历下区一模)如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH,④AD2=OD•DH中,正确的是_________.13.(2013•潍坊)如图,直角三角形ABC中,∠ACB=90°,AB=10,BC=6,在线段AB上取一点D,作DF⊥AB 交AC于点F,现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为A1;AD的中点E的对应点记为E1,若△E1FA1∽△E1BF,则AD=_________.14.(2013•南通)如图,在▱ABCD中,AB=6cm,AD=9cm,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=4cm,则EF+CF的长为_________cm.15.(2013•菏泽)如图所示,在△ABC中,BC=6,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE 于D,∠CBP的平分线交CE于Q,当CQ=CE时,EP+BP=_________.16.(2013•兰州)如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是_________.17.(2014•濮阳二模)二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③a+b+c>0;④当x>1时,y随x值的增大而增大;⑤当y>0时,﹣1<x<3.其中,正确的说法有_________(请写出所有正确说法的序号).18.(2013•大连)如图,抛物线y=x2+bx+与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为_________.19.(2011•日照)如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为﹣3和1;④a﹣2b+c>0.其中正确的命题是_________.(只要求填写正确命题的序号)20.(2012•长春)在平面直角坐标系中,点A是抛物线y=a(x﹣3)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为_________.三.解答题(共10小题)21.(2014•黔南州)如图,在平面直角坐标系中,顶点为(4,﹣1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3).(1)求此抛物线的解析式;(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l 与⊙C有怎样的位置关系,并给出证明;(3)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积.22.(2014•本溪)如图,直线y=x﹣4与x轴、y轴分别交于A、B两点,抛物线y=x2+bx+c经过A、B两点,与x轴的另一个交点为C,连接BC.(1)求抛物线的解析式及点C的坐标;(2)点M在抛物线上,连接MB,当∠MBA+∠CBO=45°时,求点M的坐标;(3)点P从点C出发,沿线段CA由C向A运动,同时点Q从点B出发,沿线段BC由B向C运动,P、Q的运动速度都是每秒1个单位长度,当Q点到达C点时,P、Q同时停止运动,试问在坐标平面内是否存在点D,使P、Q运动过程中的某一时刻,以C、D、P、Q为顶点的四边形为菱形?若存在,直接写出点D的坐标;若不存在,说明理由.23.(2014•义乌市)如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.(1)求该抛物线的函数解析式;(2)已知直线l的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l于点H,连结OP,试求△OPH的面积;②当m=﹣3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.24.(2014•珠海)如图,矩形OABC的顶点A(2,0)、C(0,2).将矩形OABC绕点O逆时针旋转30°.得矩形OEFG,线段GE、FO相交于点H,平行于y轴的直线MN分别交线段GF、GH、GO和x轴于点M、P、N、D,连结MH.(1)若抛物线l:y=ax2+bx+c经过G、O、E三点,则它的解析式为:_________;(2)如果四边形OHMN为平行四边形,求点D的坐标;(3)在(1)(2)的条件下,直线MN与抛物线l交于点R,动点Q在抛物线l上且在R、E两点之间(不含点R、E)运动,设△PQH的面积为s,当时,确定点Q的横坐标的取值范围.25.(2014•白银)如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2﹣3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.(1)求点M、A、B坐标;(2)连接AB、AM、BM,求∠ABM的正切值;(3)点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为α,当α=∠ABM时,求P点坐标.26.(2014•娄底)如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:(1)设△APQ的面积为S,当t为何值时,S取得最大值?S的最大值是多少?(2)如图乙,连接PC,将△PQC沿QC翻折,得到四边形PQP′C,当四边形PQP′C为菱形时,求t的值;′(3)当t为何值时,△APQ是等腰三角形?27.(2014•无锡)如图1,已知点A(2,0),B(0,4),∠AOB的平分线交AB于C,一动点P从O点出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,过点P且平行于AB的直线交x轴于Q,作P、Q关于直线OC的对称点M、N.设P运动的时间为t(0<t<2)秒.(1)求C点的坐标,并直接写出点M、N的坐标(用含t的代数式表示);(2)设△MNC与△OAB重叠部分的面积为S.①试求S关于t的函数关系式;②在图2的直角坐标系中,画出S关于t的函数图象,并回答:S是否有最大值?若有,写出S的最大值;若没有,请说明理由.28.(2014•许昌二模)将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G),使点B落在AD边上的点F处,FN与DC交于点M,连接BF与EG交于点P.(1)当点F与AD的中点重合时(如图1):①△AEF的边AE=_________cm,EF=_________cm,线段EG与BF的大小关系是EG_________BF;(填“>”、“=”或“<”)②求△FDM的周长.(2)当点F在AD边上除点A、D外的任意位置时(如图2):③试问第(1)题中线段EG与BF的大小关系是否发生变化?请证明你的结论;④当点F在何位置时,四边形AEGD的面积S最大?最大值是多少?29.(2014•红桥区二模)如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P、Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度,匀速向点C运动,点Q从点C 出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P、Q同时出发,同时停止,设运动时间为t秒,当t=2秒时.(Ⅰ)求点D的坐标,并直接写出t的取值范围;(Ⅱ)连接AQ并延长交x轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF,则△AEF的面积S是否随t的变化而变化?若变化,求出S与t的函数关系式;若不变化,求出S的值.(Ⅲ)在(Ⅱ)的条件下,t为何值时,PQ∥AF?30.(2014•定州市三模)如图,M为等腰△ABD的底AB的中点,过D作DC∥AB,连结BC;AB=8cm,DM=4cm,DC=1cm,动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC﹣CD上匀速运动,速度均为1cm/s,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(s)时,△MPQ的面积为S(不能构成△MPQ 的动点除外).(1)t(s)为何值时,点Q在BC上运动,t(s)为何值时,点Q在CD上运动;(2)求S与t之间的函数关系式;(3)当t为何值时,S有最大值,最大值是多少?(4)当点Q在CD上运动时,直接写出t为何值时,△MPQ是等腰三角形.函数的图像与相似三角形参考答案与试题解析一.选择题(共10小题)1.如图已知A1,A2,A3,…A n是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=A n﹣1A n=1,分别过点A1,A2,A3,…A n′作x轴的垂线交二次函数y=x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△P n﹣1B n﹣1P n(n>1)的面积为S n,则S n=().C D.xny=×[n(2.如图,抛物线y=x2﹣x﹣与直线y=x﹣2交于A、B两点(点A在点B的左侧),动点P从A点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点B.若使点P运动的总路径最短,则点P运动的总路径的长为().C D.x=的交点是x与直线x=x,时,﹣,﹣)﹣=的对称点x=C=+﹣C=1+==.运动的总路径的长为3.如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是﹣2,点B的横坐标是3,则以下结论:①抛物线y=ax2(a≠0)的图象的顶点一定是原点;②x>0时,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的函数值都随着x的增大而增大;③AB的长度可以等于5;④△OAB有可能成为等边三角形;⑤当﹣3<x<2时,ax2+kx<b,其中正确的结论是()4.已知抛物线y=﹣x2+1的顶点为P,点A是第一象限内该二次函数图象上一点,过点A作x轴的平行线交二次函数图象于点B,分别过点B、A作x轴的垂线,垂足分别为C、D,连结PA、PD,PD交AB于点E,△PAD与△PEA 相似吗?()=,再根据两边对应成比例且夹角相等,两三角形相似解答.PD====2=5.如图,分别过点P i(i,0)(i=1、2、…、n)作x轴的垂线,交的图象于点A i,交直线于点B i.则的值为().D.x﹣(﹣=2()+=2+﹣+﹣).6.(2012•武汉四月调考)在直角梯形ABCD中,AB∥CD,∠DAB=90°,G为AB中点,在线段DG上取点F,使FG=AG,过点F作FE⊥DG交AD于点E,连接EC交DG于点H.已知EC平分∠DEF.下列结论:①∠AFB=90°;②AF∥EC;③△EHD∽△BGF;④DH•FG=FH•DG.其中正确的是()AB====7.(2011•和平区模拟)如图,正方形ABCD中,E是BC的中点,DF=3CF,下面得出六个结论中:①△ABE∽△AEF;②△ABE∽△ECF;③△ADF∽△ABE;④△AEF∽△ECF;⑤△AEF∽△ADF;⑥△ECF∽△ADF,其中正确的个数是(),.8.(2011•武汉五月调考)如图,等腰直角△ABC中,AC=BC,∠ACB=90°,AF为△ABC的角平分线,分别过点C、B作AF的垂线,垂足分别为E、D.以下结论:①CE=DE=BD;②AF=2BD;③CE+EF=AE;④=.其中结论正确的序号是()比比,设==,=AD===9.(2010•武汉五月调考)如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=4,CD=3.下列结论①∠AED=∠ADC;②=;③AC•BE=12;④3BF=4AC,其中结论正确的个数有()10.如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BC=CD,E为梯形内一点,∠BEC=90°,将△BEC绕C 点旋转90°,使BC与DC重合,得到△DCF,连接EF交CD于点M.给出以下5个命题:①DM:MC=MF:ME;②BE⊥DF;③若sin,则;④若tan,则点D到直线CE的距离为1;⑤若M为EF中点,则点B、E、D三点在同一直线上.则正确命题的个数(),,,::),,DCN=二.填空题(共10小题)11.(2014•武侯区一模)如图,n+1个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△B n+1D n C n的面积为S n,则S n=(用含n的式子表示).=×,,故答案为:12.(2014•历下区一模)如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH,④AD2=OD•DH中,正确的是①②③④.13.(2013•潍坊)如图,直角三角形ABC中,∠ACB=90°,AB=10,BC=6,在线段AB上取一点D,作DF⊥AB 交AC于点F,现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为A1;AD的中点E的对应点记为E1,若△E1FA1∽△E1BF,则AD=.==xF==,,×=.故答案为:14.(2013•南通)如图,在▱ABCD中,AB=6cm,AD=9cm,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=4cm,则EF+CF的长为5cm.BG=4=2===,=,,15.(2013•菏泽)如图所示,在△ABC中,BC=6,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE 于D,∠CBP的平分线交CE于Q,当CQ=CE时,EP+BP=12.CECE=16.(2013•兰州)如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是﹣2<k<.时,抛物线与,×x<<17.(2014•濮阳二模)二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③a+b+c>0;④当x>1时,y随x值的增大而增大;⑤当y>0时,﹣1<x<3.其中,正确的说法有①②④(请写出所有正确说法的序号).18.(2013•大连)如图,抛物线y=x2+bx+与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为y=x2﹣x+.y=)×=,>=,x+.﹣.19.(2011•日照)如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为﹣3和1;④a﹣2b+c>0.其中正确的命题是①③.(只要求填写正确命题的序号);根据﹣20.(2012•长春)在平面直角坐标系中,点A是抛物线y=a(x﹣3)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为18.三.解答题(共10小题)21.(2014•黔南州)如图,在平面直角坐标系中,顶点为(4,﹣1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3).(1)求此抛物线的解析式;(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l 与⊙C有怎样的位置关系,并给出证明;(3)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积.,∴抛物线为;时,AB===,即,解得CE=,m+3m﹣m×(﹣m (;;,22.(2014•本溪)如图,直线y=x﹣4与x轴、y轴分别交于A、B两点,抛物线y=x2+bx+c经过A、B两点,与x轴的另一个交点为C,连接BC.(1)求抛物线的解析式及点C的坐标;(2)点M在抛物线上,连接MB,当∠MBA+∠CBO=45°时,求点M的坐标;(3)点P从点C出发,沿线段CA由C向A运动,同时点Q从点B出发,沿线段BC由B向C运动,P、Q的运动速度都是每秒1个单位长度,当Q点到达C点时,P、Q同时停止运动,试问在坐标平面内是否存在点D,使P、Q运动过程中的某一时刻,以C、D、P、Q为顶点的四边形为菱形?若存在,直接写出点D的坐标;若不存在,说明理由.y=x xx xBCO=y= x x x x x x,,,﹣)CBO=y=x x x得:x x,,(,﹣)或(,,,.CE=CQ==,t=t=.,,.(﹣,﹣)(﹣,﹣)t=(﹣,﹣==t=﹣t=,﹣×.(﹣,(﹣,﹣)或()或(﹣,)23.(2014•义乌市)如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.(1)求该抛物线的函数解析式;(2)已知直线l的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l于点H,连结OP,试求△OPH 的面积;②当m=﹣3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.x(OM CP=(×﹣=.PF=PD=(PFEF==+1PF=PFPE=PE,即aGK=FK=EH=tt+t=4﹣4,y=,)(EF=(PE=PF•PE=PF=,即=MD=(.1+244,)24.(2014•珠海)如图,矩形OABC的顶点A(2,0)、C(0,2).将矩形OABC绕点O逆时针旋转30°.得矩形OEFG,线段GE、FO相交于点H,平行于y轴的直线MN分别交线段GF、GH、GO和x轴于点M、P、N、D,连结MH.(1)若抛物线l:y=ax2+bx+c经过G、O、E三点,则它的解析式为:y=x2﹣x;(2)如果四边形OHMN为平行四边形,求点D的坐标;(3)在(1)(2)的条件下,直线MN与抛物线l交于点R,动点Q在抛物线l上且在R、E两点之间(不含点R、E)运动,设△PQH的面积为s,当时,确定点Q的横坐标的取值范围.OF,求解不等式即可.另要注意求解出结果后要考虑,=GO===1(﹣x xOF•﹣(﹣(﹣x+2y=x﹣<.<,﹣••••x x)<,﹣•)﹣x.x.<﹣+,<<<,<.25.(2014•白银)如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2﹣3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.(1)求点M、A、B坐标;(2)连接AB、AM、BM,求∠ABM的正切值;(3)点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为α,当α=∠ABM时,求P点坐标.相似,根据相似三角形对应边成比例列式求出=,==,﹣=(舍去)×的坐标为()或(,﹣26.(2014•娄底)如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:(1)设△APQ的面积为S,当t为何值时,S取得最大值?S的最大值是多少?(2)如图乙,连接PC,将△PQC沿QC翻折,得到四边形PQP′C,当四边形PQP′C为菱形时,求t的值;′(3)当t为何值时,△APQ是等腰三角形?,得出=,再根据,得出t的面积为:PH=﹣=﹣QC得出﹣t+4=﹣﹣t+4PQ=,=t ,即=5==t×PH=×t(),秒时,最大值为==﹣═﹣t+4QC=t+2t+4=t+2t=,<的值是﹣t+4PQ==,=,即=t,=5=s s或27.(2014•无锡)如图1,已知点A(2,0),B(0,4),∠AOB的平分线交AB于C,一动点P从O点出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,过点P且平行于AB的直线交x轴于Q,作P、Q关于直线OC的对称点M、N.设P运动的时间为t(0<t<2)秒.(1)求C点的坐标,并直接写出点M、N的坐标(用含t的代数式表示);(2)设△MNC与△OAB重叠部分的面积为S.①试求S关于t的函数关系式;②在图2的直角坐标系中,画出S关于t的函数图象,并回答:S是否有最大值?若有,写出S的最大值;若没有,请说明理由.,解得x=点坐标为(,,•×+×)﹣•)代入得,x+t﹣的横坐标为﹣(×2t+.28.(2014•许昌二模)将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G),使点B落在AD边上的点F处,FN与DC交于点M,连接BF与EG交于点P.(1)当点F与AD的中点重合时(如图1):①△AEF的边AE=3cm,EF=5cm,线段EG与BF的大小关系是EG=BF;(填“>”、“=”或“<”)②求△FDM的周长.(2)当点F在AD边上除点A、D外的任意位置时(如图2):③试问第(1)题中线段EG与BF的大小关系是否发生变化?请证明你的结论;④当点F在何位置时,四边形AEGD的面积S最大?最大值是多少?。