云南省普洱市数学八年级上学期期末复习专题4 尺规作图

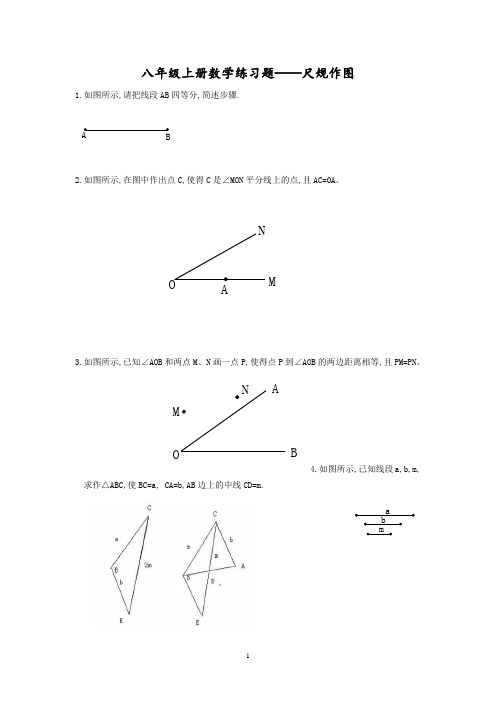
八年级上册数学练习题——尺规作图1.如图所示,请把线段AB 四等分,简述步骤.AB2.如图所示,在图中作出点C,使得C 是∠MON 平分线上的点,且AC=OA 。

NMAO3.如图所示,已知∠AOB 和两点M 、N 画一点P,使得点P 到∠AOB 的两边距离相等,且PM=PN 。

NM BAO4.如图所示,已知线段a,b,m,求作△ABC,使BC=a, CA=b,AB 边上的中线CD=m.mb a5.已知三个自然村A 、B 、C 的位置如图所示,现计划建一所小学,使其到A 、B 、C 三个自然村的距离相等,请你设计出学校所在的位置O,(不写画法,保留画图痕迹)CBA6.如图所示,已知AB .求证:(1)确定AB 的圆心O;(2)过点A 且与⊙O 相切的直线.(注:作图要求利用直尺和圆规,不写作法,但要求得保留作图痕迹)ABCBO7.如图所示,已知B 、C 是⊙O 上的两点.求作⊙O 上一点P,使得PB=PC.(保留作图痕迹,不写作法和证明)8.如图所示,已知线段a,求作:(1)△ABC,使AB=BC=CA=a;(2)⊙O,使它内切于△ABC.(说明:要求写出作法)a9.如图所示,一块直角三角形形状的木板余料, 木匠师傅要在此余料上锯出一块圆形的木板制做凳面,要想使锯出的凳面的面积最大.(1)请你试着用直尺和圆规画出此圆(要求尺规作图,保留作图痕迹,不写作法和证明). (2)若此Rt △ABC 的两直角边分别为30cm 和40cm,试求此圆凳面的面积.CBA10.如图，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：（用直尺画图） （1）画出格点△ABC （顶点均在格点上）关于直线DE 对称的△A 1B 1C 1；（3分） (2)在DE 上画出点P ，使PC PB +1最小；（2分） （3）在DE 上画出点Q ，使QC QA +最小。

（2分）EDA BC11.贵港市政府计划修建一处公共服务设施，使它到三所公寓A 、B 、C 的距离相等。

初中数学⼈教版⼋年级上册尺规作图（习题及答案）初中数学⼈教版⼋年级上册实⽤资料尺规作图（习题）巩固练习1.下列作图语⾔描述正确的是（）A．延长线段AB⾄点C，使AB=ACB．过∠AOB内部⼀点P，作∠AOB的平分线C．以点O为圆⼼，AC长为半径作弧D．在射线OA上截取OB=a，BC=b，则有OC=a+b2.已知边长作等边三⾓形．已知：线段a．求作：等边△ABC，使△ABC的三边长均为a．a作法：（1）作线段_____________；（2）分别以______，______为圆⼼，_______为半径作弧，两弧交于________；（3）连接________，_________．____________________．3.按下列要求作图，保留作图痕迹，不写作法．已知：如图，∠ABC．求作：∠DEF，使∠DEF=32∠ABC．A4.已知∠AOB=45°，点P在边OA上．请以点P为顶点，射线P A为⼀边作∠APC=∠O（作出所有可能的图形）．5.如图，分别过A，B两个加油站的公路l1，l2相交于点O，现准备在∠AOB内建⼀个油库，要求油库的位置点P满⾜在两个加油站的连线上，且到两条公路l1，l2的距离相等．请⽤尺规作图作出点P（保留作图痕迹）．6.请画出草图，并根据图形完成下列各题：（1）在△ABC中，AD平分∠BAC交BC于点D，过点B作BF∥AD交CA 的延长线于点F，则AF和AB的数量关系是_________________．（2）在△ABC中，点D是BC上的⼀点，过D作DE∥AC交AB于点E，DF∥AB交AC于点F，则∠EDF与∠A的数量关系是__________________．（3）已知，在锐⾓△ABC中，AD⊥BC于点D，CE⊥AB于点E，若AD与CE所夹的锐⾓是58°，则∠ABC=______．（4）已知，在锐⾓△ABC中，∠BAC=50°，AD平分∠BAC交BC于点D，BE⊥AC于点E，若∠EBC=20°，则∠ADC=_______．思考⼩结阅读材料：尺规作图是起源于古希腊的数学课题．只使⽤圆规和直尺，并且只准许使⽤有限次，来解决不同的平⾯⼏何作图题．古希腊的安那萨哥拉斯⾸先提出作图要有次数限制．他因政治上的纠葛，被关进监狱，并被判处死刑．在监狱⾥，他思考改圆成⽅以及其他有关问题，⽤来打发令⼈苦恼的⽆所事事的⽣活．他不可能有规范的作图⼯具，只能⽤⼀根绳⼦画圆，⽤随便找来的破⽊棍作直尺，当然这些尺⼦上不可能有刻度．另外，对他来说，时间是不多了，因此他很⾃然地想到要有限次地使⽤尺规解决问题．尺规作图三⼤难题：①化圆为⽅问题求⼀个正⽅形的边长，使其⾯积与⼀已知圆的⾯积相等；②三等分⾓问题求⼀⾓，使其⾓度是⼀已知⾓度的三分之⼀；③倍⽴⽅问题求⼀⽴⽅体的棱长，使其体积是⼀已知⽴⽅体的⼆倍．【参考答案】1. C2.作法：（1）作线段AB使AB=a；（2）分别以点A，点B为圆⼼，a长为半径作弧，两弧交于点C；（3）连接AC，BC．△ABC即为所求．3.略4.略（有两种情况）5.略6.（1）AF=AB（2）∠EDF=∠A（3）58°（4）85°。

八上数学教师辅导讲义学员编号：年级：新初二课时数：学员姓名：辅导科目：数学学科教师：赵老师课题尺规作图授课日期及时段教学目的教学内容一、知识梳理（一）尺规作图的定义：尺规作图是指用没有刻度的直尺和圆规作图。

（二）五种基本作图：1、作一条线段等于已知线段；已知：如图，线段a .求作：线段AB,使AB = a . 訂〈己知）作法：A 1H p①作射线AP;:作线段等干记知线段）②在射线AP上截取AB=a .则线段AB就是所求作的图形。

2、作一个角等于已知角；3、作已知线段的垂直平分线；已知：如图，线段MN.求作：点O,使MO=NQ即0是MN的中点）作法：完美WORD 格式.整理①分别以M N为圆心，大于1/2MN的相同线段为半径画弧，两弧相交于P, Q;②连接PQ交MN于O.则点O就是所求作的MN的中点。

（试问：PQ与MN有何关系？）4、作已知角的角平分线；已知：如图，/ AOB求作：射线OP,使/ AOP=Z BOP （即卩OP平分/ AOB 。

作法：①以O为圆心，任意长度为半径画弧，分别交OA OB于M N;②分别以M N为圆心，大于1/2MN的相同线段为半径画弧，两弧交/ AOB内于P;③作射线OP则射线OP就是/ AOB的角平分线。

5、过一点作已知直线的垂线；①以已知点为圆心，以任意长为半径作弧，交直线于②分别以A、B为圆心，以大于1/2AB长为半径分别作弧,两弧分别交于点M点N;③连接MN则直线MN为所求作的直线。

6、过直线外一点作直线的平行线（三）尺规作图拓展（1）已知三边作三角形。

已知：如图，线段a, b, c.求作：△ ABC 使AB = c , AC = b , BC = a.作法：（作线段的中点）（作角平分线）B两点;--------------------- b（巳知）（已知三边作三凭形）作线段AB = c ;以A 为圆心b 为半径作弧，以 B 为圆心 为半径作弧与前弧相交于 C ;连接AC, BG则厶ABC 就是所求作的三角形。

云南初二初中数学期末考试班级:___________ 姓名：___________ 分数：___________一、选择题1.下面有4个汽车标致图案，其中是轴对称图形的是 ( )①②③④A．②③④B．①②③C．①③④D．①②④2.在实数，，，，，，，7.1010010001中，无理数有（）A．1个B．2个C．3个D．4个3.下列运算正确的是（）A．= ±5B．C．D．4.等腰三角形一腰上的高与另一腰的夹角是50°，则这个等腰三角形的底角为（）A．20°B．70°C．20°或70°D．40°或140°5.如图所示的计算程序中，y与x之间的函数关系所对应的图象应为（）6.如图，从边长为（a＋4）cm的正方形纸片中剪去一个边长为cm的正方形，剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则矩形的面积为（）.A．B．C．D．7.古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”，而把1、4、9、16 … 这样的数称为“正方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（）A．13 = 3+10B．25 =" 9+16"C．36 = 15+21D．49 = 18+318.如图，在直角梯形ABCD中，动点P从点A开始沿A→B→C→D的路径匀速前进到点D为止，在这个过程中，△APD的面积S随时间t的变化关系用图象表示正确的是（）二、填空题1.的平方根是2.如图是汽车牌照在水中的倒影，则该车牌照上的数字是．3.已知，，则的值为 .4.分解因式＝。

5.如图，在△ABC中，边AB的垂直平分线分别交BC、AB于点D、E，AE=3cm，△ADC•的周长为9cm，则△ABC的周长是 .6.如图，∠B、∠C的平分线相交于F，过点F作DE∥BC，交AB于D，交AC于E，那么下列结论正确的是 .①△BDF、△CEF都是等腰三角形；②DE＝BD＋CE；③BD＝CE；④△ADE的周长为AB＋AC.7.如图，是在同一坐标系内作出的一次函数y 1、y 2的图象l 1、l 2，设y 1＝k 1x ＋b 1，y 2＝k 2x ＋b 2，则方程组的解是___ ____.三、解答题1.①计算：②计算③先化简，再求值.［］，其中，2.如图：已知在中，，为边的中点，过点作，垂足分别为．（1）求证：DE=DF ； （2）若，BE=1，求的周长．3.如图，中，，将沿着一条直线折叠后，使点与点重合（图②）．（1）在图①中画出折痕所在的直线．设直线与分别相交于点，连结．（尺规作图，保留作图痕迹，不要求写画法）（2分）（2）请你找出完成问题（1）后所得到的图形中的等腰三角形．（用字母表示，不要求证明）（2分）4.如图：在平面直角坐标系中A( - 1, 5 ), B( - 1, 0 ) C( - 4, 3 ).（1）在图中作出△ABC 关于y 轴对称图形△A 1B 1C 1, 直接在图中写出C 1的坐标(２分)（2）在x轴上找一点P, 使得PA＋PC的值最小，并求出P点坐标。

数学-八年级上-尺规作图练习题Document图1 图21 用直尺和圆规作一个角等于已知角，如图，能得出∠A′O′B′=∠AOB的依据是（）A．（SAS）B．（SSS）C．（ASA）D．（AAS）2 如图，下面是利用尺规作∠AOB的角平分线OC的作法，在用尺规作角平分线过程中，用到的三角形全等的判定方法是（）作法：①以O为圆心，适当长为半径画弧，分别交OA，OB于点D，E；②分别以D，E为圆心，大于DE的长为半径画弧，两弧在∠AOB内交于一点C；③画射线OC，射线OC就是∠AOB的角平分线．A．ASA B．SAS C．SSS D．AAS3 如图，已知在Rt△ABC中，∠ABC=90°，点D是BC边的中点，分别以B、C为圆心，大于线段BC长度一半的长为半径画弧，两弧在直线BC上方的交点为P，直线PD交AC于点E，连接BE，则下列结论：①ED⊥BC；②∠A=∠EBA；③EB平分∠AED；④ED=AB中，一定正确的是（）A．①②③B．①②④C．①③④D．②③④图3 图44 如图，分别以线段AC的两个端点A，C为圆心，大于AC的长为半径画弧，两弧相交于B，D两点，连接BD，AB，BC，CD，DA，以下结论：①BD垂直平分AC；②AC平分∠BAD；③AC=BD；④四边形ABCD是中心对称图形．其中正确的有（）A．①②③B．①③④C．①②④D．②③④第1页5 观察图中尺规作图痕迹，下列结论错误的是（）A．PQ为∠APB的平分线B．PA=PB C．点A、B到PQ的距离不相等D．∠APQ=∠BPQ图5 图7 图86 已知△ABC的三条边长分别为3，4，6，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（）A．6条B．7条C．8条D．9条7 尺规作图作∠AOB的平分线方法如下：以O为圆心，任意长为半径画弧交OA，OB于C，D，再分别以点C，D 为圆心，以大于CD长为半径画弧，两弧交于点P，作射线OP．由作法得△OCP≌△ODP的根据是（）A．SAS B．ASA C．AAS D．SSS8 如图，点C在∠AOB的边OB上，用尺规作出了∠BCN=∠AOC，作图痕迹中，弧FG是（）A．以点C为圆心，OD为半径的弧B．以点C为圆心，DM为半径的弧C．以点E为圆心，OD为半径的弧D．以点E为圆心，DM为半径的弧9 如图，在△ABC中，按以下步骤作图：②分别以B，C为圆心，以大于BC的长为半径作弧，两弧相交于M，N两点；②作直线MN交AB于点D，连接CD，若CD=AC，∠B=25°，则∠ACB的度数为．图9 图1010 如图，在△ABC中，AC=BC，∠B=70°，分别以点A、C为圆心，大于AC的长为半径作弧，两弧相交于点M、N，作直线MN，分别交AC、B C于点D、E，连结AE，则∠AED的度数是°．第2页图15 图1616 如图，△ABC中，∠C=90°，∠A=30°．（1）用尺规作图作AB边上的中垂线DE，交AC于点D，交AB于点E．（保留作图痕迹，不要求写作法和证明）；（2）连接BD，求证：BD平分∠CBA．17 已知△ABC中，∠A=25°，∠B=40°．（1）求作：⊙O，使得⊙O经过A、C两点，且圆心O落在AB边上．（要求尺规作图，保留作图痕迹，不必写作法）（2）求证：BC是（1）中所作⊙O的切线．18 如图，在Rt△ABC中，∠ACB=90°．（1）先作∠ABC的平分线交AC边于点O，再以点O为圆心，OC为半径作⊙O（要求：尺规作图，保留作图痕迹，不写作法）；（2）请你判断（1）中AB与⊙O的位置关系，并证明你的结论．/paper/34276/答案1 B 解：作图的步骤：①以O为圆心，任意长为半径画弧，分别交OA、OB于点C、D；②任意作一点O′，作射线O′A′，以O′为圆心，OC长为半径画弧，交O′A′于点C′；③以C′为圆心，CD长为半径画弧，交前弧于点D′；④过点D′作射线O′B′．所以∠A′O′B′就是与∠AOB相等的角；作图完毕．在△OCD与△O′C′D′，，∴△OCD≌△O′C′D′（SSS），∴∠A′O′B′=∠AOB，显然运用的判定方法是SSS．2 C 解：如图，连接EC、DC．根据作图的过程知，在△EOC与△DOC中，，△EOC≌△DOC（SSS）．故选：C．3 B 解：根据作图过程可知：PB=CP，∵D为BC的中点，∴PD垂直平分BC，∴①ED⊥BC正确；∵∠ABC=90°，∴PD∥AB，∴E为AC的中点，∴EC=EA，∵EB=EC，∴②∠A=∠EBA正确；③EB平分∠AED错误；④ED=AB正确，故正确的有①②④，4 C 解：①∵分别以线段AC的两个端点A，C为圆心，大于AC的长为半径画弧，∴AB=BC，∴BD垂直平分AC，故此小题正确；②在△ABC与△ADC中，∵，∴△ABC≌△ADC（SSS），∴AC平分∠BAD，故此小题正确；③只有当∠BAD=90°时，AC=BD，故本小题错误；④∵AB=BC=CD=AD，∴四边形ABCD是菱形，∴四边形ABCD是中心对称图形，故此小题正确．5 C 解：∵由图可知，PQ是∠APB的平分线，∴A，B，D正确；∵PQ是∠APB的平分线，PA=PB，∴点A、B到PQ的距离相等，故C错误．6 B 解：如图所示：当BC=AC1，AC=CC2，AB=BC3，AC4=CC4，AB=AC5，AB=AC6，BC7=CC71时，都能得到符合题意的等腰三角形．故选：B．7 D 解：∵以O为圆心，任意长为半径画弧交OA，OB于C，D，即OC=OD；以点C，D为圆心，以大于CD长为半径画弧，两弧交于点P，即CP=DP；在△OCP和△ODP中，，∴△OCP≌△ODP（SSS）8 D 解：根据作一个角等于已知角可得弧FG是以点E为圆心，DM为半径的弧．9 105°解：由题中作图方法知道MN为线段BC的垂直平分线，∴CD=BD，∵∠B=25°，∴∠DCB=∠B=25°，∴∠ADC=50°，∵CD=AC，∴∠A=∠ADC=50°，∴∠AC D=80°，∴∠ACB=∠ACD+∠BCD=80°+25°=105°，10 50 解：∵由作图可知，MN是线段AC的垂直平分线，∴CE=AE，∴∠C=∠CAE，∵AC=BC，∠B=70°，∴∠C=40°，∴∠AED=50°，11 30°解：∵AB∥CD，∴∠ACD+∠CAB=180°，又∵∠ACD=120°，∴∠CAB=60°，由作法知，AM是∠CAB的平分线，∴∠MAB=∠CAB=30°．12 作OD的垂线OM，取OM=OA，连接MD，以MD为斜边作等腰直角三角形△MND，以O为圆心，以MN为半径作弧，交BC于Q，交AD于P，弧PQ即为所求．解：作OD的垂线OM，取OM=OA，连接MD，以MD为斜边作等腰直角三角形△MND，以O为圆心，以MN为半径作弧，交BC于Q，交AD于P，弧PQ即为所求．13 8 解：由题意可得出：PQ是AB的垂直平分线，∴AE=BE，∵在△ABC中，∠C=90°，∠CAB=60°，∴∠CBA=30°，∴∠EAB=∠CAE=30°，∴CE=AE=4，∴AE=8．14 解：（1）如图所示：（2）DE∥AC∵DE平分∠BDC，∴∠BDE=∠BDC，∵∠ACD=∠A，∠ACD+∠A=∠BDC，∴∠A=∠BDC，∴∠A=∠BDE，∴DE∥AC．15解：（1）∵由题意可知MN是线段AC的垂直平分线，∴∠ADE=90°；（2）∵在Rt△ABC中，∠B=90°，AB=3，AC=5，∴BC==4，∵MN是线段AC的垂直平分线，∴AE=CE，∴△ABE的周长=AB+（AE+BE）=AB+BC=3+4=7．16 （1）解：如图所示，DE就是要求作的AB边上的中垂线；（2）证明：∵DE是AB边上的中垂线，∠A=30°，∴AD=BD，∴∠ABD=∠A=30°，∵∠C=90°，∴∠ABC=90°﹣∠A=90°﹣30°=60°，∴∠CBD=∠ABC﹣∠ABD=60°﹣30°=30°，∴∠ABD=∠CBD，∴BD平分∠CBA．17 解：（1）作图如图1：（2）证明：如图2，连接OC，∵OA=OC，∠A=25°∴∠BOC=50°，又∵∠B=40°，∴∠BOC+∠B=90°∴∠OCB=90°∴OC⊥BC∴BC是⊙O的切线．18 解：（1）如图：（2）AB与⊙O相切．证明：作OD⊥AB于D，如图．∵BO平分∠ABC，∠ACB=90°，OD⊥AB，∴OD=OC，∴AB与⊙O相切．。

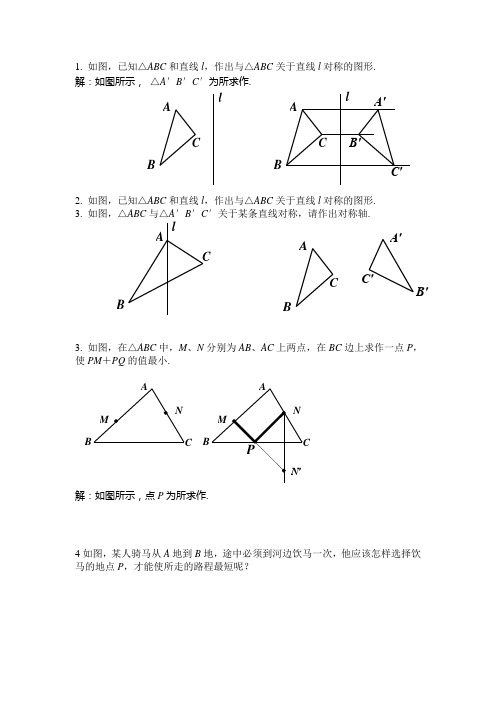
1. 如图，已知△ABC 和直线l ，作出与△ABC 关于直线l 对称的图形. 解：如图所示， △A ′B ′C ′为所求作.2. 如图，已知△ABC 和直线l ，作出与△ABC 关于直线l 对称的图形.3. 如图，△ABC 与△A ′B ′C ′关于某条直线对称，请作出对称轴.3. 如图，在△ABC 中，M 、N 分别为AB 、AC 上两点，在BC 边上求作一点P ，使PM ＋PQ 的值最小.4如图，某人骑马从A 地到B 地，途中必须到河边饮马一次，他应该怎样选择饮马的地点P ，才能使所走的路程最短呢？MNA B5. 如图，已知牧马营地在A 处，每天牧马人要赶着马群先到河边饮水，再到草地吃草，然后回到营地. 试设计出最短的放牧路线.A′B′C′AB C l l C B A A B C l B B A′B′C′CB AA营地草地河6. 如图，A 为马厩，B 为帐篷，牧马人某一天要从马厩牵出马，先到草地边某一处牧马，再到河边饮马，然后回到帐篷. 请你帮他确定这一天的最短路线.M河草7. 如图，△ABC 的三个顶点的坐标分别为A (－2，3)，B (－3，1)，C (－1，2)，分别作出与△ABC 关于y 轴和x 轴对称的图形，并标出各对称点的坐标.8. 如图，△ABC 的三个顶点的坐标分别为A (－2，3)，B (－分别作出与△ABC 关于直线m （直线x ＝1）和直线n （直线y ＝－1）轴对称的图形，并标出各对称点的坐标.9五种基本作图：①作一条线段等于已知线段； ②作一个角等于已知角；③平分已知角（作角平分线）； ④作线段的垂直平分线；⑤经过一点作已知直线的垂线.10 如图，作△ABC ，使得BC =a 、AC =b 、∠C =∠1.11已知△ABC ，求作点P ，使点P 到三边AB 、BC 、CA 的距离相等.12 如图，已知△ABC ，求作点P ，使点P 到三个顶点A 、B 、C 的距离相等.点P 在直线l 上ab13，某地由于居民增多，要在公路边增加一个公共汽车站，A 、B 是路边两个新建小区，这个公共汽车站建在什么位置，能使两个小区到车站的路程一样长？ 14如图，有分别过A 、B 两个加油站的公路1l 、2l 相交于点O ，现准备在∠AOB 内建一个油库，要求油库的位置点P 满足到A 、B 两个加油站的距离相等，而且P 到两条公路1l 、2l 的距离也相等.15 电线部门要修建一座电视信号发射塔P . 如图，按照设计要求，发射塔到两个城镇A 、B 的距离必须相等，到两条高速公路m 和n 的距离也必须相等.发射塔P 应建在什么地方？16 如图，某住宅小区拟在休闲场地的三条道路上修建三个凉亭A 、B 、C 且凉亭用两两连通. 如果凉亭A 、B 的位置已经选定，那么凉亭C 建在什么位置，才能使工程造价最低？要求用尺规作图．．．．．．．.BCB CM N A B l。

八上数学尺规作图归纳总结(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（八上数学尺规作图归纳总结(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为八上数学尺规作图归纳总结(word版可编辑修改)的全部内容。

八上数学教师辅导讲义学员编号：年级：新初二课时数：学员姓名: 辅导科目：数学学科教师：赵老师课题尺规作图授课日期及时段教学目的教学内容一、知识梳理（一)尺规作图的定义：尺规作图是指用没有刻度的直尺和圆规作图。

（二）五种基本作图：1、作一条线段等于已知线段;已知：如图，线段a .求作：线段AB，使AB = a .作法：①作射线AP;②在射线AP上截取AB=a .则线段AB就是所求作的图形。

2、作一个角等于已知角；3、作已知线段的垂直平分线；已知：如图，线段MN。

求作：点O，使MO=NO(即O是MN的中点）.作法：①分别以M、N为圆心,大于1/2MN的相同线段为半径画弧，两弧相交于P，Q;②连接PQ交MN于O．则点O就是所求作的ＭＮ的中点。

(试问：PQ与ＭＮ有何关系?)4、作已知角的角平分线；已知：如图，∠AOB，求作：射线OP，使∠AOP＝∠BOP（即OP平分∠AOB）.作法：①以O为圆心,任意长度为半径画弧,分别交OA，OB于M，N；②分别以M、Ｎ为圆心，大于1/2MN的相同线段为半径画弧，两弧交∠AOB内于Ｐ；③作射线OP。

则射线OP就是∠AOB的角平分线。

5、过一点作已知直线的垂线；①以已知点为圆心，以任意长为半径作弧，交直线于A、B两点；②分别以A、B为圆心，以大于1/2AB长为半径分别作弧,两弧分别交于点M、点N；③连接MN，则直线MN为所求作的直线.6、过直线外一点作直线的平行线（三）尺规作图拓展（1）已知三边作三角形.已知：如图，线段a,b，c。

《尺规作图》课堂笔记
一、基本概念和定义
1.尺规作图：只使用圆规和无刻度直尺进行的作图方法。

2.基本作图：通过尺规可以完成的基本图形绘制。

二、尺规作图的基本步骤和要求
1.明确题目要求，确定需要绘制的图形。

2.选择合适的圆心和半径，用圆规进行作图。

3.使用无刻度直尺进行连线，完成图形。

4.标记必要的角度和长度信息。

5.检查图形是否符合题目要求，进行调整。

三、常见图形的尺规作图方法
1.等分线段：利用圆规和无刻度直尺将线段等分为指定份数。

2.作一个角等于已知角：利用圆规截取已知角两边等长线段，再在无刻度直尺上
画出等长线段，连接两端点得到所求角。

3.作已知线段的垂直平分线：分别以线段两端点为圆心，以大于线段长度一半为
半径画弧，两弧交于两点，连接这两点即为所求垂直平分线。

4.作一个角大于、小于或等于已知角：通过截取和比较已知角两边等长线段来得
到所求角。

四、注意事项
1.圆规使用时要固定好圆心，保持半径不变。

2.无刻度直尺只能用来进行连线和画直线，不能进行度量。

3.作图过程中要保持图形清晰、整洁，避免混淆。

4.完成作图后要进行检查，确保符合题目要求。

初中数学八年级上学期期末复习专题4尺规作图一、单选题1 .下列作图语言中，正确的是（）A.过点P作直线AB的垂直平分线B ,延长射线OA到B点C.延长线段AB到 C ,使BC=ABD .过N AOB内一点P ,作N AOB的平分线2 .如图，已知线段AB ,以下作图不可能的是（）I ■IA 0 BA.在AB上取一点C使AC=BCB.在AB的延长线上取一点C使BC=ABC.在BA的延长线上取一点C ,使BC=ABD .在BA的延长线上取一点C ,使BC=2AB3 .用直尺和圆规作一个角等于已知角，其依据是（）A . SSSB . SASC. ASAD . AAS4 .如图，用尺规作图作N AOC=N AOB的第一步是以点0为圆心,以任意长为半径画弧①，分别交OA,OB于点E,F ,那么第二步的作图痕迹②的作法是（）A .以点F为圆心，OE长为半径画弧B .以点F为圆心，EF长为半径画弧C.以点E为圆心，OE长为半径画弧D .以点E为圆心，EF长为半径画弧5 .如图所示，已知△ ABC （ AC < AB < BC ）,用尺规在线段BC上确定一点P ,使得PA+ PC = BC ,则符合要求的作图痕迹是（）A .如图① 以B为圆心，BA长为半径画弧交BC于点PB .如图②作AC中垂线交BC于点PC.如图③以C为圆心，CA长为半径画弧交BC于点PD.如图④作AB 中垂线交BC于P6 .下列四种基本尺规作图分别表示：①作一个角等于已知角；②作一个角的平分线；③作一条线段的垂直平分线；④过直线外一点P作已知直线的垂线。

则对应作法7 .如图，已知MBC ,用尺规在AC上确定一点P ,使PB+PC = AC ,则下列选项中，一定符合要求的作图痕迹是8 .下列各条件中，能作出睢一的SBC的是A . AB = 4 , BC = 5 , AC = 10B . AB = 5 , BC = 4 , zA = 40℃ . zA = 90°z AB =10D.zA = 60° , zB = 50° , AB = 59 .如图，在△.0C上确定一点P ，使点 等，则符合要求的作图痕迹是（10 .小明用尺规作图作3BC 边AC 上的高BH ，作法如下：1①分别以点D , E 为圆心，大于，DE 的长为半径作弧，两弧交于F ;②作射线BF,交边AC 于点H ; ③以B 为圆心，BK 长为半径作弧，交直线AC 于点D 和E ;④取一点K ,使K 和B 在AC 的两侧;所以，BH 就是所求作的高.其中顺序正确的作图步骤是（）A.①②③④B .④③②①C .②④③①D .④③①②二、填空题11 .如图，在RfABC 中，zC=90° ,以顶点A 为圆心，适当长为半径画弧，分 别交AC , AB 于点M 、N ,再分别以点M 、N 为圆心，大于 MN 的长半径 .用直尺和圆规在边BC 、点B 的距离相画弧，两弧交于点P ,作射线AP ,交边BC于点D ,若CD=4 , AB=15 ,贝SABD的面积是.12 .已知底边a和底边上的高h ,在用尺规作图方法作这个等腰aCDE ,使DE=a , CB=h时，需用到的作法有：①在MN上截取BC=h ;②作线段DE=a ;③作线段DE的垂直平分线MN ,与DE交于点B ;④连接CD , CE , △CDE就是所求的等腰三角形.则正确作图步骤的序号是.13 .如图，用尺规作图作〃一个角等于已知角〃的原理是：因为△D'O'C^4DOC , 所以N DOC'=/DOC。