下载文档原格式
陕西省公务员历年面试真题贾东平整理目录<<2008年陕西公务员面试真题>> (4)2008年6月陕西宝鸡公务员考试检查员面试真题 (4)2008年6月12日陕西杨凌公务员考试面试真题 (4)2008年6月14日陕西省政府公务员考试面试真题 (4)2008年6月17日陕西省委公务员考试面试真题 (4)2008年6月21日陕西铜川政府公务员考试面试真题 (4)2008年6月22日陕西药监公务员考试面试真题 (5)2008年6月28日上午陕西咸阳公务员考试面试真题 (5)2008年6月29日陕西质监系统公务员考试面试真题 (5)2008年6月29日上午陕西劳教系统公务员面试真题 (5)2008年5月国税系统公务员面试真题解析 (5)2008年7月19日下午陕西省公务员录用考试面试题 (6)2008年7月19日上午陕西省公务员录用考试面试题 (6)2008年7月20日下午陕西公务员录用考试面试题 (7)<<2009年陕西公务员面试真题>> (7)2009年7月5日陕西省宝鸡市政府部门公务员考试面试真题 (7)2009年7月5日陕西省咸阳市公安系统公务员考试面试真题 (7)2009年7月6日陕西省街道办公务员考试面试真题 (7)2009年7月9日陕西汉中政府部门公务员面试真题 (7)2009年7月11日陕西省公务员考试面试真题 (8)2009年7月11日陕西省西安市公务员考试面试真题 (8)2009年7月11日陕西省安康市公务员考试面试真题 (8)2009年7月12日陕西省公务员录用考试面试真题 (8)2009年7月13日陕西省公务员录用考试面试真题 (8)<<2010年陕西公务员面试真题>> (9)6月8日咸阳面试题 (9)6月9日咸阳面试题 (9)6月10号咸阳面试 (9)10月陕西法官检察官考试初任面试真题 (9)2010年西安公务员面试真题：11月12日-14日面试题 (9)2010年11月12日陕西西安公务员面试真题 (9)2010年11月13日陕西公务员面试真题 (10)2010年11月14日陕西务员面试真题 (10)<<2011年陕西公务员面试真题>> (10)陕西工商系统14日上午考题： (10)1、有人说高考加分有利于学生综合素质的拓展，有人反对。
2008年高考真题精品解析2008年普通高等学校招生全国统一考试（北京卷）（理科） 测试题 2019.91,若实数满足则的最小值是（ ）A ．0B ．1C．92,已知数列对任意的满足，且，那么等于（ ）A ．B ．C ．D ．3,过直线上的一点作圆的两条切线，当直线关于对称时，它们之间的夹角为（ ）A ．B ．C ．D ．4,如图，动点在正方体的对角线上．过点作垂直于平面的直线，与正方体表面相交于．设，，则函数的图象大致是（ ）5,已知函数（）的最小正周期为．（Ⅰ）求的值；（Ⅱ）求函数在区间上的取值范围．6,如图，在三棱锥中，，，，．（Ⅰ）求证：；（Ⅱ）求二面角的大小；x y ，1000x y x y x ⎧-+⎪+⎨⎪⎩，，，≥≥≤23x yz +={}n a *p q ∈N ，p q p q a a a +=+26a =-10a 165-33-30-21-y x =22(5)(1)2x y -+-=12l l ，12l l ，y x =30456090P 1111ABCD A B C D -1BD P 11BB D D M N ，BP x =MN y =()y f x =2π()sin sin 2f x x x x ωωω⎛⎫=++ ⎪⎝⎭0ω>πω()f x 2π03⎡⎤⎢⎥⎣⎦，P ABC -2AC BC ==90ACB ∠=AP BP AB ==PC AC ⊥PC AB ⊥B AP C --（Ⅲ）求点到平面的距离．7,甲、乙等五名奥运志愿者被随机地分到四个不同的岗位服务，每个岗位至少有一名志愿者．（Ⅰ）求甲、乙两人同时参加岗位服务的概率； （Ⅱ）求甲、乙两人不在同一个岗位服务的概率；（Ⅲ）设随机变量为这五名志愿者中参加岗位服务的人数，求的分布列． 8,已知函数，求导函数，并确定的单调区间．9,已知菱形的顶点在椭圆上，对角线所在直线的斜率为1．（Ⅰ）当直线过点时，求直线的方程； （Ⅱ）当时，求菱形面积的最大值．10,对于每项均是正整数的数列，定义变换，将数列变换成数列．对于每项均是非负整数的数列，定义变换，将数列各项从大到小排列，然后去掉所有为零的项，得到数列； 又定义．设是每项均为正整数的有穷数列，令．（Ⅰ）如果数列为5，3，2，写出数列；（Ⅱ）对于每项均是正整数的有穷数列，证明； （Ⅲ）证明：对于任意给定的每项均为正整数的有穷数列，存在正整数，当时，．测试题答案CAPB A B C D ，，，A ξA ξ22()(1)x bf x x -=-()f x '()f x ABCD A C ，2234x y +=BD BD (01)，AC 60ABC ∠=ABCD 12n A a a a ：，，，1T 1T A 1()T A ：12111n n a a a ---，，，，12m B b b b ：，，，2T 2T B 2()T B 2221212()2(2)m mS B b b mb b b b =+++++++0A 121(())(012)k k A T T A k +==，，，0A 12A A ，A 1(())()S T A S A =0A K k K ≥1()()k k S A S A +=1, 【标准答案】: B【试题分析】: 解出可行域的顶点，带入验证。
2008年普通高等学校招生全国统一考试理科数学(必修+选修Ⅱ)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．第Ⅰ卷1至2页．第Ⅱ卷3至10页．考试结束后，将本试卷和答题卡一并交回．第Ⅰ卷注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上．2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．不能答在试题卷上．3．本卷共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 参考公式：如果事件A B ，互斥，那么 球的表面积公式如果事件A B ，相互独立，那么 其中R 表示球的半径()()()P A B P A P B = 球的体积公式如果事件A 在一次试验中发生的概率是p ，那么 34π3V R =n 次独立重复试验中事件A 恰好发生k 次的概率 其中R 表示球的半径一、选择题1．设集合{|32}M m m =∈-<<Z ，{|13}N n n M N =∈-=Z 则，≤≤（ ）A ．{}01，B ．{}101-，，C ．{}012，，D ．{}1012-，，，【答案】B【解析】{}1,0,1,2--=M ，{}3,2,1,0,1-=N ，∴{}1,0,1-=N M【高考考点】集合的运算，整数集的符号识别。
【评注】历年来高考数学第一个小题一般都是集合问题，都超简单。
其实集合问题是可以出难题的，但高考中的集合问题比较简单。
需要注意的是：很多复习书都把集合作为高考数学复习的起点，我认为这是不妥当的，高中的集合问题涉及到的集合知识并不多（就是一种表达方式），其难度主要体现在知识的综合性上，学生应当先学习其他知识，再在集合中综合。
建议把“数学的基本运算”作为高考数学复习的起点，学生花1个月的时间温习、强化初等数学的基本运算是必要的，重要的，也是值得的。
数学的基本运算具体包括的内容可以参考本人编写的《高考数学复习专用教材》 2．设a b ∈R ，且0b ≠，若复数3()a bi +是实数，则（ ） A ．223b a = B ．223a b =C ．229b a =D ．229a b =【答案】A【解析】i b b a ab a i b ab bi a a bi a )3()3(33)(322332233-+-=--+=+，因是实数且0b ≠，所以2232303a b b b a =⇒=-【高考考点】复数的基本概念、基本运算，立方和公式（基本运算）【评注】很多学生没有学习过立方和公式，不会用立方和公式一步到位地展开，有人按32()()()a bi a bi a bi +=++进行展开，也有人按3()()()()a bi a bi a bi a bi +=+++进行展开，还有人用二项式定理进行展开，这都是可行的思路。
2008年高考真题精品解析2008年普通高等学校招生全国统一考试（四川卷）（理科） 测试题 2019.91,( )（Ａ）（Ｂ）（Ｃ）（Ｄ）2,直线绕原点逆时针旋转，再向右平移１个单位，所得到的直线为( )（Ａ）（Ｂ）（Ｃ）（Ｄ）3,若，则的取值范围是：( )（Ａ） （Ｂ） （Ｃ） （Ｄ）4,从甲、乙等10个同学中挑选4名参加某项公益活动，要求甲、乙中至少有1人参加，则不同的挑选方法共有( ) （Ａ）种（Ｂ）种（Ｃ）种（Ｄ）种5,已知等比数列中，则其前3项的和的取值范围是( ) （Ａ） （Ｂ）（Ｃ） （Ｄ） 6,设是球心的半径上的两点，且，分别过作垂线于的面截球得三个圆，则这三个圆的面积之比为：( ) （Ａ）（Ｂ）（Ｃ）（Ｄ）7,设直线平面，过平面外一点与都成角的直线有且只有：( )（Ａ）１条（Ｂ）２条（Ｃ）３条（Ｄ）４条8,设，其中，则是偶函数的充要条件是( ) （Ａ）（Ｂ）（Ｃ）（Ｄ）9,设定义在上的函数满足，若，则( )()2tan cot cos x x x +=tan x sin x cos x cot x 3y x =0901133y x =-+113y x =-+33y x =-113y x =+02,sin απαα≤≤>α,32ππ⎛⎫ ⎪⎝⎭,3ππ⎛⎫ ⎪⎝⎭4,33ππ⎛⎫ ⎪⎝⎭3,32ππ⎛⎫ ⎪⎝⎭70112140168()n a 21a =3S (],1-∞-()(),01,-∞+∞[)3,+∞(][),13,-∞-+∞,M N O OP NP MN OM ==,,N M O OP 3,5,63,6,85,7,95,8,9l ⊂ααA ,l α030()()sin f x x ωϕ=+0ω>()f x ()01f =()00f =()'01f =()'00f =R ()f x ()()213f x f x ⋅+=()12f =()99f =（Ａ） （Ｂ） （Ｃ） （Ｄ）10,已知抛物线的焦点为，准线与轴的交点为，点在上且，则的面积为( )（Ａ） （Ｂ） （Ｃ） （Ｄ）测试题答案1, 【解】：∵故选D2, 【解】：∵直线绕原点逆时针旋转的直线为，从而淘汰（Ｃ），（D ）又∵将向右平移１个单位得，即故选A 3, 【解】：∵ ∴ ，即又∵ ∴，∴ ，即 故选C4, 【解】：∵从10个同学中挑选4名参加某项公益活动有种不同挑选方法；从甲、乙之外的8个同学中挑选4名参加某项公益活动有种不同挑选方法；∴甲、乙中至少有1人参加，则不同的挑选方法共有种不同挑选方法 故选C5, 【解1】：∵等比数列中 ∴当公比为1时，，；当公比为时，， 从而淘汰（Ａ）（Ｂ）（Ｃ）1321322132:8C y x =F x K ACAK AF =AFK ∆481632()22222sin cos sin cos tan cot cos cos cos cos sin sin cos x x x x x x x x x x x x x +⎛⎫+=+=⋅ ⎪⎝⎭cos cot sin xx x ==3y x =09013y x =-13y x =-()113y x =--1133y x =-+sin αα>sin 0αα>12sin 2sin 023πααα⎛⎫⎛⎫=-> ⎪ ⎪ ⎪⎝⎭⎝⎭02απ≤≤5333πππα-≤-≤03παπ≤-≤4,33x ππ⎛⎫∈ ⎪⎝⎭410C 48C 4410821070140C C -=-=()n a 21a =1231a a a ===33S =1-1231,1,1a a a =-==-31S =-故选D ；【解2】：∵等比数列中 ∴∴当公比时，；当公比时，∴ 故选D6, 【解】：设分别过作垂线于的面截球得三个圆的半径为，球半径为，则：∴∴这三个圆的面积之比为： 故选D7,【解】：如图，和成角的直线一定是以A 为顶点的圆锥的母线所在直线，当，直线都满足条件 故选Ｂ8, 【解】：∵是偶函数∴由函数图象特征可知必是的极值点， ∴ 故选D9, 【解】：∵且 ∴，，，，，，()n a 21a =312321111S a a a a q q q q ⎛⎫=++=++=++⎪⎝⎭0q>31113S q q =++≥+=0q<31111S q q ⎛⎫=---≤-=- ⎪⎝⎭(][)3,13,S ∈-∞-+∞,,N M O OP 123,,r r r R 22222222222212325182,,39393r R R R r R R R r R R R ⎛⎫⎛⎫⎛⎫=-==-==-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭222123::5:8:9r r r =5,8,9α030030ABC ACB ∠=∠=,AC AB ()()sin f x x ωϕ=+()()sin f x x ωϕ=+0x =()f x ()'00f =()()213f x f x ⋅+=()12f =()12f =()()1313312f f ==()()13523f f ==()()1313752f f ==()()13925f f ==∴ ，∴故选C10,【解】：∵抛物线的焦点为，准线为 ∴设，过点向准线作垂线，则 ∵，又 ∴由得，即，解得∴的面积为 故选B()221132n f n n ⎧⎪-=⎨⎪⎩为奇数为偶数()()1399210012f f =⨯-=2:8C y x =()20F ，2x =-()20K -，()00A x y ，A AB ()02B y -，AK AF =()0022AF AB x x ==--=+222BK AK AB =-()22002y x =+()20082x x =+()24A ±，AFK ∆01144822KF y ⋅=⨯⨯=。
08年全国卷精选15.一个T 型电路如图所示，电路中的电110R =Ω,23120,40R R =Ω=Ω.另有一测试电源，电动势 为100V ，内阻忽略不计。
则A.当cd 端短路时，ab 之间的等效电阻是40ΩB. 当ab 端短路时，cd 之间的等效电阻是40ΩC. 当ab 两端接通测试电源时， cd 两端的电压为80 VD. 当cd 两端接通测试电源时， ab 两端的电压为80 V【解析】本题考查电路的串并联知识。
当cd 端短路时，R 2与R 3并联电阻为30Ω后与R 1串联，ab 间等效电阻为40Ω，A 对；若ab 端短路时，R 1与R 2并联电阻为8Ω后与R 3串联，cd 间等效电阻为128Ω，B 错；但ab 两端接通测试电源时，电阻R 2未接入电路，cd 两端的电压即为R 3的电压，为U cd = 4050×100V=80V ，C 对；但cd 两端接通测试电源时，电阻R 1未接入电路，ab 两端电压即为R 3的电压，为U ab = 40160×100V=25V ，D 错。
答案：AC16.如图所示，同一平面内的三条平行导线串有两个最阻R 和r ，导体棒PQ 与三条导线接触良好；匀强磁场的方向垂直纸面向里。
导体棒的电阻可忽略。
当导体棒向左滑动时，下列说法正确的是A.流过R 的电流为由d 到c ，流过r 的电流为由b 到aB.流过R 的电流为由c 到d ，流过r 的电流为由b 到aC.流过R 的电流为由d 到c ，流过r 的电流为由a 到bD.流过R 的电流为由c 到d ，流过r 的电流为由a 到b【解析】本题考查右手定则的应用。
根据右手定则，可判断PQ 作为电源，Q 端电势高，在PQcd 回路中，电流为逆时针方向，即流过R 的电流为由c 到d ，在电阻r 的回路中，电流为顺时针方向，即流过r 的电流为由b 到a 。
当然也可以用楞次定律，通过回路的磁通量的变化判断电流方向。
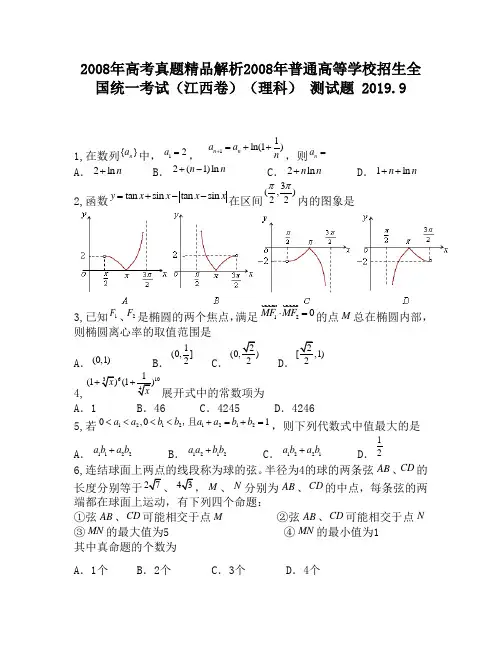
2008年高考真题精品解析2008年普通高等学校招生全国统一考试（江西卷）（理科） 测试题 2019.91,在数列中，， ，则A ．B ．C ．D ．2,函数在区间内的图象是3,已知、是椭圆的两个焦点，满足的点总在椭圆内部，则椭圆离心率的取值范围是A ．B ．C ．D ．4,展开式中的常数项为 A ．1 B ．46 C ．4245 D ．42465,若，则下列代数式中值最大的是A ．B ．C ．D ．6,连结球面上两点的线段称为球的弦。
半径为4的球的两条弦、的长度分别等于、、分别为、的中点，每条弦的两端都在球面上运动，有下列四个命题：①弦、可能相交于点 ②弦、可能相交于点 ③的最大值为5 ④的最小值为1 其中真命题的个数为A ．1个B ．2个C ．3个D ．4个{}n a 12a =11ln(1)n n a a n +=++n a =2ln n +2(1)ln n n +-2ln n n +1ln n n ++tan sin tan sin y x x x x=+--3(,)22ππ1F 2F 120MF MF ⋅=M (0,1)1(0,]2(0,22610(1(1+121212120,01a a b b a a b b <<<<+=+=,且1122a b a b +1212a a b b +1221a b a b +12AB CD M N AB CD AB CD M AB CD N MN MN7,电子钟一天显示的时间是从00:00到23:59的每一时刻都由四个数字组成，则一天中任一时刻的四个数字之和为23的概率为A ．B ．C ．D ．8,已知函数，，若对于任一实数，与至少有一个为正数，则实数的取值范围是A ．B ．C ．D ． 9,在中，角所对应的边分别为，，，求及 10,某柑桔基地因冰雪灾害，使得果林严重受损，为此有关专家提出两种拯救果林的方案，每种方案都需分两年实施；若实施方案一，预计当年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4；第二年可以使柑桔产量为上一年产量的1.25倍、1.0倍的概率分别是0.5、0.5. 若实施方案二，预计当年可以使柑桔产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5； 第二年可以使柑桔产量为上一年产量的1.2倍、1.0倍的概率分别是0.4、0.6. 实施每种方案，第二年与第一年相互独立。
2008年高考真题精品解析2008年普通高等学校招生全国统一考试（全国卷Ⅰ）（理科） 测试题 2019.91,函数）A ．B ．C ．D ．2,汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程看作时间的函数，其图像可能是（ ）3,在中，，．若点满足，则（ ） A ．B ．C ．D ．4,设，且为正实数，则（ ） A ．2B ．1C ．0D ． 5,已知等差数列满足，，则它的前10项的和（ ）A ．138B ．135C ．95D ．236,若函数的图像与函数的图像关于直线对称，则（ ）A ．B ．C ．D ．7,设曲线在点处的切线与直线垂直，则（ ）A ．2B ．C ．D ．8,为得到函数的图像，只需将函数的图像（ ）y ={}|0x x ≥{}|1x x ≥{}{}|10x x ≥{}|01x x ≤≤s t ABC △AB =c AC =b D 2BD DC =AD =2133+b c 5233-c b 2133-b c 1233+b c a ∈R 2()a i i +a =1-{}n a 244a a +=3510a a +=10S =(1)y f x =-1y =y x =()f x =21x e -2x e 21x e +22x e +11x y x +=-(32)，10ax y ++=a =1212-2-πcos 23y x ⎛⎫=+ ⎪⎝⎭sin 2y x =A ．向左平移个长度单位B ．向右平移个长度单位C ．向左平移个长度单位D ．向右平移个长度单位9,设奇函数在上为增函数，且，则不等式的解集为（ ）A ．B ．C ．D ． 10,若直线通过点，则（ ） A ．B ．C ．D ．测试题答案1, C. 由2, A ．根据汽车加速行驶，匀速行驶，减速行驶结合函数图像可知； 3, A. 由，， 4, D.5, C. 由 6, B.由7, D.由 8, A.只需将函数的图像向左平移个单位得到函数的图像. 5π125π125π65π6()f x (0)+∞，(1)0f =()()0f x f x x --<(10)(1)-+∞，，(1)(01)-∞-，，(1)(1)-∞-+∞，，(10)(01)-，，1x y a b +=(cos sin )M αα，221a b +≤221a b +≥22111a b +≤22111a b +≥()10,0,1,0;x x x x x -≥≥≥=得或212s at =s vt =212s at =-()2AD AB AC AD -=-322AD AB AC c b =+=+1233AD c b =+()()()22221210,1a i i a ai i a a i a +=+-=-+->=-243511014,104,3,104595a a a a a d S a d +=+=⇒=-==+=()()()()212121,1,y x x y x e f x e f x e --=⇒=-==()3212211,','|,2,21121x x y y y a a x x x =+==+=-=--==----55cos 2sin 2sin 2,3612y x x x πππ⎛⎫⎛⎫⎛⎫=+=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭sin 2y x =5π12πcos 23y x ⎛⎫=+ ⎪⎝⎭9, D ．由奇函数可知，而，则，当时，；当时，，又在上为增函数，则奇函数在上为增函数，.10, D ．由题意知直线与圆有交点，则.另解：设向量，由题意知由可得()f x ()()2()0f x f x f x x x --=<(1)0f =(1)(1)0f f -=-=0x >()0(1)f x f <=0x <()0(1)f x f >=-()f x (0)+∞，()f x (,0)-∞01,10x x <<-<<或1x y a b +=221x y +=22111a b +1,≥11(cos ,sin ),(,)a b ααm =n =cos sin 1a b αα+=⋅≤m n m n cos sin 1a b αα=+≤。
2008年真题D品。
同时为弥补需求的波动，可能再额外持有250件作为后备或安全库存。
则该物品的平均库存量将为（）A.250B.500C.750D.10009.假设某商场彩电销售量情况如（）使用加权移动平均法计算彩电第四天的预测销售量A.30B.31C.32D.3310.波动库存是指（）A.由于物料必须从一处移动到另一处而产生的库存B.以大于目前所需要的数量来获得物品造成的库存C.由于不能准确预测销售数量、生产数量和时机而持有的库存D.为迎接高峰销售季节、市场营销推进计划或工厂停产期而预先建立起来的库存11.运输规模经济的特点是（）A.随装运规模的增长，使每单位重量的运输成本下降B.随装运规模的增长，使每单位重量的运输成本上升C.每单位距离的运输成本随距离的增加而减少D. 每单位距离的运输成本随距离的增长12.有效顾客响应应用于（）A.品牌选择性强的行业B.食品行业C.百货业D.重工业13.反映供应链上、下节点企业之间关系的绩效评价指标是（）A.价格指标B.质量指标C.成本指标D.满意度指标14.均衡计分卡模型包括哪几类指标（）A.客户指标、财务指标、内部运营指标和学习成长指标B.客户指标、财务指标、柔性指标C.客户指标、柔性指标、刚性指标和敏捷性指标D.财务指标、柔性指标、刚性指标和学习成长指标15.柔性评价指标的目标是（）A为了描述系统创新能力 B.为了描述系统盈利能力C.为了描述系统组织能力D.为了描述系统应对环境变化的能力二、多项选择题（每小题2分，共计20分）16.与推式供应链模式相比，拉式模式的优势表现在（）A.能够全面衡量业绩，更易于实施控制B.支持产品的不断变化C.提高经营效率D.改进质量，降低单位成本E.改进质量，降低单位成本17.下列关于物流存储功能的描述正确的有（）A.包括任何跨空间的物质实体的流动B.是物流体系中唯一的静态环节，是物流体系上的一个结点C.是物流运动空间和时间上的两大支持之一D.制定和完善物流业务管理规矩E.为将货物配送给用户，在物流中心进行必要的加工活动而进行保护18.MRP系统的三个主要依据包括（）A.主生产计划B.物流清单C.库存信息D.人员安排 E作业流程控制19.下列关于JIT的描述正确的有（）A.目标是最小化库存、提高产品质量、最大化生产效率和提供最佳客户服务水平B.在JIT中，理想的批量是一个单位，安全库存是不必要的，库存根本不应存在C.JIT具有向零库存进军、实现最大化节约、最大限度的降低废品的优势D. JIT的基本原理是以需定供，适时适量生产E. JIT的基本原理是以产定销，保存一定的库存量20.下列关于供应链伙伴关系和传统企业关系的描述正确的是（）A.传统关系的基础是联盟，而供应链伙伴关系的基础是交易B.传统关系的基础是交易，而供应链伙伴关系的基础是联盟C传统关系维系时间比较短，而供应链关系关系维持是长期的D.传统关系性质是敌对关系，而供应链关系性质是合作E.传统关系信息共享程度较低，而供应链关系拥有广泛的产品、营销和物流信息共享21.广义的库存可以理解为（）A.仅仅指的是在仓库中处于暂时停滞状态的物资B.用于将来目的的、暂时处于闲置状态的资源C资源停滞的位置，可以是在仓库里、生产线上D.资源的闲置状态可能由任何原因引起E.资源停滞的位置，可以是在非仓库的任何位置22.指导运输运作管理的两条基本原理是（）A.规模经济B.规模不经济C.距离经济D.边际效益递减规律E.边际效益递增规律23.有效捕获的构成要素包括（）A.POS机扫描和店铺单品预测B.店铺的电子收货系统、单品的价格和促销数据库C.计算机辅助订货系统、集成的采购订单管理D.配送系统、仓库的电子收货E直接出货、自动化的会计系统24.下列说法正确的有（）A.产销率越接近1，说明资源利用程度越低B. 产销率越接近1，说明供应链成品库存量越小C.平均产销绝对偏差指标值越大，说明供应链成品库存量越大，库存费用越高D.产需率大于1，则说明上层企业对下层企业的需求量缺乏调研或调研不准确E.供应链核心企业产需率指标数值小于1，则说明供应链生产能力不足，不能快速响应市场需求25.构成EDI系统的三个要素是（）A.EDI软件和硬件B.信息共享C通信网络 D.数据标准化 E.数据采集三、名词解释（本大题共5小题，每小题3分，共15分）26.现代物流管理27.牛鞭效应28.再订货点29.供应商管理库存30.快速响应四、简答题（本大题共5小题，每小题5分，共计25分）31.简述供应链的基本特征32.简述ERP系统的主要管理思想33.简述运输网络模型设计方案的主要类型34.简述影响承运人决策的因素35.简述ECR的最终目标五、案例分析题（本大题共1小题，每小题10分，共10分）36.随着市场经济的发展，企业对于客户满意度的重视程度日益增强。
2008年高考真题精品解析2008年普通高等学校招生全国统一考试（湖北卷）（理科） 测试题 2019.91,已知函数（Ⅰ）将函数化简成（，，）的形式；（Ⅱ）求函数的值域.2,袋中有20个大小相同的球，其中记上0号的有10个，记上号的有个（=1,2,3,4）.现从袋中任取一球.表示所取球的标号. （Ⅰ）求的分布列，期望和方差；（Ⅱ）若, ,,试求a,b 的值.3,如图，在直三棱柱中，平面侧面. （Ⅰ）求证：；（Ⅱ）若直线与平面所成的角为,二面角的大小为，试判断与的大小关系，并予以证明.4,如图，在以点为圆心，为直径的半圆中，，是半圆弧上一点，，曲线是满足为定值的动点的轨迹，且曲线过点.（Ⅰ）建立适当的平面直角坐标系，求曲线的方程；（Ⅱ）设过点的直线l 与曲线相交于不同的两点、. 若△的面积不小于，求直线斜率的取值范围.17()()cos (sin )sin (cos ),(,).12f t g x x f x x f x x ππ==⋅+⋅∈()g x sin()A x B ωϕ++0A >0ω>[0,2)ϕπ∈()g x n n n ξξa b ηξ=+1E η=11D η=111ABC A B C -ABC ⊥11A ABB AB BC ⊥AC 1A BC θ1A BC A --ϕθϕO ||4AB =ADB OD AB ⊥P 30POB ∠=︒C ||||||MA MB -M C P C D C E FOEF l5,水库的蓄水量随时间而变化，现用表示时间，以月为单位，年初为起点，根据历年数据，某水库的蓄水量（单位：亿立方米）关于的近似函数关系式为（Ⅰ）该水库的蓄求量小于50的时期称为枯水期.以表示第1月份（）,同一年内哪几个月份是枯水期？（Ⅱ）求一年内该水库的最大蓄水量（取计算）.6,已知数列和满足：,其中为实数，为正整数.（Ⅰ）对任意实数，证明数列不是等比数列； （Ⅱ）试判断数列是否为等比数列，并证明你的结论；（Ⅲ）设,为数列的前项和.是否存在实数，使得对任意正整数，都有?若存在，求的取值范围；若不存在，说明理由.7,设(其中表示z 1的共轭复数)，已知z 2的实部是，则z 2的虚部为 .8,在△中，三个角的对边边长分别为,则的值为 .9,已知函数,,其中,为常数，则方程的解集为 . 10,已知函数,等差数列的公差为.若,则.t t 124(1440)50,010,()4(10)(341)50,1012.x t t e t V t t t t ⎧⎪-+-+<≤=⎨⎪--+<≤⎩1i t i -<<1,2,,12i = 2.7e ={}n a {}n b 1a λ=124,(1)(321),3n n n n n a a n b a n +=+-=--+λn λ{}n a {}n b 0a b <<n S {}n b n λn n a S b<<λ211z z iz =-1z 1-ABC ,,A B C 3,4,6a b c ===cos cos cos bc A ca B ab C ++2()2f x x x a =++2()962f bx x x =-+x R ∈,a b ()0f ax b +=()2xf x ={}x a 2246810()4f a a a a a ++++=212310log [()()()()]f a f a f a f a ⋅⋅⋅⋅=测试题答案1, 解：（Ⅰ）（Ⅱ）由得 在上为减函数，在上为增函数， 又（当）， 即故g(x)的值域为2, 解：（Ⅰ）的分布列为：∴ 1sin 1cos ()cos sin 1sin 1cos xx g x xxxx --=+++2222(1sin )(1cos )cos sin cos sin x x x xx x --=+1sin 1cos cos sin .cos sin x xx x x x--=+17,,cos cos ,sin sin ,12x x x x x π⎛⎤∈π∴=-=- ⎥⎝⎦1sin 1cos ()cos sin cos sin x x gx x x x x --∴=+--sin cos 2x x =+- 2.4x π⎛⎫+- ⎪⎝⎭1712x ππ≤＜，55.443x πππ+≤＜sin t 53,42ππ⎛⎤ ⎥⎝⎦35,23ππ⎛⎤ ⎥⎝⎦5535sin sin ,sin sin()sin 34244x πππππ∴≤+＜＜17,2x π⎛⎤∈π ⎥⎝⎦1sin()2)23424x x ππ-≤+-≤+--＜＜，)2,3.⎡-⎣ξ1113101234 1.5.22010205E ξ=⨯+⨯+⨯+⨯+⨯=2222211131(0 1.5)(1 1.5)(2 1.5)(3 1.5)(4 1.5) 2.75.22010205ξ=-⨯+-⨯+-⨯+-⨯+-⨯=（Ⅱ）由，得a 2×2.75＝11，即又所以 当a=2时，由1＝2×1.5+b,得b=-2;当a=-2时，由1＝-2×1.5+b ，得b=4.∴或即为所求.3,（Ⅰ）证明：如图，过点A 在平面A 1ABB 1内作AD ⊥A 1B 于D ，则由平面A 1BC ⊥侧面A 1ABB 1,且平面A 1BC 侧面A 1ABB 1=A 1B,得 AD ⊥平面A 1BC,又BC 平面A 1BC ，所以AD ⊥BC.因为三棱柱ABC-A 1B 1C 1是直三棱柱，则AA 1⊥底面ABC ，所以AA 1⊥BC. 又AA 1AD=A,从而BC ⊥侧面A 1ABB 1， 又AB 侧面A 1ABB 1，故AB ⊥BC.（Ⅱ）解法1：连接CD ，则由（Ⅰ）知是直线AC 与平面A 1BC 所成的角，是二面角A 1-BC-A 的平面角，即于是在Rt △ADC 中，在Rt △ADB 中，由AB ＜AC ，得又所以解法2：由（Ⅰ）知，以点B 为坐标原点，以BC 、BA 、BB 1所在的直线分别为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系，设AA 1=a,AC=b,D a D η=ξ22.a =±,E aE b η=ξ+2,2a b =⎧⎨=-⎩2,4a b =-⎧⎨=⎩⊂⊂ACD ∠1ABA ∠1,,ACD ABA ∠=θ∠=ϕsin ,AD AC θ=sin ,ADAB ϕ=sin sin θϕ＜，02πθϕ＜，＜，θϕ＜，AB=c,则 B(0,0,0), A(0,c,0),于是设平面A 1BC 的一个法向量为n=(x,y,z)，则由得 可取n=(0,-a,c)，于是与n 的夹角为锐角，则与互为余角.所以于是由c ＜b即又所以4, （Ⅰ）解法1：以O 为原点，AB 、OD 所在直线分别为x 轴、y 轴，建立平面直角坐标系，则A （-2，0），B （2，0），D(0,2),P （1,3），依题意得｜MA ｜-｜MB ｜=｜PA ｜-｜PB ｜＝221321)32(2222＝）（+--++＜｜AB ｜＝4.∴曲线C 是以原点为中心，A 、B 为焦点的双曲线. 设实平轴长为a ，虚半轴长为b ，半焦距为c ，1(0,,),C A c a 221(,0,0),(0,,),BC b c BA c a =-=221(,,0),(0,0,).AC b c c AA a =--=10,0,n BA n BC ⎧=⎪⎨=⎪⎩0,0,cy az +=⎧=0n AC ac AC =＞，ββθsin cos n AC n AC b a θ-β==11cos BA BA BA BAa ϕ==sin ϕ=sin sin ,θϕ＜0,2πθϕ＜，＜,θϕ＜则c ＝2，2a ＝22，∴a 2=2,b 2=c 2-a 2=2.∴曲线C 的方程为12222=-y x .解法2：同解法1建立平面直角坐标系，则依题意可得｜MA ｜-｜MB ｜=｜PA ｜-｜PB ｜＜ ｜AB ｜＝4.∴曲线C 是以原点为中心，A 、B 为焦点的双曲线.设双曲线的方程为a b y a x (12222=-＞0，b ＞0）.则由 .4,11)3(222222=+=-b a b a 解得a 2=b 2=2,∴曲线C 的方程为.12222=-y x(Ⅱ)解法1：依题意，可设直线l 的方程为y ＝kx+2，代入双曲线C 的方程并整理得（1-K 2）x 2-4kx-6=0.∵直线l 与双曲线C 相交于不同的两点E 、F ，⇔ ②设E （x ，y ），F(x 2,y 2)，则由①式得x 1+x 2=k x x k k --=-16,14212,于是 ｜EF ｜＝2212221221))(1()()(x x k x y x x -+=++-22210(4)46(1)0k k k ⎧-≠⎪⎨∆=-+⨯->⎪⎩∴1k k ≠±⎧⎪⎨<<⎪⎩(1k k ∈≠±∴且＝.132214)(1222212212kk k x x x x k --⋅+=-+⋅+而原点O 到直线l 的距离d ＝212k +，∴S △DEF =.132213221122121222222kk k k k k EF d --=--⋅+⋅+⋅=⋅若△OEF 面积不小于22,即S △OEF 22≥，则有解得.22,022********2≤≤-≤--⇔≥--k k k k k ③综合②、③知，直线l 的斜率的取值范围为解法2：依题意，可设直线l 的方程为y ＝kx+2，代入双曲线C 的方程并整理，得（1-K 2）x 2-4kx-6=0.∵直线l 与双曲线C 相交于不同的两点E 、F ，∴⇔. . ②设E(x 1,y 1),F(x 2,y 2),则由①式得｜x 1-x 2｜=.132214)(22221221kk kx x x x --=-∆=-+ ③当E 、F 在同一去上时（如图1所示）， S △OEF ＝;21212121x x OD x x OD S S ODE ODF -⋅=-⋅=-∆∆当E 、F 在不同支上时（如图2所示）.+=∆∆ODFOEF S S S △ODE =.21)(212121x x OD x x OD -⋅=+⋅综上得S △OEF ＝,2121x x OD -⋅于是由｜OD ｜＝2及③式，得S △OEF =.132222kk --若△OEF 面积不小于2则有即,22,2≥∆OEF S[1k k ∈≠±且22210(4)46(1)0k k k ⎧-≠⎪⎨∆=-+⨯->⎪⎩1k k ≠±⎧⎪⎨<⎪⎩(1k k ∈≠±∴且.22,022*******2≤≤-≤-⇔≥--k k k k k 解得 ④综合②、④知，直线l 的斜率的取值范围为5, （Ⅰ）①当时，，化简得,解得，或，又，故.②当时，，化简得, 解得，又,故.综合得,或；故知枯水期为1月，2月，3月，11月，12月共5个月. (Ⅱ)(Ⅰ)知：V(t)的最大值只能在（4，10）内达到.由V ′（t ）=),8)(2(41)42341(41241-+-=++-t t c t t c tt令V ′(t)=0,解得t=8(t=-2舍去).当t 变化时，V ′(t) 与V (t)的变化情况如下表：由上表，V(t)在t ＝8时取得最大值V(8)＝8e 2+50-108.52(亿立方米). 故知一年内该水库的最大蓄水量是108.32亿立方米 6, （Ⅰ）证明：假设存在一个实数λ，使｛a n ｝是等比数列，则有a 22=a 1a 3,即,094949494)494()332(222=⇔-=+-⇔-=-λλλλλλλ矛盾.所以｛a n ｝不是等比数列.(Ⅱ)解：因为b n+1=(-1)n+1［a n+1-3(n-1)+21］=(-1)n+1(32a n-2n+14)[1k k ∈≠±且010t <≤124()(1440)5050x V t t t e =-+-+<214400t t -+>4t <10t >010t <≤04t <<1012t <≤()4(10)(341)5050V t t t =--+<(10)(341)0t t --<41103t <<1012t <≤1012t <≤04t <<1012t <≤=32(-1)n ·（a n -3n+21）=-32b n又b 1x-(λ+18),所以当λ＝－18，b n =0(n ∈N +),此时｛b n ｝不是等比数列： 当λ≠－18时，b 1=(λ+18) ≠0,由上可知b n ≠0，∴321-=+n a b b (n ∈N +).故当λ≠-18时，数列｛b n ｝是以－（λ＋18）为首项，－32为公比的等比数列.(Ⅲ)由（Ⅱ）知，当λ=-18,b n =0,S n =0,不满足题目要求.∴λ≠-18，故知b n = -（λ+18）·（－32）n-1，于是可得 S n =-要使a<S n <b 对任意正整数n 成立，即a<-53(λ+18)·［1－（－32）n ］〈b(n ∈N +)①当n 为正奇数时，1<f(n),1)(95;35<≤≤n f n 为正偶数时，当 ∴f(n)的最大值为f(1)=35,f(n)的最小值为f(2)= 95, 于是，由①式得95a<-53(λ+18),<.1831853--<<--⇔a b b λ当a<b ≤3a 时，由－b-18≥=-3a-18，不存在实数满足题目要求；当b>3a 存在实数λ，使得对任意正整数n,都有a<S n <b,且λ的取值范围是（－b-18,-3a-18）7, 解：设，由复数相等8, 解：由余弦定理，原式.321·)18(53⎥⎦⎤⎢⎣⎡+n ）－（－ λ1,z x yi =+21z bi =-+1()()()bi x yi i x yi x y y x i -+=+--=-+-()1b y x x y ⇒=-=--=163699361616936612222+-+-+-=++=9, 解：由题意知所以 ，所以解集为。
2008年普通高等学校招生全国统一考试（全国卷2数学）理科数学(必修+选修Ⅱ)第Ⅰ卷一、选择题1．设集合{|32}M m m =∈-<<Z ，{|13}N n n M N =∈-=Z 则，≤≤（ ） A ．{}01，B ．{}101-，，C ．{}012，，D ．{}1012-，，，2．设a b ∈R ，且0b ≠，若复数3()a bi +是实数，则（ ） A ．223b a = B ．223a b =C ．229b a =D ．229a b =3．函数1()f x x x=-的图像关于（ ） A ．y 轴对称 B ． 直线x y -=对称 C ． 坐标原点对称 D ． 直线x y =对称4．若13(1)ln 2ln ln x e a x b x c x -∈===，，，，，则（ ） A ．a <b <cB ．c <a <bC ． b <a <cD ． b <c <a5．设变量x y ，满足约束条件：222y x x y x ⎧⎪+⎨⎪-⎩，，．≥≤≥，则y x z 3-=的最小值（ ）A ．2-B ．4-C ．6-D ．8-6．从20名男同学，10名女同学中任选3名参加体能测试，则选到的3名同学中既有男同学又有女同学的概率为（ ） A ．929B ．1029C ．1929D ．20297．64(1(1的展开式中x 的系数是（ ） A ．4-B ．3-C ．3D ．48．若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ，两点，则MN 的最大值为（ ） A ．1BCD ．29．设1a >，则双曲线22221(1)x y a a -=+的离心率e 的取值范围是（ ）A．B．C ．(25)，D．(210．已知正四棱锥S ABCD -的侧棱长与底面边长都相等，E 是SB 的中点，则AE SD ，所成的角的余弦值为（ ）A ．13B ．3C ．3D ．2311．等腰三角形两腰所在直线的方程分别为20x y +-=与740x y --=，原点在等腰三角形的底边上，则底边所在直线的斜率为（ ） A ．3B ．2C ．13-D ．12-12．已知球的半径为2，相互垂直的两个平面分别截球面得两个圆．若两圆的公共弦长为2，则两圆的圆心距等于（ ） A ．1B ．2C ．3D ．2第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分．把答案填在题中横线上．13．设向量(12)(23)==，，，a b ，若向量λ+a b 与向量(47)=--，c 共线，则=λ ．14．设曲线ax y e =在点(01)，处的切线与直线210x y ++=垂直，则a = ．15．已知F 是抛物线24C y x =：的焦点，过F 且斜率为1的直线交C 于A B ，两点．设FA FB >，则FA 与FB 的比值等于 ．16．平面内的一个四边形为平行四边形的充要条件有多个，如两组对边分别平行，类似地，写出空间中的一个四棱柱为平行六面体的两个充要条件：充要条件① ； 充要条件② ． （写出你认为正确的两个充要条件）三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分10分） 在ABC △中，5cos 13B =-，4cos 5C =．（Ⅰ）求sin A 的值；（Ⅱ）设ABC △的面积332ABC S =△，求BC 的长． 18．（本小题满分12分）购买某种保险，每个投保人每年度向保险公司交纳保费a 元，若投保人在购买保险的一年度内出险，则可以获得10 000元的赔偿金．假定在一年度内有10 000人购买了这种保险，且各投保人是否出险相互独立．已知保险公司在一年度内至少支付赔偿金10 000元的概率为41010.999-．（Ⅰ）求一投保人在一年度内出险的概率p ；（Ⅱ）设保险公司开办该项险种业务除赔偿金外的成本为50 000元，为保证盈利的期望不小于0，求每位投保人应交纳的最低保费（单位：元）． 19．（本小题满分12分）如图，正四棱柱1111ABCD A BC D -中，124AA AB ==，点E 在1CC 上且EC E C 31=． （Ⅰ）证明：1AC ⊥平面BED ； （Ⅱ）求二面角1A DE B --的大小．20．（本小题满分12分）设数列{}n a 的前n 项和为n S ．已知1a a =，13n n n a S +=+，*n ∈N ．（Ⅰ）设3n n n b S =-，求数列{}n b 的通项公式； （Ⅱ）若1n n a a +≥，*n ∈N ，求a 的取值范围．21．（本小题满分12分）设椭圆中心在坐标原点，(20)(01)A B ，，，是它的两个顶点，直线)0(>=k kx y 与AB 相交于点D ，与椭圆相交于E 、F 两点．（Ⅰ）若6ED DF =，求k 的值；（Ⅱ）求四边形AEBF 面积的最大值． 22．（本小题满分12分） 设函数sin ()2cos xf x x=+．（Ⅰ）求()f x 的单调区间；（Ⅱ）如果对任何0x ≥，都有()f x ax ≤，求a 的取值范围．AB CD EA 1B 1C 1D 12008年参考答案和评分参考一、选择题1．B 2．A 3．C 4．C 5．D 6．D 7．B 8．B 9．B 10．C 11．A 12．C部分题解析：2. 设a b ∈R ，且0b ≠，若复数3()a bi +是实数，则（ ）A ．223b a =B ．223a b =C ．229b a =D ．229a b =，解：33223()33()()a bi a a bi a bi bi +=+++ （←考查和的立方公式，或二项式定理）3223(3)(3)a a b a b b i =-+- （←考查虚数单位i 的运算性质）R ∈ （←题设条件） ∵a b ∈R ，且0b ≠∴ 2330a b b -=（←考查复数与实数的概念） ∴ 223b a =. 故选A.6. 从20名男同学，10名女同学中任选3名参加体能测试，则选到的3名同学中既有男同学又有女同学的概率为（ ） A ．929B ．1029C ．1929D ．2029思路1：设事件A ：“选到的3名同学中既有男同学又有女同学”，其概率为：211220102010330()C C C C P A C += （←考查组合应用及概率计算公式） 201910910202121302928321⨯⨯⨯+⨯⨯⨯=⨯⨯⨯⨯ （←考查组合数公式） 10191010109102914⨯⨯+⨯⨯=⨯⨯ （←考查运算技能）2029=故选D.思路2：设事件A ：“选到的3名同学中既有男同学又有女同学”，事件A 的对立事件为A ：“选到的3名同学中要么全男同学要么全女同学”其概率为：()1()P A P A =- （←考查对立事件概率计算公式）3320103301C C C +=- （←考查组合应用及概率计算公式）2019810983213211302928321⨯⨯⨯⨯+⨯⨯⨯⨯=-⨯⨯⨯⨯（←考查组合数公式） 2019181098302928⨯⨯+⨯⨯=⨯⨯ （←考查运算技能）2029=故选D.12.已知球的半径为2，相互垂直的两个平面分别截球面得两个圆．若两圆的公共弦长为2，则两圆的圆心距等于（ ） A ．1B ．2C ．3D ．2分析：如果把公共弦长为2的相互垂直的两个截球面圆，想成一般情况，问题解决起来就比较麻烦，许多考生就是因为这样思考的，所以浪费了很多时间才得道答案；但是，如果把公共弦长为2的相互垂直的两个截球面圆，想成其中一个恰好是大圆，那么两圆的圆心距就是球心到另一个小圆的距离3，问题解决起来就很容易了. 二、填空题13．2 14．2 5．3+16．两组相对侧面分别平行；一组相对侧面平行且全等；对角线交于一点；底面是平行四边形． 注：上面给出了四个充要条件．如果考生写出其他正确答案，同样给分． 三、解答题 17．解：（Ⅰ）由5cos 13B =-，得12sin 13B =， 由4cos 5C =，得3sin 5C =．所以33sin sin()sin cos cos sin 65A B C B C B C =+=+=． ··············································· 5分 （Ⅱ）由332ABC S =△得133sin 22AB AC A ⨯⨯⨯=， 由（Ⅰ）知33sin 65A =，故65AB AC ⨯=， ················································································································ 8分又sin 20sin 13AB B AC AB C ⨯==， 故2206513AB =，132AB =． 所以sin 11sin 2AB A BC C ⨯==． ····························································································· 10分18．解：各投保人是否出险互相独立，且出险的概率都是p ，记投保的10 000人中出险的人数为ξ，则4~(10)B p ξ，．（Ⅰ）记A 表示事件：保险公司为该险种至少支付10 000元赔偿金，则A 发生当且仅当0ξ=， ················································································································································· 2分()1()P A P A =-1(0)P ξ=-=4101(1)p =--，又410()10.999P A =-，故0.001p =． ······················································································································· 5分 （Ⅱ）该险种总收入为10000a 元，支出是赔偿金总额与成本的和． 支出 1000050000ξ+，盈利 10000(1000050000)a ηξ=-+，盈利的期望为 1000010000500E a E ηξ=--，······················································ 9分由43~(1010)B ξ-，知，31000010E ξ-=⨯，4441010510E a E ηξ=--⨯4443410101010510a -=-⨯⨯-⨯．0E η≥4441010105100a ⇔-⨯-⨯≥1050a ⇔--≥ 15a ⇔≥（元）．故每位投保人应交纳的最低保费为15元． ········································································ 12分19．解法一：依题设知2AB =，1CE =．（Ⅰ）连结AC 交BD 于点F ，则BD AC ⊥． 由三垂线定理知，1BD AC ⊥．···························································································· 3分 在平面1ACA 内，连结EF 交1AC 于点G ， 由于1AA ACFC CE== AB CD E A 1 B 1 C 1 D 1FH G故1Rt Rt A AC FCE △∽△，1AAC CFE ∠=∠， CFE ∠与1FCA ∠互余．于是1AC EF ⊥． 1AC 与平面BED 内两条相交直线BD EF ，都垂直， 所以1AC ⊥平面BED ． ······································································································· 6分 （Ⅱ）作GH DE ⊥，垂足为H ，连结1A H ．由三垂线定理知1A H DE ⊥，故1A HG ∠是二面角1A DE B --的平面角． ······································································ 8分EF =CE CF CG EF ⨯==3EG ==． 13EG EF =，13EF FD GH DE ⨯=⨯=又1AC ==11AG AC CG =-=．11tan A GA HG HG∠== 所以二面角1A DE B --的大小为 ······························································· 12分 解法二：以D 为坐标原点，射线DA 为x 轴的正半轴， 建立如图所示直角坐标系D xyz -．依题设，1(220)(020)(021)(204)B C E A ，，，，，，，，，，，．(021)(220)DE DB == ，，，，，，11(224)(204)AC DA =--=，，，，，． ······················································································· 3分 （Ⅰ）因为10AC DB = ，10AC DE =， 故1AC BD ⊥，1AC DE ⊥． 又DB DE D = ，所以1AC ⊥平面DBE ． ········································································································ 6分 （Ⅱ）设向量()x y z =，，n 是平面1DA E 的法向量，则DE ⊥n ，1DA ⊥ n ．故20y z +=，240x z +=．令1y =，则2z =-，4x =，(412)=-，，n ． ··································································· 9分 1AC ，n 等于二面角1A DE B --的平面角，111cos 42AC AC AC ==，n n n ． 所以二面角1A DE B --的大小为arccos 42． ······························································ 12分 20．解：（Ⅰ）依题意，113n n n n n S S a S ++-==+，即123n n n S S +=+，由此得1132(3)n n n n S S ++-=-． ·························································································· 4分 因此，所求通项公式为13(3)2n n n n b S a -=-=-，*n ∈N ．① ·············································································· 6分 （Ⅱ）由①知13(3)2n n n S a -=+-，*n ∈N ， 于是，当2n ≥时，1n n n a S S -=-1123(3)23(3)2n n n n a a ---=+-⨯---⨯ 1223(3)2n n a --=⨯+-，12143(3)2n n n n a a a --+-=⨯+-22321232n n a --⎡⎤⎛⎫=+-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦，当2n ≥时，21312302n n n a a a -+⎛⎫⇔+- ⎪⎝⎭≥≥9a ⇔-≥．又2113a a a =+>．综上，所求的a 的取值范围是[)9-+∞，． ········································································· 12分 21．（Ⅰ）解：依题设得椭圆的方程为2214x y +=， 直线AB EF ，的方程分别为22x y +=，(0)y kx k =>． ··············································· 2分 如图，设001122()()()D x kx E x kx F x kx ，，，，，，其中12x x <， 且12x x ，满足方程22(14)4k x +=，故21x x =-=．①由6ED DF = 知01206()x x x x -=-，得021215(6)77x x x x =+==；由D 在AB 上知0022x kx +=，得0212x k=+． 所以212k =+ 化简得2242560k k -+=，解得23k =或38k =． ············································································································ 6分 （Ⅱ）解法一：根据点到直线的距离公式和①式知，点E F ，到AB 的距离分别为1h ==2h ==····································································· 9分又AB ==AEBF 的面积为121()2S AB h h =+ 12===≤当21k =，即当12k =时，上式取等号．所以S 的最大值为 ······························· 12分 解法二：由题设，1BO =，2AO =．设11y kx =，22y kx =，由①得20x >，210y y =->， 故四边形AEBF 的面积为BEF AEF S S S =+△△222x y =+ ······························································································································ 9分===当222x y =时，上式取等号．所以S 的最大值为·················································· 12分 22．解： （Ⅰ）22(2cos )cos sin (sin )2cos 1()(2cos )(2cos )x x x x x f x x x +--+'==++． ····································· 2分当2π2π2π2π33k x k -<<+（k ∈Z ）时，1cos 2x >-，即()0f x '>； 当2π4π2π2π33k x k +<<+（k ∈Z ）时，1cos 2x <-，即()0f x '<． 因此()f x 在每一个区间2π2π2π2π33k k ⎛⎫-+ ⎪⎝⎭，（k ∈Z ）是增函数， ()f x 在每一个区间2π4π2π2π33k k ⎛⎫++ ⎪⎝⎭，（k ∈Z ）是减函数． ···································· 6分 （Ⅱ）令()()g x ax f x =-，则第11页（共11页） 22cos 1()(2cos )x g x a x +'=-+ 2232cos (2cos )a x x =-+++ 211132cos 33a x ⎛⎫=-+- ⎪+⎝⎭． 故当13a ≥时，()0g x '≥． 又(0)0g =，所以当0x ≥时，()(0)0g x g =≥，即()f x ax ≤． ······························ 9分 当103a <<时，令()sin 3h x x ax =-，则()cos 3h x x a '=-． 故当[)0arccos3x a ∈，时，()0h x '>．因此()h x 在[)0arccos3a ，上单调增加．故当(0arccos3)x a ∈，时，()(0)0h x h >=， 即sin 3x ax >．于是，当(0arccos3)x a ∈，时，sin sin ()2cos 3x x f x ax x =>>+． 当0a ≤时，有π1π0222f a ⎛⎫=> ⎪⎝⎭≥． 因此，a 的取值范围是13⎡⎫+∞⎪⎢⎣⎭，． ····················································································· 12分。
机密*启用前2008年天津市高等院校“高职升本科”招生统一考试英语本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)两部分。
第1卷1至8页，第Ⅱ卷9至10页。
共150分。
考试时间120分钟。
第I卷(选择题共95分)注意事项：1．答第1卷前，考生务必将自己的姓名、准考号、考试科目涂写在答题卡上，并将本人考试用条形码贴在答题卡的贴条形码处。
2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其他答案标号，答在试卷上的无效。
3．考试结束，监考入将本试卷和答题卡一并收回。
Part I. Grammar and Vocabulary (15 points)Directions:There are 15 sentences, each with a blank. Under each sentence, there are four choices marked A, B, C and D. Read the sentences and the choices carefully and then choose the one that best completes the sentence.1. When I leave the research institute next week, I ______ there for 17 years.A. shall be workingB. shall have workedC. will workD. have worked2. We're going to the bookstore in Jim's car. You can come with us ______ you can meet us there later.A. butB. andC. thenD. or3. ---You know Mr. Green has been iii for days?---Yes, I wonder if he is ______ better now.A. someB. muchC. noD. many4. In Britain people ______ four million tons of potatoes every year.A. swallowB. disposeC. consumeD. exhaust5. Does ______ surprise you to know that the wonderful invention was made by atwelve-year-old schoolboy?A. heB. thatC. thisD. it6. ---I'm taking my driving test tomorrow.--- ______ !A. Good luckB. CheersC. Come onD. Congratulations7. At first I was worried about the employment prospect. Four years of study later, I’verealized I ______.A. didn't need to worry'B. mustn't have worriedC. needn't have worriedD. couldn't have worried8. ______ his great achievements in chemistry, he was considered as one of the mostoutstanding scientists of the century.A. In terms ofB. On behalf ofC. On the basis ofD. in the form of9. I could hardly ______ the ship in the distance.A. look outB. make outC. make upD. see through10. I was not ______ by his many arguments, so finally we agreed to differ.A. convictedB. confirmedC. concernedD. convinced11. Human beings are superior to animals______ they can use language as a tool tocommunicate.A. in whichB. for whichC. in thatD. for that12. He is well ______ with the literature of America.A. acquaintedB. informedC. enlightenedD. acknowledged13. John did quite well in his exams, ______ how little he studied.A. considerB. consideredC. consideringD. to consider14. The manager spoke highly of such ______ as loyalty, courage and truthfulness shown byhis employees.A. virtuesB. featuresC. propertiesD. characteristics15. The police are always ready to give a hand to ______ needs help.A. whoB. whomC. whomeverD. whoeverPart II. Cloze Test (30 points)Directions: There are 20 blanks in the following passage. For each blank there are four choices marked A, B, C and D. Read the passage' carefully and choose the one that fits right into the passage.The United States is well-known for its network of major highways designed to help a driver get from one place to another in the shortest possible time. 16 these wide modem roads are generally 17 and well maintained, with 18 sharp curves (转弯) and many straight 19 , a direct route is not always the most 20 one. Large highways often pass 21 scenic areas and interesting small towns. Furthermore, these highways generally 22__ large urban centers, which means that they become crowded with 23 traffic during rush hours, 24 the 'fast, direct' way becomes a very slow route.However, there is 25 always another route to take 26 you are not in a hurry. Not far from the 27 new 'superhighways', there are often older, 28 heavily traveled roads which go through the countryside. 29 of these are good two-lane roads; others are uneven roads 30 through the country. These secondary routes may go up steep slopes, along high 31 , or down frightening hillsides to towns 32 ill deep valleys. Through these less direct routes, longer and slower, they generally go to places 33 the air is cleanand the scenery, is beautiful, and the driver may have a 34 to get a flesh 35 of the world.16. A. Although B. Since C. Because D. Therefore17. A. stable B. splendid C. smooth D. complicated18. A. little B. few C. much D. many19. A. selections B. separations C. series D. sections20. A. terrible B. possible C. enjoyable D. profitable21. A. to B. into C. over D. by22. A. lead B. connect C. collect D. communicate23. A. large B. fast C. high D. heavy24. A. when B. for C. but D. that25. A. yet B. still C. almost D. quite26. A. unless B. if C. as D. since27. A. relatively B. regularly C. respectively D. reasonably28. A. and B. less C. more D. or29. A. All B. Several C. Lots D. Some30. A. driving B. crossing C. curving D. traveling31. A. rocks B. cliffs C. roads D. paths32. A. lying B. laying C. laid D. lied33. A. there B. when C. which D. where34. A. space B. period C. chance D. spot35. A. view B. variety C. visit D. videoPart III. Reading Comprehension ( 50 points )Directions:There are four passages in this part. Each passage is followed by a number of questions for comprehension. For each of them there are four choices marked A, B, C and D. Choose the one that fits best according to the information given in the passage you have just read.Passage OneMost people do not think of fishes and other marine animals as having voices, and of those who are aware of the fact that many of them can "speak", few understand that these "conversations" have significance. Actually, their talk may be as meaningful as much of our own. For example, some sea animals use their "voices" to locate their food in the ocean expanses; others, to let their fellows know of their whereabouts; and still others, as a means of obtaining mates. Sometimes, "speaking" may even mean the difference between life and death to a marine animal. It appears in some cases that when a predator (食肉动物) approaches, the prey depends on no more than the sounds it makes to escape.Fish sounds are important to man, also. By listening to them he can learn a great dealabout the habits of the creatures that make them, the size of the schools they form, the patterns of their migrations, and the nature of the environments in which they live. He can also apply this information to the more effective utilization of the listening posts he has set up to detect enemy submarines (潜水艇) . A knowledge of fish sounds can avoid confusion and unneeded effort when a "new" sound is picked up and the sound sentry (岗哨) must decide whether or not to call an alert.36. Among the people who know that many sea animals have voices, few______.A. could understand their conversationsB. realize that they can make speechesC. could understand the significance of their conversationsD. realize that they can communicate37. By listening to sounds fishes make, man can learn all the following except_______.A. their habitsB. their environmentsC. their sizesD. the usual pattern of their migrations38. In some cases, when a predator approaches, fishes depend on ______.A. the sounds of their fellows to escapeB. the sounds of the approaching enemy to escapeC. none of the sounds it makes to escapeD. their prey to escape39. The last sentence means that a knowledge of fish sounds can help man to______.A. detect enemy submarinesB. pick up new soundsC. avoid confusion in fishing activitiesD. avoid unneeded effort in fish sound studies40. Which of the following statements can be inferred from the passage?A. Fish sounds cannot be transmitted through air.B. Hearing in fishes is more acute than in people.C. Fishes only "speak" to communicate with each other.D. Researchers are engaged in studying the significance of fish sounds.Passage TwoWhen Louis Braille was three years old, he became blind in both eyes as the result of an accident in his father's harness shop. His father, determined that Louis should not suffer the usual fate of blind persons at that time and become a beggar, kept him in the village school until he was ten and then entered him in the institution des Jeunes Aveugles in Paris. Louis learned to read from the three books engraved in large raised letters in the Institution library. He did exceptionally well both in academic work and at the piano and the organ, and was soon helping to teach the younger children.In 1819, the same year that Louis entered the Institution, Charles Barbier, an army captain, reported to the Academy of Sciences on a system of raised dots and dashes which enabled soldiers to read messages in the dark. Later, Barbier brought his invention to the Institution. After experimenting with it, young Braille produced a writing system using only dots, from which he gradually devised 63 separate combinations representing the letters in the French alphabet. At the request of an Englishman, he later added the letter "w", accents and punctuation marks, and mathematical signs. Although government bureaucracy prevented immediate official adoption, his system was used at the Institution as long as the director, Dr. Pignier, was in office. Pignier's successor insisted on returning to the officially approved former system, but students continued to use Braille's method secretly. Eventually, its superiority was established and it was adopted throughout France.41. Louis-Braille first learned to read with the aid of _______.A. his fatherB. special books at the InstitutionC. the village school teacherD. Captain Barbier's system of dots and dashes42. Louis's father kept him at the village school until he was ten because his father______.A. wanted Louis to help him in the harness shopB. thought it was not worthwhile to have Louis work when he was youngC. did not want Louis to live the same sort of life as that of other blind peopleD. wanted Louis to remain with the family as long as possible43. Louis Braille did all of the following things EXCEPT______.A. teaching young children at the InstitutionB. developing a writing system for the blindC. learning to play musical instruments wellD. encouraging students to use his method secretly44. Charles Barbier originally devised his writing system for______.A. the Academy of SciencesB. blind childrenC. military personnelD. the English government45. Braille's method was not adopted officially for some time because______.A. the students preferred the former methodB. the large library collection would then have been uselessC. Dr. Pignier's successor disliked Braille's methodD. the government was slow to approve itPassage ThreeOne hundred and thirteen million Americans have at least one bank-issued credit card.They give their owners automatic credit in stores, restaurants, and hotels, at home, across the country, and even abroad, and they make many banking services available as well. More and more of these credit cards can be read automatically, making it possible to withdraw or deposit money in scattered locations, whether or not the local branch bank is open. For many of us the "cashless society" is not on the horizon --- it's already here.While computers offer these conveniences to consumers, they have many advantages for sellers too. Electronic cash registers can do much more than simply ring up sales. They can keep a wide range of records, including who sold what, when, and to whom. This information allows businessmen to keep track of their list of goods by showing which items are being sold and how fast they are moving. Decisions to reorder or return goods to suppliers can then be made. At the same time these computers record which hours are busiest and which employees are the most efficient, allowing personnel and staffing assignments to be made accordingly. And they also identify preferred customers for promotional campaigns. Computers are relied on by manufacturers for similar reasons. Computer-analyzed marketing reports can help to decide which products to emphasize now, which to develop for the future, and which to drop. Computers keep track of goods in stock, of raw materials on hand, and even of the production process itself.Numerous other commercial enterprises, from theaters to magazine publishers, from gas and electric utilities to milk processors, bring better and more efficient services to consumers through the use of computers.46. According to the passage, the credit card enables its owner to______.A. obtain more convenient services than other people doB. exchange foreign currency wherever he wishes toC. enjoy greater trust from the storekeeperD. withdraw as much money from the bank as he wishes to47. From the last sentence of the first paragraph we learn that_______.A. many Americans do not like using credit cards todayB. nowadays many Americans do not pay in cashC. in the future all the Americans will use credit cardsD. it is now more convenient to use credit cards than before48.The underlined phrase "ring up sales" in Paragraph 2 most probably means______.A. record sales on a cash registerB. keep track of the goods in stockC. make an order of goodsD. call the sales manager49.The underlined word "identify" in Paragraph 2 most probably means______.A. observeB. pick outC. associate withD. spot50. What is this passage mainly about?A. Advantages of credit cards in business.B. Significance of automation in commercial enterprises.C. Conveniences brought about by computers in business.D. Approaches to the commercial use of computers.Passage FourToo often young people get themselves employed quite by accident, not knowing what lies in the way of opportunity for promotion, happiness and security. As a result, they are employed doing jobs that afford them little or no satisfaction. Our school leavers face so much competition that they seldom care what they do as long as they can earn a living. Some stay long at a job and learn to like it; others quit from one to another looking for something to suit them. The young graduates who leave the university look for jobs that offer a salary up to their expectations.Very few go out into the world knowing exactly what they want and realizing their own abilities. The reason behind all this confusion is that there never has been a proper vocational guidance in our educational institution. Nearly all grope (摸索) in the dark and their chief concern when they look for a job is to ask what salary is like. They never bother to think whether they are suited for the job or, even more important, whether the job suits them. Having a job is more than merely providing yourself and your dependants with daily bread and some money for leisure and entertainment. It sets a pattern of life and, in many ways, determines social status in life, selection of friends, leisure and interest.In choosing a career you should first consider the type of work which will suit your interest. Nothing is more pathetic than taking on a job in which you have no interest, for it will not only discourage your desire to succeed in life but also ruin your talents and ultimately make you an emotional wreck (受到严重伤害的人) and a bitter person.51. The reason why some people are unlikely to succeed in life is that______.A. they have too high expectationsB. they have ruined their talentsC. they have taken on an unsuitable jobD. they change their jobs frequently52. The difficulty in choosing a suitable job lies mainly in that______.A. schools fail to offer students appropriate vocational guidanceB. many employees have no working experienceC. young people only care about how much they can earnD. much competition has to be faced53. Which of the following statements is most important according to the passage?A. Your job must set a pattern of life.cehuaB. Your job must suit your interest.C. Your job must not ruin your talents.D. Your job must offer you a high salary.54.The underlined word "pathetic" in Paragraph 3 most probably means______.A. miserableB. disgustingC. wonderfulD. touching55. The best title for this passage would be______.A. How to Choose a JobB. What Can a Good Job OfferC. Earning a LivingD. Correct Attitude to Job-hunting机密*启用前2008年天津市高等院校“高职升本科”招生统一考试英语 第Ⅱ卷(非选择题共55分)注意事项：1．答第Ⅱ卷前，考生须将密封线内的项目填写清楚。
