第十二届全国华罗庚金杯少年数学邀请赛决赛试卷初一组答案及详细解析

1第十二届全国“华罗庚金杯”少年数学邀请赛第十二届全国“华罗庚金杯”少年数学邀请赛初赛试卷（初一组）（时间：2007年3月24日 10∶00～11∶00）一、选择题（每小题10分）以下每小题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题的圆括号内．1． 算式 321(1)21(1)2(1)1-⨯----+⨯-+等于（ ）．(A) 2- (B) 1- (C) 1 (D) 22． 新制作的渗水防滑地板是形状相同的长方形．如图1，三块这样的地板可以拼成一个大的长方形．如果大长方形的周长为150厘米，则一块渗水妨滑地板的面积是（ ）平方厘米． (A) 450 (B) 600 (C) 900 (D) 1 350 3． 如果一个多项式的各项的次数都相同，则称该多项式为齐次多项式．例如：32322x xy xyz y +++是3次齐次多项式．若22323m xy xy z ++是齐次多项式，则m 等于（）．(A) 1(B) 2(C) 3(D) 44． 若x y y x +=-，则有（ ）． (A) y ＞0，x ＜0(B) y ＜0，x ＞0(C) y ＜0，x ＜0(D) x =0，y ≥0或y =0，x ≤05． 设a b ＞0，cd＞0．有如下四个结论： (1) 如果 ad ＞bc ，则必定有 a b ＞c d ．(2) 如果 ad ＞bc ，则必定有 a b ＜cd． (3) 如果 ad ＜bc ，则必定有a b ＜c d ．(4) 如果 ad ＜bc ，则必定有 a b ＞c d． 其中正确结论的个数是（ ）． (A) 0 (B) 1 (C) 2(D) 3图1第十二届全国“华罗庚金杯”少年数学邀请赛6． 已知a 是整数，则以下四个代数式中，不可能得整数值的是（ ）．(A)325a + (B)23a- (C)316a + (D)527a -二、填空题（每小题10分）7． 如图2，空心圆柱底面圆环的外径和内径之比为2∶1，若保持内径不变，外径扩大成内径的3倍，则扩大后的空心圆柱的体积是原来的体积的 倍．8． 图3是某车间的1至12月的产量图表，记月份为n ，1至5月份的产量为20an +，6至12月份的产量为2bn -，则ab 等于 ．9． 相同的正方块码放在桌面上，从正面看，如图4；从侧面看，如图5．则正方块最多有 个，最少有 个．10．甲种签字笔每支3.5元，乙种签字笔每支2.65元．班上的同学每人出了相同的钱凑在一起买了两种签字笔若干支，将这些笔分给同学们，每人3支多2支，每人4支少13支．该班里有 名同学，每人至少要出 元钱．三、解答题（30分钟完成）11、（15分）若记号“*”表示球两个有理数的平均数的运算，即*2a ba b += （1）对于任意三个有理数a 、b 、c ， 等式(*)(*)(*)()*(222)222a b ca ab bc c a b c ++=++++是否成立？ （2）试写出一个两边都含有运算符号“*”和“+”且对于任意四个有理数a 、b 、c 、d 都成立的等式。

2007年第十二届“华罗庚金杯”少年数学邀请赛初赛一、选择题1、算式10.2530.53120.751342+⨯+⨯-+等于（ ）。

（A ）3 （B ）2 （C ）1 （D ）0解答：原式=5351422393342+=+= 选B2、折叠一批纸鹤，甲同学单独折需要半小时，乙同学单独折需要45分钟。

甲、乙两同学共同折叠需要（ ）。

（A ）12分钟 （B ）15分钟 （C ）18分钟 （D ）20分钟 解答：111304518+= 1÷118=18分钟 需要18分钟 选C3、如图，将四条长为16厘米，宽为2厘米的长方形纸条垂直相交平放在桌面上，则桌面被盖住的面积是（ ）。

（A ）72cm 2 （B ）128cm 2 （C ）124cm 2 （D ）112cm 2 解答：16×2×4=128平方厘米 2×2×4=16平方厘米128-16=112平方厘米 盖住的面积是112平方厘米 选D4、地球表面的陆地面积和海洋面积之比是29:71，其中陆地的四分之三在北半球。

那么南、北半球海洋面积之比是（）。

（A）284：29 （B）284：87 （C）87：29 （D）171：113解答：陆地面积占29100北半球陆地占293871004400⨯=北半球海洋占12-87400=113400南半球海洋占71113171100400400-=171113:400400=171:113 南、北半球海洋面积之比是171:113 选D5、一个长方体的长、宽、高恰好是3个连续的自然数，并且它的体积的数值等于它的所有的棱长之和的数值的2倍，那么这个长方体的表面积是（）。

（A）74 （B）148 （C）150 （D）154解答：设宽为n，则长为n+1，高为n-1（n+n+1+n-1）×4×2=24n 24=4×6 所以n=5（5×4+5×6+6×4）×2=148 表面积为148 选B6、从和为55的10个不同的非零的自然数中，取出3个数后，余下的数之和是55的711，则取出的三个数的积最大等于（）。

第十二届全国“华罗庚金杯”少年数学邀请赛决赛试卷（初一组）一、填空（每题10分，共80分） 1、计算：=⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛--⨯-3553134217685.17130998-解析：3576306113999820171315130130⎛⎫⎛⎫⎛⎫-⨯--⨯-=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2、“b 的相反数与a 的差的一半的平方”的代数表达式为 。

解析：2222⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛--a b a b 或3、规定符号“⊕”为选择两数中较大者，规定符号“⊙”为选择两数中较小者，例如：3⊕5=5，3⊙5=3，则解析：400.726001271211211367⨯==+ 已知 5-=-n m ，1322=+n m ，那么 44n m += 97 。

解析：4、22224422222()(5)6,()(6)()()2=m n m n m n m n m n m n -=-→⨯=-⨯=-+=+-代入数据，原式975、用一些棱长是1的小正方体码放成一个立体，从上向下看这个立体，如图1，从正面看这个立体，如图2，则这个立体的表面积最多是 48 。

图1（从上向下看） 图2（从正面看）解析：从两个视图可知，该立体的排布最多如图所示，则表面积最多为48 6、满足不等式|13|22|1|3+>--n n n 的整数n 的个数是 5 。

解析：n-1=0 则n=1， 3n+1=0 则n=-1/3当n-1>=0时，n>=1， 3(n-1)-2n>2(3n+1)，5n<-5 ，n<-1, 则n 无解当-1/3<n<1时，3(1-n)-2n>2(3n+1)，3-5n>6n+2，n<1/11 ,则-1/3<n<1/11…（1） 当n<=-1/3时,3(1-n)-2n>2(-3n-1),n>-5,则-5<n<=-1/3…（2） 由（1）、（2）得:-5<n<1/11,则整数n 的个数是: n=-4.-3.-2.-1.0共5个7、某年级原有学生280人，被分为人数相同的若干个班。

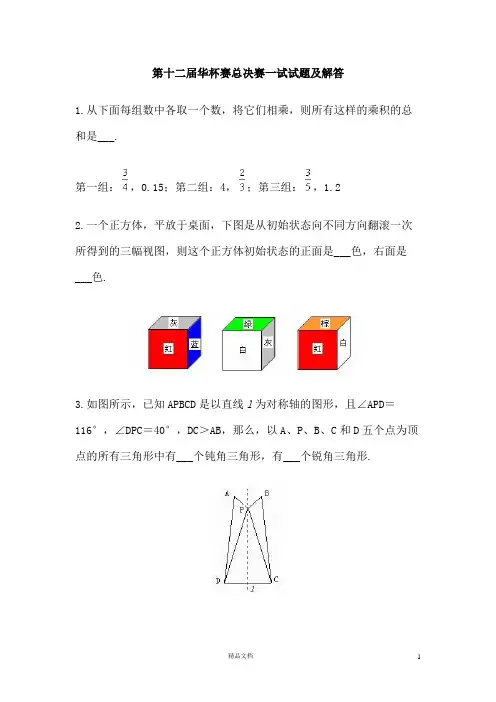
第十二届华杯赛总决赛一试试题及解答1.从下面每组数中各取一个数，将它们相乘，则所有这样的乘积的总和是___.第一组：，0.15；第二组：4，；第三组：，1.22.一个正方体，平放于桌面，下图是从初始状态向不同方向翻滚一次所得到的三幅视图，则这个正方体初始状态的正面是___色，右面是___色.3.如图所示，已知APBCD是以直线l为对称轴的图形，且∠APD＝116°，∠DPC＝40°，DC＞AB，那么，以A、P、B、C和D五个点为顶点的所有三角形中有___个钝角三角形，有___个锐角三角形.4.A、B、C三项工程的工作量之比为1∶2∶3，由甲、乙、丙三个工程队分别承担，同时开工，若干天后，甲完成的工作量是乙未完成工作量的二分之一，乙完成的工作量是丙未完成工作量的三分之一，丙完成的工作量等于甲未完成的工作量，则甲、乙、丙三个队的工作效率的比是多少？5.将1分、2分、5分和1角的硬币投入19个盒子中，使每个盒子里都有硬币，且任何两个盒子里的硬币的钱数都不相同。

问：至少需要投入多少硬币？这时，所有的盒子里的硬币的总钱数至少是多少？6.下图是一种电脑射击游戏的示意图，线段CD、EF和GH的长度都是20厘米，O、P、Q是它们的中点，并且位于同一条直线AB上，AO＝45厘米，OP＝PQ＝20厘米，已知CD上的小圆环的速度是每秒5厘米，EF 上的小圆环的速度是每秒9厘米，GH上的小圆环的速度是每秒27厘米。

零时刻，CD、EF、GH上各有一个小圆环从左端点同时开始在线段上匀速往返运动。

问：此时，从点A向B发射一颗匀速运动的子弹，要想穿过三个圆环，子弹的速度最大为每秒多少厘米？1.解：设总和为S，则S＝＝（0.75＋0.15）×（）＝0.9×（2.4＋4.8＋0.4＋0.8）＝0.9×8.4＝7.562.解：红面与灰、蓝、棕、白面相邻，故知红面与绿面相对；同理可知白面与蓝面相对，灰面与棕面相对。

第十一届全国“华罗庚金杯〞少年数学邀请赛决赛试题解答〔初一组〕一. 填空1 计算：()()⎥⎦⎤⎢⎣⎡-÷+⎪⎭⎫ ⎝⎛-⨯÷⎭⎬⎫⎩⎨⎧-⨯⎥⎦⎤⎢⎣⎡---342)2(5833225.01631=( ).答：47解：原式(){}235130254388.⎡⎤⎛⎫⎡⎤=---⨯÷⨯-- ⎪⎢⎥⎣⎦⎝⎭⎣⎦()144187⎛⎫=-÷-= ⎪⎝⎭.2 当2m π=时，多项式31am bm ++的值是0，那么多项式31452a b ππ++＝〔 〕.答：5.解：根据 38210a b ππ++=，即()3311458215522a b a b ππππ++=+++=，故原式的值为5.3 将假设干本书籍分给几名小朋友，如果每人分4本书，就还余下20本书，如果每人分8本书，就有1名小朋友虽然分到了一些书，但是缺乏8本, 那么共有〔 〕名小朋友. 答：6.解：设共有x 名小朋友，由题意，04208(1)8x x <+--<，02848x <-<推出75<<x ，得6=x .4 图16中的长方形ABCD 是由四个等腰直角三角形和一个正方形EFGH 拼成. 长方形ABCD 的面积是120平方厘米，那么正方形EFGH 的面积等于〔 〕平方厘米. 答：10.图16解法1：如图16a ，延长BF 交DC 于N 点，延长EH 交BC 于M 点，由条件可知1122CE CM CN CB ===，DA DE CB CN ===，所以 CM=MB ＝CE=EN =ND . 将长方形ABCD 的长边3等分，短边2等分，如图1a 所示，连接对应的等分点，分成网格图形， 数一数，长方形ABCD 恰好等于12个正方形EFGH 的面积，由于长方形ABCD 的面积为120平方厘米，所以正方EFGH 的面积等于10平方厘米.解法 2：设正方形EFGH 的边长为x ，根据题意，图1中的四个三角形为等腰直角三角形，那么三角形EHC 的直角边长为x ，三角形CGB 的直角边长为x 2， 三角形ABF 的直角边长为x 3，三角形ADE 的斜边长为x 4.并且，正方形EFGH 的面积＝2x ，三角形EHC 的面积＝22x ，三角形CGB 的面积＝2222)2(x x =，三角形ABF 的面积＝292)3(22x x =， 三角形ADE 的面积＝2⨯三角形CGB 的面积＝24x .因此120=2222221242922x x x x x x =+++， 故102=x ，即正方形EFGH 的面积等于10平方厘米.5 满足方程2006182006|x |--+=的所有x 的和为〔 〕. 答： 4012.解：根据绝对值的性质，逐步去除等式2006182006|x |--+=绝对值符号，得到2006120068x --=-，2006120068x -=+-，()2006120068x =++-，或()2006120068x =-+-由表达式可以看到，x 有2个不同的解，它们的和是：图2图16a()2006120068++-＋()20061200684012-+-=.6 一个存有一些水的水池，有一个进水口和假设干个口径相同的出水口, 进水口每分钟进水3立方米.假设同时翻开进水口和三个出水口, 池中水16分钟放完; 假设同时翻开进水口与五个出水口, 池中水9分钟放完. 池中原有水〔 〕立方米. 答: 288.解: 设每个出水口每分钟放出水x 立方米, 池中原有水y 立方米， 那么3163165939x yx y⨯⨯=⨯+⎧⎨⨯⨯=⨯+⎩， 解上面二元一次方程组，()4845482721x -=-=，7x =〔立方米〕，316748288y =⨯⨯-=〔立方米〕. 7 20062005122006220052)1(164834221-++-++-+-=+ k k k S ，小于S 的最大的整数是〔 〕. 解答：因为，2005200620052006123420052006248162212342005200602481622S =-+-++-⎛⎫⎛⎫⎛⎫=-+-++-> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2005200620042005200620052006123420052006248162212345200420052006248163222211320032006 1.283222S =-+-++-⎛⎫⎛⎫⎛⎫=-------- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭<-----< 因此小于S 的最大的整数是0.8 如图17，数轴上标有21n +个点，它们对应的整数是:(),1,,2,1,0,1,2,,1,n n n n ------.为了确保从这些点中可以取出2006个，其中任何两个点之间的距离都不等于4，那么n 的最小值是〔 〕.答： 2005.解：① 将数轴上的21n +个点，自左端开始，连续8个点为一组，每组仅取右边4个点，这样就可以确保所取出的点，其中任意两点之间的距离不等于 4. 从多少组中才能取出2006个点？既然，200645012=⨯+，即从501组可以取出2004个点，另外，再从第502组中取出2个点，就得到2006个点. 所以，850124010⨯+=.即数轴上至少有4010个点，就能够确保从这4010个点中取出2006个，其中任意两点之间的距离不等于4.214010n +≥，2005n ≥.当n =2005时，可以取 -2005，-2004，-2003，-2002，-1997，-1996，-1995，-1994，，-2005+8k ，-2004+8k ，-2003+8k ，-2002+8k ，，1995，1996，1997，1998，2003，2004,共2006个，其中任何两个数所代表的两个点之间的距离都不等于4.② 当2004=n 时，数轴上连续点的个数是214009n +=. 此时，将距离是4的2个点配对，共有2004对，另外还有单独的一个点，从每个配对中只取一个点，否那么一定有2个点的距离是4, 连同单独的一个点，一共可以取出2005个点，但是要求取出2006个点，不得不将某个配对的两个点都取出，它们的距离是4. 所以，当2004=n 时，任取2006个点，一定有2个点，距离是4. 当2004<n 时，补足至4009个点，就可以说明n 的最小值是2005.二. 解答以下各题〔要求写出简要过程〕9 图18中，ABCD 是矩形，6BC cm =，10AB cm =，AC 和BDCD 为轴旋转一周，那么阴影局部扫过的立体的体积是多少立方厘米？〔π 取3.14〕图18图17解: 〔见小学组决赛第11题解答〕 10 将21个整数：109832101238910,,,,,,,,,,,,,------分为个数不相等的六组数，分别计算各组的平均值，那么这六个平均值的和最大是多少？ 解: 将21个整数分为个数不相等的6组，各组的个数分别为1、2、3、4、5、6个. 既然是求六组个平均值的和的最大值，应当将数值大的分在整数个数少的组中. 所以，可以如下分组：10第一组第二组98第三组765第四组4321第五组－1－2－3－4第六组－5－6－7－8－9－10计算上述六组整数的平均值的和：1098765432101567891012345611110862272221172.+--=＋＋＋＋＋＋－－2－3－4－－－－－－＋＋＋＋＋＝＋＋ 答：最大的和是1172.评注和说明：下面说明理由.六组数分别为{}{}{}{}{}{}112123123412345123456,,,,,,,,,,,,,,,,,,,,a b b c c c d d d d e e e e e f f f f f f ，那么各组数平均数的和为()()()()()12123126111212312341234512345623660302015121060b bc c c f f f a a b b c c cd d d de e e e ef f f f f f ++++++++++++++++++++++++++++++=我们要使得这个分数最大，只要使得分子最大. 先考虑让那一个字母取10，显然是1a ，这样能使总和最大；同理，让12,b b 取8，9对总和的奉献是最大的……以此类推，{}{}{}{}{}{}10,8,9,5,6,7,1,2,3,4,4,3,2,1,0,10,9,8,7,6,5----------是我们得到的分组结果.这一过程无非就是把我们的解题过程用代数式翻译了一遍.为了同学们能多体会字母代表数的抽象性，这里再介绍一种更为一般一些的方法.()()()()()()()()61121231234123451234561091019100;S a b b c c c d d d d e e e e e f f f f f f =++++++++++++++++++++=+++++-++-+-=()()()()()()51121231234123451093445S a b b c c c d d d d e e e e e =++++++++++++++≤+++-+-=；()()()411212312341092155S a b b c c c d d d d =+++++++++≤++++=；()()3112123109640S a b b c c c =+++++≤+++=；()2112109827S a b b =++≤++=； 1110S a =≤因而有()()()()()1212312611121231234123451234561234562366030201512106030105321060b bc c c f f f a a b b c c cd d d de e e e ef f f f f f S S S S S S ++++++++++++++++++++++++++++++=+++++=()11240102251659060300270225165906035,2a b b +++++≤++++≤= 该不等式在{}{}{}{}{}{}112123123412345123456,,,,,,,,,,,,,,,,,,,,a b b c c c d d d d e e e e e f f f f f f 分别取{}{}{}{}{}{}10,8,9,5,6,7,1,2,3,4,4,3,2,1,0,10,9,8,7,6,5----------时恰好能取到等号，因此最大值为352. 11 当5431013231241000m ,,,,,,,,,=----时，从等式()()2123150m x m y m ++-+-=可以得到10个关于x 和y 的二元一次方程，问这10个方程有没有公共解？如果有，求出这些公共解？解：分别取0m =和1m =，我们得到两个方程：210340x y x y ++=⎧⎨--=⎩ 先求两个方程的公共解，把它们看作二元一次方程组，解得：1,1-==y x .把1,1-==y x 代入()()212315m x m y m ++-+-，值恒为0. 此即意味着：当5431013231241000m ,,,,,,,,,=----时，()()212315m x m y m ++-+-＝0成立.所以，1,1-==y x 是对应的10个方程的的公共解.答：这些方程的公共解是 1,1-==y x .12 平面上有5条直线，其中任意两条都不平行，那么在这5条直线两两相交所成的角中，至少有一个角不超过36度. 说明理由.解：在平面上任取一点O ，过O 点作的5条直线的平行线12345,,,,l l l l l . 将以O 为中心的周角分为10个彼此依次相邻的小的角，记为12910,,,,θθθθ.每个小角iθ〔1,2,,9,10i =〕都等于这5条直线相交的一个交角.这10个小角的和恰等于360，即.12910360θθθθ++++=，根据抽屉原理，至少有一个小角不超过36.三. 解答以下各题〔要求写出详细过程〕13 如图19，A 、B 和C 是圆周的三等分点，甲、乙、丙三只蚂蚁分别从A 、B 、C 三个点同时出发，甲和乙沿圆周逆时针爬行，丙顺时针爬行. 甲、乙、丙三只蚂蚁爬行的速度之比是8:6:5，求出三只蚂蚁所有的会合地点. 解：① 设圆周的周长为3L ，甲的速度为v 8，乙的速度为v 6，丙的速度为v 5；甲第一次追上乙时，爬行的时间和爬行的路程分别是：甲爬行的时间＝862L L v v v =-, 甲爬行的路程＝842Lv L v=， ABAC A图19因为圆周的周长为3L ，即甲在Ｂk+1(k 是整数)次追上乙时，甲爬行的时间＝322L kLv v+， 甲爬行的路程＝3822L kL v v v ⎛⎫+⨯= ⎪⎝⎭()412314L kL L k L +=+⨯+因为()314k L ⨯+是圆周周长的整数倍，所以，甲在B 点追上乙. ② 在时刻322L kLv v+，( 丙爬行的路程＝3315362222L kL k v L kL L v v ⎛⎫⎛⎫+⨯=++- ⎪ ⎪⎝⎭⎝⎭，当k ＝1时，上式是35922L kL v L L v v ⎛⎫+⨯=+ ⎪⎝⎭因为丙是从C 出发顺时针爬行，所以，丙爬行至B 处，意味着甲、乙、丙能够在B 点会合.答；甲、乙、丙仅仅在B 处集合. 14 m, n 都是正整数，并且),11)(11()311)(311)(211)(211(m m A +-+-+-=),11)(11()311)(311)(211)(211(nn B +-+-+-=① 证明：A =m m 21+, n n B 21+=； ② 假设,261=-B A 求 m 和n 的值. 解：①111111(1-)(1+)(1-)(1+)(1-)(1+)2233111111(1-)(1-)(1-)(1+)(1+)(1+)23231213411 ;23232A m m m m m m m m m m==-++=⨯⨯⨯⨯⨯⨯⨯=同样，nn B 21+=②由题设，11111222226m n A B m n m n ++-=-=-=，11113m n -=111131313nm n n+=+=， 所以，1313nm ,n=+ ()13131313131313131313n n m ,n n n+-⨯===-+++ 即13+n 是1313⨯的因数，1313⨯只有3个因数：1，13，132. 所以，13+n=132，n =132 –13=156, m =12.〕评注和说明：另一方法可以求出正整数m,n ，使11113m n -=. 设()1m Ka,n Kb,a,b ===，代入上式，11113b a Ka Kb Kab --==. ()b a -和a,b 都互质，一定整除K .记Kd b a=-是正整数，b a >那么有 1113dab =. 由上式和b a >，1311b ,a ,d ===. 所以，K ＝12，m 和n 有唯一解，12156m ,n ==.。

第十届全国”华罗庚金杯”少年数学邀请赛决赛试题:初一组一. 填空(每题10分,共80分)1.①计算: 22111134413(12)(0.5)(2)22412433⎡⎤-⨯-÷-÷⨯-⨯--=⎣⎦ . ②已知: 0abc ≠且0a b c ++=,则a b b c c a a b b c c a++= . 2.m 和n 均不为零, 233x y 和2235m nx y ++-是同类项,则322332233395369m m n mn n m m n mn n -++=+-+ . 3.由于浮力的作用,金放在水里秤量和它的重量比较,在水中的”重量”会减少119;银放在水里秤量和它的重量相比较,在水中的”重量”会减少110.某个只含有金银成分的古文物,重量是150克,在水中秤量,”重量”是141克,则古文物中金占 %.(精确到1%)4.图1是几何学中非常著名的美丽的轴对称的图形,它有 条对称轴.5.甲加工一种零件,乙加工另一种零件.甲用A 型机器需要6小时才能完成任务,用B 型机器效率降低60%;乙用B 型机器需要10小时才能完成任务,用A 型机器效率提高20%.如果甲用A 型机器,乙用B 型机器同时开始工作,中途某一时刻交换使用机器,甲和乙同时完成任务.则甲完成任务所用的时间是 小时.6.一个直角三角形三条边的长度是3,4,5.如果分别以各边为轴旋转一周,得到三个立体,那么三个立体中最大的体积和最小的体积的比是 .7.一列自然数0,1,2,3……，2005，……，2024.第一个数是0,从第二个数开始,每一个都比它前一个大1,最后一个是2004.现在将这列自然数排成以下数表:3 8 15 (1)2 7 14 (4)5 6 13 …… 9 10 11 12 ………… …… …… …… ……规定横排为行，竖排为列，则2005在数表中位于第 行和第 列。

8。

(31)635m x x -=-是关于x 的方程，为确保该方程的解是负整数，m 能取的最大 值 。

华罗庚金杯少年数学邀请赛口试试题第01届华罗庚金杯少年数学邀请赛口试试题1. 这是七巧板拼成的正方形，正方形边长20厘米，问七巧板中平行四边形的一块（如右图中阴影部分）的面积是多少？2．从所有分母小于10的真分数中，找出一个最接近0.618的分数。

3．有49个小孩子，每人胸前有一个号码，号码从1到49各不相同，请你挑选出若干个小孩，排成一个圆圈，使任何相邻两个小孩的号码数的乘积小于100，你最多能挑选出多少个小孩子？4．有一路公共汽车，包括起点和终点站共有15个车站，如果有一辆车，除终点到站外，每一站上车的乘客中，恰好各有一位乘客从这一站到以后的每一站，为了使每位乘客都有座位，问这辆公共汽车最少要有多少个座位？5．正方形的树林每边长1000米，里面有白杨树和榆树，小明从树林的西南角走入树林，碰见一株白杨树就往正北走，碰见一株榆树就往正东走，最后他走了东北角上，问：小明一共走了多少米的距离？6．自然数按从小到大的顺序排成螺旋形，在2处拐第一个弯，在3处拐第二个弯，在5处拐第三个弯……问拐第二十个弯的地方是哪一个数？第02届华罗庚金杯少年数学邀请赛口试试题1、如下图是一个对称的图形，黑色部分面积大还是阴影部分面积大？2、你能不能将自然数1到9分别填入右面的方格中，使得每个横格中的三个数之和都是偶数？3、司机开车按顺序到五个车站接学生到学校（如下图），每个站都有学生上车，第一站上了一批学生，以后每站上车的人数都是前一站上车人数的一半，车到学校时，车上最少有多少学生？4、如图中五个正方形的边长分别是1米、2米、3米、4米、5米。

问：白色部分面积与阴影部分面积之比是多少？5、用1、2、3、4、5这五个数两两相乘，可以得到10个不同的乘积，问乘积中是偶数多还是奇数多？6、7、将右边的硬纸片沿虚线折起来，便可作成一个正方体，问：这个正方体的2号面对面是几号面？（如下图）8、下面是一个11位数，它的每三个相邻数之和都是20，你知道打“？”的数字是几？9、有八张卡片，右图分别写着自然数1到8，从中取出三张，要使这三张卡片上的数字之和为9，问有多少种不同的取法？第03届华罗庚金杯少年数学邀请赛团体决赛口试1．一条白色的正方形手帕，它的边长是18厘米，手帕上横竖各有二道红条，如右图阴影所示部分，红条宽都是2厘米．问：这条手帕白色部分的面积是多少？2．伸出你的左手，从大拇指开始如图所示的那样数数字，1，2，3，……，问：数到1991时，你数在那个手指上？3．有3个工厂共订300份吉林日报，每个工厂订了至少99份，至多101份．问：一共有多少种不同的订法？4．图上有两条垂直相交的直线段AB、CD，交点为E（如下图）．已知：DE=2CE，BE=3AE．在AB和CD上取3个点画一个三角形．问：怎样取这3个点，画出的三角形面积最大？5．如下图中有两个红色的圆，两个蓝色的圆，红色圆的直径分别是1992厘米和1949厘米，蓝色圆的直径分别是1990厘米和1951厘米．问：红色二圆面积大还是蓝色二圆面积大？6．在一张9行9列的方格纸上，把每个方格所在的行数和列数加起来（如下图），填在这个方格中，例如a=5＋3=8．问：填入的81个数字中，奇数多还是偶数多？7．能不能在下式：1□2□3□4□5□6□7□8□9=10的每个方框中，分别填入加号或减号，使等式成立？8．把一个时钟改装成一个玩具钟（如右图），使得时针每转一圈，分针转16圈，秒针转36圈．开始时3针重合．问：在时针旋转一周的过程中，3针重合了几次？（不计起始和终止的位置）．9．将1，2，3，4，5，6，7，8这8个数分成3组，分别计算各组数的和．已知这3个和互不相等，且最大的和是最小的和的2倍．问：最小的和是多少？10.这是一个棋盘，将一个白子和一个黑子放在棋盘线交叉点上，但不能在同一条棋盘线上．问：共有多少种不同的放法（如下图）？11.这是两个圆，它们的面积之和为1991平方厘米，小圆的周长是大圆周长的90％（如右图）．问：大圆的面积是多少？12.有一根1米长的木条，第一次去掉它的，第二次去掉余下木条的；第三次又去掉第二次余下木条的，等等；这样一直下去，最后一次去掉上次余下木条的．问：这根木条最后还剩下多长？13.这是一个楼梯的截面图（如下图），高2.8米，每级台阶的宽和高都是20厘米．问：此楼梯截面的面积是多少？14.请找出6个不同的自然数，分别填入6个括号中，使这个等式成立．第04届华罗庚金杯少年数学邀请赛团体决赛口试1．2×3×5×7×11×13×17这个算式中有七个数连乘，请回答：最后得到的乘积中，所有数位上的数字和是多少？请讲一讲你是怎样算的？2．这是一个中国象棋盘（图中小方格都是相等的正方形，“界河”的宽等于小正方形边长），黑方有一个“象”，它只能在1，2，3，4，5，6，7位置中的一个，红方有两个“相”，它们只能在8，9，10，11，12， 13，14中的两个位置．问：这三个棋子（一个“象”和两个“相”）各在什么位置时，以这三个棋子为顶点构成的三角形的面积最大？3．将一根长为374厘米的合金铝管截成若干根36厘米和24厘米两种形状的短管（加工损耗忽略不计）问：剩余部分的管子最少是多少厘米？4．乙两人同时从A出发向B行进，甲速度始终不变，乙在走前面路程时，速度为甲的2倍，而走后面路程时，速度是甲的，问甲、乙二人谁选到B？请你说明理由。