机械原理课后答案7章
- 格式:docx
- 大小:251.96 KB
- 文档页数:8


机械原理孙恒课后答案机械原理孙恒课后答案【篇一:机械原理(第七版) 孙桓主编第7章】ss=txt>1.设某机器的等效转动惯量为常数,则该机器作匀速稳定运转的条件是,作变速稳定运转的条件是。
2.机器中安装飞轮的原因,一般是为了,同时还可获得的效果。
3.在机器的稳定运转时期,机器主轴的转速可有两种不同情况,即稳定运转,在前一种情况,机器主轴速度是,在后一种情况,机器主轴速度是。
4.机器中安装飞轮的目的是和。
7.机器等效动力学模型中的等效质量(转动惯量)是根据的原则进行转化的,因而它的数值除了与各构件本身的质量(转动惯量)有关外,还与。
8.机器等效动力学模型中的等效力(矩)是根据则进行转化的,等效质量(转动惯量)是根据的原则进行转化的。
9.机器等效动力模型中的等效力(矩)是根据的原则进行转化的,因而它的数值除了与原作用力(矩)的大小有关外,还与有关。
10.若机器处于起动(开车)阶段,则机器的功能关系应是,机器主轴转速的变化情况将是。
11.若机器处于停车阶段,则机器的功能关系应是,机器主轴转速的变化情况将是。
12.用飞轮进行调速时,若其它条件不变,则要求的速度不均匀系数越小,飞轮的转动惯量将越,在满足同样的速度不均匀系数条件下,为了减小飞轮的转动惯量,应将飞轮安装在轴上。
13.当机器运转时,由于负荷发生变化使机器原来的能量平衡关系遭到破坏,引起机器运转速度的变化,称为,为了重新达到稳定运转,需要采用来调节。
14.在机器稳定运转的一个运动循环中,运动构件的重力作功等于因为。
15.机器运转时的速度波动有速度波动两种,前者采用,后者采用进行调节。
16.若机器处于变速稳定运转时期,机器的功能特征应有,它的运动特征是。
17.当机器中仅包含机构时,等效动力学模型中的等效质量(转动惯量)是常量,若机器中包含机构时,等效质量(转动惯量)是机构位置的函数。
18.设作用于机器从动件上的外力(矩)为常量,且当机器中仅包含机构时,等效到主动件上的等效动力学模型中的等效力(矩)亦是常量,若机器中包含机构时,等效力(矩)将是机构位置的函数。

第七章 机械的运转及其速度波动的调节题7-7如图所示为一机床工作台的传动系统,设已知各齿轮的齿数,齿轮3的分度圆半径r 3,各齿轮的转动惯量J 1、J 2、J 2`、J 3,因为齿轮1直接装在电动机轴上,故J 1中包含了电动机转子的转动惯量,工作台和被加工零件的重量之和为G 。
当取齿轮1为等效构件时,试求该机械系统的等效转动惯量J e 。
解:根据等效转动惯量的等效原则,有∑=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=ni i Si Si i e J v m J 122ωωω 212133212221221⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+=''ωωωωωωωv g G J J J J J e 2322123232213221222121⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+='''Z Z Z Z r g G Z Z Z Z J Z Z J Z Z J J J e 题7-9已知某机械稳定运转时其主轴的角速度ωs =100rad/s ,机械的等效转动惯量J e =0.5Kg ·m 2,制动器的最大制动力矩M r =20N ·m (该制动器与机械主轴直接相联,并取主轴为等效构件)。
设要求制动时间不超过3s ,试检验该制动器是否能满足工作要求。
解:因此机械系统的等效转动惯量J e 及等效力矩M e 均为常数,故可利用力矩形式的机械运动方程式dtd J Me e ω= 其中:25.020m kg m N M M r e ⋅=⋅-=-= ωωωd d d M J dt r e 025.0205.0-=-=-= ()s t S S 5.2025.0025.0==--=∴ωωω由于 s s t 35.2<= 所以该制动器满足工作要求。
题7-11 在图a 所示的刨床机构中,已知空程和工作行程中消耗于克服阻抗力的恒功率分别为P 1=367.7W 和P 2=3677W ,曲柄的平均转速n=100r/min ,空程中曲柄的转角φ1=120°。

第7章作业7—1等效转动惯量和等效力矩各自的等效条件是什么?7—2在什么情况下机械才会作周期性速度波动?速度波动有何危害?如何调节?答: 当作用在机械上的驱动力(力矩)周期性变化时,机械的速度会周期性波动。
机械的速度波动不仅影响机械的工作质量,而且会影响机械的效率和寿命。
调节周期性速度波动的方法是在机械中安装一个具有很大转动惯量的飞轮。
7—3飞轮为什么可以调速?能否利用飞轮来调节非周期性速度波动,为什么?答: 飞轮可以凋速的原因是飞轮具有很大的转动惯量,因而要使其转速发生变化.就需要较大的能量,当机械出现盈功时,飞轮轴的角速度只作微小上升,即可将多余的能量吸收储存起来;而当机械出现亏功时,机械运转速度减慢.飞轮又可将其储存的能量释放,以弥补能最的不足,而其角速度只作小幅度的下降。
非周期性速度波动的原因是作用在机械上的驱动力(力矩)和阻力(力矩)的变化是非周期性的。
当长时问内驱动力(力矩)和阻力(力矩)做功不相等,机械就会越转越快或越转越慢.而安装飞轮并不能改变驱动力(力矩)或阻力(力矩)的大小也就不能改变驱动功与阻力功不相等的状况,起不到调速的作用,所以不能利用飞轮来调节非周期陛速度波动。
7—4为什么说在锻压设备等中安装飞轮可以起到节能的作用?解: 因为安装飞轮后,飞轮起到一个能量储存器的作用,它可以用动能的形式把能量储存或释放出来。
对于锻压机械来说,在一个工作周期中,工作时间很短.而峰值载荷很大。
安装飞轮后.可以利用飞轮在机械非工作时间所储存能量来帮助克服其尖峰载荷,从而可以选用较小功率的原动机来拖动,达到节能的目的,因此可以说安装飞轮能起到节能的作用。
7—5由式J F =△W max /(ωm 2 [δ]),你能总结出哪些重要结论(希望能作较全面的分析)? 答:①当△W max 与ωm 一定时,若[δ]下降,则J F 增加。
所以,过分追求机械运转速度的均匀性,将会使飞轮过于笨重。
②由于J F 不可能为无穷大,若△W max ≠0,则[δ]不可能为零,即安装飞轮后机械的速度仍有波动,只是幅度有所减小而已。
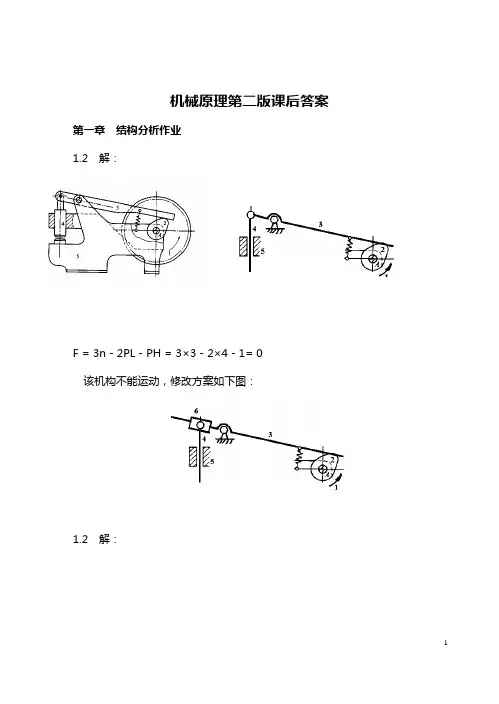
机械原理第二版课后答案第一章结构分析作业1.2 解:F = 3n-2PL-PH = 3×3-2×4-1= 0该机构不能运动,修改方案如下图:1.2 解:(a)F = 3n-2PL-PH = 3×4-2×5-1= 1 A点为复合铰链。
(b)F = 3n-2PL-PH = 3×5-2×6-2= 1B、E两点为局部自由度, F、C两点各有一处为虚约束。
(c)F = 3n-2PL-PH = 3×5-2×7-0= 1 FIJKLM为虚约束。
1.3 解:F = 3n-2PL-PH = 3×7-2×10-0= 11)以构件2为原动件,则结构由8-7、6-5、4-3三个Ⅱ级杆组组成,故机构为Ⅱ级机构(图a)。
2)以构件4为原动件,则结构由8-7、6-5、2-3三个Ⅱ级杆组组成,故机构为Ⅱ级机构(图b)。
3)以构件8为原动件,则结构由2-3-4-5一个Ⅲ级杆组和6-7一个Ⅱ级杆组组成,故机构为Ⅲ级机构(图c)。
(a) (b) (c)第二章 运动分析作业2.1 解:机构的瞬心如图所示。
2.2 解:取作机构位置mmmm l /5=μ图如下图所示。
1.求D 点的速度V D13P D V V =而 25241314==P P AE V V E D ,所以 s mm V V E D /14425241502524=⨯==2. 求ω1s rad l V AE E /25.11201501===ω3. 求ω2因 98382412141212==P P P P ωω ,所以s rad /46.0983825.1983812=⨯==ωω4. 求C 点的速度V Csmm C P V l C /2.10154446.0242=⨯⨯=⨯⨯=μω2.3 解:取作机构位置mmmm l /1=μ图如下图a 所示。
1. 求B2点的速度V B2V B2 =ω1×L AB =10×30= 300 mm/s 2.求B3点的速度V B3V B3 = V B2 + V B3B2 大小 ? ω1×L AB ? 方向 ⊥BC ⊥AB ∥BC取作速度多边mms mm v /10=μ形如下图b 所示,由图量得:mmpb 223= ,所以smm pb V v B /270102733=⨯=⨯=μ由图a 量得:BC=123 mm , 则mmBC l l BC 1231123=⨯=⨯=μ3. 求D 点和E 点的速度V D 、V E利用速度影像在速度多边形,过p 点作⊥CE ,过b 3点作⊥BE ,得到e 点;过e 点作⊥pb 3,得到d 点 , 由图量得:mmpd 15=,mmpe 17=,所以smm pd V v D /1501015=⨯=⨯=μ ,smm pe V v E /1701017=⨯=⨯=μ;smm b b V v B B /17010173223=⨯=⨯=μ4. 求ω3srad l V BC B /2.212327033===ω5. 求nB a 222212/30003010s mm l a ABn B =⨯=⨯=ω6. 求3B aa B3 = a B3n + a B3t = a B2 + aB3B2k + aB3B2τ大小 ω32LBC ? ω12LAB 2ω3VB3B2 ? 方向 B →C ⊥BC B →A ⊥BC ∥BC 22233/5951232.2s mm l a BCn B =⨯=⨯=ω223323/11882702.222s mm V a B B k B B =⨯⨯=⨯=ω取作速度多边mms mm a 2/50=μ形如上图c 所示,由图量得:mmb 23'3=π ,mmb n 20'33=,所以233/11505023's mm b a a B =⨯=⨯=μπ2333/10005020's mm b n a at B =⨯=⨯=μ7. 求3α233/13.81231000s rad l a BC tB ===α8. 求D 点和E 点的加速度aD 、a E利用加速度影像在加速度多边形,作e b 3'π∆∽CBE ∆, 即BE eb CEeCBb 33''==ππ,得到e 点;过e 点作⊥3'b π,得到d 点 , 由图量得:mm e 16=π,mmd 13=π,所以2/6505013s mm d a a D =⨯=⨯=μπ ,2/8005016s mm e a a E =⨯=⨯=μπ 。
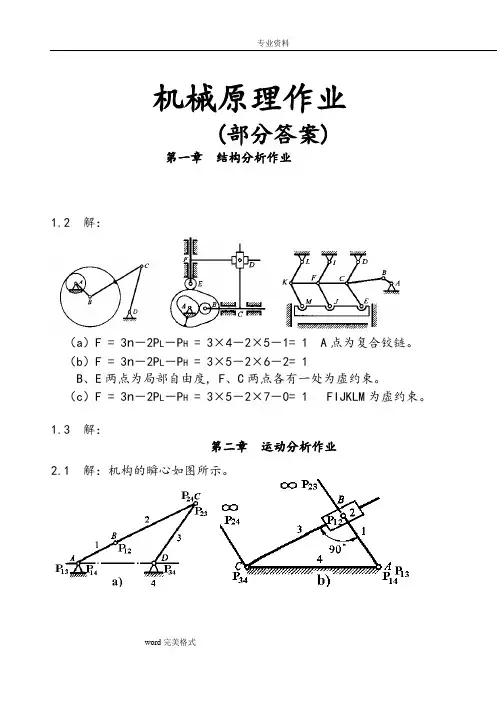
机械原理作业(部分答案)第一章结构分析作业1.2 解:(a)F = 3n-2P L-P H = 3×4-2×5-1= 1 A点为复合铰链。
(b)F = 3n-2P L-P H = 3×5-2×6-2= 1B、E两点为局部自由度, F、C两点各有一处为虚约束。
(c)F = 3n-2P L-P H = 3×5-2×7-0= 1 FIJKLM为虚约束。
1.3 解:第二章运动分析作业2.1 解:机构的瞬心如图所示。
2.2 解:取mmmm l /5=μ作机构位置图如下图所示。
1.求D 点的速度V D13P D V V =而 25241314==P P AE V V E D ,所以 s mm V V E D /14425241502524=⨯==2. 求ω1s rad l V AE E /25.11201501===ω3. 求ω2因 98382412141212==P P P P ωω ,所以s rad /46.0983825.1983812=⨯==ωω 4. 求C 点的速度V Csmm C P V l C /2.10154446.0242=⨯⨯=⨯⨯=μω2.3 解:取mmmm l /1=μ作机构位置图如下图a 所示。
1. 求B 2点的速度V B2V B2 =ω1×L AB =10×30= 300 mm/s 2.求B 3点的速度V B3V B3 = V B2 + V B3B2大小 ? ω1×L AB ? 方向 ⊥BC ⊥AB ∥BC 取mm s mm v /10=μ作速度多边形如下图b 所示,由图量得:mmpb 223= ,所以smm pb V v B /270102733=⨯=⨯=μ由图a 量得:BC=123 mm , 则mmBC l l BC 1231123=⨯=⨯=μ3. 求D 点和E 点的速度V D 、V E利用速度影像在速度多边形,过p 点作⊥CE ,过b 3点作⊥BE ,得到e 点;过e 点作⊥pb 3,得到d 点 , 由图量得:mmpd 15=,mmpe 17=,所以smm pd V v D /1501015=⨯=⨯=μ , smm pe V v E /1701017=⨯=⨯=μ;smm b b V v B B /17010173223=⨯=⨯=μ4. 求ω3s rad l V BC B /2.212327033===ω5. 求n B a 222212/30003010smm l a AB n B =⨯=⨯=ω6. 求3B aa B3 = a B3n + a B3t = a B2 + a B3B2k + a B3B2τ 大小 ω32L BC ? ω12L AB 2ω3V B3B2 ?方向 B →C ⊥BC B →A ⊥BC ∥BC 22233/5951232.2s mm l a BCn B =⨯=⨯=ω223323/11882702.222s mm V a B B k B B =⨯⨯=⨯=ω取mms mm a 2/50=μ作速度多边形如上图c 所示,由图量得:mmb 23'3=π ,mmb n 20'33=,所以233/11505023's mm b a a B =⨯=⨯=μπ2333/10005020's mm b n a at B =⨯=⨯=μ7. 求3α233/13.81231000s rad l a BC tB ===α8. 求D 点和E 点的加速度a D 、a E利用加速度影像在加速度多边形,作e b 3'π∆∽CBE ∆, 即 BE eb CE e CB b 33''==ππ,得到e 点;过e 点作⊥3'b π,得到d 点 , 由图量得:mm e 16=π,mmd 13=π,所以2/6505013s mm d a a D =⨯=⨯=μπ ,2/8005016s mm e a a E =⨯=⨯=μπ 。
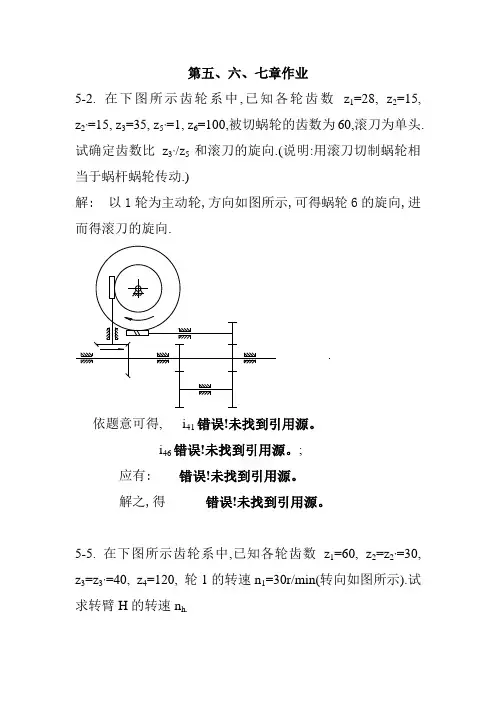
第五、六、七章作业5-2. 在下图所示齿轮系中,已知各轮齿数z1=28, z2=15, z2’=15, z3=35, z5’=1, z6=100,被切蜗轮的齿数为60,滚刀为单头.试确定齿数比z3’/z5和滚刀的旋向.(说明:用滚刀切制蜗轮相当于蜗杆蜗轮传动.)解: 以1轮为主动轮,方向如图所示,可得蜗轮6的旋向,进而得滚刀的旋向.依题意可得, i41错误!未找到引用源。
i46错误!未找到引用源。
;应有: 错误!未找到引用源。
解之,得错误!未找到引用源。
5-5. 在下图所示齿轮系中,已知各轮齿数z1=60, z2=z2’=30, z3=z3’=40, z4=120, 轮1的转速n1=30r/min(转向如图所示).试求转臂H的转速n h.解:图中的周转齿轮系,其转化轮系的传动比的计算公式为i H14错误!未找到引用源。
由此可解得: 错误!未找到引用源。
(负号表示与n1反向) ;5-8. 在下图所示齿轮系中,已知各轮齿数z1=20, z2=40, z3=20, z4=80, z4’=60, z5=50,z5’=55, z6=65, z6’=1, z7=60, 轮1、3的转速n1=n3=3000r/min(转向如图所示). 试求转速n7.解依题意, 错误!未找到引用源。
n2错误!未找到引用源。
i 34错误!未找到引用源。
对于周围齿轮系4’-5-5’-6; 此转化轮系的传动比计算公式为:i H 36错误!未找到引用源。
;由此解出 错误!未找到引用源。
(负号表示与n 2反向);进而n 7=错误!未找到引用源。
;5.12 在如图所示齿轮系中,已知各轮齿数1z =20,2z =40,3z =35,'3z =30,''3z =1,4z =20,5z =75,'5z =80,6z =30,7z =90,8z =30,9z =20,10z =50,轮1的转速1n =100r/min,试求轮10的转速10n 。
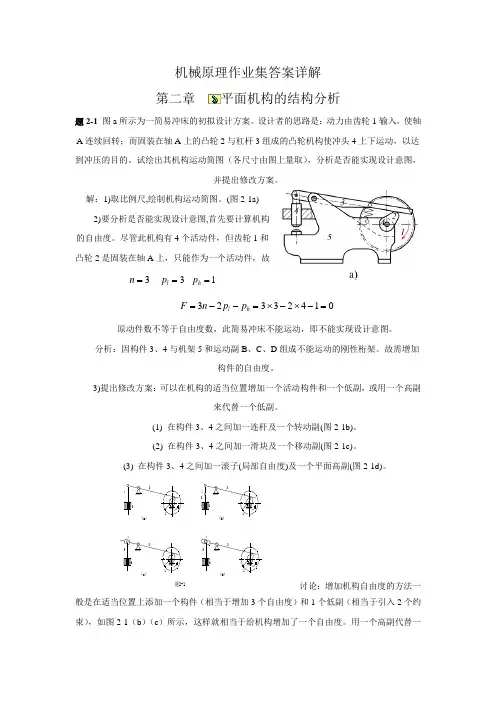
机械原理作业集答案详解 第二章平面机构的结构分析题2-1 图a 所示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动,以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析是否能实现设计意图,并提出修改方案。
解:1)取比例尺,绘制机构运动简图。
(图2-1a) 2)要分析是否能实现设计意图,首先要计算机构的自由度。
尽管此机构有4个活动件,但齿轮1和凸轮2是固装在轴A 上,只能作为一个活动件,故3=n 3=l p 1=h p01423323=-⨯-⨯=--=h l p p n F原动件数不等于自由度数,此简易冲床不能运动,即不能实现设计意图。
分析:因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。
故需增加构件的自由度。
3)提出修改方案:可以在机构的适当位置增加一个活动构件和一个低副,或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-1b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-1c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-1d)。
11(c)题2-1(d)54364(a)5325215436426(b)321讨论:增加机构自由度的方法一般是在适当位置上添加一个构件(相当于增加3个自由度)和1个低副(相当于引入2个约束),如图2-1(b )(c )所示,这样就相当于给机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度,如图2-1(d )所示。
题2-2 图a 所示为一小型压力机。
图上,齿轮1与偏心轮1’为同一构件,绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽,摆杆4上的滚子6嵌在凹槽中,从而使摆杆4绕C 轴上下摆动。
同时,又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。

《机械原理》课后习题答案第2章(P27)2-2 计算下列机构的自由度,如遇有复合铰链、局部自由度、虚约束等加以说明。
(a)n=3,p l=3 F=3*3-2*3=3(b)n=3,p l=3,p h=2 F=3*3-2*3-2=1 (B处有局部自由度)(c)n=7,p l=10 F=3*7-2*10=1(d)n=4,p l=4,p h=2 F=3*4-2*4-2=2 (A处有复合铰链)(e)n=3,p l=4 F=3*3-2*4=1 (A或D处有虚约束)(f)n=3,p l=4 F=3*3-2*4=1 (构件4和转动副E、F引入虚约束)(g)n=3,p l=5 F=(3-1)*3-(2-1)*5=1 (有公共约束)(h)n=9,p l=12,p h=2 F=3*9-2*12-2=1 (M处有复合铰链,C处有局部自由度)2-3 计算下列机构的自由度,拆杆组并确定机构的级别。
(a)n=5,p l=7 F=3*5-2*7=1由于组成该机构的基本杆组的最高级别为Ⅱ级杆组,故此机构为Ⅱ级机构。
(b)n=5,p l=7 F=3*5-2*7=1此机构为Ⅱ级机构。
(c)n=5,p l=7 F=3*5-2*7=1拆分时只须将主动件拆下,其它构件组成一个Ⅲ级杆组,故此机构为Ⅲ级机构。
2-4 验算下列运动链的运动是否确定,并提出具有确定运动的修改方案。
(a)n=3,p l=4,p h=1 F=3*3-2*4-1=0 该运动链不能运动。
修改方案如下图所示:(b)n=4,p l=6 F=3*4-2*6=0 该运动链不能运动。
修改方案如下图所示:或第3章(P42)3-2 下列机构中,已知机构尺寸,求在图示位置时的所有瞬心。
(a)(b)(c)(a) v3=v P13=ω1P14P13μl3-6 在图示齿轮连杆机构中,三个圆互作纯滚,试利用相对瞬心P13来讨论轮1与轮3的传动比i13。
第5章(P80)5-2 一铰接四杆机构(2)机构的两极限位置如下图:(3)传动角最大和最小位置如下图:5-3题略解:若使其成为曲柄摇杆机构,则最短杆必为连架杆,即a 为最短杆。
第二章2-1 何谓构件?何谓运动副及运动副元素?运动副是如何进行分类的?答:参考教材5~7页。
2-2 机构运动简图有何用处?它能表示出原机构哪些方面的特征?答:机构运动简图可以表示机构的组成和运动传递情况,可进行运动分析,也可用来进行动力分析。
2-3 机构具有确定运动的条件是什么?当机构的原动件数少于或多于机构的自由度时,机构的运动将发生什么情况?答:参考教材12~13页。
2-5 在计算平面机构的自由度时,应注意哪些事项?答:参考教材15~17页。
2-6 在图2-22所示的机构中,在铰链C、B、D处,被连接的两构件上连接点的轨迹都是重合的,那么能说该机构有三个虚约束吗?为什么?答:不能,因为在铰链C、B、D中任何一处,被连接的两构件上连接点的轨迹重合是由于其他两处的作用,所以只能算一处。
2-7 何谓机构的组成原理?何谓基本杆组?它具有什么特性?如何确定基本杆组的级别及机构的级别? 答:参考教材18~19页。
2-8 为何要对平面高副机构进行“高副低代"?“高副低代”应满足的条件是什么?答:参考教材20~21页。
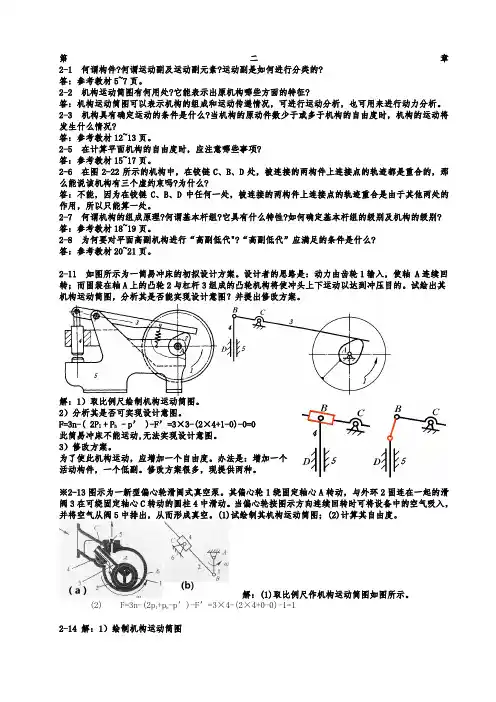
2-11 如图所示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴 A连续回转;而固装在轴A上的凸轮2与杠杆3组成的凸轮机构将使冲头上下运动以达到冲压目的。
试绘出其机构运动简图,分析其是否能实现设计意图?并提出修改方案。
解:1)取比例尺绘制机构运动简图。
2)分析其是否可实现设计意图。
F=3n-( 2P l +P h –p’ )-F’=3×3-(2×4+1-0)-0=0此简易冲床不能运动,无法实现设计意图。
3)修改方案。
为了使此机构运动,应增加一个自由度。
办法是:增加一个活动构件,一个低副。
修改方案很多,现提供两种。
※2-13图示为一新型偏心轮滑阎式真空泵。
其偏心轮1绕固定轴心A转动,与外环2固连在一起的滑阀3在可绕固定轴心C转动的圆柱4中滑动。
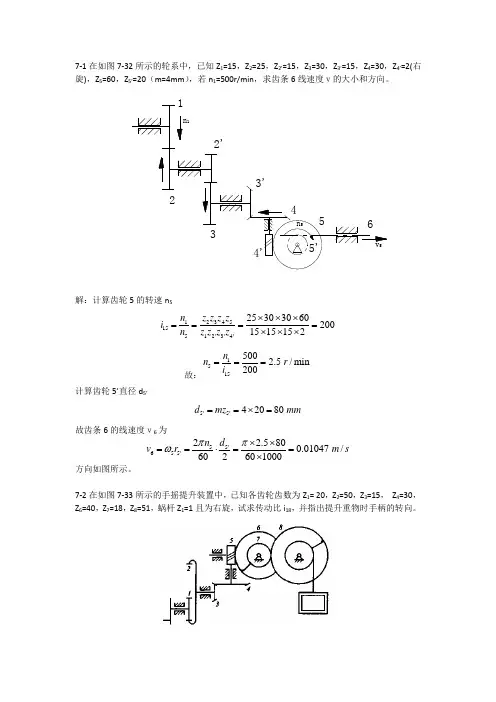
7-1在如图7-32所示的轮系中,已知Z 1=15,Z 2=25,Z 2’=15,Z 3=30,Z 3’=15,Z 4=30,Z 4’=2(右旋),Z 5=60,Z 5’=20(m=4mm ),若n 1=500r/min ,求齿条6线速度v的大小和方向。
解:计算齿轮5的转速n 52345115512'3'4'253030602001515152z z z z n i n z z z z ⨯⨯⨯====⨯⨯⨯故:15155002.5 /min 200n n r i ===计算齿轮5’直径d 5’5'5'42080 d mz mm==⨯=故齿条6的线速度v6为55'655'2 2.5800.01047 /602601000n d v r m s ππω⨯⨯==⋅==⨯方向如图所示。
7-2在如图7-33所示的手摇提升装置中,已知各齿轮齿数为Z 1= 20,Z 2=50,Z 3=15, Z 4=30,Z 6=40,Z 7=18,Z 8=51,蜗杆Z 1=1且为右旋,试求传动比i 18,并指出提升重物时手柄的转向。
解:246811881357503040515682015118z z z z i z z z z ωω⨯⨯⨯====⨯⨯⨯提升重物时手柄的转向如图所示。
7-3在如图7-34所示的轮系中,已知各齿轮齿数为Z 1= 20,Z 2=30,Z 3=18, Z 4=68,齿轮1的转速n 1=500r/min ,试求系杆H的转速n H 的大小及方向。
解:1241441330685.672018H H H n n z z i n n z z -⨯==-=-=--⨯40n =115.6715022.496.67 6.67H HH n n n n n -====方向与n 1相同。
7-4在如图7-35所示的双级行星齿轮减速器中,各齿轮齿数为Z 1= Z 6 =20,Z 2=30,Z 3=Z 4=40,Z 2=Z 5=10,试求:(1) 固定齿轮4时的传动比i 1H2; (2) 固定齿轮3时的传动比i 1H2。
第二章 平面机构的结构分析题2-1 图a 所示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动,以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析是否能实现设计意图,并提出修改方案。
解:1)取比例尺,绘制机构运动简图。
(图2-1a) 2)要分析是否能实现设计意图,首先要计算机构的自由度。
尽管此机构有4个活动件,但齿轮1和凸轮2是固装在轴A上,只能作为一个活动件,故3=n3=l p 1=h p01423323=-⨯-⨯=--=h l p p n F原动件数不等于自由度数,此简易冲床不能运动,即不能实现设计意图。
分析:因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。
故需增加构件的自由度。
3)提出修改方案:可以在机构的适当位置增加一个活动构件和一个低副,或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-1b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-1c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-1d)。
1(c)题2-154364(a)53221讨论:增加机构自由度的方法一般是在适当位置上添加一个构件(相当于增加3个自由度)和1个低副(相当于引入2个约束),如图2-1(b )(c )所示,这样就相当于给机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度,如图2-1(d)所示。
题2-2 图a所示为一小型压力机。
图上,齿轮1与偏心轮1’为同一构件,绕固定轴心O连续转动。
在齿轮5上开有凸轮轮凹槽,摆杆4上的滚子6嵌在凹槽中,从而使摆杆4绕C轴上下摆动。
同时,又通过偏心轮1’、连杆2、滑杆3使C轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G使冲头8实现冲压运动。
试绘制其机构运动简图,并计算自由度。
第七章 机械的运转及其速度波动的调节题7-7如图所示为一机床工作台的传动系统,设已知各齿轮的齿数,齿轮3的分度圆半径r 3,各齿轮的转动惯量J 1、J 2、J 2`、J 3,因为齿轮1直接装在电动机轴上,故J 1中包含了电动机转子的转动惯量,工作台和被加工零件的重量之和为G 。
当取齿轮1为等效构件时,试求该机械系统的等效转动惯量J e 。
解:根据等效转动惯量的等效原则,有∑=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=ni i Si Si i e J v m J 122ωωω 2322123232213221222121⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+='''Z Z Z Z r g G Z Z Z Z J Z Z J Z Z J J J e 212133212221221⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+=''ωωωωωωωv g G J J J J J e 题7-9已知某机械稳定运转时其主轴的角速度ωs =100rad/s ,机械的等效转动惯量J e =0.5Kg ·m 2,制动器的最大制动力矩M r =20N ·m (该制动器与机械主轴直接相联,并取主轴为等效构件)。
设要求制动时间不超过3s ,试检验该制动器是否能满足工作要求。
解:因此机械系统的等效转动惯量J e 及等效力矩M e 均为常数,故可利用力矩形式的机械运动方程式dtd J Me e ω= 其中:25.020m kg m N M M r e ⋅=⋅-=-= ωωωd d d M J dt r e 025.0205.0-=-=-= ()st S S 5.2025.0025.0==--=∴ωωω由于 s s t 35.2<= 所以该制动器满足工作要求。
题7-11 在图a 所示的刨床机构中,已知空程和工作行程中消耗于克服阻抗力的恒功率分别为P 1=367.7W 和P 2=3677W ,曲柄的平均转速n=100r/min ,空程中曲柄的转角φ1=120°。
华东理工大学机械原理第7章齿轮习题及答案(全)华东理工大学机械原理第7章齿轮--习题及答案(全)练习7-9在图示的渐开线齿阔中,基圆半径rb?100mm,试求出:1)当rk?135mm时,渐开线的展角?k,渐开线压力角?k和渐开线在k点的曲率半径?k。
002)什么时候?K渐开线在200、25和30°时的压力角?K和rk。
解:1)rk?rb/cos?kcos?k?rb100??0.741rk135K42.2oktankk0.17022krksink90.68mm2)什么时候?K20点,?K51点15分,rk?经常预算/预算?K159.42毫米?K25点,?K54o5,rk?经常预算/预算?K170.47毫米?K30点,?K56点28分?经常预算/预算?K181.02毫米7-10今测得一渐开线直齿标准齿轮齿顶圆直径da?110mm,齿根圆直径df?87.5mm,**齿数Z?20.尝试确定齿轮的模数m、齿顶高度系数HA和径向间隙系数C。
解:da?m(z?2ha*)df?m(z?2ha*?2c*)df?D爸爸d?mz?m?5mm替换到溶液中,以获得:ha*?1,c*?0.25*7-11已知有一个外啮合的渐开线直齿轮,齿数为Z1?20,m?2毫米,z2?41哈?1.c*?0.25,??200,求:1)当一对齿轮为标准齿轮时,尝试计算分度圆直径D1和D2、基圆直径db1和DB2、齿顶圆直径DA1和DA2、齿根圆直径DF1和df2、齿距P、齿厚s和分度圆上的齿槽宽度E。
2)当该对齿轮为标准齿轮且为正确安装时的中心距,求齿轮1的齿顶压力角?a1,齿顶处齿廓的曲率半径?a1。
解决方案:1)D1?mz1?40毫米,d2?mz2?82毫米db1?mz1cos??37.59mm,db2?mz2cos??77.05mmda1?m(z1?2ha*)?44mm,da2?m(z2?2ha*)?86mmdf1?m(z1?2ha?2c)?35毫米,df2?m(z2?2ha?2c)?77mmp??M6.28毫米,s?0.5? M3.14毫米,e?0.5便士?3.14平方毫米?a1?阿卡斯?a1?***db1?31.3ODA1R12?rb12?11.43毫米7-12渐开线标准齿轮的基圆和齿根圆重合时的齿数为多少(考虑正常齿和短齿两种情况)?齿数为多少时基圆大于齿根圆?解决方案:DB?mzcosdf?m(z?2ha?2c)若为正常齿,则ha*?1,c?0.25***通过数据库?df?Z41分贝?df?Z41如果牙齿较短,ha*?0.8,c?零点三由db?df,?z?36,由db?df,?z?367-13已知外啮合渐开线标准直齿轮的传动比为i12?2.4,模数m?5毫米,压力*角??20,ha?1,c?0.25,中心距a=170mm,试求该对齿轮的齿数z1、z2,分度圆O**直径D1、D2、齿顶圆直径DA1、DA2、基圆直径db1、DB2。
第二章平面机构的结构分析题2-1 图a 所示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动,以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析是否能实现设计意图,并提出修改方案。
解:1)取比例尺,绘制机构运动简图。
(图2-1a) 2)要分析是否能实现设计意图,首先要计算机构的自由度。
尽管此机构有4个活动件,但齿轮1和凸轮2是固装在轴A 上,只能作为一个活动件,故3=n 3=l p 1=h p01423323=-⨯-⨯=--=h l p p n F原动件数不等于自由度数,此简易冲床不能运动,即不能实现设计意图。
分析:因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。
故需增加构件的自由度。
3)提出修改方案:可以在机构的适当位置增加一个活动构件和一个低副,或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-1b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-1c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-1d)。
11(c)题2-1(d)54364(a)5325215436426(b)321讨论:增加机构自由度的方法一般是在适当位置上添加一个构件(相当于增加3个自由度)和1个低副(相当于引入2个约束),如图2-1(b )(c )所示,这样就相当于给机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度,如图2-1(d )所示。
题2-2 图a 所示为一小型压力机。
图上,齿轮1与偏心轮1’为同一构件,绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽,摆杆4上的滚子6嵌在凹槽中,从而使摆杆4绕C 轴上下摆动。
同时,又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。
机械原理课后全部习题答案目录第1章绪论 (1)第2章平面机构的结构分析 (3)第3章平面连杆机构 (8)第4章凸轮机构及其设计 (15)第5章齿轮机构 (19)第6章轮系及其设计 (26)第8章机械运动力学方程 (32)第9章平面机构的平衡 (39)第一章绪论一、补充题1、复习思考题1)、机器应具有什么特征?机器通常由哪三部分组成?各部分的功能是什么?2)、机器与机构有什么异同点?3)、什么叫构件?什么叫零件?什么叫通用零件和专用零件?试各举二个实例。
4)、设计机器时应满足哪些基本要求?试选取一台机器,分析设计时应满足的基本要求。
2、填空题1)、机器或机构,都是由组合而成的。
2)、机器或机构的之间,具有确定的相对运动。
3)、机器可以用来人的劳动,完成有用的。
4)、组成机构、并且相互间能作的物体,叫做构件。
5)、从运动的角度看,机构的主要功用在于运动或运动的形式。
6)、构件是机器的单元。
零件是机器的单元。
7)、机器的工作部分须完成机器的动作,且处于整个传动的。
8)、机器的传动部分是把原动部分的运动和功率传递给工作部分的。
9)、构件之间具有的相对运动,并能完成的机械功或实现能量转换的的组合,叫机器。
3、判断题1)、构件都是可动的。
()2)、机器的传动部分都是机构。
()3)、互相之间能作相对运动的物件是构件。
()4)、只从运动方面讲,机构是具有确定相对运动构件的组合。
()5)、机构的作用,只是传递或转换运动的形式。
()6)、机器是构件之间具有确定的相对运动,并能完成有用的机械功或实现能量转换的构件的组合。
()7)、机构中的主动件和被动件,都是构件。
()2 填空题答案1)、构件2)、构件3)、代替机械功4)、相对运动5)、传递转换6)、运动制造7)、预定终端8)、中间环节9)、确定有用构件3判断题答案1)、√2)、√3)、√4)、√5)、×6)、√7)、√第二章 机构的结构分析2-7 是试指出图2-26中直接接触的构件所构成的运动副的名称。
7-1在如图7-32所示的轮系中,已知Z 1=15,Z 2=25,Z 2’=15,Z 3=30,Z 3’=15,Z 4=30,Z 4’=2(右旋),Z 5=60,Z 5’=20(m=4mm ),若n 1=500r/min ,求齿条6线速度v的大小和方向。
解:计算齿轮5的转速n 52345115512'3'4'253030602001515152z z z z n i n z z z z ⨯⨯⨯====⨯⨯⨯故:15155002.5 /min 200n n r i ===计算齿轮5’直径d 5’5'5'42080 d mz mm==⨯=故齿条6的线速度v6为55'655'2 2.5800.01047 /602601000n d v r m s ππω⨯⨯==⋅==⨯方向如图所示。
7-2在如图7-33所示的手摇提升装置中,已知各齿轮齿数为Z 1= 20,Z 2=50,Z 3=15, Z 4=30,Z 6=40,Z 7=18,Z 8=51,蜗杆Z 1=1且为右旋,试求传动比i 18,并指出提升重物时手柄的转向。
解:246811881357503040515682015118z z z z i z z z z ωω⨯⨯⨯====⨯⨯⨯提升重物时手柄的转向如图所示。
7-3在如图7-34所示的轮系中,已知各齿轮齿数为Z 1= 20,Z 2=30,Z 3=18, Z 4=68,齿轮1的转速n 1=500r/min ,试求系杆H的转速n H 的大小及方向。
解:1241441330685.672018H H H n n z z i n n z z -⨯==-=-=--⨯40n =115.6715022.496.67 6.67H HH n n n n n -====方向与n 1相同。
7-4在如图7-35所示的双级行星齿轮减速器中,各齿轮齿数为Z 1= Z 6 =20,Z 2=30,Z 3=Z 4=40,Z 2=Z 5=10,试求:(1) 固定齿轮4时的传动比i 1H2; (2) 固定齿轮3时的传动比i 1H2。
解:固定齿轮4时轮系如图所示,齿轮1,2,3组成定轴轮系,齿轮6,5,4和系杆H2组成行星轮系。
62544644265640220H H H n n z z z i n n z z z -==-=-=-=--4610, n n n ==,可得12212122/1213H H H H n n n n n i -=---=--=固定齿轮3时轮系如图所示,齿轮1,2,3组成行星轮系,齿轮6,5,4和系杆H2组成差动轮系。
62544644265640220H H H n n z z z i n n z z z -==-=-=-=-- 23311133112140220HH H z z z n n i n n z z z -==-=-=-=--30,n =,可得113H n n =,因为6141, H n n n n ==故143n n =则621214221212121223/12139/5H H H H H H H H n n n nn n n nn n n n i n n --==----=--==7-5如图7-36所示的复合轮系中,设已知n 1=3549r/min ,又各齿轮齿数为Z 1= 36,Z 2=60,Z 3=23,Z 4=49,Z 4’=69,Z 5=31,Z 6 =131,Z 7=94,Z 8=36,Z 9=167,试求行星轮架H的转速n H。
解:齿轮1,2,3,4组成定轴轮系,齿轮4’,5,6和7,8,9组成两个行星轮系。
12414413146049 3.5536233549999.5/min 3.55 3.55n z z i n z z n n r ⨯====⨯===4'75664'6674'54'131 1.9069H n n z z z i n n z z z -==-=-=-=--64'40,n n n ==解得7344.66/minn r =。
78997997871671.7894HH H n n z z z i n n z z z -==-=-=-=--90n =解得123.98/minH n r =。
7-6如图7-37a 、b 所示为两个不同结构的锥齿轮周转轮系,已知各齿轮齿数为Z 1= 20,Z 2=24,Z 2’=30,Z 3=40,n 1=200r/min ,n 3=-100r/min ,求两种结构中行星轮架H的转速n H?a) b)解:a)轮系为差动轮系23113312'3124401.620301.6 1.6(100)200600/min 0.60.6H H H H z z n n i n n z z n n n r -⨯====-⨯-⨯--===-b)轮系为差动轮系7-7在如图7-38所示的三爪电动卡盘的传动机构中,各齿轮齿数为Z 1= 6,Z 2= Z 2’=25,Z 3=57,Z 4=56,求传动比i 14。
解:30n =解得10.095H n n =。
解得:i 41=0.002,故i 14=1/ i 41=1/0.002=500。
7-8如图7-39所示为纺织机械中的差动轮系,各齿轮齿数为Z 1= 30,Z 2=25,Z 3=Z 4=24, Z 5=18,Z 6=121,n 1=48~200r/min ,n H=316r/min ,求n 6=?解:解得23113312'3124401.620301.6 1.6(100)20015.38/min 2.6 2.6H H H H z z n n i n n z z n n n r -⨯==-==--⨯+⨯-+===2331133121579.56HH H z z z n n i n n z z z -==-=-=-=--12414412'11414125569.336250.0959.330.09510.0959.33/0.095HH H n n z z i n n z z n n n n n n -⨯==-=-=--⨯-=---=--224611661352524121(1) 5.60302418H H H z z z n n i n n z z z -⨯⨯==-==-⨯⨯1616 4.648 4.6316268/min 5.6 5.64.6200 4.6316295/min 5.6 5.6H H n n n r n n n r ++⨯===++⨯===故n 6=268~295r/min 。
7-9如图7-40所示轮系中,已知Z 1= 22, Z 3=88, Z 3’=Z 5,试求传动比i 15=?解:左边为定轴轮系,右边为差动轮系533', ,H n n n n ==34553'553'43'1n z z zi n z z z ==-=-=-则:35,n n =-故解得i 15=9。
7-10如图7-41所示为手动起重葫芦,已知Z 1= Z 2’=10,Z 2= 20,Z 3=40,传动效率η=0.9,为提升重Q=10kN 的重物,求必须施加于链轮A上的圆周力P。
解:计算传动比i ABn A =n 1,n B =n H 。
故i AB =i 1H233113312188422H H H z z z n n i n n z z z -==-=-=-=--1555154/142n n n n n n -=----=--in A A A AAB out B B B BBA AB N PV P R PR i N QV Q R QR QR P R i ωηωη=====3 0,n =7-11在如图7-42所示的行星轮系中,已知各轮齿数Z 1,Z 2,Z 2’, Z 3, Z 3’和Z 4,试求传动比i 1H。
解:234114412'3'H HH z z z n n i n n z z z -==-4 0,n =234112'3'234112'3'/111H H z z z n n z z z z z z i z z z -=-=-23113312'204081010H H H z z n n i n n z z -⨯==-=-=--⨯11131/1819HH H H HAB n n n n i n i i --===---==10800.90.253209B A AB QR P kNR i η⨯===⨯。