2015-2016学年高中数学 第1章 3统计图表课时作业

§3统计图表课时目标会用统计图表分析数据，获取有用的信息，并明确四种统计图表各自的特点．1．统计图表是__________________的重要工具．2．四种常用的统计图表，______________、______________、____________、__________.一、选择题1．如图所示是从一批产品中抽样得到的数据的条形统计图，由图可看出数据出现机会最大的范围是( )A．(8.1,8.3) B．(8.2,8.4)C．(8.4,8.5) D．(8.6,8.7)2．把过期的药品随意丢弃，会造成对土壤和水体的污染，危害人们的健康．如何处理过期药品，有关机构随机对若干家庭进行调查，调查结果如图，其中对过期药品处理不正确的家庭达到( )A．79% B．80% C．18% D．82%3．某校为了了解学生的课外阅读情况，随机调查了50名学生，得到他们在某一天课外阅读所用时间的数据，结果用如图的条形图表示，根据条形图可得这50名学生这一天平均每人的课外阅读时间为( )A．0.6小时 B．0.9小时C．1.0小时 D．1.5小时A．0.13 B．0.39 C．0.52 D．0.645．一个容量为35的样本数据，分组后，组距与频数如下：[5,10)，5个；[10,15)，12个；[15,20)，7个；[20,25)，5个；[25,30)，4个；[30,35)，2个．则样本在区间[20，＋∞)上的频率为( )A．20% B．69%6．某市高三数学抽样考试中，对90分以上(含90分)的成绩进行统计，其频率分布直方图如图所示，若130～140分数段的人数为900人，则90～100分数段的人数为________．7．甲、乙两名运动员在某个赛季一些场次中得分的茎叶图如图所示，则水平发挥较好的运动员是______．8．将容量为n的样本中的数据分成6组，绘制频率分布直方图．若第一组至第六组数据的频率之比为2∶3∶4∶6∶4∶1，且前三组数据的频数之和等于27，则n＝________.9．下图是某保险公司提供的资料，在1万元以上的保险单中，有821少于2.5万元，那么不少于2.5万元的保险单有________万元．三、解答题10．为了对两个城市进行调查，在A、B两座城市各安放了仪器，测量两个城市的噪音的分贝数．为了解这两个城市的噪音情况，调查人员分别同时取12个时刻的声音分贝11．台州某校七(1)班同学分三组进行教学活动，对七年级400名同学最喜欢喝的饮料种类情况、八年级300名同学零花钱的最主要用途情况、九年级300名同学完成家庭作业时间情况进行了全面调查，并分别用扇形图、频数分布直方图、表格来描述整理得到的数据．九年级同学完成家庭作业时间情况统计表(1)七年级400名同学中最喜欢喝“冰红茶”的人数是多少？(2)补全八年级300名同学中零花钱的最主要用途情况的频数分布直方图；(3)九年级300名同学中完成家庭作业的平均时间大约是多少小时？(结果保留一位小数)能力提升1213．贵阳市是我国西部的一个多民族城市，总人口数为370万(2000年普查统计)．如图1和图2所示的是2000年该市各民族人口的统计图，请你根据统计图提供的信息回答下列问题．(1)2000年贵阳市少数民族的总人口数是多少？(2)2000年贵阳市总人口中的苗族所占的百分比是多少？(3)若2000年贵阳市参加中考的学生有40 000人，则参加中考的少数民族的学生人数约为多少？答案 知识梳理1．表达和分析数据 2.条形统计图 扇形统计图 折线统计图 茎叶图 作业设计 1．B 2.D3．B [由题意可知50人每人一天的课外阅读时间为150(5×0＋20×0.5＋10×1.0＋10×1.5＋5×2.0)＝0.9(小时)．] 4．C [样本数据落在[10,40)上的频数为13＋24＋15＝52，故其频率为52100＝0.52.]5．C [由题意，样本中落在[20，＋∞)上的频数为5＋4＋2＝11，∴在区间[20，＋∞)上的频率为1135≈0.31.]6．8 100解析 设该市高三总人数为x ，则0.005×10x ＝900，即x ＝18 000，∴90～100分数段的人数为18 000×0.045×10＝8 100.7．甲 8．60解析 ∵n·2＋3＋42＋3＋4＋6＋4＋1＝27，∴n ＝60.9．91解析 不少于1万元的占700万元的21%，为700×21%＝147万元.1万元以上的保险单中，超过或等于2.5万元的保险单占1321，金额为1321×147＝91(万元)，故不少于2.5万元的保险单有91万元．10．解 茎叶图表示如下．从茎叶图中可以看出，城市A 噪音环境好一些．11．解 (1)400×(1－25%－25%－10%)＝400×40%＝160(人)． (2)补全频数分布直方图如图所示．(3)1300(50×1＋80×1.5＋2×120＋2.5×50)≈1.78(小时)．12．解用条形统计图、折线统计图和扇形统计图来分别表示如下：由上可得，用条形统计图与扇形统计图来表示较为合适．13．解(1)15%×370＝55.5(万人)，即2000年贵阳市少数民族的总人口数是55.5万人．(2)40%×15%＝6%，∴2000年贵阳市总人口中的苗族所占的百分比是6%.(3)40 000×15%＝6 000(人)，即2000年贵阳市参加中考的少数民族的学生约有6 000人．11。

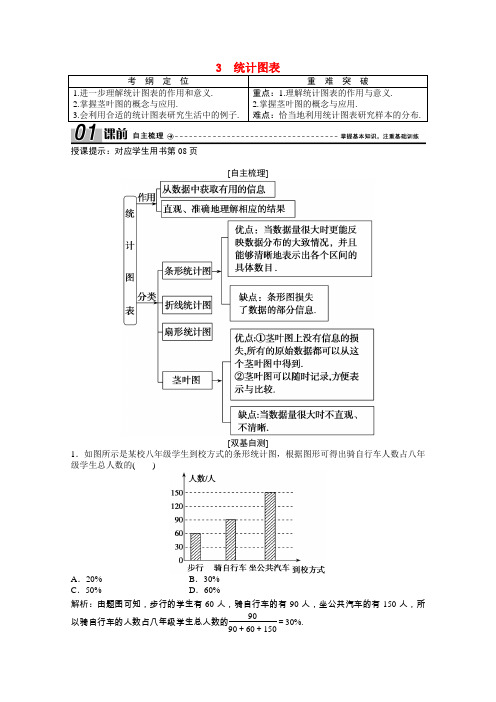
考纲定位重难突破1.进一步理解统计图表的作用和意义.2.掌握茎叶图的概念与应用.3.会利用合适的统计图表研究生活中的例子. 重点：1.理解统计图表的作用与意义.2.掌握茎叶图的概念与应用.难点：恰当地利用统计图表研究样本的分布.授课提示：对应学生用书第08页[自主梳理][双基自测]1．如图所示是某校八年级学生到校方式的条形统计图，根据图形可得出骑自行车人数占八年级学生总人数的()A．20%B．30%C．50% D．60%解析：由题图可知，步行的学生有60人，骑自行车的有90人，坐公共汽车的有150人，所以骑自行车的人数占八年级学生总人数的9090＋60＋150＝30%.答案：B2．如图为某校高三(1)班的男女比例图表，已知该班共有学生55人，则该班男生比女生约多()A．13人B．21人C．24人D．34人解析：55×(62%－38%)＝55×24%≈13(人)．答案：A3．如图表示8位销售员一个月销售商品数量的茎叶图，则销售数据分别为______(单位：百件)．解析：由茎叶图可知销售数据都是两位数，分别为45，45，52，56，57，58，60，63.答案：45，45，52，56，57，58，60，63授课提示：对应学生用书第08页探究一条件统计图[典例1]“国际无烟日”来临之际，小彬就公众在餐厅吸烟的态度进行了调查，并将调查结果制作成如图所示的统计图，请根据图中的信息回答下列问题：(1)被调查者中，不吸烟者中赞成在餐厅彻底禁烟的人数是多少？(2)被调查者中，希望在餐厅设立吸烟室的人数是多少？(3)求被调查者中赞成在餐厅彻底禁烟的频率；(4)某市现有人口370万，根据图中的信息估计这个城市现有人口中赞成在餐厅彻底禁烟的人数．[解析](1)由条形图可知，被调查者中，不吸烟者中赞成在餐厅彻底禁烟的有97人．(2)由条形图可知，被调查者中，希望在餐厅设立吸烟室的人共有35＋28＝63人．(3)由97＋2397＋23＋35＋28＋10＋7＝0.6，可知被调查者中赞成在餐厅彻底禁烟的频率为0.6.(4)因为370×0.6＝222，所以此城市现有人口中赞成在餐厅彻底禁烟的约有222万人．条形统计图分两种，一种是频数条形图(纵轴为频数)，另一种是频率条形图(纵轴为频率)．1．为了丰富校园文化生活，某校计划在午间校园广播台播放“百家讲坛”的部分内容．为了了解学生的喜好，抽取若干名学生进行问卷调查(每人只选一项内容)，整理调查结果，绘制统计图如图所示．请根据统计图提供的信息回答以下问题：(1)求抽取的学生数；(2)若该校有3 000名学生，估计喜欢收听易中天《品三国》的学生人数；(3)估计该校喜欢收听刘心武评《红楼梦》的女学生人数占全校学生人数的百分比． 解析：(1)从统计图上可以看出，喜欢收听于丹析《庄子》的男生有20人，女生有10人，喜欢收听《故宫博物馆》的男生有30人，女生有15人，喜欢收听于丹析《论语》的男生有30人，女生有38人，喜欢收听易中天《品三国》的男生有64人，女生有42人，喜欢收听刘心武评《红楼梦》的男生有6人，女生有45人，所以抽取的学生数为20＋10＋30＋15＋30＋38＋64＋42＋6＋45＝300(人)．(2)喜欢收听易中天《品三国》的男生有64人，女生有42人，共有106人，占所抽取总人数的比例为106300，由于该校有3 000名学生，因此可以估计喜欢收听易中天《品三国》的学生有106300×3 000＝1 060(名)．(3)该校喜欢收听刘心武评《红楼梦》的女学生人数约占全校学生人数的比例为45300×100%＝15%.探究二 折线统计图与扇形统计图[典例2] 右图是根据某市3月1日至3月10日的最低气温(单位：℃)的情况绘制的折线统计图，试根据折线统计图反应的信息，绘制该市3月1日到10日最低气温(单位：℃)的条形统计图和扇形统计图．[解析] 该城市3月1日至10日的最低气温(单位：℃)情况如下表： 日期 1 2 3 4 5 6 7 8 9 10最低气温－3－20－1120－12 2条形统计图如图所示．扇形统计图如图所示．1．折线统计图是用一个单位长度表示一定的数量，根据数量的多少描出各点，然后把各点用线段顺次连接起来．折线统计图不但可以表示出数量的多少，而且能够清楚地表示数量增减变化的情况，即折线统计图能够清晰地反映数据的变化情况．2．扇形统计图中，用圆面代表总体，圆面中的各个扇形分别代表总体中的不同部分，扇形的大小反映部分占总体的百分比的大小．扇形统计图可以很清楚地表示各部分数量同总数之间的关系，即扇形统计图能清楚地表示出各部分在总体中所占的百分比．2．某摩托车厂2015年第三、四季度各月产量如下表：月份789101112月产量(辆)300350450540700600解析：建立直角坐标系，用横坐标表示月份，用纵坐标表示月产量，描出每个月份的对应点，连成折线，得到折线统计图如图，由图可知，10月和11月这两个相邻月的月产量增长幅度最大．探究三 茎叶图[典例3] 某中学高二(2)班甲、乙两名学生自进入高中以来，每次数学考试成绩情况如下： 甲：95，81，75，91，86，89，71，65，76，88，94，110，107；乙：83，86，93，99，88，103，98，114，98，79，78，106，101.画出两人数学成绩的茎叶图，并根据茎叶图对两人的成绩进行比较．[解析] 甲、乙两人数学成绩的茎叶图如图所示．从这个茎叶图上可以看出，乙同学的得分情况是大致对称的，中位数是98；甲同学的得分情况也大致对称，中位数是88.因此乙同学的成绩比较稳定，总体情况比甲同学好．画茎叶图的步骤第一步，将数据分为“茎”(高位)和“叶”(低位)两部分．第二步，将表示“茎”的数字按大小顺序由上到下排成一列．第三步，将各个数据的“叶”按次序写在其茎的左、右两侧．3．某市各地中小学每年都要进行学生体质健康测试，测试总成绩满分为100分，规定测试成绩在[85，100]之间为体质优秀；在[75，85)之间为体质良好；在[60，75)之间为体质合格；在[0，60)之间为体质不合格．现从某校高三年级的300名学生中随机抽取30名学生的体质健康测试成绩，其茎叶图如下：(1)试估计该校高三年级体质为优秀的学生人数；(2)根据以上30名学生的体质健康测试成绩，现采用分层抽样的方法，从体质为优秀和良好的学生中抽取5名，则优秀与良好的学生应各抽多少名？解析：(1)根据题意，样本中体质为优秀的学生人数为10，故该校高三年级体质为优秀的学生人数为1030×300＝100. (2)依题意，体质为良好和优秀的学生人数之比为15∶10＝3∶2，所以从体质为良好的学生中抽取的人数为35×5＝3， 从体质为优秀的学生中抽取的人数为25×5＝2. 三种统计图的综合应用[典例]1957年世界人口30亿，17年后(即1974年)增加了10亿，即达到40亿；又过了13年达到50亿；到1999年全世界总人口达60亿．以此速度，人口学专家预测到2025年，世界人口将达到80亿；而到2050年人口将超过90亿，其中亚洲人口最多，将达到52.68亿，北美洲3.92亿，欧洲8.28亿，拉丁美洲及加勒比地区8.09亿，非洲17.68亿．有一位同学根据以上提供的数据制作了三幅统计图(如图(1)(2)(3))，请根据这些统计图完成下列问题．(1)三幅统计图分别表示了什么内容？(2)从哪幅统计图中最能看出世界人口的总体变化情况？(3)2050年非洲人口大约将达到多少亿？你是从哪幅统计图中得到这个数据的？(4)2050年亚洲人口比其他各洲人口的总和还要多，你从哪幅统计图中可以明显地得到这个结论？[解析](1)世界人口变化情况折线统计图清楚地反映了世界人口的变化情况；2050年世界人口分布预测扇形统计图反映了各洲人口在世界人口分布中所占的百分比；2050年世界人口分布预测条形统计图反映了各洲2050年的具体人口数．(2)从世界人口变化情况折线统计图中看出．(3)从2050年世界人口分布预测条形统计图中可得到，2050年非洲人口大约为17.68亿．(4)从2050年世界人口分布预测扇形统计图中得到．[感悟提高]同一问题用不同的统计图表表示出来，可根据各统计图表的特点、应用范围反映出不同的问题．针对需解决的问题及统计图表的功能，可选择画出相应的统计图表或用三种统计图综合解释现实生活中的问题．[随堂训练] 对应学生用书第10页1．如图是甲、乙、丙、丁四组人数的扇形统计图的部分结果，根据扇形统计图的情况可以知道丙、丁两组人数和为( )A ．250B ．150C ．400D ．300解析：甲组人数是120，占30%，则总人数是12030%＝400，则乙组人数是400×7.5%＝30，则丙、丁两组人数和为400－120－30＝250.答案：A2．对“小康县”的经济评价标准：①年人均收入不低于7 000元；②年人均食品支出不高于年人均收入的35%.某县有40万人，年人均收入如下表如示，年人均食品支出如图所示，则该年人均收入/元0 2 000 4 000 6 000 8 000 10 000 12 000 16 000 人数/万人 6 3 5 5 6 7 5 3A ．是小康县B ．达到标准①，未达到标准②，不是小康县C ．达到标准②，未达到标准①，不是小康县D ．两个标准都未达到，不是小康县 解析：由题中图表可知年人均收入为(2 000×3＋4 000×5＋6 000×5＋8 000×6＋10 000×7＋12 000×5＋16 000×3)÷40＝7 050(元)，达到了标准①；年人均食品支出为(1 400×3＋2 000×5＋2 400×13＋3 000×10＋3 600×9)÷40＝2 695(元)，则年人均食品支出占年人均收入的2 6957 050×100%≈38.2%>35%，未达到标准②.所以不是小康县．答案：B3．如图是某市5月1日至5月7日每天最高、最低气温的折线统计图，在这7天中，日温差最大的一天是________．解析：由图可知5月1日的温差为12 ℃，5月2日的温差为12 ℃，5月3日的温差为11 ℃，5月4日的温差为10.5 ℃，5月5日的温差为12.5 ℃，5月6日的温差为10 ℃，5月7日的温差为10 ℃.答案：5月5日。

课时作业 4 统计图表|基础巩固|(25分钟，60分)一、选择题(每小题5分，共25分) 1．对某校2017年高中毕业生去向调查如下A ．条形统计图B ．扇形统计图C ．折线统计图D ．茎叶图解析：扇形统计图、条形统计图和折线统计图，均可以将统计中的所有数据所占整体百分比直观显示出来，但最佳的统计图表应当是扇形统计图，其显示得更为直观．答案：B2．某市近几年连年干旱，市政府采取措施扩大水源，措施之一是投资增建水库，如图是该市目前水源结构的扇形统计图，根据图中圆心角的大小算出黄河水在总供水中所占的百分比是( )A ．64%B ．60%C ．54%D ．74%解析：230.4°360°×100%＝64%.故选A.答案：A3．如图①和图②分别是我国1997年～2000年全国初中生在校人数和全国初中学校数的统计图．由图可知，从1997年～2000年，我国初中生在校人数( )A．逐年增加，学校数也逐年增加B．逐年增加，学校数却逐年减少C．逐年减少，学校数也逐年减少D．逐年减少，学校数却逐年增加解析：由两个条形统计图可以看出，人数是逐年增加的，而学校数却在逐年减少．答案：B4．某超市连锁店统计了甲、乙两个城市的各16台自动售货机在中午12：00至13：00间的销售金额，并用茎叶图表示如图．则有( )A.甲城市销售额多，乙城市销售额不够稳定B．甲城市销售额多，乙城市销售额稳定C．乙城市销售额多，甲城市销售额稳定D．乙城市销售额多，甲城市销售额不够稳定解析：乙城市的销售额明显多于甲，且甲的销售额比乙分散，不够稳定．故选D.答案：D5．如图是2015年各级学校每10万人口中平均在校生的人数扇形统计图，则下列结论正确的是( )A．2015年有6%的高中生升入高等学校B．2015年全国高等学校在校生6 000人C．2015年各级学校10万人口平均在校生数高等学校学生占6%D．2015年高等学校的学生比高中阶段的学生多解析：由扇形统计图可以看出，2015年各级学校每10万人口中平均在校生的人数所占的百分比分别为：幼儿园占8%，高等学校占6%，高中阶段占12%，初中阶段占26%，小学占48%，A项中应是高等学校在校学生，B项中6 000人应是平均数，D项显然错误．答案：C二、填空题(每小题5分，共15分)6．某班一次单元测试后，解答题部分的抽样成绩的茎叶图如图所示，则图中内数字所表示的学生的原始成绩是________.解析：根据“茎”是十位数，“叶”是个位数，易知学生的原始成绩为45.答案：457．某售票窗口在3月1日至8日的售票情况如图所示，由图可知，售票最多的日期是________；售票最少的日期是________；前4天共售票________张．解析：由题图可知，售票最多的日期是3月2日；最少的日期是3月3日与3月7日；前4天共售票8＋14＋7＋12＝41(张)。

高中数学第一章统计 1.3 统计图表课后训练北师大版必修3A．都一样B．茎叶统计图C．扇形统计图D．折线统计图2．某校为了了解学生的课外阅读情况，随机调查了50名学生，得到他们在某一天各自课外阅读所用的时间的数据，结果用条形统计图(如下图)表示．根据条形统计图可得这50名学生这一天平均每人的课外阅读时间为( )．A．0.6小时 B．0.9小时 C．1.0小时 D．1.5小时3．如图所示的是某中学高一年级学生参加课外活动人数的扇形统计图，若参加舞蹈类课外活动的学生有42人，则参加球类活动的学生有( )．A．145人 B．147人 C．149人 D．151人4．如图是根据《山东统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图．图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字，右边的数字表示城镇居民百户家庭人口数的个位数字．从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为( )．A．304.6 B．303.6 C．302.6 D．301.65．甲、乙两个城市2010年4月中旬，每天的最高气温统计图如图所示，这9天里，气温比较稳定的城市是________．6．如图所示是CBA篮球联赛中，甲、乙两名运动员某赛季一场次得分的茎叶图，则平均得分高的运动员是________．7．某著名饮食品牌在某地开了甲、乙两家连锁店，一周内的每天回头客的数量统计结果如下：甲：52 51 49 48 53 48 49乙：60 65 40 35 25 65 60用茎叶图分析哪个连锁店的客源比较稳定．8．某同学从一本英文杂志中截取了含有1 200个字母的一段小文章，欲研究六个字母的使用频率，我们不妨用1,2,3,4,5,6来代替这六个字母，发现它们出现的次数分别为18,19,21,22,20,20.(1)列出样本数据的统计表；(2)画出数据的条形统计图；(3)画出数据的折线统计图．解：(1)统计表如下：某家电商场经销A，B，C三种品牌的彩电，五月份共获利48 000元．已知A种品牌彩电每台可获利100元，B种品牌彩电每台可获利144元，C种品牌彩电每台可获利360元．请你根据相关信息，补全彩电销售台数的条形统计图和所获利润的百分数的扇形统计图(如图所示)．各品牌彩电销售台数的条形统计图各品牌彩电所获利润的百分数的扇形统计图参考答案1. 答案：C2. 答案：B解析：这50名学生这一天平均每人的课外阅读时间为(0×5＋0.5×20＋1.0×10＋1.5×10＋2.0×5)÷50＝0.9(小时)．3. 答案：B解析：设参加球类活动的学生有x 人，根据统计图得1264236012614454x =-(++)，解得x ＝147.故选B. 4. 答案：B解析：由茎叶图可知1997年至2006年我省城镇居民百户家庭的人口数分别为291,291,295,298,302,306,310,312,314,317.故平均数为110(291＋291＋295＋298＋302＋306＋310＋312＋314＋317)＝303.6.5. 答案：甲城市6. 答案：甲7. 解：茎叶图如下：由茎叶图看出，甲连锁店的回头客数量比较集中，所以甲连锁店的客源比较稳定． 8.(2)(3)数据的折线统计图如图所示9. 解：从条形统计图可知，销售A 种品牌彩电的数量为120台， 所以销售A 种品牌彩电共获利：120×100＝12 000(元)， 所以A 种品牌彩电所获利润的百分数为12000100%25%48000⨯＝.从扇形统计图可知，B 种品牌彩电所获利润的百分数为30%， 所以销售B 种品牌彩电共获利：48 000×30%＝14 400(元)， 由于B 种品牌彩电每台可获利144元，所以销售B种品牌彩电的数量为14 400÷144＝100(台)．根据扇形统计图中所有扇形表示的百分比之和为1，所以C种品牌彩电所获利润的百分数为1－30%－25%＝45%，所以销售C种品牌彩电共获利：48 000×45%＝21 600(元)，由于C种品牌彩电每台可获利360元，所以销售C种品牌彩电的数量为21 600÷360＝60(台)．补全彩电销售台数的条形统计图和所获利润的百分数的扇形统计图如下图所示．各品牌彩电销售台数的条形统计图各品牌彩电所获利润的百分数的扇形统计图。

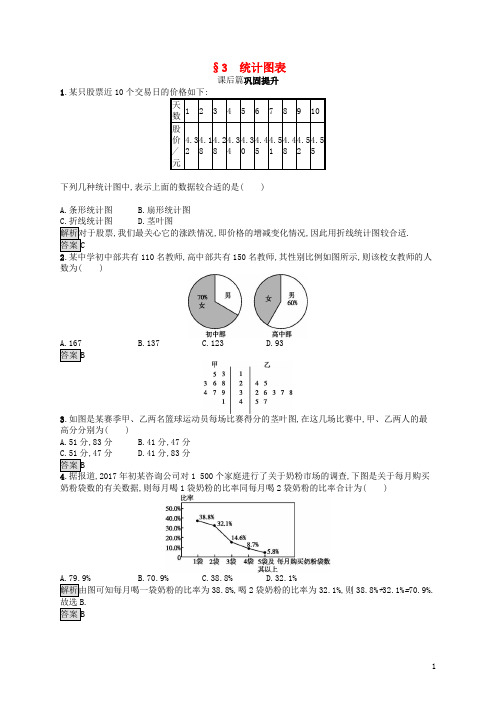
§3统计图表课后篇巩固提升1.某只股票近10个交易日的价格如下:天数1 2 3 4 5 6 7 8 9 10股价/元4.324.184.284.344.34.454.514.484.524.55下列几种统计图中,表示上面的数据较合适的是()A.条形统计图B.扇形统计图C.折线统计图D.茎叶图解析对于股票,我们最关心它的涨跌情况,即价格的增减变化情况,因此用折线统计图较合适.答案C2.某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为()A.167B.137C.123D.93答案B3.如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,在这几场比赛中,甲、乙两人的最高分分别为()A.51分,83分B.41分,47分,47分 D.41分,83分答案B,2017年初某咨询公司对1 500个家庭进行了关于奶粉市场的调查,下图是关于每月购买奶粉袋数的有关数据,则每月喝1袋奶粉的比率同每月喝2袋奶粉的比率合计为()9% B.70.9% C.38.8% D.32.1%解析由图可知每月喝一袋奶粉的比率为38.8%,喝2袋奶粉的比率为32.1%,则38.8%+32.1%=70.9%.答案B5.某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用的时间的数据,结果用下面的条形统计图表示.根据条形统计图可得这50名学生这一天平均每人的课外阅读时间为()A.0.6时B.0.9时C.1.0时D.1.5时解析这50名学生这一天平均每人的课外阅读时间为(0×5+0.5×20+1.0×10+1.5×10+2.0×5)÷50=0.9(时).答案B6.一家大型公司共有员工1 000名,为了比较他们的收入状况,公司收集了他们9月份的工资数据共1 000个,要比较该公司员工的收入差距,用统计图比较简便.解析由于1 000个数据是比较多的,因此用茎叶图不现实.如果用折线统计图,绘图是一个很复杂的工作,而采用条形统计图,可以看出员工的收入差别情况,故采用条形统计图最为简便.答案条形7.某班学生在课外活动中参加文娱、美术、体育小组的人数之比为3∶1∶6,则在扇形统计图中表示参加体育小组人数的扇形对应的圆心角的度数是.解析所求圆心角的度数是×100%×360°=216°.答案216°,分别随机抽取了16台,记录了某一上午各自的销售情况(单位:元):甲:18,8,10,43,5,30,10,22,6,27,25,58,14,18,30,41;乙:22,31,32,42,20,27,48,23,38,43,12,34,18,10,34,23.(1)请你画出这两组数据的茎叶图;(2)将这两组数据进行比较分析,你能得到什么结论?解:(1)这两组数据的茎叶图如图所示.(2)甲城市该上午的销售情况不太稳定;乙城市该上午的销售情况比较稳定.9.导学号36424010为了了解学生参加体育活动的情况,某校对学生进行了随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4种情况可供选择:①1.5时以上②1~1.5时③0.5~1时④0.5时以下下图是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:(1)本次一共调查了多少名学生.(2)在图(1)中将②对应的部分补充完整.若该校有3 000名学生,你估计全校有多少名学生平均每天参加体育活动的时间在0.5时以下? 解(1)从题图中知,选①的共60人,占总人数的百分比为30%,所以总人数为60÷30%=200,即本次一200名学生.(2)被调查的学生中,选②的有200-60-30-10=100(人),补充完整的条形统计图如图所示.(3)3 000×5%=150,估计全校有150名学生平均每天参加体育活动的时间在0.5时以下.。

课时作业05统计图表
(限时：10分钟)
1．下面哪种统计图没有数据信息的缺失，所有的原始数据都可以从该图中得到( A．条形统计图B．茎叶图
(限时：30分钟) 南美洲面积占地球陆地总面积的11.9%；
北美洲面积占地球陆地总面积的16.1%；
．乙
．无法确定
由茎叶图知甲的成绩有7次集中在80～90间，而乙的成绩则比较分散，故甲的成绩要比乙的成绩要稳定．
由图容易看出甲组成绩较集中，即甲组的成绩更整齐一些．
．某地农村某户农民年收入如下(单位：元)：
打工收入养殖收入其他收入
3 600 2 357843 请用不同的统计图来表示上面的数据．。

统计图表-备课资料1.. 2.计图表3.练习1.14012010080604020140年份12010080604020.时间时间该市总人口×该县..4 4 4333份4443333.示2211..入..我们用条形图和折线图表示上面数据.56129130133134135136138141142143144145绩人数6129130133134135136138141142143144145成绩人数5.我们可以用象形统计图、条形图、茎叶图来分别表示：甲乙976611525400094112233445586438639831 图1－3－30 乙11223344556600101020203030404050506060得分得分频数频数1002345甲乙5 25 49 76 6 1 19 483 4 63 6 83 8 91图1－3－31 图1－3－326.我们可先对每位同学进行调查，把他们一周的活动时间记录下来，然后对数据进行初步整理，最后从学过的四种统计表中选择其中的一种或几种把它们表示出来.根据数据的特点，我们可以采用象形统计图、条形统计图、茎叶图来表示，但最宜用茎叶图来表示，不但形象.而且信息也不会丢失.在进行调查时，要设计科学、合理的调查方案，以利于数据的搜集.互动学习知识链接1.常用抽样方法有哪些?它们各自有什么特点?我们用普查或抽查的方法搜集2.请选择适当的抽样方法解决下列问题.（1）从50名同学中抽取10名同学进行智商测试；（2）对我国各类职业的年收入情况作一个调查；21世纪（3）对10000件产品抽样调查其质量状况.答案：1.常用抽样方法有简单随机抽样、分层抽样、系统抽样.各自特点分别为：简单随机抽样：简便易行，一般适用于总体的个体数较少的情况.分层抽样：主要适用于总体由明显差异的几部分组成的情形.系统抽样：主要适用于总体无明显差异的几部分组成并且总体中的个体数较多的情况.2.（1）简单随机抽样.因为总体中的个体数较少，用最简单的简单随机抽样较好.（2）分层抽样.因为不同的职业，其年收入差距较大，为此可按职业类别进行分层.（3）系统抽样.因为总体中的个体数较大，并且又无明显差异的几部分组成，故选用系统抽样. 到数据，但搜集到的数据一般乱而多，我们无法将其包含的信息统统理解并加以表达，这就需要对数据进行整理和分析，将其转化成可以直接利用的形式，并从中获取相应的信息，统计图表正是表达和分析数据的重要工具，并且还可以直观地、准确地理解相应结果.知识总结在统计活动中，一个很重要的步骤是对调查数据进行整理，而整理数据的常用方法有统计表和统计图，用统计图来表示统计数据，显得更加直观、形象. 常用的统计图有条形统计图、扇形统计图、折线统计图和茎叶统计图.它们都有各自的特点和用途.其中条形统计图的特点是便于看出和比较各种数量的多少；扇形统计图能够清楚地表示出各部分在总体中所占的百分比；折线统计图不但可以表示出数量的多少，而且能够清楚地表示数量增减变化的情况；茎叶统计图有两个突出的优点：其一，统计图上没有信息的损失，所有的原始数据都可以从茎叶图中得到，其二，茎叶图可以随时记录，方便表示与比较.但是，当数据量很大或有多组数据时，茎叶图就不那么直观、清晰了.条形统计图虽然损失了数据的部分信息，但当数据量很大时，却更能直观地反映数据分布的大致情况，并且能够清晰地表示出各个区间的具体数目.在面对实际问题时，我们常常根据不同的需要，结合各种统计图的特点，选择合适的统计图来进行表示.。

§3统计图表一、非标准1.某支股票近10个交易日的价格如下:天数 1 2 3 4 5 6 7 8 9 10股价/元4.324.184.284.344.34.454.514.484.524.55下列几种统计图中,表示上面的数据较合适的是( )A.条形统计图B.扇形统计图C.折线统计图D.茎叶图解析:对于股票,我们最关心它的涨跌情况,即价格的增减变化情况,因此用折线统计图较合适.答案:C2.某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用的时间的数据,结果用条形统计图(如下图)表示.根据条形统计图可得这50名学生这一天平均每人的课外阅读时间为( )A.0.6时B.0.9时C.1.0时D.1.5时解析:这50名学生这一天平均每人的课外阅读时间为(0×5+0.5×20+1.0×10+1.5×10+2.0×5)÷50=0.9(时).答案:B3.如图是甲、乙、丙、丁四组人数的扇形统计图的部分结果,根据扇形统计图的情况可以知道丙、丁两组人数和为( )A.250B.150C.400D.300解析:甲组人数是120,占30%,则总人数是=400.则乙组人数是400×7.5%=30,则丙、丁两组人数和为400-120-30=250.答案:A4.如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得的最高分分别为( )A.51,83B.41,47C.51,47D.41,83答案:B5.甲、乙两班学生的体育成绩的条形统计图如图所示,不用计算,体育成绩好的班级是( )A.甲班B.乙班C.甲、乙一样D.无法确定解析:由两个条形统计图中各部分的人数可知乙班学生的体育成绩好一些.答案:B6.某校开展“爱我海西、爱我家乡”摄影比赛,9位评委对参赛作品A给出的分数如茎叶图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91.复核员在复核时,发现有一个数字(茎叶图中的x)无法看清.若记分员计算无误,则数字x应该是( )A.1B.2C.4D.6解析:若x≤4,因为平均分为91,所以总分应为637,即637=89+89+92+93+92+91+90+x,所以x=1.若x>4,637≠89+89+92+93+92+91+94=640,不合题意.答案:A7.某班学生在课外活动中参加文娱、美术、体育小组的人数之比为3∶1∶6,则在扇形统计图中表示参加体育小组人数的扇形对应的圆心角的度数是.解析:所求圆心角的度数是×100%×360°=216°.答案:216°8.如图是某市5月1日至5月7日每天最高、最低气温的折线统计图,在这7天中,日温差最大的一天是,最大日温差等于℃.解析:逐一计算发现,5月5日的日温差最大,最大日温差为24.5-12=12.5(℃).答案:5月5日12.59.如图①②是某单位的各项支出情况,根据图中提供的信息,回答下列问题:(1)2013年管理费支出的金额是多少?(2)2013年总支出比2012年增加多少?增加了百分之几?解:由题图①可知2013年的总支出为8万元,2012年总支出为6万元;由题图②可知管理费占总支出的10%.(1)2013年管理费支出为8×10%=0.8(万元).(2)2013年总支出比2012年增加8-6=2(万元),比2012年增加了≈33.33%.10.有关部门从甲、乙两个城市所有的自动售货机中,分别随机抽取了16台,记录了某一上午各自的销售情况(单位:元):甲:18,8,10,43,5,30,10,22,6,27,25,58,14,18,30,41;乙:22,31,32,42,20,27,48,23,38,43,12,34,18,10,34,23.(1)请你画出这两组数据的茎叶图;(2)将这两组数据进行比较分析,你能得到什么结论?解:(1)这两组数据的茎叶图如图所示.(2)甲城市该上午的销售情况不太稳定;乙城市该上午的销售情况比较稳定.。