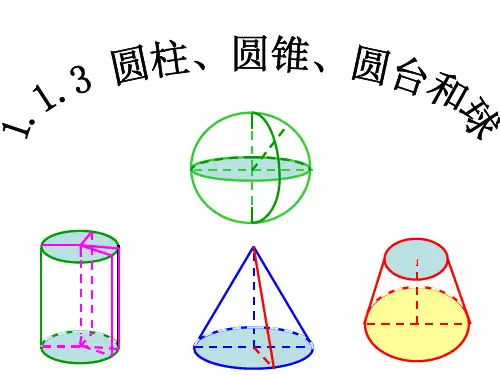
圆柱、圆锥、圆台、球

似三角形的性质得
3 r 3 l 4r
解得l=9.
所以，圆台的母线长为9cm.
例2. 我国首都北京靠近北纬40度。
求北纬40度纬线的长度约为多少千米 （地球半径约为6370千米）?
解：如图，设A是北纬40°圈上一点，AK 是它的半径，所以 OK⊥AK，
设c是北纬40°的纬线长， 因为∠OAK= ∠AOB = 40°，
3．表示方法：用表示它的轴的字母表示， 如圆柱OO’ .
4．有关性质： （1）用平行于底面的平面去截，截面都 是圆。 （2）圆柱、圆锥、圆台的轴截面分别是 全等的矩形、全等的等腰三角形、全等的 等腰梯形；
5.侧面展开图：
（1）圆柱的侧面展开图是矩形。 （2）圆锥的侧面展开图是扇形. （3）圆台的侧面展开图是扇环.
所以 c=2π·AK=2π·OA·cos∠OAK =2π·OA·cos40° ≈2×3.1416×6370×0.7660 ≈3.066×104(km)，
即北纬40°的纬线长约为3.066×104km.
练习： 1、圆柱的轴截面是正方形，它的面
h
积为9 ,求圆柱的高与底面的周长。
(h=3， c=2πr=3π)
即O到截面圆心O1的距离；
（4）大圆与小圆：球面被经过球心的平面截 得的圆叫做球的大圆， 被不经过球心的平面截得的圆叫做球 的
小圆；
5．球面距离：在球面
上，两点之间的最短距
离就是经过这两点的大
A
圆在这两点间的一段劣
弧的长度。这个弧长叫 B
做两点的球面距离。
O
三．旋转体的概念
由一个平面图形绕着一条直线旋转产生的 曲面所围成的几何体叫做旋转体，这条直线 叫做旋转体的轴。比如常见的旋转体有圆柱、 圆锥、圆台和球.

矩形
O
(3)平行于轴的边旋转而成的 曲面叫做圆柱的侧面. (4)无论旋转到什么位置,不垂直 于轴的边都叫做圆柱的母线.
A’
O
B’
A
O1
B
侧面 轴
母线 底面
2、圆柱的表示法：用表示它的轴的字母 表示，如圆柱OO1.
二、 圆锥的结构特征:
S
S
直角三角形
O A
1、定义:以直角三角形 的一条直角边所在直线 为旋转轴，其余两边旋 转而成的面所围成的旋 转体叫做圆锥.
柱、锥、台体的关系 棱柱、棱锥、棱台之间有什么关系？圆柱、圆锥、 圆台之间呢？柱、锥、台体之间有什么关系？
上底扩大 上底缩小
柱
台
锥
体
上底扩大
体
上底缩小
体
旋转体
例1 将下列平面图形绕直线AB旋转一周， 所得的几何体分别是什么？
B B B A 图3
A
A 图1
图2
BAC 45 例2 如图，AB为圆弧BC所在圆的直径， . 将这个平面图形绕直线AB旋转一周，得到一个组 合体，试说明这个组合体的结构特征.
线是圆柱的母线．
（
）
（2）圆台所有的轴截面是全等的等腰梯形．（ ）
（3）与圆锥的轴平行的截面是等腰三角形．（ ）
多面体
旋转体
简单几何体
旋转体 多面体
球
圆 柱
圆 锥
圆 台
棱 柱
棱 锥
棱 台
几何体的分类
柱体
锥体
台体
球
简单几何体的结构特征
柱体 棱柱 圆柱
锥体
台体 棱台 圆台
球
棱锥 圆锥
台体与锥体的关系 圆台和棱台统称为台体．它们是由平行与底面的 平面截锥体，得到的底面和截面之间的部分．

2．圆柱、圆锥、圆台的关系
探究点 1 旋转体的结构特征 判断下列各命题是否正确．
(1)一直角梯形绕下底所在直线旋转一周，所形成的曲面围成 的几何体是圆台； (2)圆锥、圆台中过轴的截面是轴截面，圆锥的轴截面是等腰 三角形，圆台的轴截面是等腰梯形； (3)到定点的距离等于定长的点的集合是球．
【解】 (1)错误．直角梯形绕下底所在直线旋转一周所形成 的几何体是由一个圆柱与一个圆锥组成的简单组合体，如图 所示．
(3)圆台的截面 ①平行于圆台底面的截面都是圆面，如图(1)所示．
②过轴的截面(简称轴截面)是全等的等腰梯形，如图(2)所示． ③圆台的母线 l、高 h 和上下两底面圆的半径 r、R 组成一个 直角梯形，且有 l2＝h2＋(R－r)2 成立，圆台的有关计算问题， 常归结为解这个直角梯形．
(4)球的截面 ①球心和截面圆心的连线垂直于截面． ②球心到截面的距离 d 与球的半径 R 及截面圆的半径 r 有如 下关系：r＝ R2－d2．
简单组合体的结构特征
1．圆柱、圆锥、圆台、球的结构特征
定义及结构特征
图形及记法
定义：以__矩__形____的一边所在 直线为旋转轴，其余三边旋转
形成的面所围成的旋转体叫做
圆柱
_圆__柱_____ 特征：(1)圆柱的轴垂直于底面，
所有母线互相平行且相等
记作：__圆__柱__O__′O____
(2)底面是平行且全等的两个圆
截得圆台的圆锥的母线长为 12 cm，求圆台的母线长．
【解】 如图是圆台的轴截面，由题意知 AO＝
2 cm，A′O′＝1 cm，SA＝12 cm．
由 A′O′ ＝ SA′ ， 得 AO SA
SA′
＝
A′O′ AO

圆柱圆锥圆台球的表面积和体积圆柱、圆锥、圆台、球是我们数学中经常遇到的几何图形，它们的表面积和体积也是我们需要掌握的基本概念。

下面我们来分别介绍它们的表面积和体积。

一、圆柱圆柱是由一个圆形和一个平行于圆底的矩形组成的几何体。

它的表面积包括圆底面积、侧面积和顶面积三部分。

其中，圆底面积为πr²，侧面积为2πrh，顶面积同圆底面积为πr²。

因此，圆柱的表面积为2πr²+2πrh。

圆柱的体积为底面积乘以高，即V=πr²h。

二、圆锥圆锥是由一个圆锥形底面和一个顶点连通而成的几何体。

它的表面积包括锥底面积、侧面积和母线长度三部分。

其中，锥底面积为πr²，母线长度为l=√(h²+r²)，侧面积为πrl。

因此，圆锥的表面积为πr²+πrl。

圆锥的体积为底面积乘以高再除以3，即V=πr²h/3。

三、圆台圆台是由一个圆形底面和一个上方与底面平行的圆环面连通而成的几何体。

它的表面积包括圆底面积、圆环侧面积和上底面积三部分。

其中，圆底面积为πr₁²，上底面积为πr₂²，圆环侧面积为π(r₁+r₂)l，其中l为斜高。

因此，圆台的表面积为πr₁²+πr₂²+π(r₁+r₂)l。

圆台的体积为底面积乘以高再除以3，即V=(πr₁²+πr₂²+πr₁r₂)h/3。

四、球球是由一个圆形转动一周形成的几何体，它的表面积和体积是所有几何体中最容易计算的。

球的表面积为4πr²，球的体积为4/3πr³。

圆柱、圆锥、圆台、球的表面积和体积都是由其底面积和高或半径计算得出的。

通过学习和掌握这些几何体的公式，我们可以更好地理解和运用它们在实际生活中的应用。

以半圆的直径所在直线为旋转轴,半圆面旋转一周形 成的旋转体叫做球体,简称球
有关 半圆的圆心叫做球的球心;半圆的半径叫做球的半径;
概念 半圆的直径叫做球的直径
图形
表示 球常用表示球心的字母表示,如上图中的球表示为球 法O
1 2 34
知识梳理
知识拓展1.球面的定义:与定点的距离等于定长的所有点的集合 (轨迹)叫做球面.
3.圆台
定义
用平行于圆锥底面的平面去截圆锥,底面与截面之间的部 分叫做圆台(圆台也可以看作是以直角梯形垂直于底边的 腰为旋转轴,其余三边旋转形成的面所围成的旋转体)
图形
有关概 念
原圆锥的底面和截面分别叫做圆台的下底面和上底面.与 圆柱和圆锥一样,圆台也有轴、侧面、母线,如上图所示, 轴为 O'O,A'A,B'B 为母线
概念 叫做圆锥的顶点,OA(或 OB)叫做底面☉O 的半径 表示 圆锥用表示它的轴的字母表示,上图中的圆锥可表示为 法 圆锥 SO
规定:棱锥与圆锥统称为锥体.
知识梳理
1 2 34
归纳总结圆锥的简单性质: (1)圆锥有无数条母线,它们有公共点即圆锥的顶点,且长度相等.
(2)平行于底面的截面都是圆,如图①所示. (3)过轴的截面都是全等的等腰三角形,如图②所示. (4)过任意两条母线的截面是等腰三角形,如图③所示.
12
2.圆柱、圆锥、圆台、球的结构特征比较 剖析:如下表所示.
结构特征 圆柱
两个底面
底面
是平行且
形状
半径相等
的圆
侧面
展开
矩形
图形状
母线
平行且相 等
圆锥 只有一个 底面,且底 面是圆
扇形
相交于顶 点

组合体
简单组合体
日常生活中我们常用到的日用品，比如：消毒液、 暖瓶、洗洁精等的主要几何结构特征是什么？ 由柱、锥、台、球组成了一些简单的组合体．认 识它们的结构特征要注意整体与部分的关系．
圆柱
圆台
圆柱
简单组合体
走在街上会看到一些物体，它们的主要几何结构特 征是什么？
简单组合体
一些螺母、带盖螺母又是有什么主要的几何结构特 征呢？
90° 60° 66.5°北极圈
40°
20° 30° 0° 20° 40° 60° 90° 60° 90° 120° 150° 赤道 23.5° 南回归线 23.5° 北回归线
南极圈 66.5°
P地的纬度就是经过 P点的球半径和赤道 平面所成的线面角 ∠POA的度数
北极
G
r R
P
O
A
南极
球面离
简单组合体
蒙古大草原上遍布蒙古包，那么蒙古包的主要几 何结构特征是什么？
简单组合体
居民的住宅又有什么主要几何结构特征？
简单组合体
下图是著名的中央电视塔和天坛，你能说说它们的 主要几何结构特征吗？
你能从旋转体的概念说说它们是由什么图形旋转而 成的吗？
旋转体
你能想象这条曲线绕轴旋转而成的几何图形吗？
O S
O
2、表示：如圆锥SO。
圆台
O1 O
用一个平行于圆锥底面的平面去截 圆锥,底面与截面之间的部分是圆台.
思考：圆柱、圆锥和圆台都是旋转体，当 底面发生变化时，它们能否互相转化？
上底扩大 上底缩小
思考：圆柱、圆锥、圆台过轴的截面分 别是什么图形？
例1. 用一个平行圆锥底面的平面截这个 圆 锥，截得圆台上下底面半径的比是1：4，截 去的圆锥的母线长是3cm,求圆台的母线长。

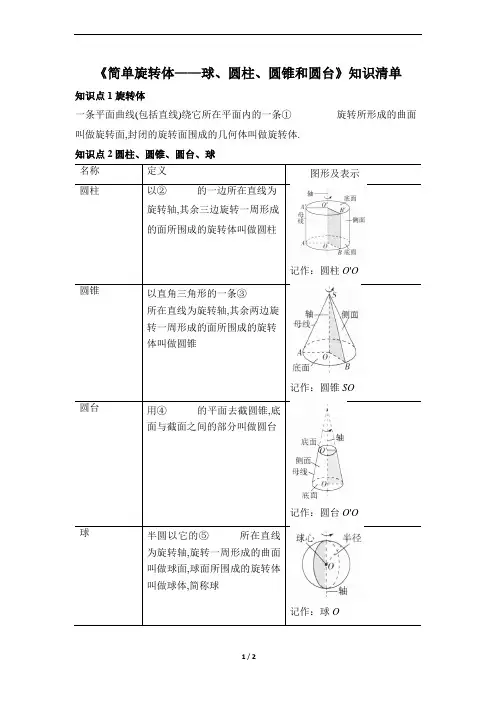
《简单旋转体——球、圆柱、圆锥和圆台》知识清单
知识点1 旋转体
一条平面曲线(包括直线)绕它所在平面内的一条①_________旋转所形成的曲面叫做旋转面,封闭的旋转面围成的几何体叫做旋转体.
知识点2圆柱、圆锥、圆台、球
记作：圆柱O'O
记作：圆锥SO
记作：圆台O'O
记作：球O
【答案】
①定直线②矩形③直角边④平行于圆锥底面⑤直径
【知识辨析】判断正误, 正确的画“√”, 错误的画“×”.
1.圆锥、圆台中过轴的截面是轴截面,圆锥的轴截面是等腰三角形,圆台的轴截面是等腰梯形.( )
2.圆台上底面圆周上任意一点与下底面圆周上任意一点的连线都是圆台的母线.( )
【答案】
1.√
2.×经过圆台的轴的平面截圆台得到的等腰梯形的腰才是圆台的母线.如图,
PP
1是母线,而PB不是母线.。

图中圆柱表示为 圆柱O′O _________
类别
定义 直角三角 以_________ 形的一条直 ___________ 角边 _____所在直 线为旋转轴, 其余两边旋 转形成的面 所围成的旋 转体
相关概念
图形
圆 锥
轴 旋转轴 轴：_______叫做圆锥的轴. 垂直于轴的边 侧面 底面：_____________旋转 直角三 而成的圆面.侧面：_______ 母线 角形的斜边 ___________旋转而成的曲 面.母线：无论旋转到什么 不垂直于轴的边 位置,_______________.锥 底面 棱锥和圆锥 体：___________统称为 锥体 图中圆锥表示 圆锥SO 为_______
图形 半径
球
直径 球O 图中的球表示为____
2.简单组合体的结构特征
(1)概念：由简单几何体组合而成的几何体.
拼接 (2)两种基本形式：一种是由简单几何体_____而成,一种是由
截去 挖去 简单几何体_____或_____一部分而成.
1.“判一判”理清知识的疑惑点(正确的打“√”,错误的打 “×”). (1)圆台的母线与轴平行.( ) ) )
类别
定义
相关概念 轴：圆锥的轴.底面： 截面 圆锥的底面和_____.侧 底 面：圆锥的侧面在___ 面与截面 _________之间的部分. 母线：圆锥的母线在底 面与截面之间的部分. 棱台和圆台 台体：___________统 称为台体
图形 底面 侧面 母线
轴
圆 台
平行于 用_______圆 锥底面的平 面去截圆锥, 截面 底面与_____ 之间的部分
试着解答下面的问题,并归纳常见组合体的类型及识别组 合体的要诀. 1.如图所示的组合体的结构特征是( A.由两个四棱锥组合成的 B.由一个三棱锥和一个四棱锥组合成的 C.由一个四棱锥和一个四棱柱组合成的 D.由一个四棱锥和一个四棱台组合成的 )

图形
用表示它的轴的字母，即表示两底面__圆__心____的字母表示，上图 表示法 中的圆柱可记作圆柱___O_′_O_____ 规定 __圆__柱____和__棱__柱____统称为柱体
[归纳总结] 圆柱的简单性质： (1)圆柱有无数条母线，它们互相平行且相等． (2)平行于底面的截面是与底面大小相同的圆，如图①所示． (3)过轴的截面(轴截面)都是全等的矩形，如图②所示． (4)过任意两条母线的截面是矩形，如图③所示．
⑥球的半径是球面上任意一点和球心的连线段； ⑦球面上任意三点可能在一条直线上； ⑧用一个平面去截球，得到的截面是一个圆面． [思路分析] 准确理解旋转体的定义，在此基础上掌握各旋转体的性质，才 能更好地把握它们的结构特征，以作出准确的判断． [解析] ①以直角三角形的一条直角边为轴旋转一周才可以得到圆锥；②以 直角梯形垂直于底边的一腰为轴旋转一周可得到圆台；③它们的底面为圆面； ④正确；作球的一个截面，在截面的圆周上任意取四点，则这四点就在球面 上，故⑤错误；根据球的半径定义可知⑥正确；球面上任意三点一定不共线， 故⑦错误；用一个平面去截球，一定截得一个圆面，故⑧正确．
在 Rt△SOA 中，∠ASO＝45°，所以 SO＝AO＝3x cm， 又 SO′＝A′O′＝x cm，所以 OO′＝2x cm. 又 S 轴截面＝12×(2x＋6x)×2x＝392(cm2)，所以 x＝7. 综上可知，圆台的高 OO′＝14 cm，母线长 AA′＝ 2OO′＝14 2(cm)， 上、下底面半径分别为 7 cm 和 21 cm.
综上可知，圆台的高 OO′＝14 cm，母线长 AA′＝ 2OO′＝14 2(cm)， 上、下底面的半径分别为 7 cm 和 21 cm.
方法二 圆台的轴截面如图所示，根据题意可设圆台的上、下底面半径分别 为 x cm 和 3x cm，延长 AA′，BB′交 OO′的延长线于点 S(O′，O 分别为上、 下底面圆心)．

o′
o
圆台的性质: 1、圆台的母线长都相等. 2、平行于底面的截面 都是圆. 3、圆台的轴通过两底面圆的圆心,并 且与底面垂直. 4、轴截面(经过圆台轴的平面截圆台所得的 截面)是全等的等腰梯形,腰长就是母线长.
例1 .用一个平行于圆锥底面的平面截这 个圆锥，截得圆台上下底面半径的比是 1 ：4，截去的圆锥的母线长是3cm，求 圆台的母线长.
圆锥的性质:
①圆锥的轴通过底面圆的圆心,并且 与底面垂直. ②圆锥的母线长都相等.
③平行于底面的截面都是圆. ④轴截面(经过圆锥轴的平面截圆锥所 得的截面)是全等的等腰三角形. ⑤圆锥的侧面展开图是扇形,底面圆周长 与母线长分别对应扇形的弧长和半径.
知识探究（三）：圆台的结构特征
思考1:用一个平行于圆锥底面的平面去 截圆锥，截面与底面之间的部分叫做圆 台.圆台可以由什么平面图形旋转而形成？
顶点
轴 母线
底面
侧面
母线
旋转轴叫做圆锥的轴，垂直于轴的边旋转 而成的圆面叫做圆锥的底面，斜边旋转而 成的曲面叫做圆锥的侧面，斜边在旋转中 的任何位置叫做圆锥侧面的母线.
思考3：经过圆锥任意两条母线的截面是 什么图形？
思考4：经过圆锥的轴的截面称为轴截面， 你能说出圆锥的轴截面有哪些基本特征 吗？
以矩形的一边所在直线为旋转轴，其 余三边旋转形成的面所围成的旋转体.
思考2：在圆柱的形成中，旋转轴叫做圆柱的轴， 垂直于轴的边旋转而成的圆面叫做圆柱的底面， 平行于轴的边旋转而成的曲面叫做圆柱的侧面， 平行于轴的边在旋转中的任何位置叫做圆柱侧面 的母线. 你能结合图形正确理解这些概念吗？ 轴 侧面
h
h
l
l
(l 3 (5 1) 5)
问题：

五.旋转体的概念 由一个平面图形绕着一条直线旋转产生 旋转体, 的曲面所围成的几何体叫做旋转体 的曲面所围成的几何体叫做旋转体,这条 直线叫做旋转体的轴 直线叫做旋转体的轴.比如常见的旋转体 圆柱,圆锥,圆台和球. 有圆柱,圆锥,圆台和球.
六.组合体 由柱, 由柱,锥,台,球等基本几何体组合而 成的几何体称为组合体.组合体可以通过 成的几何体称为组合体. 把它们分解为一些基本几何体来研究
h
h
l
l
(l = 3 + (5 1) = 5)
2 2
例2. 我国首都北京靠近北纬40度. 我国首都北京靠近北纬40度 求北纬40度纬线的长度约为多少千米 求北纬40度纬线的长度约为多少千米 (地球半径约为6370千米)? 地球半径约为6370千米 千米)
解:如图,设A是北纬40°圈上一点, 是北纬40°圈上一点, 如图, AK是它的半径,所以 OK⊥AK, AK是它的半径, OK⊥AK, 是它的半径 设c是北纬40°的纬线长, 是北纬40°的纬线长, 因为∠AOK= OAK=40° 因为∠AOK=∠OAK=40°, 所以 c=2πAK=2πOAcos∠OAK =2πAK=2πOAcos∠ =2π OAcos40° =2πOAcos40° ≈2×3.1416×6370× ≈2×3.1416×6370×0.7660 ≈3.066×104(km), ≈3.066×104(km), 即北纬40°的纬线长约为3.066× 即北纬40°的纬线长约为3.066×104km.
上底面 侧面
母线 母线 轴
下底面
3.圆台的表示方法:用表示它的轴的字 圆台的表示方法: 母表示,如圆台OO' 母表示,如圆台OO'.
4.圆台具有以下性质: 圆台具有以下性质: 圆台的底面是两个半径不等的圆, 底面是两个半径不等的圆 (1)圆台的底面是两个半径不等的圆,两圆 所在的平面互相平行又都和轴垂直; 所在的平面互相平行又都和轴垂直; 平行于底面的截面是圆 截面是圆; (2)平行于底面的截面是圆; 通过轴的各个截面是轴截面 轴截面, (3)通过轴的各个截面是轴截面,各轴截面 是全等的等腰梯形 是全等的等腰梯形; 等腰梯形; 任意两条母线 它们延长后会相交 母线( 延长后会相交) (4)任意两条母线(它们延长后会相交)确 定的平面,截圆台所得的截面是等腰梯形; 定的平面,截圆台所得的截面是等腰梯形; 母线都相等,各母线延长后都相交于一 (5)母线都相等,各母线延长后都相交于一 点.

圆柱圆锥圆台球的表面积和体积公式
圆柱圆锥圆台球的表面积和体积如下：
球：全面积=4πR^2=πD^2；【R---球半径，D---球直径，π---圆周率（=3.14159....) 】
体积=(4/3)πR^3=(1/6)πD^3 【^2---平方符号，^3----立方符号】圆锥：侧面积=πRl全面积=πR(l+R)；【全面积=侧面积+底面积】体积=(1/3)πR^2*H
式中，R---圆锥底面圆的半径，H----圆锥的高，l----圆锥母线的长度，l=√(R^2+H^2)。

圆台：侧面积=π（R1+R2)l ；全面积=πR1(l+R1)+πR2(l+R2)；体积=(1/3)πH(R1^2+R2^2+R1*R2),式中，R1和R2分别是圆台的下底和上底的半径，l----圆台的母线长度，i=√[H^2+(R1-R2)^2]，H----圆台的高。

体积的国际单位制是立方米。

一件固体物件的体积是一个数值用以形容该物件在三维空间所占有的空间。

一维空间物件（如线）及二维空间物件（如正方形）在三维空间中均是零体积的。

垂直于侧棱并与每条 侧棱都相交的截面 经过旋转轴的截面 过高的中点平行于 底面的截面
轴截面
中截面
棱柱、棱锥、棱台 圆柱、圆锥、圆台
七、小结
一、常见旋转体—圆柱、圆锥、圆台由来及相关概念
用表示轴的字母来表示 二、圆柱、圆锥、圆台的表示法：
三、圆柱、圆锥、圆台的性质： 性质1：平行于底面的截面都是圆 性质2：圆柱的轴截面是全等的矩形 圆锥的轴截面是全等的等腰三角形 圆锥的轴截面是全等的等腰梯形
说明：在解题过程中，如果问题都集中在某个截 面上，为了直观起见，不妨将该截面移出来单独研究， 这种将立体问题转化为平面问题的方法在今后应用极为 广泛，必须牢牢掌握并能熟练运用。
回顾小结
•
•
（1）圆柱、圆锥、圆台和球的概念
（2）运动变化、类比联想的观点
•
（3）分解复杂的组合体
课外作业
1.请同学们课后找一找生活中具有圆柱、圆锥、 圆台和球几何结构特征的实物.
O S
O’
O
O
O
记作：
记作：
记作：
圆柱O’O
圆锥SO
圆台O’O
四、圆柱、圆锥、圆台的性质
性质1： 平行于底面的截面都是圆,
过旋转轴的截面 称为旋转体的轴截面 定 义：
性质2：圆柱的轴截面是 全等的 矩形 圆锥的轴截面是 全等的 等腰三角形 圆台的轴截面是 全等的 等腰梯形 S
O’
O’
O
O
O
建构数学
∵⊙Ｏ’ ∥ ⊙O ∴O’A’ ∥OA
＝ ∴⊿ O’SA’O’ A’ ︰OA SA’ ︰SA （∴ ∽⊿ SAO ）
即： x ：4x ＝ (y－10)︰ y 4 (y－10) ＝ y y ＝

球心
A
直径
C
O
大圆
B
建构数学
矩形
直角三角形
直角梯形
半圆
圆柱
圆锥
圆台
球
建构数学
轴
底面
母线
圆柱 轴 底面 侧面 母线
圆锥 旋转前不动的一边所在的直线 垂直于轴的边旋转所成的圆面 不垂直于轴的边旋转所成的曲面 不垂直于轴的边
圆台
圆柱、圆锥、圆台、球的结构特征比较
结构特征
定义 底面 侧面展开 图 两底面是平行且 半径相等的圆 矩形 平行且相等 圆 扇形 两底面平行但 半径不相等 扇环 无
2．下列命题中正确的是（Ａ ）
Ａ．以直角三角形的一直角边为轴旋转所得的旋转体是圆锥 Ｂ．以直角梯形的一腰为轴旋转所得的旋转体是圆台 Ｃ．圆柱、圆锥、圆台都有两个底面 Ｄ．圆锥的侧面展开图为扇形，这个扇形所在圆的半径等于 圆锥底面圆的半径 3．下面几何体中，过轴的截面一定是圆面的是（Ｃ ）
Ａ．圆柱
Ｂ．圆锥
圆 柱 的 结 构 特 征
圆柱：以矩形的一边所在的直线为旋 转轴，其余三边旋转形成的曲面所围 成的几何体叫做圆柱。
底面 轴 母线
侧面
圆柱和棱柱统称为柱体。
圆柱用表示它的轴的字母表示。
圆锥：以直角三角形的一条直角边所在的直线 为旋转轴，其余两边旋转形成的曲面所围成的 A 圆 几何体叫做圆锥。
锥 的 结 构 特 征
1. 下列几个命题中，①两个面平行且相似，其余各面都是梯 形的多面体是棱台．②有两个面互相平行，其余四个面都 是等腰梯形的六面体是棱台．③各侧面都是正方形的四棱 柱一定是正方体．④分别以矩形两条不等的边所在直线为 旋转轴，将矩形旋转，所得到的两个圆柱是两个不同的圆 柱． 其中正确的有（Ａ）个． Ａ．１ Ｂ．２ Ｃ．３ Ｄ．４

圆柱,圆锥,圆台,球的结构特征圆柱、圆锥、圆台和球作为常见的基本几何体，它们在我们日常生活以及工程建设中都有着很广泛的应用。

下面我们将从它们的结构特征、性质及应用等方面，来一一介绍。

首先，圆柱的结构特征主要表现为：底面为圆形，顶面也为圆形，并且底面和顶面之间的部分是由直线“母线”沿着底面一圈一圈绕而成的。

圆柱的体积公式为V=πr²h，而表面积公式为S=2πrh+2πr²。

其特点是在数值比较大的情况下，其体积和面积都会相对比较大。

其次，圆锥的结构特征主要表现为：底面为圆形，顶点在底面上方，并且从底面至顶点的长度正好是圆锥的高。

圆锥的体积公式为V=1/3πr²h，表面积公式为S=πr（r+√(r²+h²))。

圆锥的特点是其顶点聚焦，靠近锥顶的部分空间比较小，因此在设计制图中应该注意其空间的利用。

再次，圆台的结构特征主要表现为：底面和顶面都是圆形，而其母线是两个圆之间的连接线。

圆台的体积公式为V=1/3πh（r1²+r2²+r1r2）,表面积公式为S=π（r1+r2）√((r1-r2)²+h²)。

圆台的特点是底面和顶面大小相似，但高度相对比较小，因此在工程设计制图中，在保证空间利用的基础上，可根据实际要求，灵活选择底面和顶面的大小。

最后，球的结构特征主要体现为：球体的表面处处与它的内部半径相等，即球体从内到外半径处处相等。

球的体积公式为V=4/3πr³，表面积公式为S=4πr²。

由于球形的几何特征具有对称性和向心性，因此常被应用于建筑物的圆形设计、机械制造中的球面旋转等方面。

在实际生产制造和设计过程中，掌握圆柱、圆锥、圆台和球的结构特征、性质及应用等方面，可更好地发挥其应用价值和优势。

同时，在园艺、建筑设计、机械制造等领域中的当代工程设计和生产制造中，借鉴和应用这些几何体的空间特性，也能够创造出更加美观且实用的产品设计。