非球面检测系统的设计
- 格式:docx
- 大小:769.68 KB
- 文档页数:18


非球面在线检测的系统误差分离与修正郭隐彪;郭江;柯晓龙;朱永炉【摘要】为了解决非球面在线检测的系统误差问题,针对系统误差产生的机理、误差的数学模型、分离方法以及补偿方法进行了研究.提出一种将空间误差投影到不同平面上进行分析从而解决测量系统误差的新方法并建立了各系统误差的数学模型.根据最小二乘法的基本思想,建立了基于标准球面的系统误差分离数学模型,得到了各参数的最小二乘估计值,并利用误差修正模型进行了校正.利用标准球面进行测量实验,验证了该方法的有效性和精确性.实验结果表明所提出的解决测量系统误差的思路可行,最终可使测量系统精度达到1 μm数量级,从而满足精磨阶段在线检测的需要.【期刊名称】《纳米技术与精密工程》【年(卷),期】2010(008)005【总页数】6页(P416-421)【关键词】非球面;在线检测;误差分离与补偿修正【作者】郭隐彪;郭江;柯晓龙;朱永炉【作者单位】厦门大学物理与机电工程学院,厦门,361005;厦门大学物理与机电工程学院,厦门,361005;厦门大学物理与机电工程学院,厦门,361005;厦门大学物理与机电工程学院,厦门,361005【正文语种】中文【中图分类】TG76随着先进光学元件的设计和制造技术的不断发展,各种精密光学元件尤其是非球面光学元件被广泛地应用于各种高清晰度电视、高速复印机及航天、航空、国防等行业中,这就对其中光学元件的加工和检测技术提出了更高的要求[1-3].严格来讲,非球面的加工和检测技术是一个整体.在某种程度上,获得高质量的非球面的关键技术在于能否提供可靠的、行之有效的检测结果指导加工.为了提高光学元件补偿加工阶段的面形精度,目前主要采用在线检测.在线检测系统通过将测量传感器固定在机床上可实现对光学元件面形的在机测量,避免了因重新裝夹引入的误差,有利于进行补偿加工,从而获得面形精度更好的光学元件[4-7].然而实际测量系统中,由于测量传感器安装不精确使被测工件的理想坐标系与测量坐标系之间总是不可能完全重合,从而在测量结果中引入了坐标系不重合误差.当采用接触式测量时,由于测头本身的精度问题或沾有油污或在长期使用过程中的磨损,当测头有半径误差Δr时,即产生测头半径误差.因此,要准确地反映面形误差就必须进行有效的误差分离与修正.针对这一问题,本文中建立了一种基于标准件的系统误差分离模型,得到了各参数的最小二乘估计值,并利用误差修正模型进行校正,消除了系统误差的影响,提高了测量结果的精确度.1 系统误差分析与建模由于系统误差对加工精度影响最大,因此在精度较高的非球面检测中,求出检测系统的系统误差对后续的误差修正有重要的指导作用.其中系统误差主要分为坐标系不重合误差和测头半径误差.1.1 坐标系不重合误差非球面光学元件的面形测定主要有接触式和非接触式两种方式,但无论采用哪种方式,在测量中都会存在坐标系不重合误差.坐标系不重合误差包括测量坐标系与工件坐标系(即工件的理想坐标系)原点定位误差和倾角误差.1.1.1 原点定位误差原点定位误差主要是由于测杆摆放不直等原因,使得测量坐标系与工件坐标系的原点发生了位置偏移造成的,此误差会对非球面面形的测定产生较大影响.如图1(a)和1(b)所示,坐标系X′Y′Z′为工件理想坐标系,坐标系XYZ为测量坐标系.由图可知,在X、Y、Z轴方向分别产生的误差为ΔX、ΔY、ΔZ,取ΔX、ΔZ合成方向大小为ΔU.由ΔX、ΔY、ΔZ共同作用所产生的Y轴方向的面形误差为EΔX(θ)=ΔY+ΔUtan θ(1)式中:故(2)式中:α为在XZ投影平面内,两坐标系原点连线与X轴夹角;β为在UY投影平面内,两坐标系原点连线与U轴夹角;θ为被测点切线角,对于某个被测点,切线角θ是确定的,0≤θ≤45°.1.1.2 坐标系倾角误差由于测量夹具存在倾角等原因,使得光学元件的测量坐标系与工件坐标系在X轴和Z轴方向存在倾角ΔτX和ΔτZ,故产生倾角误差,如图2(a)和(b)所示,此误差也会对面形的测定产生影响.其中坐标系XYZ为测量坐标系,坐标系X′Y′Z′为工件坐标系,坐标系X″Y″Z″为测量坐标系XYZ绕X轴旋转得到的过渡坐标系.图1 原点定位误差对测量精度的影响图2 坐标系倾角误差对测量精度的影响设A点在测量坐标系XYZ下的坐标为(X,Y,Z),与B点对应的点在过渡坐标系下坐标即为B点在测量坐标系下的坐标,设为(X″,Y″,Z″);与C点对应的点在工件坐标系下坐标即为C点在过渡坐标系下的坐标,设为(X′,Y′,Z′),则A点和B点的坐标满足以下关系:(3)B点和C点的坐标满足以下关系(4)根据测量坐标系A点的坐标可算出B点的坐标和θA,再由B点的坐标算出C点的坐标和θB.由倾角ΔτX所产生的误差为B点到C点的竖直距离,即(5)由倾角ΔτZ所产生的误差为A点到B点的竖直距离,即(6)于是总的面形误差为EΔτ(θ)=EΔτZ(θA)+EΔτX(θB)=(7)1.2 测头半径误差当采用接触式测量时,由于测头半径精度问题,也会引入一定的误差,从而对面形测定产生影响.如图 3(a)和3(b)所示,测头半径误差也会对非球面的面形测定产生影响.由图3(b)可知,由Δr所产生的Y轴方向的面形误差为式中Δr为测头半径误差.图3 测头半径误差对测量精度的影响2 误差分离与修正方法2.1 误差分离方法由于测量装置在安装过程中或多或少会引入坐标系原点定位误差ΔX、ΔY、ΔZ和倾角误差ΔτZ、ΔτX,其中接触式测量还可能引入Δr,因此必须对测量数据进行系统误差分离.但是这些误差并不容易由实验检测直接得出,因此本文根据最小二乘法的基本思想,建立了基于标准件的系统误差分离数学模型,借助计算机技术,采用合适的算法,编写程序,自动分离出测量系统误差ΔX、ΔY、ΔZ、ΔτZ、ΔτX 和Δr.结合式(2)、式(7)和式(8)可知,由测量引入的面形误差可表示为E(θ)=EΔX(θ)+EΔτ(θ)+EΔr(θ)=(9)假设有n个被测点,对于第i(i=1,2,…,n)个被测点,式(9)可表示为E(θi)=EΔX(θi)+EΔτ(θi)+EΔr(θi)=(10)令ΔX=a,cos α=b,tan β=c,tan ΔτZ=dtan ΔτX=e,Δr=f则则式(10)变为(11)设被测点i的实测面形误差为Ei(i=1,2,…,n),定义以下函数:(12)由最小二乘原理可知,要使S(a,b,c,d,e,f)=min,则有成立,故可得到以下方程组:(13)由于采用标准件,故式(13)中Ei=0.利用非线性最小二乘法编程解此方程组即可得a、b、c、d、e、f的值,也就分离出了相应的测量误差ΔX、α、β、ΔτZ、ΔτX、Δr,进而得到ΔX、ΔY、ΔZ、ΔτZ、ΔτX和Δr.2.2 误差修正方法基于以上误差分离的结果,本文中对系统误差进行了有效的修正.2.2.1 测头半径误差的修正在接触式测量中,测量所得数据为测头球心坐标值,为了得到被测点的实际坐标值,必须对测量数据进行坐标变换,同时考虑到测头半径误差Δr的影响,变换公式为(14)式中:(X,Z,Y)为测头球心坐标;(X′,Z′,Y′)为被测量点实际坐标.2.2.2 坐标系原点定位误差的修正由误差分离得到的ΔX、α、β,可得到坐标变换公式为(15)2.2.3 坐标系倾角误差的修正由误差分离得到的ΔτZ和ΔτX,可得坐标变换公式为(16)式中:(X,Z,Y)为测量坐标系下坐标;(X′,Z′,Y′)为工件坐标系下坐标.3 误差分离与修正实验本文的误差分离与修正实验通过采用电感测微仪在瑞士Magerle磨床上搭建在线检测系统对口径为 210 mm的标准凹面球面进行在线检测来完成.标准凹面球面的半径为4 785.148 mm.最大高度差PV=52 nm,均方差RMS=7.830 nm,故此标准凹面球面可以被用作标准件使用.测量传感器采用电感测微仪,测头半径为1.33 mm,测量档位为第1档,测量范围为±3 mm、分辨率为0.1 μm、示值误差为0.06 μm.实际测量采用子午线式测量轨迹对该标准件进行测量.测量坐标系的建立以夹具台面为XZ平面,以标准球面表面对称中心为原点进行测量,实际的测量结果见图4(a).其中,各条子午线间夹角为10°,检测步长为1 mm,对标准凹面球面表面半径为104 mm以内的区域进行检测,每条子午线上采集207个点,共计3 726个点.将实际测量得到的每条子午线上的点绕测量坐标系的Y轴旋转到XY平面上,得到的结果如图4(b)所示.从图中可以看到,由于存在系统误差,所以测量轨迹没有重合在一起.经过对测量数据进行数据预处理,利用上述基于标准件的误差分离方法建立误差分离模型并进行误差分离后,得到系统误差分离的参数如表1所示.将经过误差修正得到的数据结果绕工件理想坐标系的Y轴旋转到同一平面上得到的结果如图5(a)所示,减去利用半径为4 785.148 mm标准圆的残差分布如图5(b)所示.由残差结果可知各点的误差在1 μm以内,经过误差分离和修正后的结果满足实际要求.表1 误差分离参数ΔXΔZΔY7.7637×10-30.151424.6082ΔτXΔτZΔr-7.6905×10-24.8023×10-21.0699×10-2注:结果保留5位有效数字,切线角θ的计算代入理论球面方程进行.图4 实际测量结果图5 误差修正结果4 结论在非球面检测中,为了提高测量精度既可通过改善硬件设备,也可通过合理的误差分离与修正算法进行补偿.本文中对在线检测系统的误差情况进行了研究,得到以下结论.(1)分析了系统误差产生的原因以及各系统误差对测量精度的影响,完成了对坐标系不重合误差和测头半径误差数学模型的建立.(2)根据最小二乘法的基本思想,建立了基于标准件的系统误差分离模型,得到了各参数的最小二乘估计值,并利用误差修正模型进行校正,消除了系统误差的影响,提高了测量结果的精确度.进一步进行了误差分离与修正实验,实验结果表明所提出的解决测量系统误差的思路可行,最终可使测量系统精度达到1 μm数量级,从而满足精磨阶段在线检测的需要.【相关文献】[1] Sazedur M,Saleh T,Lim H S,et al. Development of an on-machine profile measurement system in ELID grinding for machining aspheric surface with softwarecompensation[J]. International Journal of Machine Tools and Manufacture,2008,48(7/8):887-895.[2] 万勇建,范斌,袁家虎,等.大型非球面主镜细磨中的一种在线检测技术[J]. 光电工程,2005,32(1):1-4.Wan Yongjian,Fan Bin,Yuan Jiahu,et al . An online measuring technique for lapping large aspherical mirror[J].Opto-electron Eng,2005,32(1):1-4(in Chinese).[3] Gan S W,Lim H S, Rahman M,et al. A fine tool servo system for global position error compensation for a miniature ultra-precision lathe[J].International Journal of Machine Tools and Manufacture,2007,47(7/8):1302-1310.[4] Arai Y,Gao Wei,Shimizu Hiroki Su,et al. On-machine measurement of asperical surface profile[J].Nanotechnology and Precision Engineering,2004,2(3):210-216. [5] 叶军君,兰劲,郭隐彪.非球面检测误差分析和误差补偿策略研究[J] . 中国机械工程,2007,18(23):2793-2796.Ye Junjun,Lan Jin,Guo Yinbiao. Research on error analysis and compensation of aspheric surface measurement [J].Chinese Mechanical Engineering,2007,18(23):2793-2796(in Chinese).[6] 郭隐彪,黄元庆,田波,等. 非轴对称非球面平行磨削误差补偿技术研究[J].机械工程学报,2002,38(5):118-121.Guo Yinbiao, Huang Yuanqing, Tian Bo, et al. Study on compensation of parallel grinding non-axisymmetric aspheric surfaces[J]. Chinese Journal of Mechanical Engineering,2002,38(5): 118-121 (in Chinese).[7] 黄浩,郭隐彪,王振忠,等. 轴对称非球面加工误差分离及补偿技术[J].机械工程学报,2005,41(12):177-181.Huang Hao,Guo Yinbiao,Wang Zhenzhong, et al. Error separation and compensation technology of axisymmetric aspheric machining[J]. Chinese Journal of Mechanical Engineering,2005,41(12):177-181(in Chinese).。






超高精度非球面检测技术研究1、本文概述随着现代光学技术的飞速发展,非球面光学元件在各种高精度光学系统中发挥着越来越重要的作用。
非球面由于能够减少光学系统中的球面像差和色差,提高成像质量,已成为高性能光学系统设计的关键部件。
非球面的制造和检测技术比传统的球面光学元件复杂得多,尤其是对于超高精度非球面形状检测,需要更严格的技术要求。
本文旨在对超高精度非球面的检测技术进行深入研究。
首先介绍了非球面光学元件的应用背景和重要性,然后详细阐述了当前非球面检测中存在的主要问题和挑战。
通过对现有检测技术的分析和比较,本文提出了一种新的超高精度检测方法,可以有效提高非球面检测的精度和效率。
文章随后对所提出的检测技术进行了详细的理论分析和数学建模,验证了该方法的理论可行性。
本文还设计了一系列实验来验证所提出方法的实际有效性,并通过与其他现有技术的比较,展示了新方法的优势和潜在的应用价值。
本文总结了研究成果,展望了非球面检测技术的未来发展趋势,为相关领域的研究人员和工程师提供了有益的参考和启示。
2、超高精度非球面检测技术的理论基础在现代光学制造和精密工程领域,非球面的设计和制造是实现高性能光学系统的关键。
超高精度非球面检测技术的理论基础主要涉及几何光学、物理光学、光学检测原理和数据处理方法。
几何光学为非球面提供了一种基本的定义和描述方法。
非球面是指不满足球面方程旋转对称性的光学表面。
这些类型的曲面通常是通过数学表达式或多项式来定义的,例如泽尼克多项式,它可以描述曲面形状的局部曲率和形状偏差。
物理光学进一步解释了光与非球面之间相互作用的原理。
当光波穿过非球面或从非球面反射时,其传播和偏转特性会受到表面细节的影响。
非球面几何参数的精确测量和控制对于确保光学系统的性能至关重要。
光学检测的原理包括干涉测量、散斑测量和聚焦测量等技术。
干涉测量是一种常用的高精度检测方法,通过比较参考光和测试光之间的相位差来测量表面形状。
散斑测量利用光的散射特性来评估表面质量。


摘要非球面因其具有更高的自由度,有利于简化结构、减小像差等球面无法比拟的优势,越来越广泛地应用于光学设计中,但国内高精度非接触式非球面检测系统研制一直比较落后,国外检测设备也非常昂贵,限制了非球面技术在中小型企业及院校的进一步推广。
为了解决这一问题,本文提出了一种基于激光扫描技术的非球面测量方法,利用细激光束扫描非球面的轮廓面得到非球面的面形曲线,论文完成的工作和创新点主要包括以下几个方面:1、分析现有的各种非球面测量系统的优缺点,考虑操作环境、实际需求等因素选择激光扫描式测量方案。
分析以往激光扫描式测量方案的结构形式,提出一种在光路中加入反射镜的方案,用直线和旋转扫描机构带动反射镜进行扫描,增大了系统的测量范围并减小系统的复杂程度。
2、以往的激光扫描方案,通过测量反射光束在CCD上的位置进行测角,CCD的大小和精度限制了测量精度的提高,本课题首次提出通过PSD寻找光斑中心实现改进型自准直测量的方式来进行角度测量,提高了系统的测量精度。
3、针对提出的方案设计完整光路,选型合适的光电器件。
在LightTools中对完整光路进行建模,确定光路中各个光学元件的位置和参数以及扫描机构的量程及精度。
分析模拟数据发现需要在光路中加入缩束镜,根据LightTools中模拟数据设置参数,在CODEV中进行优化设计。
4、设计缩束镜和反射镜固定组件的机械结构,在系统各部分光机器件加工完成后进行装配和调试,并选择合适的非球面进行系统测试,采集直线位移、旋转角度以及PSD探测的数据。
5、利用迭代算法处理收集到的数据,重现待测非球面的面形,并与理论面形作比对,分析测量精度和产生误差的原因。
关键词:非球面,激光扫描,高精度,非接触式,光线对中ABSTRACTBecause of some incomparable features of the aspheric surface such as greater design freedom, the convenience of reducing the system structure and the ability of reducing the aberration, the aspheric surface is more widely used in the optical design. However in our country, the development of high precision and non-contact aspheric testing system is relatively backward, which limits the further popularization and application in minor enterprise and colleges.In order to solve this problem, this paper presents a new method based on laser scanning for measuring the aspheric surface. Scanning the outline of aspheric surface by thin laser beam to obtain aspherical surface shape curve. The work and innovation of the paper mainly include the following aspects:1、Analyzing the merits and drawbacks of various kinds of aspheric measurement system, and considering the operational environment, the actual demand and other factors , choosing a laser scanning measurement scheme at last. The paper analyzes the structure of laser scanning measurement scheme in the past, and proposes a scheme which can increase the measuring range of the system and reduce the complexity of the system by adding a mirror in the optical path and being driven by a straight line and a scanning mechanism.2、In the previous laser scanning, angle measurement is performed by measuring the position of the reflected light beam on the CCD. The size and precision of CCD limits the accuracy of the measurement. In this paper, making the light beam in the center of PSD to measure the angle is put forward for the first time, which improves the measurement accuracy of the system.3、Designing the optical path and selecting suitable optical devices based on the proposed scheme. In LightTools, the modeling of optical path is finished, which is in order to ensure the positions, parameters of each optical elements in the optical path and the range and precision of the scanning mechanism. By analyzing the simulation data, we find that a shrinking beam lens is needed to join the optical path. Parameters of the lens is set according to the simulated data in LightTools. And the shrinking beam lens is optimized in CODEV.4、The mechanical structure of shrinking beam lens and fixed components of reflector is designed. The paper has assembled and debugged the each part of the optical devices after they are machined, chosen suitable aspheric surface to carry out system test, and collected the data of the linear displacement, rotation angle and PSD detection.5、To process the collected data, using iterative algorithm to reproduce the shape of the aspheric surface which is measured. The results are compared with the theoretical results to analyze the measurement accuracy and the causes of error.KEY WORDS:Aspheric surface,Laser scan,High precision,Non-contact measurement,Laser shaft alignment目录摘要 (I)ABSTRACT (II)第1章绪论 (1)1.1 课题背景 (1)1.2研究意义 (2)1.3 国内外研究现状 (2)1.3.1 国外研究现状 (2)1.3.2 国内研究现状 (4)1.4 课题主要内容 (5)第2章系统测量原理和方案 (6)2.1非球面测量系统工作原理 (6)2.1.1光学非球面 (6)2.1.2现有测量方案结构分析 (6)2.2系统测量方案 (10)2.2.1激光扫描式系统方案 (10)2.2.2激光扫描式测量系统结构 (12)2.3本章小结 (12)第3章系统的光路设计与模型搭建 (14)3.1系统总体光路布局与分析 (14)3.1.1系统测量光路布局 (14)3.1.2系统光路分析 (15)3.2光器件选型 (16)3.2.1 激光器 (16)3.2.2PSD位敏探测器 (17)3.3系统光路设计 (18)3.3.1设计工具简介 (18)3.3.2系统光路搭建 (20)3.3.3扫描机构精度分析 (23)3.3.4缩束镜设计 (25)3.3.5 光学元件选型 (31)3.4 本章小结 (33)第4章系统的结构设计与调试 (34)4.1 机械结构设计 (34)4.1.1 缩束镜机械设计 (34)4.1.2扫描机构机械设计 (36)4.1.3反射镜机械固定件设计 (37)4.2系统光机器件装配 (39)4.2.1缩束镜的装配 (39)4.2.2反射镜安装 (40)4.2.3 扫描机构安装 (41)4.3 待测样品介绍 (41)4.3.1 紫外照明球面 (42)4.3.2 照明均匀非球面 (42)4.3.3 激光扩角缩束非球面 (43)4.4 系统调试 (44)4.4.1 激光光束的水平调整 (44)4.4.2 反射镜的位置和姿态调整 (44)4.4.3 光学元件共轴性调整 (44)4.4.4PSD位置和姿态调整 (45)4.4.5 安装待测非球面 (45)4.5本章小结 (45)第5章数据采集与处理 (47)5.1数据采集 (47)5.1.1数据采集系统介绍 (47)5.1.2测量数据采集 (48)5.2数据处理 (49)5.2.1 迭代算法 (49)5.2.2面形曲线分析与拟合 (51)5.2.3 系统误差分析 (54)5.3本章小结 (54)第6章总结与展望 (56)6.1全文总结 (56)6.2课题展望 (57)参考文献 (58)附录 (62)发表论文和参加科研情况说明 (68)致谢 (69)第1章绪论1.1 课题背景随着光学精密加工工艺的发展,非球面光学元件以其简化系统结构和尺寸、校正多种像差、明显改善成像质量[1][2]、增加系统设计自由度等优势,在国防航空航天系统[3][4]、红外探测技术、医用内窥镜、民用照明工程[5]、空间遥感技术[6]等领域中得到越来越广泛的应用。
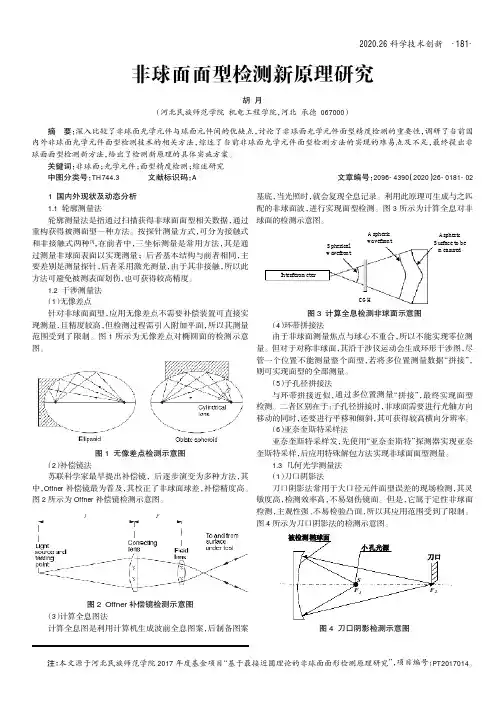
2020.26科学技术创新非球面面型检测新原理研究胡月(河北民族师范学院机电工程学院,河北承德067000)1国内外现状及动态分析1.1轮廓测量法轮廓测量法是指通过扫描获得非球面面型相关数据,通过重构获得被测面型一种方法。
按探针测量方式,可分为接触式和非接触式两种[1],在前者中,三坐标测量是常用方法,其是通过测量非球面表面以实现测量;后者基本结构与前者相同,主要差别是测量探针,后者采用激光测量,由于其非接触,所以此方法可避免被测表面划伤,也可获得较高精度。
1.2干涉测量法(1)无像差点针对非球面面型,应用无像差点不需要补偿装置可直接实现测量,且精度较高,但检测过程需引入附加平面,所以其测量范围受到了限制。
图1所示为无像差点对椭圆面的检测示意图。
图1无像差点检测示意图(2)补偿镜法苏联科学家最早提出补偿镜,后逐步演变为多种方法,其中,Offner 补偿镜最为普及,其校正了非球面球差,补偿精度高。
图2所示为Offner 补偿镜检测示意图。
图2Offner 补偿镜检测示意图(3)计算全息图法计算全息图是利用计算机生成波前全息图案,后制备图案基底,当光照时,就会复现全息记录。
利用此原理可生成与之匹配的非球面波,进行实现面型检测。
图3所示为计算全息对非球面的检测示意图。
图3计算全息检测非球面示意图(4)环带拼接法由于非球面测量焦点与球心不重合,所以不能实现零位测量。
但对于对称非球面,其沿干涉仪运动会生成环形干涉图,尽管一个位置不能测量整个面型,若将多位置测量数据“拼接”,则可实现面型的全部测量。
(5)子孔径拼接法与环带拼接近似,通过多位置测量“拼接”,最终实现面型检测。
二者区别在于:子孔径拼接时,非球面需要进行光轴方向移动的同时,还要进行平移和倾斜,其可获得较高横向分辨率。
(6)亚奈奎斯特采样法亚奈奎斯特采样发,先使用“亚奈奎斯特”探测器实现亚奈奎斯特采样,后应用特殊解包方法实现非球面面型测量。
1.3几何光学测量法(1)刀口阴影法刀口阴影法常用于大口径元件面型误差的现场检测,其灵敏度高,检测效率高,不易划伤镜面。
光学非球面新型检测原理与技术嘿,大家知道吗?在光学的奇妙世界里,有个超厉害的东西叫光学非球面新型检测原理与技术呢!想象一下,我们的眼睛就像是超级精密的光学仪器,能看到五彩斑斓的世界,而光学非球面就是让我们能看得更清晰、更准确的关键之一。
那这个检测原理与技术到底是怎么回事呢?简单来说,就好像我们要去检查一个特别复杂的拼图是不是完整无缺。
我们需要非常仔细地去观察每一个小块,看看它们是不是都在正确的位置上,有没有缺失或者变形。
光学非球面的检测也是这样,要对那些曲面进行超级精细的“扫描”,确保它们的形状和性能都符合要求。
比如说,就像我们在挑选一个完美的足球,我们要看看它的表面是不是光滑,有没有凹凸不平的地方。
如果有,那这个足球踢起来可能就不那么顺手啦!同样的道理,光学非球面如果有一点点瑕疵,都会影响到整个光学系统的表现哦。
在这个检测过程中,有各种各样的技术和工具就像我们的小助手一样。
它们能帮助我们发现那些微小的问题,就像放大镜能让我们看清蚂蚁身上的细节一样。
而且,这些技术还在不断进步和发展呢,就像我们的手机不断更新换代一样,变得越来越厉害。
想象一下,如果没有这些先进的检测原理与技术,我们的眼镜可能就没那么清晰,相机拍出来的照片可能就没那么美,那些高科技的光学设备可能就没法正常工作啦。
所以啊,光学非球面新型检测原理与技术可真是太重要啦,它们就像是光学世界里的守护天使,让一切都变得更加
美好和清晰呢!。
非球面光学元件检测方法利用计算机软件控制空间光调制解调器(SLM)形成检测所需的图样,此调制图样经过光学系统投射到光学元件上,得到反射图样,再进行后期数据处理。
该系统可以完成对反射图样的判读处理、自动采集、波面和波差值的三维立体图[2],原理框架图如图1所示。
图1 非球面检测原理的框架图为了更好的达到实验设计的要求,实验之前,对某些数值需要进行计算机模拟。
模拟过程的光学原理:系统投射出的平行光经过非球面被测物体反射到投影系统,经过投影系统的透射与立方棱镜的反射最后投射到CCD摄像机的接收面。
进行计算机模拟的目的:(1)完成理论计算,被测元件与参考球面垂轴距离y,CCD摄像机接收面上检测距离d,算出他们之间的公式关系;(2)借助计算机和C语言,模拟出垂轴距离,与计算出的垂轴距离作比较,并输出各自的数据;(3)根据输出的数据,利用excel进行制表,作出根据理论计算得到的非球面曲线和模拟出的非球面曲线。
2.1.2 理论计算将半反半透镜'P、透镜L、接收屏和非球面按照如图2所示放置,向此光路系统透射入一与光轴平行的光线HA,经透镜L汇聚交于非球面,再反射到透镜L 上,形成另一束与光轴平行但方向相反的光线BG。
若此时将非球面换为参考球面,球心与透镜L的焦距重合,光线按原路返回。
假设非球面与参考球面的同球心误差为h,平行入射光线与平行反射光线在接收屏上的间距为d,取非球面的方程为抛物线方程进行理论计算。
郎奇检验法系统组成及工作原理此检测方法选用的装置包括光源、Ronchi光栅(透射式黑白线性光栅)、CCD 图像采集装置和被检反射镜面,如图3所示。
透射过的Ronchi光栅的像经过被测非球面的反射回落到光栅上,前提是光栅在被放置在非球面的曲率中心位置,从而产生莫尔条纹,根据莫尔条纹的变形来计算出被检镜面的面形误差,其中的莫尔条纹可以看作是由衍射和干涉共同作用产生的结果。
其检测具体过程如下:(1)绘制及刻划Ronchi光栅,分为两个步骤:第一步是根据被加工镜面的方程和检测光路来计算出郎奇光栅方程。
高精度非球面透镜的加工与检测摘要:针对非球面透镜高精度的加工需求,提出了一种组合式抛光技术。
在采用不用研抛参数的条件下将自动化研抛系统与离子研抛机相结合,从而提高了系统对非球面透镜的加工能力。
通过仿真分析与实验测试,验证了提高表面精度的设计理念。
关键词:透镜加工;非球面;离子抛光机;仿真计算1 引言大口径不是球面的元件由于具有不需要中心遮蔽,可以改善成像质量,让系统结构更简单等优点,现已是空间相机和超大功率的激光器等光学装置的重要器件之一[1]。
随着科学技术的进步,目前的大尺寸光学系统在器件表面质量、加工效率方面都有了很大的提高,远超出古典光学在系统设计中的要求从频域上看,光学器件的制作误差可分为低频段的误差、中频段的误差还有高频段的误差三种。
中频段的误差可分为两个频段:SD1、PSD2。
分段的频率是0.4 mm-1。
高频相位的误差在8.3到100 mm-1之间[2]。
大口径不是球面零件的常规加工工艺是采用铣磨出形状、散粒研磨和抛光等工艺,使其达到与球面形态最接近,然后采用人工修整抛光或者数控机床把球面再变成非球面。
这种把零件抛光成球面,然后再从球面到非球面的加工方法存在着很大的缺陷。
2 设计思路为解决以上问题,改善非球面的加工效率和精确度,各种先进的工艺技术(抛光技术例如磁流变、离子束、气囊、等离子体技术等)被开发出来并且迅速发展。
同时,以先进的制造技术为基础,开发了多种工艺的加工方法。
位于英国的Zeeko公司的Walker等人提出了一种利用超精密研磨加气囊抛光的技术来加工欧洲大型望远镜制造所需要的大型非球面零件。
所制得的米级口径的六边形不是球面光学器件的面形误差PV可达62纳米, RMS可达11纳米。
位于美国的QED公司的 Dumas等人[3]提出了一种新的抛光工艺,即将 MRF技术与常规的沥青抛光技术相结合,应用于非球面研磨出形以后再抛光的加工。
为了满足高精确度批量生产离轴型的非球面零件需求,本文研究了一种混合的抛光工艺,以达到高效率生产非球面零件的目的。