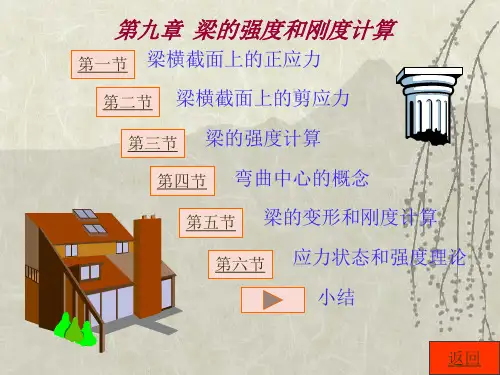
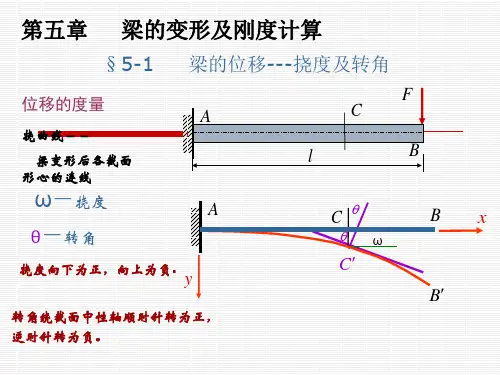
例7-2 18号工字钢制成的简支梁如图所示。试求D截面上a、b两 点处的正应力。 解:(1)求D截面的弯矩: MD=30kN.m (2)确定中性轴位置 和截面惯性矩: 查型钢表 IZ=1660cm4 (3)求D截面a、b两点的正应力: 180 y a yb 10 .7 79.3mm; 2 M D ya 30 10 3 79 .3 10 3 a 143 .3MPa; 8 z 1660 10
max
105 0 0
M max
d , b(截面尺寸取整!)
(3)确定梁的 许可荷载
M max M Wz P ; M Qmax [Q ] [ ] A [ P ](取[ P ]为[ P ] . ) h/2
b h2 bh3 2 y1bdy ( y ); I z , 2 4 12
η沿截面高度按 抛物线规律变化。
Q h2 6Q h 2 2 ( y ) 3 ( y 2 ); 2I z 4 bh 4
h 6Qh 2 3 Q y , 0; y 0, max ; 3 2 4bh 2 bh
返回 下一张 上一张 小结
二、正应力公式的推导:
(一)变形几何关系:
取梁微段dx考虑变形 几何关系,得应变规律:
S yd y ; dx d
当M>0时:y>0,ε>0,为受拉区;y<0,ε<0,为受压区。 (二)物理关系: y 由假设2及虎克定律,梁横 E E 截面上的正应力变化规律为: 此式表明:梁横截面上任一点的正应力,与该点距中性轴 (z轴)的距离y成正比,而与该点距y轴的距离z无关。正应 力沿截面高度呈直线规律分布。中性层处y=0,ζ=0;上下边 缘处有ymax,故有ζmax。 返回 下一张 上一张 小结