【真卷】2017年湖北省武汉市高三二月调考数学试卷(文科)

湖北省2017年高考文科数学试题及答案(Word版)湖北省2017年高考文科数学试题及答案本次高考文科数学试题共分为选择题和填空题两部分。

选择题部分1.已知集合A={x|x0}，则B=（）。

A。

AB。

A∩BC。

BD。

B的补集解析：将3-2x>0化简得x<3/2，所以B={x|x<3/2}，与A 没有交集，所以B的答案为B。

2.为评估一种农作物的种植效果，选了n块地作试验田。

这n块地的亩产量（单位：kg）分别为x1，x2，…，xn，下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是（）。

A。

x1，x2，…，xn的平均数B。

x1，x2，…，xn的标准差C。

x1，x2，…，xn的最大值D。

x1，x2，…，xn的中位数解析：稳定程度越高，说明亩产量的波动越小，所以选项B的标准差可以用来评估。

3.下列各式的运算结果为纯虚数的是（）。

A。

i(1+i)²B。

i²(1-i)C。

(1+i)²D。

i(1+i)解析：将各式展开得到i(1+i)²=2i，i²(1-i)=-2i，(1+i)²=2i，i(1+i)=i+i²=-1，所以答案为D。

4.如图，正方形ABCD内的图形来自中国古代的太极图。

正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称。

在正方形内随机取一点，则此点取自黑色部分的概率是（）。

A。

1/4B。

π/8C。

1/2D。

4/y²解析：由于黑色部分和白色部分关于正方形的中心成中心对称，所以黑色部分的面积等于白色部分的面积，即1/2.又因为随机取一点，所以概率为1/2，所以答案为C。

5.已知F是双曲线C：x²/9-y²/4=1的右焦点，P是C上一点，且PF与x轴垂直，点A的坐标是(1,3)。

则△APF的面积为（）。

A。

3B。

2C。

3/3D。

2/3解析：双曲线的焦距为c=√(a²+b²)，其中a=3，b=2，所以c=√(3²+2²)=√13.由于F是右焦点，所以F的横坐标为3.由于PF与x轴垂直，所以△APF是一个直角三角形，且AP=√(1-3²/4)=√7/2，所以△APF的面积为1/2*√7/2*√(13-3) =1/2*√(7*10) = √70/2 = 5/√2，化简得3/3，所以答案为C。

' $# 12 $# $!"( ! 0 !") !" "' ! 0 !"# ! $( # "& ! " 1 $ 3 4 5 % ( & 3 4 5 '6 3 4 5 )1 $ 3 4 5 % 7 8) 3 4 5 '6 5 7 8' 3 4 5 )1 $5 7 8% 3 4 5 % !5 $ $ 5 7 8 )6 ' 1 $5 7 8%3 4 5 % 5 7 8 %1 $5 7 8% 3 4 5 % " 9% : %: 5 7 8% 4 5 %1 !;%1 "% !;3 ' $ $ ) $ '1 )0 %1 0 0 ' )0 ' 3 4 5 1 '5 7 8) 4 5 )0 1 '5 7 8) 4 5 )1 '5 7 8) !3 !3 ' $
分 别 为 中 点 又 平 面 平 面 平 面 平 面 平 面 平 面
设 试 连 作 于 考 平 面 学 又 平 面 大'%1)%2!%11槡 在 直 角 三 角 形 % ' 1中 ) . ' 范 % 1 槡 ' 1 *%中 点 , 到 平 面 *. '距 离 为 ,为 师 $ $ 中 " " ' 槡 '# 1 " 槡 1 # 3 + 分 $ "$ ' $ 华 9*. 面 ) % ' . (平 *. 1 " ,为 *%中 点 , 到 平 面 ) % ' .距 离 为 $ " '# 槡 3 槡 1 # ' " 1 ' ' 依 题 意 3 1 $ 3 6 3 " '# 槡 '# @ #@ '@ $1 $ 槡 "" 分 6 槡 ' $ '

湖北省各地2017届高三最新考试数学文试题分类汇编统计与概率2017.02一、选择、填空题 1、（荆、荆、襄、宜四地七校考试联盟2017届高三2月联考）从数字1,2,3,4中任取两个不同的数字构成一个两位数，这个两位数大于20的概率是 A ．14 B ．34 C ．13 D ．232、（荆州市五县市区2017届高三上学期期末）经统计，用于数学学习的时间（单位：小时）与成绩（单位：分）近似于线性相关关系．对某小组学生每周用于数学的学习时间x 与数学成绩y 进行数据收集如下：由表中样本数据求得回归方程为y bx a =+，则点(,)a b 与直线11018=+y x 的位置关系是（ ）A ．点在直线左侧B ．点在直线右侧C ．点在直线上D ．无法确定3、（天门、仙桃、潜江市2017届高三上学期期末联合考试）对于一个容量为N 的总体抽取容量为n 的样本，当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为P 1，P 2，P 3，则 A ．P 1= P 2＜P 3B ．P 2= P 3＜P 1C ．P 1= P 2=P 3D ．P 1= P 3＜P 24、（天门、仙桃、潜江市2017届高三上学期期末联合考试）已知集合{|28}M x x =-≤≤，2{|320}N x x x =-+≤，在集合M 中任取一个元素x ,则“x M N ∈ ”的概率为A ．110B ．16C ．310D ．125、（天门、仙桃、潜江市2017届高三上学期期末联合考试）为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁~18岁的男生体重（kg ），得到频率分布直方图如下根据上图，可得这100名学生中体重在).,.[564556的学生人数是 ▲ ．6、（武汉市2017届高三毕业生二月调研考）从装有3个红球和2个白球的袋中任取3个球，则所取的3个球中至少有2个红球的概率是 A.12 B. 25 C. 710 D.357、（武汉市武昌区2017届高三1月调研）已知某射击运动员每次射击击中目标的概率都为，现采用随机模拟的方法估计该运动员4次射击至少3次击中目标的概率：先由计算器产生0到9之间取整数值的随机数，指定0,1表示没有击中目标，2,3,4,5,6,7,8,9表示击中目标，再以每4个随机数为一组，代表4次射击的结果，经随机模拟产生了如下20组随机数： 7527 0293 7140 9857 0347 4373 8636 6947 1417 4698 0371 6233 2616 8045 6011 3661 9597 7424 7610 4281 据此估计，该射击运动员4次射击至少3次击中目标的概率为8、（孝感市七校教学联盟2017届高三上学期期末）一个棱长为4的正方体涂上红色后，将其切成棱长为1的小正方体，置于一密闭容器搅拌均匀，从中任取一个，则取到两面涂红色的小正方体的概率为（ ） A.18 B.38 C. 827 D.12279、（孝感市2017届高三上学期期中）从4，5，6，7，8这5个数中任取两个数，则所取两个数之积能被3整除概率是（ ）A ．B ．C ．D ．二、解答题1、（黄冈市2017届高三上学期期末）某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下：甲运动员得分：13,51,23,8,26,38,16,33,14,28,39；乙运动员得分：49,24,12，31,50,31,44,36,15,37,25,36,39.（1）用十位数为茎，在答题卡中画出原始数据的茎叶图；（2）用分层抽样的方法在乙运动员得分十位数为2,3,4的比赛中抽取一个容量为5的样本，从该样本中随机抽取2场，求其中恰有1场得分大于40分的概率.2、（荆、荆、襄、宜四地七校考试联盟2017届高三2月联考）某手机厂商推出一款6吋大屏手机，现对500名该手机使用者（200名女性，300名男性）进行调查，对手机进行打分，打分的频数分布表如下：计算具体值，给出结论即可）；（Ⅱ）分别求女性用户评分的众数，男性用户评分的中位数；（Ⅲ）如果评分不低于70分，就表示该用户对手机“认可”，否则就表示“不认可”，附：()()()()()22n ad bcKa b c d a c b d-=++++3、（荆门市2017届高三元月调考）某中学对高三学生进行体能测试，已知高三某文科班有学生30人，立定跳远的测试成绩用茎叶图表示如下图（单位：cm）；男生成绩在195cm 以上（包括195cm）定义为“合格”，成绩在195cm以下（不包括195cm）定义为“不合格”；女生成绩在185cm以上（包括185cm）定义为“合格”，成绩在185cm以下（不包括185cm）定义为“不合格”.（Ⅰ）求女生立定跳远测试成绩的中位数；（Ⅱ）若在男生中按成绩是否合格进行分层抽样，抽取6人，求抽取成绩为“合格”的学生人数；（Ⅲ）若从（Ⅱ）的抽取6名男生中任意选取4人，求这4人中至少有3人“合格”的概率.4、（荆州市五县市区2017届高三上学期期末）某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程（单次充电后能行驶的最大里程），被调查汽车的续驶里程全部介于50公里和300公里之间，将统计结果分成5组：[50，100），[100，150），[150，200），[200，250），[250，300]，绘制成如图所示的频率分布直方图．（Ⅰ）求直方图中x的值；（Ⅱ）求续驶里程在[200，300]的车辆数；（Ⅲ）从续驶里程在[200，300]的车辆中随机抽取2辆车，求其中恰有一辆车的续驶里程为[200，250）的概率．5、（武汉市2017届高三毕业生二月调研考）如图所示茎叶图记录了甲、乙两组5名工人制造某种零件的个数（1）求甲组工人制造零件的平均数和方差；（2）分别从甲、乙两组中随机选取一个工人，求这两个工人制造的零件总数不超过20的概率.6、（武汉市武昌区2017届高三1月调研）我国上是世界严重缺水的国家，城市缺水问题较为突出，某市政府为了鼓励居民节约用水，计划在本市试行居民生活用水定额管理，即确定一个合理的居民月用水量标准x （吨），用水量不超过x 的部分按平价收费，超过x 的部分按议价收费，为了了解全市民月用水量的分布情况，通过抽样，获得了100位居民某年的月用水量（单位：吨），将数据按照[)0,0.5，[)0.5,1，…，[]4,4.5分成9组，制成了如图所示的频率分布直方图.（Ⅰ）求直方图中a 的值；（Ⅱ）已知该市有80万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由； （Ⅲ）若该市政府希望使85%的居民每月的用水量不超过标准x （吨），估计x 的值，并说明理由；7、（襄阳市优质高中2017届高三1月联考） 某研究小组到社区了解参加健美操运动人员的情况，用分层抽样的方法抽取了40人进行调查，按照年龄分成五个小组：[](](](](]30,40,40,50,50,60,60,70,70,80，并绘制成如图所示的频率分布直方图.（1）求该社区参加健美操运动人员的平均年龄；（2）如果研究小组从该样本中年龄在[]30,40和(]70,80的6人中随机地抽取出2人进行深入采访，求被采访的2人，年龄恰好都在(]70,80内的概率.8、（孝感市七校教学联盟2017届高三上学期期末）孝汉城铁于12月1日开通，C5302、C5321两列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况，分别在两个车次各随机抽取了100名旅客进行调查，下面是根据调查结果，绘制了乘车次数的频率分布直方图和频数分布表。

湖北省武汉市2017届高中毕业生二月调研考试试题（文）本试卷总分值为150分考试时间为120分钟一.选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1. 已知全集U =R ，集合A ={x |x 2﹣2x ＞0}，则C U A 等于( )A ．{x |0≤x ≤2}B ．{x |0＜x ＜2}C ． {x |x ＜0或x ＞2}D ．{x |x ≤0或x ≥2} 2. cos600的值是（）A ．32B ．32-C ．12-D ．123. 由函数()sin 2f x x =的图像得到()cos(2)3g x x π=-的图像，可将()f x 的图象（）A ．向左平移12π个单位 B ．向右平移6π个单位 C ．向左平移6π个单位 D ．向右平移12π个单位4．函数xx x f 2)1ln()(-+=的零点所在的大致区间是( )A. )1,0(B. )2,1(C. ),2(eD. )4,3( 5. 函数()1cos2f x x =-的周期是（） A.2πB. 2πC. πD. 4π6. 函数的图象大致是（）7．函数()(0,2)y f x =在上是增函数，函数(2)y f x =+是偶函数，则下列结论正确的是（）A.57(1)()()22f f f <<B.57()(1)()22f f f <<C.75()()(1)22f f f <<D.75()(1)()22f f f <<22xy x =-8. 偶函数)(x f y =满足)1()1(-=+x f x f ，且1[-∈x , ]0时，943)(+=xx f , 则)5(log 31f 的值为( )A ．－1B ．35-C ．95- D ．1 9. 在ABC ∆所在的平面上有一点P ，满足→→→→=++AB PC PB PA ，则PBC ∆与ABC ∆的面积之比是( ) A ．13 B ．12 C ．34 D．2310．已知()22x x f -=，若0m n <<时满足()()f m f n =，则mn 的取值范围为（）A ．(]4,0B ．(]2,0C ．()2,0D ．(]2,0 11. 已知函数(21)(2)()log (1)(2) a a x a x f x x x -+<⎧=⎨-≥⎩是R 上的减函数，则实数a 的取值范围是（）11 [,)3.2A 21 [,)5.2B 2 [).,15C 1(0,).2D12. 定义域为R 的函数()f x 满足条件：①1212[()()]()0f x f x x x -->1212(,,)x x R x x +∈≠； ②()()0f x f x +-=()x R ∈；③(3)0f -=.则不等式()0x f x ⋅<的解集是（） A. {}|3003x x x -<<<<或 B. {}|303x x x <-≤<或 C. {}|33x x x <->或 D. {}|303x x x -<<>或二、填空题（本大题共4小题，每小题5分，共20分．） 13．计算：．14．函数f （x ）=2sin （ωx +φ）（ω＞0，且|φ|＜的部分图象如图所示，则f （π）的值为 ．15．若→OA =)8,2(，→OB =)2,7(-，则31→AB =_________．43310.25()log 18log 22-⨯-+-=16.已知222(1),0(),4(3),0x k a x f x a R x x a x ⎧+-≥=∈⎨-+-<⎩，对任意非零实数1x ，存在唯一的非零实数212()x x x ≠，使得12()()f x f x =成立，则实数k 的取值范围是 .三、解答题：（本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．） 17.（10分）已知角α的终边经过点P(-4，3)， （1）求)tan()cos()sin(απααπ+-+-的值;（2）求1sin cos cos sin 22+-+αααα的值．18.（12分）已知函数21)(-+=x x x f 的定义域为集合A ，函数 a a x a x x g +++-=22)12()(的定义域为集合B ．（1）求集合A 、B ；（2）若A B A = ，求实数a 的取值范围．19.（12分）已知6x π=是函数)2sin()(ϕ+=x x f )20(πϕ<<图象的一条对称轴．（1）求函数)(x f 的解析式；（2）求函数)(x f -的单调增区间；（3）作出函数()f x 在[]0,x π∈上的图象简图（列表，画图）．20.（12分）已知函数f （x ）=2cos 2ωx +2sinωxcosωx ﹣1（ω＞0）的最小正周期为π．（1）求f （）的值；（2）求函数f （x ）的单调递增区间及其图象的对称轴方程．21.（12分）已知函数])2,0[(1)23(∈-=-x x f x，函数3)2()(+-=x f x g . （1）求函数)(x f y =与)(x g y =的解析式，并求出()f x ，()g x 的定义域; （2）设)()]([)(22x g x g x h +=，试求函数)(x h y =的最值22（本题满分12分）已知函数2()log (41)()x f x kx k =++∈R 是偶函数. （1）求k 的值；（2）设函数24()log (2)3xg x a a =⋅-，其中0.a >若函数()f x 与()g x 的图象有且只有一个交点，求a 的取值范围.参考答案一、选择题题号 1 234 567891011 12 答案AC A BC AD D D CBA二、填空题（本大题共有4小题，每小题5分共20分．把答案填在题中横线上）13． 6 14．﹣15. (3,2)--16．0k ≤或8k ≥17.解：(1);154（2）5418.解：（1）10212x x x x +≥⇒>≤--或，22(21)01x a x a a x a x a -+++≥⇒≥+≤或 ),1[],(),,2(]1,(+∞+-∞=+∞--∞=a a B A（2）11211≤≤-⇒⎩⎨⎧≤+-≥⇒⊆⇔=a a a B A A B A 19. 解：（1）)62sin()(π+=x x f ；（2）函数()x f 的增区间为Z k k k ∈++],65,3[ππππ （3）列表x6π 512π23π 1112ππ26x π+6π 2π π32π 2π136π()f x1211-12()x f 在],0[π∈x 上的图象简图如下图所示：20.解：（1）函数f （x ）=2cos 2ωx +2sinωxcosωx ﹣1=cos 2ωx +sin 2ωx =2sin （2ωx +），因为f （x ）最小正周期为π，所以=π，解得ω=1， 所以f （x ）=2sin （2x +），f （）=2sin=1．（2）由2kπ﹣≤2x +≤2kπ+，k ∈z ，可得kπ﹣≤x ≤kπ+，k ∈z ，所以，函数f （x ）的单调递增区间为，k ∈z ． 由 2x +=kπ+可得x =kπ+，k ∈z ．所以，f （x ）图象的对称轴方程为x =kπ+，k ∈z ．…21.解：（1）设32xt =-∈（t [-1,7]，则3log (t 2)x =+, 于是有3()log (t 2)1f t =+-，[1,7]t ∈-，∴3()log (2)1f x x =+-()[1,7]x ∈-，根据题意得3()(2)3log 2g x f x x =-+=+，又由721≤-≤-x 得91≤≤x ， ∴2log )(3+=x x g ()[1,9]x ∈（2）∵3()log 2,[1,9]g x x x =+∈∴要使函数22()[()]()h x g x g x =+有意义，必须21919x x ⎧≤≤⎨≤≤⎩∴13x ≤≤，∴222223333()[()]()(log 2)2log (log )6log 6h x g x g x x x x x =+=+++=++ （13x ≤≤）设x t 3log =,则66)(2++=t t x h ()332-+=t )10(≤≤t 是()1,0上增函数,∴0=t 时min )(x h =6,1=t 时13)(max =x h ∴函数()y h x =的最大值为13，最小值为6．22. 解：（1）∵2()log (41)()x f x kx k =++∈R 是偶函数， ∴2()log (41)()x f x kx f x --=+-=对任意x R ∈恒成立, 即：22log (41)2log (41)x x x kx kx +--=++恒成立，∴1k =-（2）令2,xt =则43t >，因而等价于关于t 的方程24(1)103a t at ---=（*）在4(,)3+∞上只有一解① 当1a =时，解得34(,)43t =-∉+∞，不合题意； ② 当01a <<时，记24()(1)13h t a t at =---，其图象的对称轴203(1)a t a =<- ∴函数24()(1)13h t a t at =---在(0,)+∞上递减，而(0)1h =- ∴方程（*）在4(,)3+∞无解③ 当1a >时，记24()(1)13h t a t at =---，其图象的对称轴203(1)a t a =>- 所以，只需4()03h <，即1616(1)1099a a ---<，此恒成立∴此时a 的范围为1a > 综上所述，所求a 的取值范围为1a >。

2017年湖北省武汉市高三二月调考数学试卷（文科）一、选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，有且只有一项符合题目要求.1．（5分）复数z满足（z+2i）i=1+i，则z=（）A．1+3i B．1﹣3i C．﹣1+3i D．﹣1﹣3i2．（5分）设集合M={x|0≤x≤3}，N={x|x2﹣3x﹣4＜0}，则M∩N=（）A．[﹣1，3]B．（﹣1，3）C．[0，3]D．[﹣1，4]3．（5分）命题“y=f（x）（x∈M）是奇函数”的否定是（）A．∃x∈M，f（﹣x）=﹣f（x） B．∀x∈M，f（﹣x）≠﹣f（x）C．∀x∈M，f（﹣x）=﹣f（x）D．∃x∈M，f（﹣x）≠﹣f（x）4．（5分）非零向量满足，且与的夹角为，则=（）A．B．C．D．25．（5分）设x，y满足约束条件，则z=x﹣3y的最大值为（）A．4 B．C．D．26．（5分）执行如图所示的程序框图，若输出的结果为80，则判断框内应填入（）A．n≤8？B．n＞8？C．n≤7？D．n＞7？7．（5分）已知直线l：mx+y﹣1=0（m∈R）是圆C：x2+y2﹣4x+2y+1=0的对称轴，过点A（﹣2，m）作圆C的一条切线，切点为B，则|AB|为（）A．4 B．C．D．38．（5分）从装有3个红球和2个白球的袋中任取3个球，则所取的3个球中至少有2个红球的概率是（）A．B．C．D．9．（5分）为了得到函数y=sin2x+cos2x的图象，可以将函数y=cos2x﹣sin2x的图象（）A．向右平移个单位B．向左平移个单位C．向右平移个单位D．向左平移个单位10．（5分）已知直线y=2x﹣3与抛物线y2=4x交于A，B两点，O为坐标原点，OA，OB的斜率分别为k1，k2，则（）A．B．2 C．D．11．（5分）如图是某个几何体的三视图，其中正视图为正方形，俯视图是腰长为2的等腰直角三角形，则该几何体外接球的直径为（）A．2 B．C．D．12．（5分）若函数f（x）=ae x﹣x﹣2a有两个零点，则实数a的取值范围是（）A．B． C．（﹣∞，0）D．（0，+∞）二、填空题：本大题共4小题，每小题5分，共20分.13．（5分）函数f（x）=的定义域为．14．（5分）在△ABC中，角C=60°，tan+tan=1，则tan•tan=．15．（5分）在平面直角坐标系中，设A、B、C是曲线y=上三个不同的点，且D、E、F分别为BC、CA、AB的中点，则过D、E、F三点的圆一定经过定点．16．（5分）若函数f（x）=ln（ax2+x）在区间（0，1）上单调递增，则实数a的取值范围为．三、解答题：本大题共5小题，共70分.解答应写出必要的文字说明或推理、验算过程.17．（12分）各项均为正数的等比数列{a n}的前n项和为S n，满足．（1）求a1及通项公式a n；（2）若，求数列{b n}的前n项和T n．18．（12分）如图，在三棱柱ABC﹣A1B1C1中，AB⊥平面BCC1B1，为CC1的中点．（1）求证：DB1⊥平面ABD；（2）求点A1到平面ADB1的距离．19．（12分）如图所示茎叶图记录了甲、乙两组5名工人制造某种零件的个数（1）求甲组工人制造零件的平均数和方差；（2）分别从甲、乙两组中随机选取一个工人，求这两个工人制造的零件总数不超过20的概率．20．（12分）已知椭圆的左、右焦点分别为F1，F2，离心率为，F2与椭圆上点的连线的中最短线段的长为．（1）求椭圆Γ的标准方程；（2）已知Γ上存在一点P，使得直线PF1，PF2分别交椭圆Γ于A，B，若，求直线PB的斜率．21．（12分）已知函数f（x）=xe x﹣ae2x（a∈R）恰有两个极值点x1，x2（x1＜x2）．（1）求实数a的取值范围；（2）求证：f（x2）＞﹣．四．请考生在第22、23两题中任选一题作答，如果两题都做，则按照所做的第一题给分；作答时，请用2B铅笔将答题卡上相应的题号涂黑．选修4-4：参数方程与极坐标系22．（10分）以原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的方程为，⊙C的极坐标方程为ρ=4cosθ+2sinθ．（1）求直线l和⊙C的普通方程；（2）若直线l与圆⊙C交于A，B两点，求弦AB的长．23．（10分）（1）求函数y=2|x﹣1|﹣|x﹣4|的值域；（2）若不等式2|x﹣1|﹣|x﹣a|≥﹣1在x∈R上恒成立，求实数a的取值范围．2017年湖北省武汉市高三二月调考数学试卷（文科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，有且只有一项符合题目要求.1．（5分）复数z满足（z+2i）i=1+i，则z=（）A．1+3i B．1﹣3i C．﹣1+3i D．﹣1﹣3i【解答】解：由（z+2i）i=1+i，得，∴z=1﹣3i．故选：B．2．（5分）设集合M={x|0≤x≤3}，N={x|x2﹣3x﹣4＜0}，则M∩N=（）A．[﹣1，3]B．（﹣1，3）C．[0，3]D．[﹣1，4]【解答】解：∵集合M={x|0≤x≤3}，N={x|x2﹣3x﹣4＜0}={x|﹣1＜x＜4}，∴M∩N={x|0≤x≤3}=[0，3]．故选：C．3．（5分）命题“y=f（x）（x∈M）是奇函数”的否定是（）A．∃x∈M，f（﹣x）=﹣f（x） B．∀x∈M，f（﹣x）≠﹣f（x）C．∀x∈M，f（﹣x）=﹣f（x）D．∃x∈M，f（﹣x）≠﹣f（x）【解答】解：命题“y=f（x）（x∈M）是奇函数”的否定，∃x∈M，f（﹣x）≠﹣f （x），故选：D．4．（5分）非零向量满足，且与的夹角为，则=（）A．B．C．D．2【解答】解：∵，且；∴=；又；∴；∴．故选B．5．（5分）设x，y满足约束条件，则z=x﹣3y的最大值为（）A．4 B．C．D．2【解答】解：由约束条件作出可行域如图，联立，得A（﹣2，﹣2），化目标函数z=x﹣3y为y=，由图可知，当直线y=过点A时，直线在y轴上的截距最小，z有最大值为﹣2+6=4．故选：A．6．（5分）执行如图所示的程序框图，若输出的结果为80，则判断框内应填入（）A．n≤8？B．n＞8？C．n≤7？D．n＞7？【解答】解：模拟程序的运行，可得S=0，n=1，a=3执行循环体，S=3，a=5不满足条件，执行循环体，n=2，S=8，a=7不满足条件，执行循环体，n=3，S=15，a=9不满足条件，执行循环体，n=4，S=24，a=11不满足条件，执行循环体，n=5，S=35，a=13不满足条件，执行循环体，n=6，S=48，a=15不满足条件，执行循环体，n=7，S=63，a=17不满足条件，执行循环体，n=8，S=80，a=19由题意，此时满足条件，退出循环，输出的S结果为80，则判断框内应填入n＞7？故选：D．7．（5分）已知直线l：mx+y﹣1=0（m∈R）是圆C：x2+y2﹣4x+2y+1=0的对称轴，过点A（﹣2，m）作圆C的一条切线，切点为B，则|AB|为（）A．4 B．C．D．3【解答】解：∵圆C：x2+y2﹣4x+2y+1=0，即（x﹣2）2+（y+1）2 =4，表示以C（2，﹣1）为圆心、半径等于2的圆．由题意可得，直线l：mx+y﹣1=0经过圆C的圆心（2，﹣1），故有2m﹣1﹣1=0，∴m=1，点A（﹣2，1）．∵AC=，CB=R=2，∴切线的长|AB|==4．故选A．8．（5分）从装有3个红球和2个白球的袋中任取3个球，则所取的3个球中至少有2个红球的概率是（）A．B．C．D．【解答】解：从装有3个红球和2个白球的袋中任取3个球，基本事件总数n==10，所取的3个球中至少有2个红球包含的基本事件个数：m==7，∴所取的3个球中至少有2个红球的概率：p==．故选：C．9．（5分）为了得到函数y=sin2x+cos2x的图象，可以将函数y=cos2x﹣sin2x的图象（）A．向右平移个单位B．向左平移个单位C．向右平移个单位D．向左平移个单位【解答】解：∵y=sin2x+cos2x=（sin2x+cos2x）=cos2（x﹣）y=cos2x﹣sin2x=（cos2x﹣sin2x）=cos2（x+）=cos2[（x+）﹣]，∴只需将函数y=cos2x﹣sin2x的图象向右平移个单位可得函数y=sin2x+cos2x 的图象．故选：A．10．（5分）已知直线y=2x﹣3与抛物线y2=4x交于A，B两点，O为坐标原点，OA，OB的斜率分别为k1，k2，则（）A．B．2 C．D．【解答】解：直线y=2x﹣3与抛物线y2=4x联立，可得y2﹣2y﹣6=0，∴y=1±，∴A（2+，1+），B（2﹣，1﹣），∴=+=，故选A．11．（5分）如图是某个几何体的三视图，其中正视图为正方形，俯视图是腰长为2的等腰直角三角形，则该几何体外接球的直径为（）A．2 B．C．D．【解答】解：由题意可知三视图复原的几何体如图：四棱锥S﹣BCDE，是正方体的一部分，正方体的棱长为2；所以几何体外接球为正方体外接球，该几何体外接球的直径为2．故选D．12．（5分）若函数f（x）=ae x﹣x﹣2a有两个零点，则实数a的取值范围是（）A．B． C．（﹣∞，0）D．（0，+∞）【解答】解：函数f（x）=ae x﹣x﹣2a的导函数f′（x）=ae x﹣1，当a≤0时，f′（x）≤0恒成立，函数f（x）在R上单调，不可能有两个零点；当a＞0时，令f′（x）=0，得x=ln，函数在（﹣∞，ln）递减，在（ln，+∞）递增，所以f（x）的最小值为f（ln）=1﹣ln﹣2a=1+lna﹣2a，令g（a）=1+lna﹣2a，（a＞0），g′（a）=，a，g（a）递增，a递减，∴∴f（x）的最小值为f（ln）＜0，函数f（x）=ae x﹣x﹣2a有两个零点；综上实数a的取值范围是：（0，+∞），故选：D．二、填空题：本大题共4小题，每小题5分，共20分.13．（5分）函数f（x）=的定义域为[0，1] ．【解答】解：要使函数有意义，则x﹣x2≥0，即x2﹣x≤0，解得0≤x≤1，即函数的定义域为[0，1]．故答案：[0，1]．14．（5分）在△ABC中，角C=60°，tan+tan=1，则tan•tan=1﹣．【解答】解：由题意：角C=60°，tan+tan=1，根据cot=tan（）=，可得：=，解得：tan•tan=故答案为：115．（5分）在平面直角坐标系中，设A、B、C是曲线y=上三个不同的点，且D、E、F分别为BC、CA、AB的中点，则过D、E、F三点的圆一定经过定点（1，0）．【解答】解：曲线y=的对称中心为（1，0），取过对称中心直线与曲线交于A，B，A，B中点为对称中心（1，0），∴过D、E、F三点的圆一定经过定点（1，0）．故答案为（1，0）．16．（5分）若函数f（x）=ln（ax2+x）在区间（0，1）上单调递增，则实数a的取值范围为a≥﹣．【解答】解：若函数f（x）=ln（ax2+x）在区间（0，1）上单调递增，即函数g（x）=ax2+x在（0，1）递增，a=0时，g（x）=x在（0，1）递增，符合题意，a＞0时，g（x）的对称轴x=﹣＜0，g（x）在（0，1）递增，符合题意，a＜0时，需满足g（x）的对称轴x=﹣≥1，解得：a≥﹣，综上，a≥﹣，故答案为：a≥﹣．三、解答题：本大题共5小题，共70分.解答应写出必要的文字说明或推理、验算过程.17．（12分）各项均为正数的等比数列{a n}的前n项和为S n，满足．（1）求a1及通项公式a n；（2）若，求数列{b n}的前n项和T n．【解答】解：（1）∵各项均为正数的等比数列{a n}的前n项和为S n，满足，∴n=1时，S3=4S1+6，∴a1+a2+a3=4a1+6，①n=2时，a1+a2+a3+a4=4（a1+a2）+6，②由②﹣①，得，∴q2=4，∵q＞0，∴q=2，由①式知，∴a1（1+2+4）=4a1+6，3a1=6，解得a1=2，∴．（2）∵，∴T n=，③∴=，④由③﹣④，得：=﹣=﹣=1﹣﹣，∴T n=2﹣．18．（12分）如图，在三棱柱ABC﹣A1B1C1中，AB⊥平面BCC1B1，为CC1的中点．（1）求证：DB1⊥平面ABD；（2）求点A1到平面ADB1的距离．【解答】证明：（1）在平面四边形BCC1B1中，∵BC=CD=DC1=1，∠BCD=60°，∴BD=1，∵B1D=，BB1=2，∴∠BDB1=90°，∴B1D⊥BD，∵AB⊥面BB1C1C，∴AB⊥DB1，∴B1D与平面ABD内两相交直线AB和BD同时垂直，∴DB1⊥平面ABD．解：（2）对于四面体A1﹣ADB1，A1到直线DB1的距离即A1到面BB1C1C的距离，A1到B1D的距离为2，设A1到面B1D的距离为h，为直角三角形，==，△ADB∴=，∵==2，D到平面AA 1B1的距离为，∴==，∵=，∴，解得h=．∴点A1到平面ADB1的距离为．19．（12分）如图所示茎叶图记录了甲、乙两组5名工人制造某种零件的个数（1）求甲组工人制造零件的平均数和方差；（2）分别从甲、乙两组中随机选取一个工人，求这两个工人制造的零件总数不超过20的概率．【解答】解：（1）甲组工人制零件数为：9，9，10，10，12，∴甲组工人制造零件的平均数：=（9+9+10+10+12）=10，方差为S2=[（9﹣10）2+（9﹣10）2+（10﹣10）2+（10﹣10）2+（12﹣10）2]=．（2）由题意甲、乙两组工人制造零件中的个数分别是：甲：9，9，10，10，12；乙：8，9，9，10，11，甲组中5名工人分别记为a，b，c，d，e，乙组5名工人分别记为A，B，C，D，E，分别从甲、乙两组中随机选取1个工人，共有25种方法，制造零件总数超过20的有：eB，eC，eD，eE，dE，cE，共6种，∴这两个工人制造的零件总数不超过20的概率：p=1﹣=．20．（12分）已知椭圆的左、右焦点分别为F 1，F2，离心率为，F2与椭圆上点的连线的中最短线段的长为．（1）求椭圆Γ的标准方程；（2）已知Γ上存在一点P，使得直线PF1，PF2分别交椭圆Γ于A，B，若，求直线PB的斜率．【解答】解：（1）椭圆的离心率为，∴=，…①右焦点F2与椭圆上点的连线的中最短线段的长为，即a﹣c=﹣1；…②由①②解得a=，c=1，∴b==1；∴椭圆Γ的标准方程是+y2=1；（2）设点P（x0，y0），A（x1，y1），B（x2，y2），则直线l PA的方程为：x=my﹣1；由，消去x，得（m2+1）y2﹣2my﹣1=0；则y0•y1=﹣，又=，∴m=；∴=﹣=﹣=（m2+2）=[+2]=+2=+2﹣；∴=3+2x0，∴2+2x0=2，解得x0=﹣，∴P（﹣，±），∴K PB===；故直线PB的斜率为±．21．（12分）已知函数f（x）=xe x﹣ae2x（a∈R）恰有两个极值点x1，x2（x1＜x2）．（1）求实数a的取值范围；（2）求证：f（x2）＞﹣．【解答】解：（1）f′（x）=e x（x+1﹣2ae x），要使f（x）恰有2个极值点，则方程x+1﹣2ae x=0有2个不相等的实数根，令g（x）=x+1﹣2ae x，g′（x）=1﹣2ae x；（i）a≤0时，g′（x）＞0，g（x）在R递增，不合题意，舍，（ii）a＞0时，令g′（x）=0，解得：x=ln，当x＜ln时，g′（x）＞0，g（x）在（﹣∞，ln）递增，且x→﹣∞时，g（x）＜0，x＞ln时，g′（x）＜0，g（x）在（ln，+∞）递减，且x→+∞时，g（x）＜0，∴g（x）max=g（ln）=ln+1﹣2a•=ln＞0，∴＞1，即0＜a＜；（2）证明，由（1）知：x1＜ln＜x2，且x1，x2满足x+1﹣2ae x=0，∴x2+1﹣2a=0，即2a=x2+1，∴f（x2）=（x2﹣1），其中x2＞ln，∴f′（x2）=•x2，∵0＜a＜，∴x2＞ln＞0，∴f′（x2）＞0，∴f（x2）在（ln，+∞）递增，∴f（x2）＞f（ln）=（ln﹣1）=﹣，令g（a）=﹣，则g′（a）=，∵0＜a＜，∴ln2a＜0，∴g′（a）＜0，∴g（a）在（0，）递减，∴g（a）＞g（）=﹣，故f（x2）＞g（a）＞﹣，∴f（x2）＞﹣．四．请考生在第22、23两题中任选一题作答，如果两题都做，则按照所做的第一题给分；作答时，请用2B铅笔将答题卡上相应的题号涂黑．选修4-4：参数方程与极坐标系22．（10分）以原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的方程为，⊙C的极坐标方程为ρ=4cosθ+2sinθ．（1）求直线l和⊙C的普通方程；（2）若直线l与圆⊙C交于A，B两点，求弦AB的长．【解答】解：（1）直线l的方程为，可得：ρsinθcos﹣ρcosθsin=﹣⇔﹣y﹣x=即：．⊙C的极坐标方程为ρ=4cosθ+2sinθ．可得：ρ2=4ρcosθ+2ρsinθ，⇔x2+y2=4x+2y即：x2+y2﹣4x﹣2y=0，故得直线l的普通方程为：；⊙C的普通方程为：x2+y2﹣4x﹣2y=0．（2）由x2+y2﹣4x﹣2y=0，可知圆心为（2，1），半径r=，那么：圆心到直线的距离d=，∴|AB|=2故得直线l与圆⊙C交于A，B两点间的弦AB 长为．23．（10分）（1）求函数y=2|x﹣1|﹣|x﹣4|的值域；（2）若不等式2|x﹣1|﹣|x﹣a|≥﹣1在x∈R上恒成立，求实数a的取值范围．【解答】解：（1）∵y=2|x﹣1|﹣|x﹣4|==，故函数的值域是[﹣3，+∞）；（2）f（x）=2|x﹣1|﹣|x﹣a|，①a≥1时，f（x）==，而2a﹣2＞1﹣a，此时f（x）的最小值是1﹣a，故只需1﹣a≥﹣1，∴1≤a≤2；②a＜1时，f（x）==，此时a＜1时，﹣1+a＜2﹣2a，f（x）的最小值是a﹣1，只需a﹣1≥﹣1，0≤a＜1，综上，a的范围是[0，2]．赠送：初中数学几何模型举例【模型四】几何最值模型：图形特征：l运用举例：1. △ABC中，AB=6，AC=8，BC=10，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为AP的中点，则MF的最小值为B2.如图，在边长为6的菱形ABCD中，∠BAD＝60°，E为AB的中点，F为AC上一动点，则EF+BF的最小值为_________。

2o
的
概率
文科 数学试 卷
第 4 页( 共 6 X )
20
( 本 小题 满 分 1 2 分 )
L
知 椭圆 厂
丁+
下
\
2
点 的 连 线 中最 短 线 段 长 刀
厂 的 标 准 方程 œû 求椭 1
n )
L
知 /
l 存在
点
P
使得 直线
PF
Hale Waihona Puke 1P1分别 交椭 圆 厂 于 僶 召 若 P F
=
2 1
à 求
红线
第
23
题 为 选 考题 考 生 根 据 要 求做 答 丅
5
本 大题 共 4 小 题 每 小 题
分
13
丁丁 下的定 义 域 为 乕僜 函数 乿
CA A B
16
的 中点
=
则过
ln
D E F 三
2
点的圆
定经 过 定点
,
若函数j (x )
(
· ×
+
x
) 在区间(0
1
) 上 单调 递增 则实数
a
的取 值 范 围 为
T
,
U
n
文 科 数学 试 卷
第
3
页( 共 6 页)
18
( 本 小 题 满 分 12 分 )
如图 在三 棱柱
D
ABC
A , 吕 C,
中
AB 上 平 面 B B , C , C
,
L B CC ,
-
子A B
=
BB
-
,
2
BC
-
1
,

湖北省武汉市2017届高中毕业生二月调研考试试题（理）一、选择题（12×5=60）1．已知全集为R ，集合}0|{≥=x x A ，}086|{2≤+-=x x x B ，则=B C A R （ ）A ．}0|{≤x xB ．}42|{≤≤x xC ．20|{<≤x x 或}4>xD ．20|{<≤x x 或}4≥x2．函数)2(log )(23x x x f +-=的单调递减区间为（ ）A ．),1(+∞B ．)2,1(C ．)1,0(D ．)1,(-∞3．已知y x ,为正实数，则（ ）A ．y x y x lg lg lg lg 222+=+ B ．y x y x lg lg )lg(222⨯=+ C ．y x y x lg lg lg lg 222+=⨯ D ．y x xy lg lg )lg(222⨯=4．对于函数)(x f 在定义域内用二分法的求解过程中得到(2015)0,(2016)0f f << (2017)f 0>，则下述描述正确的是（ ）A ．函数)(x f 在（2015，2016）内不存在零点B ．函数)(x f 在（2016，2017）内不存在零点C ．函数)(x f 在（2016，2017）内存在零点，并且仅有一个D ．函数)(x f 在（2015，2016）内可能存在零点5．两圆229x y +=和221816450x y x y +-++=的公切线有（ ）条A ．1B ．2C ．3D ．46．棱长为a 的正四面体的外接球和内切球的体积比是（ ）A ．9:1B ．4:1C ．27:1D ．8:17．已知,a b R ∈,直线230ax y +-=与直线(1)20a x by -++=平行，则2a b 的最小值是（ ）A 、0B 、12-C 、12D 、14-8．已知两条异面直线a,b 所成的角为050 ，则过空间任意一点P 与a,b 所成的角均为065的直线共有（ ）条A 、1B 、2C 、3D 、49．过点()2,1作圆()1122=+-y x 的两条切线，切点分别为A 、B ，则直线AB 的方程为（ ）A.20x y +-=B.30x y +-=C.230x y --=D.230x y +-=10．若函数a x x x f +-=24)(有4个零点，则实数a 的取值范围是（ ）A . )0,4(- B. []4,0 C. )4,0( D. []0,4-11．如图，网格纸上小正方形的边长为1，若粗线画出的是某几何体的三视图，则此几何体的体积为（ ）A. 12B. 10C. 8D. 612．已知P 是直线:40l x my ++= 上一动点，PA 、PB 是圆22:20C x y x +-= 的两条切线，切点分别为A 、B ，若四边形PACB的最小面积为2，则实数m =( )A 、2或-2B 、2C 、-2D 、无数个取值二、填空题（4×4=16）13．直线2550x y +-+=被圆22240x y x y +--=截得的弦长等于 ；14．在上定义运算：，若不等式()()4x a x a +⊕-<对任意实数都成立，则的取值范围是 ；15．已知正三棱柱111ABC A B C -的体积为934，底面边长为3 ，若O 为底面111A B C 的中心，则OA 与平面ABC 所成角的大小为 ；16．下列命题：①奇函数)(x f 必满足0)0(=f ；②函数()log (32)1a f x x =-+的图象过定点()1,1R ⊕(1)x y x y ⊕=-xa③,A R B R +==，11:+=→x y x f ，则f 为A 到B 的映射；④在同一坐标系中，x y 2=与2x y -=-的图象关于原点O 对称．其中真命题的序号是 (把你认为正确的命题的序号都填上)．二、解答题（第17题10分，其余5题各12分，共计70分）17．（本小题满分 10分） 已知集合{}013A x x =≤-≤,，{}3log 1B x x =>．(1)求B A ，B A ；(2)已知集合{}R a a x x C ∈<<=,1，若A C ⊆，求实数a 的取值范围．18．（本小题满分12分）已知函数2()log (21)g x x =-，2()log (2)f x x =+，（1）求不等式)()(x f x g ≥的解集；（2）在（1）的条件下求函数)()(x f x g y +=的值域．19．（本小题满分12分） 如图所示，在三棱锥中，23AB BC ==，平面平面，于点D ，2AD =，4CD =，3PD =．求三棱锥的体积；证明：为直角三角形．20．（本小题满分12分）已知一个圆与x 轴相切，圆心在直线20x y -= 上，又圆心为整点（即横纵坐标为整数），且被直线2x = 所截得的弦长为2.(1)求此圆的方程；(2)过点（3，3）作此圆的切线，求切线方程.21．（本小题满分12分）如图，在四棱锥P ﹣ABCD 中，P A ⊥平面ABCD ，AB =BC =2，∠ABD =∠CBD =60° .（1） 求证：BD ⊥平面P AC ；（2）若四棱锥P ﹣ABCD 的体积是43，∠BCD =90°,求点C 到平面PBD 的距离．22．（本小题满分12分）已知=)(x f 21x a x -+是奇函数，=)(x g 21x bx ++为偶函数. （1）求,a b 的值 ；（2）对任意R x ∈不等式m x g x g x f -<)()()(2恒成立，求m 的取值范围.参考答案1-5 CBDDB 6-10 CBCAA 11-12 BA13．4 14．35(,)22- 15．030 16．②③④ 17．解：(1) {}013A x x =≤-≤{}14x x =≤≤， …………………… 1分 {}3log 1B x x =>{}3x x =>， ………… 3分B A {}14x x =≤≤{}3x x > {}34x x =<≤， …………4分 B A {}14x x =≤≤{}3x x > {}1≥=x x ……… 5分（2）①当1≤a 时，φ=C ，此时A C ⊆,所以符合题意1≤a ；…… 7分②当1>a 时，A C ⊆，则14a <≤；综合①②，可得a 的取值范围是(],4-∞． ………………10分18．解：（1）由)()(x f x g ≥ 得22log (21)log (2)x x -≥+则有∴不等式)()(x f x g ≥的解集为{}3x x ≥. …………5分（2）=+=)()(x f x g y 22log (21)log (2)x x -++ 2log (21)(2)x x =-+22log (232)x x =+-…………7分 令2232t x x =+-，则t y 2log =由（1）可得{}3x x ≥.，函数2232t x x =+-的对称轴为3[3,)4x =-∉+∞， 所以3t =时，min 25t =，即25t ≥又∵t y 2log =在[25,)t ∈+∞上单调递增，∴当3x ≥时，22log 252log 5y ≥=，∴所求函数的值域为[)22log 5,+∞. ……12分 19．解：（1）证明：因为平面平面，平面平面， 平面，，所以平面．………………1分记边上的中点为，在△中，因为，所以． 因为23AB BC ==，6AC =，3BE =．………3分所以△的面积1332S AC BE =⨯= ……………………4分 因为3PD =，所以三棱锥的体积1333333⨯⨯=．………6分 （2）证明：因为，所以△为直角三角形．因为PD=3,CD=4所以PC=5………7分连接，在△中，因为，3BE = ，，所以BD=2……9分由（1）知平面，又平面，所以．在△中，因为，PD=3，BD=2 所以13PB = …………………………………10分在中，因为23BC =，13PB = ,5PC = ，所以．所以为直角三角形．…………………………………………………………12分20．解：（1）22(2)(1)1x y -+-= ………………6分（2）3430x y -+=或x=3（过程略）………………12分21．解：（1）证明：在ABC ∆中，因为AB= BC=2，∠ABD=∠CBD=60°,BO AC OC OA ∴⊥=(等腰三角形三线合一)------------3分又 PA ⊥平面ABCDBD PA ∴⊥PA 与AC 交于CBD ∴⊥面PAC-------------------------------------------------------6分（2）因为AB= BC=2，∠ABD=∠CBD=60° ，∠BCD=90°4,23BD AC ∴==1423432ABCD S ∴=⨯⨯= 11434333P ABCD ABCD V S PA PA -∴=⨯⨯=⨯⨯= 3PA ∴= ----------------------------------------------8分OC OA = ,故C 到面PBD 的距离等于A 到面PBD 的距离， 作AH OP ⊥于H ，A 到面PBD 的距离即AH ，在OPA ∆中，,3323PA OA OP AH AH =⨯=⨯32AH ∴= 故C 到面PBD 的距离等于32.---------------------------------------------12分 22．解：（1）1)(2+-=x a x x f 是奇函数， 1(-x)a -x -),()(22+--=-=-∴x a x x f x f 即，0=∴a 又1)(2++=bx x x g 是偶函数，)()(x g x g =-∴，0=∴b .所以0,0==b a ………………………………………………6分（2）由（1）知1)(,1)(22+=+=x x g x x x f . m x x x x x x g x f -+<=++=∴12)1(12)()(2222， 对任意122+-<x x m R x ∈恒成立，又0)1(12x 22≥-=+-x x .∴0<m .………………………………………………………………………12分。

2017高考仿真卷·文科数学(二)(考试时间:120分钟试卷满分:150分)第Ⅰ卷选择题(共60分)一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知i是虚数单位,则复数=()A.-2+iB.iC.2-iD.-i2.已知集合M={x|x2-4x<0},N=,则M∪N=()A.[-2,4)B.(-2,4)C.(0,2)D.(0,2]3.采用系统抽样的方法从1 000人中抽取50人做问卷调查,为此将他们随机编号为1,2,3,…,1 000,适当分组后,在第一组中采用简单随机抽样的方法抽到的号码为8.若编号落入区间[1,400]上的人做问卷A,编号落入区间[401,750]上的人做问卷B,其余的人做问卷C,则抽到的人中,做问卷C的人数为()A.12B.13C.14D.154.已知命题p:函数y=ln(x2+3)+的最小值是2;命题q:“x>2”是“x>1”的充分不必要条件.则下列命题是真命题的是()A.p∧qB.( p)∧( q)C.( p)∧qD.p∧( q)5.已知点A是抛物线C1:y2=2px(p>0)与双曲线C2:=1(a>0,b>0)的一条渐近线的交点,若点A到抛物线C1的焦点的距离为p,则双曲线C2的离心率等于()A. B. C. D.6.某产品的广告费用x(单位:万元))的统计数据如下表:根据表中数据求得回归直线方程为=9.5x+,则等于()A.22B.26C.33.6D.19.57.设a,b,c分别是△ABC的内角A,B,C所对边的边长,则直线sin A·x-ay-c=0与bx+sin B·y+sin C=0的位置关系是()A.平行B.重合C.垂直D.相交但不垂直8.如图,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,若V =,则球O的表面积是()正四棱锥P-ABCDA.4πB.8πC.12πD.16π9.已知变量x,y满足线性约束条件若目标函数z=kx-y仅在点(0,2)处取得最小值,则k的取值范围是()A.k<-3B.k>1C.-1<k<1D.-3<k<110.某几何体的三视图如图所示,当a+b取最大值时,这个几何体的体积为()A. B. C. D.11.已知M是△ABC内一点(不含边界),且=2,∠BAC=30°.若△MBC,△MCA,△MAB的面积分别为x,y,z,记f(x,y,z)=,则f(x,y,z)的最小值为()A.26B.32C.36D.4812.已知集合M={(x,y)|y=f(x)},若对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,则称集合M是“商高线”.给出下列四个集合:①M=;②M={(x,y)|y=sin x+1};③M={(x,y)|y=log2x};④M={(x,y)|y=e x-2}.其中是“商高线”的序号是()A.①②B.②③C.①④D.②④第Ⅱ卷非选择题(共90分)二、填空题(本大题共4小题,每小题5分,共20分)13.执行如图所示的程序框图,若输入x=0.1,则输出的m的值是.14.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=3x+m(m为常数),则f(-log35)的值为.15.关于函数f(x)=2(sin x-cos x)cos x的下列四个结论:①函数f(x)的最大值为;②把函数f(x)=sin 2x-1的图象向右平移个单位后可得到函数f(x)=2(sin x-cos x)·cos x的图象;③函数f(x)的单调递增区间为,k∈Z;④函数f(x)的图象的对称中心为,k∈Z.其中正确的结论有个.16.已知数列{a n}满足a1=,a n-1-a n=(n≥2),则该数列的通项公式为.三、解答题(本大题共6小题,满分70分,解答须写出文字说明、证明过程或演算步骤)17.(本小题满分12分)在△ABC中,角A,B,C的对边分别为a,b,c,已知A=,sin B=3sin C.(1)求tan C的值;(2)若a=,求△ABC的面积.18.(本小题满分12分)国家教育部要求高中阶段每学年都要组织学生进行“国家学生体质健康数据测试”,方案要求以学校为单位组织实施.某校对高一(1)班的同学按照“国家学生体质健康数据测试”的项目进行了测试,并对测试成绩进行统计,其频率分布直方图如图所示,若分数在[90,100]上的人数为2.(1)请求出分数在[70,80)内的人数;(2)现根据测试成绩从第一组和第五组(从低分段到高分段依次分为第一组,第二组,…,第五组)中任意选出2人,形成搭档小组.若选出的2人成绩差大于30,则称这2人为“互补组”,试求选出的2人为“互补组”的概率.19.(本小题满分12分)如图,在正方体ABCD-A1B1C1D1中,E,F分别为AB,BB1的中点.(1)求证:EF⊥平面A1D1B;(2)若AA1=2,求三棱锥D1-DEF的体积.20.(本小题满分12分)已知椭圆C的中心在原点,焦点在x轴上,长轴长为4,且点在椭圆C上.(1)求椭圆C的方程;(2)设P是椭圆C长轴上的一个动点,过P作斜率为的直线l交椭圆C于A,B两点,求证:|P A|2+|PB|2为定值.21.(本小题满分12分)设函数f(x)=.(1)求证:f(x)在(0,1)和(1,+∞)内都是增函数;(2)若在函数f(x)的定义域内,不等式af(x)>x恒成立,求a的取值范围.请考生在第22、23两题中任选一题做答,如果多做,则按所做的第一题评分.22.(本小题满分10分)选修4—4:坐标系与参数方程在平面直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C:ρcos2θ=2a sin θ(a>0),过点P(-4,-2)的直线l的参数方程为(t为参数),直线l与曲线C分别交于点M,N.(1)写出C的直角坐标方程和l的普通方程;(2)若|PM|,|MN|,|PN|成等比数列,求a的值.23.(本小题满分10分)选修4—5:不等式选讲已知函数f(x)=|x-1|+|x+1|.(1)求不等式f(x)≥3的解集;(2)若关于x的不等式f(x)>a2-x2+2x在R上恒成立,求实数a的取值范围.参考答案2017高考仿真卷·文科数学(二)1.B解析(方法一)=i.(方法二)=i.2.A解析∵M={x|0<x<4},N={x|-2≤x≤2},∴M∪N=[-2,4).3.A解析若采用系统抽样的方法从1 000人中抽取50人做问卷调查,则需要分为50组,每组20人.若第一组抽到的号码为8,则以后每组抽取的号码分别为28,48,68,88,108,…,所以编号落入区间[1,400]上的有20人,编号落入区间[401,750]上的有18人,所以做问卷C的有12人.4.C解析因为命题p为假命题,命题q为真命题,所以( p)∧q为真命题.5.C解析因为点A到抛物线C1的焦点的距离为p,所以点A到抛物线准线的距离为p.所以点A的坐标为.所以双曲线的渐近线方程为y=±2x.所以=2,所以b2=4a2.又b2=c2-a2,所以c2=5a2.所以双曲线的离心率为.6.B解析由题意知=2,=45.又由公式,得=26,故选B.7.C解析因为,所以两条直线斜率的乘积为=-1,所以这两条直线垂直.8.D解析连接PO,由题意知,PO⊥底面ABCD,PO=R,S正方形ABCD=2R2.因为V正四棱锥P-ABCD=,所以·2R2·R=,解得R=2,所以球O的表面积是16π.9.D解析如图,作出不等式组所表示的平面区域.由z=kx-y得y=kx-z,要使目标函数z=kx-y 仅在点A(0,2)处取得最小值,则阴影部分区域在直线y=kx+2的下方,故目标函数线的斜率k 满足-3<k<1.10.D解析由该几何体的三视图可得其直观图为如图所示的三棱锥,且从点A出发的三条棱两两垂直,AB=1,PC=,PB=a,BC=b.可知P A2+AC2=a2-1+b2-1=6,即a2+b2=8.故(a+b)2=8+2ab≤8+2,即a+b≤4,当且仅当a=b=2时,a+b取得最大值,此时P A=,AC=.所以该几何体的体积V=×1×.11.C解析由=2,∠BAC=30°,可得S△ABC=1,即x+y+z=1.故(x+y+z)=1+4+9+≥14+4+6+12=36,当且仅当x=,y=,z=时等号成立.因此,f(x,y,z)的最小值为36.12.D解析若对于函数图象上的任意一点M(x1,y1),在其图象上都存在点N(x2,y2),使OM⊥ON,则函数图象上的点的集合为“商高线”.对于①,若取M(1,1),则不存在这样的点;对于③,若取M(1,0),则不存在这样的点.②④都符合.故选D.13.0解析若输入x=0.1,则m=lg 0.1=-1.因为m<0,所以m=-1+1=0.所以输出的m的值为0.14.-4解析因为f(x)是定义在R上的奇函数,所以f(0)=1+m=0.所以m=-1.所以f(-log35)=-f(log35)=-(-1)=-4.15.2解析因为f(x)=2sin x·cos x-2cos2x=sin 2x-cos 2x-1=sin-1,所以其最大值为-1.所以①错误.因为函数f(x)=sin 2x-1的图象向右平移个单位后得到函数f(x)=sin-1=sin-1的图象,所以②错误.由-+2kπ≤2x-+2kπ,k∈Z,得函数f(x)的单调递增区间为,k∈Z,即为,k'∈Z.故③正确.由2x-=kπ,k∈Z,得x=,k∈Z,故④正确.16.a n=解析因为a n-1-a n=(n≥2),所以,所以.所以,…,.所以.所以.所以a n=(n≥2).经检验,当n=1时也适合此公式.所以a n=.17.解(1)∵A=,∴B+C=.∴sin=3sin C.∴cos C+sin C=3sin C.∴cos C=sin C.∴tan C=.(2)由,sin B=3sin C,得b=3c.在△ABC中,由余弦定理得a2=b2+c2-2bc cos A=9c2+c2-2×(3c)×c×=7c2.∵a=,∴c=1,b=3.∴△ABC的面积为S=bc sin A=.18.解(1)由频率分布直方图可知分数在[50,60)内的频率为0.1,[ 60,70)内的频率为0.25,[80,90)内的频率为0.15,[90,100]上的频率为0.05.故分数在[70,80)内的频率为1-0.1-0.25-0.15-0.05=0.45.因为分数在[90,100]上的人数为2,频率为0.05,所以参加测试的总人数为=40.所以分数在[70,80)内的人数为40×0.45=18.(2)因为参加测试的总人数为=40,所以分数在[50,60)内的人数为40×0.1=4.设第一组[50,60)内的同学为A1,A2,A3,A4;第五组[90,100]上的同学为B1,B2,则从中选出2人的选法有(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),(A3,B1),(A3,B2),( A4,B1),(A4,B2),(B1,B2),共15种,其中2人成绩差大于30的选法有(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2),共8种,则选出的2人为“互补组”的概率为.19.(1)证明如图,连接AB1.因为E,F分别为AB与AB1的中点,所以EF∥AB1.因为AB1⊥A1B,所以EF⊥A1B.又因为D1A1⊥平面ABB1A1,平面ABB1A1⊃EF,所以D1A1⊥EF.又因为A1B∩D1A1=A1,所以EF⊥平面A1D1B.(2)解如图,连接DB.因为BB1∥DD1,所以.所以=S△DEB·DD1=×2=.20.(1)解因为2a=4,所以a=2.又因为焦点在x轴上,所以设椭圆方程为=1.将点代入椭圆方程得b2=1,所以椭圆方程为+y2=1.(2)证明设点P(m,0)(-2≤m≤2),可得直线l的方程是y=,由方程组消去y得2x2-2mx+m2-4=0.(*)设A(x1,y1),B(x2,y2),则x1,x2是方程(*)的两个根.所以x1+x2=m,x1x2=.所以|P A|2+|PB|2=(x1-m)2++(x2-m)2+=(x1-m)2+(x1-m)2+(x2-m)2+(x2-m)2=[(x1-m)2+(x2-m)2]=-2m(x1+x2)+2m2]=[(x1+x2)2-2m(x1+x2)-2x1x2+2m2]=[m2-2m2-(m2-4)+2m2]=5.所以|P A|2+|PB|2为定值.21.(1)证明由题意可得f'(x)==(x>0,x≠1).令g(x)=2ln x-,则g'(x)=.当0<x<1时,g'(x) <0,g(x)是减函数,g(x)>g(1)=0.于是f'(x)=g(x)>0,故f(x)在(0,1)内为增函数.当x>1时,g'(x)>0,g(x)是增函数,g(x)>g(1)=0,于是f'(x)=g(x)>0,故f(x)在(1,+∞)内为增函数.(2)解af(x)-x=-x=.令h(x)=-ln x(x>0),则h'(x)=.令φ(x)=ax2-x+a,当a>0,且Δ=1-4a2≤0,即a≥时,此时φ(x)=ax2-x+a>0在(0,1),(1,+∞)内恒成立,所以当a≥时,h'(x)>0在(0,1),(1,+∞)内恒成立,故h(x)在(0,1),(1,+∞)内是增函数,若0<x<1,则h(x)< h(1)=0,所以af(x)-x=h(x)>0;若x>1,则h(x)>h(1)=0,所以af(x)-x=h(x)>0,所以当x>0,x≠1时都有af(x)>x成立.当0<a<时,h'(x)<0,解得<x<,所以h(x)在内是减函数,h(x)<h(1)=0.故af(x)-x=h(x)<0,不符合题意.当a≤0时,x∈(0,1)∪(1,+∞),都有h'(x)<0,故h(x)在(0,1),(1,+∞)内为减函数,同理可知,在(0,1),(1,+∞)内,af(x)-x=h(x)<0,不符合题意.综上所述,a≥,即a的取值范围是.22.解(1)曲线C的直角坐标方程为x2=2ay(a>0),直线l的普通方程为x-y+2=0.(2)将直线l的参数方程与C的直角坐标方程联立,得t2-2(4+a)t+8(4+a)=0.(*)由Δ=8a(4+a)>0,可设点M,N对应的参数分别为t1,t2,且t1,t2是方程(*)的根,则|PM|=|t1|,|PN|=|t2|,|MN|=|t1-t2|.由题设得(t1-t2)2=|t1t2|,即(t1+t2)2-4t1t2=|t1t2|.由(*)得t1+t2=2(4+a),t1t2=8(4+a)>0.则有(4+a)2-5(4+a)=0,解得a=1或a=-4.因为a>0,所以a=1.23.解(1)原不等式等价于解得x≤-或x≥.故原不等式的解集为.(2)令g(x)=|x-1|+|x+1|+x2-2x,则g(x)=当x∈(-∞,1]时,g(x)单调递减;当x∈[1,+∞)时,g(x)单调递增.故当x=1时,g(x)取得最小值1.因为不等式f(x)>a2-x2+2x在R上恒成立,所以a2<1,解得-1<a<1.所以实数a的取值范围是(-1,1).。

湖北省部分重点中学2017届高三第二次联考高三数学试卷（文科） 第Ⅰ卷（选择题）一、选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，有且只有一项符合题目要求.1. 设复数321i z i =-（i 为虚数单位），z 则的虚部为A. iB.i -C. 1-D.12. 已知集合{}2|230A x x x =-->，集合{}|04B x x =<<，则()R C A B =A. []1,3-B. ()0,3C. (]0,3D.()3,43.已知实数,,a b c 满足不等式01a b c <<<<，且2,3,ln a b M N P c -===，则,,M N P 的大小关系是A. P N M <<B.P M N <<C. M P N <<D.N P M << 4.为了求函数()237xf x x =+-的一个零点（精确度0.05），某同学已经利用计算器得()()1.50.32843, 1.250.8716f f ==-，则还需用二分法等分区间的次数为A. 2次B. 3次C. 4次D.5次5.某三棱锥的三视图如图所示，则该三棱锥的体积为 A.23 B. 1 C. 13D. 2 6.已知点()()5,0,5,0A B -，直线,AM BM 的交点为M ，,AM BM 的斜率之积为1625-，则点M 的轨迹方程是 A.2212516x y -= B. 2212516x y += C.()22152516x y x -=≠± D.()22152516x y x +=≠± 7.已知变量,x y 满足约束条件2328x y y x x y +≥⎧⎪≤⎨⎪-≤⎩，则目标函数3z x y =-的最大值为A. 2B. 11C. 16D. 188.数列{}n a 的通项公式为2n a n kn =+，那么2k ≥-是{}n a 为递增数列的 A.充分不必要条件 B. 必要不充分条件 C.充要条件 D.既不充分也不必要条件9.如图，在直三棱柱111ABC A B C -中，190,CAB AC AB AA ∠=== ,则异面直线11,AC A B 所成角的余弦值为 A. 14-B. 14C. 12-D.1210.如图所示()sin y x ωϕ=+的图象可以由sin y x ω=的图象沿x 轴经怎样的平移得到的A.沿x 轴向左平移6π个单位 B.沿x 轴向左平移3π个单位 C.沿x 轴向右平移6π个单位 D. 沿x 轴向右平移6π个单位11.过抛物线24y x =的焦点F 的直线与其交于,A B 两点，AF BF >,如果5AF =，那么BF =B. 54C. 52D.3212.已知函数()2sin 3f x x x =-，若对任意[]()()22,2,30m f ma f a ∈--+>的恒成立，则a 的取值范围是A. ()1,1-B. ()(),13,-∞-+∞C. ()3,3-D.()(),31,-∞-+∞第Ⅱ卷（非选择题）二、填空题：本大题共4小题，每小题5分，共20分.13.若向量2,1a b == ，,a b 的夹角为120，则a b +=.14.若,,41a b R a b +∈+=，则11a b+的最小值为 . 15.我国古代数学家赵爽利用“勾股圈方图”巧妙的证明了勾股定理，成就了我国古代数学的骄傲，后人称之为“赵爽弦图”.他是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形，若直角三角形中较小的锐角记为θ，大正方形的面积为25，小正方形的面积为1，则sincos22θθ+= .16.设()21,1ln ,1x x f x x x ⎧-<=⎨≥⎩，若函数()()1g x f x ax =--有4不同的零点，则a 的取值范围为 .三、解答题：本大题共6小题，共70分.解答应写出必要的文字说明或推理、验算过程. 17.（本题满分12分）已知数列{}n a 是等差数列，其前n 项和为n S ，39524,30.a a S +== （1）求数列{}n a 的通项公式； （2）求数列21n n a a +⎧⎫⎨⎬⋅⎩⎭的前n 项和n T .18.（本题满分12分）在ABC ∆中,角,,A B C 的对边分别是,,a b c ，若()()2sin 2sin 2sin .a A b c B c b C =-+-（1）求角A ;（2）若2a b =，求ABC ∆的面积.19.（本题满分12分）如图，在斜三棱柱111ABC A B C -中，侧面11ACC A 是边长为4的菱形，BC ⊥平面11ACC A ，2CB =,点1A 在底面ABC 上的射影D 为棱AC 的中点，点A 在平面1ACB 内的射影为E . （1）证明：E 为1AC 的中点； （2）求三棱锥11A B C C -的体积.20.（本题满分12分）已知动圆P 与圆(22:25E x y ++=相切，且与圆(22:1F x y +=都内切，记圆心P 的轨迹为曲线C.（1）求曲线C 的方程；（2）直线l 与曲线C 交于点A,B ，点M 为线段AB 的中点，若1OM =，求AOB ∆面积的最大值.21.（本题满分12分）已知函数()()2ln f x x x ax x a a R =+-+∈在其定义域内有两个不同的极值点.（1）求a 的取值范围；（2）设()f x 的两个极值点分别为12,x x ，证明：212.x x e ⋅>22.（本题满分10分）已知曲线C 的极坐标方程为4cos 0ρθ-=，以极点为原点，极轴为x 轴的正半轴建立平面直角坐标系，直线l 过点()1,0M ,倾斜角为.6π（1）求曲线C 的直角坐标方程与直线l 的标准参数方程； （2）设直线l 与曲线C 交于A,B 两点，求MA MB +.湖北省部分重点中学2017届高三第二次联考高三数学答案（文科）二．填空题9 15.5102 16. )1,0(2e三．解答题17.解：(1)因为数列{}n a 是等差数列，设其首项是1,a 公差是d ，由题意3966224,12a a a a +===，15515335()30,212,62a a S a a a a +==+===，可求得 12,2,2n a d a n ===. (5)分（2）因为22,2(2)n n a n a n +==+，211111()22(2)82n n a a n n n n +==⋅-⋅⋅++，1111111111(1)8324351121111(1)8212n T n n n n n n =-+-+-++-+--++=+--++ (35)=16(1)(2)n n n n +++ …………………………………………………12分 18解：在ABC ∆中.由正弦定理得：22(2)(2)a b c b c b c =-⋅+-⋅ 则：222b c a bc +-=由余弦定理可得：2221cos 222b c a bc A bc bc +-=== 3π=∴A …………………………………………………………………6分（2）若2a b ==，2431cos 222c A c +-==⋅,1c =. 所以ABC ∆的面积是1sin 2ABC S b c A =⋅⋅⋅=. ………………………12分19 (1)证明:因为,11ACC A BC 面⊥BC A BC 1平面⊆,所以111ACC A BC A 平面平面⊥交线为C A 1,过A 作C A AE 1⊥,则CB A AE 1平面⊥.又11ACC A 是菱形,AC AA =1所以E 为C A 1的中点. ……6分 (2)由题意1A D ⊥平面ABC ,321=D A338324221311111=⋅⋅⋅⋅===---ABCB BC B A C C B A V V V………12分20解: (1)由1=c 和椭圆上的点)22,1(可求得椭圆 12:22=+y x C …………4分 (2)由题意直线l 的斜率存在设为k ,设)2(:+=x k y l ,联立⎩⎨⎧=-++=022)2(22y x x k y 得 0288)21(2222=-+++k x k x k 设),(),,(2211y x B y x A ,AB 的中点设为),(00y x M0)28)(21(4)8(,214,21822222212221>-+-=∆+=++-=+k k k k ky y k k x x 则2222,212,21420220<<-+=+-=k kk y k k x ,又GB GA =,所以AB GM ⊥, )0(,1214212122122200≠-=+-++=+=k k k k k k x y k GM 解得222-=k ，222+=k （舍） 当0=k 时,显然满足题意. 所以直线l 的方程为)2(222:+-=x y l 或0=y . ……………………………12分21解: (1)1)(--=ax e x f x ,a e x f x -=')(A1①当0<a 时,0)(≥'x f (不恒为0),)(x f 在R 上单调递增,又0)0(=f ,所以当0)(),0,(<-∞∈x f x ,不合题意,舍去;②当0≥a 时,)(,0)(),ln ,(x f x f a x <'-∞∈单调递减, )(,0)(),,(ln x f x f a x >'+∞∈单调递增,1ln )(ln )(min --==a a a a f x f ,则需01ln ≥--a a a 恒成立.令1ln )(--=a a a a g ,a a g ln )(-=',当)1,0(∈a 时,)(,0)(a g a g >'单调递增, 当),1(+∞∈a 时,)(,0)(a g a g <'单调递减,而0)1(=g ,所以01ln ≤--a a a 恒成立.所以a 的取值集合为{}1. …………………………………………………………7分 (2)由(1)可得)0(01>>--x x e x ,)0)(1ln(>+>x x x ,令nx 1=,则 n n n n n n ln )1ln(1ln )11ln(1-+=+=+>,所以 ))(1ln()ln )1(ln()2ln 3(ln )1ln 2(ln 131211*∈+=-+++-+->++++N n n n n n………………………………………………………………………………12分22.解(1)由圆C 的参数方程可得圆C 的圆心为（2,0），半径为2，所以圆C 的极坐标方程为θρcos 4= .………………………………………………………4分 (2)由直线)(2123:为参数t t y t m x l ⎪⎪⎩⎪⎪⎨⎧=+=可求得直线l 的直角坐标方程为03=--m y x .由15=AB 知圆心)0,2(C 到l 距离2122=-=m d ,可得1=m 或3=m .………10分23.解(1)当1-=a 时, 231)(≥--+=x x x f 由不等式的几何意义可得2≥x ,所以2)(≥x f 的解集为{}2≥x x . …………………………………………4分(2)当存在实数x 使得2)(a x f -≤成立，则只需()2min a x f -≤，①3≤a 时，()23min a a x f -≤-=，2,323≤≤a a ；②3>a 时，()23min a a x f -≤-=，6,32≥≥a a.所以a 的取值范围为),6[]2,(+∞-∞ ………………………………………10分。

湖北省武汉市2017届⾼三毕业⽣⼆⽉调研考试⽂科数学试题及答案武汉市2017届毕业⽣⼆⽉调研测试⽂科数学第Ⅰ卷（选择题共60分）⼀、选择题：本⼤题共12⼩题，每⼩题5分，共60分.在每个⼩题给出的四个选项中，有且只有⼀项符合题⽬要求.1.复数z 满⾜()21z i i i +=+，则z =A. 13i +B. 13i -C. 13i -+D.13i --2.设集合{}{}2|03,|340M x x N x x x =≤≤=--<，则M N = A. []1,3- B. ()1,3- C. []0,3 D. []1,4-3.命题“()()y f x x M =∈是奇函数”的否定是A. ()(),x M f x f x ?∈-=-B. ()(),x M f x f x ?∈-≠-C. ()(),x M f x f x ?∈-=-D. ()(),x M f x f x ?∈-≠-4.⾮零向量,a b 满⾜()2a a b ⊥+ ，且a 与b 的夹⾓为23π，则a b = A. 12 B. 142 5.设,x y 满⾜约束条件02422y x x y x y -≤??+≤??-≤?，则3z x y =-的最⼤值为 A. 4 B. 32 C. 83- D.2 6. 执⾏如图所⽰的程序框图，若输出的结果为80，则判断框内应填⼊A. 8?n ≤B. 8?n >C. 7?n ≤D. 7?n >7.已知直线():10l mx y m R +-=∈是圆22:4210C x y x y +-++=的对称轴，过点()2,A m -作圆C 的⼀条切线，切点为B ，则AB 为A. 4B.8.从装有3个红球和2个⽩球的袋中任取3个球，则所取的3个球中⾄少有2个红球的概率是 A. 12 B. 25 C. 710 D.35 9.为了得到函数sin 2cos 2y x x =+的图象，可以将函数cos 2sin 2y x x =-的图象A. 向右平移4π个单位B. 向左平移4π个单位 C.向右平移2π个单位 D. 向左平移2π个单位 10. 已知直线23y x =-与抛物线24y x =交于,A B 两点，O 为坐标原点，,OA OB 的斜率分别为12,k k ，则1211k k + A. 12 B. 2 C. 12- D. 13- 11. 如图是某个⼏何体的三视图，其中正视图为正⽅形，俯视图是腰长为2的等腰直⾓三⾓形，则该⼏何体外接球的直径为A. 2B.12.若函数()2xf x ae x a =--有两个零点，则实数a 的取值范围是 A. 1,e ??-∞ B. 10,e ??C. (),0-∞D.()0,+∞第Ⅱ卷（⾮选择题共90分）⼆、填空题：本⼤题共4⼩题，每⼩题5分，共20分.13.函数y =的定义域为 .14. 在ABC ?中，⾓60C = ，且tantan 122A B +=，则tan tan 22A B ?=为 . 15. 在平⾯直⾓坐标系中，设,,A B C 是曲线11y x =-上两个不同的点，且,,D E F 分别为,,BC CA AB 的中点，则过,,D E F 三点的圆⼀定经过定点 .16.若函数()()2ln f x ax x =+在区间()0,1上单调递增，则实数a 的取值范围为 . 三、解答题：本⼤题共6⼩题，共70分.解答应写出必要的⽂字说明或推理、验算过程.17. 各项均为正数的等⽐数列{}n a 的前n 项和为n S ，满⾜246,.n n S S n N *+=+∈（1）求1a 及通项公式n a ；（2）若n nn b a =，求数列{}n b 的前n 项和n T .18. 如图，在三棱柱111A B C ABC -中，AB ⊥平⾯11BCC B ，11,2,1,3BCC AB BB BC D π∠====为1CC 的中点.（1）求证：1DB ⊥平⾯ABD ；（2）求点1A 到平⾯1ADB 的距离.19.（本题满分12分）如图所⽰茎叶图记录了甲、⼄两组5名⼯⼈制造某种零件的个数（1）求甲组⼯⼈制造零件的平均数和⽅差；（2）分别从甲、⼄两组中随机选取⼀个⼯⼈，求这两个⼯⼈制造的零件总数不超过20的概率.20.（本题满分12分）已知椭圆()2222:10x y a b a b Γ+=>>的左、右焦点分别为12,F F ，离⼼率为2，2F 与椭圆上点1.（1）求椭圆Γ的标准⽅程；（2）已知Γ上存在⼀点P ，使得直线12,PF PF 分别交椭圆Γ于,A B ，若()12122,20PF F A PF F B λ==> ，求直线PB 的斜率.21.（本题满分12分）已知函数()()2x x f x xe ax a R =-∈恰有两个极值点()1212,x x x x <.（1）求实数a 的取值范围；（2）求证：()21.2f x >-请考⽣在第22、23两题中任选⼀题作答，如果两题都做，则按照所做的第⼀题给分；作答时，请⽤2B 铅笔将答题卡上相应的题号涂⿊。

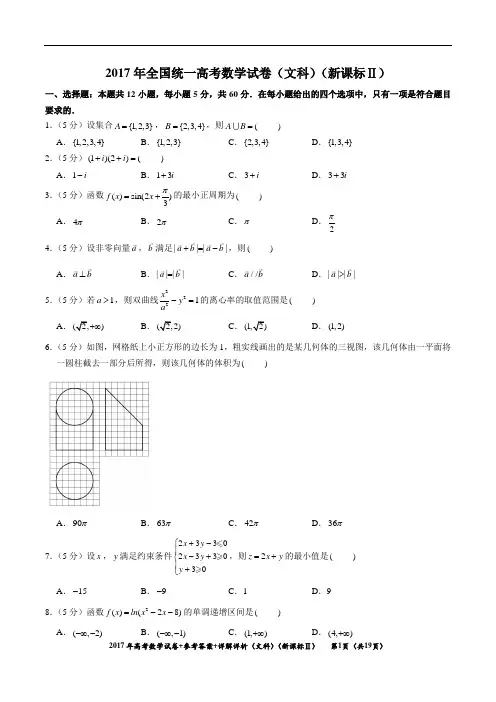
2017年全国统一高考数学试卷（文科）（新课标Ⅱ）一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）设集合{1,2,3}A =，{2,3,4}B =，则(A B = )A ．{1,2,3,4}B ．{1,2,3}C ．{2,3,4}D ．{1,3,4}2．（5分）(1)(2)(i i ++= ) A ．1i -B ．13i +C ．3i +D ．33i +3．（5分）函数()sin(2)3f x x π=+的最小正周期为( )A ．4πB ．2πC ．πD ．2π 4．（5分）设非零向量a ，b 满足||||a b a b +=-，则( ) A ．a b ⊥B ．||||a b =C ．//a bD ．||||a b >5．（5分）若1a >，则双曲线2221x y a-=的离心率的取值范围是( )A．)+∞B．C．D ．(1,2)6．（5分）如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为( )A ．90πB ．63πC ．42πD ．36π7．（5分）设x ，y 满足约束条件2330233030x y x y y +-⎧⎪-+⎨⎪+⎩，则2z x y =+的最小值是( )A ．15-B ．9-C ．1D ．98．（5分）函数2()(28)f x ln x x =--的单调递增区间是( ) A ．(,2)-∞-B ．(,1)-∞-C ．(1,)+∞D ．(4,)+∞9．（5分）甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩．老师说：你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩．看后甲对大家说：我还是不知道我的成绩．根据以上信息，则( ) A ．乙可以知道四人的成绩 B ．丁可以知道四人的成绩C ．乙、丁可以知道对方的成绩D ．乙、丁可以知道自己的成绩10．（5分）执行如图的程序框图，如果输入的1a =-，则输出的(S = )A ．2B ．3C ．4D ．511．（5分）从分别写有1，2，3，4，5的5张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( ) A ．110B ．15C ．310D ．2512．（5分）过抛物线2:4C y x =的焦点F ，3C 于点(M M 在x 轴上方），l 为C 的准线，点N 在l 上，且MN l ⊥，则M 到直线NF 的距离为( ) A 5B ．22C ．23D ．33二、填空题，本题共4小题，每小题5分，共20分 13．（5分）函数()2cos sin f x x x =+的最大值为 ．14．（5分）已知函数()f x 是定义在R 上的奇函数，当(,0)x ∈-∞时，32()2f x x x =+，则(2)f = ． 15．（5分）长方体的长、宽、高分别为3，2，1，其顶点都在球O 的球面上，则球O 的表面积为 ． 16．（5分）ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，若2cos cos cos b B a C c A =+，则B = ．三、解答题：共70分．解答应写出文字说明，证明过程或演算步骤，第17至21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17．（12分）已知等差数列{}n a 的前n 项和为n S ，等比数列{}n b 的前n 项和为n T ，11a =-，11b =，222a b +=． （1）若335a b +=，求{}n b 的通项公式； （2）若321T =，求3S ．18．（12分）如图，四棱锥P ABCD-中，侧面PAD为等边三角形且垂直于底面ABCD，12AB BC AD==，90BAD ABC∠=∠=︒．（1）证明：直线//BC平面PAD；（2）若PCD∆面积为27，求四棱锥P ABCD-的体积．19．（12分）海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：kg ），其频率分布直方图如下：（1）记A 表示事件“旧养殖法的箱产量低于50kg ”，估计A 的概率；（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：箱产量50kg <箱产量50kg旧养殖法 新养殖法（3）根据箱产量的频率分布直方图，对两种养殖方法的优劣进行比较． 附：2()P K K0.050 0.010 0.001 K3.8416.63510.8282()()()()K a b c d a c b d =++++．20．（12分）设O为坐标原点，动点M在椭圆22:12xC y+=上，过M作x轴的垂线，垂足为N，点P满足2NP NM=．（1）求点P的轨迹方程；（2）设点Q在直线3x=-上，且1OP PQ=．证明：过点P且垂直于OQ的直线l过C的左焦点F．21．（12分）设函数2()(1)x f x x e =-． （1）讨论()f x 的单调性；（2）当0x 时，()1f x ax +，求实数a 的取值范围．（二）选考题：共10分。

2017年全国统一高考新课标版Ⅱ卷全国2卷文科数学试卷及参考答案与解析一、选择题：本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合A＝{1,2,3},B＝{2,3,4},则A∪B＝( )A.{1,2,3,4}B.{1,2,3}C.{2,3,4}D.{1,3,4}2.(5分)(1＋i)(2＋i)＝( )A.1－iB.1＋3iC.3＋iD.3＋3i3.(5分)函数f(x)＝sin(2x＋)的最小正周期为( )A.4πB.2πC.πD.4.(5分)设非零向量,满足|＋|＝|－|则( )A.⊥B.||＝||C.∥D.||＞||5.(5分)若a＞1,则双曲线－y2＝1的离心率的取值范围是( )A.(,＋∞)B.(,2)C.(1,)D.(1,2)6.(5分)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A.90πB.63πC.42πD.36π7.(5分)设x,y满足约束条件,则z＝2x＋y的最小值是( )A.－15B.－9C.1D.98.(5分)函数f(x)＝ln(x2－2x－8)的单调递增区间是( )A.(－∞,－2)B.(－∞,－1)C.(1,＋∞)D.(4,＋∞)9.(5分)甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说：你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说：我还是不知道我的成绩.根据以上信息,则( )A.乙可以知道四人的成绩B.丁可以知道四人的成绩C.乙、丁可以知道对方的成绩D.乙、丁可以知道自己的成绩10.(5分)执行如图的程序框图,如果输入的a＝－1,则输出的S＝( )A.2B.3C.4D.511.(5分)从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( )A. B. C. D.12.(5分)过抛物线C：y2＝4x的焦点F,且斜率为的直线交C于点M(M在x轴上方),l为C 的准线,点N在l上,且MN⊥l,则M到直线NF的距离为( )A. B.2 C.2 D.3二、填空题,本题共4小题,每小题5分,共20分13.(5分)函数f(x)＝2cosx＋sinx的最大值为.14.(5分)已知函数f(x)是定义在R上的奇函数,当x∈(－∞,0)时,f(x)＝2x3＋x2,则f(2)＝.15.(5分)长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为.16.(5分)△ABC的内角A,B,C的对边分别为a,b,c,若2bcosB＝acosC＋ccosA,则B＝.三、解答题：共70分.解答应写出文字说明,证明过程或演算步骤,第17至21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题：共60分.17.(12分)已知等差数列{an }的前n项和为Sn,等比数列{bn}的前n项和为Tn,a1＝－1,b1＝1,a2＋b2＝2.(1)若a3＋b3＝5,求{bn}的通项公式；(2)若T3＝21,求S3.18.(12分)如图,四棱锥P－ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB＝BC＝AD,∠BAD＝∠ABC＝90°.(1)证明：直线BC∥平面PAD；(2)若△PCD面积为2,求四棱锥P－ABCD的体积.19.(12分)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位：kg),其频率分布直方图如下：(1)记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率；.K2＝.20.(12分)设O为坐标原点,动点M在椭圆C：＋y2＝1上,过M作x轴的垂线,垂足为N,点P满足＝.(1)求点P的轨迹方程；(2)设点Q在直线x＝－3上,且•＝1.证明：过点P且垂直于OQ的直线l过C的左焦点F.21.(12分)设函数f(x)＝(1－x2)e x.(1)讨论f(x)的单调性；(2)当x≥0时,f(x)≤ax＋1,求a的取值范围.选考题：共10分。

2020届湖北省武汉市2017级高三下学期2月调研仿真模拟考试数学（文）试卷★祝考试顺利★(解析版)一、单选题1.已知集合{|ln 2}A x x =>, {|B x y ==,则()R C A B ⋂=（ ）A. ()20,eB. (20,e ⎤⎦C. 22,e ⎡⎤⎣⎦D. (2,)+∞【答案】C【解析】利用集合的补集,交集运算即可求解;【详解】由题意知,{}2A x x e =>,{}2B x x =≥, ∴{}2R A x x e =≤, ∴()22,R A B e ⎡⎤=⎣⎦.故选:C2.已知复数z 满足2(1)1z i i -=+(i 为虚数单位),则z = ( )A. 1122i -+B. 1122i --C. 1122i +D. 1122i - 【答案】B【解析】先计算出z ,再利用共轭复数及概念计算出z .【详解】由于2(1)1z i i -=+,因此2111(1)22i i i z i i ++-+===--,因此11z 22i =--,故选B. 3.某中学有高中生4200人,初中生1200人,为了解学生学习情况,用分层抽样的方法从该校学生中抽取一个容量为n 的样本,已知从高中生中抽取70人,则n 为（ ）A. 100B. 150C. 200D. 90【答案】D分析：利用分层抽样的定义解答.详解：由题得420070,9042001200nn=∴=+.故答案为D.点睛：（1）本题主要考查分层抽样,意在考查学生对该知识的掌握水平.(2)分层抽样时,一般根据个体抽样前后的比例相等列方程.4.设x,y满足22022020x yx yx y--≤⎧⎪-+≥⎨⎪++≥⎩,则3z x y=-的最小值是（）A. 8B. -2C. -4D. -8【答案】C【解析】作出不等式组表示的平面区域,利用目标函数的几何意义,向上平移直线0:30l x y-=至最高点时的z即为目标函数的最小值.【详解】根据题意,作出不等式组表示的平面区域如图所示：向上平移直线0:30l x y-=,由图可知,当直线3z x y=-经过可行域的顶点时,目标函数3z x y=-有最小值,联立方程220220x yx y--=⎧⎨-+=⎩,解得22xy=⎧⎨=⎩,即2x y==时,min2324z=-⨯=-.故选:C5.已知数列{}n a为等差数列,若1598a a a++=π,则()28cos a a+的值为（）。

湖北省部分学校2017届高三毕业生（二）月调研考试数 学（文 科）试卷一、选择题（本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．） 1、下列函数中，定义域和值域相同的是（ ）A ．2y x =和2x y =B ．sin y x =和tan y x =C ．3y x =和2log y x =D ．2y x =和y x =2、定义{},x y x y A +B =+∈A ∈B ，设集合{}0,1i M =+，130,2i i --⎧⎫N =⎨⎬+⎩⎭，则集合M +N 中元素的个数为（ ）A ．4B ．3C ．2D ．13、从区间()3,3-中任取两个整数a ，b ，设点(),a b 在圆223x y +=内的概率为1P ，从区间()3,3-中任取两个实数a ，b ，直线30ax by ++=和圆223x y +=相离的概率为2P ，则（ ）A ．12P >PB ．12P <PC ．12P =PD ．1P 和2P 的大小关系无法确定4、设抛物线1C :22y x =与双曲线2C :22221x y a b-=的焦点重合，且双曲线2C 的渐近线为y =，则双曲线2C 的实轴长为（ ）A ．1 函数cos 23y x π⎛⎫=- ⎪⎝⎭的图象向右平移12π，得到函数()f x 的图象，则函数()f x 为（ ）A ．周期为π的奇函数B ．周期为π的偶函数C ．周期为2π的奇函数D ．周期为2π的偶函数6、某几何体的三视图如图所示，则该几何体中，面积最大的侧面的面积为（ ）A ．2B ．．3 7、设0x >，则“1a ≥”是“2a x x+≥恒成立”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件8、某科研所共有职工20人，其年龄统计表如下：由于电脑故障，有两个数字在表格中不能显示出来，则下列说法正确的是（ ）A ．年龄数据的中位数是40，众数是38B ．年龄数据的中位数和众数一定相等C ．年龄数据的平均数()39,40x ∈D ．年龄数据的平均数一定大于中位数 9、在三角形C AB 中，C 60∠= ，C C 6A +B =，4AB =，则AB 边上的高为（ ）A B ．203C D ．4310、如图所示，若输入的n 为10，那么输出的结果是（ ） A ．45 B ．110 C ．90 D ．55二、填空题（本大题共7小题，每小题5分，共35分．） 11、已知公比为负值的等比数列{}n a 中，154a a =，41a =-，则数列{}n a 的通项公式为 ．12、在三角形C AB 中，A ，B ，C 是三角形C AB 的内角，设函数()22C 2sinsin sin cos 2222f ππB +A A A ⎛⎫⎛⎫A =-++- ⎪ ⎪⎝⎭⎝⎭，则()f A 的最大值为 ．13、已知矩形CD AB 中，2AB =，C 1B =，点P 是D B 上任意一点，则()CBP⋅PA +P的取值范围是 ．14、设x ，y 满足约束条件()2log 221x y x y +≤⎧⎪⎨-≤⎪⎩，则z x y =+的最大值为 ．15、若函数()2sin f x x απ⎛⎫=+ ⎪⎝⎭（02απ<<）是奇函数，则方程()lg f x x =解的个数为 ．16、已知函数()2log 1f x a x =+（0a ≠），定义函数()()(),0F ,0f x x x f x x >⎧⎪=⎨-<⎪⎩，给出下列命题：①()()F x f x =；②函数()F x 是奇函数；③当0a >时，若120x x <，120x x +>，则()()12F F 0x x +>成立；④当0a <时，函数()2F 23y x x =--存在最大值，不存在最小值，其中所有正确命题的序号是 ．17、已知矩形CD AB 的周长为18，把它沿图中的虚线折成正六棱柱，当这个正六棱柱的体积最大时，它的外接球的表面积为 ．三、解答题（本大题共5小题，共65分．解答应写出文字说明、证明过程或演算步骤．）18、（本小题满分13分）设函数()()2cos cos cos 2f x x x x a x π⎛⎫=-++ ⎪⎝⎭的一个零点是12x π=．()1求函数()f x 的周期；()2求函数()f x 单调增区间． 19、（本小题满分12分）农科院分别在两块条件相同的试验田分别种植了甲、乙两种杂粮作物，从两块试验田中任意选取6颗该种作物果实，测得籽重（单位：克）数据如下： 甲种作物的产量数据：111 111 122 107 113 114乙种作物的产量数据：109110124108112115()1计算两组数据的平均数和方差，并说明哪种作物产量稳定；()2作出两组数据的茎叶图．20、（本小题满分12分）如图所示，在矩形CDA=，AB中，D1 AB=，点E是线段AB的中点，把三角形DAE沿D E折起，设折2起后点A的位置为P，F是D P的中点．()1求证：无论P在什么位置，都有F//PE；A平面C()2当点P在平面CDAB上的射影落在线段D E上时，若三棱锥CDP-E的四个顶点都在一个球上，求这个球的体积．21、（本小题满分14分）已知椭圆1C :2241x y +=，焦点在x 轴上的椭圆2C 的短轴长与1C 的长轴长相等，且其离心率为2． ()1求椭圆2C 的方程；()2若点T 满足：2OT =MN +OM +ON，其中M ，N 是2C 上的点，且直线OM ，ON 的斜率之积等于14-，是否存在两定点A ，B ，使TA +TB 为定值？若存在，求出这个定值；若不存在，请说明理由．22、（本小题满分14分）已知函数()ln 2f x x ax =-+，R a ∈是常数．()1若函数()y f x =的图象在点()(),a f a （0a >）与直线y b =相切，求a和b的值；()2若函数()=有两个零点，求实数a的取值范围．y f x。

武汉市2017届高中毕业生二月调研测试试卷绝密★启用前武汉市2017届高中毕业生二月调研测试试卷英语试题武汉市教育科学研究院命制2017.2.17本试题卷共9页。

全卷满分150分。

考试用时120分钟。

★祝考试顺利★注意事项：1.答卷前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2、选择题的作答:每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3、非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4、考试结束后，请将本试题卷和答题卡一并上交。

第一部分:听力（共两节，满分30分）做题时，先将答案划在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题;每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

例：How much is the shirt?A. £ 19.15.B. £ 9.18.C. £ 9.15.答案是C。

1. What did the man forget to do?A. Pick up milk and eggs for breakfast.B. Get some noodles for dinner.C. Put the garbage downstairs.2. What are the speakers mainly talking about?A. A presentation.B. An inspiring story.C. An Australian person.3. What will the woman probably do in ten minutes?A. Plan a party.B. Do someone a favor.C. Work on her report.4. Where does the conversation probably take place?A. In a classroom.B. In a drugstore.C. At the doctor’s.5. Who might Cathy be?A. Bill’s friend.B. The history teacher.C. Jill' s roommate.第二节（共15小题;每小题1.5分，满分22.5分）听下面5段对话或独白。

武汉市2017-2018高三数学起点调研试卷（文科含解析）2017-2018学年度武汉市部分学校新高三起点调研测试文科数学第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合，，则（）A.B.C.D.【答案】C【解析】本题选择C选项.2.设，其中是实数，则在复平面内所对应的点位于（）A.第一象限B.第二象限C.第三象限D.第四象限【答案】D【解析】由，其中是实数，得：，所以在复平面内所对应的点位于第四象限.本题选择D选项.3.函数的最小正周期为（）A.B.C.D.【答案】C【解析】∴最小正周期.本题选择C选项.4.设非零向量满足，则（）A.B.C.D.【答案】A【解析】∵非零向量满足，本题选择A选项.5.已知双曲线（）的离心率与椭圆的离心率互为倒数，则双曲线的渐近线方程为（）A.B.C.或D.或【答案】A【解析】由题意,双曲线离心率∴双曲线的渐近线方程为，即.本题选择A选项.点睛：双曲线的渐近线方程为，而双曲线的渐近线方程为(即)，应注意其区别与联系.6.一个几何体的三视图如图，则它的表面积为（）A.28B.C.D.【答案】D【解析】如图所示，三视图所对应的几何体是长宽高分别为2,2,3的长方体去掉一个三棱柱后的棱柱：ABIE-DCJH，该几何体的表面积为：.本题选择D选项.点睛：(1)以三视图为载体考查几何体的表面积，关键是能够对给出的三视图进行恰当的分析，从三视图中发现几何体中各元素间的位置关系及数量关系．(2)多面体的表面积是各个面的面积之和；组合体的表面积应注意重合部分的处理．(3)圆柱、圆锥、圆台的侧面是曲面，计算侧面积时需要将这个曲面展为平面图形计算，而表面积是侧面积与底面圆的面积之和．7.设满足约束条件，则的最大值是（）A.-15B.-9C.1D.9【答案】D【解析】x、y满足约束条件的可行域如图：z=2x+y经过可行域的A时，目标函数取得最小值，由解得A(&#8722;6,&#8722;3)，则z=2x+y的最小值是：&#8722;15.故选：A.点睛：求线性目标函数z＝ax＋by(ab≠0)的最值，当b＞0时，直线过可行域且在y轴上截距最大时，z值最大，在y轴截距最小时，z值最小；当b＜0时，直线过可行域且在y轴上截距最大时，z值最小，在y轴上截距最小时，z值最大.8.函数的单调递增区间是（）A.B.C.D.【答案】D【解析】由得：x∈(&#8722;∞,&#8722;1)∪(5,+∞)，令，则y=t，∵x∈(&#8722;∞,&#8722;1)时,为减函数；x∈(5,+∞)时,为增函数；y=t为增函数，故函数的单调递增区间是(5,+∞)，本题选择D选项.点睛：复合函数的单调性：对于复合函数y＝f[g(x)]，若t＝g(x)在区间(a，b)上是单调函数，且y＝f(t)在区间(g(a)，g(b))或者(g(b)，g(a))上是单调函数，若t＝g(x)与y＝f(t)的单调性相同(同时为增或减)，则y＝f[g(x)]为增函数；若t＝g(x)与y＝f(t)的单调性相反，则y＝f[g(x)]为减函数．简称：同增异减．9.给出下列四个结论：①命题“，”的否定是“，”；②“若，则”的否命题是“若，则”；③是真命题，则命题一真一假；④“函数有零点”是“函数在上为减函数”的充要条件. 其中正确结论的个数为（）A.1B.2C.3D.4【答案】B【解析】由题意得，根据全程命题与存在性命题的否定关系，可知①是正确的；②中，命题的否命题为“若，则”，所以是错误的；③中，若“”或“”是真命题，则命题都是假命题；④中，由函数有零点，则，而函数为减函数，则，所以是错误的，故选A。

高考衣食住用行衣：高考前这段时间，提醒同学们出门一定要看天气，否则淋雨感冒，就会影响考场发挥。

穿着自己习惯的衣服，可以让人在紧张时产生亲切感和安全感，并能有效防止不良情绪产生。

食：清淡的饮食最适合考试，切忌吃太油腻或者刺激性强的食物。

如果可能的话，每天吃一两个水果，补充维生素。

另外，进考场前一定要少喝水！住：考前休息很重要。

好好休息并不意味着很早就要上床睡觉，根据以往考生的经验，太早上床反而容易失眠。

考前按照你平时习惯的时间上床休息就可以了，但最迟不要超过十点半。

用：出门考试之前，一定要检查文具包。

看看答题的工具是否准备齐全，应该带的证件是否都在，不要到了考场才想起来有什么工具没带，或者什么工具用着不顺手。

行：看考场的时候同学们要多留心，要仔细了解自己住的地方到考场可以坐哪些路线的公交车？有几种方式可以到达？大概要花多长时间？去考场的路上有没有修路堵车的情况？考试当天，应该保证至少提前20分钟到达考场。

绝密★启用前2017年普通高等学校招生全国统一考试文科数学注意事项：1.答题前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.设集合{}{}123234A B ==，，， ，，， 则=A B U A. {}123,4，， B. {}123，， C. {}234，， D. {}134，，2.（1+i ）（2+i ）=A.1-iB. 1+3iC. 3+iD.3+3i 3.函数()fx =πsin （2x+）3的最小正周期为A.4πB.2πC. πD. 2π4.设非零向量a ，b 满足+=-b b a a 则A a ⊥b B. =b a C. a ∥b D. >b a5.若a ＞1，则双曲线x y a=222-1的离心率的取值范围是A. 2+∞（，）B. 22（，）C. 2（1，）D. 12（，）6.如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为A.90πB.63πC.42πD.36π7.设x 、y 满足约束条件2+330233030x y x y y -≤⎧⎪-+≥⎨⎪+≥⎩。