基础教育 数学课程与教学概论(常进荣等)思维导图
- 格式:xmin
- 大小:4.87 KB
- 文档页数:1

a 2 ⎪ ⎪乘法运算 ⎪ ⎪ ⎨ ⎪ ⎡ 2 ⎨ ⎥ ⎨ ⎪ 第一部分《数与式》知识点⎧ ⎧定义:有理数和无理数统称实数. ⎪ ⎪⎪ ⎪分类⎧有理数:整数与分数 ⎪⎪ 无理数:常见类型( 开方开不尽的数、与有关的数、无限不循环小数) ⎪实数⎪ ⎩ ⎧法则:加、减、乘、除、乘方、开方 ⎪ ⎨实数运算⎨ ⎪ ⎩运算定律:交换律、结合律、分配律 ⎪ ⎪ ⎪数轴(比较大小)、相反数、倒数(负倒数)科学记数法 ⎪ ⎪相关概念: ⎨ 2 ⎩ ⎩有效数字、平方根与算术平方根、立方根、非负式子(a a , a ) ⎪ ⎧ ⎧单项式:系数与次数⎪ ⎪分类⎨⎪ ⎪ ⎩多项式:次数与项数 ⎪ ⎪加减法则:(加减法、去括号(添括号)法则、合并同类项) ⎪ ⎪ ⎛ a a m 1 ⎫ ⎪ ⎪幂的运算: a m ⋅a n = a m +n ; a m ÷ a n = a m -n ;(a m )n = a mn ,(ab )m = a m b m ;( )m = ; a 0 = 1;a - p = ⎪ ⎪ ⎝ b b m ⎪整式⎨ ⎛单项式单⨯ 项式;单项式多⨯项式;多项式多项⨯式 ⎫ : 单项式单÷ 项式;多项式单÷项式 ⎪ ⎪ ⎝ ⎭ a p ⎭ ⎪ ⎪混合运算:先乘方开方,再乘除,最后算加减;同级运算自左至右顺序计算;括号优先 ⎪ ⎪ ⎪ ⎪⎧平方差公式:(a + b )(a - b ) = a 2 - b 2 ⎪ ⎪乘法公式⎨2 2 2 ⎩ ⎩完全平方公式:(a ± b ) = a ± 2ab + b ⎧ ⎧分式的定义:分母中含可变字母 ⎪ ⎪分式分⎨ 式有意义的条件:分母不为零 ⎪⎪ ⎪ ⎪⎩分式值为零的条件:分子为零,分母不为零 数与式 ⎪⎪ ⎛ a a ⨯ m a a ÷ m ⎫ ⎪分式分⎨ 式的性质:通 分=与约分; 的=根据)( ⎪⎪ ⎪ ⎝ b b ⨯ m b b ÷ m ⎭ ⎪ ⎪ ⎧通分、约分,加、减、乘、除 ⎪ ⎪ ⎪ ⎪ ⎪分式的运算⎨ ⎧先化简再求值(整式与分式的通分、符号变化) ⎪ ⎪ ⎪化简求值⎨ ⎪ ⎩ ⎩ ⎩整体代换求值 ⎪ ⎧定义:式子≥a 叫(a 二0) 根式二次根.式的意义即被开方数大于等于 0. ⎪ ⎪ ⎪ ⎪ ⎪二次根式的性质:⎢( a ) = a ; = ⎧ a (a ≥ 0) ⎤ -a (a ≤ 0) ⎪ ⎪ ⎣ ⎩ ⎦ ⎪ ⎪ ⎧最简二次根式(分解质因数法化简) ⎪ ⎪ ⎪ 二次根式⎨二次根式的相关概念同⎨ 类二次根式及合并同类二次根式 ⎪ ⎪ ⎪分母有理化(“ 单项式与多项式” 型) ⎪ ⎪ ⎩ ⎪ ⎪ ⎧⎪加减法:先化最简,再合并同类二次根式 ⎪ ⎪二次根式的运算⎨ a ⎪ ⎪ ⎪乘除法:a ⋅(b 结=果化ab 简; = ⎪ ⎩ ⎩ b ⎪ ⎪ ⎧定义:(与整式乘法过程相反,分解要彻底) ⎪ ⎪ ⎧提取公因式法:(注意系数与相同字母,要提彻底) ⎪ ⎪ ⎪ ⎧ 2 2 ⎪ ⎪ 平方差公式:a - b = (a + b )(a - b ) ⎪分解因式⎨ ⎪公式法⎨ 2 2 2⎪ ⎪方法⎨ ⎩完全平方公式:a ± 2ab + b = (a ± b ) ⎪ ⎪ ⎪十字相乘法:x 2 + (a + b )x + ab = (x + a )(x + b ) ⎪ ⎪⎪ ⎪ ⎩ ⎩分组分解法:(对称分组与不对称分组) a b ⎪ ⎪⎪ ⎩ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ 第二部分《方程与不等式》知识点 ⎧ ⎧ ⎧定义与解: ⎪ ⎪ ⎪ ⎪ ⎪一元一次方程解⎨ 法步骤:去分母、去括号、移项、合并同类项、系数化为1. ⎪ ⎪ ⎪应用:确定类型、找出关键量、数量关系⎪ ⎪ ⎩ ⎪ ⎪ ⎧⎪定义与解:⎪ ⎪二元一次方程(组)⎪解法:代入消元法、加减消元法⎪ ⎪ ⎨ ⎪方程⎨ ⎪简单的三元一次方程组: ⎪ ⎪ ⎩简单的二元二次方程组:⎪ ⎪ ⎧定义与判别式( △=b 2 - 4ac) ⎪⎪一元二次方程⎨ ⎪ ⎪ ⎪ ⎪ ⎩解法:直接开平方法、配方法、求根公式法、因式分解法. ⎧定义与根(增根): ⎪ ⎪分式方程⎨⎪ ⎩ ⎪ ⎧⎪ ⎩解法:去分母化为整式方程,解整式方程,验根. ⎧⎪1. 行程问题: ⎪ ⎪ ⎪2. 工程(效)问题: ⎪ ⎪ ⎪3. 增长率问题:(增长率与负增长率) ⎪ 4.数字问题:(数位变化) ⎪ ⎪ ⎪类型⎨ 方程与不等式 ⎪ ⎪5. 图形问题:(周长与面积(等积变换)) ⎪⎨方程的应用⎪⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ 6. 销售问题:(利润与利率) ⎪7. 储蓄问题:(利息、本息和、利息税) ⎩8. 分配与方案问题:⎪ ⎪ ⎧⎪1.线段图示法: ⎪ ⎪常用方法列⎨2表. 法: ⎪ ⎪ ⎪3.直观模型法: ⎧ ⎧一般不等式解法⎪一元一次不等式⎨ ⎪ ⎪ ⎩条件不等式解法 ⎪ ⎪ ⎧⎪解法:(借助数轴) ⎪ ⎪ ⎧1.不等式与不等式 ⎪不等式(组)⎨ ⎪ ⎪ ⎪ ⎪2.不等式与方程 一元一次不等式组⎨ ⎪ ⎪ ⎪应用不⎨3等. 式与函数 ⎪ ⎪ ⎪ ⎪ ⎪4.最佳方案问题 ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎩5. 最后一个分配问题 ⎪ ⎪⎩⎪第三部分《函数与图象》知识点⎪⎪ ⎪ ⎨ ⎪ ⎪ ⎨⎪ ⎪ ⎩ ⎪ ⎪ b ⎩ ⎪函数应用⎨ ⎪ ⎪ ⎧ ⎧①各象限内点的特点: ⎪ ⎪ ⎧x 轴:纵坐标y=0; ⎪ ⎪②坐标轴上点的特点⎨ y 轴:横坐标x=0. ⎪ ⎪ 直角坐标系⎪③平行于x 轴,y 轴的线段长度的求法(大坐标减小坐标) ④不共线的几点围成的多边形的面积求法(割补法) ⎪ ⎪ ⎪ ⎪ ⎧关于x 轴对称( x 相同,y 相反) ⎪ ⎪ ⎪ ⑤对称点的坐标关于y 轴对称( x 相反,y 相同) 关于原点O 称( x ,y 都相反)⎪ ⎧ ⎩ ⎩ ⎧ ⎧一、三象限角平分线:y=x ⎪ ⎪正比例函数:y=kx( k ≠0) (一点求解析式)⎨ ⎪函数表达式⎨ ⎩二、四象限角平分线: y=- x ⎪ ⎪一次函数:y=kx+b( k ≠0) (两点求解析式) ⎪ ⎩ 增减性: 与y=kx+b 增减性一样,k >0时,x 增大y 增大;k <0, x 增大y 减小. ⎪ ⎪一次函数⎨y=kx ⎪ ⎪平移性:y=kx+b 可由y=kx 上下平移而来;若y=k 1x+b 1与y=k 2x+b 2平行,则k 1 = k 2 , b 1 ⎪ ⎪垂直性: 若y=k x+b 与y=k x+b 垂直,则k k = -1. b 2 . ⎪ ⎪ ⎪求交点:(联立函数表达式解方程组) ⎪ ⎪正负性:观察图像y 与0 <y 时,0 的取x 值范围(图像在轴上x 方或下方时,的取值x 范围)⎪ ⎩ ⎧ k ⎪ ⎪表达式:≠=一点(k 求解0)(析式) ⎪ ⎪ x ⎪ ⎪ ⎧①区域性:>时0 ,图像在一、三象限;<k 时,0 图像在二、四象限. ⎪ ⎪ ⎪ ②增减性⎨⎧k >0在每个象限内,y 随x 的增大而减小; ⎪反比例函数性⎨ 质 ⎨ ⎪ ⎪ ⎩k <0在每个象限内,y 随x 的增大而减小. ⎪ ⎪ ⎪⎩③恒值性:(图形面积与k 值有关) 函数⎪ ⎪ ④对称性:既是轴对称图形,又是中心对称图形. ⎨ ⎪求交点:(联立函数表达式解方程组求交点坐标,还可由图像比较函数的大小) ⎪ ⎪ ⎧ ⎧①一般式:y ax 2 + bx + c 其, 中 (a ≠ 0), ⎪ ⎪ ⎪ 2 ⎪表达式②⎨ 顶点式:=y a (x - k ) +其h ,中(k (a , h ≠)0为),抛物线顶点坐标; ③交点式:= a (x - x )(x - x )其, 中,(a 、≠是0)函数x 图x 象与轴交点的横x 坐标; ⎪ ⎪ ⎩ 1 2 1 2 ⎪ ⎪ ⎧①开口方向与大小:a >0向上,a <0向下;a 越大,开口越小;越小,开口越小. ⎪ ⎪ ⎪ b ⎪ ⎪ ⎪②对称性:对称轴直线x=- ⎪ ⎪ ⎪ 2a ⎪ ⎪ ⎪ ⎧a >0,在对称轴左侧,增x 大减y 小;在对称轴右侧,增大x 增大y ; ⎪ ⎪性质⎪⎪③增减性⎨⎪ ⎪ ⎨ ⎩a <0,在对称轴左侧,增x 大增y 大;在对称轴右侧,增大x 减小y ; ⎪ ⎪ ⎪ b 4ac - b 2 ⎪二次函数⎨ ④顶点坐标:(- , ) ⎪ ⎪ ⎪ ⎪ ⎪ ⎪2a 4a 4ac - b 2 b 4ac -b 2 ⎪ ⎪ ⎪⑤最值:当a >0时, x=- ,y = ;a <0时,x=- ,y = .⎪ ⎪ ⎩ 2a 最小值最大值 4a2a 4a ⎪ ⎪示意图:画示意图五要素(开口方向、顶点、对称轴、与、x 交y 点坐标) ⎪ ⎪ ⎧a 与:c 开口方向确定a 的符号,抛物线与y 轴交点纵坐标确定c 的值; ⎪⎪ ⎪b 的符号:b 的符号由a 与对称轴位置有关:左同右异. ⎪ ⎪ ⎪ ⎪符号判断⎨Δ=b 2 - 4ac :Δ>0与x 轴有两个交点;Δ=0与x 轴有两个交点;Δ<0与x 轴无交点. ⎪ ⎪ ⎪a + b + c :当x=1时,y=a+b+c 的值.⎪ ⎪ ⎪ ⎪ ⎪ ⎩a - b + c :当x=- 1时,y=a- b+c 的值. ⎪ ⎧①求函数表达式: ⎪ ⎪⎪②求交点坐标: ⎪ ⎪③求围成的图形的面积( 巧设坐标): ⎪⎩⎩④比较函数的大小. ⎩ ⎪ ⎪ ⎪ ⎪ 1 1 2 2 1 2 ⎪⎪ ⎨ ⎪ ⎪⎪判定:⎨⎪平行于同一条直线的两条直线平行 ⎩ 第四部分《图形与几何》知识要点⎧ ⎧直线:两点确定一条直线 ⎪ ⎪ ⎪线射⎨ 线: ⎪ ⎪线段:两点之间线段最短,(点到直线的距离,平行线间的距离)⎪ ⎩ ⎪ ⎧角的分类: 锐角、直角、钝角、平角、周角. ⎪ ⎪ 0 ” ’ ” ⎪角⎪角的度量与比较:1 ,= 60 1 ;= 60 ⎪ ⎨余角与补角的性质:同角的余角(补角)相等,等角的余角(补角)相等, ⎪ ⎪ ⎩角的位置关系:同位角、内错角、同旁内角、对顶角、邻补角 几何初步 相交线⎧对顶角:对顶角相等. ⎨ ⎩垂线:定义,垂直的判定,垂线段最短. ⎪ ⎧ ⎪ ⎪ ⎪ ⎪定义:在同一平面内,不相交的两条直线叫平行线⎪ ⎪ ⎪平行线性⎨ 质:两直线平行,同位角相等、内错角相等、同旁内角互补; ⎪ ⎪ ⎧同位角相等或内错角相等或同旁内角互补,两直线平行⎪ ⎪ ⎪ 平面内,垂直于同一条直线的两直线平行⎪ ⎩⎩⎧ 的对边的邻边的对边 ⎪定义:在R A B C 中,si n =,cos = ,t an =斜边斜边的邻边⎪ ⎧ ⎪ si n 300 = 1 ,co ;s 300 = 3 , tan 300 = 3 ⎪ 2 2 3 三角函数⎨ 特殊三角函数值 0 = 2 cos 450 = 2 , tan 450 = 1 ⎪ s ⎨i n45 ,; ⎪ ⎪ 0 ⎪si n6 = 2 2 3 ,cos 600 = 1 , tan 300 = 3. ⎪ 0 2 2 ⎪ ⎩应用:要构造△t ,才能使用三角函数 .⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎧ ⎧ ⎧按边分类:不等边三角形、等腰三角形、等边三角形 ⎪ ⎪分类⎨ ⎪ ⎪ ⎩按角分类:锐角三角形、直角三角形、钝角三角形 ⎪ ⎪ ⎪⎧三边关系:两边之和大于第三边,两边之差小于第三边; ⎪ ⎪边⎨ 1 ⎪⎪ ⎪面积与周长:C a+b=c ,=S 底 高.⨯ ⎪ ⎩ 2 ⎪ ⎪ ⎧⎪三角形的内角和等于180度,外角和等于360度; 角三 角形的一个外角等于不相邻的两内角之和; ⎪ ⎪ ⎨ ⎪ ⎪ ⎪三角形的一个外角大于任何一个不相邻的内角.⎪ ⎩ ⎪一般三角形⎨ ⎧中线:一条中线平分三角形的面积⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧⎪性质:角平分线上的点到角两边的距离相等; ⎪ ⎪ ⎪角平分线判⎨ 定:到角两边的距离相等的点在角的平分线上 . ⎪ ⎪⎪ ⎪内心:三角形三条角平分线的交点,到三边距离相等. ⎪ ⎪线段⎪⎩ ⎨高:高的作法及高的位置(可以在三角形的内部、边上、外部) ⎪ ⎪⎪中位线:三角形的中位线平行于第三边且等于第三边的一半. ⎪ ⎪ ⎪ ⎪ ⎪ ⎧性质:线段垂直平分线上的点到线段两端点的距离相等; ⎪ ⎪中垂线⎪判定:到线段两端点的距离相等的点在线段的垂直平分线上.⎪ ⎪ ⎨ 三角形⎪ ⎪ ⎩⎪⎪外心:三角形三边垂直平分线的交点,到三个顶点的距离相等 ⎪⎨ ⎧ ⎧ ⎩ 等腰三角形的两腰相等、两底角相等,具有三线合一性质,是轴对称图形. ⎪ ⎪性质⎨ ⎪ ⎩等边三角形的三边上均有三线合一,三边相等,三角形等都为6度0 . ⎪ ⎧有两边相等的三角形是等腰三角形; ⎪等腰三角形⎨ ⎪有两角相等的三角形是等腰三角形;⎪ ⎪ ⎪ ⎪判定⎨ ⎪ ⎪ ⎪有一个角为6度0的等腰三角形是等边三角形; ⎪ ⎪⎩ ⎩有两个角是度0的三角 形是等边三角形. ⎪ ⎧ ⎧一个角是直角或两个锐角互余; ⎪ ⎪ ⎪直角三角形斜边上的中线等于斜边的一半; ⎪ ⎪性质⎨⎪ ⎪ ⎪ 0 ⎪ ⎪直角三角形中,30的锐角所对的直角边等于斜边的一半; ⎪直角三角形⎨ ⎪ ⎪ ⎩勾股定理:两直角边的平方和等于斜边的平方. ⎧⎪证一个角是直角或两个角互余; ⎪ ⎪判定有⎨ 一边上的中线等于这边的一半的三角形是直角三角形; ⎪ ⎪ ⎪ 2 2 2 0 ⎪ ⎪⎩ ⎩勾股定理的逆定理:若a +b =c ,则∠C = 90 . ⎪全等三角形 ⎪⎧性质⎨⎧全等三角形的对应边相等,对应角相等,周长、面积也相等; 全等三角形对应线段(角平分线、中线、高、中位线等)相等.⎪ ⎨ ⎩ ⎪判定:,S ,A ,S ,A .S AAS SSS HL⎩ ⎩⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧多边形:多边形的内角和为(n- 2)⋅ 1800 ,外角和为3600 . ⎪ ⎧定义:一组对边平行而另一组对边不平行的四边形叫做梯形. ⎪ ⎪ ⎪ ⎪ ⎧⎪直角梯形 ⎧性质:两腰相等、对角线相等,同一底上的两角相等. ⎪梯形⎨ ⎪ ⎪ ⎪特殊梯形两⎨ 腰相等的⎪梯形是⎧ 等腰梯形; ⎪等腰梯形⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ 判定对角线相等的梯形是等腰梯形; ⎨ ⎪同一底上的两角相等的梯形是等腰梯形; ⎪ ⎩ ⎩ ⎪ ⎧ ⎧两组对边分别平行且相等 ⎪ ⎪ ⎪ ⎪ ⎪性质:平行四边形的⎨两组对角分别相等 ⎪ ⎪ 两条对角线互相平分 ⎪ ⎪ ⎩ ⎪平行四边形⎪ ⎧两组对边分别平行 ⎪ 一组对边平行且相等 ⎪ ⎪ ⎪ ⎪判定:⎨两组对边分别相等的⇒四边形是平行四边形. ⎪ ⎪ ⎪两组对角分别相等 ⎪ ⎪ ⎪ ⎪ ⎪ ⎩对角线互相平分⎪ ⎩ ⎪ ⎧⎪性质⎧⎨共性:具有平行四边形的所有性质. 四边形⎨ ⎪ ⎩个性:对角线相等,四个角都是直角. ⎪矩形⎪⎨ ⎧⎪先证平行四边形,再证有一个直角; 判定先证平行四边形,再证对角线相等;⎪ ⎪ ⎨ ⎪ ⎪ ⎪三个角是直角的四边形是矩形.⎪ ⎩ ⎩ ⎪ ⎧ ⎧共性:具有平行四边形的所有性质. ⎪ ⎪性质⎨ ⎪菱形⎪ ⎪ ⎨ ⎩个性:对角线互相垂直且每条对角线平分一组对角,四条边相等. ⎧先证平行四边形,再证对角线互相垂直; ⎪ ⎪ ⎪判定先⎨ 证平行四边形,再证一组邻边相等; ⎪ ⎪⎪ ⎩ ⎩四条边都相等的四边形是菱形.⎪ ⎧⎪性质:具有平行四边形、矩形、菱形的所有性质. ⎪正方形⎨ ⎧证平行四边形矩→形正方→形 ⎪ ⎪判定⎨⎩ ⎩证平行四边形菱→形正方→形 ⎧ 1 ⎪梯形:(=上 底下底+ )⨯高=中位线高⨯ ⎪ 2 ⎪ ⎪平行四边形:底=高 ⨯ ⎪ 面积求法⎨矩形:长=宽 ⨯ ⎪ ⎪ 菱形:=底高⨯=对角线乘积的一半 ⎪ ⎪ ⎩正方形:边=长边长⨯=对角线乘积的一半 ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎩ ⎪ ⎪ ⎧ ⎧点在圆外:d >r ⎪ ⎪ ⎪点与圆的三种位置关系点⎨ 在圆上:d =r ⎪ ⎪点在圆内:d <r⎪ ⎩ ⎪ ⎧弓形计算:(弦、弦心距、半径、拱高)之间的关系 ⎪圆的轴对称性⎨垂径定理⎨⎧定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧 ⎪ ⎪ ⎩推论:平分弦(不是直径)的直径垂直于弦,并且平分线所对的弧 ⎪ ⎧ ⎧在同圆或等圆中,两条弧、两条弦、两个圆心角、两个圆周角、 ⎪五组量的关系:⎨两条弦心距中有一组量相等,则其余的各组两也分别相等. ⎩ ⎧同弧所对的圆周角是它所对圆心角的一半; ⎪ ⎪ 0 ⎪圆的中心对称性⎨圆周角与圆心角半⎨ 圆(或直径)所对的圆周角是;90 900的圆周角所对的弦是直径,所对的弧是半圆.⎪ ⎪ ⎩ ⎪⎪相交线定理:圆中两弦A 、B 相交C 于D 点,则P PA PA = P C PD. ⎪⎪ ⎪ ⎪⎩圆中两条平行弦所夹的弧相等. ⎪ ⎪ ⎪⎧ ⎪⎧相离:d >r⎪ ⎪直线和圆的三种位置关系相⎨ 切:d =r ( 距离法) 圆⎨ ⎪ ⎪相交:d <r ⎩ ⎪ ⎪ ⎧性质:圆的切线垂直于过切点的直径(或半径) ⎪ ⎪圆的切线⎨ 直线和圆的位置关系⎨ ⎩判定:经过半径的外端且垂直于这条半径的直线是圆的切线.⎪ ⎪ ⎪ ⎪弦切角:弦切角等于它所夹的弧对的圆周角 ⎪ ⎪切线长定理:如图,PA ,P B 平分PO ∠ ⎪ ⎪⎪ ⎪切割线定理:如图,PA 2 = PC PD. ⎪外心与内心: APB A P .O ⎩ ⎪ ⎧相离:外离(d >R+r ),内含(d <R- r ) C D ⎪ B ⎪圆和圆的位置关系⎪ 相⎨ 切:外切(d=R+r ),内切(d=R- r ) ⎪ ⎪相交:R- r <d <R+r ) ⎪ ⎧ ⎩ n n ⎪ ⎪弧长公式:l 弧长 = 360 2r = r 180 ⎪ ⎪ ⎪ ⎪扇形面积公式:S = n r 2 =1 ⋅l ⋅ r 圆的有关计算⎪ ⎪ ⎪ 360 2 弧长 1⎪ ⎪圆锥的侧面积:为侧底=面 ⋅圆2的r 半⋅l =径,rl 为(r 母线) l ⎪⎪圆锥的全面积:S ⎩⎩ 全 =2 r 2 +rl⎩ ⎪ ⎪ ⎪ ⎩ b d n b + d +... + n ⎪ ⎨ ⎪⎪ ⎪ ⎪ 第五部分《图形的变化》知识点⎧ ⎧ ⎧①轴对称指两个图形之间的关系,它们全等 ⎪⎪ ⎪②对应点的连线段被对称轴垂直平分 ⎪ ⎪轴对称(折叠)⎪⎨ ⎪ ⎪③对应线段所在的直线相交于对称轴上一点(或平行) 轴对称⎨⎪ ⎪ ⎩④图形折叠后常用勾股定理求线段长 ⎪ ⎪ ⎧①指一个图形 ⎪ ⎪轴对称图形⎨ ⎪ ⎪ ⎩②轴对称图形被对称轴分成的两部分全等 ⎪ ⎪ ⎧⎪①平移前后两个图形全等⎪平 移⎪②平移前后对应点的连线段相等且平行(或共线)⎨ ⎪③平移前后的对应角相等,对应线段相等且平行(或共线) ⎪ ⎩④平移的两个要素:平移方向、平移距离 ⎪ ⎧①旋转前后的两个图形全等 ⎪②旋转前后对应点与旋转中心的连线段相等,且它们的夹角等于旋转角⎪旋 转⎨⎪③旋转前后对应角相等,对应线段相等⎪ ⎪ ⎪ ⎩④旋转的三要素:旋转中心、旋转方向、旋转角 ⎪ ⎧ ⎧①大小、比例要适中 ⎪ ⎪视图的画法⎨ ⎪ ⎪ ⎩②实线、虚线要画清 ⎪视图与投影⎪⎨ ⎪⎧平行投影:平行光线下的投影,物体平行影子平行或共线 ⎪ ⎪投影⎪中心投影:点光源射出的光线下的投影,影子不平行 ⎪⎪ ⎨ ⎪ ⎪ ⎪视点、视线、盲区 ⎪ ⎩ ⎩投影的计算:画好图形,相似三角形性质的应用 图形的变化 ⎧ ⎧ a c ⎪ ⎪基本性质: = ⇔ ad = bc ⎨⎪ ⎪ ⎪⎪ b a d c a ± b c ± d 比例的性质合比性质: = ⇒ =⎪ ⎪ ⎨ ⎪ ⎪ ⎪ b d b d a c m a + b +... + m ⎪ ⎪ ⎪等比性质: ,= (条= .件.. =≠ = k ⇒ = k b + d +... + n 0) ⎪ ⎪ ⎪黄金分割:线段被B 点分成C 、两线A C 段(B >C ),满足A =C BC , ⎪ 则点C 为的A 一B 个黄金分割点 AC 2 BC AB ⎪ ⎪ ⎧ ⎧性质:相似多边形的对应边成比例、对应角相等 ⎪ ⎪相似多边形⎨ ⎪ ⎪ ⎩判定:全部的对应边成比例、对应角相等⎪ ⎪ ⎪ ⎧⎪ ⎧⎪①对应角相等、对应边成比例 ⎪ ⎪ ⎪ ⎪性质②⎨ 对应线段(中线、高、角平分线、周长)的比等于相似比 ⎪相似形⎨ ⎪ ⎪ ⎪ ⎪ ⎪③面积的比等于相似比的平方 ⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎧①有两个角相等的两个三角形相似 ⎪相似图形 ⎪ ⎪ ⎪相似三角形⎨判定 ⎪②两边对应成比例且夹角相等的两个三角形相似 ⎪⎨ ⎪ ⎪ ⎪ ⎪ ⎪③三边对应成比例的两个三角形相似 ⎪ ⎪ ⎪ ④有一条直角边与斜边对应成0比例的两个直角三角2 形相似 ⎪ ⎪ ⎪ ⎪射影定理:在△t 中A ,B ∠C ,⊥,则==90 CD , AB AC AD ⋅AB ⎪ ⎪ ⎪ ⎪ 2 2 ⎪ ⎪ ⎪ ⎪ BC =BD ⋅AB ,=D AD (⋅ B 如D 图) ⎪ ⎪ ⎪ ⎩⎪ ⎪ ⎪ ⎩ C ⎧①位似图形是一种特殊的相似图形,具有相似图形的一切性质 ⎪ ⎪ ⎪ ⎪ 位似图形②⎨ 位似图形对应点所确定的直线过位似中心 ③通过位似可以将图形放大或缩小 A D B ⎪ ⎩ ⎩ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ 第六部分《统计与概率》知识要点⎧⎪两查⎧⎨普查:总体与个体(研究对象中→心词) 抽样调查:样本与容量(无单位的数量) ⎪ ⎩ ⎪ ⎧折线图(发展趋势与波动性横→纵轴坐标单位长度要统一) ⎪三图条⎨ 形图(纵坐标起点为零高→度之比等于频数或频率之比) ⎪ ⎪扇形图(知道各量的百分比可→用加权平均数求平均值) ⎪ ⎩ ⎪ ⎧ ⎧算术平均数 ⎪ ⎪ ⎪ ⎪ 平均数参⎨ 照平均数 加权平均数⎪ ⎪ ⎩⎪三数⎨⎪ ⎪众数( 可能不止一个) ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩中位数(排序、定位) ⎪ 统计与概率⎨ ⎪ ⎧方差:s 2 = 1 ⎪ n (x - x )2 + (x - x )2 + + (x - x )2 1 2 n ⎪ ⎪(一组数据整体被扩大n ,平均数扩大倍n ,方差扩大倍n )2 ; ⎪三差(⎨⎪ 一组数据整体被增加m ,平均数增加m ,方差不变) ⎪ ⎪标准差:方差的算术平方根s ⎪ ⎪ ⎪ ⎪极差:最大数与最小数之差 ⎪ (⎩⎪ 方差与标准差均衡量数据的波动性,方差越小波动越小) ⎪ ⎧ ⎧必然事件:(概率为1) ⎪确定事件⎨ 事件⎨ ⎩不可能事件:(概率为0) ⎪ ⎪不确定事件:(概率在0与1之间)⎪ ⎩ ⎧频率:(试验值,多次试验后频率会接近理论概率) ⎪ ⎪ ⎧比例法(数量之比、面积之比等) ⎪两率⎨ ⎪ ⎨ ⎪ ⎪概率:求法列表法(返回与不返回的两步实验求概率) ⎪ ⎪ ⎪树⎩状图(返回与不返回的两步或两步以上的试验求概率 ⎪ ⎣ ⎦初中数学常考知识点I、代数部分:一、数与式:1、实数:1)实数的有关概念;常考点:倒数、相反数、绝对值(选择第 1 题)2)科学记数法表示一个数(选择题第二题)3)实数的运算法则:混合运算(计算题)4)实数非负性应用:代数式求值(选择、填空)2、代数式:代数式化简求值(解答题)3、整式:1)整式的概念和简单运算、化简求值(解答题)2)利用提公因式法、公式法进行因式分解(选择填空必考题)4、分式:化简求值、计算(解答题)、分式求取值范围(一般为填空题)(易错点:分母不为0)5、二次根式:求取值范围、化简运算(填空、解答题)二、方程与不等式:1、解分式方程(易错点:注意验根)、一元二次方程(常考解答题)2、解不等式、解集的数轴表示、解不等式组解集(常考解答题)3、解方程组、列方程(组)解应用题(若为分式方程仍勿忘检验)(必考解答题)4、一元二次方程根的判别式三、函数及其图像1、平面直角坐标系与函数1)函数自变量取值范围,并会求函数值;2)坐标系内点的特征;3)能结合图像对简单实际问题中的函数关系进行分析(选择8 题)2、一次函数(解答题)1)理解正比例函数、一次函数的意义、会画图像2)理解一次函数的性质3)会求解析式、与坐标轴交点、求与其他函数交点4)解决实际问题3、反比例函数(解答题)1)反比例函数的图像、意义、性质(两支,中心对称性、分类讨论)2)求解析式,与其他函数的交点、解决有关问题(如取值范围、面积问题)4、二次函数(必考解答题)1)图像、性质(开口、对称性、顶点坐标、对称轴、与坐标轴交点等)2)解析式的求解、与一元二次方程综合(根与交点、判别式)3)解决实际问题4)与其他函数综合应用、求交点5)与特殊几何图形综合、动点问题(解答题)II、空间与图形一、图形的认识1、立体图形、视图和展开图(选择题)1)几何体的三视图,几何体原型相互推倒2)几何体的展开图,立体模型相互推倒2、线段、射线、直线(解答题)1)垂直平分线、线段中点性质及应用2)结合图形判断、证明线段之间的等量、和差、大小关系3)线段长度的求解4)两点间线段最短(解决路径最短问题)3、角与角分线(解答题)1)角与角之间的数量关系2)角分线的性质与判定(辅助线添加)4、相交线与平行线1)余角、补角2)垂直平分线性质应用3)平分线性质与判定5、三角形1)三角形内角和、外角、三边关系(选择题)2)三角形角分线、高线、中线、中位线性质应用(辅助线)3)三角形全等性质、判定、融入四边形证明(必考解答题)4)三角形运动、折叠、旋转、平移(全等变换)、拼接(探究问题)6、等腰三角形与直角三角形1)等腰三角形的性质与判定、直角三角形的性质、勾股定理及逆定理2)等腰三角形、直角三角形与四边形或圆的综合3)锐角三角函数、特殊角三角函数、解直角三角形(解答题)4)等腰、直角、等腰直角三角形与函数综合形成的代几综合题(压轴题必考)7、多边形:内角和公式、外角和定理(选择题)8、四边形(解答题)1)平行四边形的性质、判定、结合相似、全等证明2)特殊的平行四边形:性质、判定、以及与轴对称、旋转、平移和函数等结合应用(动点问题、面积问题及相关函数解析式问题)3)梯形:一般梯形及等腰、直角梯形的性质、与平行四边形知识结合,四边形计算题,辅助线的添加等9、圆(必考解答题)1)圆的有关概念、性质2)圆周角、圆心角之间的相互联系3)掌握并会利用垂径定理、弧长公式、扇形面积公式,圆锥侧面面积、全面积公式解决问题4)圆中的位置关系:要会判断:点与圆、直线与圆、圆与圆(重点是圆与圆位置关系)5)重点:圆的证明计算题(圆的相关性质与几何图形综合)二、图形与变换1、轴对称:会判断轴对称图形、能用轴对称的知识解决简单问题2、平移:会运用平移的性质、会画出平移后的图形、能用平移的知识解决简单问题3、旋转:理解旋转的性质(全等变换),会应用旋转的性质解决问题(全等证明),会判断中心对称图形4、相似:会用比例的基本性质解题、利用三角形相似的性质证明角相等、应用相似比求解线段长度(解答题)III、统计与概率一、相关概念的理解与应用:平均数、中位数、众数、方差等(选择题)二、能利用各种统计图解决实际问题(必考,解答题)三、会用列举法(包括图表、树状图法)计算简单事件发生的概率(解答题,填空题)“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

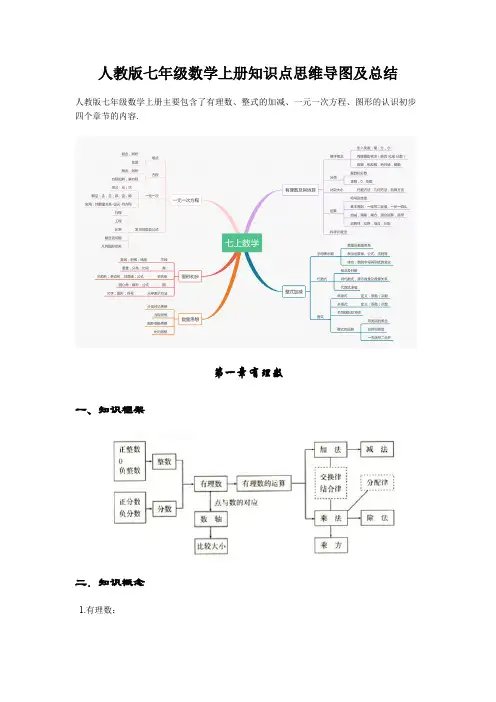
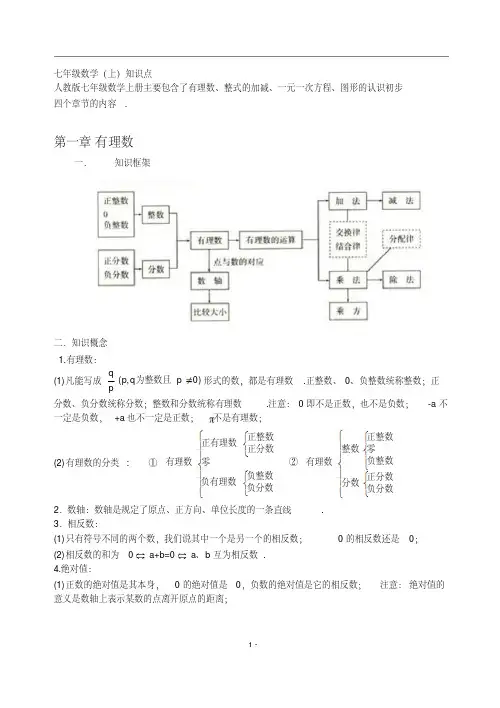
人教版七年级数学上册知识点思维导图及总结人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章有理数一、知识框架二.知识概念1.有理数:(1)凡能写成形式的数,都是有理数.正整数、0、负整数统称整数;)0p q ,p (pq ≠为整数且正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数; 不是有理数;(2)有理数的分类: ① ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 a+b=0 a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:或 ;绝对值的问题经常分类讨⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a ⎩⎨⎧<-≥=)0a (a )0a (a a 论;5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么的倒数是a ;若ab=1 a 、b 互为倒数;若ab=-1 a 、b 互为负倒数.a17. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ).10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc );(3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,.无意义即0a 13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。


42研究提起数学,总有学生叫苦连连,“听不懂”“学不会”“太枯燥”“有何用”“难不成买个橘子还需要用函数吗?”……执教多年,由于数学的学科特性如思维缜密、抽象性高等,让许多学生“谈数色变”,可数学作为基础教育学科,除了对人类的发展具有重大作用外,其本身也具有非常迷人的色彩。
如何让学生由“怕数学”到“爱数学”,是笔者一直以来不断探索并实践的课题。
思维导图是理清知识点、将零散的内容绘制到一起,形成系统性思维的重要工具,针对数学教学,我们进行了思维导图融入初中数学课堂教学案例、促进深度学习的策略研究,研究结果表明,思维导图对初中生数学思维能力有明显的提高作用,能明显增强学生的学习兴趣和深度学习。
理论学习,丰富自我内涵相关网站上有很多关于思维导图的研究,我们先后学习了曾伟、黄泳的《“思维导图”助力初中数学难点学习》,方永进的《“思维导图”是数学课本不错的“补丁”》,张冬梅的《思维导图在初中数学重难点问题教学中的应用策略》,吴志丹《协作构建思维导图在数学复习课中的应用探究》,樊雅琴、王炳皓、王伟《深度学习国内外研究综述》,马云鹏的《深度学习的理解与实践模式-以小学数学学科为例》等相关资料,加深了对思维导图的理解。
我们发现,用思维导图串联知识点、归类题型,记录题目的解题思路,可突破教学中的重难点;在复习课中使用思维导图,将广阔的知识点链接起来,变“浅学”为“博学”,“学会”为“会学”,可提高学生分析问题、解决问题的能力;思维导图的构建将知识网络化、系统化,对培养学生的逻辑思维、创造力思维、发散思维,以及提高对数学的理解具有促进作用。
设计思维导图,融入课堂教学在思维导图融入课堂教学的案例研究中,我们经过探索,最终确定了课堂引入思维导图、课堂小结思维导图的应用研究,知识发散型思维导图课堂应用实例研究,课本案例教学实例研究等一系列系统地将思维导图融入课堂教学案例的研究过程以及研究方案,并在日常教学中将思维导图融入课堂教学。

初中数学知识体系,7张图教你全局思考模式!用正确的思维模式去梳理解决问题好多同学一面对数学知识就头疼,不能全面清晰地去分析解决问题,那是因为你没有用正确的思维方法去分析解决这个问题。
初中数学的学习,最重要的就是建立自己的知识体系,学会全局思考的思维模式!下面这些数学知识点的思维导图,将初中重要的知识点都整理出来了,相信一定能帮助同学们们提升数学成绩!我们一起来看看吧!1、全等三角形思维导图经过翻转、平移后,能够完全重合的两个三角形叫做全等三角形,而该两个三角形的三条边及三个角都对应相等。
2、相似三角形思维导图三角分别相等,三边成比例的两个三角形叫做相似三角形3、几何初步和三角形思维导图4、投影与视图思维导图5、圆思维导图在一个平面内,一动点以一定点为中心,以一定长度为距离旋转一周所形成的封闭曲线叫做圆。
圆有无数个点。
6、实数思维导图7、代数式思维导图这样用全局思维模式梳理出所学内容重点,然后逐一掌握学习,是不是看起来很容易,思路瞬间清晰起来!同学们在学习过程中一定要养成正确学习的好习惯,善于发现思考!下面这十条小建议希望能在你的学习过程中起到帮助。
【Tip】1、学数学要善于思考,自己想出来的答案远比别人讲出来的答案印象深刻。
2、课前要做好预习,这样上数学课时才能把不会的知识点更好的消化吸收掉。
3、数学公式一定要记熟,并且还要会推导,能举一反三。
4、学好数学最基础的就是把课本知识点及课后习题都掌握好。
5、数学80%的分数来源于基础知识,20%的分数属于难点,所以考120分并不难。
6、数学需要沉下心去做,浮躁的人很难学好数学,踏踏实实做题才是硬道理。
7、数学要想学好,不琢磨是行不通的,遇到难题不能躲,研究明白了才能罢休。
8、数学最主要的就是解题过程,懂得数学思维很关键,思路通了,数学自然就会了。
9、数学不是用来看的,而是用来算的,或许这一秒没思路,当你拿起笔开始计算的那一秒,就豁然开朗了。
10.数学题目不会做,原因之一就是例题没研究明白,所以数学书上的例题绝对不要放过。

利用思维导图解读小学数学教材思维导图是一种将思维和思考过程以可视化的方式表达出来的工具,能够帮助我们更好地理解和组织知识。
利用思维导图解读小学数学教材可以帮助我们深入理解数学知识的内涵和结构,提高学习效果。
下面是对小学数学教材进行思维导图解读的内容。
思维导图一:小学数学教材的结构- 教材基本信息:书名、年级、版次等- 教材的整体结构:导学、微课、教案、作业、课件等内容- 各章节的内容:每章的名称、内容概述、学习目标等- 教材的教学理念和教学方法:启发式教学、探究式学习等- 教材与学生生活和实践的联系:引导学生将数学知识应用到实际生活中思维导图二:小学数学教材的核心知识点- 数的认识:自然数、整数、有理数等的认识和比较- 数的运算:加法、减法、乘法、除法等的基本运算和应用- 分数和小数:分数和小数的认识、比较和运算- 几何图形:平面几何图形的认识、性质和应用- 数据与统计:数据的收集、整理、分析和表示方法- 代数与方程:代数表达式、方程的认识和应用思维导图三:小学数学教材的教学目标和方法- 教学目标:培养学生数学思维和解决问题的能力,提高数学素养- 启发式教学:通过提出问题、引导探究等方式激发学生的兴趣和思考能力- 模型建构:通过模拟实际情境和问题,帮助学生理解和应用数学知识- 课堂互动:引导学生主动参与和合作,培养学生的合作精神和团队意识- 个性化教学:根据学生的兴趣、能力和学习风格,调整教学内容和策略思维导图四:小学数学教材的教学资源和评价方式- 教学资源:教师课件、学生教材、辅导材料等的使用和推荐- 新媒体技术:利用电子教学、网络资源等辅助教学和学习- 评价方式:课堂作业、小测验、期中期末考试等方式进行评价- 反馈和辅导:根据评价结果进行学生辅导和个别化教学- 学习与考试策略:培养学生的学习方法和考试技巧,提高学习效果思维导图五:小学数学教材的拓展应用和综合训练- 拓展应用:将数学知识应用到实际生活和其他学科中- 跨学科整合:与科学、语文、体育等学科进行综合训练和实践活动- 数学思维训练:培养学生的逻辑思维、问题解决和创新能力- 数学竞赛和课外活动:参加数学竞赛、讲座、实验等拓展学生的数学视野 - 数学思维游戏:通过数学游戏、益智玩具等方式激发学生的兴趣和动力。

2023最新小学数学课程标准内附思维导图建议收藏第一部分前言数学素养是现代社会每一个公民应该具备的基本素养。
作为促进学生全面发展教育的重要组成部分,数学教育既要使学生掌握现代生活和学习中所需要的数学知识与技能,更要发挥数学在(培养人)的理性思维和创新能力方面的不可替代的作用。
一、课程性质数学课程具有基础性、普及性和发展性。
二、课程基本理念人人都能获得良好的数学教育,不同的人在数学上得到不同的发展。
三、课程设计思路符合学生的认知规律和心理特征,有利于激发学生的学习兴趣,引发数学思考;充分考虑数学本身的特点,体现数学的实质;在呈现作为知识与技能的数学结果的同时,重视学生已有的经验,使学生体验从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程。
(一)学段划分三个学段:第一学段(1~3年级)、第二学段(4~6年级)、第三学段(7~9年级)。
(二)课程目标义务教育阶段数学课程目标:分为总目标和学段目标课程目标从知识技能、数学思考、问题解决、情感态度等四个方面加以阐述。
数学课程目标包括结果目标和过程目标。
结果目标使用“了解、理解、掌握、运用”等术语表述,过程目标使用“经历、体验、探索”等术语表述(三)课程内容在各学段中,安排了四个部分的课程内容:“数与代数”“图形与几何”“统计与概率”“综合与实践”。
“综合与实践”内容设置的目的在于培养学生综合运用有关的知识与方法解决实际问题,培养学生的问题意识、应用意识和创新意识,积累学生的活动经验,提高学生解决现实问题的能力。
在数学课程中,应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想。
为了适应时代发展对人才培养的需要,数学课程还要特别注重发展学生的应用意识和创新意识。
数感主要是指关于数与数量、数量关系、运算结果估计等方面的感悟。
建立数感有助于学生理解现实生活中数的意义,理解或表述具体情境中的数量关系。
符号意识主要是指能够理解并且运用符号表示数、数量关系和变化规律;知道使用符号可以进行运算和推理,得到的结论具有一般性。

新课程高中数学知识点思维导图第一部分:集合、映射、函数、导数及微积分集合是由元素组成的整体,可以用数轴、Venn图或函数图象等方式表示。
集合具有确定性、互异性和无序性等特点。
定义域、值域、单调性、奇偶性、周期性和对称性等是函数的重要性质。
函数可以进行平移、对称、翻折和伸缩变换,最值是函数的重要特征。
对数函数、分段函数、复合函数和抽象函数等都是常见的函数类型。
函数与方程密切相关,函数在生活中有着广泛的应用。
导数是函数变化率的度量,基本初等函数的导数可以通过运用导数的运算法则求得。
导数的应用包括求极值和定积分等。
三角函数、复合函数的单调性、函数模型的建立等都是微积分的重要内容。
第二部分:三角函数与平面向量角的概念可以用弧度制或线度制表示,三角函数是角的重要性质之一。
同角三角函数之间有着密切的关系,诱导公式、和角、差角公式和二倍角公式等都是常用的公式。
三角函数的定义域、图象、对称性、最值、奇偶性、单调性和周期性等都是重要的性质。
正弦函数、余弦函数和正切函数的图象可以通过平移和伸缩变换得到,也可以用五点作图法进行绘制。
最小正周期是正弦函数和余弦函数的重要特征,对称轴和对称中心是正弦函数和余弦函数图象的重要点。
三角函数的化简、求值和证明都需要运用公式的变形和逆用。
平面向量是具有大小和方向的量,可以进行加减和数乘等运算。
向量的模、方向角和坐标等都是向量的重要性质。
向量的共线和垂直关系、平面向量的数量积和叉积等都是向量的重要概念。
概念:解析几何是一种通过运用坐标系和代数方法研究几何问题的数学分支。
线性运算:向量的加法和数乘运算。
基本定理:平面向量的基本定理包括平面向量的加法定理和数量积的几何意义。
平面向量:平面上具有大小和方向的量,可以用有向线段表示。
坐标表示:平面向量可以用坐标表示,其中x和y分别表示向量在x轴和y轴上的投影。
模:向量的大小,也称为模长或长度。
加、减、数乘几何意义:向量加法表示平移,向量减法表示连接两点的向量,数乘表示伸缩或反向。
人教版七年级数学上册知识点思维导图及总结 人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一、知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论; 5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a 1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a -b=a+(-b ).10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc );(3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a .13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b -a)n , 当n 为正偶数时: (-a)n =a n 或 (a -b)n =(b -a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a×10n的形式,其中a是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
高中数学课程内容必修课程预备知识集合(刻画一类事物的语言和工具)集合概念与表示集合的基本关系集合的基本运算常用逻辑用语必要条件、充分条件、充要条件全称量词与存在量词全称量词命题与存在量词命题的否定相等关系与不等关系等式与不等式的性质基本不等式<=ab2a+b从函数观点看一元二次方程和一元二次不等式函数函数概念与性质函数概念函数性质幂函数、指数函数、对数函数幂函数指数函数对数函数三角函数角与弧度三角函数概念与性质同角三角函数的基本不等式sinθ+2cosθ=21=cosθsinθtanθ三角恒等变换三角函数应用函数应用二分法与求解方程近似解函数与数学模型几何与代数平面向量及其应用向量概念向量运算向量基本定理及坐标表示向量应用与解三角形复数复数概念复数的运算立体几何初步基本立体图形基本图形位置关系概率与统计概率随机事件与概率随机事件的独立性统计获取数据的基本途径与相关概念抽样统计图表用样本估计总体数学建模活动与数学探究活动实际情境→提出问题→建立模型→求解模型→检验结果→实际结果选择性必修课程函数数列数列概念等差数列等比数列数学归纳法*一元函数导数及其应用导数概念及其意义导数运算导数在函数中的应用微积分的创立与发展*几何与代数空间向量与立体几何空间直角坐标系空间向量及其运算向量基本定理及坐标表示空间向量的应用平面解析几何直线与方程圆与方程圆锥曲线与方程平面解析几何的形成与发展*概率与统计计数原理两个基本计数原理排列与组合二项式定理概率随机事件的条件概率离散型随机变量及其分布列正态分布统计成对数据的统计相关性一元线性回归模型2*2列联表数学建模活动与数学探索活动选修课程A类微积分空间向量与代数概率与统计B类微积分空间向量与代数应用统计模型C类逻辑推理初步数学模型社会调查与数据分析D类美与数学音乐中的数学美术中的数学体育运动中的数学E类拓展视野的数学课程日常生活的数学课程地方特色的数学课程大学数学的先修课程。
课程课程概述“课程”一词的由来我国最早:唐 · 孔颖达《五经正义》同义:朱熹《朱子全书 · 论学》外国把课程用于教育科学的专门术语,始于英国 · 斯宾塞《什么知识最有价值》标志着课程作为专门研究领域的诞生,美 · 博比特《课程》课程的定义在我国课程具体表现为课程计划、课程标准和教材三种物化形式新课改认为,课程是教师、学生、教材、环境四个因素动态交互作用的“生态系统”古德莱德的五种课程理想的课程专家正式的课程教育行政部门领悟的课程运作的课程经验的课程课程的类型根据学科的固有属性学科课程历史最悠久、最常用、适用范围最广例:我国古代的“六艺”,古希腊的“七艺”和“武士七艺”经验课程思想源于卢梭的“自然教育”最早提出“活动课程”的是杜威根据课程内容的组织方式分科课程综合课程第一次提出“综合课程”的是怀特海基本形式相关课程(联络课程)融合课程(合科课程)将二级学科合并为一级学科广域课程(综合课程)将众多一级学科合并为一个大领域核心课程(问题课程)以问题为核心,将几门学科结合起来融合程度,从上到下,由低到高基本类型学科本位的综合课程社会本位的综合课程儿童本位的综合课程根据课程计划对课程设置实施的要求必修课程选修课程根据课程设计、开发和管理的主体国家课程(一级课程)地方课程(二级课程)省级为主校本课程(三级课程)通常以选修课或特色课的形式出现校本课程是国家课程的补充校本课程开发菲吕马克和麦克米伦最早提出“校本课程开发”的概念个性化是校本课程开发的价值追求根据课程任务基础型课程基础知识、基本技能的发展和学习动机、学习态度的培养拓展型课程拓展学生视野、发展学生的特殊能力例:文学、艺术鉴赏研究型课程培养学生的探究态度与能力根据课程呈现的形式显性的课程隐性的课程观念性隐性课程物质性隐性课程制度性隐性课程心理性隐性课程显性课程和隐性课程最主要区别:计划性课程理论知识中心结构主义代表人物:布鲁纳以学科结构为课程中心“任何学科的基础都可以用任何形式教给任何年龄阶段的任何人”学科基本结构的学习要与学生的认知发展水平相一致采用螺旋上升的方式编制课程要素主义代表人物:巴格莱课程内容应该是人类文化的“共同要素”,学习“新三艺”数学自然科学外遇永恒主义赫钦斯学生中心代表人物:杜威以社会生活的实际来组织课程教材课程组织要心理学化社会中心代表人物:布拉梅尔德、弗莱雷存在主义代表人物:奈勒确定课程的重要前提是学生为自己的存在负责反对固定课程,课程最终由学生的需要决定教材是学生自我发展和实现的手段,学生应成为教材的主宰课程重点:人文学科后现代代表人物:多尔课程标准:“4R”丰富性循环性关联性严密性“蜜蜂联欢”课程是不断展开的动态过程“教师是平等中的首席”人本主义代表人物:罗杰斯建立和实施平行课程学术型课程社会体验课程自我实现课程课程内容选择上贯彻“适切性”学校课程结构组织注重“整合”和“统整”有意义学习制约课程的因素社会知识儿童课程实际、内容、实施与评价课程目标是指导整个课程设计/课程编制最为关键的准则完整的课程目标体系结果性目标(知识领域)体验性目标(过程领域)表现性目标(制作领域)课程目标的价值取向(舒伯特)“普遍性目标”价值取向例柏拉图“哲学王洛克“绅士教育”培养德智体美劳全面发展的人《大学》”格物,致知...治国,平天下““行为目标”价值取向例记忆“cat”和“dog”两个单词能说出牛顿第二定律“生成性目标”价值取向在教育过程中自然而然生成的课程目标“表现性目标“价值取向例参观动物园,讨论最有趣的几件事使用积木展示三维形式确定课程目标的依据学习者的需要(对学生的研究)泰勒主张的首要考虑当代社会生活的需求(对社会的研究)学科知识及其发展(对学科的研究)课程设计概念:是一个有目的、有计划、有结构的产生课程计划、课程标准以及教材等系统化的活动模式目标模式泰勒“课程评价之父”《课程与教学的基本原理》“泰勒原理”目标内容方法评价步骤确定目标:学校教育应该达到哪些目标?(最关键)需要考虑学科专家的建议(学科的逻辑)学生的研究(学生的心理发展逻辑)当代社会生活的研究(社会的要求)两个筛子哲学心理学选择经验:提供哪些教育经验才能实现这些目标?组织经验:怎样才能有效地组织这些教育经验?连续性顺序性整合性评价结果:我们怎样才能确定这些目标真正得到实现?过程模式斯腾豪斯观点首倡“教师作为研究者”真正的教育是使人类更加自由、更富于创造性,因而教育的本质是“引导”教师是整个过程的核心人物,课程发展即教师发展课程内容课程内容的选择原则注重基础性贴近社会生活尊重学生经验强化价值观和道德教育课程内容的组织形式(1)直线式在我国中小学占主流螺旋式(2)纵向组织从已知到未知横向组织打破学科知识界限和传统知识体系(3)逻辑顺序按照知识的内在联系心理顺序按照学生心理发展规律课程内容的文本表现形式/课程设计的三个层次课程计划(教学计划)含义由国家教育主管部门指定的有关教学和教育工作的指导性文件。