小学数学思维导图C
- 格式:doc
- 大小:1.35 MB
- 文档页数:13
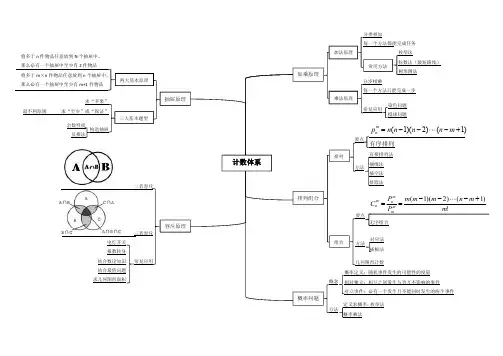
二者容斥
三者容斥
常见应用
电灯开关报数转身结合数论知识结合最值问题求几何图形面积
容斥原理
将多于n 件物品任意放到N 个抽屉中,那么必有一个抽屉中至少有2件物品将多于m ×n 件物品任意放到n 个抽屉中,那么必有一个抽屉中至少有m+1件物品
两大基本原理
求“苹果”
最不利原则
求“至少”或“保证”
构造抽屉
余数性质反推法
三大基本题型
抽屉原理
计数体系
分类相加
每一个方法都能完成任务
常用方法
枚举法
标数法(最短路线)树形图法
加法原理
分步相乘
每一个方法只能完成一步
常见应用
染色问题摸球问题
乘法原理
加乘原理
排列组合
排列
要点
方法
)
1()2)(1(+---=m n n n n p m n 有序排列
直接排列法捆绑法插空法
排除法
组合
要点
方法
几何图形计数
!
)1()2)(1(m m n m m m P P C m m m n m
n
+---=
= 无序组合
对应法插板法
概念
方法
概率定义:随机事件发生的可能性的度量相对独立:相互之间发生与否互不影响的事件对立事件:必有一个发生且不能同时发生的两个事件
定义求概率:枚举法概率乘法
概率问题。
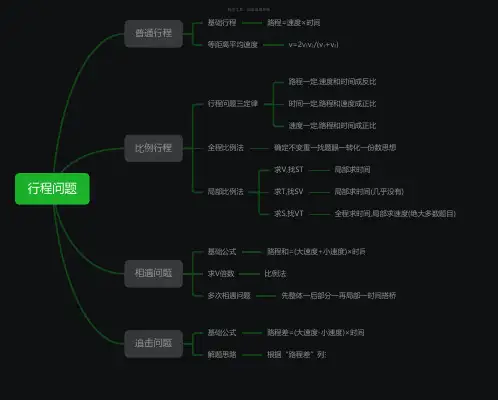
行程问题普通行程
基础行程路程=速度×时间
等距离平均速度v=2v₁v₂/(v₁+v₂)
比例行程
行程问题三定律
路程一定,速度和时间成反比
时间一定,路程和速度成正比
速度一定,路程和时间成正比
全程比例法确定不变重一找题眼一转化一份数思想
局部比例法
求V,找ST局部求时间
求T,找SV局部求时间(几乎没有)
求S,找VT全程求时间,局部求速度(绝大多数题目)相遇问题
基础公式路程和=(大速度+小速度)×时间
求V倍数比例法
多次相遇问题先整体一后部分一再局部一时间搭桥
追击问题
基础公式路程差=(大速度-小速度)×时间
解题思路根据“路程差”列式。

小学数学思维导图第五章比和比例正比例和反比例比例正比例和反比例是数学中两个重要的概念,它们可以帮助我们理解和解决许多实际问题。
在这一章节中,我们将通过思维导图的方式,深入探讨正比例和反比例的概念、性质以及它们在实际中的应用。
一、正比例1. 定义:如果两个相关联的量,它们的比值(商)始终保持不变,那么它们就是成正比例的关系。
用数学公式表示,即 y = kx,其中 k 是常数,表示比例关系。
2. 性质:a. 当一个量增大时,另一个量也会相应地增大。
b. 当一个量减小时,另一个量也会相应地减小。
c. 两个量的比值始终保持不变。
3. 应用:a. 计算速度:速度 = 路程÷ 时间。
当路程固定时,速度和时间成正比。
b. 计算工资:工资 = 工作量× 单价。
当单价固定时,工资和工作量成正比。
二、反比例1. 定义:如果两个相关联的量,它们的乘积始终保持不变,那么它们就是成反比例的关系。
用数学公式表示,即 xy = k,其中 k 是常数,表示比例关系。
2. 性质:a. 当一个量增大时,另一个量会相应地减小。
b. 当一个量减小时,另一个量会相应地增大。
c. 两个量的乘积始终保持不变。
3. 应用:a. 计算速度:速度 = 路程÷ 时间。
当路程固定时,速度和时间成反比。
b. 计算工资:工资 = 工作量× 单价。
当工作量固定时,工资和单价成反比。
小学数学思维导图第五章比和比例正比例和反比例比例三、比例关系的识别1. 正比例关系的识别:观察两个量的变化趋势,如果它们同时增加或减少,且它们的比值保持不变,那么可以判断它们成正比例关系。
例如,在绘制图表时,如果数据点在一条通过原点的直线上,那么这些数据点就表示正比例关系。
2. 反比例关系的识别:同样地,观察两个量的变化趋势,如果它们一个增加而另一个减少,且它们的乘积保持不变,那么可以判断它们成反比例关系。
例如,在绘制图表时,如果数据点在一条双曲线上,那么这些数据点就表示反比例关系。
正比例与反比例常见的量
乘法算式
两数相除,又叫作这两个数的比。
比的前项和后项同时乘或除以同一个不为0的数,比值的大小不变。
8∶4,6∶4=3∶2这样表示两个比相等
在比例里,两个内项的积等于两个外项的积
图上距离和实际距离的比,叫作这幅图的比例尺
会求平面图的比例尺
再变化过程中,如果它们相对应的每两个数的比值保持一
两个量是否成正比例关键是这个两个量的比值是否一定
再变化过程中,如果它们相对应的每两个数的积保持一
两个量是否成反比例关键是这两个量的积是否一定
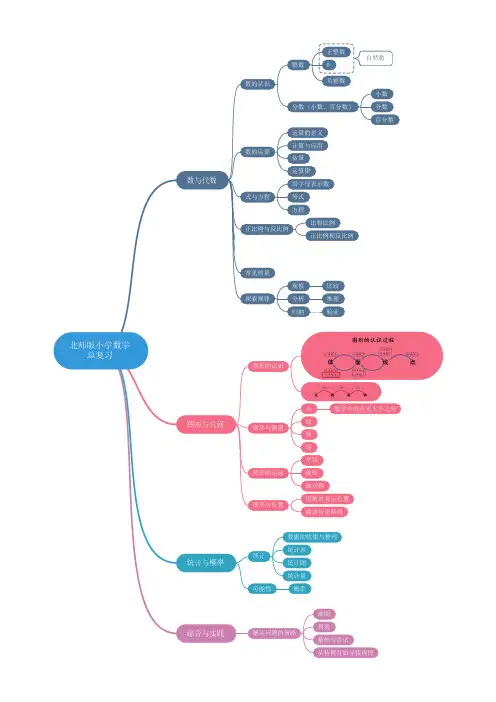
点数学中的点无大小之分
过一点可画无数条直线,过两点能画一条直线
两点之间线段最短
备注:线段只有长度没有宽度
一条射线绕着它的一个端点旋转形成的平面图形
锐角:<90°
直角:=90°
钝角:>90°
平角:=180°
周角:=360°
角的大小与长度无关,与角的张口有关
)点对点)线对边
)读数要看另一边量角器的中心点与角的顶点重合刻度线与角的一条边重合
观察角的另一条边所对的量角器上的刻度
00)画射线
)点重合、边重合
定义画法
在同一平面内,永不相交的两条线互相平行。
平移
特征
平行线间的宽度(距离)处处相同
AB ∥CD
当两条直线相交成直角时,这两条直线就互相垂直直角
点到直线的距离,垂线段最短
解决简单的实际问题
解决简单的实际问题
展开图
拐弯点
前后
同一列平移,那么第几列是不变的,同一行平移,那么第几行是平移了几格,同一列,同一行的数就相差几格2,4)。

⼩学数学公式⼤全之⼀(图形周长、⾯积、体积计算公式)思维导图剖解⼩学数学公式⼤全之⼀(图形周长、⾯积、体积计算公式)思维导图表述 思维导图表述⽂字表述1.正⽅形 C周长S⾯积a边长周长=边长×4 C=4a ⾯积=边长×边长 S=a×a 2.正⽅体 V:体积a:棱长表⾯积=棱长×棱长×6 S表=a×a×6 体积=棱长×棱长×棱长 V=a×a×a 3.长⽅形 C周长S⾯积a边长周长=(长+宽)×2 C=2(a+b) ⾯积=长×宽 S=ab 4.长⽅体 V:体积s:⾯积a:长b:宽h:⾼ (1)表⾯积=(长×宽+长×⾼+宽×⾼)×2 S=2(ab+ah+bh) (2)体积=长×宽×⾼ V=abh 5.三⾓形 s⾯积a底h⾼⾯积=底×⾼÷2 s=ah÷2 三⾓形⾼=⾯积×2÷底三⾓形底=⾯积×2÷⾼ 6.平⾏四边形 s⾯积a底h⾼⾯积=底×⾼ s=ah 7.梯形 s⾯积a上底b下底h⾼⾯积=(上底+下底)×⾼÷2 s=(a+b)×h÷2 8.圆形 S⾯积C周长∏d=直径r=半径 (1)周长=直径×∏=2×∏×半径 C=∏d=2∏r(2)⾯积=半径×半径×∏ 9.圆柱体 v:体积h:⾼s;底⾯积r:底⾯半径c:底⾯周长(1)侧⾯积=底⾯周长×⾼ (2)表⾯积=侧⾯积+底⾯积×2 (3)体积=底⾯积×⾼ (4)体积=侧⾯积÷2×半径 10.圆锥体 v:体积h:⾼s;底⾯积r:底⾯半径体积=底⾯积×⾼÷3。