当前位置：文档之家 › 自相关过程的质量控制方法_残差控制图

自相关过程的质量控制方法_残差控制图

  • 格式：pdf
  • 大小：159.16 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

品检质量控制中的统计过程控制方法

品检质量控制中的统计过程控制方法

品检质量控制中的统计过程控制方法在现代工业生产中，如何保证产品质量的稳定和可靠性是一个重要的问题。

统计过程控制（Statistical Process Control，简称SPC）是一种常用的质量控制方法，通过对生产过程中的数据进行统计和分析，帮助企业实现对质量的持续监控和改进。

本文将介绍品检质量控制中常用的统计过程控制方法，包括控制图、过程能力分析和六西格玛方法。

控制图是一种直观简单且易于理解的统计工具，用于监控生产过程中的关键指标。

控制图一般由上限线、下限线和中心线组成，中心线表示过程的平均水平，上下限线则代表了过程的变异性。

通过收集和记录采样数据，可以绘制出控制图，并根据数据的变化情况来判断过程是否处于控制状态。

常用的控制图包括均值图和极差图。

均值图用于监测过程的平均水平是否稳定。

通过对一系列样本均值的统计，绘制出均值图，可以直观地判断过程是否存在系统性变化。

如果数据点超出了控制限，就说明过程中可能存在特殊原因的影响，需要进行进一步分析和改进。

极差图则用于监控过程的变异性。

极差是指样本中最大值与最小值之间的差异，极差图通过对一系列样本极差的统计，可以判断过程的变异性是否处于控制状态。

同样，如果数据点超出了控制限，就需要进行原因分析和改进措施的制定。

除了控制图之外，过程能力分析也是品检质量控制中的重要工具。

过程能力分析的目的是评估生产过程是否具有满足需求的能力。

常用的过程能力指标包括过程平均值与规格上下限之间的距离、过程的标准偏差以及过程的允许偏差范围。

通过分析过程能力指标，可以得出生产过程是否稳定，并评估其是否满足产品质量要求。

如果过程能力指标超出了规格要求，就需要采取措施来改进过程，以提升产品质量。

六西格玛方法是一种基于统计分析的全面质量管理方法。

它将统计过程控制与过程改进相结合，致力于提高质量、降低成本和增强客户满意度。

六西格玛方法通过收集和分析大量数据来识别生产过程中的关键环节，并采取措施来减少变异性，从而提高产品质量和生产效率。

自相关过程

自相关过程

自相关过程控制院系：管理科学与工程专业：质量与可靠性工程学号：110510335 姓名：张华威自相关过程质量控制引论：自相关过程质量控制概述当质量过程呈现自相关现象时,常规控制图已经不能准确反映生产中质量的波动.常规控制图理论：质量管理的观点认为:质量具有变异性其特性值是波动的,具有规律性,但它不是通常的确定性现象的确定性规律,而是随机现象的统计规律,用数学语言来讲,就是服从某种分布。

如果出现异常情况,就必然使波动偏离原来的分布,利用统计技术就可以发现这种波动。

在现代质量管理学中，通常使用休哈特控制图进行质量控制，但休哈特控制图的原理要求数据必须复合独立正态性，即要求数据服从正态分布，所以说如果数据之间彼此具有相关性的话，休哈特控制图便不再使用。

基于以上理论基础绘制的常规控制图虽然使用简便且易于理解,但对于受控状态下一般性原因的认知过于简化。

因此为了提高控制图对特殊性原因的检测能力,当过程相关时设计控制图,必须考虑质量过程的自相关结构。

为了解决过程自相关情况下的质量控制问题,统计学家们陆续提出了一些改进方法,其中主要方法之一就是引入时间序列分析法。

以ARMA以及ARIMA 模型为基础，我们便可以对具有相关性的一组数据进行相关性分析，方差分析，以及残差分析等，通过一系列控制图，便可以达到对具有自相关性的数据进行质量控制和质量改进的目的。

一、收集或生成反应自相关生产过程的平稳时间序列ARMA（p，q）数据：0.5377 0.1183 -0.6593 -1.8273 -0.93062.3339 0.5832 -1.9769 -1.5564 -1.2791-0.9306 -0.887 -1.0862 -1.3611 -0.59951.097 -1.3821 -1.6807 -1.9456 -0.37060.5881 -0.964 -0.8627 -0.3625 -1.2301-0.6845 0.636 -1.5359 -0.8981 -0.7563-0.5994 -0.7409 -0.5368 -1.2723 -0.912-0.1624 0.1918 0.0102 0.4458 -0.05523.3173 -0.352 1.556 -0.3836 0.79214.3794 0.9989 0.5869 -0.6471 1.48871.835 -0.6952 -1.3781 -0.7324 -0.9085.2662 -0.0154 -1.3526 -1.4082 -0.42463.909 0.3363 0.2649 -2.044 0.23763.4713 1.2641 -1.3455 1.0815 2.57693.6231 2.2772 0.3677 1.5831 0.69282.648 1.6038 -0.0958 1.4235 1.30682.2868 -0.0066 1.4991 -0.0704 0.77883.4275 -0.2645 -1.2401 -0.4736 -1.15163.8088 -1.1958 -0.368 -0.4345 -0.78114.3498 1.6732 -1.7639 0.4321 -2.53073.9891 -0.1377 1.9157 -1.2463 -0.3442.092 1.1812 1.2539 -2.8234 -0.59092.96 0.3569 2.5806 -3.2347 -2.14883.7378 1.4214 0.6083 -2.1308 -1.5373 3.2458 0.0529 0.6097 -1.6445 -2.2447 3.7789 -0.9494 0.2149 -1.0098 -2.5627 3.5901 -1.8812 1.3888 -1.1285 -3.1112 2.6253 -0.7372 0.481 -0.6835 -2.858 2.6835 -1.1103 1.3587 -1.1565 -4.3651.3421 -0.9724 -1.2282 0.0787 -2.07562.3645 0.6 -0.5603 -1.6693 0.3241 0.4378 0.2999 -1.4722 -0.356 0.1171 -0.1406 0.5277 -2.4813 -1.5275 -0.1473 -0.7485 1.9415 -1.1743 -1.2054 -0.0155 -3.3607 0.3246 -1.0496 -0.5082 -0.0006 -0.4665 1.4414 -0.8436 0.4234 0.8211 -0.9163 1.6532 -2.0703 -1.0584 1.9373 -1.353 1.0153 -0.1608 0.8585 1.6819 0.4189 1.2193 -0.3513 0.7719 1.2125 -1.908 -0.2516 -0.5229 0.5756 1.736二、建立过程的时间序列模型建模步骤：a ：传统修哈特控制图分析:首先对所生成数据作正态性检验概率图P值大于0.05，服从正态分布作均值极差控制图控制图X 的Xbar 控制图检验结果检验1。

基于GARCH模型的残差控制图在股票收益波动分析中的应用研究——以IBM股票为例

基于GARCH模型的残差控制图在股票收益波动分析中的应用研究——以IBM股票为例

都 是 运 用 ＡＲ Ｍ Ａ 模 型 表 示 质 量 过 程 ． 用 自相 关 模 型 及 其 残 差 图解 决 自相 关 问题 本 文 尝 试 运 用 ＧＡ Ｒｃ Ｈ 类 模 型 及 其 残 差 控 制 图 来 解 决 控 制 过 程 中 出现 的 波动 簇 聚 问 题 。 并 以 美 国 股 票 市场 中 的 ｍ Ｍ 股 票 为 例 进 行 简单 的 实证 分 析 。 通 过 对 其 日收 益 率 序 列进 行 建模 ， 从 而 评 判该类型残差控 制图的有效性。结果表明 ： 控 制 图在 含 有 相 关 性 和 波
质 量管 理 过 程 中很 少 出 现 方差 变 动 （ 波动 ） 的 状 况 。而 控 制 图 的应 用 也 主 要在 工 业 ， 医学 等 领 域 应用 ， 没 有 过 多 的存 在 相 关 性 和 波 动 性 的 受 控
式中， ｘ ， ｝ 为 受 控过 程 中监 测 序 列 ， 为在 给 定 前 期 信 息 集 的 情 况 下， 的条件均值 （ 其 中 可 以 包含 表 示 质 量 环 境 的变 量 ，如 系 统 因素
受 控 过 程 中 应 当服 从 独 立 同 分 布 之假 定 。 实践 中我 们 可 以 看 到 ， 多数 受
般情况下 ， 自回归 异 方 差 模 型 （ Ｇ ＡＲ Ｃ Ｈ） 为
Ｙ Ｊ ｒ＝ ， Ｉ ｆ＋
控 过 程 都 存 在 自相 关 性 ， 或 者 存 在显 著 的波 动 簇 聚 性 。 尤 其 在 金融 领 域
为了解决此类 问题 ， 许多学者对此作 了研究。例如 ， 由Ａ ｌ ｗ ａ ｎ （ １ ９ ８ ８ ） 所 提 出 的针 对 受 控 过 程 中 存 在 自相 关 问题 ． 建 立 ＡＲ Ｉ ＭＡ 模 型 ， 通 过 残
自相关过程的统计控制方法研究

自相关过程的统计控制方法研究

（ ＝ ０ 曰） 曰） （ ａ （） １
② 残 差 控 制 图 残 差 控 制 图 （ ｐ ｃａ ａ ｅｃ ａｔ Ｓ ｅ ｉｌＣ ｓ ｈ ｒ， Ｓ Ｃ） 基 本 思 想 是 运 用 模 型 拟 合 的 方 法 把 自相 关 过 Ｃ 的 程 过 滤 成残 差序 列 ， 外 还 可 以 辅 以共 因 图 （ｏ 此 Ｃ ｍｍｏ ｎ Ｃ ｕ ｅｃ ａｔ ＣＣ 。 差 序 列 具 有 独 立 同 分 布 的 假 设 ， ａ ｓ ｈ ｒ， Ｃ） 残 可 采 用 传 统 的 控 制 图 方 法 进 行 控 制 。 因 图 没 有 控 制 共 界 限 ， 根 据 时 间 序 列 模 型 建 立 的 预 测 值 的运 行 图 。 是 有
在离 散过 程工业 中 ， 于采 用传 感器 的先进 测量 技术 ， 由 可 以 获 得 实 时 的 测 量 数 据 ， 据 就 有 明 显 的 自相 关 性 。 数
★国 家 ８３ 目 （ 号 ：０ １ Ａ４２ ２ ） ６项 编 ２ ０ Ａ １ ０ ０
过 程 满足某 种平 稳 时 间序 列模 型 。 若 观测 值 ｘ（ １ ２ ３， … ） 用 时 间 序 列 ＡＲ ，， … 可
② 系统 实 现 了库 存 管 理 的多 Ａｅｔ 间 的协 调 ， ｇｎ 之
也 实 现 了 Ａ ｅ ｔ 用 户 之 间 的 复 杂 交 互 。 信 转 换 部 ｇｎ 与 通
件 统 一 负 责 完 成 Ａｇ ｎ ｅ ｔ向 ＣＯ ＲＢＡ对 象 中 的 操 作 和 方 法 的 映 射 ， 在 设 计 Ａｇ ｎ 使 ｅ ｔ时 可 以 不 必 过 多 考 虑 内 部 的 通 信 机 制 ， 要 按 照 传 统 的设 计 ： 只 式 即可 ， 高 了 系 提
关键词 ： 自相 关过 程 控 制图 ＡＲ Ａ Ｍ 时 间序 列
自相关过程的统计控制状态

自相关过程的统计控制状态


残差与过程刚发生偏移时的第一个残差相比会变得非常小 ,
而难于检测出过程的偏移 。导致这一结果的原因是 AR (1)
模型对过程均值的变化作出了响应 ,均值的部分变化反映在
预测值中 。由式 (8) 可见 ,当 < > 0 时 ,均值的变化对残差的
影响减弱了 ;当 < < 0 时 ,均值的变化对残差的影响增强了 。
AR(1) 模型 , Xt 与 Xt - k 的自相关系数为 :
ρ k
=
<k , k
= 1 ,2 , …
(2)
如果模型中系数的估值 ^< 和μ^ 是准确的 ,那么 ,残差为
Rt = Xt - μ^ (1 - ^<) - ^<Xt- 1
(3)
εt 可用残差 Rt 来近似 ,此时残差的自相关性已很微弱 。用
Rt 在控制图上打点构成了一张残差控制图 ,其残差控制图
的控制界限为 :
UCL = 3
CL = 0
LCL = - 3
假设系数估值是准确的 ,那么 ,预测值 X^ t 如下式所示
X^ t = μ(1 - <) + <Xt- 1
(4)
不失一般性 ,令 X0 = μ。
现考虑由于异常原因的影响使过程均值发生变化的情
(1) E ( Xt ) = μ,对一切 t
— 76 —
(2) E( Xt - μ) ( Xt+τ - μ) = rτ 第一条性质表明过程的期望值不随时间的推移而变化 ;第二 条性质表明过程前后两个时刻的线性相关性 (统计意义) 的 强弱只依赖于两个时刻间的间隔而与它们所处的位置 t 无 关 。而平稳过程在工程技术 、自然科学和医学等领域中具有 极其广泛的代表性 ,它反映了一个过程处于稳态工作条件下 的统计性质 。
CUSUM EWMAPPT课件

CUSUM EWMAPPT课件


1
26
第26页/共69页
• 双侧CUSUM控制图可以通过同时使用两个单侧CUSUM控制图来实现，其中：上单侧与下单侧CUSUM的
参考值分别记为K1和K2，它们的ARL记为
和
。
• 单侧CUSUM控制图的ARL与双侧CUSUM控制图的ARL即
之间的关系为
L1 () L2 ()
L()
L1
()
L1 1
()
• 利用CUSUM控制图，过程偏移量可以利用点子倾斜程度的变化进行估计。并且， 通过观察倾斜程度的变化，可找到过程出现变化的起点。
14
第14页/共69页
CUSUM控制方法——V型模板
15
第15页/共69页
V型模板的应用方法： 把V型模板的O点放在 最新得到的点子Si上， 直线OP与x轴平行
每当CUSUM打 点图上出现一个 新的点子，就要 移动V型模板， 把O点移到最新 点子上，OP与x 轴平行，应用V 型模板进行控制。
内容：
• CUSUM控制及其应用 • EWMA控制及其应用 • 自相关过程的质量控制
1
第1页/共69页
2
CUSUM控制及其应用
第2页/共69页
常规控制图的不足
• 常规休哈特控制图存在着对过程小偏移不灵敏的缺陷。 • CUSUM控制图的诞生正是为了解决过程小偏移的质量控制问题。 • CUSUM控制图是1954年佩基(Page)提出的。
SH (i)
SL (i)
SH (i)
SH (i)
0
SL (i) SL (i)
或
为负值，则将其置为0；
30
第30页/共69页
• CUSUM控制图的设计原则 设计CUSUM控制图取决于对参考值K和决策值H的选择。 建议：基于对ARL的设计要求，选取参数。
实验室质量控制图制作过程

实验室质量控制图制作过程

实验室质量控制图制作过程实验室质量控制图制作过程1.1 质控血清的制备和保存（以ELISA试验检测HIV抗体为例）在每次实验中必须包含有内部对照质控血清和外部对照质控血清。

内部对照质控血清指试剂盒内提供的阳性和阴性对照血清。

内部对照是质量控制的基础。

每一次检测必须使用内部对照，而且只能在同批号的试剂盒中使用。

外部对照质控血清是为了监控检测的重复性和稳定性以及试剂盒批间或孔间差异而由实验室设置的一套对照血清，包括强阳性、弱阳性和阴性对照血清。

也可以只设置一个弱阳性对照，以该试剂盒临界值（Cut-off）的2?3倍为宜。

1.1.1 外部对照质控血清的制备HIV抗体阳性和阴性血清，56℃ 30min灭活，3000r/min，离心15min。

弱阳性对照可以用HIV抗体阴性血清梯度稀释HIV抗体强阳性血清并标定后得到。

按一年使用量配制（可加入不影响检测结果的防腐剂）用0.2μm滤膜过滤除菌。

1.1.2 外部对照质控血清的保存1.1.2.1 按一周实验用量分装、分类、标记、封口、-20℃冻存于非自动除霜冰箱中。

1.1.2.2 外部对照血清不可反复冻融，一旦融化后应该存放2?8℃，供一周内使用。

1.1.3 外部对照质控血清的使用每一次实验必须使用外部对照质控血清，以便监控实验的重复性和稳定性。

同时可以了解各批试剂盒的批间或孔间差异，绘制质量控制图。

1.1.4 外部对照质控物的质量要求质控物的管间或瓶间变异必须小于监测系统预期的变异（cv＜20%），并且质控物的成分应在稳定状态中。

质控物应无菌，并不含有影响ELISA反应的防腐剂。

1.2 质控图的建立及应用（以ELISA试验检测HIV抗体为例）最常用的质控图是Levey-Jennings质控图，使用累计和技术或趋势分析技术的图形可提供系统偏移和漂移的状况。

1.2.1 建立质控图参数外部对照质控物的平均值和标准差应建立在实验室常规使用方法对质控物重复测定的基础上。

工程质量控制的统计分析方法：相关图法

工程质量控制的统计分析方法：相关图法

(⼀) 相关图法的⽤途 相关图⼜称散布图。

在质量控制中它是⽤来显⽰两种质量数据之间关系的⼀种图形。

质量数据之间的关系多属相关关系。

⼀般有三种类型：⼀是质量特性和影响因素之间的关系;⼆是质量特性和质量特性之间的关系;三是影响因素和影响因素之间的关系。

我们可以⽤y和X分别表⽰质量特性值和影响因素，通过绘制散布图，计算相关系数等，分析研究两个变量之间是否存在相关关系，以及这种关系密切程度如何，进⽽对相关程度密切的两个变量，通过对其中⼀个变量的观察控制，去估计控制另⼀个变量的数值，以达到保证产品质量的⽬的。

这种统计分析⽅法，称为相关图法。

[例题] 在质量控制中( )是⽤来显⽰两种质量数据之间关系的⼀种图形。

A. 排列图B. 直⽅图C. 控制图D. 相关图 答案：D (⼆)相关图的绘制⽅法 [例7-5] 分析混凝⼟抗压强度和⽔灰⽐之间的关系。

1.收集数据 要成对地收集两种质量数据，数据不得过少。

本例收集数据如教材152页表7—11所⽰。

2.绘制相关图在直⾓坐标系中，⼀般x轴⽤来代表原因的量或较易控制的量，本例中表⽰⽔灰⽐;y轴⽤来代表结果的量或不易控制的量，本例中表⽰强度。

然后将数据中相应的坐标位置上描点，便得到散布图，如教材152页图7-13所⽰。

(三)相关图的观察与分析 相关图中点的集合，反映了两种数据之间的散布状况，根据散布状况我们可以分析两个变量之间的关系。

归纳起来，有以下六种类型，如教材153页图7-14所⽰。

(1)正相关(图7-14a)。

散布点基本形成由左⾄右向上变化的⼀条直线带，即随x增加，y值也相应增加，说明x与y有较强的制约关系。

此时，可通过对x控制⽽有效控制y的变化。

(2)弱正相关(图7—14b)。

散布点形成向上较分散的直线带。

随x值的增加，y值也有增加趋势，但x、y的关系不像正相关那么明确。

说明y除受x影响外，还受其他更重要的因素影响。

需要进⼀步利⽤因果分析图法分析其他的影响因素。

平稳自相关过程的残差累积和控制图

平稳自相关过程的残差累积和控制图

从以上仿真结果可以看到，用残差 CUSUM 控制图 对自相关过程进行控制，有效避免了在受控条件下发生
［1］ Peihua Qiu.Statistical Process Control［M］.Florida：Tay⁃ lor & Francis Group，2014：135-141.
［2］ 王斌会，张志雷.自相关过程的质量控制方法——残差 控制图［J］.科技管理研究，2005（6）：139-141.
然后，再运用残差 CUSUM 控制图对上面的过程进行 监控。利用回归分析法，由前 99 个受控时的观测值估计 出时间序列模型为：Yt=0.121 3+0.510 8Yt-1，σY=1.061 12， 再根据式（5）计算出残差序列的 149 个值。本文使用 SPSS 软件对残差序列进行独立性检验，确保消除过程的 相关性。由于参数 DW 值越接近于 0 时，残差项间正相关 越强；DW 值越接近于 2 时，残差项间越无相关即独立； DW 值越接近于 4 时，残差项间负相关越强。由图 3 可以 看出，DW 参数值接近于 2，可以判断残差序列不存在自 相关性［7-9］。
［6］ 王海宇，杨剑锋，徐济超，等.平稳自相关过程的 EWMA 控制图［J］.工业工程，2006，9（3）：80-83.
［7］ 孙静.自相关过程的残差控制图［J］.清华大学学报（自 然科学版），2002，42（6）：735-738.
［8］ 方浩博.自相关过程的累积和控制图及其应用研究 ［D］.郑州：郑州大学商学院，2011：20-36.
若统计量Sn＞h 或者Sn＜-h，那么可以做出过程失控
的判定。
若 要 监 测 一 个 任 意 的 均 值 偏 移 ，可 以 使 用 双 侧
CUSUM 控制图，即将上单侧累积和控制图和下单侧累积
连续型过程的二元残差T2控制图

连续型过程的二元残差T2控制图

连续型过程的二元残差T2控制图摘要：连续型过程数据的各质量特性之间存在相关关系，各质量特性自身的数据又存在自相关现象，这种相关现象影响了传统控制图的有效性。

针对此类连续生产过程，采用残差T2控制图，用钢铁联合企业的实际数据进行分析，研究了在稳定状态和不稳定状态下的传统T2控制图和残差T2控制图，比较在两种状态下两控制图的平均运行链长ARL的大小，验证了残差T2控制图能够有效的控制连续型过程的多元自相关过程。

关键词：连续型过程；残差；T2控制图；ARL0 前言统计过程控制[1]是一种运用统计技术对生产过程质量进行监控的方法，以发现和预测生产中可能出现的异常现象。

统计过程控制常用的工具是控制图，控制图[2]是休哈特博士于1924年首次提出用于质量控制的工具，用来区分生产过程中的质量波动是由系统因素引起的还是由非系统因素引起的。

传统的控制图已经比较广泛的应用在汽车制造、环保、医药等企业[3～5]。

然而，随着计算机的发展，数据采集的频率越来越快，数据自相关现象越来越普遍，而且各因素之间也不是完全独立，存在一些相关现象。

尤其是针对连续的生产过程，例如化工、冶金类行业，各个影响因素之间是相互影响的，各因素的观测值又具有自相关特性。

目前，针对这种连续生产过程已出现了一些控制多元自相关过程的方法，针对多元影响因素最常用的方法是主元分析法对多元数据进行降维处理，以及由Pan和Jarret提出的Kalman滤波方法[4]对观测值进行滤波处理。

孙静[5]分别运用单值控制图和残差控制图就受控状况和失控状况的观测值对案例进行了分析比较，当过程存在自相关时，运用残差控制图更合适，但是，当自相关参数大于0时，残差控制图检测过程异常的灵敏性有待提高。

此后，杨穆尔和孙静对二元自相关过程的残差T2控制图进行了分析[6]，探讨两个随机变量相互独立，其中一个随机变量相互独立，另一个随机变量服从一阶自回归模型的二元自相关过程。

孙静提出的残差T2控制图用于监控存在自相关现象的生产过程，但是其算例计算的数据是采用蒙特卡洛模拟而产生的仿真数据，仿真数据的产生具有很大的人为因素，而本文采用实际生产的数据，对存在自相关现象的生产过程进行监控，验证残差T2控制图的有效性。

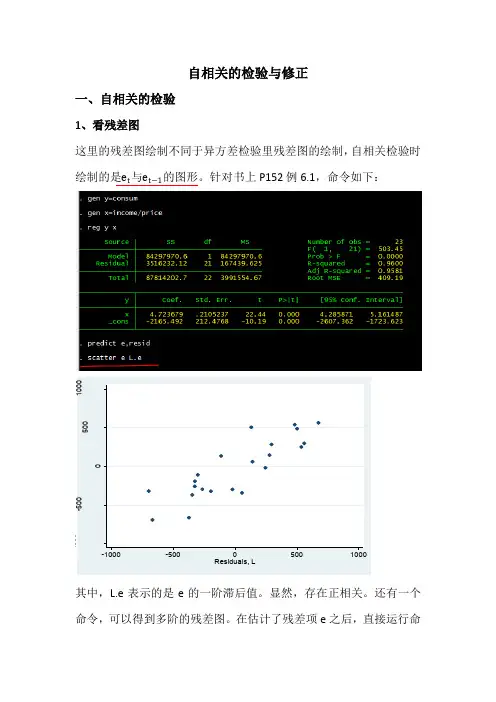
自相关的检验与修正

自相关的检验与修正

自相关的检验与修正一、自相关的检验1、看残差图这里的残差图绘制不同于异方差检验里残差图的绘制，自相关检验时绘制的是e t 与e t −1的图形。

针对书上P152例6.1，命令如下：其中，L.e 表示的是e 的一阶滞后值。

显然，存在正相关。

还有一个命令，可以得到多阶的残差图。

在估计了残差项e之后，直接运行命R e s i d u a l s令ac e 就可得到下图(ac 为autocorrelation 的缩写)：横轴表示的是滞后阶数，阴影部分表示的是相应的置信区间，在上图中，显然一阶滞后是自相关的。

补充：滞后算子L 。

L.x 表示x 的一阶滞后值，L2.x 表示二阶滞后值。

差分算子D 。

D.x 表示x 的一阶差分，D2.x 表示二阶差分。

LD.x 表示一阶差分的一阶滞后值。

需要注意的是，在使用之后算子和差分算子时，一定要事先设定时间变量。

2、DW 检验该方法出现较早，现在已经过时，主要是因为该方法只能检验一阶自相关。

命令：estat dwatson 。

经验上DW 值在1.8---2.2之间接受原假设，不存在一阶自相关。

DW 值接近于0或者接近于4，拒绝原假设，存在一阶自相关。

3、LM检验(BG检验)命令：estat bgodfrey 一阶滞后自相关检验estat bgodfrey，lags(p) P阶滞后自相关检验滞后阶数P的选取最简单的方法就是看自相关图，阴影部分以外的自相关阶数为显著。

二、自相关的处理—广义最小二乘法FGLS命令：prais y x1 x2 x3 该命令对应的是书上P147的(6.33)方法prais y x1 x2 x3，corc 该命令对应的是书上P147的(6.32)方法在自相关检验及处理上，还有比较常用的稳健标准差命令newey以及Q-Test命令，感兴趣的同学可以去查阅相关书籍。

基于GARCH型控制图的互联网金融预警实证分析——以余额宝为例

基于GARCH型控制图的互联网金融预警实证分析——以余额宝为例李红梅;王青【摘要】一般金融产品的时序数据通常具有自相关性和聚集性特征,而互联网金融是将传统金融业、信息通信技术以及互联网技术相结合的一种新型金融服务.为验证其是否也满足一般金融产品的相关属性,文章首先对以余额宝为代表的互联网金融产品的自相关性及聚集性进行了验证,其结论显示余额宝收益率数据确实具有自相关性及聚集效应(即异方差)的特征.另外,为解决这类数据的监控过程,能够对风险进行有效的报警提示,文章还提出了GARCH型残差控制图.传统的6σ控制图为静态控制限,而GARCH型控制图是动态控制限,将这种控制图应用于余额宝这种互联网金融产品进行实证分析,实证结果显示GARCH型控制图比传统控制图更敏感,对自相关过程的监控更加有效.【期刊名称】《辽宁大学学报（哲学社会科学版）》【年(卷),期】2018(046)002【总页数】7页(P38-44)【关键词】GARCH模型;残差控制图;互联网金融【作者】李红梅;王青【作者单位】辽宁大学数学院,辽宁沈阳110036;辽宁大学经济学院,辽宁沈阳110036【正文语种】中文【中图分类】F830.39一、引言互联网金融是将传统的金融业、信息通信技术和互联网技术相结合的一种新型金融服务领域。

互联网金融主要分为三种模式：第一种模式是大家熟悉的网银，这个是传统的金融借助互联网渠道为客户提供服务；第二种模式是类似支付宝的第三方支付，在用户与银行支付结算系统间建立连接的电子支付模式；第三种模式是利用互联网搭建中介平台，将资金出借方与需求方结合在一起，如人人贷（P2P）等。

本文涉及的互联网金融主要指第二种模式。

近年来，随着移动互联网的快速发展以及互联网金融产品特有的低门槛、高收益、变现灵活等特点，互联网金融产品越来越受到人们的喜爱，在移动终端上进行的金融业务也越来越多。

虽然互联网金融发展趋势迅猛，规模在不断地快速扩张，但由于互联网金融是近几年才发展起来的新兴金融业态，我国针对互联网金融进行的风险管理与预警还处在起步与探索阶段。

自相关过程控制简介.


残差控制图理论ARL的计算
当过程发生偏移时，残差值落在控制限内 的概率为
pt ( ) P(3 Rt 3 ) P[(3 E ( Rt )) / ( Rt E( Rt )) / (3 E( Rt )) / )] Z (3 E ( Rt ) / ) Z (3 E( Rt ) / )
实际问题中还需考虑时间序列的平稳性例子仍然考虑上面的例子对前200个数据采用matlab自带的函数garchfit拟合一个一阶自回归模型拟合的模型为用真实值减去该拟合模型得到的预测值即可得到残差序列我们首先检验残差序列的自相关情况003505866残差的imr控制图残差控制图的检出效果设估计的arp模型残差序列为设序列在q时刻发生偏移残差控制图的检出效果特别的对于一阶自回归模型即p1时因此若q时刻没有检出偏移以后残差显示的偏移减少检出会更加困难残差的单值移动极差控制图会不太灵敏
验证残差的自相关
验证残差的正态性
残差的I-MR控制图
残差控制图的检出效果
设估计的AR(p)模型Yˆt 1(Yt1 ) 2(Yt2 ) ... p(Yt p ) 残差序列为 Rt (Yt ) 1(Yt 1 ) 2(Yt 2 ) ... p(Yt p ) 设序列 Yt 在q时刻发生偏移Y ，即
Z i X i (1 ) Z i 1
1 Ti 2 Z i ' Zi Z i 2i 1 (1 ) 2
Zi

原因分析
SigmaY=inv(eye(4)-kron(fei,fei))*sigma；求 得
100.003 65.994 SigmaY= 65.994 121.001

自相关过程控制简介.


计算残差理论ARL的matlab语句 fei=0.6;%自回归系数 delta=1;%偏移量即多少个标准差 %p1是t=q时刻残差落在控制限内的概率 p1=normcdf(3-delta*(1/sqrt(1-fei^2)),0,1)-normcdf(3-delta*(1/sqrt(1-fei^2)),0,1); %p2是t>q各时刻残差落在控制限内的概率 p2=normcdf(3-delta*sqrt(1-fei)/sqrt(1+fei),0,1)normcdf(-3-delta*sqrt(1-fei)/sqrt(1+fei),0,1); ARLtheory=1+1*p1/(1-p2)
残差的单值控制图，偏移0.5标准差
残差的EWMA控制图偏移0.5标准差
单值控制图，偏移1个标准差
EWMA控制图，偏移1个标准差
单值控制图，偏移2个标准差
EWMA控制图，偏移2个标准差
残差控制图的检出效果
平均运行链长仿真，运行1000次，可得偏 移一个标准差，自回归系数=0.6时，可得 ARL=151.95，理论值150.00。若自回归系 数=-0.6，则ARL=7.466，理论值7.05，而 在没有自相关时，休哈特控制图偏移一个 标准差的理论ARL为43.89，在不发生偏 移时残差控制图和普通控制图ARL理论值 均为370
残差控制图的ARL
多元问题
考虑一个二元一阶向量自回归模型，误差 项需满足：均值为0、协方差矩阵为正定矩 阵且不存在自相关。
Yt (Yt 1 ) t 或写成Yt c Yt 1 t , t N 2 (0, ) , t N 2 (0, )
Z i X i (1 ) Z i 1

质量管理-质量控制-老七种工具之七：控制图

老七种工具之七：控制图
控制图是判断和预报生产过程中质量状况是否发 生波动的一种有效方法。 例如：美国某电气公司的一个工厂有3千人，制定 了5千张控制图； 美国柯达彩卷公司有5千人，制定控制图有3万 5千张，平均每人7张。 我国某飞机制造厂中的先进质量体系(AQS)中， 要求一些工序必须作控制图。
数据种类样本容量指标中心位置计数值计量值复数不良品缺陷平均数中位数平均值极差控制图r中位数控制图缺陷数控制图c单位缺陷数控制图u单值控制图x单数单值移动极差控制图xrs样本容量确定不确定不良品数控制图pn不良品率控制图p确定不确定样本容量图418控制图的种类及选用流程?计量值控制图一般适用亍以计量值为控制对象的场合
● ● ●
●
●
●●
● ● ●
μ
-3σ
(5)点子的波动呈现周期性变化，表明生产过程 有系统性因素发生。
5.控制图的两种错误判断
根据控制图的控制界限所作的判断也可能发生错 误。这种可能的错误有两种：
第一种错误是将正常判为异常； 第二种错误是将异常判为正常。
控制图的两种错误
在生产正常的情况下，点子出界的可能性为3‰。 这数值虽然很小，但这类事件总还不是绝对不能 发生的。这样，在纯粹出于偶然点子出界的场合， 我们根据点子出界判断生产过程异常就犯了虚发 警报的错误，这种错误就叫做第一种错误。
x 单值控制图（ ），中位数控制图。
（2）计数值控制图包括： 不良品数控制图， 不良品率控制图， 缺陷数控制图， 单位缺陷数控制图。
根据所要控制的质量特性和数据的种类、条件等，按图 中得箭头方向便可作出正确的选用。
计量值
数 据 种 类
计数值
样本 容量
单数 复数

基于二阶自相关过程残差控制图的改进

基于二阶自相关过程残差控制图的改进作者：魏兴龙来源：《价值工程》2018年第03期摘要：本文将以AR（2）过程为例，将CUSUM和EWMA控制图的统计量相整合，提出改进MEC和MCE两种控制图，以平均运行链长（ARL）和额外平方损失（EQL）做为评价效率的重要指标。

通过仿真分析去验证，新的控制图对于自相关模型发生均值漂移具有较好的检测效率.Abstract： In this paper， the AR （2） process is taken as an example， the statistics of CUSUM and EWMA control charts are integrated， and two control charts， MEC and MCE， are proposed. The average run length （ARL） and extra quadratic loss （EQL） are used as important index to evaluate the efficiency. Through the simulation analysis to verify， the new control chart has a good detection efficiency for the mean shift of the autocorrelation model.关键词：残差；平均运行链长；自相关；漂移；MEC；MCE；统计过程控制Key words： residual；average run length（ARL）；autoregressive；shift；Mixed EWMA-CUSUM；Mixed CUSUM-EWMA；statistical process control中图分类号：O212.1 文献标识码：A 文章编号：1006-4311（2018）03-0192-040 引言在生产过程中，为了实现统计过程的控制，提升产品的质量，控制图被认为是一种有效的控制措施。

检验自相关的常用方法

检验自相关的常用方法我之前为了弄明白检验自相关的常用方法，那可真是费了好大的劲儿。

说实话，检验自相关这事，我一开始完全就是瞎摸索。

我最先尝试的就是画图这个方法。

就像看一群蚂蚁走路一样，我把数据点一个一个画在坐标图上，试图通过肉眼看这些点是不是呈现出某种规律，要是这些点看起来像是一串一串的，就觉得可能存在自相关。

但这方法太不靠谱了，很多时候我觉得可能有自相关，可实际并不是那么回事，这全靠感觉，很容易出错。

有次我做完画图，觉得肯定有自相关，兴高采烈地跟人说我找到规律了，结果细一分析，完全不对，这可让我丢脸丢大了。

后来啊，我知道了杜宾- 沃森（Durbin - Watson）检验。

这个就比较科学了。

就像是给数据做个体检，算出杜宾- 沃森值，然后和不同的标准值比较。

如果这个值在一定的范围里，就可以大致判断有没有自相关。

不过这里面也有陷阱，这个范围有时候界限有点模糊，我刚开始的时候老是判断错，把没有自相关的数据当成有，有自相关的数据又觉得没有。

后来我就反复的试，拿很多组已知自相关情况的数据来实验，就像在迷宫里不断试错找出口一样，才慢慢掌握一点窍门儿。

还有一种方法是用相关图，这就像是一个蜘蛛网一样。

看自相关系数和偏自相关系数随着滞后阶数的变化形成的图。

当看到自相关系数不是快速趋近于零的时候，就可能存在自相关。

我记得最开始看这种图的时候，看得我眼花缭乱的，那些线在我眼里就跟乱麻似的，根本不知道啥意思。

但是经过很多次的训练，我现在看到这种图能有个大致的方向了。

不过这方法对于数据要求比较高，如果数据有些异常值或者其他的小问题，可能就会干扰判断。

总之呢，这检验自相关真不是个容易的事儿，得不断的尝试，犯错，再尝试才能找到适合的方法。

有时候一种方法失败了，别怕，再换个方法试试，总会有点收获的。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
理论分析表明 : 当过程自相关时 , 用常规控制图方法 估算的 R/ d2 (2) 是过程方差 σY 的有偏估计 , 由此导致控
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved.
2005
年第
6
期
Science
and
科技管理研究 Technology Management
Research
2005
No16
文章编号 : 1000 - 7695 (2005) 06 - 0139 - 02
自相关过程的质量控制方法 ———残差控制图
王斌会 , 张志雷
有效使用控制图能够在生产过程中科学地保证预防原 则的实现 , 减少质量的异常波动 , 从而提高产品品质 、增 强市场竞争力 。但是 , 人们在生产实践中逐渐认识到在使 用常规控制图对过程进行控制时 , 存在着一些不足之处 , 并陆续提出一些改进方法 。本文仅研究当过程存在自相关 现象从而违背常规控制图独立性假定时 , 对质量特性值控 制的残差图理论 , 希望以此对实际质量管理者提供有益的 参考 。
σ2Y = Var ( Yt)
σε2
= 1-
<2
假设在受控状态下质量特性观测值呈现自相关的系统
机理可用式 (3) 表达 , 则过程残差 et 为 : et ≡Yt - ^Yt| t - 1 , t - 2 , …
其中 ^Yt| t - 1 , t - 2 , …是 Yt 的估计值 , 令 Yt 的最小均方误 差线性估计值为 E ( Yt | Yt - 1 , Yt - 2 , …) 。在 t 时刻的估计值 是: ^Yt| t - 1 , t - 2 , … = E ( Yt| Yt - 1 , Yt - 2 , …) =μ^ + ^< ( Yt - 1 - μ^ )
然后 , 我们运用残差控制图重新对过程进行监控 。根 据时间序列理论 , 用前 200 个过程稳态下的观测值估计出 时间 序 列 模 型 , 由 于 估 计 误 差 拟 合 出 的 模 型 为 : Yt = 010078 + 016737 ( Yt - 1 + 010078) , 方差 σY = 1125 。根据式 (4) 计算出残差序列的 250 个值 , 并由式 (5) 得到的控制 限 XUCL = 3 , XCL = 0 , XLCL = - 3 , 作出残差控制图对残差 序列进行控制 。如图 2 所示 , 在前 200 个点中未有出界点且 呈随机排列 , 在第 211 个点出界显示过程均值增大 , 有异 常情况发生 。
为了解决过程自相关情况下的质量控制问题 , 统计学 家们陆续提出了一些改进方法 , 其中主要方法之一就是引 入时间序列分析法 。Alwan 和 Roberts (1988) 提出[2] , 利用 过程稳态下自相关的观测值估计时间序列模型 , 如果模型 估计准确则利用模型拟合观测值 , 其拟合后的残差序列相 互独立 , 满足常规控制图的基本假设前提 。因此 , 可以用 常规作图法对残差序列建立残差控制图进行过程监控 。此 后 , 许多同类问题的研究也都是基于这一基本思想展开的 。
3 过程模型与残差控制图
时间序列分析通常用于研究某过程的动态结构 , 分析
相邻观测值之间的依赖性 。所以当质量特性过程呈现自相
关现象时 , 我们用时间序列模型 ARMA (p , q) 表征过程仅
存在一般性原因的系统相关状况是适宜的 , 然后通过对拟
合观测值后的残差来监控过程波动 。本节将通过 ARMA 模
在实际过程中 , 参数 μ和 < 由过程稳态下的观测值估 计出 。如果两个参数估计准确 , 即 μ^ = μ, ^< = <, 则过程
残差为 :
et = Yt - ^Yt| t - 1 , t - 2 , … =εt
(4)
如果在 T 时刻 , 由于特殊性原因的影响使过程失控 ,
均值由稳态下 μ偏移到μ+δY , 则由 (3) (4) 式可知其残
型的特例 AR (1) 模型具体说明残差控制图理论 。
一阶自回归 AR (1) 过程模型 :
Yt = μ+ < ( Yt - 1 - μ) +εt t ∈Z
(3)
式中 { et} 是独立同分布的干扰序列 , εt～ N (0 , σε2 ) ,
t ∈Z 。则 AR (1) 观测序列 { Yt} 的方差 :
差序列 { et} 也随着发生变化并满足模型 :
εt
t< T
et = εt +δσY
t= T
εt + (1 - <) δσY t = T + 1 , T + 2 , … 根据时间序列模型理论 , 残差序列 { et} 满足常规控制
图独立同分布的基本假设 。所以对残差序列可用常规的休
哈特图进行控制 , 建立残差控制图 , 其中心限 CL = 0 , 上
(暨南大学经济学院统计系 , 广东广州 510632)
摘要 : 当质量过程呈现自相关现象时 , 常规控制图已经不能准确反映生产中质量的波动 。因此本文研究了 基于时间序列理论的残差控制图 , 并通过蒙特卡洛模拟方法表明 , 残差控制图能够较好解决过程自相关条件下 的质量控制问题 。
关键词 : 常规控制图 ; 残差控制图 ; 蒙特卡洛模拟 中图分类号 : F204 文献标识码 : A
式中 , yt 为在 t 时刻的观测值 , μ为过程均值常数 , εt ～ iid (0 , σε2 ) 。常规控制图的控制限一般设定是 μ ±3σε。
在生产实践中 , 参数由过程稳态下的观测值估计 , 其中 1/ n ∑Yi 为中心控制线μ的无偏估计 , 过程标准差 σε 的无偏
估计值一般用 R/ d2 (2) , 其中 d2 (2) = 2/ π是无偏估计
首先 , 我们研究在忽视过程自相关而认为观测值相互 独立条件下 , 用常规控制图方法对过程进行控制时的问题 。 根据式 (1) (2) 用前 200 个过程稳态下的观测值估计出方 差σY = 017160 , 均值 μ= - 0104 , 由此设定的控制限 XUCL = 21108 , XCL = - 0104 , XLCL = - 21188 。如图 1 所示 , 虽然在 第 202 个点即出界表明过程异常 , 但在过程处于稳态下的 前 200 个点中 , 有 12 个点出界 。说明当过程正相关时 ,由于 σY 被低估 ,导致控制限间距过紧 ,虚假报警增多 。因此 ,在自 相关条件下使用常规控制图会带来大量的误判信息 ,给实际 质量控制工作带来误导 ,控制图的监控效果大大降低 。
的修正系数 , 离差均值 R 定义 :
n
nRi
=
1 n-
1 i =2
|
Yi -
Yi - 1 |
(2)
如点子逐点上升或下降 。我们通过控制图观察数据的
变化发现失控现象 , 并希望解释产生失控的原因 ———即特
殊原因或可归因原因 。通过纠正措施消除特殊原因 , 使过
程重新处于统计控制状态 。
从以上模拟结果表明用残差控制图对自相关过程进行 控制是适宜的 , 有效避免了在受控状况下虚发报警现象的 出现 , 而且控制效果较好 。因此 , 在实际质量管理中如果 过程自相关时 , 建议考虑使用残差控制图 。
图 1 休哈特图
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved.
殊原因 。
在统计过程控制中 , 如果过程仅存在一般性原因时 , 过
程被认为处于统计控制状态 。通常在常规控制图理论中 , 统
计控制状态被假定成一个随机过程 ———过程是由独立同分
布的随机变量产生的 。即产品质量特性值{ yt} 可表示为 :
yt = μ+εt
(1)
收稿日期 : 2004 - 11 - 12 基金项目 : 广东省科技计划攻关项目 , (编号 : 2004B10101010)
下控制限 CLR :
CLR = ±LRσε
(5)
其中 LR 是控制限系数 , 一般取 LR = 3 。当观测值表现
为个别极端值出界或非随机的点序列 , 则说明生产的稳态
过程被破坏 , 有异常情况发生 , 应采取措施查出原因并加
以消除 。
4 案例分析
我们通过运用蒙特卡洛模拟方法进一步研究质量过程 自相关条件下的残差控制图理论 , 说明残差图的制作方法 , 并与常规控制图进行比较 。假设质量过程稳态时为 AR (1) 过程如式 (3) 所示 , 令参数 φ = 016 , μ = 0 , εt ～ N ( 0 , 1) 。通过计算机程序随机模拟过程变化 , 并产生 250 个仿 真数据 。其中前 200 个受控数据由模型 Yt = 016 Yt - 1 +εt 随 机产生 ; 若在第 200 点与 201 点之间时过程失控 , 均值偏移 1σY , 则失控状况下的第 201 个数据由模型 Yt =σY + 016 Yt - 1 +εt 随机产生 , 其余 49 个数据由模型 Yt = (1 - 016) σY + 016 Yt - 1 +εt 随机产生 。
1 常规控制图理论
质量管理的观点认为 : 质量具有变异性其特性值是波
动的 , 具有规律性 , 但它不是通常的确定性现象的确定性
规律 , 而是随机现象的统计规律 , 用数学语言来讲 , 就是
服从某种分布 。如果出现异常情况 , 就必然使波动偏离原
来的分布 , 利用统计技术就可以发现这种波动 。戴明在休
哈特理论基础上将产生质量波动的原因分成两类 : 一般性