下载文档原格式
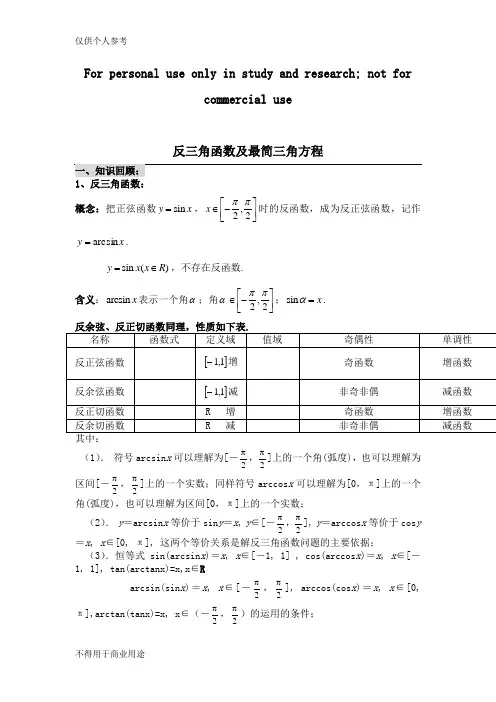
For personal use only in study and research; not forcommercial use反三角函数及最简三角方程概念：把正弦函数sin y x =，,22x ππ⎡⎤∈-⎢⎥⎣⎦时的反函数，成为反正弦函数，记作x y arcsin =.sin ()y x x R =∈，不存在反函数.含义：arcsin x 表示一个角α；角α,22ππ⎡⎤∈-⎢⎥⎣⎦；sin x α=.（1）． 符号arcsin x 可以理解为[－2π，2π]上的一个角(弧度)，也可以理解为区间[－2π，2π]上的一个实数；同样符号arccos x 可以理解为[0，π]上的一个角(弧度)，也可以理解为区间[0，π]上的一个实数； （2）． y ＝arcsin x 等价于sin y ＝x , y ∈[－2π，2π], y ＝arccos x 等价于cos y ＝x , x ∈[0, π], 这两个等价关系是解反三角函数问题的主要依据； （3）．恒等式sin(arcsin x )＝x , x ∈[－1, 1] , cos(arccos x )＝x , x ∈[－1, 1], tan(arctanx)=x,x ∈Rarcsin(sin x )＝x , x ∈[－2π，2π], arccos(cos x )＝x , x ∈[0, π],arctan(tanx)=x, x ∈（－2π，2π）的运用的条件；（4）． 恒等式arcsin x ＋arccos x ＝2π, arctan x ＋arccot x ＝2π的应用。
2（1）．含有未知数的三角函数的方程叫做三角方程。
解三角方程就是确定三角方程是否有解，如果有解，求出三角方程的解集； （2）．解最简单的三角方程是解简单的三角方程的基础，要在理解三角方程的基础上，熟练地写出最简单的三角方程的解； （3）．要熟悉同名三角函数相等时角度之间的关系在解三角方程中的作用； 如：若sin sin αβ=，则sin (1)k k απβ=+-；若cos cos αβ=，则2k απβ=±；若tan tan αβ=，则a k πβ=+；若cot cot αβ=，则a k πβ=+； （4）．会用数形结合的思想和函数思想进行含有参数的三角方程的解的情况和讨论。
三角函数公式大全表格初中数学三角函数公式大全1.正弦函数的定义：sinθ=a/b2.余弦定义：cosθ=b/a3.正切公式：tanθ=a/b4.反正弦公式：sin-1θ = c/d5.反余弦公式：cos-1θ = d/c6.反正切公式：tan-1θ = c/d7.正弦双曲线：y=a/b*sinθ8.余弦双曲线：y=b/a*cosθ9.正弦型应用：y=a+b*sin(c*x+d)10.余弦型应用：y=a+b*cos(c*x+d)11.正弦型的解析解：x=(b/c)*sin(θ-d)+Ay=(a/c)*sin(θ-d)+B12.余弦型的解析解：x=(b/c)*cos(θ-d)+A y=(a/c)*cos(θ-d)+B13.正弦函数的导数：y'=a*b*cosθ14.余弦函数的导数：y'=-a*b*sinθ15.正弦函数的倒数：y'=a/b16.余弦函数的倒数：y'=b/a17.正弦三角关系：sin2θ + cos2θ = 118.正弦函数的积分：∫sinθdθ = -cosθ+C19.余弦函数的积分：∫cosθdθ = sinθ+C20.正切函数的导数：y'=a*b*sec2θ21.正切函数的倒数：y'=b/a*secθ22.正切函数的积分：∫tanθdθ = -ln|cosθ|+C23.正弦函数的复值：sin2θ = 2*sinθ*cosθ24.余弦函数的复值：cos2θ =cos2θ-sin2θ25.正切函数复值：tan2θ =2*tanθ/(1-tan2θ)。
在Excel中，你可以使用内置的反三角函数来计算角度的反函数值。
下面是几个常用的反三角函数及其Excel函数的示例：
反正弦函数（arcsin）：返回给定数字的反正弦（以弧度为单位）。
Excel函数：ASIN(number)
反余弦函数（arccos）：返回给定数字的反余弦（以弧度为单位）。
Excel函数：ACOS(number)
反正切函数（arctan）：返回给定数字的反正切（以弧度为单位）。
Excel函数：ATAN(number)
反正切函数（arctan2）：返回x 和y 坐标的反正切（以弧度为单位）。
Excel函数：ATAN2(x, y)
这些函数使用的是弧度作为单位，如果需要结果以角度显示，可以将弧度值乘以180/π进行转换。
例如，要计算反正弦函数的值，可以在Excel中使用以下公式：
=ASIN(number)
其中，number是一个介于-1和1之间的值。
请注意，Excel中的三角函数接受的参数为弧度值，所以如果你有角度值，需要将其转换为弧度值后再进行计算。
三角函数公式大全表格304560
三角函数是数学中极为重要的一部分，涉及到三角关系的求解和它们之间的关系。
以下是30度、45度和60度的三角函数公式的详细表格。
1. 正弦函数（sin）：
角度，正弦值
30度，0.5
45度，√2/2（约等于0.707）
60度，√3/2（约等于0.866）
2. 余弦函数（cos）：
角度，余弦值
30度，√3/2（约等于0.866）
45度，√2/2（约等于0.707）
60度，0.5
3. 正切函数（tan）：
角度，正切值
30度，√3/3（约等于0.577）
45度，1
60度，√3（约等于1.732）
4. 反正弦函数（arcsin）：
正弦值，角度
0.5，30度
√2/2，45度
√3/2，60度
5. 反余弦函数（arccos）：
余弦值，角度
√3/2，30度
√2/2，45度
0.5，60度
6. 反正切函数（arctan）：
正切值，角度
√3/3，30度
1，45度
√3，60度
7.对于余切函数、反余切函数等其他三角函数，可以通过这些已知的三角函数来计算。
这是一个简单的三角函数表格，包括了常见的30度、45度和60度的三角函数值和对应的反函数值。
通过这些值，我们可以在解决三角关系和问题时进行计算和推导。
需要注意的是，三角函数的值和角度都可以根据单位圆和三角恒等式进行推导，例如平方和恒等式、余切与正弦和余弦的关系等等。
这些三角函数的值和关系在数学和物理等领域有广泛的应用，特别是在解决三角关系、图像处理、信号处理等方面。
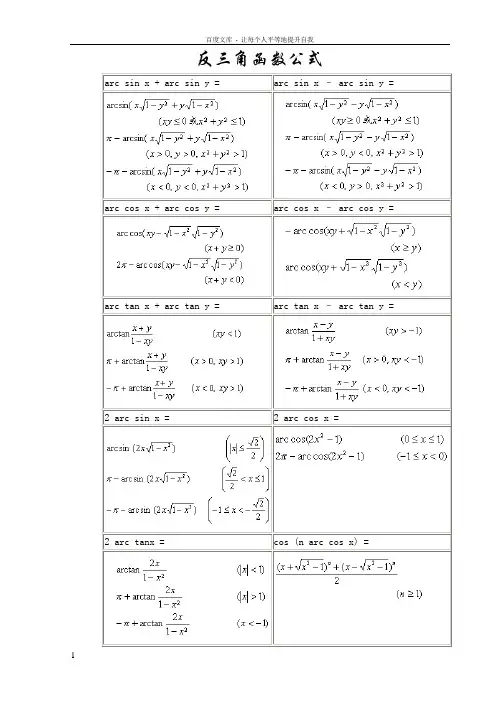
反三角函数公式arc sin x + arc sin y = arc sin x – arc sin y = arc cos x + arc cos y = arc cos x – arc cos y = arc tan x + arc tan y = arc tan x – arc tan y = 2 arc sin x = 2 arc cos x =2 arc tanx = cos (n arc cos x) =反三角函数图像与特征反正弦曲线图像与特征反余弦曲线图像与特征拐点(同曲线对称中心)：，该点切线斜率为1拐点(同曲线对称中心)：，该点切线斜率为－1 反正切曲线图像与特征反余切曲线图像与特征拐点(同曲线对称中心)：，该点切线斜率为1 拐点：，该点切线斜率为－1：渐近线：名称反正割曲线反余割曲线方程图像顶点渐近线反三角函数的定义域与主值范围函数主值记号定义域主值范围反正弦若，则反余弦若，则反正切若，则反余切若，则反正割若，则反余割若，则一般反三角函数与主值的关系为式中n为任意整数.反三角函数的相互关系arc sin x = arc cos x = arc tan x = arc cot x =sin x = x-x3/3!+x5/5!-...(-1)k-1*x2k-1/(2k-1)!+... (-∞<x<∞)cos x = 1-x2/2!+x4/4!-...(-1)k*x2k/(2k)!+... (-∞<x<∞)arcsin x = x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... (|x|<1)arccos x = π - ( x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... ) (|x|<1)arctan x = x - x^3/3 + x^5/5 - ... (x≤1)ArcSin(x) 函数功能：返回一个指定数的反正弦值，以弧度表示，返回类型为Double。
excel的反三角函数
Excel中的反三角函数
Excel是一款功能强大的表格处理工具，它内置了众多的数学函数，其中反三角函数是其中一种强大的函数，它可以用于计算三角函数的反函数，从而轻松解决复杂的三角函数问题。
Excel中的反三角函数，主要包括以下几种：
1、反正弦函数 ASIN：该函数是求正弦函数反函数的。
其格式为：ASIN（数值），返回的结果是以弧度表示的角度值，0°表示 PI/2，90°表示 PI/4，180°表示 0，270°表示-PI/4，360°表示- PI/2。
2、反余弦函数ACOS：该函数是求余弦函数反函数的。
其格式为：ACOS(数值)，返回的结果是以弧度表示的角度值，其中0°表示PI，90°表示 PI/2，180°表示 0，270°表示- PI/2，360°表示- PI。
3、反正切函数ATAN：该函数是求正切函数反函数的。
其格式为：ATAN(数值)，返回的结果是以弧度表示的角度值，其中0°表示PI/2，45°表示 PI/4，90°表示 0，135°表示- PI/4，180°表示- PI/2。
以上就是Excel中的反三角函数的具体内容，它们可以帮助我们轻松解决复杂的三角函数问题。
- 1 -。
三角函数公式大全表格高中
三角函数是高中数学中非常重要的内容，这里为大家提供了三角函数的公式大全表格，方便大家参考。
一、正弦函数sin(x)
正弦函数的定义：对于任意角x，它对应的正弦值为x所对的直角边与斜边的比值。
正弦函数的公式为：sin(x) = y/r
二、余弦函数cos(x)
余弦函数的定义：对于任意角x，它对应的余弦值为x所对的邻边与斜边的比值。
余弦函数的公式为：cos(x) = x/r
三、正切函数tan(x)
正切函数的定义：对于任意角x，它对应的正切值为x所对的直角边与邻边的比值。
正切函数的公式为：tan(x) = y/x
四、反正弦函数arcsin(x)
反正弦函数的定义：如果y/r = x，则arcsin(x) = y。
五、反余弦函数arccos(x)
反余弦函数的定义：如果x/r = y，则arccos(x) = y。
六、反正切函数arctan(x)
反正切函数的定义：如果y/x = x，则arctan(x) = y。
三角函数的公式大全表格就介绍到这里，希望对大家学习三角函数有所帮助。
反三角函数求导公式表反三角函数求导公式表是高等数学中重要的一个概念。
它是求解反三角函数导数问题的方便方法。
在此文档中，我们将深入讨论反三角函数求导公式表的意义、公式及其推导方法以及具体例子。
反三角函数的意义在高等数学中，反三角函数是指与三角函数相反的函数，用来描述弧度或角度对应的三角函数值。
反三角函数通常用表示成f(x)=sin^{-1}(x)，f(x)=cos^{-1}(x)，f(x)=tan^{-1}(x)等形式。
它们是基本三角函数sin、cos、tan的反函数，在不同应用场合有着广泛的应用。
反三角函数的求导公式对于反三角函数求导公式，我们有以下公式：1. (sin^{-1}(x))' = \frac{1}{\sqrt{1-x^2}}2. (cos^{-1}(x))' = -\frac{1}{\sqrt{1-x^2}}3. (tan^{-1}(x))' = \frac{1}{1+x^2}推导反三角函数的求导公式以下是反三角函数求导公式的推导方法：1. (sin^{-1}(x))'令 y = sin^{-1}(x)，则x = sin(y)，对x求导得到：\frac{dx}{dy} = cos(y)再对y求导得到：\frac{dy}{dx} = \frac{1}{cos(y)} =\frac{1}{\sqrt{1-x^2}}2. (cos^{-1}(x))'令 y = cos^{-1}(x)，则x = cos(y)，对x求导得到：\frac{dx}{dy} = -sin(y)再对y求导得到：\frac{dy}{dx} = -\frac{1}{sin(y)} = -\frac{1}{\sqrt{1-x^2}}3. (tan^{-1}(x))'令 y = tan^{-1}(x)，则x = tan(y)，对x求导得到：\frac{dx}{dy} = cos^2(y)再对y求导得到：\frac{dy}{dx} = \frac{1}{cos^2(y)} =\frac{1}{1+x^2}反三角函数求导公式的应用反三角函数求导公式可用于解决各种实际问题，例如：求曲线的斜率、解决极限、求导等等。
完整三角函数公式表
以下是完整的三角函数公式表：
1.正弦函数（Sine Function）:
o sin(θ) = 对边 / 斜边
o cos(θ) = 邻边 / 斜边
o tan(θ) = 对边 / 邻边
2.余弦函数（Cosine Function）:
o cos(θ) = 邻边 / 斜边
o sec(θ) = 斜边 / 邻边
3.正切函数（Tangent Function）:
o tan(θ) = 对边 / 邻边
o cot(θ) = 邻边 / 对边
4.反正弦函数（Arcsine Function）:
o arcsin(x) = θ，其中 sin(θ) = x
5.反余弦函数（Arccosine Function）:
o arccos(x) = θ，其中 cos(θ) = x
6.反正切函数（Arctangent Function）:
o arctan(x) = θ，其中 tan(θ) = x
7.余切函数（Cotangent Function）:
o cot(θ) = 邻边 / 对边
o csc(θ) = 斜边 / 对边
这些是常见的三角函数及其反函数。
通过使用这些公式，您可以计算给定角度的三角函数值或根据给定的三角函数值计算相应的角度。
请注意，这里列出的公式适用于弧度制下的角度，如果您需要在度数制下使用，需要进行相应的转换。
常用反三角函数公式表在数学的广袤领域中，反三角函数是一个重要的概念，它们在解决各种数学问题和实际应用中都发挥着关键作用。
接下来，让我们一同深入了解常用的反三角函数公式。
首先，我们来认识一下反三角函数的基本定义。
反三角函数是三角函数的反函数，包括反正弦函数（arcsin）、反余弦函数（arccos）、反正切函数（arctan）等。
反正弦函数 arcsin 的定义域为-1, 1，值域为π/2, π/2。
其主要公式有：sin(arcsin x) ＝ x ，对于－1 ≤ x ≤ 1 。
arcsin(x) ＝ arcsin x ，这体现了反正弦函数的奇偶性。
反余弦函数arccos 的定义域同样为-1, 1，值域为0, π。
相关公式为：cos(arccos x) ＝ x ，－1 ≤ x ≤ 1 。
arccos(x) ＝π arccos x 。
反正切函数 arctan 的定义域为 R，值域为(π/2, π/2)。
常见公式有：tan(arctan x) ＝ x ， x ∈ R 。
arctan(x) ＝ arctan x 。
接下来，让我们看看一些涉及反三角函数的运算公式。
arcsin x ＋ arccos x ＝π/2 ，对于－1 ≤ x ≤ 1 。
这个公式表明了反正弦函数和反余弦函数之间的特殊关系。
当涉及到两个反正弦函数的和与差时，有如下公式：arcsin x ＋ arcsin y ＝arcsin(x√（1 y²) ＋y√（1 x²)），但要注意－1 ≤ x, y ≤ 1 且 x²＋y² ≤ 1 。
arcsin x arcsin y ＝arcsin(x√（1 y²) y√（1 x²)），同样需要满足特定条件。
对于反余弦函数的和与差，也有相应的公式：arccos x ＋ arccos y ＝arccos(xy √（1 x²)√（1 y²)），－1 ≤ x, y ≤ 1 。
