基本变形公式总结

不等式的常用变形公式一、加减法变形公式不等式的加减法变形公式是我们在解不等式问题时经常使用的一种变形方式。

具体表达如下：1. 加法变形公式：对于不等式 a < b，如果两边同时加上相同的数 c，不等式的方向不变，即 a + c < b + c。

例如，对于不等式2x - 3 < 5，我们可以通过加法变形公式将其变形为 2x - 3 + 3 < 5 + 3，得到 2x < 8。

2. 减法变形公式：对于不等式 a < b，如果两边同时减去相同的数 c，不等式的方向不变，即 a - c < b - c。

例如，对于不等式 3x + 4 > 7，我们可以通过减法变形公式将其变形为 3x + 4 - 4 > 7 - 4，得到 3x > 3。

二、乘法变形公式不等式的乘法变形公式是解决不等式问题时常用的另一种变形方式。

具体表达如下：1. 正数乘法变形公式：对于不等式 a < b，如果两边同时乘以一个正数 c（c > 0），不等式的方向不变，即 ac < bc。

例如，对于不等式 2x < 6，我们可以通过正数乘法变形公式将其变形为 2x * 3 < 6 * 3，得到 6x < 18。

2. 负数乘法变形公式：对于不等式 a < b，如果两边同时乘以一个负数 c（c < 0），不等式的方向改变，即 ac > bc。

例如，对于不等式-3x > 9，我们可以通过负数乘法变形公式将其变形为 -3x * (-3) > 9 * (-3)，得到 9x < -27。

三、除法变形公式除法变形公式是不等式中应用较少的一种变形方式，但在特定情况下仍然有一定的应用价值。

具体表达如下：对于不等式 a < b，如果两边同时除以一个正数 c（c > 0），不等式的方向不变，即 a/c < b/c。

例如，对于不等式4x > 12，我们可以通过除法变形公式将其变形为 4x / 4 > 12 / 4，得到 x > 3。

代数式恒等变形法则归纳引言代数式是代数学中的基础概念之一，它用字母和常数通过运算符号相连而成。

在数学中，我们常常需要对代数式进行变形，以达到简化、分解、合并或者推导等目的。

代数式的变形是数学问题解决过程中重要的一环，它不仅能提高计算效率，还能揭示代数运算的本质。

在代数式的变形中，恒等变形法则是重要的基础工具，本文将对代数式的恒等变形法则进行归纳总结。

一、基本变形法则1. 加法法则：•加法结合律：a+(b+c)=(a+b)+c•加法交换律：a+b=b+a•加法零元：a+0=a #### 2. 乘法法则：•乘法结合律：$a \\cdot (b \\cdot c) = (a \\cdot b) \\cdot c$•乘法交换律：$a \\cdot b = b \\cdot a$•乘法零元：$a \\cdot 0 = 0$•乘法单位元：$a \\cdot 1 = a$二、分配律1. 左分配律：对于任意的a,b,c，有$a \\cdot (b + c) = a \\cdot b + a \\cdot c$ #### 2. 右分配律：对于任意的a,b,c，有$(a + b) \\cdot c = a \\cdot c + b \\cdot c$三、幂运算法则1. 幂运算与乘法运算：•幂运算与乘法运算的交换律：$(a \\cdot b)^n = a^n \\cdot b^n$•幂运算与乘法运算的结合律：$(a^n)^m = a^{n \\cdot m}$ #### 2.幂运算的乘方法则：•幂运算的乘方法则1：$a^n \\cdot a^m = a^{n + m}$•幂运算的乘方法则2：$(a^n)^m = a^{n \\cdot m}$•幂运算的乘方法则3：$(a \\cdot b)^n = a^n \\cdot b^n$四、指数运算法则1. 指数运算与乘法运算：•指数运算与乘法运算的交换律：$(a \\cdot b)^n = a^n \\cdot b^n$•指数运算与乘法运算的结合律：$(a^n)^m = a^{n \\cdot m}$ #### 2.指数运算的指数法则：•指数运算的指数法则1：$a^n^m = a^{n \\cdot m}$•指数运算的指数法则2：$(a^n)^m = a^{n \\cdot m}$•指数运算的指数法则3：$(a^m)^n = a^{m \\cdot n}$五、因式分解法则1. 公因式提取法则：•公因式提取法则1：ax+ay=a(x+y)•公因式提取法则2：$a \\cdot b + a \\cdot c = a \\cdot (b + c)$ ####2. 公式分解法则：•差的平方公式：a2−b2=(a+b)(a−b)•平方差公式：a2−b2=(a−b)(a+b)•完全平方公式：a2+2ab+b2=(a+b)2•完全平方公式：a2−2ab+b2=(a−b)2六、合并同类项法则合并同类项法则：将含有相同字母指数的项合并为一个项•合并同类项法则1：ax+bx=(a+b)x•合并同类项法则2：ax2+bx2=(a+b)x2•合并同类项法则3：ax n+bx n=(a+b)x n结论恒等变形法则在代数式的变形中起着重要的作用。

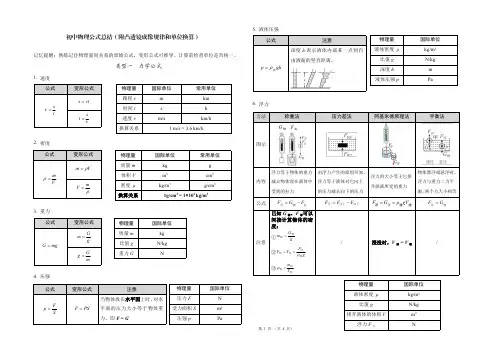
记忆提醒：熟练记住物理量间关系的原始公式，变形公式可推导。

计算前检查单位是否统一
初中物理公式总结（附凸透镜成像规律和单位换算）。

类型一力学公式
2.密度
3.重力
4.压强
5.液体压强
6.浮力
浮力等于物体的重力
减去物体浸在液体中
由浮力产生的原因可知，
浮力的大小等于它排
开排液所受的重力
物体漂浮或悬浮时，
浮力与重力二力平
衡，两个力大小相等
液
gV
ρ
G=
=
排
7.机械功
8.机械功率
9.杠杆的平衡条件
10.有用功总功机械效率（1）斜面
（2）※竖直滑轮组
（3）水平滑轮组
图示
表示物体沿这个力的方向上移动的距离。

表示与动滑轮相连的绳子段数；表示物体上升的高度；端移动的距离；
表示物体的重力；G 动轮的重力；F 拉表示绳端的拉力。

注意：
n
表示与动滑轮相连的绳子段数；s 表示物体移动的距离；s 表示
类型二热学公式
11.比热容
12.热值
（1）热值与质量
（2）热值与体积
13.热效率：被利用起来的能量与全部放出的能量之比
类型三电学公式
16.电功电热
I =I 1=I 2I =I 1+I 2U =U 1=U 2
111+=
17.电功率
补充必背
凸透镜成像规律
附：单位换算
=1×103kg
1g =1×10-31h =3600s
1cm =1×10-2m。

公式大全—公式变形—精华引言在初中政治研究中，公式变形是一个重要的知识点。

通过掌握公式的变形规律，可以帮助同学们更好地理解和应用政治知识。

本文将提供人教版初中政治的公式大全，并对其中一些常见的公式变形进行精华总结。

公式大全以下是人教版初中政治的公式大全：1. 人数变化公式：N1 / N2 = A1 / A2 (N代表人数，A代表面积)2. 平均值公式：A = (a₁ + a₂ + ... + an) / n (A代表平均值，a₁到an代表待求平均值的数)3. 百分数公式：百分数 = (部分 / 全部) × 100%4. 增长率公式：增长率 = (现在值 - 原始值) / 原始值 × 100%5. 负增长率公式：负增长率 = (原始值 - 现在值) / 原始值 × 100%6. 总和公式：总和 = 项数 ×平均值公式变形精华在初中政治中，公式变形可以帮助我们灵活运用公式解决各类问题。

下面是一些公式变形的精华总结：1. 人数变化公式变形：N1 = N2 × (A1 / A2)人数变化公式变形：N1 = N2 × (A1 / A2)2. 平均值公式变形：(a₁ + a₂ + ... + an) = A × n平均值公式变形：(a₁ + a₂ + ... + an) = A × n3. 百分数公式变形：部分 = 百分数 ×全部 / 100%百分数公式变形：部分 = 百分数 ×全部 / 100%4. 增长率公式变形：现在值 = (1 + 增长率 / 100%) ×原始值增长率公式变形：现在值 = (1 + 增长率 / 100%) ×原始值5. 负增长率公式变形：现在值 = (1 - 负增长率 / 100%) ×原始值负增长率公式变形：现在值 = (1 - 负增长率 / 100%) ×原始值6. 总和公式变形：平均值 = 总和 / 项数总和公式变形：平均值= 总和 / 项数这些公式变形的精华总结可以帮助同学们更便捷地解决各种数值计算问题。

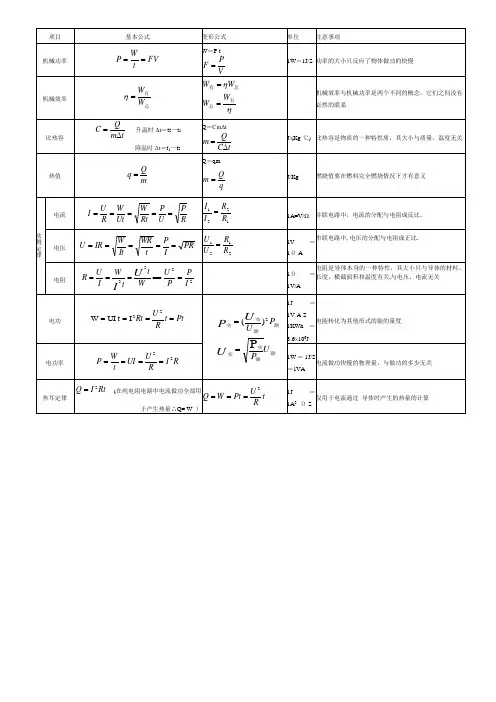
初中物理公式汇总速度公式：v =s t物理量单位公式变形：求路程——s =vt求时间——t=s/v物理量单位v ——速度m/s km/h s ——路程m km t ——时间s h单位换算：1 m=10dm=102cm=103mm 1h=60min=3600 s ；1min=60s 1 m/s =3.6 km/h重力与质量的关系：G = mgG ——重力N m ——质量kgg ——重力与质量的比值g=9.8N/kg ；粗略计算时取g=10N/kg 。

密度公式：m ρ=V物理量单位ρ——密度kg/m 3g/cm 3m ——质量kg g V ——体积m 3cm 3物理量单位单位换算：1kg=103 g1g/cm 3=1×103kg/m 31m 3=106cm 31L=1dm 3=10-3m 31mL=1cm 3=10-6m 3浮力公式：F 浮=G物–F示F 浮=G 排=m 排gF 浮——浮力N G 物——物体的重力NF 示——物体浸没液体中时弹簧测力计的读数N物理量单位F 浮=ρ液gV 排F 浮——浮力N ρ——密度kg/m 3V 排——物体排开的液体的体积m 3g=9.8N/kg ，粗略计算时取g=10N/kgG 排——物体排开的液体受到的重力Nm 排——物体排开的液体的质量kgF 浮=G物物理量单位F 提示：或悬浮时浮——浮力N[当物体处于漂浮]G 物——物体的重力N压强公式：物理量单位面积单位换算：P=F/S （固体）p ——压强Pa 或N/m 2注意：S 是受力面积，指 1 cm 2=10--4m 2F ——压力N 有受到压力作用的那部 1 mm 2=10--6m 2S ——受力面积m 2分面积液体压强公式：物理量单位p ——压强Pa 或N/m 2p =ρgh ρ——液体密度kg/m 3注意：深度是指液体内部某一点h ——深度m 到自由液面的竖直距离；杠杆的平衡条件：g=9.8N/kg 物理量F ——动力，粗略计算时取单位N g=10N/kg1F 提示：应用杠杆平衡条件解题时，L 1L 1=F 2L 2L 1——动力臂m 1、L 2的FF 2——阻力N单位只要相同即可，无须国际单位；1L 2LL 2——阻力臂m 或写成：F21滑轮组：物理量单位1F ——动力NF =n G总G 总——总重N （当不计滑轮重、绳重及摩擦时，G 总=G 物）（G 总= G 物+G 动）n ——承担物重、与动滑轮相连的绳子段数物理量单位s =nhs ——动力通过的距离m h ——重物被提升的高度m n ——承担物重的绳子段数对于定滑轮而言：∵n=1∴F =G物s = h对于动滑轮而言：∵n=2∴F =12（G物+G动）s =2 h功的公式：W=F s物理量单位W——动力做的功JF——动力Ns——物体在力的方向上通过的距离m提示：克服重力做功或重力做功（即竖直方向）：W=G h功率公式：WP=t物理量单位P——功率WW——总功Jt——时间s单位换算：1W=1J/s1马力=735W1kW=103W公式变形：W=Pt 机械效率：η=W有用物理量单位η——机械效率W有——有用功J W总×100%W总——总功J热量计算公式：提示：机械效率η没有单位，用百分率表示，且总小于1 W有=G h [对于所有简单机械]W总=F s[对于杠杆、滑轮和斜面]W总=P t[对于起重机和抽水机等电动机]物体吸热或放热物理量单位Q =c m△t Q——吸收或放出的热量Jc——比热容J/(kg·℃)m——质量kg△t——温度差℃提示：当物体吸热后，终温t高于初温t，△t=t-t当物体放热后，终温t低于初温t，△t =t-tC水=4.2×103 J/(kg·℃)物理量单位电流定义式：I——电流A提示：电流等于1s内通过导体横截面的电荷量。

常用的14个恒等变形公式作为数学中的基本工具之一，恒等变形在各种数学问题中都扮演着关键的角色。

本文将介绍14个常用的恒等变形公式，这些公式的掌握对于提高数学学习成绩和应对高考、数学竞赛等考试都有着重要的作用。

一、基本恒等变形1.加减同项式的恒等变形∵a+b+c+d+e+f=0∴a+b+c=-(d+e+f)2.去分母的恒等变形∵a/c=b/d∴ad=bc3.两边平方式的恒等变形∵a=c·d·e·f∴e·f=a/(c·d)4.拆分因式的恒等变形∵a²-b²=(a+b)(a-b)∴(a+b)(a-b)=a²-b²二、平方恒等变形5.一次二次(a+b)²=a²+2ab+b²(a-b)²=a²-2ab+b²6.和差二次cos(a+b)=cosacosb-sinasinbcos(a-b)=cosacosb+sinasinb7.平方差a²-b²=(a+b)(a-b)8.完全平方a²+2ab+b²=(a+b)²a²-2ab+b²=(a-b)²三、三角函数恒等变形9.正弦cos²(a)+sin²(a)=1sin(a+b)=sinacosb+cosasinbsin(a-b)=sinacosb-cosasinb10.余弦sin²(a)+cos²(a)=1cos(a+b)=cosacosb-sinasinbcos(a-b)=cosacosb+sinasinb11.正切tan(a+b)=(tana+tanb)/(1-tanatanb) tan(a-b)=(tana-tanb)/(1+tanatanb) 12.双角sin2a=2sina·cosacos2a=cos²(a)-sin²(a)=2cos²(a)-1=1-2sin²(a)13.半角sin(a/2)=√[(1-cos(a))/2]cos(a/2)=√[(1+cos(a))/2]tan(a/2)=sin(a)/(1+cos(a))14.万能公式sin(a±b)=(sinacosb±cosasinb)cos(a±b)=(cosacosb∓sinasinb)可以通过这些公式的使用，将复杂的数学运算转换成简单而直观的形式，使数学问题的解决变得更加容易和高效。

指数与对数恒等变形公式摘要：一、引言二、指数恒等变形公式1.指数的运算性质2.常见指数恒等变形公式三、对数恒等变形公式1.对数的运算性质2.常见对数恒等变形公式四、总结正文：一、引言在数学中，指数和对数是两个非常基础且重要的概念。

它们广泛应用于各种数学问题，包括代数、微积分、概率等。

对于许多实际问题，我们需要对指数和对数进行一些变形操作，以得到更简洁或更易于处理的表达式。

这就需要我们掌握一些基本的恒等变形公式。

二、指数恒等变形公式1.指数的运算性质指数运算的基本性质包括：a^(m * n) = (a^m)^n 和a^(m/n) =(a^m)^(1/n)。

这些性质可以帮助我们在进行指数运算时简化计算。

2.常见指数恒等变形公式一些常见的指数恒等变形公式包括：(a^m)^n = a^(m * n)a^(m/n) = (a^m)^(1/n)(ab)^n = a^n * b^na^0 = 1 (a ≠ 0)三、对数恒等变形公式1.对数的运算性质对数运算的基本性质包括：log_a(mn) = log_a(m) + log_a(n) 和log_a(m^n) = n * log_a(m)。

这些性质可以帮助我们在进行对数运算时简化计算。

2.常见对数恒等变形公式一些常见的对数恒等变形公式包括：log_a(mn) = log_a(m) + log_a(n)log_a(m^n) = n * log_a(m)log_a(1) = 0 (a > 0, a ≠ 1)log_a(a) = 1 (a > 0, a ≠ 1)四、总结指数和对数恒等变形公式是数学中非常基础且重要的概念。

掌握这些公式可以帮助我们简化复杂的数学运算，更容易地解决问题。

常用公式变形大全1. 一次函数的标准方程：y = kx + b变形为：x=(y-b)/k，k≠02. 二次函数的标准方程：y = ax² + bx + c变形为：x = (-b ± √(b²-4ac))/(2a)，a ≠ 03.圆的一般方程：(x-h)²+(y-k)²=r²变形为：x² + y² - 2hx - 2ky + h² + k² - r² = 04.三角函数对称性：sin(-θ) = -sin(θ)cos(-θ) = cos(θ)tan(-θ) = -tan(θ)cot(-θ) = -cot(θ)5.三角函数的和差化简公式：sin(α ± β) = sinαcosβ ± cosαsinβcos(α ± β) = cosαcosβ ∓ sinαsinβtan(α ± β) = (tanα ± tanβ)/(1 ∓ tanαtanβ)6.三角函数的倍角化简公式：sin(2α) = 2sinαcosαcos(2α) = cos²α - sin²α = 2cos²α - 1 = 1 - 2sin²αtan(2α) = (2tanα)/(1 - tan²α)7.幂函数的指数运算法则：a^m*a^n=a^(m+n)(a^m)^n=a^(m*n)(ab)^m = a^m * b^m(a/b)^m=(a^m)/(b^m)8.对数函数运算法则：log(ab) = loga + logblog(a/b) = loga - logblog₁₀a^n = nlog₁₀aloga(b) = logc(b)/logc(a)，其中c为底数9.指数函数与对数函数的反函数关系：loga(a^x) = xa^(loga(x)) = x，其中a > 0，a ≠ 1，x > 010.等比数列的前n项和公式：Sₙ=a₁(1-q^n)/(1-q)，其中a₁为首项，q为公比11.二项式展开公式（二项式系数）：(a+b)^n=C(n,0)a^n+C(n,1)a^(n-1)b+C(n,2)a^(n-2)b²+...+C(n,k)a^(n-k)b^k+...+C(n,n)b^n其中C(n,k)为组合数，表示从n个元素中选取k个元素的组合数，公式为C(n,k)=n!/(k!(n-k)!)这里列举的只是一些常见的公式变形，实际上还有很多公式可以进行变形以适用于不同的问题。

初中所有的物理公式以及变形公式一、运动学公式1.速度公式[ v = ] 其中，v表示速度，s表示位移，t表示时间。

2.加速度公式[ a = ] 其中，a表示加速度，Δv表示速度改变量，t表示时间。

3.加速度的变形公式[ v = u + at ] 其中，v表示末速度，u表示初速度，a表示加速度，t表示时间。

4.位移公式（匀变速直线运动）[ s = (u + v)t ] 其中，s表示位移，u表示初速度，v表示末速度，t表示时间。

5.匀变速直线运动的位移公式[ s = ut + at^2 ] 其中，s表示位移，u表示初速度，a表示加速度，t表示时间。

6.力的公式[ F = ma ] 其中，F表示力，m表示质量，a表示加速度。

二、功与能量公式1.功的定义[ W = Fs ] 其中，W表示功，F表示力，s表示位移，θ表示力和位移之间的夹角。

2.重力势能的计算公式[ E_p = mgh ] 其中，E_p表示重力势能，m表示物体的质量，g表示重力加速度，h 表示物体的高度。

3.动能公式[ E_k = mv^2 ] 其中，E_k表示动能，m表示物体的质量，v表示物体的速度。

4.机械能守恒定律对于一个只受重力的物体： [ E_p + E_k = ]三、热学公式1.热传导公式[ Q = k A ] 其中，Q表示传热量，k表示导热系数，A表示传热面积，ΔT表示温度差，d表示热传导距离。

2.内能变化公式[ U = Q + W ] 其中，ΔU表示内能变化，Q表示吸收的热量，W表示做功。

3.理想气体状态方程[ pV=nRT ] 其中，p表示气体的压强，V表示气体的体积，n表示气体的物质的量，R 表示气体常数，T表示气体的温度。

四、光学公式1.光的传播速度公式[ v = c ] 其中，v表示光的速度，c表示真空中的光速。

2.薄透镜成像公式[ = + ] 其中，f表示透镜的焦距，d_o表示物距，d_i表示像距。

3.放大倍数公式[ = = - ] 其中，β表示放大倍数，H_i表示像的高度，H_o表示物的高度，d_i表示像距，d_o表示物距。