Fisher线性判别分析实验(模式识别与人工智能原理实验1)

一、实验意义及目的掌握Fisher分类原理，能够利用Matlab编程实现Fisher线性分类器设计，熟悉基于Matlab算法处理函数，并能够利用算法解决简单问题。

二、算法原理Fisher准则基本原理：找到一个最合适的投影周，使两类样本在该轴上投影之间的距离尽可能远，而每一类样本的投影尽可能紧凑，从而使分类效果为最佳。

内容：（1）尝试编写matlab程序，用Fisher线性判别方法对三维数据求最优方向w的通用函数（2）对下面表1-1样本数据中的类别w1和w2计算最优方向w（3）画出最优方向w 的直线，并标记出投影后的点在直线上的位置（4）选择决策边界，实现新样本xx1=（-0.7，0.58，0.089）,xx2=（0.047，-0.4，1.04）的分类三、实验内容（1）尝试编写matlab程序，用Fisher线性判别方法对三维数据求最优方向w的通用函数程序清单：clcclear all%10*3样本数据w1=[-0.4,0.58,0.089;-0.31,0.27,-0.04;-0.38,0.055,-0.035;-0.15,0.53,0.011;-0.35,.47,0.034;0.17,0.69,0.1;-0.011,0.55,-0.18;-0.27,0.61,0.12;-0.065,0.49,0.0012;-0.12,0.054,-0.063];w2=[0.83,1.6,-0.014;1.1,1.6,0.48;-0.44,-0.41,0.32;0.047,-0.45,1.4;0.28,0.35,3.1;-0.39,-0.48,0.11;0.34,-0.079,0.14;-0.3,-0.22,2.2;1.1,1.2,-0.46;0.18,-0.11,-0.49];W1=w1';%转置下方便后面求s1W2=w2';m1=mean(w1);%对w1每一列取平均值结果为1*3矩阵m2=mean(w2);%对w1每一列取平均值结果为1*3矩阵S1=zeros(3);%有三个特征所以大小为3S2=zeros(3);for i=1:10%1到样本数量ns1=(W1(:,i)-m1)*(W1(:,i)-m1)';s2=(W2(:,i)-m2)*(W2(:,i)-m2)';S1=S1+s1;S2=S2+s2;endsw=S1+S2;w_new=transpose(inv(sw)*(m1'-m2'));%这里m1m2是行要转置下3*3 X 3*1 =3*1 这里提前转置了下跟老师ppt解法公式其实一样%绘制拟合结果数据画图用y1=w_new*W1y2=w_new*W2;m1_new=w_new*m1';%求各样本均值也就是上面y1的均值m2_new=w_new*m2';w0=(m1_new+m2_new)/2%取阈值%分类判断x=[-0.7 0.0470.58 -0.40.089 1.04 ];m=0; n=0;result1=[]; result2=[];for i=1:2%对待观测数据进行投影计算y(i)=w_new*x(:,i);if y(i)>w0m=m+1;result1(:,m)=x(:,i);elsen=n+1;result2(:,n)=x(:,i);endend%结果显示display('属于第一类的点')result1display('属于第二类的点')result2figure(1)scatter3(w1(1,:),w1(2,:),w1(3,:),'+r'),hold onscatter3(w2(1,:),w2(2,:),w2(3,:),'sg'),hold onscatter3(result1(1,:),result1(2,:),result1(3,:),'k'),hold onscatter3(result2(1,:),result2(2,:),result2(3,:),'bd')title('样本点及实验点的空间分布图')legend('样本点w1','样本点w2','属于第一类的实验点','属于第二类的实验点')figure(2)title('样本拟合结果')scatter3(y1*w_new(1),y1*w_new(2),y1*w_new(3),'b'),hold onscatter3(y2*w_new(1),y2*w_new(2),y2*w_new(3),'sr')（2）对下面表1-1样本数据中的类别w1和w2计算最优方向w（3）画出最优方向w 的直线，并标记出投影后的点在直线上的位置最优方向w 的直线投影后的位置（4）选择决策边界，实现新样本xx1=（-0.7，0.58，0.089）,xx2=（0.047，-0.4，1.04）的分类决策边界取法：分类结果：四、实验感想通过这次实验，我学会了fisher线性判别相关的分类方法，对数据分类有了初步的认识，尽管在过程中有不少中间量不会算，通过查阅网络知识以及模式识别专业课ppt等课件帮助，我最终完成了实验，为今后继续深入学习打下良好基础。

实验一、二维随机数的产生1、实验目的（1） 学习采用Matlab 程序产生正态分布的二维随机数 （2） 掌握估计类均值向量和协方差矩阵的方法（3） 掌握类间离散度矩阵、类内离散度矩阵的计算方法（4） 熟悉matlab 中运用mvnrnd 函数产生二维随机数等matlab 语言2、实验原理多元正态分布概率密度函数：11()()2/21/21()(2)||T X X d p X eμμπ---∑-=∑其中：μ是d 维均值向量：Td E X μμμμ=={}[,,...,]12Σ是d ×d 维协方差矩阵：TE X X μμ∑=--[()()]（1）估计类均值向量和协方差矩阵的估计 各类均值向量1ii X im X N ω∈=∑ 各类协方差矩阵1()()iTi iiX iX X N ωμμ∈∑=--∑（2）类间离散度矩阵、类内离散度矩阵的计算类内离散度矩阵：()()iTi iiX S X m X m ω∈=--∑， i=1,2总的类内离散度矩阵：12W S S S =+类间离散度矩阵：1212()()Tb S m m m m =--3、实验内容及要求产生两类均值向量、协方差矩阵如下的样本数据，每类样本各50个。

1[2,2]μ=--，11001⎡⎤∑=⎢⎥⎣⎦，2[2,2]μ=，21004⎡⎤∑=⎢⎥⎣⎦ （1）画出样本的分布图；（2） 编写程序，估计类均值向量和协方差矩阵；（3） 编写程序，计算类间离散度矩阵、类内离散度矩阵； （4）每类样本数增加到500个，重复（1）-（3）4、实验结果(1)、样本的分布图(2)、类均值向量、类协方差矩阵根据matlab 程序得出的类均值向量为：N=50 : m1=[-1.7160 -2.0374] m2=[2.1485 1.7678] N=500: m1=[-2.0379 -2.0352] m2=[2.0428 2.1270] 根据matlab 程序得出的类协方差矩阵为：N=50: ]0628.11354.01354.06428.1[1=∑ ∑--2]5687.40624.00624.08800.0[N=500：∑--1]0344.10162.00162.09187.0[∑2]9038.30211.00211.09939.0[(3)、类间离散度矩阵、类内离散度矩阵根据matlab 程序得出的类间离散度矩阵为：N=50： ]4828.147068.147068.149343.14[=bS N=500： ]3233.179843.169843.166519.16[b =S根据matlab 程序得出的类内离散度矩阵为：N=50：]0703.533088.73088.71052.78[1=S ]7397.2253966.13966.18975.42[2--=S ]8100.2789123.59123.50026.121[=W SN=500: ]5964.5167490.87490.86203.458[1--=S ]8.19438420.78420.70178.496[2=S ]4.24609071.09071.06381.954[--=W S5、结论由mvnrnd 函数产生的结果是一个N*D 的一个矩阵，在本实验中D 是2，N 是50和500.根据实验数据可以看出，当样本容量变多的时候，两个变量的总体误差变小，观测变量各个取值之间的差异程度减小。

模式识别FISHER线性判别实验
人工知能领域中的模式识别是计算机实现人类识别物体的能力的一种
技术。

它的主要目的是根据给定模式的样本及其特征，自动识别出新的样
本的特征并做出判断。

其中最著名的技术之一就是FISHER线性判别法。

FISHER线性判别法基于正态分布理论，通过计算样本的统计特征来
分类，它是一种基于参数的最优分类算法。

算法的基本思想是通过计算两
个类别的最大类间差异度，以及最小类内差异度，来有效地分类样本。

具
体而言，FISHER线性判别法即求出一个线性超平面，使这个超平面把样
本区分开来，使样本离类中心向量之间的距离最大，同时使类中心向量之
间的距离最小。

FISHER线性判别法的具体实现过程如下：
1.准备好建立模型所需要的所有数据:训练样本集，其样本特征与对
应的类标号。

2.确定每个类的类中心向量c_1，c_2，…，c_m，其中m为类的数目。

3.根据类中心向量求出类间离散度矩阵S_b和类内离散度矩阵S_w。

4.将S_b与S_w相除，得到S_b/S_w，从而求出矩阵的最大特征值
λ_1及最小特征值λ_n。

5.将最大特征值λ_1进行特征值分解，求出其特征向量w，求出判
定函数：
f(x)=w·x+w_0。

6.根据判定函数，将样本进行分类。

Fisher 线性判别分类器成员姓名： 学号：莫文敏 201111921217 赵越 201111921229 顾瑞煌 201111921104一、实验目的1.实现基于FISHER 分类的算法程序；2.能够根据自己的设计加深对FISHER 分类的认识；3.掌握FISHER 分类的原理、特点。

二、实验设备1.手提电脑2.MATLAB三、FISHER 算法原理线性判别函数的一般形式可表示成0)(w X W X g T +=其中⎪⎪⎪⎭⎫ ⎝⎛=d x x X 1 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=d w w w W 21但是，在应用统计方法解决模式识别的问题时，经常会遇到“维数风暴”的问题，因此压缩特征空间的维数在此时十分重要，FISHER 方法实际上是涉及维数压缩的问题。

把多为特征空间的点投影到一条直线上，就能把特征空间压缩成一维，这在数学上是很容易做到的。

但是在高维空间里很容易一分开的样品，把它们投射到任意一条直线上，有可能不同类别的样品就混在一起，无法区分了，如图5-16（a ）所示，投影1x 或2x 轴无法区分。

若把直线绕原点转动一下，就有可能找到一个方向，样品投射到这个方向的直线上，各类样品就能很好地分开，如图5-16（b ）所示。

因此直线方向的选择是很重要的。

一般来说总能找到一个最好的方向，使样品投射到这个方向的直线上很容易分开。

如何找到这个最好的直线方向以及如何实现向最好方向投影的变换，这正是FISHER 算法要解决的基本问题，这个投影变换正是我们寻求的解向量*W 。

样品训练集以及待测样品的特征总数目为n ，为找到最佳投影方向，需要计算出各类样品的均值、样品类内离散度矩阵i S 和总类间矩阵w S 、样品类间离散度矩阵b S ，根据FISHER 准则找到最佳投影向量，将训练集内所有样品进行投影，投影到一维Y 空间，由于Y 空间是一维的，则需要求出Y 空间的划分边界点，找到边界点后，就可以对待测样品进行一维Y 空间的投影，判断它的投影点与分界点的关系将其归类。

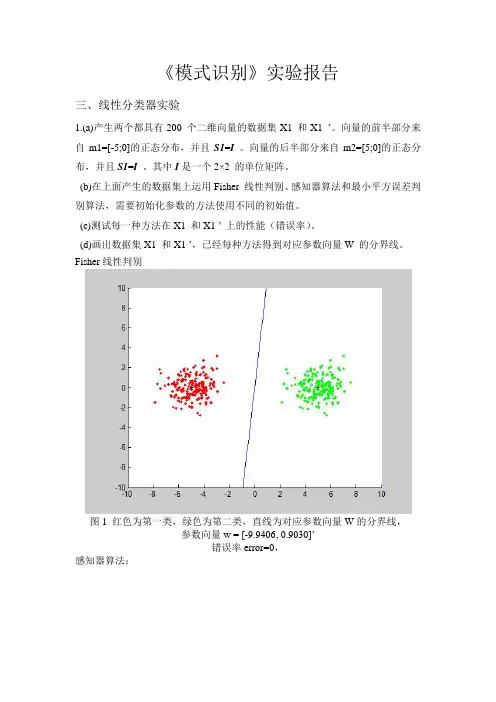
《模式识别》实验报告三、线性分类器实验1.(a)产生两个都具有200 个二维向量的数据集X1 和X1 ’。

向量的前半部分来自m1=[-5;0]的正态分布，并且S1=I 。

向量的后半部分来自m2=[5;0]的正态分布，并且S1=I。

其中I是一个2×2 的单位矩阵。

(b)在上面产生的数据集上运用Fisher 线性判别、感知器算法和最小平方误差判别算法，需要初始化参数的方法使用不同的初始值。

(c)测试每一种方法在X1 和X1 ’ 上的性能（错误率）。

(d)画出数据集X1 和X1 ’，已经每种方法得到对应参数向量W 的分界线。

Fisher线性判别图1 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数向量w = [-9.9406, 0.9030]’错误率error=0，感知器算法：图2 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[0.1;0.1]；迭代次数iter=2参数向量w = [-4.8925, 0.0920]’错误率error=0图3 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[1; 1]；迭代次数iter=2参数向量w = [-3.9925, 0.9920]’错误率error=0图4 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[10; 10]；迭代次数iter=122参数向量w = [-5.6569, 7.8096]’错误率error=0图5 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[50; 50]；迭代次数iter=600参数向量w = [-27.0945, 37.4194]’错误率error=0图6 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[50; 100]；迭代次数iter=1190参数向量w = [-54.0048, 74.5875]’错误率error=0最小平方误差判别算法：图7 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[0.1; 0.1]；参数向量w = [-0.1908, -0.0001]’错误率error=0图8 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[0.5; 0.5]；参数向量w = [-0.1924, 0.1492]’错误率error=0图9 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[1; 0.5]；参数向量w = [-0.1914, 0.0564]’错误率error=0图10 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[1; 1]；参数向量w = [-0.1943, 0.3359]’错误率error= 0.00502.重复1.中的实验内容，数据集为X2 和X2 ’。

Fisher 线性判别原理原始数据：111212122212p p n n np n px x x x x x X x x x ⨯⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦ 寻找关于X 的线性组合，使得Y Xa =，其中121p p a a a a ⨯⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦为p 维列向量。

使得111212111212222211221p p p p n n p np n n a x a x a x y a x a x a x y Y Xa a x a x a x y ⨯+++⎡⎤⎡⎤⎢⎥⎢⎥+++⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥+++⎢⎥⎣⎦⎣⎦对于Y 中的每个分量来说，离差平方和为：22211()nniii i y y yny ==-=-∑∑令11111n n n H I n⨯⨯'=-，则有：[][][][]121212121212100101011(111)0011111111111111n n n n n n y y Y HY y y y n y n n n y y y y y n nn y nn n y y y y y y y y y ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥'=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎡⎤---⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥---⎢⎥⎣⎦⎡⎤⎢⎥⎢⎥=---⎢⎥⎢⎣⎦22211()n nii i i y ny y y ==⎥=-=-∑∑而21()()nii y y Y HY Xa HXa a X HXa a Ta ='''''-====∑若n 个原始数据X 来自J 个不同的组，每个组有j n 个数据，12++J n n n n +=。

将X ，Y 重新标记为：111(1)(1)(1)11121(1)(1)(1)21222(1)(1)(1)12()()()11121()()()21222()()()12J J J pp n n n p J J J p J J J p J J J n n n p n p x x x x x x x x x X x x x x x x x x x ⨯⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦1(1)1(1)2(1)()1()2()J n J J J n y y y Y y y y ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦，Y Xa = 其中(j)表示其属于第j 组的数据。

模式识别Fisher线性判别实验实验三 Fisher线性判别实验姓名:徐维坚学号:2220103484 日期:2012/7/7 一、实验目的:1)加深对Fisher线性判别的基本思想的认识和理解。

2)编写实现Fisher线性判别准则函数的程序。

二、实验原理:1.基本原理:一般情况下，我们总可以找到某个方向，使得这个方向的直线上，样本的投影能分开的最好，而Fisher法所要解决的基本问题就是找到这条最好的、最易于分类的投影线。

X先从d维空间到一维空间的一维数学变换方法。

假设有一集合包含N个d维样本，其中个属于类的样本记为子集，个属于类的样本记为。

x,x,...,x,N,XNX212N11122若对的分量做线性组合可得标量 xN T， n,1,2,...,Ny,wxinn这样便得到N个一维样本组成的集合，并可分为两个子集和。

的绝对值是无关ywYYn12紧要的，它仅使乘上一个比例因子，重要的是选择的方向，从而转化为寻找最好的投ywn*w影方向，是样本分开。

2.基本方法:先定义几个基本参量:m(1)各类样本均值向量 i1m,x,i,1,2 ,iNx,XiSS(2)样本类内离散度矩阵和总类内离散度矩阵 i,TS,(x,m)(x,m),i,1,2 i,iix,XiS,S，S ,12S(3)样本类间离散度矩阵 bTS,(m,m)(m,m) 1212b(m,m)我们希望投影后，在低维空间里个样本尽可能的分开些，即希望两类均值越大越12Authord: Vivid Xu;好，同时希望各类样本内部尽量密集，即越小越好。

因此，我们定义Fisher 准则函数为 Si2,(mm)12 ,J(w)F，SS12但不显含，因此必须设法将变成的显函数。

wwJ(w)J(w)FF由式子111TTTm,y,wx,w(x),wm ,,,iiNNN,,,yYxXxXiiiiii2TT2TTT (m,m),(wm,wm),w(m,m)(m,m)w,wSw12121212bTTTTT22S,(y,m),(wx,wm),w(x,m)(x,m)w,wSw ,,iiiiii,,yYyYii从而得到TwSwbJw， (),FTwSw,*w采用Lagrange乘子法求解它的极大值TT L(w,,),wSw,,(wSw,c),b**对其求偏导，得，即 Sw,,Sw,0b,** Sw,,Swb,从而我们很容易得到*,1*,1T* ,w,S(Sw),S(m,m)R,其中R,(m,m)w,,b1212R*1,w,S(m,m) ,12,R/,忽略比例因子，得*1, w,S(m,m),12这就是我们Fisher准则函数J(w)取极大值时的解。

实验一、Fisher线性判别算法一、实验目的1、掌握Fisher线性判别算法基本编程。

二、实验内容1、Fisher线性判别算法程序设计用现有的训练样本，实现Fisher线性判别，画出效果图。

取不同的测试样本，观察结果。

三、实验原理1、算法原理步骤四、实验预习1、学习Matlab编程的有关知识。

2、提前预习Fisher线性判别算法。

五、实验报告1、总结出实验的详细步骤。

2、写出调试正确的程序及运行结果。

六、参考程序：参考程序1s1=[1 0.5;0.5 1], s2=[1 -0.5;-0.5 1]u1=[2 0]', u2=[2,2]'s=s1+s2ss=inv(s);w=ss*(u1-u2);y0=w'*(u1+u2)/2x=[1 2]'y=w'*x2A=[9 8 7;7 6 6;10 7 8;8 4 5;9 9 3;8 6 7;7 5 6];B=[8 4 4;3 6 6;6 3 3;6 4 5;8 2 2];s=size(A,1);t=size(B,1);u1=mean(A);u2=mean(B);DA=A-repmat(u1,s,1);DB=B-repmat(u2,t,1);S=DA'*DA+DB'*DB;w=inv(S)*(u1-u2) ';y0=w'*(u1+u2) '/2%编程产生投影后的数据，第一类样本向w上投影后的数据放y1中，第二类样本向w上投影后的%数据放y2中figure(2)for i=1:10plot3(y1(i)*w(1),y1(i)*w(2),y1(i)*w(3),'rx')hold onplot3(y2(i)*w(1),y2(i)*w(2),y2(i)*w(3),'bp')hold off。

F i s h e r线性判别分析实验(模式识别与人工智能原理实验1)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN实验1 Fisher 线性判别分析实验一、摘要Fisher 线性判别分析的基本思想：通过寻找一个投影方向（线性变换，线性组合），将高维问题降低到一维问题来解决，并且要求变换后的一维数据具有如下性质：同类样本尽可能聚集在一起，不同类的样本尽可能地远。

Fisher 线性判别分析，就是通过给定的训练数据，确定投影方向W 和阈值y0，即确定线性判别函数，然后根据这个线性判别函数，对测试数据进行测试，得到测试数据的类别。

二、算法的基本原理及流程图 1 基本原理（1）W 的确定各类样本均值向量mi样本类内离散度矩阵i S 和总类内离散度矩阵w S12w S S S =+样本类间离散度矩阵b S在投影后的一维空间中，各类样本均值T i i m '= W m 。

样本类内离散度和总类内离散度 T T i i w w S ' = W S W S ' = W S W 。

样本类间离散度T b b S ' = W S W 。

Fisher 准则函数满足两个性质：·投影后，各类样本内部尽可能密集，即总类内离散度越小越好。

·投影后，各类样本尽可能离得远，即样本类间离散度越大越好。

根据这个性质确定准则函数，根据使准则函数取得最大值，可求出W ：-1w 12W = S (m - m ) 。

（2）阈值的确定实验中采取的方法：012y = (m ' + m ') / 2。

（3）Fisher 线性判别的决策规则T x S (x m)(x m ), 1,2ii ii X i ∈=--=∑T1212S (m m )(m m )b =--对于某一个未知类别的样本向量x，如果y=W T·x>y0，则x∈w1；否则x∈w2。

fisher判别法Fisher判别分析的基本思想：选取适当的投影方向，将样本数据进行投影，使得投影后各样本点尽可能分离开来，即：使得投影后各样本类内离差平方和尽可能小，而使各样本类间的离差平方和尽可能大。

为了克服“维数灾难”，人们将高维数据投影到低维空间上来，并保持必要的特征，这样，一方面数据点变得比较密集一些，另一方面，可以在低维空间上进行研究。

fisher判别法是判别分析的方法之一，它是借助于方差分析的思想，利用已知各总体抽取的样品的p维观察值构造一个或多个线性判别函数y=l′x其中l= (l1，l2…lp)′，x= (x1，x2，…，xp)′，使不同总体之间的离差(记为B)尽可能地大，而同一总体内的离差(记为E)尽可能地小来确定判别系数l=(l1，l2…lp)′。

数学上证明判别系数l恰好是|B-λE|=0的特征根，记为λ1≥λ2≥…≥λr>0。

所对应的特征向量记为l1，l2，…lr，则可写出多个相应的线性判别函数，在有些问题中，仅用一个λ1对应的特征向量l1所构成线性判别函数y1=l′1x不能很好区分各个总体时，可取λ2对应的特征向量l′2建立第二个线性判别函数y2=l′2x，如还不够，依此类推。

有了判别函数，再人为规定一个分类原则(有加权法和不加权法等)就可对新样品x判别所属。

Fisher判别法是根据方差分析的思想建立起来的一种能较好区分各个总体的线性判别法，由Fisher在1936年提出。

该判别方法对总体的分布不做任何要求。

Fisher判别法是一种投影方法，把高维空间的点向低维空间投影。

在原来的坐标系下，可能很难把样品分开，而投影后可能区别明显。

一般说，可以先投影到一维空间(直线)上，如果效果不理想，在投影到另一条直线上(从而构成二维空间)，依此类推。

每个投影可以建立一个判别函数。

论文(设计)《模式识别》题目Fisher线性判别的基本原理及应用Fisher判别准则一、基本原理思想Fisher线性判别分析的基本思想：通过寻找一个投影方向（线性变换，线性组合），将高维问题降低到一维问题来解决，并且要求变换后的一维数据具有如下性质：同类样本尽可能聚集在一起，不同类的样本尽可能地远。

Fisher线性判别分析，就是通过给定的训练数据，确定投影方向W和阈值y0，即确定线性判别函数，然后根据这个线性判别函数，对测试数据进行测试，得到测试数据的类别。

二、算法的实现及流程图1 算法实现 （1）W 的确定x 1m x, 1,2ii X ii N ∈==∑各类样本均值向量mi样本类内离散度矩阵和总类内离散度矩阵Tx S (x m )(x m ), 1,2ii i i X i ∈=--=∑样本类间离散度矩阵T1212S (m m )(m m )b =--在投影后的一维空间中，各类样本均值。

样本类内离散度和总类内离散度。

样本类间离散度。

Fisher 准则函数满足两个性质：·投影后，各类样本内部尽可能密集，即总类内离散度越小越好。

·投影后，各类样本尽可能离得远，即样本类间离散度越大越好。

根据这个性质确定准则函数，根据使准则函数取得最大值，可求出W ：。

（2）阈值的确定采取的方法：【1】【2】【3】（3）Fisher 线性判别的决策规则对于某一个未知类别的样本向量x ，如果y=W T·x>y0，则x ∈w1；否则x ∈w2。

2 流程图归一化处理载入训练数据三、实验仿真1.实验要求试验中采用如下的数据样本集:ω1类： (22,5),(46,33),(25,30),(25,8),(31, 3),(37,9),(46,7),(49,5),(51,6),(53,3)(19,15),(23,18),(43,1),(22,15),(20,19),(37,36),(22,22),(21,32),(26,36),(23,39)(29,35),(33,32),(25,38),(41,35),(33,2),(48,37)ω2类: (40,25),(63,33),(43,27),(52,25),(55,27),(59,22) ,(65,59),(63,27)(65,30),(66,38),(67,43),(52,52),(61,49) (46,23),(60,50),(68,55) (40,53),(60,55),(55,55) (48,56),(45,57),(38,57) ,(68,24)在实验中采用Fisher线性判别方法设计出每段线性判别函数。

具体要求
1、复习感知器算法； 2、写出实现批处理感知器算法的程序 1）从 a=0 开始，将你的程序应用在 ω1 和 ω2 的训练数据上。记下收敛的步 数。 2）将你的程序应用在 ω2 和 ω3 类上，同样记下收敛的步数。 3）试解释它们收敛步数的差别。 3、提高部分：ω3 和 ω4 的前 5 个点不是线性可分的，请手工构造非线性映 射，使这些点在映射后的特征空间中是线性可分的，并对它们训练一个感
本实验通过编制程序让初学者能够体会 Fisher 线性判别的基本思路，理解线性判别的 基本思想，掌握 Fisher 线性判别问题的实质。
2、[实验内容]
1．实验所用样本数据如表 2-1 给出（其中每个样本空间（数据）为两维， x 1 表示第一维的值、x 2 表示第二维的值），编制程序实现 ω1、ω 2 类 ω 2、ω 3 类的分类。分析分类器算法的性能。
x1 X
xd
根据 Fisher 选择投影方向 W 的原则，即使原样本向量在该方向上的投影能兼顾类间分
布尽可能分开，类内样本投影尽可能密集的要求，用以评价投影方向 W 的函数为：
J F (W ) (m~S~112m~S~222)2
W * SW1(m1 m2 )
上面的公式是使用 Fisher 准则求最佳法线向量的解，该式比较重要。另外，该式这种
2
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电通，力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置，机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2，荷试而下卷且高总可中体保资配障料置2试时32卷，3各调需类控要管试在路验最习；大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试，况卷要下安加与全强过，看度并25工且52作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资；中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整，高核或中对者资定对料值某试，些卷审异弯核常扁与高度校中固对资定图料盒纸试位，卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接案资要，料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气，设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术，技槽以来术、及避管系免架统不等启必多动要项方高方案中式；资，对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资，件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调，并试合且技理进术利行，用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活：。。在对对分于于线调差盒试动处过保，程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试，题技应，术采作是用为指金调发属试电隔人机板员一进，变行需压隔要器开在组处事在理前发；掌生同握内一图部线纸故槽资障内料时，、，强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试，卷卷线试切缆验除敷报从设告而完与采毕相用，关高要技中进术资行资料检料试查，卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

fisher线性判别
fisher 判决⽅式是监督学习，在新样本加⼊之前，已经有了原样本。

原样本是训练集，训练的⽬的是要分类，也就是要找到分类线。

⼀⼑砍成两半！
当样本集确定的时候，分类的关键就在于如何砍下这⼀⼑！
若以⿊⾊的来划分，很明显不合理，以灰⾊的来划分，才是看上去合理的
1.先确定砍的⽅向
关键在于如何找到投影的向量u，与u的长度⽆关。

只看⽅向
找到样本点的中⼼均值m1，m2，以及在向量u上的投影的m1~，m2~。

因为u的⽅向与样本点都有关，所以需要考虑⼀个含有所有样本点的表达式
不妨算出离差阵
算出类内离差矩阵，两个都要求出来，并求和
并且投影的离差阵
根据聚类的理想情况，类内距离⼩，类间距离⼤，所以就⽤类间去处理类内，我们现在的变量是向量u，我们就对u求导，算出max存在的时后u的条件。

为了⽅便化简，引⼊⼀个参数不要以为下⾯除以是向量，（1*2）*（2*2）（2*1）=1 维度变成1，这是⼀个常数。

当求导公式
分⼦为0的时候，推出
所以
⽽且是（1*2）*（2*1）等于1，也是⼀个常数
到此为⽌，u的⽅向已经确定了
2.具体切哪⼀个点。

a，切
切投影均值的终点
2.
切贝叶斯概率的⽐例点
⽅向和具体点均已找到，分析完毕。

实验1 Fisher线性判别实验一、实验目的应用统计方法解决模式识别问题的困难之一是维数问题，低维特征空间的分类问题一般比高维空间的分类问题简单。

因此，人们力图将特征空间进行降维，降维的一个基本思路是将d维特征空间投影到一条直线上，形成一维空间，这在数学上比较容易实现。

问题的关键是投影之后原来线性可分的样本可能变为线性不可分。

一般对于线性可分的样本，总能找到一个投影方向，使得降维后样本仍然线性可分。

如何确定投影方向使得降维以后，样本不但线性可分，而且可分性更好（即不同类别的样本之间的距离尽可能远，同一类别的样本尽可能集中分布），就是Fisher线性判别所要解决的问题。

本实验通过编制程序让初学者能够体会Fisher线性判别的基本思路，理解线性判别的基本思想，掌握Fisher线性判别问题的实质。

二、实验要求1、改写例程，编制用Fisher线性判别方法对三维数据求最优方向W的通用函数。

2、对下面表1-1样本数据中的类别ω1和ω2计算最优方向W。

3、画出最优方向W的直线，并标记出投影后的点在直线上的位置。

表1-1 Fisher线性判别实验数据4、选择决策边界，实现新样本xx1=（-0.7,0.58,0.089），xx2=（0.047,-0.4,1.04）的分类。

5、提高部分（可做可不做）：设某新类别ω3数据如表1-2所示，用自己的函数求新类别ω3分别和ω1、ω2分类的投影方向和分类阈值。

表1-2 新类别样本数据三、部分参考例程及其说明求取数据分类的Fisher投影方向的程序如下：其中w为投影方向。

clear %Removes all variables from the workspace.clc %Clears the command window and homes the cursor.% w1类训练样本，10组，每组为行向量。

w1=[-0.4,0.58,0.089;-0.31,0.27,-0.04;-0.38,0.055,-0.035;-0.15,0.53,0. 011;-0.35,0.47,0.034;...0.17,0.69,0.1;-0.011,0.55,-0.18;-0.27,0.61,0.12;-0.065,0.49,0.0012;-0 .12,0.054,-0.063];% w2类训练样本，10组，每组为行向量。

实验一 Bayes 分类器设计【实验目的】对模式识别有一个初步的理解，能够根据自己的设计对贝叶斯决策理论算法有一个深刻地认识，理解二类分类器的设计原理。

【实验原理】最小风险贝叶斯决策可按下列步骤进行：(1)在已知)(i P ω，)(i X P ω，i=1,…，c 及给出待识别的X 的情况下，根据贝叶斯公式计算出后验概率： ∑==cj iii i i P X P P X P X P 1)()()()()(ωωωωω j=1,…，x(2)利用计算出的后验概率及决策表，按下面的公式计算出采取i a ,i=1,…，a 的条件风险∑==cj j jii X P a X a R 1)(),()(ωωλ,i=1,2,…,a(3)对(2)中得到的a 个条件风险值)(X a R i ,i=1,…，a 进行比较，找出使其条件风险最小的决策k a ，即()()1,min k i i aR a x R a x ==则k a 就是最小风险贝叶斯决策。

【实验内容】假定某个局部区域细胞识别中正常（1ω）和非正常（2ω）两类先验概率分别为 正常状态：P （1ω）=0.9； 异常状态：P （2ω）=0.1。

现有一系列待观察的细胞，其观察值为x ：-3.9847 -3.5549 -1.2401 -0.9780 -0.7932 -2.8531 -2.7605 -3.7287 -3.5414 -2.2692 -3.4549 -3.0752 -3.9934 2.8792 -0.9780 0.7932 1.1882 3.0682-1.5799 -1.4885 -0.7431 -0.4221 -1.1186 4.2532 已知类条件概率是的曲线如下图：)|(1ωx p )|(2ωx p 类条件概率分布正态分布分别为N （-2，0.25）、N （2,4）试对观察的结果进行分类。

【实验要求】1)用matlab 完成基于最小错误率的贝叶斯分类器的设计，要求程序相应语句有说明文字，要求有子程序的调用过程。

Fisher 判别
各类样本均值
1
mi Ni yi y, i 1, 2
样本类内离散度和总类内离散度
Si ( y mi )2, i 1,2 yi
样本类间离散度
Sw S1 S2 Sb (m1 m2 )2
以上定义描述d维空间样本点到一向量投影的分 散情况，因此也就是对某向量w的投影在w上的 分布。样本离散度的定义与随机变量方差相类似
Sw1(m1 m2 )R
w*
R
Sw1(m1
m2 )
Sw1(m1 m2 )
10
8
判别函数的确定
Fisher 判别
前面讨论了使Fisher准则函数极大的d维向 量w*的计算方法，判别函数中的另一项w0 （阈值）可采用以下几种方法确定：
w0
m1
2
m2
w0
N1m1 N2m2 N1 N2
m
w0
m1
m2 2
lnP(1) / P( 1 y wT x w0 0 x 2
Fisher线性判别
线性判别函数y=g(x)=wTx:
• 样本向量x各分量的线性加权 • 样本向量x与权向量w的向量点积 • 如果|| w ||=1，则视作向量x在向量w上的投
影
Fisher准则的基本原理：找到一个最合适的 投影轴，使两类样本在该轴上投影之间的距 离尽可能远，而每一类样本的投影尽可能紧 凑，从而使分类效果为最佳。
Si (x mi )(x mi )T , i 1,2 xi
Sw S1 S2
样本类间离散度矩阵Sb：Sb (m1 m2 )(m1 m2 )T
离散矩阵在形式上与协方差矩阵很相似，但协方 差矩阵是一种期望值，而离散矩阵只是表示有限 个样本在空间分布的离散程度

机器学习：线性判别式分析（LDA）1.概述线性判别式分析（Linear Discriminant Analysis），简称为LDA。

也称为Fisher线性判别（Fisher Linear Discriminant，FLD），是模式识别的经典算法，在1996年由Belhumeur引⼊模式识别和⼈⼯智能领域。

基本思想是将⾼维的模式样本投影到最佳鉴别⽮量空间，以达到抽取分类信息和压缩特征空间维数的效果，投影后保证模式样本在新的⼦空间有最⼤的类间距离和最⼩的类内距离，即模式在该空间中有最佳的可分离性。

LDA与PCA都是常⽤的降维技术。

PCA主要是从特征的协⽅差⾓度，去找到⽐较好的投影⽅式。

LDA更多的是考虑了标注，即希望投影后不同类别之间数据点的距离更⼤，同⼀类别的数据点更紧凑。

但是LDA有两个假设:1.样本数据服从正态分布，2.各类得协⽅差相等。

虽然这些在实际中不⼀定满⾜，但是LDA被证明是⾮常有效的降维⽅法，其线性模型对于噪⾳的鲁棒性效果⽐较好，不容易过拟合。

2.图解说明(图⽚来⾃⽹络)可以看到两个类别，⼀个绿⾊类别，⼀个红⾊类别。

左图是两个类别的原始数据，现在要求将数据从⼆维降维到⼀维。

直接投影到x1轴或者x2轴，不同类别之间会有重复，导致分类效果下降。

右图映射到的直线就是⽤LDA⽅法计算得到的，可以看到，红⾊类别和绿⾊类别在映射之后之间的距离是最⼤的，⽽且每个类别内部点的离散程度是最⼩的（或者说聚集程度是最⼤的）。

3.图解LAD与PCA的区别(图⽚来⾃⽹络）两个类别，class1的点都是圆圈，class2的点都是⼗字。

图中有两条直线，斜率在1左右的这条直线是PCA选择的映射直线，斜率在 -1左右的这条直线是LDA选择的映射直线。

其余不在这两条直线上的点是原始数据点。

可以看到由于LDA考虑了“类别”这个信息（即标注），映射后，可以很好的将class1和class2的点区分开。

D与PCA的对⽐(1)PCA⽆需样本标签,属于⽆监督学习降维;LDA需要样本标签,属于有监督学习降维。