分数指数幂的运算

亲爱的同学们，大家好！今天，我们将进一步讨论分数指数幂的同底数运算，希望通过今天的学习，能够让大家掌握这个知识点，并且能够熟练运用同底数运算规则求解。

我们来复习一下分数指数幂的定义。

分数指数幂，就是指数为分数的幂，例如2的1/2次方，2的2/3次方等等。

在这种情况下，我们需要首先理解分数指数幂的含义，我们以2的1/2次方为例，这个式子可以写成根号2，也就是2的平方根。

因此，我们也可以推广到其他的分数指数幂中，例如2的2/3次方，可以写成2的3次方根号2。

接下来，我们将讨论同底数运算的规则。

同底数运算的规则非常简单，就是将同一底数的指数相加，例如2的3次方乘以2的5次方，可以写成2的8次方。

用公式表示，就是a的m 次方乘以a的n次方，等于a的m+n次方。

在进行同底数运算的时候，有时候我们需要进行一些化简，例如对于3的1/2次方乘以9的3/2次方，我们可以先将9的3/2次方化简为（3的2次方）的3/2次方，接着可以将3的1/2次方写成3的1次方的1/2次方，然后代入同底数运算的公式中，即可得到3的2次方。

除了同底数运算，我们还需要学习同底数约分的方法。

同底数约分的方法非常简单，就是对于同一底数，将指数相减即可。

例如2的5次方除以2的3次方，可以写成2的（5-3）次方，也就是2的2次方。

在进行同底数约分的时候，有时候我们需要注意，即需要将分数指数幂的平方根或者三次方根化成分数形式，例如8的1/6次方可以写成（2的3次方）的1/6次方，然后化成分数形式，变成（2的1次方）的1/3次方，这样就可以进行同底数运算了。

让我们来看几个例子，来加深理解。

例子1：计算2的2/3次方乘以2的5/3次方。

答案：这个时候我们需要将指数相加，得到2的7/3次方。

例子2：计算3的1/2次方乘以9的3/2次方。

答案：这个时候我们需要进行一些化简，将9的3/2次方化简为（3的2次方）的3/2次方，接着可以将3的1/2次方写成3的1次方的1/2次方，然后代入同底数运算的公式中，即可得到3的2次方。

分数指数幂运算
分数指数幂运算是将一个分数作为底数，另一个分数作为指数进行计算的运算。

如果分数指数是正数，可以按照分数的定义进行计算。

例如，计算2^1/3，可以先计算2的立方根，再将结果与自身相乘，即2^1/3 = (∛2)^3 = 2。

如果分数指数是负数，可以使用倒数的概念进行计算。

例如，计算2^(-1/3)，可以先计算2的立方根的倒数，再将结果与自身相乘，即2^(-1/3) = 1/(∛2)。

如果分数指数是分数形式，可以使用乘法的性质进行计算。

例如，计算2^(2/3)，可以将指数分解为2×(1/3)，然后先计算2的立方根，再将结果平方，即2^(2/3) = (∛2)^2 = 2^(1/3) ×
2^(1/3) = (∛2) × (∛2)。

需要注意的是，分数指数运算可能会得到无理数的结果，因此可能需要进行近似运算或使用特定的表达式表示结果。

(m - n )4 p 6⋅ q 5a a a 3 6a 9 6 3a 9 4 a3 1 3x 3 x -23、⎛ 3 6 a 9 ⎫ ⎛ 6 3 a 9 ⎫ ⎪ 根式与分数指数幂的运算（1）一、根式与指数转化1、用分数指数幂表达下列各式：(1) 3 x 2 =（2） 4 (a + b )3 （ a + b > 0 ） =（3）3 (m - n )2 =（4） （ m > n ）=m 3（5） （ｐ＞０）=（6） =m（7）（9）4 (- a )2（式中a > 0 ）= （8）3 ab 2（10）（11） =（12）( )4⋅ ()4=32、将52 写为根式44⎪ ⎪ ⎝ ⎭ ⎝ ⎭等于（ C ）A 、a 16B 、a 8C 、a 4D 、a 24、已知x 5 = -2009 ，则x =（用根式表达）⎛ 8 - 6 ⎫ - 1 25、 a 5 b 5 ⎪ ⎝ ⎭⋅ 5 a 4 ÷ 5 b 3 (a ≠ 0, b ≠ 0)⎛ ⎫46、已知a ≥0，化简3 ⎪ = a7 (3 6⎝a 9 )4 ⋅ (6 3 ⎭a 9 )44、将表达成指数幂形式，其成果为 a- 8 ⎛ ⎫58、 ⎪ ⎪ ⎝ ⎭4 化成分数指数幂为 ________ 159、将(3 6 a 9 )4 ⋅ (6 3 a 9 )4 ( a >0)表达成指数幂形式，其成果为 a 4 .x 3 x 2 4 x 31 1a a(-2)4481⨯ 392 6 12 227 9 ⎭ ⎛ 6 ⎫ 7 3 二、求值1 求值：3 - 64 =； = ； 4 (3 -π)4 =3 42、 +3、22 ⨯ 23 =3 42216 - 34、(22 ) 3 =35、23⨯ 23=236 36、求值：( ) 814 =7、(1) 252 =（２） 27 3 =（３）( ) 2 =49（4）( 25)- 24=（5） =（6） 2 ⨯ ⨯ =[(- )2 ]-1-8、22 等于（）A ． B ．C D ． 2 2- 1 ⎛ 1 ⎫-23( )9、计算：0.0273- - ⎪ ⎝ ⎭+ 2564 - 3-1 + - 1 = 。

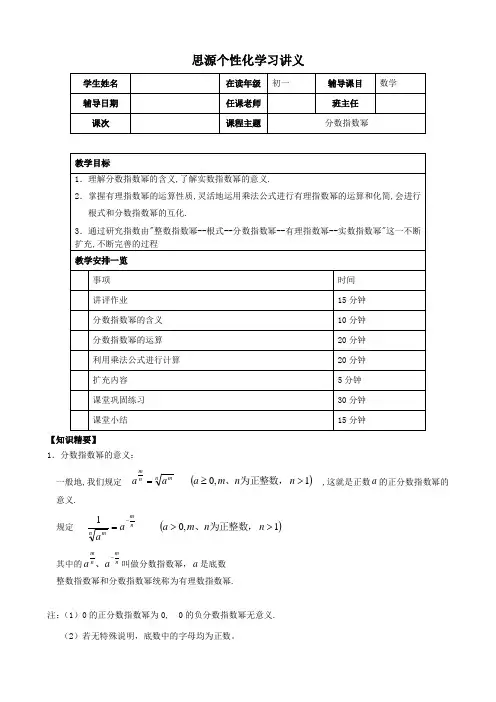
思源个性化学习讲义【知识精要】1．分数指数幂的意义： 一般地,我们规定 n m nm a a = ()1,0>≥n n m a 为正整数，、 ,这就是正数a 的正分数指数幂的意义. 规定nm n maa-=1()1,0>>n n m a 为正整数，、其中的nm nm a a -、叫做分数指数幂，a 是底数整数指数幂和分数指数幂统称为有理数指数幂.注：（1）0的正分数指数幂为0, 0的负分数指数幂无意义. （2）若无特殊说明，底数中的字母均为正数。

2. 当a >0时，整数指数幂的运算性质，对于有理指数幂也同样适用.即对于任意有理数r ,s ,均有下面的运算性质：设q p b a 、,0,0>>为有理数（1）q p q p qp q p a a a a a a -+=÷=⋅，（2）()pq qpa a =（3）()p p pp p pb a b a b a ab =⎪⎭⎫ ⎝⎛=，【热身练习】1. 把下列方根化为分数指数幂的形式（1）310 （2）32101（3）3100 （4）41002. 求值(1)21169 (2)3264 (3) 239- (4)⎪⎪⎭⎫ ⎝⎛-43256（ ）A.3B.3-C.3±D.81 4．当a _________时，式子23a 有意义 5. 若0>a ，则43a 和53-a 用根式形式表示分别为 和6.56b a 和mm 3用分数指数幂形式表示分别为 和【精解名题】 1. （1）23425-⎪⎭⎫⎝⎛= ；（2） 63125.132⨯⨯= ________2. 计算：631010⨯=__________________3.3151写成幂的形式______________4.化为分数指数幂的形式为 ___________________5. 583221)22(--化为分数指数幂得 _________________________6.式子 （ ）7. 已知32121=+-aa ，求下列各式的值。

课 题 函数奇偶性与分数指数幂的运算教学目标 理解函数奇偶性的判断方法和判断要点，会使用函数的奇偶性来解答相关问题；梳理清楚分数指数幂的运算性质和计算方法，明白在解答时具体的运用和思路。

重点、难点 重点：掌握函数奇偶性、分数指数幂的重点性质和计算方法。

难点：和所学知识糅合使用，将初中知识牵扯如高中的使用中。

考点及考试要求理解并掌握函数奇偶性在解答形象问题和抽象问题时的运用办法，能够把奇偶性等问题掌握；明白分数指数幂的计算，学会分数指数幂的计算要领和方法。

教学内容知识点一：函数奇偶性1.函数奇偶性的定义函数奇偶性：（1）奇函数⎪⎩⎪⎨⎧==+--=-0)0(03)2(0)()()()()1(f x x f x f x f x f ，则可以为）若（图象关于原点对称或（2）偶函数⎩⎨⎧=--=-轴对称图象关于或y x f x f x f x f )2(0)()()()()1(例题讲解11 .若3)3()2()(2+-+-=x k x k x f 是偶函数，讨论函数)(x f 的单调区间？2 定义在R 上的偶函数)(x f 在)0,(-∞是单调递减，若)2()6(a f a f <-，则a 的取值范围是如何？注意：用定义判断函数奇偶性的步骤是[来源学科网ZXXK](1)、先求定义域，看是否关于原点对称；(2)、再判断()()f x f x -=- 或 ()()f x f x -= 是否恒成立； （3）、作出相应结论.2 函数按是否有奇偶性可分为四类：n m nm a a= (a ＞0,m ,n ∈N *,且n ＞1)针对性练习一、填空题1.整数指数幂：0);1(0);(0,).n n a a a a n N a a a a n N *-*⋅⋅⋅⋅=∈=≠=≠∈个（2.整数指数幂的运算性质：（1）(,)m n a a m n Z ⋅=∈；（2）()(,)m n a m n Z =∈；（3）(,,0)mn a m n Z a a=∈≠；（4）()()m ab m Z =∈.[来源:Z#xx#]3.根式的运算性质：（1）当n 为任意正整数时，()nna =.（2）当n 为奇数时，nna =；当n为偶数时，.nna ==（3）根式的基本性质：(0).npmp a a =≥例题讲解1 化简：41233332233382()42a a b b aa b ab a--÷-⨯++a ·3a 25a ·3a(式原式＝11111213333333321111111223333352[()(2)]2()()(2)(2)()a a b a b a a aa ab b a a --⋅÷⨯+⋅+⋅ ＝51116333111336(2)2a a a a b a ba-⨯⨯-＝12233.a a a a ⨯⨯=课堂练习1 ：已知102m =，则m 等于 （ ）10.2A10.2B -10.2C10.2D ±2.：（1）下列根式与分数指数幂的互化正确的是 （ ）12.()(0)A x x x -=-> 1623.(0)B y y y =< 43341.()(0)C xx x-=> 133.(0)D x x x -=-≠3. 若0,n m <<，则222222m mn n m mn n ++--+等于（ ）.2A m .2B n .2C m - .2D n-§X§K]4.若02522<+-x x ，则2441x x +-+2 | x －2|等于 （ ） （A ） 54-x （B ）3- （C ）3 （D ）x 45-5.函数210)2()5()(--+-=x x x f 的定义域是 （ ）（A ）}2,5 ,|{≠≠∈x x R x x 且 （B ）}2|{>x x （C ）}5|{>x x （D ）}5,52|{><<x x x 或6. 计算122[(2)]--的结果是 （ ）（A ）2 （B ）2- （C ）22（D ）22-7 把322-化成分数指数幂的形式是 （ ） （A ）122--（B ）122- （C ）132-（D ）562-求值1.：求值：（1）88(2)x -； （2）33322(12)-+-；3.()41-30-0.753370.064()-2+168-⎡⎤--+⎣⎦; 4. 3-2013+26+-1.03-423-2⎛⎫⎛⎫⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭;化简（1）设33,x -<<求222169x x x x -+-++的值.（2）用分式指数幂的形式表示下列各式.1..(0)a a a >2. 42233.()(0)b b -->[来源:学+科+网Z+X+X+K]课后作业试 题批 阅。

近似数的精确度分数指数幂及运算
在数学中，我们经常会遇到需要进行近似数的计算，这时候我们需要考虑到近似数的精确度。

近似数的精确度是指我们所得到的近似数与真实值之间的误差大小。

在实际应用中，我们需要根据具体情况来确定近似数的精确度，以保证计算结果的准确性。

在分数的运算中，我们需要注意分母的大小，因为分母越大，分数的精确度就越高。

例如，1/2和1/1000相比，1/2的精确度要高得多。

在进行分数的加减乘除运算时，我们需要先将分数化为相同的分母，然后再进行运算。

这样可以避免分母不同导致的误差。

指数幂是数学中常见的运算方式，它可以用来表示一个数的幂次方。

例如，2的3次方等于8，即2³=8。

在进行指数幂的计算时，我们需要注意底数和指数的大小关系。

如果底数比较大，指数比较小，那么我们可以直接计算出结果。

但如果底数比较小，指数比较大，那么我们需要使用科学计数法来表示结果，以保证精确度。

在运算中，我们还需要注意数值的精确度。

例如，当我们进行小数的加减乘除运算时，我们需要注意小数点后的位数，以保证计算结果的精确度。

如果小数点后的位数太多，我们可以使用四舍五入的方法来保留合适的位数。

在数学中，我们需要根据具体情况来确定近似数的精确度，以保证计算结果的准确性。

在分数、指数幂和运算中，我们需要注意数值
的大小关系和精确度，以避免误差的产生。

指数运算规律一、指数法则1. 幂的乘方：(a^m)^n = a^(m×n) (m,n都是正数) ；2. 同底数幂的乘法：a^m×a^n = a^(m+n) (m,n都是正数) ；3. 同底数幂的除法：a^m / a^n = a^(m-n) (a≠0, m,n都是正数，且m>n) ；4. 幂的乘方：(a^m)^n = a^(m×n) (m,n都是正数) ；5. 积的乘方：(ab)^n = a^n×b^n (n是正整数) 。

二、指数运算性质1. 零指数幂：0^n=1 (n∈Z*)；2. 负整数指数幂：a^(-n)=1/a^n (a≠0, n∈N*)；3. 特殊值法：令字母取不同的值代入进行验证。

三、指数运算技巧1. 分散注意，将难点各个击破；2. 利用分配律简化运算；3. 利用同底数幂的乘除法法则进行简化；4. 利用幂的乘方运算法则进行简化；5. 利用积的乘方运算法则进行简化；6. 利用非零数的0次幂等于1的性质进行简化；7. 利用整体代入的思想简化运算。

四、指数运算的规律1. 负指数表示的是倒数：a^(-n) = 1/a^n2. 分数指数幂：根号[a^(2n)] = a^n，根号[a^(2n-1)] = |a|^n3. 指数为无理数时，视为实数：例如，e^(πi) + 1 = 04. 指数运算中，负数可以引入：例如，e^(-x) = 1/e^x5. 指数函数与对数函数的互为反函数：指数函数和对数函数具有反函数性质，即如果y=a^x，那么x=log_a y。

五、指数运算的应用1. 在物理学中的应用：指数函数在物理学中有广泛的应用，例如在放射性衰变、电路中的RC或LC振荡器、光的吸收和发射等过程中，都可以看到指数函数的身影。

2. 在金融学中的应用：在金融学中，复利计算就是一个典型的指数问题。

复利是指本金及其产生的利息一并计算，也就是利上有利。

复利计算的特点是：把上期末的本利和作为下一期的本金，在计算时每一期本金的数额是不同的。

§指数与指数幂的运算（2）1.理解分数指数幂的概念；2.掌握根式与分数指数幂的互化；3.掌握有理数指数幂的运算.一、课前准备：（预习教材P 50~P 53，找出疑惑之处） 复习1：一般地，若n x a =，则x 叫做a 的，其中1n >,n *∈N .简记为：.的式子就叫做，具有如下运算性质：n =；=. 复习2：整数指数幂的运算性质：（1）=⋅n m a a ；（2）()m n a = ；（3）()n ab =.二、新课导学 ※学习探究：引例：a >01025a a ===；23a =，= .新知：规定分数指数幂如下：*(0,,,1)m na a m n N n =>∈>；*1(0,,,1)mnm naa m n N n a-==>∈>.试试：（1）将下列根式写成分数指数幂形式：=；=；=(0,)a m N *>∈.（2）将下列分数指数幂写成根式形式：322=；255=；436-=；32-a= )0(≠a .反思：①0的正分数指数幂为 ； 0的负分数指数幂 .②分数指数幂有什么运算性质？小结：规定了分数指数幂的意义后，指数的概念就从整数指数推广到了有理数指数，那么整数指数幂的运算性质也同样可以推广到有理数指数幂．指数幂的运算性质：（0,0,,a b r s Q >>∈）s r s r a a a +=；rs s r a a =)(；rr r b a ab =)(．※典型例题 例1求值：=328；=-2125；=-5)21(；=-43)8116(.例2用分数指数幂的形式表示下列各式(0)b >： （1）=•a a 3；（2）a 2•√a 23=；（3）=•3a a；例3计算（式中字母均正）：（1）)3()6)(2(656131212132b a b a b a -÷-（2）88341)(-nm例4计算：（1）4325)12525(÷- （2）)0(322>•a aa a小结：在进行指数幂的运算时，一般地，化指数为正指数，化根式为分数指数幂，对含有指数式或根式的乘除运算，还要善于利用幂的运算法则.反思：①结论：无理指数幂.（结合教材P 53利用逼近的思想理解无理指数幂意义）②无理数指数幂(0,)a a αα>是无理数是一个确定的实数．实数指数幂的运算性质如何？三、总结提升 ※学习小结①分数指数幂的意义；②分数指数幂与根式的互化；③有理指数幂的运算性质.1. 用分数指数幂表示下列各式：=32x)0(>x ；=+44)(b a；=-32)(n m)(n m >；=-4)(n m)(n m >.=56q p)0(>p ；=mm 3.2.计算下列各式=23)4936(；=-814121aa a ；=⨯⨯63125.132；=---)221(2323131x x x课后作业1.化简下列各式：=623b a a b；=a aa2121；=•••415643)(mm m m m2.计算下列各式（式中字母均正）：=1274331aa a ；=÷654332a a a；=-124331)(yx；(16s 2t −625r 4)−32= ； =-÷---)32(431313132a a ba；=----)4)(3)(2(324132213141y x y xyx；=-+--)32)(32(41214121yx y x；=-÷----)6()3(43221314141yxy x x；。

分数指数幂定义
分数指数幂是一个数的指数为分数，正数的分数指数幂是根式的另一种表示形式。

负数的分数指数幂并不能用根式来计算，而要用到其它算法，是高中代数的重点。

分数指数幂是一个数的指数为分数，如2的1/2次幂就是根号2。

分数指数幂是根式的另一种表示形式，
即n次根号(a的m次幂)可以写成a的m/n次幂。

幂是指数值，如8的1/3次幂=2
一个数的b分之a次方等于b次根号下这个数的a次方
重点:
1、分数指数幂的含义的理解。

2、根式与分数指数幂的互化。

3、有理指数幂的运算性质。

难点:
1、分数指数幂概念的理解。

2、有理指数幂的运算和化简。

分数指数幂的混合运算是初中数学中一个非常重要的概念，掌握好这个概念可以为学生以后的数学学习打下坚实的基础。

在前一篇教案中，我们介绍了分数指数幂的基本概念和乘除混合运算的方法。

在本篇教案中，我们将为大家介绍一个非常重要的内容，那就是分数指幂的运算的优先级顺序。

一、认识优先级顺序在进行分数指数幂的混合运算中，我们需要知道哪些运算符先进行，哪些运算符后进行。

例如，我们知道在一般的四则运中，乘法和除法的优先级要高于加法和减法。

那么在分数指数幂的混合运算中，我们又该如何确定优先级顺序呢？二、分数指幂混合运算的优先级顺序1、先执行指数运算在分数指幂混合运算中，指数运算的优先级最高。

什么是指数运算呢？我们知道，在一个数a 的b次方中，b就是指数，a就是底数。

例如，“2的3次方”中的2就是底数，3就是指数。

因此，当我们遇到分数指数幂混合运算的式子时，首先要做的就是先进行指数运算。

例如，下面这个式子：2^(1/2) × 3^4 × 5^(1/3)我们应该先进行指数运算。

其中，“2的1/2次方”相当于根号2，“5的1/3次方”相当于3次方根号5。

因此，原式可以化简为：√2 × 3^4 × ³√52、其次执行分数运算在分数指数幂的混合运算中，分数运算的优先级次于指数运算。

当指数运算计算完成后，我们要进行的就是分数运算。

在进行分数运算时，我们需要注意分母的通分问题。

例如：1/(2^3) + 2/(3^2) - 3/(5^3)其中，2的3次方相当于8，3的2次方相当于9，5的3次方相当于125。

因此，我们要进行分母的通分操作，得到：125/(2^3 × 5^3) + 500/(3^2 × 5^3) - 24/(2^3 × 3^2 × 5^3)再进行分子的加减操作，得到最终结果。

3、最后执行乘除运算在分数指数幂混合运算中，乘除运算的优先级最低。

分数指数幂课时目标1. 理解分数指数幂的意义，会进行方根和分数指数幂间的转化；2. 理解有理数数指数幂的运算性质，并能熟练应用于计算；知识精要1. 分数指数幂把指数的取值范围扩大到分数，规定：(0)m na a =≥m na-=(0)a >，其中m ，n 为正整数，1n >.m na 和m na-叫做分数指数幂，a 是底数.注：当m 与n 互素时，如果n 为奇数，那么分数指数幂中的底数a 可为负数. 2. 有理数指数幂整数指数幂和分数指数幂统称为有理数指数幂. 3. 有理数指数幂运算性质设0,0a b >>，,p q 为有理数，那么 （1）()p q pq a a =，p q p q a a a -÷= （2）()p q pq a a =（3）(),()ppppp p a a ab a a b b==4. 分数指数幂的运算（1）应用幂的运算性质进行分数指数幂的运算.（2）将方根化成幂的形式后能运用幂的性质，可使运算简便，所得结果中如有分数指数幂一般应化为方根.热身练习1. 把下列方根化为幂的形式（1 （2） （3（4） （5 （6说明：根据1na =0a ≥）进行求解，但要记住：当n 是偶数时，若0a <，则没有意义. 2. 计算（1）131()27- （2）238()27（3）121()16-（4）0.57(1)9（5）12(32) （6）3121)64(3. 计算（1）138()27（2）21331010⨯ （3）112228⨯（4）111362a a a ÷g （5）211055(25)⨯4. 利用幂的运算性质运算：（1 （2 （3精解名题例1 计算（1）43555÷⋅ （2）251232)3(32)27(2-+---（3）643321648⋅÷⋅ （4）1243aaa a ⋅⋅（5）05321)15(125)259(+---（6）34141331064.028|48|÷⨯--（7）4141241)21()41()21(+⋅+⋅-a a a （8）)4()2(3312161326561y x y x y x ⨯-÷（9）212131])27[()3()6427(-+---- （10）22121])32()32[(--++例2 94,24==βα，求βα2122-的值.例3 ）（，求下列各式的值已知121211:3--+=+x x xx ）（222-+x x例4 的值，求已知32131313133124---++⨯⨯=a a a a .例5 化简a b c备选例题例1 已知13x x -+=，求下列各式的值：（1）1122x x -+；（2）3322x x -+.例2 已知210(0)xaa =>，求x xx xa a a a--+-的值.例3 已知：01522≤--x x ，化简25109622+--++x x x x .巩固练习1.用幂的形式表示下列各数 （1）6 35-323-（2）3m 错误!未找到引用源。