下载文档原格式
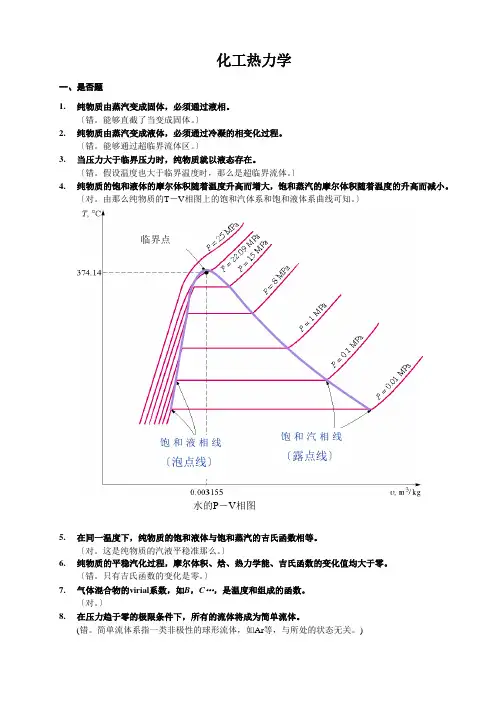
化工热力学一、是否题1. 纯物质由蒸汽变成固体，必须通过液相。
〔错。
能够直截了当变成固体。
〕2. 纯物质由蒸汽变成液体，必须通过冷凝的相变化过程。
〔错。
能够通过超临界流体区。
〕3. 当压力大于临界压力时，纯物质就以液态存在。
〔错。
假设温度也大于临界温度时，那么是超临界流体。
〕4. 纯物质的饱和液体的摩尔体积随着温度升高而增大，饱和蒸汽的摩尔体积随着温度的升高而减小。
〔对。
由那么纯物质的T －V 相图上的饱和汽体系和饱和液体系曲线可知。
〕5. 在同一温度下，纯物质的饱和液体与饱和蒸汽的吉氏函数相等。
〔对。
这是纯物质的汽液平稳准那么。
〕6. 纯物质的平稳汽化过程，摩尔体积、焓、热力学能、吉氏函数的变化值均大于零。
〔错。
只有吉氏函数的变化是零。
〕 7. 气体混合物的virial 系数，如B ，C …，是温度和组成的函数。
〔对。
〕8. 在压力趋于零的极限条件下，所有的流体将成为简单流体。
(错。
简单流体系指一类非极性的球形流体，如Ar 等，与所处的状态无关。
)饱和液相线〔泡点线〕饱和汽相线〔露点线〕水的P －V 相图 临界点二、选择题1. 指定温度下的纯物质，当压力低于该温度下的饱和蒸汽压时，那么气体的状态为〔 〕(C 。
参考P －V 图上的亚临界等温线。
)A. 饱和蒸汽B. 超临界流体C. 过热蒸汽2. T 温度下的过冷纯液体的压力P〔A 。
参考P －V 图上的亚临界等温线。
〕 3. T 温度下的过热纯蒸汽的压力P〔B 。
参考P －V 图上的亚临界等温线。
〕 4. 纯物质的第二virial 系数B〔A 。
virial 系数表示了分子间的相互作用，仅是温度的函数。
〕5. 能表达流体在临界点的P-V 等温线的正确趋势的virial 方程，必须至少用到〔A 。
要表示出等温线在临界点的拐点特点，要求关于V 的立方型方程〕 6. 关于纯物质，一定温度下的泡点压力与露点压力是 (A) A 相同的 B 不同的7. 关于纯物质，一定温度下泡点与露点，在P －T 图上是 (A) A 重叠的 B 分开的8． 关于纯物质，一定温度下泡点与露点，在P-V 图上是 (B) A 重叠的 B 分开的 9. 泡点的轨迹称为 (A) A 饱和液相线 B 饱和汽相线 10. 露点的轨迹称为 (B) A 饱和液相线 B 饱和汽相线 11. 关于混合物，PR 方程常数a 的表达式∑∑==-=3131)1(i j ij jj ii jik a a yy a 中的相互作用参数k ij ，i ＝j 时，其值 (A)A 为1B 为0C 从实验数据拟合得到，在没有实验数据时，近似作零处理A. >()T P sB. <()T P sC. =()T P sA. >()T P sB. <()T P sC. =()T P sA 仅是T 的函数B 是T 和P 的函数C 是T 和V 的函数D 是任何两强度性质的函数A. 第三virial 系数B. 第二virial 系数C. 无穷项D. 只需要理想气体方程纯物质的P －V 相图P C V C12. 关于混合物，PR 方程常数a 的表达式∑∑==-=3131)1(i j ij jj ii jik a a yy a 中的相互作用参数k ij ，i ≠j 时，其值 ( C )A 为1B 为0C 从实验数据拟合得到，在没有实验数据时，近似作零处理 三、运算题1. 由饱和蒸汽压方程，在合适的假设下估算水在25℃时的汽化焓。
化工热力学课后答案(填空、判断、画图)第1章 绪言一、是否题1. 封闭体系的体积为一常数。
（错）2. 封闭体系中有两个相βα,。
在尚未达到平衡时，βα,两个相都是均相敞开体系；达到平衡时，则βα,两个相都等价于均相封闭体系。
（对） 3. 理想气体的焓和热容仅是温度的函数。
（对）4. 理想气体的熵和吉氏函数仅是温度的函数。
（错。
还与压力或摩尔体积有关。
）5. 封闭体系的1mol 气体进行了某一过程，其体积总是变化着的，但是初态和终态的体积相等，初态和终态的温度分别为T 1和T 2，则该过程的⎰=21T T V dT C U ∆；同样，对于初、终态压力相等的过程有⎰=21T T P dT C H ∆。
（对。
状态函数的变化仅决定于初、终态与途径无关。
）二、填空题1. 状态函数的特点是：状态函数的变化与途径无关，仅决定于初、终态 。
2. 封闭体系中，温度是T 的1mol 理想气体从(P i ，V i )等温可逆地膨胀到(P f ，V f )，则所做的功为()f i rev V V RT W ln =(以V 表示)或()i f rev P P RT W ln = (以P 表示)。
3. 封闭体系中的1mol 理想气体(已知igP C )，按下列途径由T 1、P 1和V 1可逆地变化至P 2，则A 等容过程的 W = 0 ，Q =()1121T P P R C igP⎪⎪⎭⎫ ⎝⎛--，U =()1121T PP R C igP⎪⎪⎭⎫⎝⎛--，H =1121T P P C ig P ⎪⎪⎭⎫ ⎝⎛-。
B 等温过程的 W =21lnP P RT -，Q =21ln P PRT ，U = 0 ，H = 0 。
第2章Ｐ－Ｖ－Ｔ关系和状态方程一、是否题1. 纯物质由蒸汽变成液体，必须经过冷凝的相变化过程。
（错。
可以通过超临界流体区。
）2. 当压力大于临界压力时，纯物质就以液态存在。
（错。
若温度也大于临界温度时，则是超临界流体。
化工热力学课后答案第1章 绪言一、是否题1. 封闭体系的体积为一常数。
（错）2. 封闭体系中有两个相βα,。
在尚未达到平衡时，βα,两个相都是均相敞开体系；达到平衡时，则βα,两个相都等价于均相封闭体系。
（对）3. 理想气体的焓和热容仅是温度的函数。
（对）4. 理想气体的熵和吉氏函数仅是温度的函数。
（错。
还与压力或摩尔体积有关。
）5. 封闭体系的1mol 气体进行了某一过程，其体积总是变化着的，但是初态和终态的体积相等，初态和终态的温度分别为T 1和T 2，则该过程的⎰=21T T V dT C U ∆；同样，对于初、终态压力相等的过程有⎰=21T T P dT C H ∆。
（对。
状态函数的变化仅决定于初、终态与途径无关。
）二、填空题1. 状态函数的特点是：状态函数的变化与途径无关，仅决定于初、终态 。
2. 封闭体系中，温度是T 的1mol 理想气体从(P i ，V i )等温可逆地膨胀到(P f ，V f )，则所做的功为()f i rev V V RT W ln =(以V 表示)或()i f rev P P RT W ln = (以P 表示)。
3. 封闭体系中的1mol 理想气体(已知igP C )，按下列途径由T 1、P 1和V 1可逆地变化至P 2，则A 等容过程的 W = 0 ，Q =()1121T P P R C igP⎪⎪⎭⎫ ⎝⎛--，错误！未找到引用源。
U =()1121T PP R C igP⎪⎪⎭⎫⎝⎛--，错误！未找到引用源。
H = 1121T P P C ig P ⎪⎪⎭⎫ ⎝⎛-。
B 等温过程的 W =21lnP P RT -，Q =21ln P PRT ，错误！未找到引用源。
U = 0 ，错误！未找到引用源。
H = 0 。
C 绝热过程的 W =()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛--11211igPC RigPP P R V P R C ，Q = 0 ，错误！未找到引用源。
化工热力学课后答案第1章绪言—、是否题1. 封闭体系的体积为一常数。
（错）2. 封闭体系中有两个相， 。
在尚未达到平衡时，， 两个相都是均相敞开体系；达到平衡时，则，两个相都等价于均相封闭体系。
（对）3. 理想气体的焓和热容仅是温度的函数。
（对）4. 理想气体的熵和吉氏函数仅是温度的函数。
（错。
还与压力或摩尔体积有关。
）5. 封闭体系的1mol 气体进行了某一过程， 其体积总是变化着的， 但是初态和终态的体积相T 2等，初态和终态的温度分别为 T ［和丁2，则该过程的 UC V dT ;同样，对于初、终态T iT 2压力相等的过程有 HC p dT 。
（对。
状态函数的变化仅决定于初、 终态与途径无关。
）T 1二、填空题状态函数的特点是： ________ 。
封闭体系中，温度是 T 的1mol 理想气体从（P , V ）等温可逆地膨胀到（P ，V f ），则所做的 功为 W revRTl nV i V f （以 V 表示）或 W rev RT l nP f P （以 P 表示）。
C PP T1T 1。
1.3. 封闭体系中的imol 理想气体（已知C pg ），按下列途径由T 、P i 和V 可逆地变化至P 2,则A 等容过程的 W = _，Q= Cp 1RP 2 P 2P i/C Pg RP 1 1 T 1 ， H=B等温过程的RTln l，^RTln t，U= 0 ，H=_0 ___ 。
解:EOSW revV 2 b RTl n丄 V 1 bRTln 纟V 1999In 2 1.0007222. 对于c P为常数的理想气体经过一绝热可逆过程，状态变化符合下列方程解: 3. 解: T 1 P 1（1），其式又是如何？以上a 、b 、 理想气体的绝热可逆过程,C ；gRdTT 22a Rb TT 1aln 旦 b T 2T1RT dV V cT dTCigC !，试问，对于C P a bTcT 2的理想气体，上述关系c 为常数。
第 3章均相封闭体系热力学原理及其应用一、是否题1. 体系经过一绝热可逆过程,其熵没有变化。
2. 吸热过程一定使体系熵增,反之,熵增过程也是吸热的。
3. 热力学基本关系式 dH=TdS+VdP只适用于可逆过程。
4. 象 dU=TdS-PdV等热力学基本方程只能用于气体,而不能用于液体或固相。
5. 当压力趋于零时, ((0, , ≡-P T M P T M ig (M 是摩尔性质。
6.[](0ln , P PR P T S S ig+-与参考态的压力 P 0无关。
纯物质逸度的完整定义是,在等温条件下, f RTd dG ln =。
7. 理想气体的状态方程是 PV=RT, 若其中的压力 P 用逸度 f 代替后就成为了真实流体状态方程。
8. 当0→P 时, ∞→P f 。
9. 因为⎰⎪⎭⎫⎝⎛-=PdP P RT V RT 01ln ϕ,当0→P 时, 1=ϕ,所以, 0=-P RT V 。
10. 逸度与压力的单位是相同的。
11. 吉氏函数与逸度系数的关系是 ((ϕln 1, , RT P T G P T G ig ==-。
12. 由于偏离函数是两个等温状态的性质之差, 故不可能用偏离函数来计算性质随着温度的变化。
13. 由于偏离函数是在均相体系中引出的概念, 故我们不能用偏离函数来计算汽化过程的热力学性质的变化。
14. 由一个优秀的状态方程,就可以计算所有的均相热力学性质随着状态的变化。
二、选择题1. 对于一均匀的物质,其 H 和 U 的关系为(B 。
因 H =U +PVA. H ≤UB. H>UC. H=UD. 不能确定2. 一气体符合 P=RT/(V-b 的状态方程从 V 1等温可逆膨胀至 V 2,则体系的∆S 为(C 。
b V b V R b V R dV T P dV V S S V V V V V V V T --=-=⎪⎭⎫⎝⎛∂∂=⎪⎭⎫⎝⎛∂∂=⎰⎰⎰12ln 212121∆ A. bV bV RT --12lnB. 0C. bV bV R --12lnD. 12lnV V R 3. 对于一均相体系, VP T S T T S T ⎪⎭⎫⎝⎛-⎪⎭⎫⎝⎛∂∂∂∂等于(D 。
化⼯热⼒学答案（3章）3-1. 物质的体积膨胀系数β和等温压缩系数k 的定义分别为：1P V V T β=，1TV k V P =- ?。
试导出服从Vander Waals 状态⽅程的β和k 的表达式。
解：Van der waals ⽅程2 RT a P V b V=--由Z=f(x,y)的性质1y x z z x y x y z =- ? ?得 1T P VP V T V T P=- ? ? ???? ⼜ ()232TP a RTV VV b =-- VP R T V b= ?-所以 ()2321P a RT V V b V T RV b -??-??=-??-()()3232P RV V b V T RTV a V b -= ?-- 故 ()()22312PRV V b V V T RTV a V b β-==--()()222312T V V b V k V P RTV a V b -=-= ?-- 3-2. 某理想⽓体借活塞之助装于钢瓶中，压⼒为，温度为93℃，反抗⼀恒定的外压⼒ MPa ⽽等温膨胀，直到两倍于其初始容积为⽌，试计算此过程之U ?、H ?、S ?、A ?、G ?、TdS ?、pdV ?、Q和W 。
解：理想⽓体等温过程，U ?=0、H ?=0∴ Q =-W =21112ln 2V V V V RTpdV pdV dV RT V==== J/mol ∴ W = J/mol⼜ PP dT V dSC dP T T=- ?理想⽓体等温膨胀过程dT =0、P V R T P= ? ∴ R dS dP P=-∴ 222111ln ln ln2S P P P S P SdS R d P R PR ?==-=-=??=(mol·K)A U T S ?=?-?=-366×= J/(mol·K)G H T S A ?=?-?=?= J/(mol·K)TdS T S A =?=??= J/(mol·K)21112ln 2V V V V RTpdV pdV dV RT V==== J/mol 3-3. 试求算1kmol 氮⽓在压⼒为、温度为773K 下的内能、焓、熵、V C 、p C 和⾃由焓之值。
