下载文档原格式
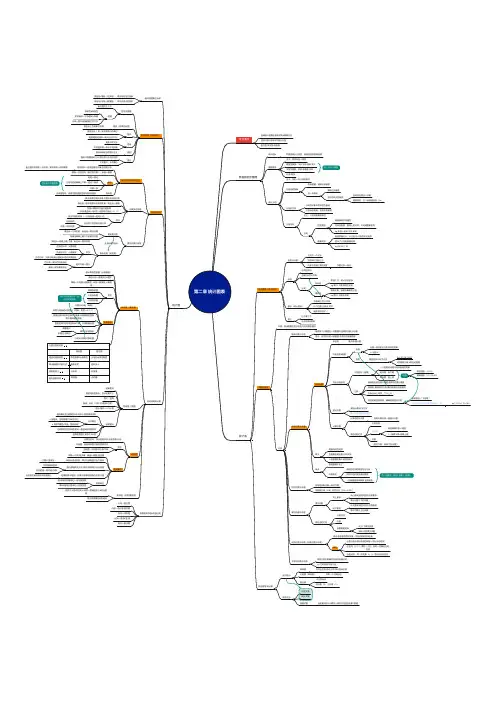
条形图直方图第二章 统计图表学习重点各种统计图表的基本结构&编制方法各种次数分布表&次数分布图直方图条形图线形图数据的初步整理统计指标对数据统计分类后，得到的各种数量结果数据排序含义：顺序标准→排列数值型数据：大小长短高低多少字符型数据：拼音笔画数字母升序/降序进一步划分等级统计分组含义：特征→划分到组别中分组前的准备校核数据：消除记录误差进一步核实删除过失数据变异性较大的数据没有充足理由→不删删除原则：三个标准差准则（3σ）分组时注意以研究对象本质特性为基础分类标志明确，包括所有数据分组标志含义：分组所依据的特性分类性质类别根据事物不同属性反映在组别、种类上的不同，不说明数量差异e g.年龄→老年中年青年数量类别依据取值大小，以分组/不分组的形式排序显示了分类的数量信息e g.96 86 77 63统计表组成要素（基本结构）表号及标题之间空一个汉字居中排在顶线上方长度不宜超过表的宽度字数过多→转行标目分类的项目含单位&百分号等分类纵标目表格上方，统计分析指标e g.表2-1 尽职情况的评定横标目表格左侧，被研究事物的分组e g.表2-1 非常不尽职数字（统计指标）不带单位百分号等以个位数/小数点对齐缺数字的项划“—”表注位于表下方补充说明&解释次数分布表作用：表示数据在各分组区间内的散布情况分类简单次数分布表依据每个分数值在一列数据中出现的次数/总计数适合：按类别分的计数数据连续性的测量数据分组次数分布表编制步骤求全距最大数最小数决定组距&组数组距任意一组的起点与终点间的距离＝全距/K 组数数据总体分布为正态K =1.87*(N-1)2/5N 为数据个数 K 取近似整数列出分组区间分组区间（组限）一个组的起点值与终点值间的距离起点值：组下限终点值：组上限组限表述组限：10~19精确组限：9.5~19.499注意最高组区间含最大数据最低组含最小数据最高组/最低组的下限最好是组距的整数倍在纵坐标上排序，下小上大表述组限呈现表格，精确组限登记次数呈现表格→“下组限~”分组区间分界点的值登记到上一组e g.179.5→170~180登记次数画线计数卌/写正字第一次登记后要再核实计算次数计算各组总次数各组次数总和＝数据总个数表包含的栏目分组区间组中值每组精确下限+½组距½（精确下限+精确上限）次数（相对次数：频率百分次数）意义将数列排列成序各数据出现次数分布状况一组数据的集中&差异情况缺点原始数据不见了归组效应假设各区间的数据均匀分布用组中值代表各原始数据→忽略数据原来情况造成误差同一组数据，组距↑误差↑（有限）相对次数分布表将各组实际次数→相对次数用频数比率（f/N ）或百分比（f/N ×100％）累加次数分布表累加次数向上累加从小数端逐区间进行次数累加表示上限以下的次数向下累加从大数端逐区间进行次数累加表示下限以上的次数表包含的栏目分组区间次数根据需要选择向上/下累加次数实际/相对累加次数双列次数分布表（相关次数分布表）表示有联系的两列变量（同组/质被试的结果）编制①按分组次数分布表的编制→得出分组区间②竖列（小下）横列（小左）各有一变量的分组区间③登记时，同一对变量（x ，y ）登记在相应格子不等距次数分布表等距分组不能确切反映实际情况时e g.工资级别年龄分组其他常用统计表按内容分简单表只列出名称地点时序统计指标名称分组表（单向表）只有一个分类标志复合表≥2分类标志双向表（2）三向表（3）按形式分定性式表统计式表函数式表自变量X 的大小顺序→排列对应的因变量Y 数值统计图一般采用直角坐标系横坐标/横轴（分类轴）：表示组别/自变量X 纵坐标/纵轴（数值轴）：表示次数/因变量Y 组成要素（基本结构）图号及图题置于图的正下方图题说明性&专指性资料复杂→大标题&小标题字体→图中使用的最大号文字图目（刻度线标签）横坐标上各种单位名称图尺横纵坐标上用一定距离表示的单位数据值相差悬殊→断尺法/回尺法图形避免书写文字不同图形线→表示不同结果图例表示&标明各种图形含义图注图形中需要借助文字/数字加以补充说明的文字要少，字号要小次数分布图直方图（等距直方图）矩形面积→连续性随机变量的次数分布直方图的总面积→总次数；矩形面积→该组频数横轴→分组区间（有时组中值）；纵轴→频数制作组距→底边分组区间的精确上下限→底边二端点次数→高组织图没有画矩形，使直方图包围的面积成封闭图形各矩形间不留空隙次数多边形图表示连续性随机变量次数分布的线形图横坐标→组中值表示的连续变量；纵坐标→频数为使计算面积与直方图相等→折线画至前一组&后一组的组中值点（x ，0）作用显示次数的轮廓（→分布曲线→经验公式）比较多个同质的次数分布组距相同次数→相对次数累加次数分布图累加直方图横坐标→分组区间；纵坐标→累加次数能看出精确上限以下的累加次数累加曲线（递加线）横坐标→精确上限/下限；纵坐标→累加次数形状正偏态分布：大数端缓负偏态分布：小数端缓正态分布：大数小数端分组数目&各组次数相当相对次数→图尺百分数→累加百分数曲线频率→累加频率曲线其他常用统计图条形图（直条图）表示离散型数据（计数数据）条形长短→数量大小&差异横轴→分类轴计数数据；纵轴→数量轴计量数据类型简单条形图分组条形图分段条形图①比较的长条拼在一起②必须有图例绘制要点尺度从0开始（纵轴）条宽与间隔的比例适当（间隔：条宽＝0.5~1）直条的排列顺序可按时间数量比较事物的固有序列具体情况来定图形区域中条形的顶端&下端，少用数据标签调节过长的条形调整图尺折叠法回转法分组&分段复式条形图与直方图的区别描述的数据类型称名数据/计数数据分组的连续性数据表示数据多少的方式直条长短面积大小横轴的意义分类轴刻度值图形直观形状有间隔无间隔圆形图（饼图）绘制要点描述间断性资料，显示比重大小图式：圆周基线：半径（12时时钟指针位置）部分/整体＝X/360度绘制要点基线确定后按顺时针由大而小/固有顺序排列分开扇区a 用线条，注明简要文字&百分比b 用不同颜色/线条，图例说明比较两种性质类似的资料→直径&排列顺序同各扇区度数之和等于360度线形图连续性资料，表示函数关系/变化趋势/比较类型折线图：连接条形图中条形顶部中点曲线图：折线修匀后较平滑绘制要点横轴→时间/自变量；纵轴→频数/因变量纵轴从零点开始，零点与横轴相交处为原点（对数尺度除外）线与横轴间无文字/数目线条粗于坐标格线不同线要有图例比较的线一般不超过5条若横轴表示组距，刻度只需表明组距起点/组中值点应画在该组段中点的垂线上对数单位横/纵轴取对数单位→半对数曲线横&纵轴取对数单位→对数曲线散点图（点图散布图）相同大小圆点的多少/疏密→数量的多少&变化趋势表示两现象的相关趋势根据表现作用&内容分类分布→直方图内容→条形图圆形图变化→线形图比较→直条圆线相关→散点图连接矩形右端点。
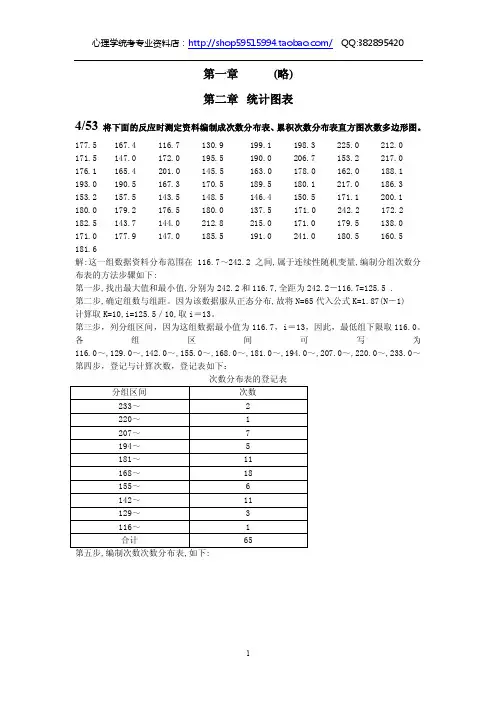
《心理统计学》重要知识点第二章 统计图表简单次数分布表的编制：Excel 数据透视表列联表（交叉表）：两个类别变量或等级变量的交叉次数分布，Excel 数据透视表直方图（histogram ）：直观描述连续变量分组次数分布情况，可用Excel 图表向导的柱形图来绘制 散点图（Scatter plot ）：主要用于直观描述两个连续性变量的关系状况和变化趋向。
条形图（Bar chart ）：用于直观描述称名数据、类别数据、等级数据的次数分布情况。
简单条形图：用于描述一个样组的类别（或等级）数据变量次数分布。
复式条形图：用于描述和比较两个或多个样组的类别(或等级)数据的次数分布。
圆形图（circle graph ）、饼图（pie graph ）：用于直观描述类别数据或等级数据的分布情况。
线形图（line graph ）：用于直观描述不同时期的发展成就的变化趋势；第三章 集中量数● 集中趋势和离中趋势是数据分布的两个基本特征。
● 集中趋势：就是数据分布中大量数据向某个数据点集中的趋势。
● 集中量数：描述数据分布集中趋势的统计量数。
● 离中趋势：是指数据分布中数据分散的程度。
● 差异量数：描述数据分布离中趋势（离散程度）的统计量数 ● 常用的集中量数有：算术平均数、众数（M O ）、中位数（M d ） 1．算术平均数（简称平均数，M 、X 、Y ）：nx X i∑= Excel 统计函数AVERAGE算术平均数的重要特性：（1）一组数据的离均差（离差）总和为0，即0)(=-∑x x i（2）如果变量X 的平均数为X ，将变量X 按照公式bx a y +=转换为Y 变量后，那么，变量Y 2．中位数（median ，M d ）：在一组有序排列的数据中，处于中间位置的数值。
中位数上下的数据出现次数各占50%。
3．众数（mode ，M O ）：一组数据中出现次数最多的数据。
4．算术平均数、中数、众数之间的关系。
心理统计学一．描述统计（一）统计图表 1、统计图次数分布图——①直方图：用以矩阵的面积表示连续性随即变量次数分布的图形。
②次数多边形图：一种表示连续性随机变量次数分布的线形图，属于次数分布图。
③累加次数分布图：分为累加直方图和累加曲线图；其中累加曲线的形状大约有三种：一种是曲线的上枝长于下枝（正偏态），另一种是下枝长于上枝（负偏态），第三种是上枝，下枝长度相当（正态分布）。
其他统计图：条形图：用于离散型数据资料； 圆形图：用于间断性资料；线形图：更多用于连续性资料，凡预表示两个变量之间的函数关系，或描述某种现象在时间上的发展趋势，或一种现象随另一种现象变化的情况，用这种方法比较好。
散点图： 2、统计表①简单次数分布表 ②分组次数分布表③相对次数分布表：将次数分布表中各组的实际次数转化为相对次数，即用频数比率表示。
④累加次数分布表⑤双列次数分布表：对有联系的两列变量用同一个表来表示其次数分布。
（二）集中量数 1、算术平均数M1nii XX N==∑优点：反应灵敏；计算严密；计算简单；简明易解；适合于进一步用代数方法演算；较少受抽样变动的影响；缺点：受极端数据的影响；若出现模糊不清的数据时，无法计算平均数； 计算和运用平均数的原则： 同质性原则；平均数与个体数值相结合的原则； 平均数与标准差、方差相结合原则； 性质：①在一组数据中每个变量与平均数之差的总和等于零②在一组数据中，每一个数都加上一个常数C ，所得的平均数为原来的平均数加常数C ③在一组数据中，每一个数都乘以一个常数C ，所得的平均数为原来的平均数乘以常数C 2、中数：Md 按顺序排列在一起的一组数据中居于中间位置的数，即这组数据中，一般数据比它大，一般数据比它小。
注意计算方法；3、众数：Mo 是指在次数分布中出现次数最多的那个数值；三者的关系：正偏态分布中，M>Md>Mo 负偏态分布中，M<Md<MoMo=3Md-2M （自己推导一下）（三）差异量数差异量数就是对一组数据的变异性，即离中趋势特点进行度量和描述的统计量，也称为离散量数。
心理统计学目录一、描述统计 (3)(一)、统计图表 (3)1.统计图 (3)2.统计表 (3)(二)、集中量数 (3)1.算术平均数 (3)2.中数 (3)3.众数 (4)(三)、差异量数 (4)1.离差与平均差 (4)2.方差与标准差 (4)(四)、相对量数 (5)1.百分位数 (5)2.百分等级 (5)3.标准分数 (6)（五）、分布性状-偏态和峰度 (6)（六）、相关量数 (6)1.积差相关 (6)2.斯皮尔曼等级相关 (7)3.肯德尔等级相关 (8)4.点二列相关 (9)5.二列相关 (9)6.Φ相关 (10)7.相关系数差异的显著性检验 (10)8.数据类型与相关系数类型 (10)二、推断统计 (11)(一)、推断统计的数学基础 (11)1.概率 (11)2.概率分布 (11)3. 样本平均数分布 (14)4. 抽样原理与抽样方法 (14)(二)、参数估计 (14)1.点估计、区间估计与标准误 (14)2.总体平均数的估计 (14)3.标准差与方差的估计 (15)(三)、假设检验 (15)1.假设检验的原理 (15)2.样本与总体平均数差异的检验 (15)3.两样本平均数差异的检验 (16)4.方差齐性的检验 (17)5.卡方检验 (18)6.非参数检验 (20)(四)、方差分析 (21)1.方差分析的原理与基本过程 (21)2.完全随机设计（独立组设计）的方差分析 (22)3.随机区组设计（重复测量设计）的方差分析 (22)4.协方差分析 (24)5.多因素方差分析 (24)6.事后检验 (24)(五) 、统计功效与效果量 (25)(六)、一元线性回归分析 (26)1.一元线性回归方程的建立、检验及应用 (26)2.可化为一元线性回归的曲线方程 (27)(七)、多元统计分析初步 (28)1. 多元线性回归分析 (28)2. 主成分分析 (28)3. 因素分析 (29)一、描述统计(一)、统计图表1.统计图条形图、帕累托图（曲线函数二阶导数正负转折点位于前半段为正偏态，位于后半段则为负偏态）、饼图、环形图、直方图、箱线图、垂线图（将同一样本或类别的多个取值的散点用一条垂线连接起来，用垂线的长度和垂线上的各个点来反映某个样本或类别取值的差异及其分布状况）、误差图（以均值为中心，加减一定倍数的标准差绘制而成，展示多个样本或分类的不同取值的分布状况和离散状况）、散点图、雷达图（可先对数据进行标准化处理）、轮廓图（折线图）。
