《电路分析》二阶电路教案
- 格式:ppt
- 大小:431.00 KB
- 文档页数:35


二阶电路教学设计摘要:本文旨在设计一份针对二阶电路的教学设计,通过理论和实践相结合的方式,帮助学生全面了解和掌握二阶电路的基本原理、特性和应用。
本文主要分为三个部分:理论知识介绍、实验设计和实验报告分析。
一、理论知识介绍1.1 二阶电路的基本概念介绍二阶电路的定义、特点和基本分类,包括有源二阶电路和无源二阶电路的区别。
1.2 二阶电路的频率响应特性介绍二阶电路的频率响应特性,包括幅频特性和相频特性,并解释其背后的原理。
1.3 二阶电路的传递函数介绍二阶电路的传递函数表示方法,包括标准形式、零极点形式和极点频率形式,并讲解如何通过传递函数计算电路的频率响应特性。
1.4 二阶电路的稳态响应和暂态响应介绍二阶电路的稳态响应和暂态响应的概念和计算方法,以及二阶电路的阻尼比、共振频率和带宽的定义和计算。
二、实验设计2.1 实验目的明确本次实验的主要目的和学习要点,包括了解二阶电路的基本特性、掌握二阶电路的频率响应特性测量方法等。
2.2 实验器材和仪器列出本次实验所需的器材和仪器清单,包括二阶电路示波器、信号发生器、电流电压表等。
2.3 实验步骤和操作详细描述实验的具体步骤和操作流程,包括搭建电路、调节仪器、测量数据等。
2.4 实验数据记录与分析记录并分析实验过程中的数据,包括幅频特性曲线和相频特性曲线的绘制,以及对实验数据的解读和分析。
三、实验报告分析在实验报告分析阶段,要求学生根据实验数据和理论知识,对实验结果进行分析和总结,包括对二阶电路的频率响应特性的理解、实验结果与理论计算结果的比较和分析,发现实验中的问题并提出改进措施等。
结论:通过本次二阶电路的教学设计,学生能够全面了解和掌握二阶电路的基本原理、特性和应用。
通过理论和实践相结合的学习方式,学生能够更好地理解电路原理,掌握实验操作技巧,并能够独立进行电路实验设计和数据分析。
这样的教学设计有助于提高学生的实践能力和创新意识,培养学生的问题解决能力和团队合作精神。


第七章二阶电路重点要求:1. 理解二阶电路零输入响应过渡过程的三种情况;2. 了解二阶电路的阶跃响应和冲击响应。
3.学习数学中的拉普拉斯变换的定义、性质及反变换的方法;4.掌握用拉普拉斯变换求解电路的过渡过程的方法。
1§7-1 二阶电路的零输入响应二阶电路:由二阶微分方程描述的电路。
典型的二阶电路是RLC串联电路。
求全响应方法:1.经典法(时域分析法)全响应= 稳态分量(强制分量) + 暂态分量(自由分量)2.拉普拉斯变换法(频域分析法)2响应曲线:U 0u C , u L , i 0ωtiu Cu L§7-1 二阶电路的零输入响应220p ααω=−±−一. 问题的提出经典法解动态电路过渡过程存在的问题:对较复杂的电路,联立求解微分方程特别是定积分常数比较困难。
若激励不是直流或正弦交流时,特解不容易求得。
二. 拉氏变换法用积分变换的原理简化求解电路过渡过程时域电路解微分方程时域响应f(t)取拉斯变换复频域电路解代数方程复频域响应F(s)取拉斯反变换7.2 动态电路的复频域分析应用拉氏变换法进行电路分析称为电路的一种复频域分析方法,也叫运算法!是数学中的一种积分变换.优点:对复杂电路﹑无稳态情况﹑换路时出现强迫跃变等用拉氏变换法较经典法方便。
三. 拉普拉斯变换的定义设函数f(t)在0≤t ≤∞时有定义,则积分称为原函数f(t)的拉普拉斯变换(象函数)。
()dte tf s F st∫∞−−=0)(式中s=σ+ j ω----复频率。
单位:熟悉的变换:相量法⎩⎨⎧=∫∞+∞−)s (21)(ds e F j t f stj c j c π反变换正变换ZH1.象函数F (s)存在的条件:∞<∫∞−−dt et f st0)(说明:电路分析中的函数都能满足上述条件。
2. 在电路中积分的下限定义为“0-”, 更有实际意义(将奇异函数也包括在内)。
[][]⎩⎨⎧==−)( )()( )( S F t f t f S F 1简写正变换反变换在电路分析中通常直接查表得到。




二阶电路课程设计一、课程目标知识目标:1. 学生能理解并掌握二阶电路的基本概念,包括RLC串联电路和并联电路的特性。
2. 学生能够运用相关公式计算二阶电路的响应,分析其暂态过程和稳态过程。
3. 学生能够解释二阶电路中振荡现象的产生原因及其影响。
技能目标:1. 学生能够运用所学知识,正确绘制二阶电路的原理图,并进行电路分析。
2. 学生能够运用相关公式和参数,计算二阶电路的时域响应和频域响应。
3. 学生能够通过实验和仿真软件,验证二阶电路的理论知识,并解决实际问题。
情感态度价值观目标:1. 培养学生对电路分析的兴趣,激发他们探索科学问题的热情。
2. 培养学生严谨的科学态度,使他们能够客观、理性地看待电路现象。
3. 培养学生的团队协作精神,提高他们在学术交流和合作学习中的沟通能力。
课程性质:本课程为电子信息工程及相关专业的高年级专业课程,旨在帮助学生深入理解二阶电路的原理和应用。
学生特点:学生已具备一定的电路基础知识,具有较强的逻辑思维能力和动手能力。
教学要求:结合学生特点和课程性质,本课程要求教师采用理论教学与实践操作相结合的方式,注重启发式教学,引导学生主动探索,提高分析问题和解决问题的能力。
通过课程学习,使学生能够将所学知识应用于实际电路设计和分析中。
二、教学内容1. 二阶电路概述- RLC串联电路和并联电路的基本概念- 二阶电路的阶跃响应、冲激响应及其特性2. 二阶电路的数学模型- 二阶电路微分方程的建立- 二阶电路的特征方程和特征根- 二阶电路的状态方程和输出方程3. 二阶电路的时域分析- 阶跃响应和冲激响应的计算- 暂态过程和稳态过程的判断与计算- 过渡过程的能量转换与损耗4. 二阶电路的频域分析- 幅频特性与相频特性- 传递函数与波特图- 频率响应的实验验证5. 二阶电路的振荡现象- 振荡产生的原因及条件- 振荡频率与品质因数的计算- 振荡电路的设计与应用6. 二阶电路仿真与实验- Multisim、PSpice等仿真软件的应用- 二阶电路实验方案的设计与实施- 实验结果的分析与讨论教学内容依据课程目标,遵循科学性和系统性原则,按照教学大纲的安排进行。
第七章二阶电路一、教学基本要求1、了解二阶电路零状态响应、零输入响应、全响应的物理意义和概念。
2、会分析简单的二阶电路。
二、教学重点与难点1. 教学重点: (1).二阶电路的方程和特征根(2). 二阶电路的零输入响应、零状态响应、全响应的概念(3). 二阶电路过渡过程的过阻尼、欠阻尼及临界阻尼的概念及分析(4). 二阶电路的阶跃响应。
2.教学难点:1.应用基尔霍夫定律和电感、电容的元件特性建立动态电路方程;2. 二阶电路的过阻尼、欠阻尼及临界阻尼放电过程分析方法和基本物理概念。
三、本章与其它章节的联系:本章讨论的仍是线性电路,因此前面讨论的线性电路的分析方法和定理全部可以用于本章的分析中。
第 9 章讨论的线性电路的正弦稳态响应就是动态电路在正弦激励下的稳态分量的求解。
四、学时安排总学时:2五、教学内容§7.1 二阶电路的零输入响应二阶电路是指用二阶微分方程来描述的电路。
下面主要通过分析RLC 串联电路来说明求二阶电路响应的方法。
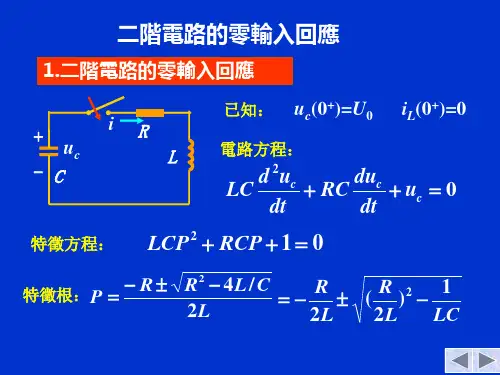
1.方程和初始条件图 7.1图7.1所示的RLC串联电路在t=0时刻闭合开关,设电容原本充有电压U0,此电路的放电过程是二阶电路的零输入响应问题。
电路的KVL方程及元件的VCR 为:若以电容电压为变量,从以上方程中消去其他变量得二阶齐次微分方程:初始条件为:u C (0+)= U 0 ,i (0+)=0 ,或若以电感电流为变量,则方程为:初始条件为:i (0+)=0 ,根据得:2.二阶微分方程的解及其物理意义以电容电压为变量,电路方程为:从中得特征方程:特征根为:上式表明特征根仅与电路参数和结构有关,而与激励和初始储能无关。
当R、L、C的参数不同,特征根为不同的形式。
下面分三种情况讨论。
(1)当时,特征根为两个不相等的负实根,电路处于过阻尼状态。
此时方程的解为:由初始条件:,得:即:因此电容电压为:电流为:电感电压为:图7.2给出了电容电压、电流和电感电压随时间变化的波形,从中可以看出,电容电压和电流始终不改变方向,且最终衰减至零,说明电容始终在释放能量,称过阻尼放电。
第十二章 二阶电路12.1 二阶电路的零输入响应12.1.1 RLC 串连电路1. 建立关于u C 的电路方程u C +u L +u R =u C +L di L dt +Ri L =0, i L =C du C dt{LC d 2u C dt 2+RC du C dt +u C =0u C (0+)=u C (0−)=U 0, i L (0+)= i L (0−)=0这是一个常系数线性齐次二阶微分方程。
2. 确定特解(稳态解)u CP =03. 确定通解特征方程为:LCP 2+RCP +1=0特征根为P =−R 2L ±√(R 2L )2−1LC所以u C 的通解为:u C ℎ=A 1e P 1t +A 2e P 2t4. 写出全解u C =u Cp +u C ℎ=A 1e P 1t +A 2e P 2t其中RC L u L u C i LP 1=−R 2L +√(R 2L )2−1LC ,P 2=−R 2L −√(R 2L )2−1LC5. 确定待定系数由给定初始条件u C (0+)=U 0=[A 1e P 1t +A 2e P 2t ]|t=0+=A 1+A 2 i L (0+)=0=C du C dt |t=0+=C[P 1A 1e P 1t +P 2A 2e P 2t ]|t=0+=[A 1P 1+A 2P 2]C即:{A 1+A 2=U 0A 1P 1+A 2P 2=0解得:{ A 1=P 2U 0P 2−P 1A 2=−P 1U 0P 2−P 1 代入通解,并整理得零输入相应:u C =U 0P 2−P 1(P 2e P 1t −P 1e P 2t ) i L =C du C dt =U 0CP 1P 2P 2−P 1(e P 1t −e P 2t )=U 0L (P 2−P 1)(e P 1t −e P 2t ) u L =L di L dt =U 0P 2−P 1(P 1e P 1t −P 2e P 2t ) 均为t ≥0时,下同。