两个一次函数绝对值的和与差求最值的方法探究

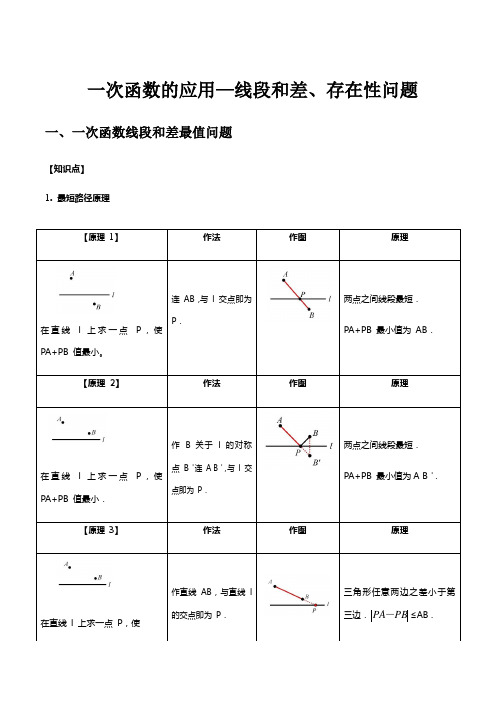
一次函数的应用—线段和差、存在性问题一、一次函数线段和差最值问题【知识点】1. 最短路径原理【原理1】作法作图原理在直线l 上求一点P，使PA+PB 值最小。

连AB，与l 交点即为P．两点之间线段最短．PA+PB 最小值为AB．【原理2】作法作图原理在直线l 上求一点P，使PA+PB 值最小．作 B 关于l 的对称点B＇连A B＇，与l 交点即为P．两点之间线段最短．PA+PB 最小值为A B＇．【原理3】作法作图原理在直线l 上求一点P，使作直线AB，与直线l的交点即为P．三角形任意两边之差小于第三边．≤AB .PBPA－（1）求线段和最小时动点坐标或直线解析式； （2）求三角形周长最小值；（3）求线段差最大时点的坐标或直线解析式。

3. 口诀：“和小异，差大同”（一）一次函数线段和最小值问题【例题讲解】★★☆例题1．在平面直角坐标系xOy 中，y 轴上有一点P ，它到点(4,3)A ，(3,1)B 的距离之和最小，则点P 的坐标是( ) A ．(0,0)B ．4(0,)7C ．5(0,)7D ．4(0,)5【答案】C的值最大 .【原理 4】作法作图原理在直线 l 上求一点 P ，使的值最大 .作 B 关于 l 的对称点 B ＇作直线 A B ＇，与 l 交点即为 P ．三角形任意两边之差小于第三边．≤A B ＇ .PB PA －PB PA －PB PA －【解析】解：作A 关于y 轴的对称点C ，连接BC 交y 轴于P ，则此时AP PB +最小，即此时点P 到点A 和点B 的距离之和最小，(4,3)A ，(4,3)C ∴-，设直线CB 的解析式是y kx b =+，把C 、B 的坐标代入得：3413k bk b =-+⎧⎨-=+⎩，解得：47k =-，57b =，4577y x ∴=-+，把0x =代入得：57y =， 即P 的坐标是5(0,)7，故选：C ．【备注】本题考查了轴对称-最短路线问题，一次函数的解析式，坐标与图形性质等知识点，关键是能画出P 的位置，题目比较典型，是一道比较好的题目．★★☆练习1．如图，在平面直角坐标系中，已知点(2,3)A ，点(2,1)B -，在x 轴上存在点P 到A ，B 两点的距离之和最小，则P 点的坐标是 ．【答案】(1,0)-【解析】解：作A 关于x 轴的对称点C ，连接BC 交x 轴于P ，则此时AP BP +最小，A 点的坐标为(2,3)，B 点的坐标为(2,1)-，(2,3)C ∴-，设直线BC 的解析式是：y kx b =+，把B 、C 的坐标代入得：2123k b k b -+=⎧⎨+=-⎩解得11k b =-⎧⎨=-⎩．即直线BC 的解析式是1y x =--，当0y =时，10x --=，解得：1x =-，P ∴点的坐标是(1,0)-．故答案为：(1,0)-．【备注】本题考查了一次函数图象上点的坐标特征，用待定系数法求一次函数的解析式，轴对称-最短路线问题的应用，关键是能找出P 点，题目具有一定的代表性，难度适中．★★☆练习2．如图，直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点，以线段AB 为边在第一象限内作正方形ABCD ．若点P 为x 轴上的一个动点，求当PC PD +的长最小时点P 的坐标．【答案】详见解析【解析】解：直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点，则点A 、B 的坐标分别为：(0,3)，(4,0)，如图所示，过点C 作CH x ⊥轴交于点H ，90ABO BAO ∠+∠=︒，90ABO CBH ∠+∠=︒，CBH BAO ∴∠=∠，又90AOB CHB ∠=∠=︒，AB BC =，()AOB BHC AAS ∴∆≅∆，4CH OB ∴==，3HB OA ==，故点(7,4)C ，同理可得点(3,7)D ，确定点C 关于x 轴的对称点(7,4)C '-，连接C D '交x 轴于点P ，则此时PC PD +的长最小，将点C '、D 的坐标代入一次函数表达式并解得： 直线CD 的表达式为：116144y x =-+， 当0y =时，6111x =，故点61P，0)．(11【备注】本题考查的是一次函数上坐标点的特征，涉及到点的对称性、正方形性质等，本题的难点在于：通过证明三角形全等，确定点C、D的坐标．★★☆例题2．在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，3OB=，D为边OB的中点，若E为x轴上的一个动点，当CDE∆的周长最小时，求点E OA=，4的坐标()A．(3,0)-B．(1,0)C．(0,0)D．(3,0)【答案】B【解析】解：如图，作点D关于x轴的对称点D'，连接CD'与x轴交于点E，连接DE．若在边OA上任取点E'与点E不重合，连接CE'、DE'、D E''由DE CE D E CE CD D E CE DE CE'+'=''+'>'='+=+，可知CDE∆的周长最小．OB=，D为边OB的中点，42∴=，OD∴，(0,2)D在矩形OACB 中，3OA =，4OB =，D 为OB 的中点，3BC ∴=，2D O DO '==，6D B '=，//OE BC ，Rt ∴△D OE Rt '∽△D BC '，∴OE D OBC D B '=' 即236OE = 1OE =，∴点E 的坐标为(1,0)故选：B ．【备注】此题主要考查轴对称--最短路线问题，解决此类问题，一般都是运用轴对称的性质，将求折线问题转化为求线段问题，其说明最短的依据是三角形两边之和大于第三边．★★☆练习1．如图，在平面直角坐标系中，点A 、B 的坐标分别为(1,4)和(3,0)，点C 是y 轴上的一个动点，连接AC 、BC ，当ABC ∆的周长最小值时，ABC ∆的面积为 ．【答案】3【解析】解：如图，作点A 关于y 轴的对称点A '，连接A B '交y 轴于点C '，此时ABC ∆'的周长最小，设直线A B ' 的解析式为y kx b =+，(1,4)A '-，(3,0)B ，∴430k b k b -+=⎧⎨+=⎩，1k ∴=-，3b =，∴直线A B ' 的解析式为3y x =-+，当0x =时，3y =，(0,3)C ∴'，ABC AA BAA C S SS∆'''∴=-11242122=⨯⨯-⨯⨯ 413=-=．所以ABC ∆'的面积为3．故答案为：3．【备注】本题考查了轴对称、最短路线问题、坐标与图形性质、三角形的面积，解决本题的关键是掌握轴对称的性质．★★☆练习2．如图，在平面直角坐标系中，直线122y x =+与x 轴、y 轴分别交于A 、B 两点，以AB 为边 在第二象限内作正方形ABCD ．（1）求点A 、B 的坐标，并求边AB 的长；（2）求点C 和点D 的坐标；（3）在x 轴上找一点M ，使MDB ∆的周长最小，请求出M 点的坐标，并直接写出MDB ∆的周长最小值．【答案】详见解析【解析】解： （1）对于直线122y x =+， 令0x =，得到2y =；令0y =，得到4x =-，(4,0)A ∴-，(0,2)B ，即4OA =，2OB =， 则224225AB =+=；（2）过D 作DE x ⊥轴，过C 作CF y ⊥轴，四边形ABCD 为正方形，AB BC AD ∴==，90ABC BAD BFC DEA AOB ∠=∠=∠=∠=∠=︒，90FBC ABO ∠+∠=︒，90ABO BAO ∠+∠=︒，90DAE BAO ∠+∠=︒，FBC OAB EDA ∴∠=∠=∠，()DEA AOB BFC AAS ∴∆≅∆≅∆，2AE OB CF ∴===，4DE OA FB ===，即426OE OA AE =+=+=，246OF OB BF =+=+=，则(6,4)D -，(2,6)C -；（3）如图所示，连接BD ，找出B 关于y 轴的对称点B '，连接DB '，交x 轴于点M ，此时BM MD DM MB DB +=+'='最小，即BDM ∆周长最小，(0,2)B ，(0,2)B ∴'-，设直线DB '解析式为y kx b =+，把(6,4)D -，(0,2)B '-代入得：642k b b -+=⎧⎨=-⎩，解得：1k =-，2b =-，∴直线DB '解析式为2y x =--，令0y =，得到2x =-，则M 坐标为(2,0)-， 此时MDB ∆的周长为21062+．【备注】本题属于一次函数综合题，涉及的知识有：待定系数法求一次函数解析式，坐标与图形性质，勾 股定理，全等三角形的判定与性质，正方形的性质，对称性质，以及一次函数与坐标轴的交点，熟练掌握 性质及定理是解本题的关键（二）一次函数线段差最大值问题【例题讲解】★★☆例题1．已知，如图点(1,1)A ，(2,3)B -，点P 为x 轴上一点，当||PA PB -最大时，点P的坐标为( )A ．1(,0)2B ．5(,0)4C ．1(,0)2-D ．(1,0)【答案】A【解析】解：作A 关于x 轴对称点C ，连接BC 并延长交x 轴于点P ， (1,1)A ，C ∴的坐标为(1,1)-，连接BC ，设直线BC 的解析式为：y kx b =+，∴123k b k b +=-⎧⎨+=-⎩， 解得：21k b =-⎧⎨=⎩， ∴直线BC 的解析式为：21y x =-+， 当0y =时，12x =， ∴点P 的坐标为：1(2，0)，当B ，C ，P 不共线时，根据三角形三边的关系可得：||||PA PB PC PB BC -=-<，∴此时||||PA PB PC PB BC -=-=取得最大值．故选：A ．【备注】此题考查了轴对称、待定系数法求一次函数的解析式以及点与一次函数的关系．此题难度较大，解题的关键是找到P 点，注意数形结合思想与方程思想的应用．★★☆练习1．平面直角坐标系中，已知(4,3)A 、(2,1)B ，x 轴上有一点P ，要使PA PB -最大，则P 点坐 标为【答案】(1,0)【解析】解：(4,3)A 、(2,1)B ，x 轴上有一点P ，||PA PB AB ∴-，∴当A ，B ，P 三点共线时，PA PB -最大值等于AB 长，此时，设直线AB 的解析式为y kx b =+，把(4,3)A 、(2,1)B 代入，可得3412k b k b =+⎧⎨=+⎩， 解得11k b =⎧⎨=-⎩， ∴直线AB 的解析式为1y x =-，令0y =，则1x =，P ∴点坐标为(1,0)，故答案为：(1,0)． 【备注】本题主要考查了坐标与图形性质，利用待定系数法求得直线AB 的解析式是解决问题的关键． ★★☆练习2．如图，在平面直角坐标系中，点A 的坐标为(0,4)，点B 的坐标为(6,0)，点P 在一次函数1322y x =+的图象上运动，则PB PA -的最大值为( )A ．2B ．233C ．4D ．143【答案】C【解析】解：如图，作点A 关于直线1322y x =+的对称点K ，连接AK 交直线于H ，连接PK ．AK PH ⊥，(0,4)A ，∴直线AK 的解析式为24y x =-+，由132224y x y x ⎧=+⎪⎨⎪=-+⎩，解得12x y =⎧⎨=⎩， (1H ∴，20，AH KH =，(2,0)K ∴．PB PA PB PK KB ∴-=-，∴当点P 在BK 的延长线上时，P B P K BK '-'=的值最大，最大值为624-=，故选：C ．【备注】本题考查一次函数图象上的点的特征、轴对称等知识，解题的关键是学会利用对称解决最值问题 属于中考常考题型．【题型知识点总结】一次函数最短路径问题注意事项：1. 根据“和小异，差大同”判断是否需要作对称；2. 作对称时注意要选取动点运动的直线为对称轴作某一定点的对称点。

一类多个绝对值求和型函数最值问题的求解方法作者：王联宪来源：《中学教学参考·理科版》2010年第09期近年来,高考和竞赛常出现多个绝对值求和型函数的最值问题,该类型问题常常采用分类分段讨论去绝对值符号的办法来解决,但往往因分段区间太多而难以有效解决.若利用以下命题,则可以化繁为易,迅速解题.命题:设y=︱x-︱+︱x-︱+︱x-︱+…+︱x-︱,求y达到最小值的条件:(1)当n=2k时,x∈值达到最小;(2)当n=2k-1时时,y值达到最小.证明:利用绝对值的几何意义,可以方便的证明.(1)当n=2k时,若︱x-︱+︱x-︱-当且仅当x∈时等号成立,︱x-︱+︱x--︱--当且仅当x∈-时等号成立,…︱x-︱+︱x-︱-当且仅当x∈时等号成立.因为是以上各区间的公共的子区间,所以当且仅当x∈时,以上各式的等号能同时成立,y值才能达到最小.若时,当且仅当时,以上各式的等号能同时成立,y值才能达到最小.(2)当n=2k-1时,︱x-︱+︱x--︱--当且仅当∈-时等号成立,︱x-︱+︱x--︱--当且仅当∈-时等号成立,…︱x--︱+︱x-︱--当且仅当x∈-时等号成立;︱x-︱≥0,当且仅当时等号成立.因为是以上各区间唯一公共的元素,所以当且仅当时,以上各式的等号能同时成立,y值才能达到最小.【例1】 y=︱x-1︱+︱x-2︱+︱x-3︱+…+︱x-19︱,求y的最小值.解析:该式共19项,中项为10,由以上定理知,当且仅当x=10时,y值达到最小.即当x=10时【例2】 (第19届“希望杯”高二年级2试)如果对于任意实数x,都有y=︱x-1︱+︱x-2︱+︱x-3︱+…+︱x-2008︱≥m成立,那么m的最大值是().A.1003×1004B.10042C.1003×1005D.1004×1005解析:m的最大值,即是y的最小值.绝对值和式共2008项,中间两项分别是1004和1005,当且仅当x∈[1004,1005]时,y值能达到最小,取x=1004或x=1005代入2,故选B.【例3】 y=︱x-1︱+︱x-2︱+︱x-3︱︱x-4︱求x的解集.解析:该式共4项,中间两项分别是2和3,当且仅当x∈[2,3]时所以原不等式的解集是{x︱x3｝.【例4】 (2009,上海)某地街道呈现东西和南北方向的网格状,相邻街距都是1.两街道相交的点称为格点,若以互相垂直的两条街道为轴建立直角坐标系,现有下述格点(-2,2),(3,1),(3,4),(-2,3),(4,5),(6,6)为报刊零售点.请确定一个格点(除报刊零售点外)为发行点,使6个报刊零售点沿街道到发行站的路程和最短,求该发行点的坐标.解析:设格点为(x,y),则该格点到各零售点的距离之和为:︱x+2︱+︱x+2︱+︱x-3︱+︱x-3︱+︱x-4︱+︱x-6︱+︱y-1︱+︱y-2︱+︱y-3︱+︱y-4︱+︱y-5︱+︱y-6︱.x系列共6项,中间两项都为3,当且仅当x=3时,这一部分和值达到最小;y系列共6项,中间两项为3和4,当且仅当y∈[3,4]时,这一部分和值达到最小.所以(x,y)可取点(3,3)或(3,4),由题意舍去(3,4),所以只能选(3,3).【例5】求y=︱-1︱+︱-2︱+︱-3︱+︱-4︱+︱-5︱的最小值.解析:令则y=︱t-1︱+︱t-2︱+︱t-3︱+︱t-4︱+︱t-5︱,共5项,中间项为3,当t=3即时【例6】求y=︱︱+︱-1︱︱-2︱︱-4︱+︱-6︱的最小值.解析:令则y=︱t+1︱+︱t-1︱+︱t-2︱+︱t-4︱+︱t-6︱,共5项,中项为2,当且仅当t=2即x=4时【例7】求y=︱x2+2x-1︱+︱x2+2x-2︱+︱x2+2x-3︱的最小值.解析:令t=x2+2x,则y=︱t-1︱+︱t-2︱+︱t-3︱,共3项,中项为2,当且仅当t=2即x2+2x=2时,y有最小值,对x2+2x=2求解,得x=-1±3,此时练习:(1)求y=︱x+1︱+︱2x-6︱+︱3x-6︱的最小值.(2)求y=︱x-6︱+︱12x-6︱的最小值.分析:(1)y=︱x+1︱+︱x-2︱+︱x-2︱︱x-2︱︱x-3︱+︱x-3︱,共6项,中间两项都为2,代入x=2即可.(2)y=12(︱x-6︱+︱x-6︱+︱x-12︱),中间项为6,代入x=6即可.(责任编辑金铃)。

初中数学中求最值的几种常见方法仪陇县实验学校 李洪泉在生活实践中，人们经常面对求最值的问题：如在一定方案中，往往会讨论什么情况下花费最低、消耗最少、产值最高、获利最大等；在解数学题时也常常求某个变量的最大值或最小值。

同时，探求最值也是中考或一些高中学校自主招生考试中的一个热点内容，是初高中知识衔接的重要内容。

这类问题涉及变量多，综合性强，技巧性强，要求学生要有较强的数学转化思想和创新意识。

下面从不同的角度讨论如何求一些问题的最值。

一 、根据绝对值的几何意义求最值 实数的绝对值具有非负性，0a ≥，即a 的最小值为0，但根据绝对值的代数意义求一些复杂问题的最值就要采用分类讨论法，比较麻烦。

若根据绝对值的几何意义求最值就能够把一些复杂的问题简单化。

例1：已知13M x x =-++，则M 的最小值是 。

【思路点拨】用分类讨论法求出13x x -++的最小值是4,此时31x -≤≤。

如果我们从绝对值的几何意义来看此题,就是在数轴上求一点,使它到点1和点3-的距离之和为最短。

显然,若3x <-,距离之和为[1(3)]2(3)4x --+-->;若31x -≤≤,距离之和为1(3)4--=;若1x >,距离之和为[1(3)]2(1)4x --+->。

所以, 当31x -≤≤时,距离之和最短,最小值为4。

故M 的最小值为4。

二、利用配方法求最值完全平方式具有非负性，即2()0a b +≥。

一个代数式若能配方成2()m a b k ++的形式，则这个代数式的最小值就为k 。

例2：设,a b 为实数，求222a ab b a b ++--的最小值。

【思路点拨】一是将原式直接配方成与,a b 的完全平方式有关的式子可以求出最小值。

二是引入参数设222a ab b a b t ++--=，将等式整理成关于a 的二次方程，运用配方法利用判别式求最值。

解：(方法一) 配方得：当10,10,2b a b -+=-=即0,1a b ==时，上式中不等号的等式成立，故所求的最小值222222222(1)21331()242413()(1)1124a ab b a b a b a b b b a b b b a b ++--=+-+--=++---=++--≥-为1-。

含绝对值函数综合问题一、含绝对值函数的最值1、含一个绝对值的一次绝对值函数的最值、单调性、对称性（1）()||f x x =的图像是以原点为顶点的“V ”字形图像；函数在顶点处取得最小值“(0)0f =”，无最大值；在函数(,0],[0,)x ∈-∞↓+∞↑；对称轴为：0x =（2）()||(0)f x kx b k =+≠图像是以(,0)b k-为顶点的“V ”字形图像；在顶点取得最小值：“()0b f k -=”，无最大值；函数在(,],[,)b b x k k ∈-∞-↓-+∞↑；对称轴为：b x k=- （3）函数()||(0)f x k x b k =+≠： 0k >时，函数是以(,0)b -为顶点的“V ”字形图像；函数在顶点取得最小值：“()0f b -=”，无最大值；函数在(,],[,)x b b ∈-∞-↓-+∞↑；对称轴为：x b =-0k <时，是以(,0)b -为顶点的倒“V ”字形图像，函数在顶点取得最大值：“()0f b -=”，无最小值；函数在(,],[,)x b b ∈-∞-↑-+∞↓；对称轴为：x b =-2、含两个绝对值的一次绝对值函数的最值、单调性、对称性（1）函数()||||()f x x m x n m n =-+-<的图像是以点(,),(,)A m n m B n n m --为折点的“平底形”图像；在[,]x m n ∈上的每点，函数都取得最小值n m -，无最大值；函数在(,],[,)x m x n ∈-∞↓∈+∞↑ ，在[,]x m n ∈无单调性；对称轴为2m n x +=。

（2）函数()||||f x x m x n =---： 当m n >时，()f x 是以点(,),(,)A m n m B n m n --为折点的“Z 字形”函数图像；在(,]x n ∈-∞上的每点，函数都取得最大值m n -，在[,)x m ∈+∞上的每点，函数都取得最小值n m -；函数在[,]x n m ∈↓，在(,]x n ∈-∞及[,)x m ∈+∞上无单调性；对称中心为(,0)2m n +； 当n m >时，()f x 是以点(,),(,)A m m n B n n m --为折点的“反Z 字形”函数图像； 在(,]x m ∈-∞上的每点，函数都取得最小值m n -，在[,)x n ∈+∞上的每点，函数都 取得最大值n m -；函数在[,]x m n ∈↑，在(,]x n ∈-∞及[,)x m ∈+∞上无单调性；对称中心为(,0)2m n +； （3）()||||()f x a x m b x n m n =-+-<图像是以(,()),(,())A m f m B n f n 为折点的折线。

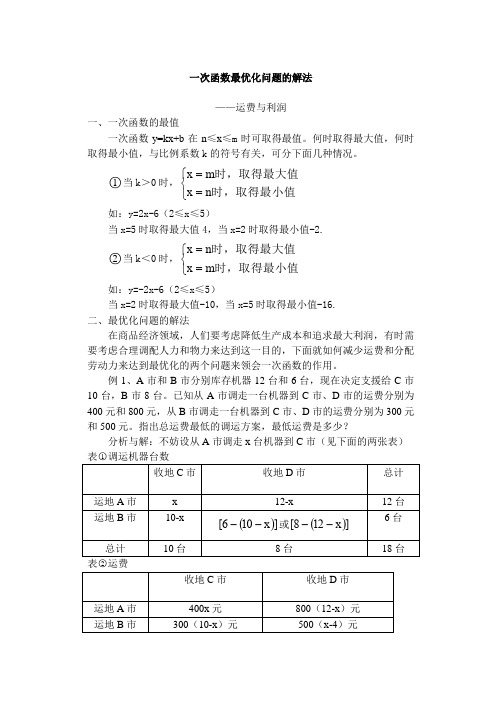
一次函数最优化问题的解法——运费与利润一、一次函数的最值一次函数y=kx+b 在n ≤x ≤m 时可取得最值。

何时取得最大值，何时取得最小值，与比例系数k 的符号有关，可分下面几种情况。

○1当k ＞0时，⎩⎨⎧==时，取得最小值时，取得最大值n x m x 如：y=2x-6（2≤x ≤5）当x=5时取得最大值4，当x=2时取得最小值-2.○2当k ＜0时，⎩⎨⎧==时，取得最小值时，取得最大值m x n x 如：y=-2x-6（2≤x ≤5）当x=2时取得最大值-10，当x=5时取得最小值-16. 二、最优化问题的解法在商品经济领域，人们要考虑降低生产成本和追求最大利润，有时需要考虑合理调配人力和物力来达到这一目的，下面就如何减少运费和分配劳动力来达到最优化的两个问题来领会一次函数的作用。

例1、A 市和B 市分别库存机器12台和6台，现在决定支援给C 市10台，B 市8台。

已知从A 市调走一台机器到C 市、D 市的运费分别为400元和800元，从B 市调走一台机器到C 市、D 市的运费分别为300元和500元。

指出总运费最低的调运方案，最低运费是多少？分析与解：不妨设从A 市调走x 台机器到C 市（见下面的两张表） 表○1调运机器台数 收地C 市收地D 市 总计 运地A 市 x 12-x12台 运地B 市 10-x ()]x 10[6--或()]x 12[8--6台 总计10台8台18台表○2运费 收地C 市 收地D 市 运地A 市 400x 元 800（12-x ）元 运地B 市300（10-x ）元500（x-4）元由上表可以看出：总运费y=400x+800（12-x ）+300（10-x ）+500（x-4） 化简得：y=-200x+9700要想运输方案能够实施，调运机器台数必须为非负数所以：⎪⎪⎩⎪⎪⎨⎧≥≥≥≥04-x 0x -100x -120x 解得：4≤x ≤10.所以,当x=10时，总运费y 取得最小值，最低运费为7700元。

一次函数与线段和的最小值研究“一次函数与线段和的最小值”问题是一个重要的数学课题。

数学可以用来分析现实中出现的很多有趣问题，而该问题就是一个好的例子。

本文的目的是在详细的数学分析的基础上，解决“一次函数与线段和的最小值”的问题。

在分析本问题之前，我们先来看看“函数”和“线段”的定义。

函数是指把元素输入到函数中，然后可以得到输出的函数称为函数。

在数学中，函数可以用公式来表示。

比如，一次函数一般用公式y=ax+b 表示，其中a,b是常数，而x是变量。

线段是指由两点确定的线，它们可以表示为y=kx+m，其中k,m也是常数，x也是变量。

解决“一次函数与线段和的最小值”的问题，我们最重要的是找到一次函数与线段的最低点。

由于一次函数可以表示为y=ax+b，而线段可以表示为y=kx+m，我们可以把两个函数组合起来，得到一个新的函数：y=ax+b+kx+m。

为了求出最低点，我们把y=ax+b+kx+m的偏导数设为0，得到x=-(b+m)/(a+k)，此时x的值就是函数的最低点，最小值就是y=-(b+m)/(a+k)。

因此，解决一次函数与线段和的最小值的问题的方法是：首先把一次函数和线段组合起来，得到新的函数，然后把函数的偏导数设为0，当x=-(b+m)/(a+k)时，最小值就是y=-(b+m)/(a+k)。

以上就是分析“一次函数与线段和的最小值”问题的结果：当x=-(b+m)/(a+k)时，最小值就是y=-(b+m)/(a+k)。

本文讨论了一次函数与线段和的最小值的问题，在数学分析的基础上，用偏导数的方法找到了解决该问题的方法：当x=-(b+m)/(a+k)时，最小值就是y=-(b+m)/(a+k)。

这就是一次函数与线段和的最小值。

本文对具有重要意义的数学问题进行了分析，提供了一种解决方案，对进一步研究和解决相关问题有一定的参考价值。

二元一次函数最值问题二元一次函数最值问题_【八上数学】函数、一次函数必考知识点(上)-csdn博客一、知识概念1、常量与变量在某一变化过程中，数值保持不变的量叫常量．在某一变化过程中，可以取不同数值的量叫变量．2、自变量与因变量，函数一般地，设在一个变化的过程中，有两个变量x和y，如果对于变量x的每一个值，变量y都有唯一的值与它对应，我们称y是x的函数，其中，x是自变量，y是因变量．3、函数的三种表示方法(1)列表法：具体地反映了函数与自变量的数值对应关系．(2)图象法：直观地反映了函数随自变量的变化而变化的规律．(3)解析法：准确地反映了函数与自变量之间的数量关系．4、一次函数和正比例函数一般地，形如y＝kx＋b(k，b为常数，且k≠0)的函数，叫做一次函数，y是x的一次函数，当b＝0，即y＝kx(k为常数且k≠0)时，称y是x的正比例函数．正比例函数一定是一次函数，一次函数不一定是正比例函数．5、待定系数法求一次函数关系式过程(1)设函数表达式y＝kx＋b；(2)根据已知条件列出关于k，b的方程(组)；(3)解方程(组)；(4)把求出的k，b值代回到表达式中．二、典型例题1、函数相关概念2、函数表示及自变量取值范围3、一次函数的概念及判定4、待定系数法运用例1：若y与x－1成正比例，且x＝2时，y＝6，则x＝－2时，y＝___．分析：我们可以设y＝k(x－1)，把x＝－2，y＝6代入，也可直接把(－2，6)代入，求得k的值，得函数的关系式，再把x＝－2代入，求得y的值．【互动必读】一文教你查询往期文章、直接下载！【重难突破】九上圆中最值问题汇编【网红模型】“对称问题”涉及的16个必考点全梳理【八上数学】全等三角形16个必考点全梳理【中考数学】三角形面积综合探究【七上数学】《有理数》月考好题精选【八上数学】等腰三角形五大考点，必须收藏！【干货汇总】一文搞定相似三角形基本模型【八上数学】《线段、角的轴对称性》必会书写格式！【初三数学】2020中考好题精选【九上数学】一文搞定“圆”中最常用12条结论【必读】很重要！各年级首次月考最实用应对方案【干货整理】涉及三角形的20个必考点全覆盖【最值系列】隐圆(2)定边对定角【专题突破】一文搞定初中数学网格问题【七上数学】《有理数》全章16个必考点全梳理！【压轴专题】图形的运动——翻折【八上数学】《轴对称》最全知识点汇总【七上数学】新学期21个必考知识点，必备！【初中数学】12张表汇齐全部重点知识，超实用！【八上数学】全等辅助线—截长补短&半角【七上数学】有理数运算典型易错题分析(下)【最值系列】隐圆(1)定点定长型【干货分享】初中数学常见解题方法梳理【九上数学】圆中的辅助线--直角、直径的互化【七上数学】有理数运算典型易错题分析(上)【干货】怎样帮助初一新生快速适应初中学习?【解题分享】巧借“对称变换”，妙解最值问题【模型突破】利用辅助圆求解动点最值问题【模型必读】相似模型全梳理，附送20道绝妙好题【中考热点】定角定高模型初探【最值模型】两点之间，线段最短！(1)【中考压轴】因动点产生的三角形相似问题【三周年特辑】对一道二次函数压轴题的探究！【考前突破】中考易错考点全整理【专题提升】几何综合图形关系的再探究【中考2020】“线段最值”系列之——轨迹思想【专题突破】特殊三角形必考解题策略汇编【专题突破】几何最值问题12小类模型全梳理【好题欣赏】由一道比例定值题引发的联想【中考2020】初中数学常见几何模型解析完整版【中考真题】函数交点问题全解析【解题探究】一类线段最值问题的本源解法——斜大于直【中考必读】几何线段最值求法大全【中考数学】中考专题复习指导兼谈核心素养命题【中考压轴】最短路径问题2【中考压轴】最短路径问题(1)。

一次函数最值的求法“一次函数最值问题”既是一次函数的应用,又是中考的热点问题。

其中利润问题的“何时费用最低？何时利润最高？”等问题是一个现实生活中的最值问题。

也是考试的高频题目。

在解题过程中，需要将实际问题转化为数学问题，构造数学模型，构建目标函数，通过一次函数的y随着x的变化趋势，可使问题得以解决。

一次函数y=kx+b中，x、y的取值范围是一切实数．如果缩小x的取值范围，一次函数值就会有最大值或最小值一次函数的“最值”由一次函数的性质决定，与函数解析是中k值的大小以及x的范围相关。

⑴k＞0时，y随x增大而增大．因此，x取最小值时，y有最小值；x取最大值时，y有最大值．⑵k＜0时，y随x增大而减小．因此，x取最小值时，y有最大值；x取最大值时，y有最小值．k值、自变量的取值范围与函数最大值、最小值的对应情况如下表：求一次函数的最大值与最小值，采用“极端值法”．即用x的端点值，根据函数的k 值，对应求出函数的最值。

例题：某厂工人小王某月工作的部分信息如下：信息一：工作时间：每天上午8∶00~12∶00，下午14∶00~18∶00，每月25天；信息二：生产甲、乙两种产品，并且按规定每月生产甲产品的件数不少于60件．生产产品件数与所用时间之间的关系见下表：生产甲产品件数（件） 生产乙产品件数（件） 所用总时间（分）1010 350 30 20 850信息三：按件计酬，每生产一件甲产品可得1.50元，每生产一件乙产品可得2.80元． 根据以上信息，回答下列问题：（1）小王每生产一件甲种产品，每生产一件乙种产品分别需要多少分？（2）小王该月最多能得多少元？此时生产甲、乙两种产品分别多少件？解：（1）设生产一件甲种产品需x 分钟，生产一件乙种产品需y 分钟，由题意得：10103503020850x y x y +=⎧⎨+=⎩ 解得：1520x y =⎧⎨=⎩所以生产一件甲产品需要15分钟，生产一件乙产品需要20分钟．（2）设生产甲种产品共用了x 分钟，生产乙种产品需用(25860)x ⨯⨯-分钟，则生产甲种产品15x 件，生产乙种产品2586020x ⨯⨯-件． 258601.5 2.81520x x w ⨯⨯-∴=⨯+⨯总额120000.1 2.820x x -=+⨯ 0.116800.14x x =+-0.041680x =-+∵6015x ≥， ∴900x ≥∵-0.04<0∴当x 取最小值900时w 取得最大值为0.0490016801644w =-⨯+=（元）甲生产了9006015=（件）， 乙生产了25860900120009005552020⨯⨯--==（件） 所以小王该月最多能得到1644元,此时生产甲、乙两种产品分别为60件和555件.。

一次绝对值求和函数最值的几何求法
例1. 求函数21)(-++=x x x f 的最小值
解一：分段讨论法
解二：绝对值三角不等式
解三：绝对值得几何意义
变式1：求函数212)(-++++=x x x x f 的最小值
变式2：求函数4212)(-+-++++=x x x x x f 的最小值
拓展一：系数为1的绝对值求和函数最值的几何求法 设n n a x a x a x a x x f a a a a -++-+-+-=<<<< 321321)(,，设使)(x f 取最小值的x 为：
当n 为奇数时，x 取中间那个实数2
1+=n a x
当n 为偶数时，x 可取中间两个数之间任何一个实数
拓展二：系数为整数的绝对值求和函数最值的几何求法
例2.（1）求函数2212)(++++-=x x x x f 的最小值
（2）求函数102322212)(-++-+-+-=x x x x x f 的最小值（25）
拓展三：系数是有理数的绝对值求和函数最值的几何求法
例3.求函数211213141161)(-+-++=x x x x f 的最小值（1829）。