盘管换热器相关计算

一、铜盘管换热器相关计算条件：600kg 水 6小时升温30℃单位时间内换热器的放热量为q q=GC ΔT=600*4.2*10^3*30/(6*3600)= 3500 w 盘管内流速1m/s ，管内径为0.007m ，0.01m ， 盘管内水换热情况：定性温度40℃ 定性温度50℃ 管径0.014m Re 21244.31 Re 25179.86 管径0.20mRe 30349.01Re 35971.22湍流范围：Re=10^4~1.2*10^5 物性参数： 40℃饱和水参数。

黏度—653.3*10^-6 运动黏度—0.659 *10^-6 普朗特数—4.31 导热系数—63.5*10^2 w/(m. ℃) 求解过程：盘管内平均水温40℃为定性温度时换热铜管的外径，分别取d1=0.014m d2=0.02m 努谢尔特准则为0.4f8.0ff Pr 023Re.0*2.1Nu =＝ 1.2*0.023*21244.310.84.310.4=143.4（d1）0.4f8.0ff Pr 023Re.0*2.1Nu =＝ 1.2*0.023*30349.010.84.310.4=190.7（d2）管内对流换热系数为l Nu h ff i λ⋅==143.4*0.635/0.014=6503.39 （d1） lNu h ff i λ⋅==190.7*0.635/0.02=6055.63 （d2） 管外对流换热系数格拉晓夫数准则为（Δt=10）23/υβtd g Gr ∆==9.8*3.86*10^-4*10*.0163/(0.659*10^-6)2=356781.6（d1）23/υβtd g Gr ∆==9.8*3.86*10^-4*10*.0223/(0.659*10^-6)2=927492.9（d2）其中g=9.8 N/kgβ为水的膨胀系数为386*10^-6 1/K自然对流换热均为层流换热（层流范围：Gr=10^4~5.76*10^8）25.023w wPr t g l 525.0Nu ⎪⎪⎭⎫ ⎝⎛⋅∆=να=0.525(356781.6*4.31)0.25=18.48755 （d1）25.023w wPr t g l 525.0Nu ⎪⎪⎭⎫⎝⎛⋅∆=να=0.525(927492.9*4.31)0.25=23.47504（d2）其中Pr 普朗特数为4.31 对流换热系数为dNu m λα==18.48755*0.635/0.014=838.5422（d1）dNu m λα==23.47504*0.635/0.014=677.5749（d2）其中λ为0.635w/(m. ℃) .传热系数Uλδ++=o i h 1h 1U 1=1/6503.39+1/838.5422+1/393=0.003891 U=257.0138 （d1）λδ++=o i h 1h 1U 1=1/6055.63+1/677.5749+1/393=0.004186 U=238.9191 （d2）h i －螺旋换热器内表面传热系数 J/㎡·s ·℃ h o －螺旋换热器外表面传热系数 J/㎡·s ·℃ δ－螺旋换热器管壁厚 m δ=1mλ－管材的导热系数 J/m ·s ·℃ λ=393W/m ℃k o －分别为管外垢层热阻的倒数（当无垢层热阻时k o 为1） J/㎡·s ·℃ 自来水 k o =0.0002㎡℃/W 换热器铜管长度 dq l απ70==3500/10/257.0138/3.14/0.014=27.1（d1） A=1.53dq l απ70==3500/10/238.9191/3.14/0.022=21.2（d2） A=1.65二、集热面积的相关计算（间接系统）条件：加热600kg 水，初始水温10℃，集热平面太阳辐照量17MJ/㎡以上，温升30℃，⎪⎪⎭⎫⎝⎛⋅⋅+⋅=hx hx CL R c IN AU A U F 1A A =9.5㎡ 式中IN A —间接系统集热器总面积，㎡L R U F —集热器总热损系数，W/（㎡·℃）对平板集热器，L R U F 宜取4～６W/（㎡·℃） 对真空管集热器，L R U F 宜取１～２W/（㎡·℃）取1hx U —环热器传热系数，W/（㎡·℃） hx A —换热器换热面积，㎡c A —直接系统集热器总面积，㎡ )1(J f)t t (C Q A L cd T i end w w c ηη--=w Q —日均用水量，kgw C —水的定压比热容，kJ/（kg ·℃） end t —出水箱内水的设计温度，℃i t —水的初始温度，℃f —太阳保证率，%；根据系统的使用期内的太阳辐照、系统经济以用户要求等因素综合考虑后确定，宜为30%～80% 取1T J —当地集热采光面上的年平均日太阳辐照量kJ/㎡η—集热器的年平均集热效率；根均经验值宜为0.25～0.5 取0.6 cdη—出水箱和管路的热损失率；根据经验取值宜为0.20～0.30 取L0.2结论：1）换热器入口流速在1 m/s 左右2）保证换热器内的平均温度在40℃左右3）换热器的入口压力不低于0.2 5MPa三、换热器计算 1.传热面积TU Q A ∆=(2.1.1)A — 传热面积 ㎡Q —传热量 J/sU —传热系数 J/㎡·s ·℃ ΔT －平均温度差 ℃2.平均温度差（考虑逆流情况）c1h2c2h1c1h2c2h1T T T T ln )T T ()T (T T -----=∆（2.2.1） 其中T c —冷流体温度 ℃ T h —热流体温度 ℃下标1为入口温度，下标2为出口温度 当c1h2c2h1T T T T --≤2时，可用算数平均值计算，即2)T T ()T (T c1h2c2h1-+-（2.2.2） 3.传热系数U)A A (k 11)k 1h 1()A A (h 1U 1io i o o o i o i ++++=λδη（2.3.1）h i －螺旋换热器内表面传热系数 J/㎡·s ·℃ h o －螺旋换热器外表面传热系数 J/㎡·s ·℃ δ－螺旋换热器管壁厚 mλ－管材的导热系数 J/m ·s ·℃k i ,k o －分别为管内外垢层热阻的倒数（当无垢层热阻时k i ,k o 均为1） J/㎡·s ·℃ηo －为肋面总效率（如果外表面为肋化，则ηo ＝1）ioA A －为换热管的外表面积与内表面积之比； 4.螺旋管内表面传热系数lNu h ff i λ⋅=（2.4.1） 其中h i —管内表面传热系数 J/㎡·h ·℃f Nu —努塞尔数f λ—流体导热系数 W/m ·K换热器设计流量为：4L/min ～14L/min ， 管内为湍流时实验关联式验证范围：Re f ＝104～1.2×105,Pr f ＝0.1～120，l/d ≥60; 管内径d 为特征长度。

盘管计算公式盘管计算公式在暖通空调系统中，盘管是常用的换热设备之一。

为了能够正确地选择和设计盘管，我们需要掌握一些与盘管相关的计算公式。

本文将列举一些与盘管计算相关的公式，并提供相应的例子进行解释说明。

散热量计算公式1. 直流盘管散热量计算公式直流盘管的散热量可以通过以下公式进行计算：Q = m * cp * ΔT其中， - Q 表示散热量（单位为瓦特，W） - m 表示流经盘管的水质量流量（单位为千克/秒，kg/s） - cp 表示水的比热容（单位为焦耳/千克·摄氏度，J/kg·°C） - ΔT 表示冷却水的进出水温差（单位为摄氏度，°C）例如，如果一台直流盘管中的冷却水的水质量流量为 kg/s，水的比热容为kJ/kg·°C，冷却水的进出水温差为10°C，则该盘管的散热量为：Q = * * 10 = kW2. 双管盘管散热量计算公式双管盘管的散热量计算相对复杂一些，可以通过以下公式进行计算：Q = m * cp * ΔT1 + m * cp * ΔT2 + 2 * m * cp * ΔT3 + m * cp * ΔT4其中， - Q 表示散热量（单位为瓦特，W） - m 表示流经盘管的水质量流量（单位为千克/秒，kg/s） - cp 表示水的比热容（单位为焦耳/千克·摄氏度，J/kg·°C） - ΔT1、ΔT2、ΔT3、ΔT4 分别表示冷却水的进出水温差（单位为摄氏度，°C）例如，一台双管盘管中的冷却水的水质量流量为 kg/s，水的比热容为kJ/kg·°C，冷却水的四个进出水温差分别为10°C、5°C、8°C和12°C，则该盘管的散热量为：Q = * * 10 + * * 5 + 2 * * * 8 + * * 12 = kW流通水量计算公式1. 直流盘管流通水量计算公式直流盘管的流通水量可以通过以下公式进行计算：m = Q / (cp * ΔT)其中， - m 表示流经盘管的水质量流量（单位为千克/秒，kg/s）- Q 表示散热量（单位为瓦特，W） - cp 表示水的比热容（单位为焦耳/千克·摄氏度，J/kg·°C） - ΔT 表示冷却水的进出水温差（单位为摄氏度，°C）例如，如果一台直流盘管的散热量为 kW，水的比热容为kJ/kg·°C，冷却水的进出水温差为10°C，则流经该盘管的水质量流量为：m = * 1000 / ( * 10) = kg/s2. 双管盘管流通水量计算公式双管盘管的流通水量计算公式与散热量计算公式类似，可以使用相同的公式进行计算。

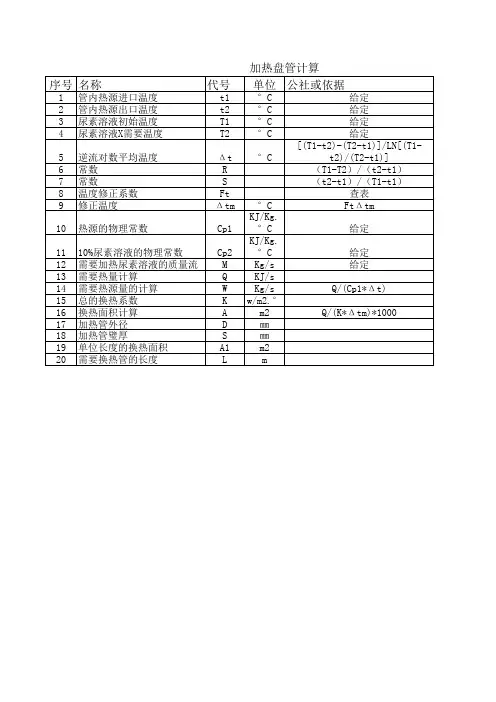
加热盘管计算书
.
'. 加热盘管计算书
由已知：开式集热水箱，有效容积20吨，高度2米
1.20吨水由5℃加热至55℃
由公式：Q=Cm△t
Q: 为所需热量，单位：KJ
C：水的比热容，取值：4.12KJ/kg*℃
△t：温差，单位：℃
通过计算得：Q=4120000KJ
由公式：P=Q/t
P：为加热盘管的功率，单位：KW
Q：为加热所需热量，单位：KJ
t：为盘管加热时间，取值6h，即21600s 通过计算得：P≈190KW
2.水箱内通过间接加热的加热盘管对其进行加热
由公式
F：为换热盘管面积
C: 由换热量及盘管内阻力选取，由经验取1.2的余量
e：为结垢影响系数，取值0.8
K：为传热系数，取值3KW/㎡*℃
△t：为换热前后温度差，取值10℃
通过计算得：F=9.5㎡
3.盘管长度计算
我们选用DN32的管路，已知DN32管道的外径为34mm
其1m的外表面积：由计算公式S=L*C
S：为外表面积，单位㎡
L：为管道长度，单位m
C：为管道周长，单位m 通过计算得S=0.133136㎡
因此的总的换热盘管长度：L=F/S≈72m。

热水盘管散热计算公式热水盘管是一种常见的散热设备，广泛应用于暖通空调系统中。

它通过热水循环流过盘管内部，将热量传递给空气，从而实现散热的目的。

在设计和使用热水盘管时，需要对其散热性能进行计算和评估。

本文将介绍热水盘管散热计算的基本原理和公式。

热水盘管的散热性能可以通过热传导和对流传热来描述。

热传导是指热水在盘管内部传递热量的过程，而对流传热则是指热水和空气之间通过对流传递热量的过程。

在实际的热水盘管散热计算中，需要考虑这两种传热方式的影响。

首先，我们来看热传导的计算。

热传导的计算可以通过热传导方程来描述，其基本形式为：q = k A (T1 T2) / L。

其中，q表示热传导率，单位为W/m2；k表示热传导系数，单位为W/(m·K)；A表示传热面积，单位为m2；T1和T2分别表示热水和空气的温度，单位为摄氏度；L表示传热距离，单位为m。

在热水盘管的散热计算中，需要根据盘管的结构和材料来确定热传导系数和传热面积。

同时，还需要考虑热水和空气之间的温度差和传热距离。

通过这个公式，可以计算出热传导在散热过程中的贡献。

接下来，我们来看对流传热的计算。

对流传热的计算可以通过对流换热系数和对流传热面积来描述，其基本形式为：q = h A (T1 T2)。

其中，q表示对流传热率，单位为W；h表示对流换热系数，单位为W/(m2·K)；A表示传热面积，单位为m2；T1和T2分别表示热水和空气的温度，单位为摄氏度。

在热水盘管的散热计算中，对流换热系数是一个重要的参数。

对流换热系数受到多种因素的影响，包括流体的性质、流速、传热面积等。

通过对流换热系数和传热面积的计算，可以得到对流传热在散热过程中的贡献。

综合考虑热传导和对流传热的影响，热水盘管的总散热率可以通过以下公式来计算：q = q_conduction + q_convection。

其中，q_conduction表示热传导的贡献，q_convection表示对流传热的贡献。

换热器换热面积计算表copper3/8h:25.4w:22152.4请输入红色字体排数=2（排）L=716.00（mm ）每英寸P 片、片数=13.00（片）H=609.6（mm ）孔高1英寸=25.40（mm ）盘管数=124总片数P=L /25.4*P 片1. 总片数P=716.0025.4013.00366（片）812.8孔数=H /25.4482. 孔数=609.6025.4024（个）每片面积A=H *22-孔数*（9.52/2）2*3.143. 每片面积A=609.6022.002422.6576 3.1411703.72326（mm 2）每片间隔=25.40/P 片4. 每片间隔=25.4013.00 1.95（mm ）1排有几片=L / 每排间隔5. 1排有几片=716.00 1.95366（片）1排总翅片面积=序号5*序号36. 1排总翅片面积=36611703.724288907.72（mm 2）总翅片面积=序号6* 排数7. 总翅片面积=4288907.7228577815.44（mm 2）单根铜管面积= 3.14*9.52*L8. 单根铜管面积= 3.149.52716.0021403.2448（mm 2）1排铜管数=H /25.49. 1排铜管数=609.6025.4024（mm 2）铜管总面积=序号8序号9*排数10. 铜管总面积=21403.2424 2.001027355.75（mm 2）单盘管面积=序号7+序号10最终结果盘管总面积=单盘管面积*盘管数18.1830（m 2）单盘管面积=17155630.891027355.7518182986.6418.18303/8"热交器换热面积计算1英寸=25.4mm L ：热交长度W ：热交宽度（m 2）H ：热交高度。

风机盘管换热量计算公式风机盘管是一种常见的空调设备，主要用于室内空气调节。

在使用风机盘管时，我们通常需要计算它的换热量，以确保室内空气的舒适度。

本文将介绍风机盘管换热量的计算公式以及相关内容。

一、风机盘管换热量的计算公式风机盘管的换热量可以通过以下公式进行计算：Q = m × C × ΔT其中，Q表示换热量，m表示空气的质量流量，C表示空气的比热容，ΔT表示空气的温度变化。

二、空气质量流量的计算空气质量流量是指单位时间内通过风机盘管的空气质量。

它可以通过以下公式计算：m = ρ × V其中，m表示空气质量流量，ρ表示空气的密度，V表示空气的体积流量。

空气的密度可以通过以下公式计算：ρ = P / (R × T)其中，ρ表示空气的密度，P表示空气的压力，R表示空气的气体常数，T表示空气的温度。

空气的体积流量可以通过以下公式计算：V = A × v其中，V表示空气的体积流量，A表示风机盘管的截面积，v表示空气的流速。

三、空气的比热容的计算空气的比热容是指单位质量的空气在温度变化时所吸收或释放的热量。

它可以通过以下公式计算：C = Cp / M其中，C表示空气的比热容，Cp表示空气的定压比热容，M表示空气的摩尔质量。

空气的定压比热容可以通过查表或使用近似公式进行估算。

四、空气温度变化的计算空气温度变化可以通过以下公式计算：ΔT = T2 - T1其中，ΔT表示空气的温度变化，T2表示空气的出口温度，T1表示空气的入口温度。

五、其他影响因素的考虑在实际计算中，还需要考虑其他因素对风机盘管换热量的影响，例如空气的相对湿度、风机盘管的效能等。

这些因素可以通过实测或使用经验值进行估算。

六、实际应用举例假设某风机盘管的空气质量流量为1000 kg/h，空气的入口温度为20°C，出口温度为10°C，风机盘管的截面积为1 m²，空气的流速为10 m/s。

盘管换热器换热系数1. 引言1.1 引言盘管换热器是一种常用的换热设备，其换热系数是评价其换热效率的重要指标之一。

换热系数是指在单位时间内，单位面积内传热量与温度差之比，是描述换热器传热性能的一个重要参数。

在工程实践中，正确地计算和调节盘管换热器的换热系数，可以提高换热效率，节约能源，减少成本，保证设备安全运行。

本文将围绕盘管换热器换热系数展开讨论，从定义、影响因素、计算方法、调节方法以及应用领域等方面进行深入分析。

希望通过本文的阐述，读者能够更加全面地了解盘管换热器换热系数的重要性和影响因素，掌握正确的计算和调节方法，更好地应用于实际工程中。

换热器在现代工业生产中扮演了至关重要的角色，其性能的优劣直接影响到工艺的效率和产品的质量。

深入研究盘管换热器的换热系数，对于工程技术人员和相关领域的研究者来说具有重要意义。

通过不断的学习和实践，我们可以更好地利用盘管换热器的性能优势，推动工业生产的持续发展。

2. 正文2.1 盘管换热器换热系数的定义盘管换热器换热系数是指在盘管换热器中，单位时间内从一个流体传递给另一个流体的热量与传热面积和温度差的比值。

换热系数的大小直接影响到换热器的换热效率，是评价换热效果的重要参数之一。

在盘管换热器中，热量传递主要通过液体或气体流过管内外壁表面来实现，而换热系数的大小受到多种因素的影响。

这些因素包括流体性质、流动状态、管道布局等，都会对换热系数产生影响。

换热系数的计算方法一般可以通过实验数据处理、理论分析、数值模拟等手段得到。

对于盘管换热器来说，一般采用平均传热系数来计算，并考虑传热面积、传热过程中的阻力等因素。

为了提高盘管换热器的换热效率，可以采取一些调节方法，比如改变流体速度、增加传热面积、优化管道布局等。

这些方法可以有效地提高换热系数，从而达到节能减排、提高换热效率的目的。

盘管换热器换热系数的应用领域非常广泛，包括化工、电力、冶金、航空航天等领域。

通过合理设计和优化，可以实现盘管换热器在不同领域的高效应用，为工业生产提供可靠的换热解决方案。