fuzzy_control模糊控制算法

A

x1


x2


xn
例：设论域U={钢笔，衣服，台灯，纸}，他们属于学习用品的隶属度分别 为:1， 0， 0.6， 0.8，则模糊集合学习用品可分别用向量表示法和扎德 表示法表示如下：
学习用品 （1 0 0.6 0.8）
学习用品=
模糊控制概述
~ ~
1 0 0.6 0.8 钢笔 衣服 台灯 纸
模糊控制
模糊控制是以模糊集理论、模糊语言变量 和模糊逻辑推理为基础的一种智能控制方法， 它是从行为上模仿人的模糊推理和决策过程的 一种智能控制方法。 该方法首先将操作人员或专家经验编成模 糊规则，然后将来自传感器的实时信号模糊化， 将模糊化后的信号作为模糊规则的输入，完成 模糊推理，将推理后得到的输出量加到执行器 上。

(1)求每条规则的蕴含关系 （Ai and Bi 采用求交运算，蕴含关 系采用最小蕴含）

1.0 1.0 0.6 0.2 A1 and B1 A1 B1 A1T B1 0.5 0
R1的运算
1.0 0.6 0.2 0.5 0.5 0.2 0 0 0
例：若A={a，b，c}，B={1，2}，则 A×B={(a, 1) (a, 2) (b, 1) (b, 2) (c, 1) (c, 2)} (a, 2) (a, 1) (a , 1) (b, 1)
元素之间可以互换位置。
B×A={(1, a) (1, b) (1, c) (2, a) (2, b) (2, c)} 0.5 0.5 0.5]
模糊推理的例子

(4)计算输出量的模糊集合
C ' ( A ' and B ') R

➢ 实验法是人为地向系统施加某种测试信号，记录其输 出响应，用适当的数学模型去逼近输入-输出间的关系。
传统的控制理论都是以被控对象和 控制系统的数学模型为基础，进行 数学分析和研究的理论。 杂的控制系统，虽然不能建立起 数学模型，无法用传统控制方法 进行控制，可是凭借丰富的实际 操作经验，技术工人却能够通过 “艺术性”的操作获得满意的控 制效果。
➢ 模糊控制是一种基于自然语言控制规则、模糊逻辑 推理的计算机控制技术，它不依赖于控制系统的数 学模型，而是依赖于由操作经验、表达知识转换成 的“模糊规则”，因此实现了人的某些职能，属于 一种智能控制。
模糊控制的基本思想
虽然模糊控制和专家系统一样都需要利用专家知 识， ➢ 但专家系统是把人类语言符号直接转换成计算机 语言， ➢ 而模糊控制则是把人类语言首先先转换成数字或 数学函数，再与物理系统结合在一起，加以利用。 ➢ 模糊控制是基于丰富操作经验总结出来的，用自 然语言表达控制策略，或通过大量实际操作数据 归纳总结出的控制规律，用计算机予以实现的自 动控制。 ➢ 它与传统控制的最大不同，在于不需要知道控制 对象的数学模型，而需要积累对设备进行控制的 操作经验或数据。
➢ 作为人类思维外壳的自然语言，当然就带有模糊性， 这是计算机所不能理解的。
➢ 模糊控制是以模糊集合理论和模糊逻辑推理为基础， 把专家用自然语言表达的知识和控制经验，通过模 糊理论转换成数学函数，再用计算机进行处理。
➢ 模糊理论形式上是利用规则进行逻辑推理，但其逻 辑值可取0与1间连续变化的任何值，因此可以采取 数值计算方法予以处理。
➢ 然而， 人们却可以根据多年的工作实践，把控制 它们的操作经验总结成类似上述的语言操作规则， 按照这些带有模糊性的、用自然语言表述的规则， 实现对它们的有效控制，模糊控制基本上解决了 用计算机模仿人类对这类系统进行的自动控制问 题。

模糊逻辑跟踪控制
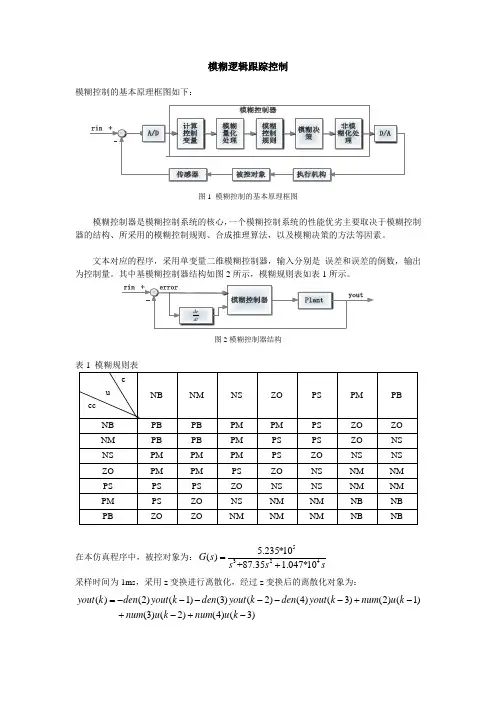
模糊控制的基本原理框图如下：
图1 模糊控制的基本原理框图
模糊控制器是模糊控制系统的核心，一个模糊控制系统的性能优劣主要取决于模糊控制器的结构、所采用的模糊控制规则、合成推理算法，以及模糊决策的方法等因素。

文本对应的程序，采用单变量二维模糊控制器，输入分别是 误差和误差的倒数，输出为控制量。

其中基模糊控制器结构如图2所示，模糊规则表如表1所示。

de dt
图2模糊控制器结构
表1 模糊规则表
在本仿真程序中，被控对象为：5
3245.235*10()+87.35 1.047*10G s s s s
=+
采样时间为1ms ，采用z 变换进行离散化，经过z 变换后的离散化对象为：
()(2)(1)(3)(2)(4)(3)(2)(1) (3)(2)(4)(3)
yout k den yout k den yout k den yout k num u k num u k num u k =------+-+-+-
其中，反模糊化采用“Centroid”方法，方波响应及控制器输出结果如图3和图4所示：。

第六章 模糊控制算法§6.1 §6.2 §6.3 §6.4 §6.5 §6.6 §6.7 模糊数学基础知识 模糊控制概述 精确量的Fuzzy化 模糊控制算法的设计 输出信息的Fuzzy判决 Fuzzy控制器查询表的建立 Fuzzy控制器实例1§6.1 模糊数学基础知识™6.1.1 普通集合及其运算规则 ™6.1.2 Fuzzy集合 ™6.1.3 Fuzzy关系矩阵的运算26.1.1 普通集合及其运算规则：1.基本概念：UAB①论域：指在考虑一个具体问题时，先将议题局限在 一定范围内，这个范围称为论域，常用U表示； ②元素： 指论域中的每个对象，常用小写字母 a、b、c表示； ③ 集合：指对于一个给定论域，其中具有某种相同 属性的、确定的、可以彼此区别的元素的 全体，常用A、B、C、X、Y、Z等表示。

例：论域为U = { 1,2,3,4,5,6 } 偶数集合A = { 2,4,6 }，奇数集合B = { 1,3,5 }32.普通集合的表示法：① 列举法（枚举法）：当集合的元素数目有限时，可将其中的元素一 一列出，并用大括号括起，以表示集合。

例：论域为U = { 1,2,3,4,5,6 }，则用列举法表示 偶数集合A = { 2,4,6 }，奇数集合B = { 1,3,5 }② 描述法（定义法）：当集合的元素数目无限时，可通过元素的定义来 描述 , 即A={x | p(x)}, 其中x为集合A的元素(x∈A)， p(x)是x应满足的条件。

例：A = {x | 25 ≤ x ≤ 50 } ，U ＝{ x |x≥ 0的实数 }4③ 特征函数法：由于元素a与集合A的关系只能有a∈A和a∈A 两种情况，故集合A可以通过函数 1， a∈A CA(a)= 来表示。

0， a∈A CA(a)称为集合A的特征函数，它只能取0，1两个值。

模糊控制理论 Fuzzy Control在传统的控制领域里，控制系统动态模式的精确与否是影响控制优劣的最主要关键， 系统动态的信息越详细，则越能达到精确控制的目的。

然而，对于复杂的系统，由于 变量太多，往往难以正确的描述系统的动态，于是工程师便利用各种方法来简化系统 动态，以达成控制的目的，但却不尽理想。

换言之，传统的控制理论对于明确系统有 强而有力的控制能力，但对于过于复杂或难以精确描述的系统，则显得无能为力了。

因此便尝试着以 模糊数学 来处理这些控制问题。

自从Zadeh 发展出模糊数学之后，对于不明确系统的控制有极大的贡献，自七 年代以后，便有一些实用的模糊控制器相继的完成，使得我们在控制领域中又向前迈 进了一大步，在此将对模糊控制理论做一番浅介。

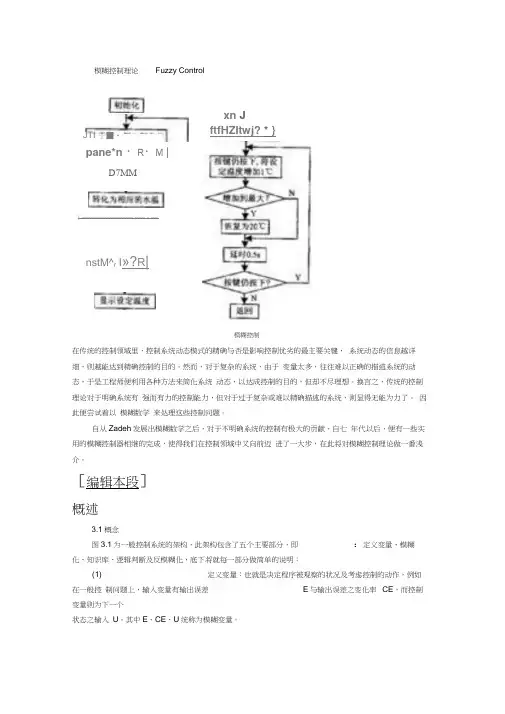
［编辑本段］概述3.1概念图3.1为一般控制系统的架构，此架构包含了五个主要部分，即 ：定义变量、模糊化、知识库、逻辑判断及反模糊化，底下将就每一部分做简单的说明：(1) 定义变量：也就是决定程序被观察的状况及考虑控制的动作，例如在一般控 制问题上，输入变量有输出误差 E 与输出误差之变化率 CE ，而控制变量则为下一个状态之输入 U 。

其中E 、CE 、U 统称为模糊变量。

xn JftfHZItwj? * }D7MMnstM^r I »?R |pane*n ・R ・M |JTI 于■•|| ----------------------------- ------ - ----模糊控制(2) 模糊化(fuzzify ):将输入值以适当的比例转换到论域的数值，利用口语化变量来描述测量物理量的过程，依适合的语言值( linguisitc value )求该值相对之隶属度，此口语化变量我们称之为模糊子集合( fuzzy subsets )。

(3) 知识库：包括数据库( data base )与规则库(rule base )两部分，其中数据库是提供处理模糊数据之相关定义；而规则库则藉由一群语言控制规则描述控制目标和策略。

➢ 作为人类思维外壳的自然语言，当然就带有模糊性， 这是计算机所不能理解的。
➢ 模糊控制是以模糊集合理论和模糊逻辑推理为基础， 把专家用自然语言表达的知识和控制经验，通过模 糊理论转换成数学函数，再用计算机进行处理。
➢ 模糊理论形式上是利用规则进行逻辑推理，但其逻 辑值可取0与1间连续变化的任何值，因此可以采取 数值计算方法予以处理。
• 互克性定理 ：随着系统复杂性的增加，人 们对其特性做出精确而有意义的描述会随 之降低，直至达到一个阈值。一旦超过它， 精确和有意义两者将会相互排斥。即，事 物越复杂，人们对它们的认识就越模糊。
3. 模糊控制的特点及展望
模糊控制理论，特别是应用方面在20世纪80年 代末90年代初取得了突飞猛进的发展，能被人 们广泛接受，是因为它有一下一些优点。
➢ 模糊控制是一种基于自然语言控制规则、模糊逻辑 推理的计算机控制技术，它不依赖于控制系统的数 学模型，而是依赖于由操作经验、表达知识转换成 的“模糊规则”，因此实现了人的某些职能，属于 一种智能控制。
模糊控制的基本思想
虽然模糊控制和专家系统一样都需要利用专家知 识， ➢ 但专家系统是把人类语言符号直接转换成计算机 语言， ➢ 而模糊控制则是把人类语言首先先转换成数字或 数学函数，再与物理系统结合在一起，加以利用。 ➢ 模糊控制是基于丰富操作经验总结出来的，用自 然语言表达控制策略，或通过大量实际操作数据 归纳总结出的控制规律，用计算机予以实现的自 动控制。 ➢ 它与传统控制的最大不同，在于不需要知道控制 对象的数学模型，而需要积累对设备进行控制的 操作经验或数据。
• 1993年美国IEEE神经网络协会创办了国际性模糊 专业杂志《Fuzzy System （模糊控制）》，
从此模糊控制制被人们公认为是智能控制的一个 重要分支。

不同PID控制算法的温控器在温度控制中的应用仪表制造有限公司工程师在本文介绍各种PID控制算法的温控器的控制特性、功能及主要应用场合，对大家合理选用用于温度控制的温控器具有很强实用性。

常用温控器控制算法包括常规PID、模糊控制、神经网络、Fuzzy-PID、神经网络PID、模糊神经网络、遗传PID及广义预测等PID算法。

常规PID控制易于建立线性温度控制系统被控对象模型；模糊控制基于规则库，并以绝对或增量形式给出控制决策；神经网络控制采用数理模型模拟生物神经细胞结构，并用简单处理单元连接成复杂网络；Puzzy-PID为线性控制，且结合模糊与PID控制优点。

1、引言温度控制系统是变参数、有时滞和随机干扰的动态系统，为达到满意的控制效果，具有许多控制方法。

故对几种常见的控制方法及其优缺点进行了分析与比较。

2、常见温度控制方法2.1 常规经典PID控制算法的PID控制PID控制即比例、积分、微分控制，其结构简单实用，常用于工业生产领域。

原理如图1。

图1 常见PID控制系统的原理框图明显缺点是现场PID参数整定麻烦，易受外界干扰，对于滞后大的过程控制，调节时间过长。

其控制算法需要预先建立模型，对系统动态特性的影响很难归并到模型中。

在我国大多数PID调节器厂家生产的温控器均为常规经典PID控制算法。

2.2 模糊PID控制算法的PID控制模糊控制(Fuzzy Control)是以模糊集合论、模糊语言变量及模糊逻辑推理为基础的计算机控制。

原理如图2。

昌晖仪表YR-GFD系列傻瓜式PID调节器使用的就是模糊控制PID控制算法。

图2 模糊控制系统原理框图2.3 神经网络PID控制算法的PID控制神经网络控制采用数理模型的方法模拟生物神经细胞结构，用简单处理单元连接形成各种复杂网络，并采用误差反向传播算法(BP)。

原理如图3：图3 神经网络控制系统的原理框图2.4 Fuzzy-PID控制算法的PID控制模糊控制不需知道被控对象的精确模型，易于控制不确定对象和非线性对象。

R=(NBe × PBu ) + ( NSe × PSu ) + (0e × 0u ) + ( PSe × NSu ) + ( PBe × NSu )
NBe × PBu = (1, 0.5, 0, 0, 0, 0, 0) × (0, 0, 0, 0, 0, 0.5,1) NSe × PSu = (0, 0.5,1, 0, 0, 0, 0) × (0, 0, 0, 0,1, 0.5, 0) 0e × 0u = (0, 0, 0.5,1, 0.5, 0, 0) × (0, 0, 0.5,1, 0.5, 0, 0) PSe × NSu = (0, 0, 0, 0,1, 0.5, 0) × (0, 0.5,1, 0, 0, 0, 0) PBe × NSu = (0, 0, 0, 0, 0, 0.5,1) × (1, 0.5, 0, 0, 0, 0, 0) 0 0 0 0 0.5 1 0 0 0 0 0 0.5 0.5 0.5 0 0 0.5 0.5 1 0 0 R= 0 0 0.5 1 0.5 0 0 0 0.5 1 0.5 0.5 0 0 0 0 0 0.5 0.5 0.5 0 1 0.5 0 0 0 0 0
学习功能
数据存储 单元
y
∗ k
e
r + —
∆
∆
k
e
e
k
c
2
e
k
Байду номын сангаас
r
模糊 控制 规则
k
∆
u
u
u
u
k −1
k
+ +
被 控 对 象
y
k
六．思考
矛盾对立统一规律： 矛盾对立统一规律：两面性 • 优点：模糊逻辑本身提供了由专家构造语 优点： 言信息并将其转化为控制策略的一种系统 的推理方法， 的推理方法，因而能够解决许多复杂而无 法建立精确数学模型系统的控制问题， 法建立精确数学模型系统的控制问题，所 以它是处理推理系统和控制系统中不精确 和不确定性的一种有效方法。从广义上讲， 和不确定性的一种有效方法。从广义上讲， 模糊控制是适于模糊推理， 模糊控制是适于模糊推理，模仿人的思维 方式， 方式，对难以建立精确数学模型的对象实 施的一种控制策略。 施的一种控制策略。它是模糊数学同控制 理论相结合的产物， 理论相结合的产物，同时也是智能控制的 重要组成部分。 重要组成部分。

模糊pid控制 python实现模糊PID控制（Fuzzy PID control）是一种基于模糊逻辑的控制方法，它结合了模糊控制和经典PID控制的优点，可以在复杂和不确定的环境中实现精确的控制。

本文将介绍模糊PID控制的原理、实现方法以及在Python中的应用。

一、模糊PID控制的原理PID控制是一种经典的控制方法，它通过比较实际输出与期望输出之间的误差，根据比例、积分和微分三个参数进行调节，使系统输出逐渐趋近于期望值。

然而，传统的PID控制方法在面对非线性、时变和不确定性系统时表现不佳。

模糊PID控制通过引入模糊逻辑来解决传统PID控制的问题。

模糊逻辑是一种能够处理模糊信息的数学方法，它可以将模糊的输入映射到模糊的输出。

模糊PID控制器通过将误差、误差变化率和误差积分三个输入量模糊化，然后根据一组模糊规则进行推理，得到模糊输出。

最后，通过解模糊化的方法将模糊输出转化为具体的控制量。

二、模糊PID控制的实现方法1. 模糊化模糊化是将具体的输入量映射到模糊集合上的过程。

常用的模糊化方法有三角隶属函数、梯形隶属函数和高斯隶属函数等。

根据具体的问题和经验，选择合适的隶属函数进行模糊化。

2. 规则库规则库是模糊PID控制的核心。

它包含了一组模糊规则，用于根据输入量的模糊值推理出输出量的模糊值。

模糊规则一般采用IF-THEN的形式，例如“IF 误差是A1 AND 误差变化率是B2 THEN 输出是C3”。

规则库的设计需要根据具体问题进行，可以基于经验或者专家知识。

3. 推理机制推理机制是根据模糊规则进行推理的过程。

常用的推理方法有最大最小合成、模糊推理和模糊推理和等。

推理机制将模糊输入与规则库进行匹配，然后根据匹配的程度计算出模糊输出的隶属度。

4. 解模糊化解模糊化是将模糊输出转化为具体的控制量的过程。

常用的解模糊化方法有最大隶属度法、面积法和重心法等。

解模糊化方法根据模糊输出的隶属度分布，计算出具体的控制量。

模糊控制算法研究——实验报告一、实验目的1、通过本次综合设计，进一步了解模糊控制的基本原理、模糊模型的建立和模糊控制的设计过程。

2提高学生有关控制系统的程序设计能力。

3熟悉MATLAB语言以及在智能控制设计中的应用。

二、实验内容1、用MATLAB中的SIMULINK工具箱，组成一个模糊控制系统。

如图：2、采用模糊控制算法，设计出能跟踪给定输入的模糊控制器，对被控系统进行仿真，绘制出系统的阶跃响应曲线。

3、改变模糊控制器中模糊变量的隶属度函数，分析隶属度函数和模糊控制规则对模糊控制效果的影响。

三、实验步骤1、启动SIMULINK。

打开MATLAB程序，并在该窗口键入SIMULINK来运行SIMULINK，或单击工具栏上SIMULINK按钮，这时SIMULINK就显示其所包含的子模块库。

2、创建一个新模型。

在FILE菜单中选择NEW-MODEL,SIMULINK就创建一个新的窗口。

3、向窗口复制模块。

例如，复制阶跃输入Step模块，具体操作为：在SIMULINK 窗口中用鼠标单击Source图标，这样就打开了Source Library中所有的模块；要从Source Library中复制Step模块，可以用鼠标单击该模块，然后拖动鼠标把它移到自己的模型窗口中，并在所需要放的位置松开鼠标，这时Step模块就出现在自己的模型窗口中。

其他需要复制的模块可参考上图，这些模块分别在Math库、Continuous库、Discontinuous库、Signal Routing库以及Sink库中找到，方法同Step模块。

在MATLAB的命令窗口输入命令Fuzzy，进入图形用户界面（GUI）窗口。

根据控制规则和所选择的隶属度函数，利用模糊推理系统（FIS）编辑器可以建立一个FIS文件，取名为fuzzycontrol.fis。

在Fuzzy Logic Toolbox中将Fuzzy Logic Controller模块找到，用鼠标将相应模块拖入窗口中即可。

模糊控制相关英语Fuzzy control (模糊控制) is a control method based on fuzzy logic, which is a mathematical framework for dealing with uncertainty and imprecision. It is used to control systems that are difficult to model or have complex dynamics.Fuzzy control works by using linguistic variables, which are variables that are expressed using natural language terms rather than precise numerical values. These linguistic variables are defined using fuzzy sets, which describe the membership function of each term. The fuzzy sets aretypically represented by fuzzy if-then rules, which incorporate expert knowledge or empirical data.Fuzzy control uses a fuzzy inference system to combine the input variables and apply the fuzzy rules to determine the output. The input variables are fuzzified, which means converting the crisp numerical values into fuzzy values based on their membership to the fuzzy sets. The fuzzy rules are then applied to the fuzzy input variables to determine the fuzzy output variables. Finally, the fuzzy output variables are defuzzified to obtain crisp numerical values for control actions.Fuzzy control has been successfully applied in various fields, such as robotics, process control, and traffic control. It has the advantage of being able to handle complex systems with imprecise or incomplete information. It can also capture the knowledge and expertise of human operators or experts in the form of linguistic rules, making it a useful tool for systems that lack mathematical models.In summary, fuzzy control is a control method based on fuzzy logic that allows for the control of systems with uncertain or imprecise information. It uses linguistic variables, fuzzy sets, and fuzzy rules to determine control actions.。

通过引入模糊逻辑，可以处理现实世界中广泛存在的模糊和不确定 性问题。
相互促进发展
模糊集合与模糊逻辑相互促进，不断发展，为解决复杂问题提供了 有力的工具。
03
模糊控制器设计
输入输出变量的确定
输入变量的确定
根据被控对象的特性和控制要求，选 择合适的输入变量，如温度、湿度、 压力等。
输出变量的确定
根据控制要求和系统性能指标，选择 合适的输出变量，如阀门开度、加热 功率等。
模糊控制算法
目录
• 模糊控制算法概述 • 模糊集合与模糊逻辑 • 模糊控制器设计 • 模糊控制算法的实现 • 模糊控制算法的优缺点 • 模糊控制算法的发展趋势与展望
01
模糊控制算法概述
模糊控制算法的定义
模糊集合
模糊集合是传统集合的扩展，它允许元素具有部分属于、部分不属于某个集合的模糊性。在模糊集合中，每个 元素都有一个隶属度，表示它属于该集合的程度。
感谢您的观看
THANKS
糊规则，计算出输出变量的隶属度函数。
模糊推理
基于专家知识和经验制定的模糊条件语句， 用于描述系统输入与输出之间的关系。模糊 规则通常采用“IF-THEN”形式，其中 “IF”部分是输入变量的模糊集合， “THEN”部分是输出变量的模糊集合。
去模糊化
将输出变量的模糊集合转换为精确值的过程 。通过选择合适的去模糊化方法（如最大值 去模糊化、最小值去模糊化、中心平均去模 糊化等），将输出变量的隶属度函数转换为 具体的输出值。
02
规则制定困难
模糊控制算法的核心是模糊规 则的制定，而模糊规则的制定 需要经验丰富的专业人员，且 往往需要反复调整和优化。
03
计算复杂度较高
对于大规模系统，模糊控制算 法的计算复杂度可能较高，需 要高性能的硬件设备才能实现 实时控制。

模糊控制介绍附件:一、模糊控制概况模糊逻辑控制(Fuzzy Logic Control)简称模糊控制(Fuzzy Control)，是以模糊集合论、模糊语言变量和模糊逻辑推理为基础的一种计算机数字控制技术。

1965年，美国的L.A.Zadeh创立了模糊集合论；1973年他给出了模糊逻辑控制的定义和相关的定理。

1974年，英国的E.H.Mamdani 首先用模糊控制语句组成模糊控制器，并把它应用于锅炉和蒸汽机的控制，在实验室获得成功。

这一开拓性的工作标志着模糊控制论的诞生。

模糊控制实质上是一种非线性控制，从属于智能控制的范畴。

模糊控制的一大特点是既具有系统化的理论，又有着大量实际应用背景。

模糊控制的发展最初在西方遇到了较大的阻力；然而在东方尤其是在日本，却得到了迅速而广泛的推广应用。

近20多年来，模糊控制不论从理论上还是技术上都有了长足的进步，成为自动控制领域中一个非常活跃而又硕果累累的分支。

其典型应用的例子涉及生产和生活的许多方面，例如在家用电器设备中有模糊洗衣机、空调、微波炉、吸尘器、照相机和摄录机等；在工业控制领域中有水净化处理、发酵过程、化学反应釜、水泥窑炉等的模糊控制；在专用系统和其它方面有地铁靠站停车、汽车驾驶、电梯、自动扶梯、蒸汽引擎以及机器人的模糊控制等。

二、模糊控制基础模糊控制的基本思想是利用计算机来实现人的控制经验，而这些经验多是用语言表达的具有相当模糊性的控制规则。

模糊控制器(Fuzzy Controller，即FC)获得巨大成功的主要原因在于它具有如下一些突出特点：模糊控制是一种基于规则的控制。

它直接采用语言型控制规则，出发点是现场操作人员的控制经验或相关专家的知识，在设计中不需要建立被控对象的精确数学模型，因而使得控制机理和策略易于接受与理解，设计简单，便于应用。

由工业过程的定性认识出发，比较容易建立语言控制规则，因而模糊控制对那些数学模型难以获取、动态特性不易掌握或变化非常显著的对象非常适用。

续变化的值。
模糊集合
2018/1/3
特征函数 隶属度函数（0～1连续变化值）
17
例：人对温度的感觉(0C ~40C的感觉)： “舒适”的温度：15C ~25C “热”：25C以上 “冷”：15C 以下 经典集合：14.99C属于“冷”；15.01 C属于舒适。 与人的感觉一致吗？
1.0
表示集合概念。 若μi＝0，可以略去该项。
2018/1/3 23
模糊集合的表达方式
3. 序偶表示法 将论域中的元素xi与隶属度A(xi)构成 序偶来表示A，则
A={(x1, A(x1)), (x2, A(x2)), …, (xn, A(xn))}
此种方法隶属度为零的项可不列入。
2018/1/3
24
差
补
对称差
2018/1/3
14
集合的运算性质
设A、B、C∈P(X)，其交、并等运算具有以下性质 (注意到它们是成对出现的)；
（1）结合律
A ( B C ) ( A B) C
A ( B C ) ( A B) C A ( B C ) ( A B) ( A C )
（2）分配律 A ( B C ) ( A B) ( A C ) （3）同一律 （4）零一律
数，关于它出现的知识的一个测量；
模糊性 — 对象无精确定义。必须要有一个函数
X→[0, 1],即隶属函数来刻画它。
从信息观点看，随机性只涉及信息的量，模糊
性关系到信息的意义、信息的定性。
2018/1/3 13
集合运算
集合的运算可以用图解来表示，称为文氏 图(Veitch图)，如图所示。
并 交
1. 向量表示法 当论域X为有限点集，即X＝{x1, x2, …, xn} 时，X上的模糊集可以用向量A来表示，即

模糊化 Fuzzifier
模糊化 信号
推理单元 Reasoning
解模糊
Defuzzifier
清晰输 出信号
e
de/dt
第一步： 模糊化

偏差（E），偏差的变化率（EC）。 要采用模糊控制的技术，首先把它们转换成模糊集 合的隶属函数。 为了便于工程实现，通常把变量范围人为的定义为 离散的若干级，所定义的级数多少取决于输入量的 分辨率。 使用最多的为三角隶属函数。

鲁棒性：
– 模糊控制系统的鲁棒性强，干扰和参数变化对控制
效果的影响被大大减弱，尤其适合于非线性、时变 及纯滞后系统的控制。
模糊控制的突出特点
1. 控制系统的设计不要求知道被控对象的精确数学 模型。 2. 控制系统的鲁棒性强，适应于解决常规控制难以 解决的非线性、时变及大纯滞后等问题。 3. 以语言变量代替常规的数学变量，易于形成专家 的“知识”。
4. 控制推理采用“不精确推理”，推理过程模仿人 的思维过程，能够处理复杂甚至“病态”系统。
模糊控制简史

1973年 Zadeh在论文Outline of a new approach
to the analysis of complex systems and decision proccesses（IEEE Trans On Systems,

模糊控制简史


1987年 the Sendai City subway成为第一个成 功应用模糊控制的大型工程 ； 模糊控制的发展最初在西方遇到了较大的阻力； 然而在东方尤其是在日本，却得到了迅速而广 泛的推广应用。 近30年来，模糊控制不论从理论上还是技术上 都有了长足的进步，成为自动控制领域中一个 非常活跃而又硕果累累的分支。

模糊PID控制方法研究Fuzzy PID Controller2 模糊控制器的设计2.1 模糊控制器的基本原理2.1.1 模糊控制器的原理模糊控制(Fuzzy Control)是以模糊集理论、模糊语言变量和模糊逻辑推理为基础的一种智能控制方法，它从行为上模仿人的模糊推理和决策过程。

模糊控制是先将操作人员或专家经验编成模糊规则，然后将来自传感器的实时信号通过模糊规则模糊化，将模糊化后的信号作为模糊规则的输入，完成模糊推理，进行解模糊化，最后将解模糊后得到的输出量加到执行器上。

图2-1是模糊控制原理框图。

图2-1 模糊控制原理框图2.1.2 模糊控制器的组成在整个控制器中，模糊控制器是整个控制系统的核心，所采用的模糊规则、合成推理算法和模糊决策的方法等都是决定整个控制器优劣的因素。

其组成如图2-2：图2-2 模糊控制器的组成框图模糊化接口是模糊控制器的输入借口，主要作用是将真实的确定量输入转换为一个模糊矢量。

数据库和规则库共同组成了控制器的知识库，数据库中存放的是所有输入、输出变的的全部模糊子集的隶属度矢量值（即经过论域等级离散化以后对应值的集合）。

在规则推理的模糊关系方程求解过程中，向推理机提供数据。

规则库是对人类长期经验的总结，将其转化成模糊控制算法，为推理机提供控制规则。

推理是模糊控制器中，根据输入模糊量，模仿人类判断时的模糊概念，运用模糊逻辑和模糊推论法进行推论，而得到模糊控制讯号。

此部分是模糊控制器的精髓所在。

解模糊借口是将推论所得到的模糊值转换为明确的控制讯号，做为系统的输入值。

2.2 模糊控制器的设计步骤通过对模糊控制器原理的研究，得出设计模糊控制器主要包括以下几项内容：（1）确定模糊控制器的输入变量和输出变量（即控制量）。

输入变量为误差e以及误差变化ec，输出变量为控制量u。

e，ec，u的模糊集均为：｛NB,NM,NS,ZO,PS,PM,PB｝。

e，ec的论域均为：｛-3，-2，-1，0，1，2，3｝。

模糊算法在PLC程序的实现摘要：模糊控制（FuzzyControl）是源于对语言变量、逻辑理论的深入研究，并结合了丰富的实际应用，从而将传统的控制方法与最新的信息处理技术相结合，构建出一种全新的、高度可靠的智能化控制系统。

通过采用本文提到的控制技术，我们能够发现它具备许多显著的优势，包括对建模的要求比传统的技术更加严格；依靠专业操作者的技术，可以更加准确的控制系统。

此外，模糊控制还具备良好的抗干扰性，特别适用于长期变化的环境。

本文旨在深入探讨PLC程序中应用的模糊算法，并对其有效性和可靠性做出详细的描述。

关键词：模糊算法；PLC程序；程序设计引言模糊控制（FuzzyControl）是一种以人类经验为基础的复杂控制方式，它以模糊的方式表达输出和输入之间的关系，而不是像传统控制那样精确的描述。

在实际工程中，许多系统和过程的复杂性超出了数学模型的范畴，因此，为了更好地控制这些系统和过程，需要采用模糊控制的方法，这种方法不仅可以避免传统数学语言的局限性，而且可以更加准确地反映出控制规则，从而达到更好的控制效果。

一、模糊控制系统简介通过对比分析，可以发现模糊控制系统和PID控制器在许多方面存在显著的不同，例如它们的算法原理、输入维数等，而这些不同又可以通过模糊控制系统来更好地体现出来。

二、模糊控制器的设计（一）明确模糊控制器的构成改变输入维数的方式将直接关系到控制的准确性，因此，应该尽可能地增加输入维数，以减少规则库中的数据，从而提高设置的复杂性。

根据操作人员的丰富经验，能够将双输入和双输出的控制结构应用于模糊控制器的设计，以获得更优质的性能和效率。

（二）确定模糊语言值在这个系统里，e和ec是由模糊语言值模糊处理而来的，它们的结果是U。

模糊语言值的取值范围包括｛负大（NB)、负中（NM)、负小（NS)、零（ZO)、正小(PS)、正中（PM)、正大（PB)}，它们的取值范围分别是｛-3、-2、-1、0、1、2、3}。