第一章第二章习题课

第一章 机械运动知识点1．长度的测量1． 长度单位及换算常用的长度单位由大到小排列为km 、m 、dm 、cm 、mm 、µm 、nm ．记忆它们之间的换算关系时，有以下方法：按单位的大小顺序记忆：先记住长度单位大小的排列顺序；再记住相邻单位之间的换算关系（如下图所示）；需进行单位换算时，根据上图便可算出所需换算的两单位之间换算关系：如要知道km 与cm 之间的换算关系，则可由图得出：3113+1+151km=101010cm=10cm=10cm ⨯⨯；又如要知道nm 与dm 之间的换算关系，则可由图得出：3311331181nm=10101010dm=10dm=10dm ---------⨯⨯⨯．知识点2．正确选择、使用刻度尺、认识长度 测量长度的工具是刻度尺。

（1）使用刻度尺测量物体长度前，首先要弄清刻度尺的量程、分度值和零刻线的位置。

（2）选择刻度尺时应根据测量的要求来选择。

（例如：要测量一支钢笔的长度，精确到mm ，则可选用分度值是1mm 、量程是150mm 左右的刻度尺；而在体育课上要测量跳远的长度，则可选用分度值是1cm 的皮卷尺。

）（3）使用刻度尺测量物体长度时，刻度线要紧贴被测物体，被测长度的一端要与刻度尺的零刻线对齐（若零刻线已磨损，则选择刻度尺上另一完好的刻度线），读数时视线要与尺面垂直，且正对刻度线读数。

知识点3．测量结果的记录 测量结果是由数字和单位组成的。

其中数字部分由准确值加上一位估计值组成。

测量结果在书写的时候一定要估读到分度值的下一位。

知识点4．实验误差（1）误差与错误：首先误差不是错误。

错误，是指由于实验方法不正确或实验时违反操作造成的，错误是能够避免的。

误差，是指测量值与真实值之间的差异。

我们不能消除误差，只能尽量减小误差。

错误与误差的最大区别是，错误可以避免，误差不能消除。

（2）误差产生的原因3种：测量仪器不够精密、测量方法不够完善、测量的人为因素。

第一章课后习题1、对N＝5、k≤3时，求解传教士和野人问题的产生式系统各组成部分进行描述（给出综合数据库、规则集合的形式化描述，给出初始状态和目标条件的描述），并画出状态空间图。

2、对量水问题给出产生式系统描述，并画出状态空间图。

有两个无刻度标志的水壶，分别可装5升和2升的水。

设另有一水缸，可用来向水壶灌水或倒出水，两个水壶之间，水也可以相互倾灌。

已知5升壶为满壶，2升壶为空壶，问如何通过倒水或灌水操作，使能在2升的壶中量出一升的水来。

3、对梵塔问题给出产生式系统描述，并讨论N为任意时状态空间的规模。

相传古代某处一庙宇中，有三根立柱，柱子上可套放直径不等的N个圆盘，开始时所有圆盘都放在第一根柱子上，且小盘处在大盘之上，即从下向上直径是递减的。

和尚们的任务是把所有圆盘一次一个地搬到另一个柱子上去（不许暂搁地上等），且小盘只许在大盘之上。

问和尚们如何搬法最后能完成将所有的盘子都移到第三根柱子上（其余两根柱子，有一根可作过渡盘子使用）。

求N＝2时，求解该问题的产生式系统描述，给出其状态空间图。

讨论N为任意时，状态空间的规模。

4、对猴子摘香蕉问题，给出产生式系统描述。

一个房间里，天花板上挂有一串香蕉，有一只猴子可在房间里任意活动（到处走动，推移箱子，攀登箱子等）。

设房间里还有一只可被猴子移动的箱子，且猴子登上箱子时才能摘到香蕉，问猴子在某一状态下（设猴子位置为a，箱子位置为b，香蕉位置为c），如何行动可摘取到香蕉。

5、对三枚钱币问题给出产生式系统描述及状态空间图。

设有三枚钱币，其排列处在"正、正、反"状态，现允许每次可翻动其中任意一个钱币，问只许操作三次的情况下，如何翻动钱币使其变成"正、正、正"或"反、反、反"状态。

6、说明怎样才能用一个产生式系统把十进制数转换为二进制数，并通过转换141.125这个数为二进制数，阐明其运行过程。

7、设可交换产生式系统的一条规则R可应用于综合数据库D来生成出D'，试证明若R存在逆，则可应用于D'的规则集等同于可应用于D的规则集。

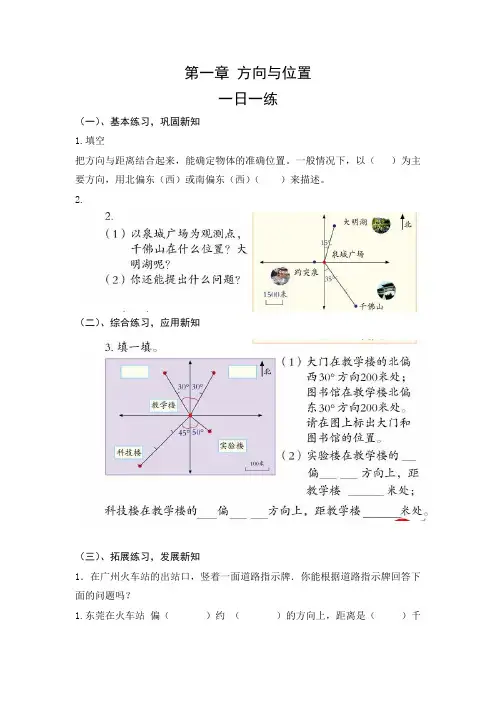
第一章方向与位置一日一练（一）、基本练习，巩固新知1.填空把方向与距离结合起来，能确定物体的准确位置。

一般情况下，以（）为主要方向，用北偏东（西）或南偏东（西）（）来描述。

2.（二）、综合练习，应用新知（三）、拓展练习，发展新知1．在广州火车站的出站口，竖着一面道路指示牌．你能根据道路指示牌回答下面的问题吗？1.东莞在火车站偏（）约（）的方向上，距离是（）千米．2.顺德在火车站偏（）约（）的方向上，距离是（）千米3.珠海在火车站偏（）约（）的方向上，距离是（）千米4.深圳在火车站偏（）约（）的方向上，距离是（）千米2如图，如果A点在广场的西南方40m处，请在图中点上小黑点，并用字母A标注出来五年级上册第一单元《方向与位置》测试试题一班级＿＿＿＿姓名＿＿＿＿＿＿得分＿＿＿＿＿＿一、填空题1、写出灰色瓷砖位置的数对。

a（，）k（，）c（，）i（，）e（，）h（，）2、如图2所示，进行“找宝”游戏，如果宝藏藏在(3，3)字母牌的下面，那么应该在字母______的下面寻找．3、如图3所示，如果点A的位置为(2，1)，那么点B的位置为______，点C的位置为______，点D和点E的位置分别为______，_______．4、观察右上图，用数对的知识解决以下问题。

（1）用数对表示正方形A、B、C、D的位置。

A（，）B（，）C（，）D（，）（2）在左图中标出E（7，5），F（7，2），G（10，2），并依次连接E、F、G、E。

这样就围成了一个（）形。

5、以灯塔为观察点：A岛在偏（）的方向上，距离是千米；B岛在偏（）的方向上，距离是千米。

二、操作题1、根据下面的数对在右图中相应位置上的圆圈里涂上颜色。

A(2,3) B(5,2)C(9,7) D(10,1)E(7,6) F(4,4)2、要求画出各景点位置。

（1）鳄鱼潭在大象馆南偏西40°方向，距离300米；（2）熊猫馆在大象馆北偏西15°方向，距离200米；（3）花果山在大象馆北偏东60°方向，距离500米；（3）麋鹿苑在大象馆南偏东50°方向，距离400米；3、填空。

生物化学（上册）课后习题第一章糖类1、环状己醛糖有多少个可能的旋光异构体？为什么？25=32因为环状己醛糖含有5个不对称碳原子。

单糖由直链变成环状结构后，羰基碳原子成为新的手性中心，导致C1差向异构化，产生两个非对映异构体。

羰基碳上形成的差向异构体称异头物。

2、含D-吡喃半乳糖和D-吡喃葡萄糖的双糖可能含有多少个异构体（不包括异头物）？含同样残基的糖蛋白上的二糖将有多少个异构体？每个单糖单位都能作为羰基供体，与另一个单糖单位的5个羟基形成糖苷键（C1,C2，C3，C4，C6），于是α-D-吡喃半乳糖-D-吡喃葡萄糖苷、β-D-吡喃半乳糖-D-吡喃葡萄糖苷、α-D-吡喃葡萄糖-D-吡喃半乳糖苷和β-D-吡喃葡萄糖-D-吡喃半乳糖苷各有五种，共5*4=20种。

糖蛋白上的二糖链其中一个单糖的C1用于连接多肽，C2，C3，C4，C6用于和另一单糖的C1形成糖苷键，算法同上，共有4*4=16个，考虑到二糖与多肽相连时的异头构象，异构体数目为16*2=32个。

5、D-葡萄糖的α、β异头物的比旋（【α】20D）分别为+112.2º和+18.7º.当α-D-吡喃葡萄糖晶体溶于水时，比旋将由+112.2º降至平衡值+52.7º.计算平衡混合液中α和β异头物的比率。

假设开链形式和呋喃形式可忽略。

忽略开链形式和呋喃形式。

设：α-D-吡喃葡萄糖所占比例x%，则β-D-吡喃葡萄糖所占比例为(100-x）%。

已知25℃,1ml溶液和1dm旋光管中，α-D-吡喃葡萄糖旋光度+112.2º，β-D-吡喃葡萄糖+18.7º，平衡时葡萄糖溶液的旋光度+52.7º。

根据平衡时旋光度是组成各成分旋光度的加和，列出关系式如下：112.2x%+18.7(100-x）%=52.7,解方程得x=36.5α-D-吡喃葡萄糖比例为36.5%，β-D-吡喃葡萄糖比例为63.5%。

《传播学概论》课程习题第一章、第二章一、填空1、传播学是研究社会信息系统及其运行规律的科学。

2、语言的产生，是完成从动物传播到人类传播之巨大飞跃的根本标志。

3、人类传播区别于动物传播的本质特征是能动性和创造性。

4、人类传播发展的阶段包括：口语传播时代、文字传播时代、印刷传播时代、电子传播时代。

5、人类传播的第一套体外化符号系统是文字。

二、名词解释1、信息：信息是物质的普遍属性，是一种客观存在的物质运动形式。

信息是由物理载体和意义构成的统一整体。

2、社会信息：除人的生物和生理信息以外的、与人类的社会活动有关的一切信息。

3、传播:社会信息的传递或社会信息系统的运行。

4、系统：由相互联系、相互制约的若干部分结合在一起并且具有特别功能的有机整体。

5、信息社会：信息成为与物质和能源同等重要甚至比之更加重要的资源，整个社会的政治、经济和文化以信息为核心价值而得到发展的社会。

三、简答1、人类社会传播的特点。

社会传播是一种信息共享活动。

社会传播是一定社会关系中进行的，又是一定社会关系的体现。

从传播的社会关系性而言，它又是一种双向的社会互动行为。

传播成立的重要前提之一，是传受双方必须要有共通的意义空间。

传播是一种行为，是一种过程，也是一种系统。

2、社会信息系统的特点。

社会信息系统是一个开放性的系统。

社会信息系统是由各种子系统相互连结、相互交织而构成的整体。

社会信息系统是一个具有双重偶然性的系统。

社会信息系统是一个自我创造、自我完善的系统。

3、信息社会的特点。

社会经济主体为以高新科技为核心的第三产业，信息和知识产业占据主导地位。

劳动力主体为信息的生产者和传播者。

交易结算主要依靠信用。

跨国贸易、全球贸易成为主流。

第三章、第四章一、填空1、信息是符号和意义的统一体。

2、符号可以分为信号和象征符两类。

3、非语言符号包括：语言符号的伴生符、体态符号和物化、活动化、程式化的 符号。

4、符号的基本功能包括：表述和理解功能、传达功能、思考功能。

自动控制理论第三版课后练习题含答案前言自动控制理论是现代自动控制技术的基础课程，课后练习题是巩固理论知识和巩固实践技能最重要的方法之一。

本文档整理了自动控制理论第三版的课后习题，提供了详细的解题思路和答案，希望能够帮助读者更好地掌握自动控制理论。

1. 第一章课后习题1.1 第一章习题1题目已知一个系统的开环传递函数为$G(s)=\\frac{1}{s(s+1)(s+2)}$，求该系统的稳定性。

解答该系统的零点为0。

该系统的极点为−1和−2。

因为系统的极点都在左半平面，没有极点在右半平面，所以该系统稳定。

1.2 第一章习题2题目已知一个系统的传递函数为$G(s)=\\frac{1}{(s+2)(s+3)}$，求该系统的单位阶跃响应。

解答该系统的传递函数可以表示为$G(s)=\\frac{A}{s+2}+\\frac{B}{s+3}$的形式，解得$A=\\frac{1}{s+3}$，$B=-\\frac{1}{s+2}$。

所以，该系统的单位阶跃响应为y(t)=1−e−2t−e−3t1.3 第一章习题3题目已知一个系统的传递函数为$G(s)=\\frac{1}{s^2+5s+6}$，求该系统的单位阶跃响应。

解答该系统的传递函数可以写成$G(s)=\\frac{1}{(s+2)(s+3)}$的形式。

所以，该系统的单位阶跃响应为$$ y(t)=1-\\frac{1}{2}e^{-2t}-\\frac{1}{3}e^{-3t} $$2. 第二章课后习题2.1 第二章习题1题目已知一个系统的传递函数为$G(s)=\\frac{1}{s^2+4s+3}$，求该系统的稳定性。

解答该系统的极点为−1和−3。

因为系统的极点都在左半平面，没有极点在右半平面，所以该系统稳定。

2.2 第二章习题2题目已知一个系统的传递函数为$G(s)=\\frac{1}{s^2+4s+3}$，求该系统的单位冲击响应。

解答该系统的传递函数可以写成$G(s)=\\frac{1}{(s+1)(s+3)}$的形式。

高等数学习题册上册第一本班级学号姓名应用数学系2第一章 函数与极限§1 函数必作习题P16－18 4 (5) (6) (8)，6，8，9，11，16，17必交习题一、一列火车以初速度0v ，等加速度a 出站，当速度达到1v 后，火车按等速运动前进；从出站经过T 时间后，又以等减速度a 2进站，直至停止。

(1) 写出火车速度v 与时间t 的函数关系式；(2) 作出函数)(t v v =的图形。

二、 证明函数12+=x xy 在),(+∞-∞内是有界的。

3三、判断下列函数的奇偶性： (1)x x x f 1sin)(2= ；(2)1212)(+-=x x x f ；(3))1ln()(2++=x x x f 。

四、 证明：若)(x f 为奇函数，且在0=x 有定义，则0)0(=f 。

4 §2 初等函数必作习题P31－33 1，8，9，10，16，17必交习题一、 设)(x f 的定义域是]1,0[，求下列函数的定义域：(1))(x e f ；(2))(ln x f ；(3))(arcsin x f ；(4))(cos x f 。

二、(1)设)1ln()(2x x x f +=，求)(x e f -；(2)设23)1(2+-=+x x x f ，求)(x f ；(3)设x x f -=11)(，求)]([x f f ，})(1{x f f 。

)1,0(≠≠x x5 三、设)(x f 是x 的二次函数，且1)0(=f ，x x f x f 2)()1(=-+，求)(x f 。

四、设⎩⎨⎧>+≤-=0,20,2)(x x x x x f ，⎩⎨⎧>-≤=0,0,)(2x x x x x g ，求)]([x g f 。

6§3 数列的极限必作习题P42 3 (3) (4)，4，5，6必交习题一、 写出下列数列的前五项 (1)3sin 31n n x n =；(2)nn n n x n ++++++=22212111 ；(3)n x n x nn n )1(1211122-=+++=-， 。

第一章第二章习题课中国石油大学能源与动力工程系China University of Petroleum Dept. of Energy and Power Engineering第一章基本概念及定义重点热力系统的选取，对工质状态的描述，状态与状态参数的关系，状态参数(p,T,V/v,U,H,S)，平衡状态，状态方程，可逆过程。

注意1.孤立系统：系统与外界既无能量传递也无物质交换2.状态参数：描述工质状态特性的各种状态的宏观物理量。

状态参数的数学特性:1212d x x x -=⎰表明：状态的路径积分仅与初、终状态有关，而与状态变化的途径无关。

0d =⎰x 表明：状态参数的循环积分为零3. 正向循环热效率：12101q q q w t -==η4. 制冷循环：制冷系数：21202q q q w q -==ε5. 热泵循环：热泵系数（供热系数）：21101q q q w q -=='ε注意：(1) 以上三式，适用于可逆循环和不可逆循环；(2) 式中q 1、q 2、w 0取绝对值。

第一章基本概念及定义第二章热力学第一定律重点热力学能U、焓H(U+pV)、热力学第一定律的实质、熟练应用热力学第一定律解决具体问题闭口系统能量方程W U Q +∆=适用于mkg 质量工质w u q +∆=适用于单位质量工质注意:该方程适用于闭口系统、任何工质、任何过程。

W U Q δd δ+=w u q δd δ+=微元过程可逆过程有δd δd w p v q T s==vp u s T v p u q d d d d d δ+=+=第二章热力学第一定律循环过程第一定律表达式⎰⎰=w q δδ结论:第一类永动机不可能制造出来对于理想气体：Tc u vd d =理想气体可逆过程：vp T c s T v p T c q v v d d d d d δ+=+=第二章热力学第一定律开口系统能量方程质量守恒原理：进入控制体的质量一离开控制体的质量=控制体中质量的增量能量守恒原理：进入控制体的能量一控制体输出的能量=控制体中储存能的增量icv W m gz c h m gz c h E Q δδ)21(δ)21(d δ1121122222+++-+++=注意:本方程适用于任何工质，稳态稳流、不稳定流动的一切过程第二章热力学第一定律稳定流动能量方程i w z g c h q δd d 21d δ2+++=适用于任何工质，稳定流动热力过程引入技术功：it w z g c w δd d 21δ2++=t t w h q w h q δd δ+=+∆=上式变为：可逆过程：p v w t d δ-=p v h s T p v h q d d d d d δ-=-=理想气体可逆过程pv T c s T p v T c q p p d d d d d δ-=-=第二章热力学第一定律功和技术功在p-V图上的表示思考题1、当真空表指示数值愈大时，表明被测对象的实际压力愈大还是愈小？答：真空表指示数值愈大时，表明被测对象的实际压力愈小。

第一章：一.判断题：1.软件就程序，编软件就是编写程序。

（）2.软件危机的主要表现是软件需求增加，软件价格上升。

()3.软件工程科学出现的主要原因是软件危机的出现。

（）4.与计算机科学的理论研究不同，软件工程是一门原理性学科（）二.选择题1.在下列选项中，（）不是软件的特征A系统性与复杂性 B 可靠性与一致性C 抽象性与智能性D 有形性与可控性2.软件危机的主要原因是：A软件工具落后 B 软件生产能力不足C 对软件的认识不够D 软件本身的特点及开发方法3.下列说法正确是的是A 20世纪50年代提出了软件工程的概念B 20世纪60年代提出了软件工程的概念C 20世纪70年代提出了客户机/服务器技术D 20世纪80年代软件工程学达到成熟4.( )是将系统化的规范的可定量的方法应用于软件的开发，运行和维护的过程。

它包括方法、工具和过程三个要素A 软件生命周期B 软件测试C 软件工程D 软件过程5.在下列选项中，（）不属于软件工程学科索要研究的基本内容。

A 软件工程材料B 软件工程目标C 软件工程原理D 软件工程过程6.软件工程的三要素是（）A技术，方法和工具 B 方法，对象和类 C 方法，工具和过程 D 过程，模型和方法7.用来辅助软件开发，运行，维护，管理，支持等过程中的活动的软件成为软件开发工具，通常也称为（）工具A CADB CAIC CAMD CASE三简答题1.与计算机硬件相比，计算机软件有哪些特点？2.软件就是程序吗？如何定义软件？3.什么是软件危机？是什么原因导致了软件危机？4.为什么说软件工程的开发能在一定程度上解决软件危机的各种弊端？5.请简述软件工程的研究内容。

6.请简述软件工程的三要素。

7.请简述软件工程的目标，过程和原则。

8.请简述软件工程的基本原则。

9.请简述现代软件工程与传统软件工程显著的区别与改进。

第二章：一判断题1.瀑布模型的最大优点是将软件开发的各个阶段划分得十分清晰。