2020年浙江省杭州二中高考数学最后一卷

2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟数学试卷6月-学生用卷一、选择题（本大题共10小题，每小题4分，共40分）1、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第1题4分 2019~2020学年江西南昌东湖区南昌市第十中学高一上学期期末第1题5分2020~2021学年四川成都成华区四川省成都列五中学高三上学期段考理科（二）第1题5分 2020~2021学年广东深圳龙岗区华中师范大学龙岗附属中学高一上学期期中第1题5分 2019~2020学年陕西宝鸡金台区宝鸡中学高三上学期期中文科第1题5分已知集合A ={x|x <1},B ={x|3x <1}，则（ ）．A. A ∩B ={x|x <0}B. A ∪B =RC. A ∪B ={x|x >1}D. A ∩B =∅2、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第2题4分 2020~2021学年河南南阳高二上学期期末文科第8题5分2018~2019学年陕西宝鸡渭滨区高二上学期期末文科第7题5分“x 2−x −6<0”的一个充分但不必要的条件是（ ）．A. −2<x <3B. 0<x <3C. −3<x <2D. −3<x <33、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第3题4分x ，y 满足约束条件{x +y −3⩾0x −2y ⩾0，则z =x −y 的最小值为（ ）． A. 1 B. −1 C. 3 D. −34、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第4题4分设某几何体的三视图如右图，则该几何体的体积为（）．A. 12B. 8C. 4D. 25、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第5题4分函数y=|x|−sin⁡(3x)的图象可能是下列图象中的（）．A.B.C.D.6、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第6题4分2019~2020学年浙江杭州西湖区浙江大学附属中学高一上学期期中第10题3分2018~2019学年四川成都高新区成都市实验外国语学校（西区）高一上学期单元测试《零点》第4题已知函数f(x)={1−|x−1|,x∈(−∞,2)12f(x−2),x∈[2,+∞)，则函数F(x)=xf(x)−1的零点个数为（）．A. 4B. 5C. 6D. 77、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第7题4分空间线段AC⊥AB，BD⊥AB，且AC:AB:BD=1:3:1，设CD与AB所成的角为α，CD与面ABC所成的角为β，二面角C−AB−D的平面角为γ，则（）．A. β⩽α⩽γ2B. β⩽γ2⩽αC. α⩽β⩽γ2D. α⩽γ2⩽β8、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第8题4分已知甲盒子中有1个黑球，1个白球和2个红球，乙盒子中有1个黑球，1个白球和3个红球，现在从甲乙两个盒子中各取1个球，分别记取出的红球的个数为ξ1，ξ2，则有（）．A. E(ξ1)>E(ξ2)，D(ξ1)>D(ξ2)B. E(ξ1)>E(ξ2)，D(ξ1)<D(ξ2)C. E(ξ1)<E(ξ2)，D(ξ1)>D(ξ2)D. E(ξ1)<E(ξ2)，D(ξ1)<D(ξ2)9、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第9题4分面积为2的△ABC中，E，F分别是AB，AC的中点，点P在直线EF上，则PC→⋅PB→+BC→2的最小值是（）．A. √2B. 2√2C. √3D. 2√310、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第10题4分已知数列{x n}满足x0=x11，(x n+1−1xn )⋅(x n+1−x n2)=0，n∈N，则x0的最大值为（）．A. 5B. 6C. 25D. 26二、填空题（本大题共7小题，共36分）11、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第11题6分已知1+3i=z⋅(1−i)，则复数z的虚部为，|z|为．12、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第12题6分双曲线x 23−y2=1的渐近线方程为，离心率为．13、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第13题6分若(1+2x)2(1−x)5=a0+a1x+a2x2+⋅⋅⋅+a7x7，则a7=，a2+ a4+a6=．14、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第14题6分在△ABC中，角A、B、C的对边分别为a、b、c，且a2−(b−c)2=(2−√3)bc，sin⁡Asin⁡B= cos2C2，则角A的大小为；若BC边上中线AM的长为√7，则△ABC的面积为．15、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第15题4分若从1,2,3,⋯,9这9个整数中同时取出4个不同的数，其和为偶数，则不同的取法共有种．16、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第16题4分设圆O圆心为坐标原点，半径为√a2−b2，圆O在第一象限的圆弧上存在一点，作圆O的切线与椭圆x 2a2+y2b2=1(a>b>0)交于A，B两点，若OA⊥OB，则椭圆的离心率为．17、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第17题4分在平面直角坐标系中，定义d(P,Q)=|x1−x2|+|y1−y2|为两点P(x1,y1)，Q(x2,y2)之间的“折线距离”，则椭圆x 22+y2=1上一点P和直线4x+3y−12=0上一点Q的“折线距离”的最小值为．三、解答题（本大题共5小题，共74分）18、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第18题14分2020~2021学年3月四川成都金牛区成都市第十八中学高二下学期月考理科第19题已知函数f(x)=sin⁡x(cos⁡x−√32sin⁡x)+√32cos2x，x∈R．(1) 求函数f(x)的最小正周期及单调递增区间．(2) 若α为锐角且f(α+π12)=−79，β满足cos⁡(α−β)=35，求sin⁡β的值．19、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第19题15分2020~2021学年5月江西南昌东湖区南昌市第二中学高二下学期月考理科第20题12分如图，平面四边形ABCD关于直线AC对称，∠A=60°，∠C=90°，CD=2．把△ABD沿BD 折起．(1) 若二面角A−BD−C的余弦值为√33，求证：AC⊥平面BCD．(2) 若AB与面ACD所成的线面角为30°时，求AC的长．20、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第20题15分已知数列{a n}，{b n}满足a1=12，a n+1=n√1+a+b∈N∗)．(1) 若b n=a n24，求证数列{1a n}是等差数列，并求数列{a n}的通项公式．(2) 若b n=a n3．①求证：0<a n⩽12．②14⋅(813)n−1⩽a n2⩽25n+3(n∈N∗)．21、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第21题15分如图，过抛物线y2=2px(p>0)焦点F的直线交抛物线于A，B两点，记以A，B为直径端点的圆为圆M．(1) 证明：圆M与抛物线的准线相切．(2) 设P=2，点A在焦点的右侧，圆M与x轴交于C，D两点，记△ANF和△ACD的面积为S1，S2，求S1S2的最大值（其中点N为圆M与抛物线准线的切点）．22、【来源】 2020年浙江杭州滨江区浙江省杭州第二中学高三下学期高考模拟6月第22题15分已知f(x)={1−x2ln⁡x,x>0 e−x−2,x⩽0．(1) 当x∈(0,+∞)时，求f(x)的最大值．(2) 若存在a∈[0,+∞)，使得关于x的方程f(x)+ax2+bx=0有三个不相同的实数根，求实数b 的取值范围．1 、【答案】 A;2 、【答案】 B;3 、【答案】 A;4 、【答案】 C;5 、【答案】 A;6 、【答案】 C;7 、【答案】 A;8 、【答案】 C;9 、【答案】 D;10 、【答案】 C;11 、【答案】2;√5;12 、【答案】y=±√33x;23√3;13 、【答案】−4;15;14 、【答案】π6;√3;15 、【答案】66;16 、【答案】√5−12;17 、【答案】3−√414;18 、【答案】 (1) T=π；[kπ−5π12,π12+kπ]，k∈Z．;(2) 6√2±415．;19 、【答案】 (1) 证明见解析．;(2) 2√3或23√3．;20 、【答案】 (1) 证明见解析，a n=2n+3．;(2)①证明见解析．②证明见解析．;21 、【答案】 (1) 证明见解析．;(2) √3．3;22 、【答案】 (1) 1+1．2e;,+∞)．(2) (−∞,−2√2)∪[1e;。

浙江杭州二中2020届高三考前热身考试（最后一卷）语文试题及答案高三杭州二中-2020学年第二学期高三年级高考热身考语文试题卷考生须知:1.本卷满分150分，考试时间150分钟；2.答题前，在答题卷指定区域填写班级、姓名、试场号及座位号；3.所有答案必须写在答题卷上，写在试卷上无效；4.考试结束后，只需上交答题卷。

一、语言文字运用(共20分)1.下列各句中，没有错别字且加点字的注音全部正确的一项是(3分)（）A.请战书叠成厚厚一摞(luò),汗水浸湿全身，摘下口罩露出印痕、压疮……这一帧帧感人的画面，让我们相信雾霾终将消散，霁(j ì)月必定到来。

B.每逢端午佳节，万人空巷、齐聚一堂，缅怀先贤、颂扬屈原，挂艾草、割菖蒲(pǔ)、赛龙舟、包粽子、办诗会，已经成为屈原故里秭(Zǐ)归千年不断的传统，成为中华大地一道独特的风景。

C.宁夏健全了研究生导师队伍管理机制，明确在导师遴(lín)选时，对存在师德问题的教师实施“一票否决”；同时，还健全了导师评聘(pìn)分离机制，破除导师资格终生制。

D.面对国家意志和香港民意，面对涉港国安立法不可逆转的事实，一些境外势力炮(páo)制谎话，无耻之犹。

面对其妄语谰(1án)言，我们的正义之声不受干扰，正义之举不会止歇。

阅读下面的文字，完成2—3题。

非虚构性文学作品《手上春秋:中国手艺人》一经出版，就荣膺中国图书评论学会4月“中国好书”榜单，好评如潮。

[甲]作者采录了五行八作的民间手艺人，如木匠、药师、制茶师、捞纸工、蜀绣传人、壮族女红传人等，书中还特地记录了“中国摩天大楼钢构第一人”陆建新。

[乙]他37年扎根建筑施工第一线，餐风宿露，参与了“三个速度”:三天一层楼(深圳国贸)、两天半一层楼(深圳地王)和两天一层楼(广州西塔)的实践。

他还主持承建了国内已封顶的100层以上钢构摩天大楼七幢中的四幢，见证了中国超高层建筑从无到有、从有到领先世界的全过程。

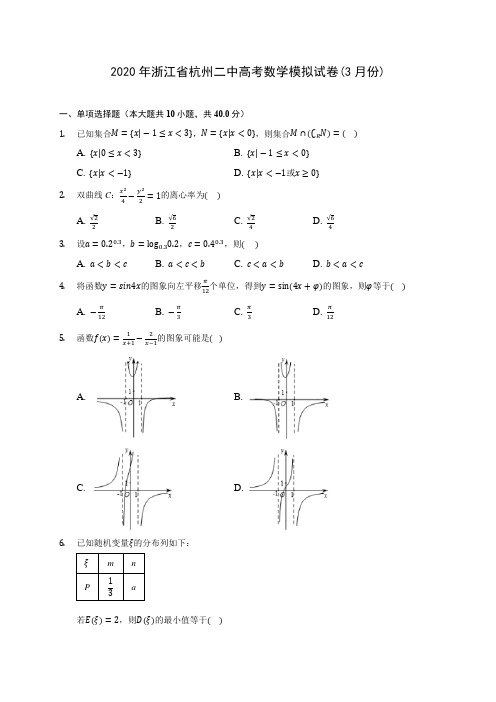
2020年浙江省杭州二中高考数学模拟试卷(3月份)一、单项选择题（本大题共10小题，共40.0分）1.已知集合M={x|−1≤x<3}，N={x|x<0}，则集合M∩(∁R N)=()A. {x|0≤x<3}B. {x|−1≤x<0}C. {x|x<−1}D. {x|x<−1或x≥0}2.双曲线C：x24−y22=1的离心率为()A. √22B. √62C. √24D. √643.设a=0.20.3，b=log0.30.2，c=0.40.3，则()A. a<b<cB. a<c<bC. c<a<bD. b<a<c4.将函数y=sin4x的图象向左平移π12个单位，得到y=sin(4x+φ)的图象，则φ等于()A. −π12B. −π3C. π3D. π125.函数f(x)=1x+1−2x−1的图象可能是()A. B.C. D.6.已知随机变量ξ的分布列如下：ξm nP 13a若E(ξ)=2，则D(ξ)的最小值等于()A. 12B. 2C. 1D. 0 7. 平面向量m⃗⃗⃗ ，n ⃗ 均为单位向量，若向量m ⃗⃗⃗ ，n ⃗ 的夹角为2π3，则|2m ⃗⃗⃗ +3n ⃗ |=( ) A. 25 B. 5 C. √7 D. 78. 如图，空间四边形ABCD 中，“AC =AD ”“BC =BD ”则AB 与CD 所成的角为( )A. 30°B. 45°C. 60°D. 90°9. 已知函数f(x)={log 2x,x >03x ,x ≤0，且函数ℎ(x)=f(x)+x −a 有且只有一个零点，则实数a 的取值范围是( ) A. [1,+∞) B. (1,+∞) C. (−∞,1) D. (−∞,1]10. 已知S n 是数列{a n }的前n 项和，a 1=1，a 2=3，数列{a n a n+1}是公比为2的等比数列，则S 10=( )A. 1364B. 1243 C. 118 D. 124二、填空题（本大题共3小题，共12.0分）11. 如图，某电子元件，是由3个电阻组成的回路，其中有4个焊点A ，B ，C ，D ，若某个焊点脱落，整个电路就不通，现在发现电路不通了，那么焊点脱落的可能情况共有__________种．12. 函数y =|x −2|+3的最小值是______ ．13. 已知向量|OA ⃗⃗⃗⃗⃗ |=√3，|OB ⃗⃗⃗⃗⃗⃗ |=1，OA⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =0，点C 在∠AOB 内，且∠AOC =60°，设OC ⃗⃗⃗⃗⃗ =λOA ⃗⃗⃗⃗⃗ +μOB ⃗⃗⃗⃗⃗⃗ (λ,μ∈R)，则λμ=______． 三、多空题（本大题共4小题，共24.0分） 14. 二项式(3x −1x )6的展开式中，常数项等于 ，二项式系数和为 15. 若实数x ，y ，满足约束条件{y ≥xx +y ≤42x −y ≥4已知点(x,y)所表示的平面区域为三角形，则实数k 的取值范围为 (1) ，若z =x +2y 有最大值8，则实数k = (2) ．16.已知一个几何体的三视图如图所示，其中正视图是直角梯形，侧视图和俯视图都是矩形，则这个几何体的体积是(1)，表面积是(2)．17.已知△ABC中，角A，B，C所对的边分别为a；b，c，△ABC的面积S=2a2sinC．(Ⅰ)ba +ab=(1)，(Ⅱ)若c=10，角C的平分线CM交边AB于点M，且|CM|=4，则b=(2)．四、解答题（本大题共5小题，共74.0分）18.已知函数f(x)=2√3sinxcosx+2cos2x−1(x∈R)).(1)求函数f(x)的最小正周期；(2)若f(x0)=65,x0∈[π4,π2]，求cos2x0的值．19.如图所示，在三棱锥A−BCD中，AB⊥平面BCD，M，N分别是AC，AD的中点，BC⊥CD．(1)求异面直线MN与BC所成的角;(2)求证：平面ACD⊥平面ABC.20.在数列{a n}中，a1=1,a n+1=√a n2−2a n+2−1,(n∈N∗)．(1)求a2,a3的值；<a2n+1．(2)证明：①0⩽a n⩽1；②a2n<1421.已知抛物线C：x2=2py(p>0)的焦点为F(0,1)．(Ⅰ)求抛物线C的方程；(Ⅱ)如图，过F作两条互相垂直的直线l1与l2，分别交抛物线C于A、B与D、E，设AB、DE的中点分别为M、N，求△FMN面积S的最小值．22.已知函数f(x)=(2x−4)e x+a(x+2)2(x>0,a∈R,e是自然对数的底数)．(1)若f(x)是(0,+∞)上的单调递增函数，求实数a的取值范围；(2)当a∈(0,1)时，证明：函数f(x)有最小值m，且m>−2e．2【答案与解析】1.答案：A解析：解：∵集合M={x|−1≤x<3}，N={x|x<0}，∴C R N={x|x≥0}，集合M∩(∁R N)={x|0≤x<3}．故选：A．推导出C R N={x|x≥0}，由此能求出集合M∩(∁R N)．本题考查交集、补集的求法，考查交集、补集定义等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．2.答案：B解析：解：双曲线C：x24−y22=1，可得a=2，b=√2，则c=√6．双曲线的离心率为：√62．故选：B．利用双曲线方程求出a，b，c，然后求解离心率即可．本题考查双曲线的简单性质的应用，是基础题．3.答案：B解析：本题考查了指数函数与对数函数、幂函数的单调性，考查了推理能力与计算能力，属于基础题．利用指数函数与对数函数、幂函数的单调性即可得出．解：∵a=0.20.3∈(0,1)，c=0.40.3∈(0,1)，由幂函数y=x0.3在(0,+∞)单调递增，∴a<c，又b=log0.30.2>log0.30.3=1，∴a<c<b．故选：B．4.答案：C解析：解：函数y =sin4x 的图象向左平移π12个单位，得到y =sin4(x +π12)的图象，就是y =sin(4x +φ)的图象，故φ=π3故选：C ．利用函数图象的平移，求出函数的解析式，与已知解析式比较，即可得到φ的值．本题是基础题，考查三角函数的图象的平移，注意平移的方向，基本知识的考查题目． 5.答案：B解析：本题考查函数的图象的识别，属于基础题．利用特殊点排除即可．解：因为f(x)=1x+1−2x−1，则f(0)=3，故排除D ；由f(−2)=−13<0，故排除C ；由f(−3)=0，故排除A ；故选B ． 6.答案：D解析：本题考查离散型随机变量的期望与方差，属于基础题.先利用概率和为1求出a 的值，再利用期望公式求出m +2n =6，然后利用方差公式得D(ξ)=13×(m −2)2+23×(n −2)2=2(n −2)2，结合二次函数的性质即可解得．解：由题意得a =1−13=23，所以E(ξ)=13m +23n =2，即m +2n =6．又D(ξ)=13×(m−2)2+23×(n−2)2=2(n−2)2，所以当n=2时，D(ξ)取最小值为0．故选D．7.答案：C解析：本题考查向量模的计算，考查单位向量的概念与向量的数量积，属于基础题．由题意可得到|m⃗⃗⃗ |=|n⃗|=1，然后利用|2m⃗⃗⃗ +3n⃗|=√(2m⃗⃗⃗ +3n⃗)2，结合向量的数量积运算进行计算即可．解：根据条件，|m⃗⃗⃗ |=|n⃗|=1，∴|2m⃗⃗⃗ +3n⃗|=√(2m⃗⃗⃗ +3n⃗)2=√4|m⃗⃗⃗ |2+12m⃗⃗⃗ ·n⃗⃗⃗⃗ +9|n⃗|2．故选C．8.答案：D解析：解：空间四边形ABCD中，取CD中点O，连结BO、AO，∵AC=AD，BC=BD，∴BO⊥CD，AO⊥CD，∵BO∩AO=O，∴CD⊥平面AOB，∵AB⊂平面AOB，∴CD⊥AB，∴AB与CD所成的角为90°．故选：D．取CD中点O，连结BO、AO，推导出CD⊥平面AOB，从而得到AB与CD所成的角为90°．本题考查异面直线所成角的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．9.答案：B解析：解：函数ℎ(x)=f(x)+x −a 有且只有一个零点，就是y =f(x)的图象与y =a −x 的图象有且只有一个交点，如图：显然当a >1时，两个函数有且只有一个交点，故选：B ．利用数形结合画出函数y =f(x)的图象，通过函数ℎ(x)=f(x)+x −a 有且只有一个零点，求出a 的范围．本题考查函数零点个数的判断，考查数形结合，考查分析问题解决问题的能力．10.答案：D解析：解：S n 是数列{a n }的前n 项和，a 1=1，a 2=3，数列{a n a n+1}是公比为2的等比数列， 可得a 2a 3a 1a 2=2，解得a 3=2，a 3a4a 2a 3=2，a 4=6，同理a 5=4，a 6=12，a 7=8，a 8=24，a 9=16，a 10=48，则S 10=1+3+2+6+4+12+8+24+16+48=124．故选：D ．利用数列的首项以及数列{a n a n+1}是公比为2的等比数列，求出数列的各项，然后求解S 10即可． 本题考查数列的递推关系式的应用，数列求和，考查计算能力．11.答案：15解析：本题考查组合的运用及分类计数原理，根据题意可得恰有i(i =1,2，3，4)个焊点脱落的可能情况为C 4i 种，进而利用分类加法计数原理即可求得结果． 解：恰有i(i =1,2，3，4)个焊点脱落的可能情况为C 4i 种，由分类加法计数原理可知，当电路不通时焊点脱落的可能情况共C 41+C 42+C 43+C 44=15(种)．故答案为15．12.答案：3解析：解：y =|x −2|+3≥3，当x =2时，取得等号． 故函数y =|x −2|+3的最小值是3，故答案为：3根据绝对值的性质即可求出函数的最小值．本题考查函数的最小值，以及绝对值函数的性质，属于基础题． 13.答案：13 解析：解：∵OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =0，∴OA ⊥OB ，以O 为原点，以OA ，OB 为坐标轴建立坐标系，则A(0,√3)，B(1,0)，设OC =ρ，则C(√32ρ,12ρ)，∵OC ⃗⃗⃗⃗⃗ =λOA ⃗⃗⃗⃗⃗ +μOB ⃗⃗⃗⃗⃗⃗ (λ,μ∈R)，∴{μ=√32ρ√3λ=12ρ，∴λμ=13．故答案为：13．建立坐标系，设OC =ρ，代入坐标运算即可求出λμ．本题考查了平面向量的基本定理，属于基础题．14.答案：−54064解析： 二项式的通项为T r+1=C 6r (3x )6−r (−1x )r=(−1)r ×36−r C 6r x 6−2r ，常数项为当6−2r =0时，即r =3时，所以T 4=(−1)3×33C 63=−540，二项式系数为C 60+C 61+⋯+C 66=26=64。

2021-2022高考数学模拟试卷注意事项：1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。

用2B 铅笔将试卷类型（B ）填涂在答题卡相应位置上。

将条形码粘贴在答题卡右上角"条形码粘贴处"。

2．作答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试题卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保证答题卡的整洁。

考试结束后，请将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．定义在R 上的函数()f x 满足(4)1f =，()f x '为()f x 的导函数，已知()y f x '=的图象如图所示，若两个正数,a b满足(2)1f a b +<，11b a ++则的取值范围是（ ）A ．(11,53)B ．1(,)(5,)3-∞⋃+∞C ．(1,53)D ．(,3)-∞2．已知12,F F 是双曲线22221(0,0)x y a b a b-=>>的左右焦点，过1F 的直线与双曲线的两支分别交于,A B 两点（A 在右支，B 在左支）若2ABF ∆为等边三角形，则双曲线的离心率为（ ） A ．3B ．5C ．6D ．73．已知集合{}2,1,0,1A =--，{}22*|,B x x a a N=≤∈，若A B ⊆，则a 的最小值为（ ）A ．1B ．2C ．3D ．44．已知函数||()()x x f x x R e=∈，若关于x 的方程()10f x m -+=恰好有3个不相等的实数根，则实数m 的取值范围为（ ） A ．(212),e eB ．(20,)2e eC ．(11,1)e+D ．21,12()ee+ 5．已知复数，则的共轭复数在复平面对应的点位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限6．已知集合(){}lg 2A x y x ==-，集合1244x B x ⎧⎫=≤≤⎨⎬⎩⎭，则A B =（ ） A ．{}2x x >-B ．{}22x x -<<C ．{}22x x -≤<D ．{}2x x <7．已知抛物线22(0)y px p =>上一点(5,)t 到焦点的距离为6，P Q 、分别为抛物线与圆22(6)1x y -+=上的动点，则PQ 的最小值为（ ）A ．211-B ．525-C ．25D ．251-8．已知抛物线2:4(0)C y px p =>的焦点为F ，过焦点的直线与抛物线分别交于A 、B 两点，与y 轴的正半轴交于点S ，与准线l 交于点T ，且||2||FA AS =，则||||FB TS =（ ） A ．25B ．2C ．72D ．39．如图在一个60︒的二面角的棱有两个点,A B ，线段,AC BD 分别在这个二面角的两个半平面内，且都垂直于棱AB ，且2,4AB AC BD ===，则CD 的长为（ ）A ．4B ．25C ．2D ．2310．已知:|1|2p x +> ，:q x a >，且p ⌝是q ⌝的充分不必要条件，则a 的取值范围是（ ） A ．1a ≤B ．3a ≤-C ．1a ≥-D ．1a ≥11．生活中人们常用“通五经贯六艺”形容一个人才识技艺过人，这里的“六艺”其实源于中国周朝的贵族教育体系，具体包括“礼、乐、射、御、书、数”.为弘扬中国传统文化，某校在周末学生业余兴趣活动中开展了“六艺”知识讲座，每艺安排一节，连排六节，则满足“数”必须排在前两节，“礼”和“乐”必须分开安排的概率为（ ） A ．760B ．16C ．1360D ．1412．已知平面向量,a b 满足||||a b =，且2)b b -⊥，则,a b 所夹的锐角为（ ）A ．6π B ．4π C ．3π D ．0二、填空题：本题共4小题，每小题5分，共20分。

2020届浙江省杭州二中高考数学统测试卷(5月份)一、单选题（本大题共10小题，共40.0分）1.若函数f(x)=cosωx在区间(0,π]上单调递减，则正实数ω的取值范围是()A. [1,2]B. (0,1)C. (12,1] D. (0,1]2.设m、n是不同的直线，α、β、γ是不同的平面，有以下四个命题：①若α//β，α//γ，则β//γ；②若α⊥β，m//α，则m⊥β；③若m⊥α，m//β，则α⊥β；④若m//n，n⊂α，则m//α．其中真命题的序号是()A. ①④B. ②③C. ②④D. ①③3.复数3+i1−3i=()A. iB. −iC. 2iD. −2i4.如图，网格纸上小正方形的边长为1，粗实线和虚线画出的是某四面体的三视图，则该多面体的各条棱中，最长的棱的长度是()A. 2√5B. 4√2C. 6D. 4√35.已知等差数列{a n}中，a1=−1，d=4，则它的通项公式是()A. a n=−4n+3B. a n=−4n−3C. a n=4n−5D. a n=4n+36.函数f(x)=√3sinx−acosx的图象的一条对称轴是x=5π3，则g(x)=asinx+cosx= Asin(ωx+φ)(A>0,ω>0)的一个初相是()A. −3π4B. −π4C. π4D. 3π47. 已知实数x ，y 满足{x ≥0y ≥0x +2y ≤2，若目标函数z =x −y 的最大值为a ，最小值为b ，则(a −bt)6展开式中t 4的系数为( )A. 200B. 240C. −60D. 608. 已知平面内一点满足，若实数满足：，则的值为( )A. 6B. 3C. 2D.9. 如图，E 、F 分别是正方形SD 1DD 2的边D 1D 、DD 2的中点，沿SE 、SF 、EF 将它折成一个几何体，使D 1、D 、D 2重合，记作D ，给出下列位置关系：①SD ⊥面EFD ； ②SE ⊥面EFD ；③DF ⊥SE ；④EF ⊥面SED.其中成立的有( )A. ①与②B. ①与③C. ②与③D. ③与④10. 已知双曲线x 2m 2−y 2=1(m >0)与抛物线y 2=4x 的准线交于A ，B 两点，O 为坐标原点，若△AOB 的面积等于1，则m =( )A. √2B. 1C. √22D. 12二、单空题（本大题共4小题，共18.0分）11. 设全集U ={1,2，3，4}，A ={1,3}，B ={1,4}，∁U (A ∪B)=______．12. 函数f(x)={x 2+2x −1,x ≥a−x 2+2x −1,x <a对于任意的实数b ，函数y =f(x)−b 至多有一个零点，则实数a 的取值范围是______ ．13. 棱锥的三视图如图所示，且三个三角形均为直角三角形，则1x +1y 的最小值为______ ．14. 已知函数，若实数满足，则实数的范围是 ．三、多空题（本大题共3小题，共18.0分）15. 若(1−x −x 2)3=a 0+a 1x +a 2x 2+⋯+a 6x 6，则a 6= (1) ，a 1+a 3+a 5= (2) ． 16. 甲、乙、丙三人参加某次招聘会，若甲应聘成功的概率为49，乙、丙应聘成功的概率均为t3(0<t <3)，且三人是否应聘成功是相互独立的．若甲、乙、丙都应聘成功的概率是1681，则t 的值是 (1) ；设ξ表示甲、乙两人中被聘用的人数，则ξ的数学期望是 (2) ．17. 已知抛物线y 2=2px(p >0)的焦点为F(2,0)，则p = (1) ，过点A(3,2)向其准线作垂线，记与抛物线的交点为E ，则|EF|= (2) ． 四、解答题（本大题共5小题，共74.0分） 18. (本题满分13分)如图，某巡逻艇在处发现北偏东相距海里的处有一艘走私船，正沿东偏南的方向以海里/小时的速度向我海岸行驶，巡逻艇立即以海里/小时的速度沿着正东方向直线追去，小时后，巡逻艇到达处，走私船到达处，此时走私船发现了巡逻艇，立即改变航向，以原速向正东方向逃窜，巡逻艇立即加速以海里/小时的速度沿着直线追击．(Ⅰ)当走私船发现了巡逻艇时，两船相距多少海里? (Ⅱ)问巡逻艇应该沿什么方向去追，才能最快追上走私船?19.如图，在四棱锥P−ABCD中，四边形ABCD是直角梯形，AB⊥AD，AB//CD，PC⊥面ABCD，AB=2AD=2CD=PC=4，E是PB的中点．(1)求证；平面EAC⊥平面PBC；(2)求三棱锥P−ACE的体积．20.等比数列{a n}的各项均为正数，且2a 1+3a 2=1，.等比数列{a n}的各项均为正数，且2a1+3a2=1，a32=9a2a6．(1)求数列{a n}的通项公式；}的前n项和．(2)设b n=log3a1+log3a2+⋯+log3a n，求数列{1b n21.已知F1，F2为椭圆C：x2a2+y2b2=1(a>b>0)的左、右两个焦点，且椭圆C上的点A(1,32)到两个焦点F1、F2的距离之和为4．(1)求椭圆C的方程，并写出其焦点F1、F2的坐标；(2)过椭圆C的右焦点F2任作一条与两坐标轴都不垂直的弦AB，若点M在x轴上，且直线MA 与直线MB关于x轴对称，求点M的坐标；(3)根据(2)中的结论特征，猜想出关于所有椭圆x2a2+y2b2=1(a>b>0)的一个一般结论(不需证明)．22.已知函数f(x)=a2x3−3ax2+2，g(x)=−3ax+3，x∈R，其中a>0．(Ⅰ)若a=1，求曲线y=f(x)在点(1,f(1))处的切线方程；(Ⅱ)求函数f(x)在区间(−1,1)上的极值；(Ⅲ)若∃x0∈(0,12]，使不等式f(x0)>g(x0)成立，求a的取值范围．【答案与解析】1.答案：D解析：本题考查三角函数的单调性，属基础题．解：∵x∈(0,π],ω>0,∴ωx∈(0,ωπ],因为函数f(x)=cosωx在区间(0,π]上单调递减，所以(0,ωπ]⊆(0,π],∴ω∈(0,1]．故选D．2.答案：D解析：解：对于①，因为α//β，α//γ，利用平面与平面平行的性质定理可得β//γ，正确；对于②，若α⊥β，m//α，则m与β关系不确定；对于③，∵m//β，∴β内存在直线与m平行，而m⊥α，所以β内存在直线与α垂直，根据面面垂直的判定定理可知α⊥β，故正确；对于④，m有可能在平面α内，故不正确；所以正确的是①③，故选：D．对每一选项进行逐一判定，不正确的只需举出反例，正确的证明一下即可．本题主要考查了平面与平面之间的位置关系，以及空间中直线与平面之间的位置关系，考查空间想象能力和推理论证能力，属于基础题．3.答案：A解析：解：3+i1−3i=(3+i)(1+3i) (1−3i)(1+3i)=3+i+9i+3i210=i．选A．把3+i1−3i 的分子分母同时乘以分母的共轭复数，得到(3+i)(1+3i)(1−3i)(1+3i)，再由复数的代数形式的乘除运算能够求出结果．本题考查复数的代数形式的乘除运算，是基础题．解题时要认真审题，仔细解答．4.答案：C解析：本题考查了不规则放置的几何体的三视图，属于中档题．作出几何体的直观图，根据三视图数据计算出最长棱即可．解：三视图对应的直观图为三棱锥A−BCD，其中正方体的棱长为4．最长棱长为CD=√22+(4√2)2=6．故选：C．5.答案：C解析：本题考查了等差数列的通项公式，考查了推理能力与计算能力，属于基础题．利用等差数列的通项公式即可得出．解：a n=−1+4(n−1)=4n−5．故选：C．6.答案：C解析：解：f(x)=√3sinx−acosx的图象的一条对称轴是x=5π3，，∴−a=−32+a2，解得a=1，∴g(x)=sinx+cosx=√2sin(x+π4)，∴g(x)的初相为π4．故选：C．根据题意，求出a，代入g(x)化简可得答案．本题考查三角函数的对称性，辅助角公式，考查运算能力，属于中档题．7.答案：D解析：解：由约束条件{x≥0y≥0x+2y≤2作出可行域如图，A(2,0)，B(0,1)，化目标函数z=x−y为y=x−z，由图可知，当直线y=x−z过A时，直线在y轴上的截距最小，z有最大值为2；当直线y=x−z过B时，直线在y轴上的截距最大，z有最小值为−1．∴a=2，b=−1．则(a−bt)6即为(2+t)6．由T r+1=C6r26−r t r，取r=4，可得展开式中t4的系数为22C64=60．故选：D．由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数求得a、b的值，代入(a−bt)6，写出展开式的通项，由x的指数等于4求得r值，则答案可求．本题考查简单的线性规划，考查了数形结合的解题思想方法，训练了二项式系数的应用，是中档题．8.答案：B解析：试题分析：根据题意可知，平面内一点满足，同时，运用向量的减法表示得到，故选B。

2020年浙江省杭州二中高考数学最后一卷一、选择题（本大题共10小题，共40.0分）1.若集合A={x|−1<2−x≤1}，B={x∈N|−x2+3x+4>0}，则A∩B=()A. {2,3}B. {0,1}C. {1,2，3}D. {1,2}2.下列说法中错误的是()A. 零向量是没有方向的B. 零向量的长度为0C. 零向量与任一向量平行D. 零向量的方向是任意的3.已知p：“x=2”，q：“x−2=√2−x”，则p是q的()A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件4.椭圆C：x2a +y2b=1(a>b>0)的左焦点为F，若F关于直线x+y=0的对称点A是椭圆C上的点，则椭圆的离心率为()A. √22B. √32C. √2−1D. √3−15.函数f(x)=1−e|x|的图像大致是()A. B.C. D.6.5位大学毕业生分配到3家单位，每家单位至少录用1人，则不同的分配方法共有()A. 25种B. 60种C. 90种D. 150种7.用反证法证明命题“设为实数，若在上单调，则至多有一个零点”时，应假设为()A. 函数f(x)至少有一个零点B. 函数f(x)至多有两个零点C. 函数f(x)没有零点D. 函数f(x)至少有两个零点8.若a>b，则()A. ln(a−b)>0B. 3a<3bC. a3−b3>0D. |a|>|b|9. 如图，已知正四面体D −ABC(所有棱长均相等的三棱锥)，P ，Q ，R 分别为AB ，BC ，CA 上的点，AP =PB ，分别记二面角D −PR −Q ，D −PQ −R ，D −QR −P 的平面角为α，β，γ，则( )A. γ<α<βB. α<γ<βC. α<β<γD. β<γ<α 10. 在数列{a n }中，若a 2n =2a 2n−2+1，a 16=127，则a 2的值为( )A. −1B. 0C. 2D. 8 二、填空题（本大题共7小题，共36.0分）11. 若复数z =−2+i ，则z⋅z i = ______ ． 12. 在(x 2−2x )7的展开式中，含x 2项的系数为________． 13. 如图，在边长为1的正方形网格中，粗线画出的是某几何体的三视图，则该几何体的长棱的长度为__________．14. 在△ABC 中，AC =√7，BC =2，B =60º，则BC 边上的高等于________。

2020年浙江省杭州二中高考数学模拟试卷（3月份）一、选择题（本大题共10小题，每小题4分，共40分）1.（4分）已知集合M={x|啜於3）,N={x|x>2},则集合MC（4N）=（）A.{x|啜少2}B.（x|x.l}C.{x|L,x<2}D.{x\2<x,,3}222.（4分）设双曲线.-匕=l（a>0）的两焦点之间的距离为10,则双曲线的离心率为（）3455A.-B.-C.-D.-55433.（4分）已知工，ycR,且x>y>0,若〃>人>1,则一定有（）A.\og a x>log^yB.sin fl x>sin^yC.ay>bxD.a x >b y4.（4分）将函数y=cos（2x+。

）的图象向右平移:个单位，得到的函数为奇函数，贝。

|切的最小值（）5.（4分）函数/（x）=e M-2cos（x-l）的部分图象可能是（）6.（4分）随机变量&的分布列如下:-101 P a b c其中。

，b,c成等差数列，则£>点的最大值为（）7.（4分）已知单位向量e v e2,且e x e2=,若向量Q满足（i一弓）一q），则1|。

1的取值范围为（）A.点—斗点+写1B.[血_?很+勺C.（0,^2+|8.（4分）在等腰梯形ABCD中，已知AB=AD=CD=1,BC=2,将AABD沿直线BD翻折成△ABD,如图，则直线&T与CD所成角的取值范围是（）A DB CA.[?,勺B.[£,勺C.[£,勺D.[0,勺32636239.（4分）已知函数/'（x）=杪*_-己°”*<2,g（x）=女+2,若函数F（x）=/（x）一g（x）在[0,[2f（x-2）,x..2+00）上只有两个零点，则实数k的值不可能为（）913A.--B.--C.--D.-132410.（4分）已知数列｛%｝满足0|=1,%=：，且3（列-*勿,土喔珥》+-=，住N*,记乌为数列｛%｝的前2〃项和，数列也｝是首项和公比都是2的等比数列，则使不等式（乌成立的最小整数"为（）A.7B.6C.5D.4二、填空题（本大题共7小题，多空题每题6分，单空题每题4分，共36分）11.（6分）若（3^--）"的展开式中所有项的系数的绝对值之和为64,贝"=；该展X开式中的常数项是.X..112.（6分）已知实数x,y满足x-2y+l,,0,若此不等式组所表示的平面区域形状为三角x+m形，则秫的取值范围为,如果目标函数z=2x-y的最小值为-1,则实数m.13.（6分）如图是一个几何体的三视图，若它的体积是-，则&=,该几何体的表面积3----为正视图12T mmm俯视图14.（6分）在AABC中，内角A,B,C所对的边分别是a,b, c.若o=a/7, c=3,A=60。

2020-2021学年浙江省杭州市第二高中高三数学理下学期期末试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 下列说法正确的是A．“为真”是“为真”的充分不必要条件；B．设有一个回归直线方程为，则变量每增加一个单位，平均减少个单位；C．若，则不等式成立的概率是；D．已知空间直线，若，，则．参考答案：B2. 设是△内一点，且，，定义，其中、、分别是△、△、△的面积，若，则的最小值是（）A．8 B．9 C．16 D．18参考答案：D略3. 已知函数的图象向右平移个单位后关于对称，当时，＜0恒成立，设，，，则的大小关系为（）A．c＞a＞b B．c＞b＞a C．a＞c＞b D．b＞a＞c参考答案：D略4. 若，则为（）A． B． C． D．参考答案：答案：C5. 点共面，若，则的面积与的面积之比为( )A. B. C. D.参考答案：D6. 已知，，则的值是（A）（B）（C）（D）参考答案：【知识点】诱导公式，二倍角公式C2 C6D解析：因为，所以，又，，，故选D.【思路点拨】由，得，，再根据二倍角公式即可求得.7. 执行右边的程序框图，如果输入a＝4，那么输出的n的值为（）A．2 B．3 C．4 D．5参考答案：B略8. 当＜m＜1时，复数z=（3m﹣2）+（m﹣1）i在复平面上对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限参考答案：D【考点】复数的代数表示法及其几何意义．【分析】当＜m＜1时，复数z的实部3m﹣2∈（0，1），虚部m﹣1∈．即可得出．【解答】解：当＜m＜1时，复数z的实部3m﹣2∈（0，1），虚部m﹣1∈．复数z=（3m﹣2）+（m﹣1）i在复平面上对应的点（3m﹣2，m﹣1）位于第四象限．故选：D．【点评】本题考查了复数的运算法则、不等式的性质、复数的几何意义，考查了推理能力与计算能力，属于基础题．9. 已知数列{a n}是等差数列，且，则的值为（）.A. B. C. D.参考答案：A 试题分析：，所以考点：1、等差数列；2、三角函数求值.10. 在中，，AB=2，AC=1，E，F为边BC的三等分点，则（）A． B． C． D．参考答案：A二、填空题:本大题共7小题,每小题4分,共28分11. 以，所连线段为直径的圆的方程是参考答案：12. 设全集设数列的各项均为正数，前项和为，对于任意的，成等差数列，设数列的前项和为，且，若对任意的实数（是自然对数的底）和任意正整数，总有．则的最小值为 .参考答案：2 .根据题意，对于任意，总有成等差数列，则对于n∈N*，总有………………①；所以（n≥2）……………………②1--②得；因为均为正数，所以（n≥2），所以数列是公差为1的等差数列，又n=1时，，解得，所以。