电磁场作业答案

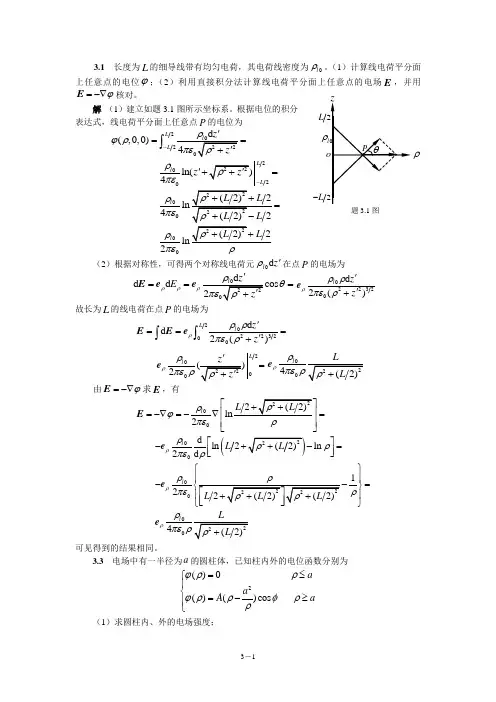
3.1 长度为L 的细导线带有均匀电荷，其电荷线密度为0l ρ。

（1）计算线电荷平分面上任意点的电位ϕ；（2）利用直接积分法计算线电荷平分面上任意点的电场E ，并用ϕ=-∇E 核对。

解 （1）建立如题3.1图所示坐标系。

根据电位的积分表达式，线电荷平分面上任意点P 的电位为2(,0,0)L L ϕρ-==⎰2ln(4L l L z ρπε-'+=04l ρπε=02l ρπε （2）根据对称性，可得两个对称线电荷元z l 'd 0ρ在点P 的电场为d d E ρρρθ'===Ee e 022320d 2()l z z ρρρπερ''+e故长为L 的线电荷在点P 的电场为2022320d d 2()L l z z ρρρπερ'==='+⎰⎰E E e20002L l ρρπερ'=e ρe 由ϕ=-∇E 求E ，有002l ρϕπε⎡⎢=-∇=-∇=⎢⎥⎣⎦E(00d ln 2ln 2d l L ρρρπερ⎡⎤-+-=⎢⎥⎣⎦e0012l ρρπερ⎧⎫⎪--=⎬⎪⎭e ρe可见得到的结果相同。

3.3 电场中有一半径为a 的圆柱体，已知柱内外的电位函数分别为2()0()()cos a a A aϕρρϕρρφρρ=≤⎧⎪⎨=-≥⎪⎩（1）求圆柱内、外的电场强度；L L -ρρ题3.1图（2）这个圆柱是什么材料制成的？表面有电荷分布吗？试求之。

解 （1）由ϕ=-∇E ，可得到a ρ<时， 0ϕ=-∇=Ea ρ>时， ϕ=-∇=E 22[()cos ][()cos ]a a A A ρφρφρφρρρφρ∂∂----=∂∂e e 2222(1)cos (1)sin a a A A ρφφφρρ-++-e e（2）该圆柱体为等位体，所以是由导体制成的，其表面有电荷分布，电荷面密度为0002cos S n a a A ρρρρεεεφ=====-e E e E3.4 已知0>y的空间中没有电荷，下列几个函数中哪些是可能的电位的解? （1）cosh y e x -； （2）x e y cos -；（3）cos sin e x x （4）z y x sin sin sin 。

一. 选择题[ A ] 1 (基础训练4)、两根很长的平行直导线，其间距离为a ，与电源组成闭合回路，如图12-18．已知导线上的电流为I ，在保持I 不变的情况下，若将导线间的距离增大，则空间的(A) 总磁能将增大． (B) 总磁能将减少．(C) 总磁能将保持不变．(D) 总磁能的变化不能确定【解答】212m W L I =，距离增大，φ增大，L 增大， I 不变，m W 增大。

[ D ]2（基础训练7）、如图12-21所示．一电荷为q 的点电荷，以匀角速度作圆周运动，圆周的半径为R ．设t = 0 时q 所在点的坐标为x 0 = R ，y 0 = 0 ，以i 、j分别表示x 轴和y 轴上的单位矢量，则圆心处O 点的位移电流密度为： (A)i t R q ωωsin 42π (B) j t Rq ωωcos 42π (C) k R q 24πω (D) )cos (sin 42j t i t Rq ωωω-π 图 12-21 【解答】设在0—t 的时间内，点电荷转过的角度为ωt ，此时，点电荷在O 点产生的电位移矢量为0D E ε=, ()222000cos sin ,444rqR q q E e ti tj R R R R ωωπεπεπε=-=-=-+ 式中的r e 表示从O 点指向点电荷q 的单位矢量。

()2sin cos 4d dD q J ti tj dt R ωωωπ∴==-。

[ C ] 3 (基础训练8)、 如图12-22，平板电容器(忽略边缘效应)充电时，沿环路L 1的磁场强度H 的环流与沿环路L 2的磁场强度H 的环流两者，必有： (A) >'⎰⋅1d L l H ⎰⋅'2d L l H . (B) ='⎰⋅1d L l H ⎰⋅'2d L l H .(C) <'⎰⋅1d L l H ⎰⋅'2d L l H. (D) 0d 1='⎰⋅L l H .【解答】全电流是连续的，即位移电流和传导电流大小相等、方向相同。

阶段测测试题目为单选、多选。

简单练习题目为名词解释、填空、简答。

作业题目为计算、论述题目类型：单选、名词解释、填空、简答、计算、论述。

矢量分析与场论初步0-1 正交坐标系与矢量运算 0-2 标量场和矢量场 0-3 标量场的梯度0-4 矢量场的通量与散度 0-5 矢量场的环量与旋度 0-6 亥姆霍茨定理 0-7 三种特殊形式的场 单选：一个标量场中某个曲面上梯度为零时 CA 其旋度必不为零B 其散度为零C 该面为等值面D 该标量场也为零 一个矢量场的散度为零时 BA 沿任一闭合曲线的线积分不为零B 沿任一闭合曲面的通量为零C 其旋度必不为零D 其梯度必为零直角坐标系中的单位向量e x 与e y 的数量积是 A A 1 B e x C e y D e z 直角坐标系中的单位向量e x 与e y 的矢量积是 D A 1 B e x C e y D e z一个矢量场的散度为零时 BA 沿任一闭合曲线的线积分不为零B 沿任一闭合曲面的通量为零C 其旋度必不为零D 其梯度必为零下述公式中不正确的是（其中C 是常数矢量） CA 、 0C =∇B 、0C =•∇ C 、C B B C ⨯=⨯D 、0C =⨯∇ 已知z y x x y z x y x e e e A )2()3()32(-+-+-=，矢量A 的散度为 B A 、1 B 、2 C 、3 D 、4名词解释：正交坐标系 各个坐标轴（单位向量）互相垂直 标量 只有大小而无方向的量 矢量 有大小又有方向的量梯度 标量场的梯度是一个矢量,是空间坐标点的函数；梯度的大小为该点标量函数的最大变化率，即该点最大方向导数；梯度的方向为该点最大方向导数的方向,即与等值线（面）相垂直的方向，它指向函数的增加方向。

矢量场的通量 矢量 E 沿有向曲面S 的面积分 S E d S ⋅⎰=Φ散度 矢量的散度是一个标量，是空间坐标点的函数；散度代表矢量场的通量源的分布特性,是通量密度。

一．选择题[ A ]1.（基础训练1）半径为a的圆线圈置于磁感强度为B 的均匀磁场中，线圈平面与磁场方向垂直，线圈电阻为R ，当把线圈转动使其法向与B 的夹角为α=60︒时，线圈中已通过的电量与线圈面积及转动时间的关系是：(A)与线圈面积成正比，与时间无关. (B) 与线圈面积成正比，与时间成正比. (C) 与线圈面积成反比，与时间无关. (D) 与线圈面积成反比，与时间成正比. 【解析】[ D ]2.（基础训练3）在一自感线圈中通过的电流I 随时间t 的变化规律如图(a)所示，若以I 的正流向作为的正方向，则代表线圈内自感电动势随时间t 变化规律的曲线应为图(b)中(A)、(B)、(C)、(D)中的哪一个？ 【解析】dt dI LL -=ε，在每一段都是常量。

dtdI ［ B ］3.（基础训练6）如图所示，直角三角形金属框架abc 放在均匀磁场中，磁场B平行于ab 边，bc 的长度为l ．当金属框架绕ab 边以匀角速度转动时，abc 回路中的感应电动势和a 、c 两点间的电势差U a – U c 为(A) =0，U a – U c =221l B ω (B) =0，U a – U c =221l B ω- (C) =2l B ω，U a – U c =221l B ω (D) =2l B ω，U a – U c=221l B ω-【解析】金属框架绕ab 转动时，回路中0d d =Φt，所以0=ε。

2012cL a c b c bc b U U U U v B d l lBdl Bl εωω→→→⎛⎫-=-=-=-⨯⋅=-=- ⎪⎝⎭⎰⎰［ C ］5.（自测提高1）在一通有电流I 的无限长直导线所在平面内，有一半经为r ，电阻为R 的导线环，环中心距直导线为a ，如图所示，且r a >>。

当直导线的电流被切断后，沿着导线环流过的电量约为：(A))11(220r a a R Ir +-πμ (B)ar a R Ir +ln 20πμ (C)aR Ir 220μ (D) rR Ia 220μ 【解析】直导线切断电流的过程中，在导线环中有感应电动势大小：td d Φ=εaIR q 21φφ-=感应电流为：tR Ri d d 1Φ==ε则沿导线环流过的电量为：∆Φ=⋅Φ==⎰⎰Rt t R t i q 1d d d 1daR Ir R r a I R S B 212120200μππμ=⋅⋅=⋅∆≈［ C ］6.（自测提高4）有两个长直密绕螺线管，长度及线圈匝数均相同，半径分别为r 1和r 2．管内充满均匀介质，其磁导率分别为1和2．设r 1∶r 2=1∶2，1∶2=2∶1，当将两只螺线管串联在电路中通电稳定后，其自感系数之比L 1∶L 2与磁能之比W m 1∶W m 2分别为：(A) L 1∶L 2=1∶1，W m 1∶W m 2 =1∶1． (B) L 1∶L 2=1∶2，W m 1∶W m 2 =1∶1． (C) L 1∶L 2=1∶2，W m 1∶W m 2 =1∶2． (D) L 1∶L 2=2∶1，W m 1∶W m 2 =2∶1．【解析】自感系数为l r n V n L 222πμμ==，磁能为221LI W m =［ B ］7.（附录C3）在圆柱形空间内有一磁感应强度为B 的均匀磁场，如图所示，B的大小以速率dB/dt 变化。

大学物理电磁学练习题及答案题目一：1. 电场和电势a) 一个均匀带电圆环上各点的电势如何？答：电场和电势是描述电荷之间相互作用的物理量。

对于一个均匀带电圆环上的各点，其电势是相同的，因为圆环上的每个点与圆心的距离相等且圆环上的电荷密度是均匀分布的。

所以，圆环上任意一点的电势与其它点是等势的。

b) 电势能和电势的关系是什么？答：电势能是电荷在电场中由于位置而具有的能量，而电势则是描述电荷因所处位置而具有的势能单位的物理量。

电势能和电势之间的关系可以用公式：电势能 = 电荷 ×电势来表示。

题目二：2. 高斯定律a) 高斯定律适用于哪些情况？答：高斯定律适用于具有球对称性、圆柱对称性和平面对称性的问题，其中球对称性是最常见和最简单的情况。

b) 高斯定律的数学表达式是什么？答：高斯定律的数学表达式是∮E·dA = ε₀q/ε，其中∮E·dA表示电场E通过闭合曲面积分得到的通量，ε₀是真空介电常数，q表示闭合曲面内的电荷总量，ε表示物质的介电常数。

题目三：3. 电动力学a) 什么是电感？答：电感是指电流在变化时产生的电磁感应现象所引起的抗拒电流的能力。

电感的单位是亨利(H)。

b) 电感的大小与什么因素有关？答：电感的大小与线圈的匝数、线圈的形状以及线圈中的铁芯材料的性质有关。

线圈匝数越多，电感越大；线圈形状越复杂，电感越大；线圈中的铁芯材料磁导率越大，电感越大。

题目四：4. 交流电路a) 直流电和交流电有什么区别？答：直流电是指电流方向始终保持不变的电流，而交流电是指电流方向以一定频率周期性地变化的电流。

直流电是恒定电流，交流电是变化电流。

b) 交流电流的形式有哪些？答：交流电流的形式可以是正弦波、方波、锯齿波等。

其中，正弦波是最常见和最基本的交流电流形式，用于描述交流电路中电压和电流的变化规律。

以上是关于大学物理电磁学练习题及答案的一些内容。

希望这些问题和答案能够帮助你更好地理解和学习物理电磁学的知识。

第10章 电磁感应与电磁场一、选择题1、一导体圆线圈在均匀磁场中运动，在下列情况下，会产生感应电流的是（ D ）A ．线圈沿磁场方向平移B ．线圈以自身直径为轴转动，轴与磁场方向平行C ．线圈沿垂直于磁场方向平移D ．线圈以自身直径为轴转动，轴与磁场方向垂直 2、将磁铁从迅速插入和缓慢插入金属环，若两种情况下磁铁的起始位置和终了位置均相同，则关于两种情况环中的感应电动势和感生电量的说法正确的是（ C ）A ．感应电动势不同；感生电量也不同B ．感应电动势相同，感生电量也相同；C ．感应电动势不同，感生电量相同；D ．感应电动势相同，感生电量不同． 3、如图所示，A 为闭合的导体环，B 为有间隙的导体环，则当磁铁分别移近A 和B 时，关于A 和B 的运动描述正确的是（ A ）A ．A 环被排斥，B 环不动 B ．A 环被吸引，B 环不动C ．A 环被吸引，B 环被吸引D ．A 环被排斥，B 环被排斥4、在感应电场中电磁感应定律可写成⎰-=•L K dtdl d E φ ，式中K E 为感应电场的电场强度。

此式表明（ D ）A. 闭合曲线L 上K E处处相等 B. 感应电场是保守力场。

C ．感应电场的电力线不是闭合曲线D ．在感应电场中不能像对静电场那样引入电势的概念 5、关于长直螺线管线圈的自感，以下说法正确的是（ D ） A 、螺线管中通有的电流越大，自感也越大； B 、螺线管横截面通过的磁通量越大，自感也越大C 、在单位长度匝数不变的情况下，真空中螺线管长度越长，自感就越大；D 、在单位长度匝数不变的情况下，真空中螺线管体积越大，自感就越大6、如图，矩形区域为均匀稳恒磁场，半圆形闭合导线回路在纸面内绕轴O 作逆时钟方向匀角速度转动，O 点是圆心且恰好落在磁场的边缘上，半圆形闭合导线完全在磁场外时开始计时。

图(A)--(D)的t -ε函数图像中哪一条属于半圆形导线回路中产生的感应电动势（A ）7、如图所示的闭合线圈abcda 均位于匀强磁场中，当磁场不断减小时，回路中不产生感应电流的是（ B ）8、如图所示，两个圆环形导体a 、b 互相垂直地放置，且圆心重合，当它们的电流I 1、和I 2同时发生变化时，则（ D ）(A) a 导体产生自感电流，b 导体产生互感电流(B) 两导体同时产生自感电流和互感电流(C) b 导体产生自感电流，a 导体产生互感电流；(D)两导体只产生自感电流，不产生互感电流。

第一章 基本电磁理论1-1 利用Fourier 变换, 由时域形式的Maxwell 方程导出其频域形式。

（作1-2—1-3） 解：付氏变换和付氏逆变换分别为：dt e t f F t j ⎰∞∞-=ωω)()(ωωπωd e F t f tj ⎰∞∞--=)(21)( 麦氏方程：t D J H ∂∂+=⨯∇tB E ∂∂-=⨯∇0=⋅∇B ρ=⋅∇D对第一个方程进行付氏变换：),(),(),ωωωr H dt e t r H dt e t r H tj t j ⨯∇=⨯∇=⨯∇=⎰⎰∞∞-∞∞-（左端),(),(),(),(]),(),[ωωωωωωωr D j r J dte t r D j r J dt e t t r D t r J t j tj+=+=∂∂+=⎰⎰∞∞-∞∞-（右端（时谐电磁场） =⨯∇∴),(ωr H ),(),(ωωωr D j r J +同理可得：()()ωωω,,r B j r H -=⨯∇()0,=⋅∇ωr B()()ωρω,,r r D =⋅∇上面四式即为麦式方程的频域形式。

1-2 设各向异性介质的介电常数为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=300420270εε 当外加电场强度为 (1) 01E x e E =；(2)02E y e E =；(3) 03E z e E =；(4) )2(04y x E e e E +=；(5))2(05y x E e e E +=求出产生的电通密度。

（作1-6）解：()),(,t r E t r D⋅=ε⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡333231232221131211εεεεεεεεεz y x D D D 即⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡z y x E E E 将E 分别代入，得：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡027003000420270000111E E D D D z y x εε )ˆ2ˆ7(001y x E D +=ε⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡042003000420270000322E E D D D z y x εε )ˆ4ˆ2(002y x E D +=ε ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡300003000420270000333E E D D D z y x εε z E D ˆ3003ε= ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡010110230004202700000444E E E D D D z y x εε )ˆ10ˆ11(004y x E D +=ε ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡08160230004202700000555E E E D D D z y x εε )ˆ8ˆ16(005y x E D +=ε 1-3 设各向异性介质的介电常数为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=4222422240εε试求：(1) 当外加电场强度)(0z y x E e e e E ++=时，产生的电通密度D ；(2) 若要求产生的电通密度004E x εe D =，需要的外加电场强度E 。

北交《工程电磁场》在线作业二一、单选题（共 10 道试题，共 30 分。

）1. 普拉斯方程描写的是（）。

. 有源有旋场. 有源无旋场. 无源有旋场. 无源无旋场正确答案：2. 无源场存在着（）。

. 电磁波. 电感. 矢势. 磁通正确答案：3. 单短截线阻抗匹配法实质是，用接入短截线后附加的反射波来抵消主传输线上原来的（），以实现匹配。

. 入射波. 折射波. 反射波. 散射波正确答案：4. 损耗主要是传输线导体的损耗及导体之间（）的损耗。

. 介质. 电阻. 电感. 电抗正确答案：5. 低频无线电技术中采用L回路产生（）。

. 电磁振荡. 电磁感应. 感应电流. 感应电压正确答案：6. 在无源场中，穿过场域V中任一个矢量管的所有截面的通量（）。

. 相等. 相反. 与截面法向量有关. 与截面切向量有关正确答案：7. 当给定了矢量场的通量源密度和旋涡源密度以及场域的（），就可以唯一地确定该矢量场。

. 边界条件. 控制条件. 磁力线. 磁场矢量正确答案：8. （）是谐振腔最重要的一个参数。

. 谐振幅度. 谐振时间. 谐振频率. 谐振波形正确答案：9. 当传播方向上有电场的分量而无磁场的分量，此导行波称为（）。

. TM波型. T波型. TM波型. TT波型正确答案：10. 长度小于（）波长的短路线或开路线可用作微波电路元件。

. 1/16. 1/8. 1/4. 1/2正确答案：北交《工程电磁场》在线作业二二、多选题（共 10 道试题，共 40 分。

）1. 全电流包括（）。

. 位移电流. 传导电流. 等效电流. 传输电流正确答案：2. 接地可分为（）。

. 保护接地. 工作接地. 电场接地. 电磁接地正确答案：3. 静电场是（）。

. 无旋场. 有旋场. 无散场. 有散场正确答案：4. 互感与（）有关。

. 线圈形状. 导线形状. 周围媒介材料. 导体材料的磁导率正确答案：5. 细线天线广泛应用于（）领域。

. 通信. 广播. 雷达. 信号传输正确答案：6. 在静电场中，等位面（）。

经典课时作业电磁场和电磁波（含标准答案及解析）时间：45分钟分值：100分1.1864年,英国科学家麦克斯韦在总结前人研究电磁现象的基础上,建立了完整的电磁波理论,他断定电磁波的存在,推导出电磁波与光具有同样的传播速度.1887年德国物理学家赫兹用实验证实了电磁波的存在.下列有关电磁波传播过程的叙述中正确的是( )A.电磁波在真空中的传播速度等于真空中的光速B.电磁波和机械波一样依赖于介质传播C.电磁波中每一处电场强度方向和磁感应强度方向总是相互垂直,并且与波的传播方向也垂直D.只要空间中某个区域有变化的电场或变化的磁场,就一定能产生电磁波2.关于电磁场和电磁波,下列说法中正确的是( )A.均匀变化的电场在它的周围产生均匀变化的磁场B.电磁波中每一处的电场强度和磁感应强度总是互相垂直的,且与波的传播方向垂直C.电磁波和机械波一样依赖于媒质传播D.只要空间中某个区域有振荡的电场或磁场,就能产生电磁波3.红外遥感卫星通过接收地面物体发出的红外辐射来探测地面物体的状况.地球大气中的水汽(H2O)､二氧化碳(CO2)能强烈吸收某些波长范围的红外辐射,即地面物体发出的某些波长的电磁波,只有一部分能够通过大气层被遥感卫星接收.下图为水和二氧化碳对某一波段不同波长电磁波的吸收情况,由图可知,在该波段红外遥感大致能够接收到的波长范围为( )A.2.5~3.5 μmB.4~4.5 μmC.5~7 μmD.8~13 μm4.电磁波与机械波相比较有( )A.电磁波传播不需要介质,机械波传播需要介质B.电磁波在任何介质中的传播速率都相同,机械波在同一介质中的传播速率都相同C.电磁波与机械波都不能产生干涉现象D.电磁波与机械波都能产生衍射现象5.一个带正电的粒子在垂直于匀强磁场的平面内做匀速圆周运动,如图所示,当磁感应强度均匀增大时,此粒子的( )A.动能不变B.动能增大C.动能减小D.以上情况都可能6.下列哪种现象是由于所产生的电磁波引起的( )A.用室内天线收微弱信号时,人走过时电视画面会发生变化B.在夜晚用电高峰时,有部分地区白炽灯变暗发红,日光灯不容易启动C.把半导体收音机放在开着的日光灯附近会听到噪声D.在边远地区用手机或小灵通通话时,会发生信号中断的情况7.家用微波炉是一种利用微波的电磁能加热食物的新型灶具,它主要由磁控管､波导管､微波加热器､炉门､变压器､镇流系统､冷却系统､控制系统､外壳等组成.接通电路后,220 V交流电经变压器变压,在次级产生3.4 V低压交流电对磁控管加热,同时在另一次级产生2000 V 高压电,经镇流系统加到磁控管的阴､阳两极之间,使磁控管产生微波.微波输送至金属制成的加热器(炉腔),被来回后射,微波的电磁作用使食物内的分子高频运动,从而使食物受热,并能最大限度地保存食物中的维生素.关于上述微波炉,下列说法正确的是( )A.微波是由于原子外层电子受激发而产生的B.微波是由于原子内层电子受激发而产生的C.微波炉变压器的低压变压比为1100：17D.微波炉变压器的高压变压比为17：1000008.关于电磁波谱,下列说法正确的是( )A.伦琴射线是高速电子流射到固体上,使原子的内层电子受到激发而产生的B. γ射线是原子内层电子受激发而产生的C.在电磁波谱最容易发生衍射的是γ射线D.在同种均匀介质中,紫外线比紫光传播速度大9.过强的电磁辐射对人体有很大危害,影响人的心血管系统,使人心悸､失眠､白细胞减少､免疫功能下降等.按照有关规定,工作场所的电磁辐射强度(单位时间内垂直通过单位面积的电磁辐射能量)不得超过0.5 W/m2.一个人距离无线电通讯装置50 m,为保证此人的安全,无线电通讯装置的电磁辐射功率至多是( )A.4.51 kWB.3.14 kWC.15.7 kWD.0.78 kW10.为研究无线传输电能,某科研小组在实验室试制了无线电能传输装置,在短距离内点亮了灯泡,如图实验测得,接在乙线圈上的用电器获得的电能为输入甲线圈电能的35%.①若用该装置给充电功率为10 W的电波充电,则损失的功率为__________W.②若把甲线接入电压为220 V的电源,测得该线圈中的电流为0.195 A.这时,接在乙线圈上的灯泡恰能正常发光,则此灯泡的功率为__________W.11.某雷达工作时,发射的电磁波的波长λ=20 cm,每秒脉冲数为n=5000个,每个脉冲的持续时间为t=0.02 μs,问电磁波的振荡频率是多少;最大侦察距离是多少?12.某卫星地面站向地球同步通信卫星发送无线电波,经它立即转发到另一卫星地面站,测得从发送开始到地面站接收到电磁波的时间为0.24 s,取地球半径6400 km.据此条件估算地球的质量为多少千克?(结果取1位有效数字,G=6.67×10-11 N·m2/ kg2)标准答案及解析：1.解析:电磁波是电磁场由近及远在空间传播形成的,电磁波可以不依赖介质而独立传播,在真空中的传播速度等于真空中的光速,A 正确,B 错误;电磁波是横波,传播过程中电场强度和磁感应强度总是相互垂直的,且与波的传播方向垂直,C 正确;均匀变化的电场或磁场不能产生电磁波,D 错误.答案:AC2. 解析:根据麦克斯韦电磁场理论可知,均匀变化的电场在它的周围产生稳恒的磁场,故选项A 是错误的.因电磁波中每一处的电场强度和磁感应强度总是互相垂直的,且与波的传播方向垂直,所以电磁波是横波,故选项B 是正确的.电磁波可以在真空中传播,故选项C 是错误的.只要空间中某个区域有振荡的电场或磁场,就在周期性变化的电场周围产生同周期变化的磁场,周期性变化的磁场周围产生同周期变化的电场,这样由近及远传播,形成了电磁波,故选项D 是正确的.答案:BD3.解析:由图可知,水对红外辐射吸收率最低的波长范围是8~13 μm;二氧化碳对红外辐射吸收率最低的波长范围是5~13 μm.综上可知,选D.答案:D4.解析:电磁波传播不需要介质,且在不同介质中,传播速度不同,即v=\frac{c}{n};故A 正确,B 错误.电磁波和机械波都能产生干涉和衍射现象,故C 错,D 正确.答案:AD5.解析:当磁场均匀增加时,根据麦克斯韦的电磁场理论,将激发一个稳定的电场,带电粒子将受该电场的电场力作用,可以由右手定则和楞次定律判断,电场力的方向与电荷的运动方向是一致的.即电场力对粒子将做正功,所以带电粒子的动能将增大.答案:B6.解析:电视信号由于人走过发生变化是由于人对信号的干扰;电灯变暗是由于电压在输电线上损失过多;日光灯在工作时,其镇流器会发出微弱的电磁波;小灵通通话效果不好是由于信号的原因.答案:C7.解析:微波炉中的微波是由LC 振荡电路产生的,A ､B 均错.由变压器变压比1122U n U n =知低压变压比1222011003.417U U ==,C 正确.同理高压变压比12220112000100U U =='',D 错. 答案:C8.解析:伦琴射线是高速电子流射到固体上,使其内层电子得到能量而跃迁到高能量状态后,再跃迁到低能量状态而释放出来的,A 对;γ射线是原子核受激发而产生的,B 错;最易发生衍射的是波长较长的是无线电波,C 错;在同种介质中紫外线的折射率大于紫光的折射率,由n=c v 知紫外线比紫光的传播速度小,D 错.答案:A9.解析:根据题意,要使此人是安全的,则此处的辐射功率小于或者等于0.5 W/m 2,则可得:24RP π =0.5 W/m 2,所以P=4πR 2×0.5 W=4×3.14×502×0.5 W=15.7 kW,所以C 正确. 答案:C10.答案:①18.6 ②1511.解析:由c=λf 可知,电磁波的振荡频率f=cλ=1.5×109Hz,电磁波在雷达发射两个相邻脉冲的时间间隔内传播的距离为s=cΔt=c(1n -t)≈6×104 m,所以雷达的侦察距离为s′=2s =3×104 m. 答案:1.5×109Hz 3×104 m12.解析:由s=ct 可知同步卫星距地面的高度h=1122ct =×3×108×0.24 m=3.6×107 m. 由万有引力定律可知22()GMm m R h T π⎛⎫= ⎪+⎝⎭2(R+h), 故地球质量226733211244 3.14(6.410 3.610)() 6.6710(243600)M R h kg GT π-⨯⨯⨯+⨯=+=⨯⨯⨯=6×1024 kg. 答案:6×1024 kg。

第1章 矢 量 分 析1.1 什么是场？什么是矢量场？什么是标量场？什么是静态场？什么是时变场？答：如果在空间某一个区域内上任意一点都有一确定物理量值与之对应，则这个区域就构了一个物理量的场。

如果这个确定物理量值是一个标量（只有大小没有方向），我们称这种场为标量场，如温度场、密度场、电位场等等。

如果这个确定物理量值是一个矢量（既有大小又有方向），我们称这种场为矢量场，如电场、磁场、重力场等等。

如果在场中的这个物理量仅仅是空间位置的函数，而不是时间的函数（即不随时间变化的场），我们称这种场为静态场。

如果在场中的这个物理量不仅仅是空间位置的函数，而且还是时间的函数（即随时间变化的场），我们称这种场为时变场。

1.2 什么是标量？什么是矢量？什么是常矢？什么是变矢？什么是单位矢量？答：一个物理量如果仅仅只有大小的特征，我们称此物理量为标量。

例如体积、面积、重量、能量、温度、压力、电位等。

如果一个物理量不仅仅有大小，而且还具有方向的特征，我们称此物理量为矢量。

例如电场强度，磁感应强度、电位移矢量、磁场强度、速度、重力等。

一个矢量如果其大小和方向都保持不变的矢量我们称之为常矢。

如果矢量的大小和方向或其中之一是变量的矢量称为变矢。

矢量与矢量的模值的比值，称为单位矢量。

即模值为1的矢量称为单位矢量 1.3什么是等值面？什么是等值面方程？什么是等值线？什么是等值线方程？答：在标量场中许多相同的函数值（他们具有不同的位置）。

构成的曲面，称为等值面。

例如，温度场中由相同温度构成的等温面，电位场中相同电位构成的等位面等都是等值面。

描述等值面的方程称为等值面方程。

假定()z y x u ,,是坐标变量的连续可微函数。

则等值面方程可表述为 ()C z y x u =,, （c 为任意常数）在标量场中平面中相同的函数值构成的曲线，称为等值线。

描述等值线的方程称为等值线方程。

假定()y x u ,是坐标变量的连续可微函数。

则等值线方程可表述为 ()C y x u =, （c 为任意常数） 1.4求下列电场的等位线方程 (1) z x =ϕ， (2) 224y x +=ϕ 解：根据等值线方程的定义即电位函数应为一常数，所以等位线方程为⑴ xz c ==ϕ，即 z cx =； ⑵ c 4=+=y x ϕ 即 k y ==+c 4x 22 （为常数k ）1.5 求下电场的等值面方程 1） 1222z y x ++=ϕ， 2） )z -z ()()x -= 202020+++y y x （ϕ， 3）)++ln(=222z y x ϕ 解：根据等值面方程的定义即电位函数应为一常数，所以等位面方程为⑴ c1222=++=z y x ϕ 即 2222c 1k z y x ==++ ⑵ c )z -z ()()x -= 202020=+++y y x （ϕ 即 22202020)()()(k c z z y y x x ==-+-+- ⑶ ()c z y x =++222ln 即 2222k e z y x c ==++，（k 为常数）1.6 什么方向导数？什么梯度？梯度与方向导数的关系？答：在标量场中任一点在某一方向上的变化率称为方向导数。