r参数贡献度分解

主成分分析‎（prin‎c ipal‎comp‎o nent‎anal‎y sis)‎是将多指标‎化为少数几‎个综合指标‎的一种统计‎分析方法，‎这种降维的‎技术而生成‎的主成分，‎能够反映原‎始变量的绝‎大部分信息‎，通常表示‎为原始变量‎的线性组合‎。

下面‎主要介绍在‎R中的主成‎分分析‎1）概念：‎①主成分‎的均值和协‎方差阵②‎主成分的总‎方差贡‎献率及累计‎贡献率③‎原始变量与‎主成分变量‎之间的相关‎系数④m‎个主成分对‎原始变量的‎贡献率⑤‎原始变量对‎主成分的影‎响2）‎从相关矩阵‎或者协方差‎矩阵出发求‎主成分‎①变量的标‎准化sc‎a le()‎3）在‎R中，可以‎用stat‎s包中的p‎r comp‎函数及pr‎i ncmp‎()函数进‎行主成分分‎析。

##‎类'f‎o rmul‎a'的S3‎方法pr‎c omp(‎f ormu‎l a, d‎a ta =‎NULL‎, sub‎s et, ‎n a.ac‎t ion,‎...)‎## ‎D efau‎l t S3‎meth‎o d:p‎r comp‎(x, r‎e tx =‎TRUE‎, cen‎t er =‎TRUE‎, sca‎l e = ‎F ALSE‎,‎ t‎o l = ‎N ULL,‎...)‎参数介‎绍：fo‎r mula‎：在公式方‎法中设定的‎没有因变量‎的公式，用‎来指明数据‎分析用到的‎数据框汇中‎的列da‎t a：包含‎在form‎u la中指‎定的数据的‎数据框对象‎，sub‎s et：向‎量对象，用‎来指定分析‎时用到的观‎测值，其为‎可选参数‎n a.ac‎t ion:‎指定处理缺‎失值的函数‎x：在默‎认的方法下‎，指定用来‎分析的数值‎型或者复数‎矩阵re‎t x：逻辑‎变量，指定‎是否返回旋‎转变量c‎e nter‎：逻辑变量‎，指定是否‎将变量中心‎化sca‎l e：逻辑‎变量，指定‎是否将变量‎标准化t‎o l：数值‎型变量，用‎来指定精度‎，小于该数‎值的值将被‎忽略。

智能化项目提成制度一、项目利润提成比例本制度所指项目利润，是指智能化项目扣除成本及税费后所得的净收益。

提成比例将根据项目利润的一定比例确定。

具体提成比例如下：项目利润（R）提成比例（P）R ≤ 10% 3%10% < R ≤ 20% 5%20% < R ≤ 30% 7%30% < R ≤ 40% 9%R > 40% 10%二、项目规模与提成分配项目规模越大，提成分配比例将根据实际情况进行相应调整。

提成分配将根据项目组成员的岗位、能力和贡献程度进行分配。

具体分配比例如下：岗位/角色分配比例项目经理 20% - 30%项目组成员 70% - 80%三、项目难度与提成分配项目难度越大，提成分配比例将根据实际情况进行相应调整。

具体分配比例如下：项目难度等级分配比例低难度项目常规分配比例中难度项目 1.2倍常规分配比例高难度项目 1.5倍常规分配比例四、团队成员贡献度与提成分配提成分配将根据团队成员的贡献程度进行分配。

具体分配比例如下：成员贡献度等级分配比例低贡献度成员常规分配比例的80% - 90%中贡献度成员常规分配比例的90% - 100%高贡献度成员常规分配比例的100% - 120%五、提成发放时间与支付方式提成发放时间将在项目验收合格并收到客户尾款后进行。

支付方式将采用现金或银行转账方式进行，具体方式将在项目经理与团队成员协商后确定。

六、提成分配争议处理机制如团队成员对提成分配存在争议，应首先进行内部协商解决。

协商无果的，可向公司领导申请调解。

调解无果的，可向公司仲裁委员会申请仲裁。

如仍有争议，可向所在地人民法院提起诉讼。

七、提成制度修订与解释权本制度自发布之日起生效，如有未尽事宜，由公司领导解释并制定补充规定。

本制度最终解释权归公司所有。

如有疑问或需要进一步了解本制度内容，请联系公司领导或咨询相关部门负责人。

R语言主成分分析模型的建立与应用主成分分析（Principal Component Analysis，简称PCA）是一种常用的降维技术和数据预处理方法。

它通过线性变换将一组可能存在相关性的高维数据转换为一组线性无关的低维数据，以实现数据降维和特征提取的目的。

在本文中，我将介绍如何使用R语言建立主成分分析模型，并应用到实际数据集中。

首先，我们需要安装并加载R语言中的主成分分析包，如“FactoMineR”和“factoextra”。

可以使用以下代码进行安装和加载：```install.packages("FactoMineR")install.packages("factoextra")library(FactoMineR)library(factoextra)```接下来，我们需要准备数据集。

假设我们有一个数据框df，其中包含了我们想要进行主成分分析的变量。

可以使用以下代码加载数据集：```df <- read.csv("your_data.csv")```在进行主成分分析之前，我们需要对数据进行预处理。

一般来说，我们需要对数据进行标准化处理，以确保各个变量之间的尺度一致。

可以使用以下代码对数据集进行标准化处理：```df <- scale(df)```接下来，我们可以使用函数“PCA”来建立主成分分析模型。

该函数需要传入数据集和一些可选参数，如主成分数目和选择的主成分标准。

以下是一个示例：```pca <- PCA(df, ncp=5, graph=FALSE)```在这个示例中，我们选择了5个主成分，并且设置参数“graph=FALSE”以禁止绘制结果图表。

主成分分析模型的具体结果可以通过打印pca对象来查看。

现在，我们可以根据建立的主成分分析模型进行数据的降维和特征提取。

可以使用以下代码提取主成分得分和主成分贡献度：```pca$ind$coord # 主成分得分pca$ind$cos2 # 主成分贡献度```主成分得分表示每个样本在不同主成分上的投影值，而主成分贡献度表示每个变量对于主成分的贡献程度。

逻辑斯蒂回归是一种常用于分类问题的统计方法，它可以用来预测二元变量的概率。

在实际应用中，我们经常需要评估每个变量对分类结果的影响程度，即变量的贡献度。

本文将介绍如何使用R语言进行逻辑斯蒂回归，并计算变量的贡献度。

一、逻辑斯蒂回归简介逻辑斯蒂回归是一种广义线性模型，通常用于处理因变量为二元变量的情况。

它通过将自变量的线性组合转化为对数几率比来进行建模，从而可以预测因变量的概率。

在R语言中，我们可以使用glm函数来拟合逻辑斯蒂回归模型。

二、建立逻辑斯蒂回归模型我们需要准备数据集，并将因变量和自变量分开。

假设我们有一个名为data的数据框，其中包含一个二元因变量y和若干自变量x1、x2、x3等。

我们可以使用以下代码来建立逻辑斯蒂回归模型：```Rmodel <- glm(y ~ x1 + x2 + x3, family = "binomial", data = data) ```在上面的代码中，y ~ x1 + x2 + x3表示因变量y与自变量x1、x2、x3之间的关系，family = "binomial"表示我们要拟合的是逻辑斯蒂回归模型，data = data表示数据集为data。

执行以上代码后，我们就可以得到一个逻辑斯蒂回归模型model。

三、计算变量的贡献度在建立好逻辑斯蒂回归模型后，我们可以通过coef函数来获取模型的系数，然后根据系数的大小来评估变量的贡献度。

具体代码如下：```Rcoefficients <- coef(model)```执行以上代码后，coefficients将会存储模型的系数。

接下来，我们可以使用如下代码来计算变量的贡献度：```Rcontribution <- abs(coefficients) / sum(abs(coefficients))```在上面的代码中，abs(coefficients)表示取系数的绝对值，sum(abs(coefficients))表示系数的绝对值之和。

r语言计算人群归因危险度的代码人群归因危险度（Attribution Risk）是指在编程和分析中，为了理解不同因素对某一结果的贡献程度，对于不同因素进行归因的程度判断。

在R语言中，可以通过各种统计方法和模型进行人群归因危险度的计算。

以下是一个简单的示例代码，用于计算人群归因危险度：```R# 创建一个数据框，包含人群数据和结果变量data <- data.frame(age = c(30, 40, 50, 60, 70),gender = c("M", "M", "F", "F", "M"),income = c(50000, 60000, 70000, 80000, 90000),health_score = c(0.3, 0.4, 0.5, 0.6, 0.7),result = c(0, 1, 0, 1, 0))# 使用逻辑回归模型计算归因危险度model <- glm(result ~ age + gender + income + health_score, data = data, family = binomial("logit"))prob <- predict(model, newdata = data, type = "response")# 计算危险度attribution_risk <- prop.table(prob)# 打印结果print(attribution_risk)```在上面的代码中，首先创建一个包含人群数据和结果变量的数据框。

然后使用逻辑回归模型来拟合数据，并使用预测函数`predict()`得到每个个体的预测概率。

最后，使用`prop.table()`函数计算危险度，结果存储在`attribution_risk`变量中。

基于R语言的主成分分析方法综述主成分分析（Principal Component Analysis，PCA）是一种常用的多变量数据分析方法，用于降维和数据可视化。

本文将综述基于R语言的主成分分析方法。

一、主成分分析的原理主成分分析是一种线性变换技术，用于将高维数据转换为低维表示。

其基本原理是通过寻找数据的主要方向，将数据在这些方向上的方差最大化，从而实现降维。

主成分分析可以用于数据的可视化、数据压缩和特征提取等领域。

主成分分析的步骤：1. 数据标准化：首先对原始数据进行标准化处理。

2. 构造协方差矩阵：根据标准化后的数据，构造协方差矩阵。

3. 计算特征值和特征向量：对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。

4. 选取主成分：根据特征值的大小，选择保留的主成分数量。

5. 构造新的特征空间：选取保留的主成分，构造新的特征空间。

6. 数据转换：将原始数据投影到新的特征空间中。

二、R语言中的主成分分析方法R语言是一种常用的统计分析软件，具有丰富的主成分分析函数和包。

下面将介绍几种常用的R语言主成分分析方法。

1. prcomp函数：prcomp函数是R语言中进行主成分分析的函数之一。

它通过奇异值分解（singular value decomposition，SVD）计算主成分。

以下是使用prcomp函数进行主成分分析的示例代码：```R# 载入数据data <- read.csv("data.csv")# 数据标准化data_scaled <- scale(data)# 主成分分析pca <- prcomp(data_scaled)# 主成分贡献度pca_variances <- pca$sdev^2pca_variances_ratio <- pca_variances / sum(pca_variances)# 主成分得分pca_scores <- pca$x```2. princomp函数：princomp函数是另一种常用的R语言主成分分析函数。

第38卷第3期2024年5月山东理工大学学报(自然科学版)Journal of Shandong University of Technology(Natural Science Edition)Vol.38No.3May 2024收稿日期:20230419第一作者:代浩然,男,2196347446@;通信作者:曹文芹,女,caowenqin@文章编号:1672-6197(2024)03-0071-08基于组合模型的球员贡献度评价代浩然,曹文芹(山东理工大学数学与统计学院,山东淄博255049)摘要:介绍了两种评价球员贡献度的统计模型,基于组合模型的优势,提出了1个组合评价模型,以2021 2022年NBA 季后赛为例,利用非参数统计中Friedman 检验进行了实证分析㊂通过基于熵权法改进的Topsis ㊁主成分综合评价与组合模型3种评价模型来探究2021 2022年NBA 总冠军金州勇士队球员的贡献,并对其贡献进行排名,采用Friedman 检验得到3种模型的结论基本一致㊂关键词:非参数统计;相关分析;组合模型;Friedman 检验中图分类号:O213文献标志码:APlayer contribution evaluation based on combination modelDAI Haoran,CAO Wenqin(School of Mathematics and Statistics,Shandong University of Technology,Zibo 255049,China)Abstract :In the paper,we firstly introduce two statistical models for evaluating player contribution,and then propose a new combined evaluation model based on the advantages of the combination model.We fi-nally performed an empirical analysis using nonparametric statistical Friedman test for the 2021 2022NBA playoffs.Golden state Warriors is the champion team,and the team is analyzed as an example using improved entropy weighting method,principal component analysis,and the combined model.We explore the contributions of Golden State Warriors players and rank their contributions.We come to a conclusionthat the three models are consistent according to the Friedman test.Keywords :nonparametric statistics;correlation analysis;composite model;Friedman test㊀㊀众所周知,NBA(national basketball association)代表全世界最高的篮球水平,如果一支球队夺得NBA 总冠军,就是拿到了篮球领域的最高荣誉㊂在2021 2022赛季,西部勇士队以4ʒ2系列赛得分击败东部凯尔特人队,夺得NBA 总冠军㊂这是勇士队时隔4年再次获得NBA 总冠军,也是队史上获得的第7个NBA 总冠军㊂然而,在2021 2022赛季初期,勇士队一直不被看好,即便最后进入总决赛,外界也认为他们无法获得总冠军㊂因此,对于这次特别的夺冠,本文对其冠军队伍展开分析,客观地展现勇士队夺冠的重要因素㊂由于球员自身身体素质的差异㊁训练方式的差别以及球员风格的不同,在竞技能力的展现上存在差异,每场比赛中球员们的表现㊁对球队的帮助以及在场时的贡献都会有所起伏,最终导致每名球员在胜利的贡献上也存在差异㊂目前国内已经有一些对球员表现的评价方法㊂许坚等[1]基于信息熵理论对篮球比赛球员贡献评价体系进行研究,最终建立球员贡献评价体系以及球员贡献值的计算公式;吴威等[2]通过主成分分析的方法构建了CBA(China basketball association)国内球员攻防能力评价模型;刘欣然[3]通过线性加权的方法得到一个球队比赛中的防守质量的综合评价分数;景怀国等[4]使用Q 型聚类分析对第30届奥运会男子篮球赛参赛队伍综合能力进行分析;李国㊀等[5]使用Topsis(technique for order preference by si-milarity to an ideal solution)评价模型对中国男子篮球队与对手攻防指标进行了综合分析;现阶段CBA 与NBA 联赛中对于球员引入了效率值来判断球员对于胜率的贡献㊂本文介绍了熵权法改进的Topsis 模型和主成分综合评价模型㊂由于这两种评价模型各有优劣,为了得到更好的评价结果,本文提出组合评价模型㊂该模型能够综合利用前两种评价模型的结果,对金州勇士队球员的贡献得分以及排名进行讨论,并通过Friedman 检验分析3种模型结果的一致性㊂1㊀综合评价模型1.1㊀基于熵权法改进的Topsis 模型与传统的Topsis 模型相比,熵权法改进的Topsis 模型主要是对待评价球员的加权决策矩阵进行了改进㊂熵权法是一种根据待评价指标来确定权重的客观打分方式,这种方法能够反映指标背后隐含的信息以此来增强各指标的差异性,以避免选取指标的差异过小而造成分析不清,从而达到全面反映各类信息的目的[6]㊂在构建数据矩阵前要先将指标转化为极大型指标㊂假定有m 个待评价对象,n 个评价指标,将所有数据构成的判断矩阵进行标准化处理,以此得到后续使用的标准化数据矩阵P :P ij =a ijðmi =1a ij ,(1)P =(P ij )m ˑn ,(2)式中:P ij 为第i 个待评价对象第j 个指标值的权重,m 为待评价对象的数量,n 为评价指标的个数,a ij 为第i 个待评价对象第j 个指标的评价值㊂熵是系统无序状态的度量,熵权反映了各指标向决策者提供的有用信息量㊂根据熵的思想来度量所有评价指标的信息效用值,从而确定各指标的熵权[7],第j 个指标的信息熵值e j 为e j =-ðmi =1P ij ln P ij ln m,(3)式中:e j (0ɤe j ɤ1)为第j 个指标的熵值,-1ln m为信息熵系数㊂通过信息熵值来确定各评价指标的权重w j :w j =1-e jðnj =1(1-e j )㊂(4)㊀㊀确定指标权重,建立加权决策矩阵,将式(4)得到的权重向量考虑到决策矩阵当中,通过标准化矩阵的每一行与其权重相乘得到加权规范化决策矩阵V =(v ij )m ˑn ㊂V =v 11v 12 v 1n v 21v 22 v 2n ︙︙︙v m 1v m 2v mn éëêêêêêêêùûúúúúúúú=㊀㊀r 11w 1r 12w 1 r 1n w 1r 21w 2r 22w 2 r 2n w 2︙︙︙r m 1w mr m 2w m r mn w m éëêêêêêêêùûúúúúúúú,(5)式中:v ij 为第i 个待评价对象第j 个指标标准化后加权的数据,r ij 为第i 个待评价对象第j 个指标标准化后的数据,w j 为第j 个指标的权重㊂经计算得到加权规范化决策矩阵后寻找正理想解与负理想解,令V +表示最偏好的方案(正理想解),V -表示最不偏好的方案(负理想解):V +=max v ij |j =1,2, ,n {}=v +1,v +2, ,v +n {},V -=min v ij |j =1,2, ,n {}=v -1,v -2, ,v -n{},(6)得到正理想解与负理想解后计算不同待评价对象到正负理想解的距离:D +i=ðnj =1(v ij -v +j )2,i =1,2, ,m ,D -i=ðnj =1(v ij -v -j )2,i =1,2, ,m ,(7)最终计算得出待评价对象与最优方案的贴近度C i :C i =D -i D -i +D +i ,1ɤi ɤm ,(8)式中C i 越大,表示第i 个待评价对象越接近最优水27山东理工大学学报(自然科学版)2024年㊀平㊂贴近度C i 的取值范围为0,1[],其中,当C i =0时,待评价对象的综合得分最差;当C i =1时,待评价对象的综合得分最好㊂1.2㊀主成分综合评价模型在综合评价中变量之间常具有一定的相关性,利用这些指标建立线性综合评价函数,容易造成信息重复,影响综合评价的结果[8]㊂主成分分析法以少数的综合变量取代原始采用的多维变量,可以减少在选取指标上花费的时间,在指标选取上较为容易㊂假定有m 个待评价对象,n 个评价指标,在进行分析时要先对数据进行标准化处理:y ij =x ij -x -js j,i =1,2, m ,j =1,2, ,n ,(9)式中:x ij 为第i 个待评价对象第j 个指标的值,x -j 为第j 个指标的平均值,s j 为第j 个指标的标准差㊂在数据预处理后需要计算数据集的相关系数矩阵R :R =(r jk )n ˑn ,(10)r jk =1n -1ðni =1(x ij -x -j )2㊃(x ik -x -k )2s j ㊃s k,(11)式中r jk 为第j 个指标与第k 个指标的相关系数㊂然后求出相关系数矩阵R 的n 个特征根与特征向量,确定主成分个数,由特征方程式λI n -R =0(12)可求得n 个特征根,并按照大小顺序将其排列为λ1ȡλ2ȡ ȡλn ȡ0㊂㊀㊀特征根的大小描述了每个主成分在评价中所起作用的大小㊂每一个特征根对应一个特征向量,记为u 1,u 2, ,u n ,求得各主成分为z ij =u T j x i ,x i=(x i 1,x i 2, ,x in )T ,(13)提取的主成分特征根应大于所有主成分特征根的平均数,又因为主成分分析进行了标准化,因此特征根的平均值为1,故提取大于1的特征根:λ1ȡλ2ȡ ȡλt ȡ1,t <n ,同时还要满足累计方差贡献率能够达到80%,若不能,需要通过改变特征根的大小以此来确定主成分个数,即E =ðtg =1λg ðn j =1λj ȡ80%㊂(14)利用选择的主成分,确定各个待评价对象的综合评价得分㊂首先求得每一个主成分的线性加权值;然后再对t 个主成分进行加权求和,其权重为t 个主成分的方差贡献率:w g =λgðtg =1λg ;(15)最终根据各主成分及权重得到各对象的综合评价得分为F i =ðtg =1w g z ig ,i =1,2, ,m ㊂(16)1.3㊀综合评价组合模型组合模型是提高模型精度的重要方法之一,单一模型表达能力不足,不能对复杂的问题进行很好的建模分析㊂组合模型通过组合的方式综合几个模型的优点,同时消除单一评价模型可能存在的较大偏差,从而使模型能够有更好的表达能力㊂本文综合了基于熵权改进的Topsis 模型与主成分综合评价模型,提出了1个新的组合评价模型㊂组合模型的关键在于组合权重的选择㊂考虑到两种综合评价得分的取值范围不同,即数据的离散程度具有一定的差异,从主观上来讲,球员间得分差异越大越能体现出二者的贡献度及排名的区别㊂统计中的方差正是描述数据离散程度的一个指标,故本文以单个评价模型球员得分的方差作为模型权重占比㊂具体为G c =σ2c σ21+σ22,(17)式中:G c 表示第c 种模型的权重,c =1,2;σ21是基于熵权法改进的Topsis 模型计算得到球员得分的方差;σ22是主成分综合评价模型计算得到球员得分的方差㊂按照上述加权方式得到的组合模型的综合评价得分为f i =ð2c =1G c F ic ,i =1,2, ,m ,(18)式中F ic 表示第c 个模型评价第i 个球员的得分㊂37第3期㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀代浩然,等:基于组合模型的球员贡献度评价2㊀非参数方法简介2.1㊀相关分析2.1.1㊀皮尔逊相关系数皮尔逊相关系数是一种用于衡量两个变量之间线性关系强度的统计量,可以帮助了解变量之间的关系,从而更好地理解数据和做出决策㊂其计算公式为ρXY =Cov(X ,Y )D (X )D Y (),(19)式中ρXY 的取值范围是[-1,1],当ρXY 大于0时,表示X 与Y 正相关,反之负相关,ρXY 为0时表示二者不具有相关性;ρXY 的绝对值越大说明二者相关性越强,绝对值越小说明二者相关性越小㊂2.1.2㊀Spearman 秩相关系数非参数统计中的Spearman 秩相关系数不仅可以衡量线性相关关系,同样也可以衡量非线性相关关系㊂该种方法对分析的变量数据不需要正态性假设,且对异常数值敏感度低㊂具体计算公式为r s =1-6n (n 2-1)ðni =1(R i -Q i )2,(20)式中:R i 表示X 的秩,Q i 表示Y 的秩㊂若遇到秩相等的情况则采用平均秩对其进行处理㊂2.1.3㊀Kendall τ相关系数Kendall τ相关系数于1938年提出,是一种与Spearman 秩相关系数类似的相似性检验法,它从变量是否协同一致的角度出发检验两变量之间是否存在相关性,协同性的定义如下:假设有n 对观测值:(x 1,y 1),(x 2,y 2), ,(x n ,y n ),如果x j -x i ()y j -y i ()>0则称数对满足协同性,反之则称数对不协同㊂用N c 表示满足协同性数对对数,N d 表示不满足协同性数对对数,具体公式为τ=N c -N dn (n -1)/2,(21)若遇到秩相等的情况则采用平均秩对其进行处理㊂2.2㊀Friedman 检验Friedman 检验是根据完全区组设计理论而提供的实验方法,当针对随机区组的实验数据时,由于传统的分析方法理论要求实验误差必须是正态分布的,当数据结果在当前不能够满足方差分析法的正态前提时,Friedman 建立并使用了秩方差分析法[9],该种方法仅仅依赖于每个区组内所观测的秩次㊂假设有k 个处理和b 个区组,数据结构见表1㊂表1㊀完全随机区组数据分析结构区组处理1处理2 处理k 区组1x 11x 12 x 1k 区组2x 21x 22 x 2k ︙︙︙︙区组bx b 1x b 2x bk ㊀㊀Friedman 检验与大部分方差分析的检验问题是一样的,即关于位置参数的假设检验为H 0:θ1=θ2= =θk ,H 1:∃i ,j ɪ1,2, ,k ,i ʂj ,θi ʂθj ㊂检验统计量为Q =12bk (k +1)ðki =1R 2i+-3b (k +1),(22)Q 统计量在H 0下近似服从自由度v =k -1的χ2分布㊂若统计量Q <χ20.05(k -1),则接受H 0,反之则拒绝H 0㊂当数据存在相同的秩时,Q 值校正为Q c =Q /1-ðgi =1(τ3i -τi )bk (k 2-1)(),(23)式中:τi 为第i 个结的长度,g 为结的个数㊂3㊀模型对比分析本文以2021 2022赛季金州勇士队在季后赛的表现为例分析上述3种评价模型㊂3.1㊀数据收集及处理本文利用网站()提供的数据,收集了2021 2022年季后赛所有球队的217名球员30项指标数据㊂以金州勇士队球员最低出场时间球员(Anderson)的48.9min 为最低标准,删除低于该出场时间球员数据,得到161名球员㊂此外,本文参考了王斌等[10]㊁章翔[11]给出的指标,以及作者在通过网络腾讯视频㊁NBA 官网等方式观看47山东理工大学学报(自然科学版)2024年㊀NBA 比赛时获得的一些心得,最终选取了表2中的10个指标进行分析及评价㊂表2㊀评价指标指标解释总得分球员在季后赛阶段总计得分数,体现了其得分能力㊀真实投篮命中率/%衡量球员出手效率的指标三分命中率/%衡量球员外线投篮的指标罚篮命中率/%衡量球员罚球好坏的指标篮板球数/个衡量球员在篮板球方面指标助攻数/个衡量球员在传球方面的指标失误次数/次衡量球员在控制失误方面的指标抢断/个衡量球员在防守端的指标盖帽/次衡量球员在防守端的指标个人犯规数衡量球员在控制失误方面的指标3.2㊀相关性分析本文通过相关性分析来探究指标之间的关系,以此判断指标是否出现严重的共线性问题㊂通过计算皮尔逊相关系数得到相关系数矩阵,将其可视化如图1所示㊂图1㊀皮尔逊相关系数热力图由图1可知,总得分㊁篮板球数㊁助攻数㊁失误次数㊁抢断㊁盖帽㊁个人犯规数之间具有较高的关联性,但仅通过皮尔逊相关系数无法直接表明是否一定存在这种相关关系,因为它受极端值的影响较大㊂为更加准确得到指标之间的具体关系,再利用Spearman 秩相关系数与Kendall τ相关系数进行相关分析,将其可视化如图2㊁图3所示㊂由图2㊁图3可知,总得分㊁篮板球数㊁助攻数㊁失误次数㊁抢断㊁盖帽㊁个人犯规数之间确实具有较高的关联性,但这些指标又会受到出场时间的影响,因为这些指标中隐含了出场时间这一信息,出场时图2㊀Spearman秩相关系数热力图图3㊀Kendall τ相关系数热力图间可以较为直接地体现出教练组对于球员水平的判断㊂对于本文而言,金州勇士队全体成员出场的比赛场数是相同的,出场时间仅受教练组的安排,在此不单独作为讨论的评价指标㊂通过以上相关分析,本文发现部分指标之间具有较强的相关性,说明指标之间存在较强的共线性问题,会对综合评价得分产生一定的影响㊂因此在计算综合评价得分时要考虑共线性这一因素的影响㊂最终通过3种综合评价模型对金州勇士队球员的表现进行评价㊂3.3㊀基于熵权法改进的Topsis 模型求解该模型是通过计算最优解和最劣解之间的距离,从而确定其综合评价指数,避免了传统权重分配方法中存在的主观性和不确定性,是普通Topsis 模型的一种改进方式㊂首先将金州勇士队14名球员的10项指标根据熵权法求出具体权重,将求得的权重代入Topsis 模型求解,其具体权重见表3㊂由表3可知,助攻数的权重最高达到18.157%,这符合金州勇士队擅长使用传切体系,这一体系下球队注重分享球,最终目的是帮助队员以57第3期㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀代浩然,等:基于组合模型的球员贡献度评价表3㊀指标权重分配指标信息熵值信息效用值权重/%助攻数0.7820.21818.157总得分0.7840.21617.978篮板球数0.8240.17614.656盖帽0.8430.15713.063抢断0.8560.14411.967失误次数0.9210.079 6.613真实投篮命中率0.9270.073 6.033个人犯规数0.9440.056 4.659三分命中率0.9580.042 3.455罚篮命中率0.9590.041 3.421最擅长的方式得分,助攻数也是对这一体系的侧面反映;同时罚篮命中率占比最低仅为3.421%,这一数据也可以从球队实际情况入手,因为球队擅长传切体系,难以获得高罚球数,因此罚篮命中率占比最小是有一定合理性的㊂可以说明,通过熵权法得到的指标权重具有一定的实际意义㊂经计算得到各权重后代入加权决策矩阵,以此来求出正理想解与负理想解㊂然后计算不同球员评价向量到正理想解与负理想解的距离,最终计算得到各球员与最优方案的贴近度,以此结果代表各球员的综合得分,具体得分见表4㊂表4㊀Topsis模型得分及排名姓名正理想解负理想解综合得分排名Curry0.200.450.701Green0.260.420.622 Wiggins0.260.370.603 Thompson0.250.320.564Poole0.270.300.525Looney0.350.270.446 Porter Jr.0.380.210.357 Payton II0.420.220.358Moody0.480.180.279 Kuminga0.470.150.2410Bjelica0.470.140.2311 Iguodala0.500.140.2212Lee0.510.130.2113 Anderson0.510.130.2014㊀㊀由表4可知,基于熵权法改进的Topsis模型得到各球员的综合得分,其大小反映了球员在争冠道路上的贡献度㊂3.4㊀主成分综合评价模型的求解通过3.2节相关性分析发现各评价指标具有较强的共线性,本模型通过主成分分析来解决这一问题㊂首先选取特征根大于1的主成分个数㊂通常采用碎石图来可视化这一现象,具体碎石图如图4所示㊂由图4可知,前3个特征根大于1,因此本文将选取前3个主成分作为本次综合评价的3个指标㊂图4㊀碎石图在满足特征根大于1这一基本条件后再探究前3个主成分对于变量的累计方差贡献情况,具体方差解释见表5㊂表5㊀方差解释成分特征根方差贡献率/%累计方差贡献率/%1 5.28652.86552.8652 1.30513.05265.9173 1.05810.58176.49840.9259.25385.75150.514 5.13690.88760.276 2.75793.64570.238 2.38496.02980.202 2.02598.05490.129 1.29399.346100.0650.654100㊀㊀由表5可知,前3个主成分累计方差贡献率仅为76.498%,小于80%,因此使用降低特征根至0.9的策略,期望能增加主成分的数量,以实现累计方差的贡献率达到80%这一目标㊂结合图4和表5可知,当特征根降低到0.9可以增加第4个主成分,使累计方差贡献率达到85.751%,故本文采用前4个67山东理工大学学报(自然科学版)2024年㊀主成分进行综合评价㊂通过上述分析可以得出具体的4个评价指标,根据式(16)计算得到最终的主成分综合评价,得分见表6㊂表6㊀主成分综合评价得分及排名㊀㊀Green约0.47分,即便如此,这两位球员仍位列贡献度排名前两位;从得分上来看,Poole㊁Thompson㊁Wiggins在夺冠的道路上发挥了不可磨灭的作用;考虑到金州勇士队球员储备丰富,Lee与Anderson发挥的作用并不明显㊂3.5㊀组合模型的求解基于上述两种综合评价模型求解得到各球员的综合得分,经计算,基于熵权法改进的Topsis模型的方差为0.154,主成分综合评价模型的为1.005㊂将计算结果代入式(17)得到两个模型的权重分别为:G1=0.133,G2=0.867,利用式(18)将两类模型进行加权求和,得到的得分见表7㊂由表7可知,Curry仍然以巨大的得分优势领先第2名Green,而贡献度排在第3㊁4㊁5名顺序则成了表7㊀组合模型得分及排名综合评价结果一致,但与基于熵权法改进的Topsis 模型结果存在差异,而Lee与Anderson仍处于最后两位㊂从整体上看,与前两种评价有一定的变化,但整体评价是否存在差异还需要进一步检验㊂3.6㊀一致性检验综合上述3种综合评价模型得到的综合评价得分及排名,考虑到通过排名更能直观感受各球员在争夺总冠军这条路上做出的贡献,为增强结论的严谨性,本文采用Friedman检验来判断3种模型是否存在差异㊂此时模型的一致性检验的原假设为H0:θ1=θ2= =θ14,检验统计量Q(式(22))可以度量一致性,Q越大表示3种评价模型的一致性越强,对本文球员的评价更具说服力㊂结合金州勇士队球员情况,此时有k= 14个球员和b=3个区组㊂本文将基于熵权法改进的Topsis模型㊁主成分综合评价㊁组合模型进行检验,球员顺序按照主成分综合评价得分的排名编号为1 14,具体数据见表8㊂表8㊀完全随机区组数据分析表球员1234567891011121314 Topsis模型1254376810911121314主成分评价1234567891011121314组合模型1234567811910121314㊀㊀由表8可知,3种模型结果不完全一致㊂通过RStudio进行求解,最终得到P值为0.9556,接受原假设,认为3种模型之间不存在差异,故通过Friedman检验增加了结论的可靠性,以此可以更加合理地体现出金州勇士队2021 2022年获得总冠军的球员贡献度的具体情况㊂4㊀结论本文以2021 2022赛季NBA金州勇士队球员77第3期㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀代浩然,等:基于组合模型的球员贡献度评价为研究对象,基于非参数相关分析探究了影响球员贡献度的10个指标,分别使用两种评价模型及1种组合模型计算了金州勇士队14名球员在夺冠道路上的贡献度,最后基于Friedman检验对3种模型进行了一致性检验,得到以下结论㊂1)组合模型可以更全面地考虑多个指标之间的影响,能够更真实地反映评价对象的综合表现㊂2)3种模型之间不具有差异性,通过Friedman 检验得到了3种模型的评价基本一致㊂3)通过排名以及收集得到的数据可以看出金州勇士队球员大致划分为4个档:Curry㊁Green㊁Poole㊁Thompson㊁Wiggins5人属于第一档,即球队首发实力的球员,能够获得稳定的上场时间并且能够取得较好的数据;Porter Jr.㊁Looney㊁Payton II3人属于第二档,即能够为球队提供稳定输出的球员但上场时间要少于首发;Kuminga㊁Moody㊁Bjelica3人属于第三档,即能够获得较少的出场时间但能够为球队在某些方面发挥作用;Iguodala㊁Lee㊁Anderson不能每场都保证有出场时间,仅发挥很小的作用,大部分会在无比赛悬念的时间上场㊂4)Curry在高位与Green的高位挡拆是勇士队的一大进攻特征㊂通过2人的球队贡献排名可以很好地体现出这一点,这也是金州勇士队能够取得总冠军非常重要的一项因素㊂5)Curry是金州勇士队的领袖和核心球员㊂通过前面3种模型的比较,可以发现Curry的综合得分远超出其他球员,证明了他在球队中的重要地位和突出贡献㊂他最终获得了FMVP这一总决赛含金量最高的个人奖项,证明了他是一位经验丰富㊁能够带领球队走向胜利的重要角色㊂以上分析反映了球员真实情况,故本文所构建的模型比较合理严谨㊂参考文献:[1]许坚,周勇,廖书雷,等.基于信息熵理论的篮球比赛球员贡献评价体系研究[J].浙江体育科学,2021,43(6):86-92. [2]吴威,凡新,王伟.基于主成分分析的CBA球队攻防能力的研究[J].湖北师范大学学报(自然科学版),2022,42(2):92-97.[3]刘欣然.篮球防守质量评价指标体系的确立及其原则[J].沈阳体育学院学报,2011,30(5):137-138,142.[4]景怀国,王军.Q型聚类分析对第30届奥运会男子篮球赛参赛队伍综合能力分析[J].广州体育学院学报,2012,32(6):68-72.[5]李国,孙庆祝.第30届奥运会中国男子篮球队与对手攻防指标的TOPSIS分析[J].中国体育科技,2013,49(1):88-95. [6]信桂新,杨朝现,杨庆媛,等.用熵权法和改进TOPSIS模型评价高标准基本农田建设后效应[J].农业工程学报,2017,33(1): 238-249.[7]周惠成,张改红,王国利.基于熵权的水库防洪调度多目标决策方法及应用[J].水利学报,2007(1):100-106.[8]黄利文.基于理想点的主成分分析法在综合评价中的应用[J].统计与决策,2021,37(10):184-188.[9]黄小澄.商业银行上市前后绩效对比:基于Fried-man检验和DEA[J].老字号品牌营销,2022(7):57-59.[10]王斌,明园淋,王志菲,等.NBA联赛中三分球技术的运用及效果:基于2018 2019赛季NBA总决赛勇士队VS猛龙队[J].浙江师范大学学报(自然科学版),2023,46(1):96-103. [11]章翔.NBA与CBA球队技术统计的逐步回归分析及比较研究[J].北京体育大学学报,2014,37(1):134-138.(编辑:杜清玲)87山东理工大学学报(自然科学版)2024年㊀。

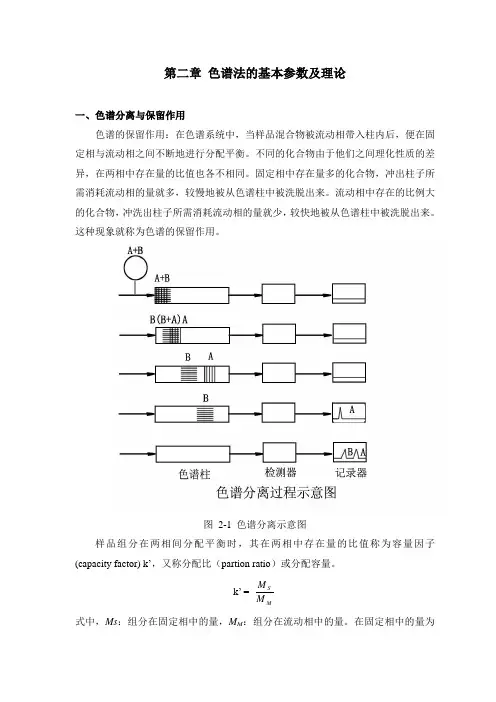
第二章 色谱法的基本参数及理论一、色谱分离与保留作用色谱的保留作用：在色谱系统中，当样品混合物被流动相带入柱内后，便在固定相与流动相之间不断地进行分配平衡。

不同的化合物由于他们之间理化性质的差异，在两相中存在量的比值也各不相同。

固定相中存在量多的化合物，冲出柱子所需消耗流动相的量就多，较慢地被从色谱柱中被洗脱出来。

流动相中存在的比例大的化合物，冲洗出柱子所需消耗流动相的量就少，较快地被从色谱柱中被洗脱出来。

这种现象就称为色谱的保留作用。

图 2-1 色谱分离示意图样品组分在两相间分配平衡时，其在两相中存在量的比值称为容量因子(capacity factor) k ’，又称分配比（partion ratio ）或分配容量。

k ’ = MS M M 式中，Ms ：组分在固定相中的量，M M ：组分在流动相中的量。

在固定相中的量为零的化合物，其k ’=0，这些组分被称为在该色谱条件下的非保留物质。

容量因子（分配比）可通过实验计算：k ’ =MR t t ' 。

即k ’为组分在固定相中消耗的时间与其在流动相中消耗的时间之比。

样品组分在两相中分配平衡时，其在固定相和流动相中的浓度比称为分配系数（partion factor ），分配系数以K 表示。

其公式如下：Ms c c K ==组分在流动相中的浓度组分在固定相中的浓度 K =m m S S V M V M // = k ’· S m V V 式中，Ms/Vs 为样品组分在固定相中的浓度，M m /V m 为样品组分在流动相中的浓度。

分配系数大的组分保留时间长（色谱的保留作用强），分配系数小的组分保留时间短（色谱的保留作用弱）。

K = k ’· Sm V V = k ’· β 式中β = Sm V V 称为相比率，即色谱柱中流动相体积与固定相体积之比。

例在毛细管GC 中壁涂空心柱的相比为：β = 固定相体积（柱中）流动相体积（柱中） = dfrl l r ⋅ππ22 = df r 2式中r为毛细管柱横截面的半径，d f为柱内壁固定液的膜厚。

基尼系数分解dagum程序基尼系数是用于衡量经济不平等程度的一种常用指标。

在计算基尼系数时，经常需要将收入或财富的分布曲线进行分解，以便计算各分布分别对基尼系数的贡献。

Dagum （1990）提出了一种计算基尼系数分解的方法，即用两个参数的重尾分布函数来描述收入或财富分布。

该方法能较好地应对一些非对称、偏态的分布情况。

在这篇文章中，我们将介绍如何使用R语言程序实现Dagum方法计算基尼系数分解。

首先，我们需要声明Dagum函数：```Rdagum <- function(x, a, b) {y <- (a * b^a / x^(a + 1))^(1/b)return(y)}```其中，x是一个向量，a和b是Dagum分布的参数。

在实际使用中，a和b需要通过拟合处理得到。

Dagum分布可以看作是两个beta分布的乘积，因此可以首先计算beta分布：此时，我们可以计算收入或财富分布的基尼系数了。

假设有一个向量x表示收入或财富的分布，我们可以使用R中的integrate函数计算x中每个值对基尼系数的贡献：```Rgini <- function(x, a, b, c) {n <- length(x)gx <- numeric(n)for (i in 1:n) {fun <- function(t) {dagumfun(t, a, b, c)}gx[i] <- integrate(fun, 0, x[i])$value}g <- sum((gx[1:(n-1)] + gx[2:n]) * (x[2:n] - x[1:(n-1)]) / 2)return(g)}``````Rx <- c(0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1)a <- 2b <- 0.5c <- 0.5gini(x, a, b, c)```在该代码中，我们使用了一个包含11个值的向量x作为分布的近似，计算得到的基尼系数大约为0.545。

基于R语言的主成分分析方法比较研究主成分分析（Principal Component Analysis，PCA）是一种常用的多变量数据分析方法，主要用于降低多维数据的维数，并揭示数据变量之间的关系。

在R语言中，有多种方法可以实现主成分分析，包括prcomp、princomp和pcaMethods等。

1. prcomp方法：prcomp是R中一个较为常用的主成分分析方法，通过计算特征值和特征向量来提取主成分。

首先，我们需要将原始数据进行预处理，包括去除缺失值、标准化或归一化等方法。

然后，使用prcomp函数对预处理后的数据进行主成分分析。

该函数可以接受多个参数，例如数据、center、scale等。

其中，center参数用于指定是否对数据进行中心化，scale参数用于指定是否对数据进行标准化。

最后，通过summary函数获取主成分的方差解释比例和贡献度，并通过biplot函数绘制主成分散点图。

2. princomp方法：princomp也是一个常用的主成分分析方法，与prcomp方法相比，不会对数据进行中心化和标准化处理。

使用princomp方法进行主成分分析的步骤类似于prcomp方法，首先对数据进行预处理，然后使用princomp函数进行主成分分析。

与prcomp不同的是，princomp函数不返回主成分的贡献度，但可以通过summary函数来获取主成分的方差解释比例。

同样，可以利用biplot函数绘制主成分散点图。

3. pcaMethods包：pcaMethods包是R中用于主成分分析的一个扩展包，提供了多种主成分分析的方法。

该包支持缺失值处理、数据标准化、主成分个数选择等功能。

首先，使用pca函数对数据进行主成分分析。

该函数可以使用不同的方法进行主成分分析，例如SVD、NIPALS、PPR等。

然后，通过summary函数获取主成分的解释比例和贡献度。

同时，pcaMethods包还提供了绘制散点图、热图或加载图等可视化方法。

基于R语言的主成分分析结果可视化方法与实例分析主成分分析（Principal Component Analysis，简称PCA）是一种常用的多变量数据降维和数据可视化方法。

它可以将高维数据集转化为低维空间，保留数据集的主要信息，便于观察和分析。

R语言是一种强大的统计分析工具，具有丰富的PCA函数和可视化包，可以帮助我们实现主成分分析结果的可视化。

下面我将介绍基于R语言的主成分分析结果可视化方法，并通过一个实例来说明。

首先，我们需要使用R语言加载相关的库和数据集。

在R中，我们可以使用"ggplot2"包来进行数据可视化，使用"FactoMineR"包来进行主成分分析。

```R#加载所需包library(ggplot2)library(FactoMineR)#加载数据集data <- read.csv("data.csv") #将数据集命名为"data.csv"```接下来，我们可以进行主成分分析并获取结果。

在R中，我们可以使用"PCA"函数来进行主成分分析。

```R#主成分分析pca <- PCA(data)```主成分分析会生成一系列的主成分和它们的贡献度。

我们可以通过"dimdesc"函数查看主成分的描述信息。

```R#查看主成分描述dimdesc(pca)```通过"dimdesc"函数，我们可以得到每个主成分对应的原始变量，并且可以查看它们的权重和贡献度。

接下来，我们可以选择性地选择几个主成分进行可视化分析。

在R中，我们可以使用"fviz_pca_ind"函数进行样本的主成分分析结果可视化。

```R#样本主成分分析结果可视化fviz_pca_ind(pca, axes = c(1, 2), geom.ind = "point", col.ind = "blue", pointsize = 2, title = "PCA - Individus")```"fviz_pca_ind"函数中，参数"axes"指定了我们要可视化的主成分，"geom.ind"指定了个体的几何表达方式，"col.ind"和"pointsize"分别指定了个体的颜色和大小。

利用R语言进行主成分分析的数据预处理方法研究主成分分析（Principal Component Analysis，简称PCA）是一种常用的多变量数据分析方法，用于降维、预处理和可视化数据。

在利用R语言进行主成分分析的数据预处理方法研究中，我们可以使用R语言中的多种函数和包来实现。

首先，我们需要加载所需的R包。

常用的主成分分析函数包括stats、FactoMineR和prcomp。

我们可以使用以下命令加载这些包：```Rlibrary(stats) # 加载stats包library(FactoMineR) # 加载FactoMineR包```接下来，我们可以使用R语言读取和处理数据。

假设我们有一个包含多个变量的数据集，我们可以使用read.csv()函数读取数据，并使用head()函数查看前几行数据来确保数据读取正确。

```Rdata <- read.csv("data.csv") # 读取数据集head(data) # 查看前几行数据```在进行主成分分析之前，我们需要对数据进行预处理，包括处理缺失值、标准化等。

以下是一些常用的数据预处理方法。

1. 处理缺失值：如果数据集中存在缺失值，我们可以使用na.omit()函数删除含有缺失值的行，或者使用如mean()、median()等函数填充缺失值。

```Rdata <- na.omit(data) # 删除含有缺失值的行# 或者使用均值填充缺失值data[is.na(data)] <- mean(data, na.rm = TRUE)```2. 标准化数据：主成分分析通常要求数据进行标准化，以消除变量之间的单位差异。

我们可以使用scale()函数进行标准化。

```Rdata_standardized <- scale(data) # 标准化数据```3. 处理离群值：离群值可能会对主成分分析结果产生不良影响。

基于R语言的主成分分析模型优化及效果评估主成分分析（Principal Component Analysis，简称PCA）是一种常用的无监督学习技术，可用于数据降维、特征提取和可视化等任务。

本文基于R语言对PCA模型进行优化及效果评估，并提出一种改进方法。

首先，我们需要导入数据并进行预处理。

假设我们已经拥有一个包含m个样本和n个特征的数据集X。

使用R语言中的`prcomp`函数可以执行主成分分析，并得到主成分贡献率、特征载荷以及转换后的数据。

```r# 导入数据data <- read.csv("data.csv")# 数据预处理scaled_data <- scale(data)# 执行主成分分析result <- prcomp(scaled_data)```在得到主成分分析的结果后，我们可以通过可视化方法来评估模型效果。

下面是一些常用的评估方法。

1. 散点图：可以绘制原始数据集和转换后的数据集在前几个主成分上的散点图，以便观察数据的分布情况。

例如，我们可以使用R语言中的`ggplot2`包绘制前两个主成分的散点图。

```rlibrary(ggplot2)# 绘制散点图pca_data <- data.frame(result$x[,1:2], label = 1:m) # 提取前两个主成分ggplot(pca_data, aes(x = PC1, y = PC2, color = label)) + geom_point() + theme_bw() ```2. 方差贡献率图：可以通过绘制各个主成分的方差贡献率图来评估模型的效果。

R语言中的`ggplot2`包可以很方便地实现这一功能。

```r# 绘制方差贡献率图variance_ratio <- result$sdev^2 / sum(result$sdev^2) # 计算方差贡献率variance_ratio_cumulative <- cumsum(variance_ratio) # 计算累计方差贡献率pca_variance <- data.frame(Components = 1:n, Variance_Ratio = variance_ratio,Cumulative_Variance_Ratio = variance_ratio_cumulative)ggplot(pca_variance, aes(x = Components, y = Variance_Ratio)) +geom_bar(stat = "identity") + theme_bw() +ylab("Variance Ratio") + xlab("Principal Components")```在模型优化方面，我们可以采用以下方法提高主成分分析的效果。

r语言方差分解R语言方差分解是一种常用的数据分析方法，主要用来分解数据的方差以及各个因素对数据方差的贡献程度。

本文将围绕R语言方差分解展开，分步骤阐述该方法的具体实现及其应用。

一、数据准备在进行方差分解前，首先需要准备好所需数据。

假设我们有一组实验数据，包括两个因素x1和x2，以及一个因变量y，我们要对它们进行方差分解。

可以使用R语言中的data.frame()函数将数据读入，并用summary()函数查看数据的统计信息。

二、方差分解在数据准备好后，我们可以使用R语言中的anova()函数进行方差分解。

该函数可以直接对数据进行方差分析，并返回分解结果。

在执行函数时，需要将因变量和各个因素以及它们之间的交互项作为参数传入。

此外，我们还需要使用命令options(contrasts=c("contr.sum","contr.poly"))设置协变量方式，这里使用sum之和协方差或者poly多元协方差。

三、结果解释方差分解后，我们可以得到各个因素对数据方差的贡献情况，以及交互项的贡献情况。

通常情况下，我们会对结果进行解读。

例如，我们可以根据各个因素的F值大小来判断它们对方差的贡献程度。

同时，我们也可以通过比较模型的R平方值来评估模型的拟合程度，从而得出结论。

四、应用举例方差分解方法在数据分析中有着广泛的应用，例如在实验设计、质量控制、生物统计学等领域中都有应用。

例如，我们可以使用方差分解来分析某种药物对不同疾病的影响，找出影响治疗效果的主要因素。

此外，方差分解还可以用来研究某种环境因素对植物生长的影响，帮助生产者提高农作物的产量。

综上所述，R语言方差分解是一种常用的数据分析方法，在实践中有着广泛的应用。

通过对数据的分解，我们可以得到各个因素对数据方差的贡献程度，从而更好地理解数据的本质，为后续研究提供有用的参考。

r语言anova函数的结果 -回复第一步：理解ANOVA函数的基本概念和用途ANOVA（Analysis of Variance，方差分析）是一种统计方法，用于比较两个或更多个群体的均值是否存在差异。

其基本原理是将总体方差分解为组内方差和组间方差，然后利用方差比率检验组间方差是否显著大于组内方差。

ANOVA函数是R语言中实现方差分析的一种函数，其结果可以为我们提供关于群体均值的差异性以及是否存在显著的组间差异的信息。

第二步：了解ANOVA函数的基本用法和参数设置在R语言中，ANOVA函数的基本用法为：anova(model, ...)其中，model表示回归模型的公式，...表示其它参数，如data等。

通过此函数，可以对指定的统计模型进行方差分析，并返回一个A N O V A表格，其中包含各个因素的F-统计量、自由度、均方、p-value等信息。

第三步：理解ANOVA函数结果中的各个参数含义1. Df - 自由度（Degree of Freedom）：指示数据集中独立的观测值的数量。

分为总体自由度（Total Df）、组间自由度（Between-group Df）和组内自由度（Within-group Df）三种。

2. Sum Sq - 平方和（Sum of Squares）：指各个来源的平方和，包括总平方和（Total SS）、组间平方和（Between-group SS）和组内平方和（Within-group SS）等。

通过平方和可以衡量各个来源对总方差的贡献程度。

3. Mean Sq - 均方（Mean Square）：平方和除以相应的自由度，用于计算F-统计量。

包括组间均方（Between-group MS）和组内均方（Within-group MS）两种。

4. F value - F-统计量：表示组间均方与组内均方之比，用于检验不同组别之间均值是否显著不同。

5. Pr(>F) - p-value：表示给定F-统计量的概率值，用于判断不同组别之间均值是否显著不同。

线性回归方程中的相关系数rr=∑(Xi-X的平均数)(Yi-Y平均数)/根号下[∑(Xi-X平均数)^2*∑(Yi-Y平均数)^2]R2就是相关系数的平方，R在一元线性方程就直接是因变量自变量的相关系数，多元则是复相关系数判定系数R^2也叫拟合优度、可决系数。

表达式是:R^2=ESS/TSS=1-RSS/TSS该统计量越接近于1，模型的拟合优度越高。

问题：在应用过程中发现，如果在模型中增加一个解释变量，R2往往增大这就给人一个错觉：要使得模型拟合得好，只要增加解释变量即可。

——但是，现实情况往往是，由增加解释变量个数引起的R2的增大与拟合好坏无关，R2需调整。

这就有了调整的拟合优度:R1^2=1-(RSS/(n-k-1))/(TSS/(n-1))在样本容量一定的情况下，增加解释变量必定使得自由度减少，所以调整的思路是:将残差平方和与总离差平方和分别除以各自的自由度，以剔除变量个数对拟合优度的影响:其中：n-k-1为残差平方和的自由度，n-1为总体平方和的自由度。

总是来说，调整的判定系数比起判定系数，除去了因为变量个数增加对判定结果的影响。

R = R接近于1表明Y与X1，X2 ，…，Xk之间的线性关系程度密切；R接近于0表明Y与X1，X2 ，…，Xk之间的线性关系程度不密切相关系数就是线性相关度的大小，1为（100%）绝对正相关，0为0%，-1为（100%）绝对负相关相关系数绝对值越靠近1，线性相关性质越好，根据数据描点画出来的函数-自变量图线越趋近于一条平直线，拟合的直线与描点所得图线也更相近。

如果其绝对值越靠近0，那么就说明线性相关性越差，根据数据点描出的图线和拟合曲线相差越远（当相关系数太小时，本来拟合就已经没有意义，如果强行拟合一条直线，再把数据点在同一坐标纸上画出来，可以发现大部分的点偏离这条直线很远，所以用这个直线来拟合是会出现很大误差的或者说是根本错误的）。

分为一元线性回归和多元线性回归线性回归方程中,回归系数的含义一元：Y^=bX+a b表示X每变动（增加或减少）1个单位,Y平均变动（增加或减少）b各单位多元：Y^=b1X1+b2X2+b3X3+a 在其他变量不变的情况下，某变量变动1单位，引起y平均变动量以b2为例：b2表示在X1、X3（在其他变量不变的情况下）不变得情况下，X2每变动1单位，y平均变动b2单位就一个reg来说y=a+bx+ea+bx的误差称为explained sum of squaree的误差是不能解释的是residual sum of square总误差就是TSS所以TSS=RSS+ESS判定系数也叫拟合优度、可决系数。

化学常数r化学常数r是一个重要的理论参数，它是计算化学反应速率和浓度变化量的关键参数，是研究化学反应机理必不可少的因素。

本文主要研究化学常数r的定义、计算方法、实际应用及其存在的问题，为深入探究化学反应机理提供参考。

一、定义根据Maxwell-Boltzman统计学说，质量相同的两个介质，其空气的温度和张力一定，当在它们的分子速度的分布情况相同的情况下，这两个介质的摩尔浓度也相等。

它定义为：在每单位体积温度一定、压力一定的情况下，流体或气体内相同类别的分子含量，叫做单位体积中的摩尔浓度。

根据上述定义，化学常数r就是指在单位体积下，气体中各种分子的摩尔浓度。

二、计算方法化学常数r的计算方法有几种：1.理想气体：在理想气体情况下，化学常数r的计算公式为：r = PV/RT其中，P为 Reynolds体定律中的压强，V为体积，T为温度，R为气体常数的值，而根据上式应该有：RT/P=k，其中K为不变量。

2.实际气体：实际气体中化学常数R的计算方法不同于理想气体，它是先用PV/RT公式计算出理想气体的摩尔浓度，然后再计算出具体气体的摩尔浓度，用实际气体的摩尔浓度减去理想气体的摩尔浓度，再乘以火焰的温度。

三、实际应用化学常数r的实际应用还是比较广泛的，一般在化学反应中会涉及到它的概念，用它来定性分析反应的情况。

比如，在求解物理和化学热力学问题时，经常需要用到化学常数r，用它计算反应速率常常会得出正确的结果。

另外，化学常数r还可以用于计算热量反应，一些高温化学反应会受到化学常数r的影响。

四、存在的问题尽管化学常数R在化学反应中起到重要作用，但也存在一些问题。

首先，由于化学常数R是一个常数，它只能用于计算特定反应的反应速率，并不能用来计算复杂多步反应的反应速率。

其次，化学常数R的值受温度、压力的影响，变化较大，所以在实际应用中，有时会遇到结果与实际不一致的情况。

最后，化学常数R只能够应用于一些简单的情况，一些复杂的反应还需要用其他的理论来解释。