黑龙江省哈尔滨市道里区九年级(上)期末数学试卷

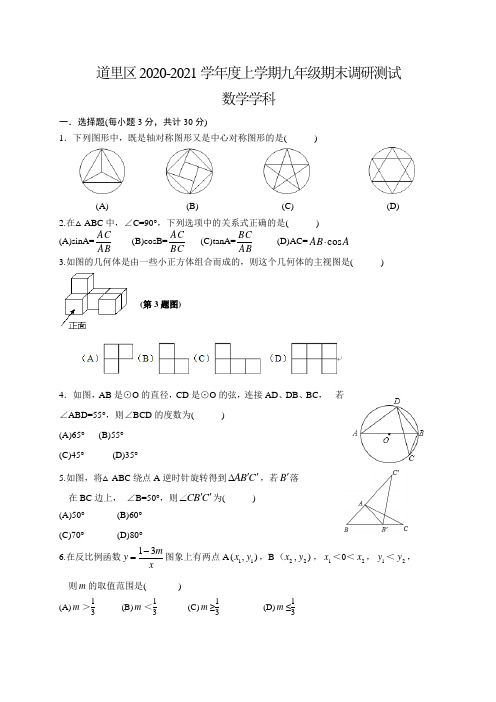
道里区2020-2021学年度上学期九年级期末调研测试数学学科一．选择题(每小题3分，共计30分)1．下列图形中，既是轴对称图形又是中心对称图形的是()(A) (B) (C) (D)2.在△ABC中，∠C=90°，下列选项中的关系式正确的是( )(A)sinA=ABAC(B)cosB=BCAC(C)tanA=ABBC(D)AC=AAB cos⋅3.如图的几何体是由一些小正方体组合而成的，则这个几何体的主视图是()4．如图，AB是⊙O的直径，CD是⊙O的弦，连接AD、DB、BC，若∠ABD=55°，则∠BCD的度数为()(A)65°(B)55°(C)45°(D)35°5.如图，将△ABC绕点A逆时针旋转得到CBA''∆，若B'落在BC边上，∠B=50°，则CBC''∠为()(A)50°(B)60°(C)70°(D)80°6.在反比例函数xmy31-=图象上有两点A),(11yx，B ),22yx（，1x＜0＜2x，1y＜2y，则m的取值范围是( )(A)m＞13(B)m＜13(C)m≥13(D)m≤13(第3题图)7.一个袋中里有4个珠子，其中2个红色，2个蓝色，除颜色外其余特征均相同，若从 这个袋中任取2个珠子，都是蓝色珠子的概率是( )(A)21(B)31 (C)41 (D)618.如图，543l l l ∥∥，1l 交543,,l l l 于E,A,C, 2l 交543,,l l l 于D,A,B,以 下结论的错误的为( )(A)AB DA AC EA = (B)CE CA BD BA = (C)DB DA CE CA = (D)DBDAEC EA =9. 如图，P 为⊙O 外一点，PA 、PB 分别切⊙O 于点A 、B ，CD 切⊙O 于点E 且分别交PA 、PB 于点C ，D ，若PA=4，则△PCD 的周长为( )(A)8 (B)7 (C)6 (D)510.如图是抛物线y 1=ax 2+bx+c(a≠0)的一部分，抛物线的顶点坐标 A(1，3)，与x 轴的一个公共点B(4，0)，直线y 2=mx+n(m≠0) 与抛物线交于A ，B 两点，下列结论:①2a-b=0；②abc ＜0；③方程 ax 2+bx+c=3有两个相等的实数根；④抛物线与x 轴的另一个公共点 是(﹣1，0)；⑤当1＜x ＜4时，有y 2＞y 1 ；其中正确的有( )个. (A)1 (B)2 (C)3 (D)4二．填空题(每题3分，共30分)11.点(-4,1)关于原点的对称点的坐标为 . 12.若反比例函数xky =的图象经过点(﹣2，3)，则k= . 13.将二次函数y=x 2+1的图象向左平移2个单位，再向下平移3个单位长度得到的图象对应的二次函数的解析式为b ax x y ++=2，则ab = ． 14.在△ABC 中，∠C=90°，cosA=23,AC=36,则BC= . 15.如图，四边形ABCD 是⊙O 的内接四边形，⊙O 的半径为4，(第8题图)(第9题图)(第10题图)∠B=135°，则AC 的长为 .16.在围棋盒中有x 颗白色棋子和y 颗黑色棋子，从盒中随机取出一 颗棋子，取得白色棋子的概率是31，如再往盒中放进4颗黑色棋子， 取得白色棋子的概率变为51，则22y x += . 17.如图，在某监测点B 处望见一艘正在作业的渔船在南偏西15° 方向的A 处，若渔船沿北偏西75°方向以60海里/小时的速度 航行，航行半小时后到达C 处，在C 处观测到B 在C 的北偏东60°方向上，则B 、C 之间的距离为 海里 .18.某种商品的进价为40元，在某段时间内若以每件x 元出售，可卖 出(100-x)件，当x= 时才能使利润最大.19.如图，⊙O 的弦AB 与半径OC 垂直，点D 为垂足，OD=DC,32=AB ,点E 在⊙O 上，∠EOA=30°，则△EOC 的面积为 .20. 如图，△ABC,∠ACB=90°，点D,E 分别在AB, BC 上， AC=AD,∠CDE=45°，CD 与AE 交于点F,若 ∠AEC=∠DEB, CE=4107,则CF= .三．解答题(60分)21.(本题7分)通过配方，确定抛物线12++=bx ax y 的顶点坐标及对称轴，其中︒-︒=45tan 30sin a ，︒⋅︒=60sin 30tan 4b .(第19题图)(第17题图)(第2020)22．(本题7分)如图，在小正方形的边长均为1的方格纸中，有线段AB ，点A ，B 均在小正方形的顶点上．(1)在图1中画出四边形ABCD ，四边形ABCD 是中心对称图形，且四边形ABCD 的面积为6，点C ，D 均在小正方形的顶点上； (2)在图2中画一个△ABE ，点E 在小正方形的顶点上，且BE=BA,请直接写出∠BEA 的余弦值．23.(本题8分)在平面直角坐标系内，点O 为坐标原点，直线4+=x y 交x 轴于点A,交y 轴于点B, 点C(2,m)在直线4+=x y 上，反比例函数xny =经过点C. (1)求m ,n 的值 ； (2)点D 在反比例函数xny =的图象上，过点D 作X 轴的垂线，点E 为垂足，若OE=3, 连接AD,求tan ∠DAE 的值(第23题图)24.(本题8分)如图，正方形ABCD,点E 在AD 上，将△CDE 绕点C 顺时针旋转90°至△CFG ，点F,G 分别为点D,E 旋转后的对应点，连接EG ,DB,DF, DB 与CE 交于点M,DF 与CG 交于点N.（1）求证BM=DN;（2）直接写出图中已经存在的所有等腰直角三角形.25.(本题10分)如图，在平面直角坐标系内，点O 为坐标原点，抛物线423412++-=x x y 交x 轴负半轴于点A,交x 轴正半轴于点B,交y 轴于点C. (1)求AB 长 ；(2)同时经过A,B,C 三点作⊙D ，求点D 的坐标 ； (3)在(2)的条件下，横坐标为10的点E 在抛物线423412++-=x x y 上，连接AE,BE, 求∠AEB 的度数.。

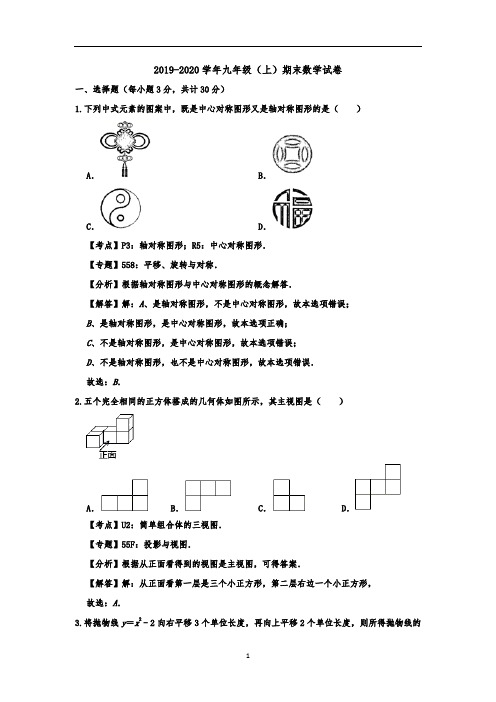
2019-2020学年九年级（上）期末数学试卷一、选择题（每小题3分，共计30分）1.下列中式元素的图案中，既是中心对称图形又是轴对称图形的是（）A．B．C．D．【考点】P3：轴对称图形；R5：中心对称图形．【专题】558：平移、旋转与对称．【分析】根据轴对称图形与中心对称图形的概念解答．【解答】解：A、是轴对称图形，不是中心对称图形，故本选项错误；B、是轴对称图形，是中心对称图形，故本选项正确；C、不是轴对称图形，是中心对称图形，故本选项错误；D、不是轴对称图形，也不是中心对称图形，故本选项错误．故选：B．2.五个完全相同的正方体搭成的几何体如图所示，其主视图是（）A．B．C．D．【考点】U2：简单组合体的三视图．【专题】55F：投影与视图．【分析】根据从正面看得到的视图是主视图，可得答案．【解答】解：从正面看第一层是三个小正方形，第二层右边一个小正方形，故选：A．3.将抛物线y＝x2﹣2向右平移3个单位长度，再向上平移2个单位长度，则所得抛物线的解析式为（）A．y＝（x+3）2B．y＝（x﹣3）2C．y＝（x+2）2+1 D．y＝（x﹣2）2+1 【考点】H6：二次函数图象与几何变换．【专题】535：二次函数图象及其性质；69：应用意识．【分析】利用二次函数图象的平移规律，左加右减，上加下减，进而得出答案．【解答】解：将抛物线y＝x2﹣2向右平移3个单位长度，得到平移后解析式为：y＝（x ﹣3）2﹣2，∴再向上平移2个单位长度所得的抛物线解析式为：y＝（x﹣3）2﹣2+2，即y＝（x﹣3）2；故选：B．4.在△ABC中，∠C＝90°，sin B＝，则tan B值为（）A．B．C．D．【考点】T3：同角三角函数的关系．【专题】55E：解直角三角形及其应用；69：应用意识．【分析】先利用平方公式计算出cos B＝，然后根据tan B＝求解．【解答】解：∵∠C＝90°，∴sin2A+cos2B＝1，∴cos B＝＝，∴tan B＝＝＝．故选：A．5.已知点P1（a，2）与点P2（﹣3，b）关于原点对称，则a﹣b的值是（）A．﹣5 B．﹣1 C．1 D．5【考点】R6：关于原点对称的点的坐标．【专题】558：平移、旋转与对称；64：几何直观．【分析】根据两个点关于原点对称时，它们的坐标符号相反可得a、b的值，进而可得答案．【解答】解：∵点P1（a，2）与点P2（﹣3，b）关于原点对称，∴a＝3，b＝﹣2，∴a﹣b＝5，故选：D．6.在反比例函数y＝图象的每一条曲线上，y都随x的增大而增大，则k的取值范围是（）A．k＞2 B．k＞0 C．k≥2 D．k＜2【考点】G4：反比例函数的性质；G6：反比例函数图象上点的坐标特征．【专题】534：反比例函数及其应用；66：运算能力；67：推理能力．【分析】根据反比例函数的性质，可求k的取值范围．【解答】解：∵反比例函数y＝图象的每一条曲线上，y都随x的增大而增大，∴k﹣2＜0，∴k＜2故选：D．7.随机掷一枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，则这个骰子向上的一面点数大于3的概率为（）A．B．C．D．【考点】X4：概率公式．【专题】11：计算题．【分析】骰子六个面出现的机会相同，求出骰子向上的一面点数大于3的情况有几种，直接应用求概率的公式求解即可．【解答】解：∵一枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，点数大于3的有4，5，6共3个，∴这个骰子向上的一面点数大于3的概率为＝．故选：A．8.关于抛物线y＝﹣（x+3）2+2，下列说法错误的是（）A．开口向下B．对称轴是直线x＝﹣3C．与y轴交点坐标（0，2）D．顶点坐标（﹣3，2）【考点】H3：二次函数的性质．【专题】535：二次函数图象及其性质；67：推理能力．【分析】由抛物线的解析式可求得开口方向、对称轴及顶点坐标，可判断A、B、D，令x ＝0求得y的值即可判断C，则可求得答案．【解答】解：∵y＝﹣（x+3）2+2，∴抛物线开口向下、对称轴为x＝﹣3、顶点坐标为（﹣3，2），故A、B、D说法是正确的；在y＝﹣（x+3）2+2中，令x＝0可得y＝﹣7，∴抛物线与y轴交点坐标（0，﹣7），∴选项C的说法是错误的，故选：C．9.如图，AB是⊙O的直径，点C，D，E在⊙O上，若∠AED＝20°，则∠BCD的度数为（）A．100°B．110°C．115°D．120°【考点】M5：圆周角定理．【分析】连接AC，根据圆周角定理，可分别求出∠ACB＝90°，∠ACD＝20°，即可求∠BCD的度数．【解答】解：连接AC，∵AB为⊙O的直径，∴∠ACB＝90°，∵∠AED＝20°，∴∠ACD＝20°，∴∠BCD＝∠ACB+∠ACD＝110°，故选：B．10.如图，平行四边形ABCD中，连接AC，在CD的延长线上取一点E，连接BE，分别交AC和AD于点G和点F，则下列结论错误的是（）A．＝B．＝C．＝D．＝【考点】L5：平行四边形的性质；S9：相似三角形的判定与性质．【专题】55D：图形的相似；69：应用意识．【分析】利用平行四边形的性质以及平行线分线段成比例定理解决问题即可．【解答】解：∵四边形ABCD是平行四边形，∴AB＝CD，BC＝AD，AB∥CD，AD∥BC，∴AB∥CE，∴＝＝，故A正确，∵AF∥BC，AB∥EC，∴＝＝，故B正确，∵AF∥BC，AB∥EC，∴＝＝，∴＝，故C正确，故选：D．二、填空题（每小题3分，共计30分)11.函数y＝的自变量x的取值范围是x≠2 ．【考点】E4：函数自变量的取值范围．【分析】根据分母不等于0列不等式求解即可．【解答】解：由题意得，x﹣2≠0，解得x≠2．故答案为：x≠2．12.若二次函数y＝x2﹣6x+3a的图象与x轴有且只有一个交点，则a的值为 3 ．【考点】HA：抛物线与x轴的交点．【专题】535：二次函数图象及其性质；66：运算能力．【分析】直接利用抛物线与x轴只有一个交点⇔b2﹣4ac＝0，进而解方程得出答案．【解答】解：∵二次函数y＝x2﹣6x+3a的图象与x轴有且只有一个交点，∴△＝b2﹣4ac＝（﹣6）2﹣4×3a＝0，解得：a＝3，故答案为：3．13.身高1.5米的小强站在旗杆旁，测得小强和旗杆在地面上的影长分别为2米和16米，则旗杆的高度为12 米．【考点】SA：相似三角形的应用．【专题】55D：图形的相似；69：应用意识．【分析】根据同一时刻同一地点物高与影长成正比求得答案即可．【解答】解：设旗杆高度为x米，根据题意得：，解得：x＝12，故答案为：12．14.一个扇形的半径为6，弧长为3π，则此扇形的圆心角为90 度．【考点】MN：弧长的计算．【专题】55C：与圆有关的计算；69：应用意识．【分析】根据弧长公式列式计算，得到答案．【解答】解：设这个扇形的圆心角为n°，则＝3π，解得，n＝90，故答案为：90．15.汽车刹车后行驶的距离s与行驶时间t（秒）的函数关系是s＝15t﹣6t2，汽车从刹车到停下来所用时间是 1.25 秒．【考点】AD：一元二次方程的应用．【分析】利用配方法求二次函数最值的方法解答即可．【解答】解：∵s＝15t﹣6t2＝﹣6（t﹣1.25）2+9.375，∴汽车从刹车到停下来所用时间是1.25秒．故答案为：1.25．16.如图，以点O为圆心的两个圆中，大圆的弦AB切小圆于点C，大圆的半径OA交小圆于点D，若OD＝3，tan∠OAB＝，则AB的长是12 ．【考点】M5：圆周角定理；MC：切线的性质；T7：解直角三角形．【专题】11：计算题；55A：与圆有关的位置关系；55E：解直角三角形及其应用；66：运算能力；67：推理能力．【分析】连接OC，由切线的性质知OC⊥AB，根据垂径定理得AB＝2AC，由tan∠OAB的值，易得OC：AC的值，进而可求出AC的长，而AB的长也可求出．【解答】解：连接OC，∵大圆的弦AB切小圆于点C，∴OC⊥AB，∴AB＝2AC，∵OD＝3，∴OC＝3，∵tan∠OAB＝＝，∴AC＝6，∴AB＝12．故答案为：12．17.科技改变生活，手机导航极大方便了人们的出行．如图，小明一家自驾到古镇C游玩，到达A地后，导航显示车辆应沿北偏西60°方向行驶6千米至B地，再沿北偏东45°方向行驶一段距离到达古镇C．小明发现古镇C恰好在A地的正北方向，则B、C两地的距离是3千米．【考点】TB：解直角三角形的应用﹣方向角问题．【专题】55E：解直角三角形及其应用．【分析】作BE⊥AC于E，根据正弦的定义求出BE，再根据正弦的定义计算即可．【解答】解：作BE⊥AC于E，在Rt△ABE中，sin∠BAC＝，∴BE＝AB•sin∠BAC＝6×＝3，由题意得，∠C＝45°，∴BC＝＝3÷＝3（千米），故答案为：3．18.如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，将△ABC绕点A逆时针旋转得到△AB′C′，点B、C的对应点分别为点B'、C′，AB′与BC相交于点D，当B′C′∥AB时，则CD＝．【考点】KQ：勾股定理；R2：旋转的性质．【专题】554：等腰三角形与直角三角形；558：平移、旋转与对称；67：推理能力．【分析】设CD＝x，由B′C′∥AB，可推得∠BAD＝∠B′，由旋转的性质得：∠B＝∠B′，于是得到∠BAD＝∠B，AC＝AC′＝4，AD＝BD＝8﹣x，由勾股定理可求解．【解答】解：设CD＝x，∵B′C′∥AB，∴∠BAD＝∠B′，由旋转的性质得：∠B＝∠B′，AC＝AC′＝6，∴∠BAD＝∠B，∴AD＝BD＝8﹣x，∴（8﹣x）2＝x2+62，∴x＝，∴CD＝，故答案为：．19.如图，CD是⊙O的直径，AB是⊙O的弦，CD⊥AB，垂足为E，连接BC、BD．点F为线段CB上一点，连接DF，若CE＝2，AB＝8，BF＝，则tan∠CDF＝．【考点】KQ：勾股定理；M2：垂径定理；M5：圆周角定理；T7：解直角三角形．【专题】559：圆的有关概念及性质；64：几何直观．【分析】连接OA，如图，设⊙O的半径为r，则OA＝r，OE＝r﹣2，利用垂径定理得到AE＝BE＝AB＝4，再利用勾股定理计算出BC＝2，42+（r﹣2）2＝r2，解得r＝5，则OE＝3，接着判断F点为BC的中点，作FH⊥CE于H，则FH＝BE＝2，HE＝CE＝1，然后利用正切的定义得到tan∠HDF的值．【解答】解：连接OA，如图，设⊙O的半径为r，则OA＝r，OE＝r﹣2，∵CD⊥AB，∴AE＝BE＝AB＝4，在Rt△BCE中，BC＝＝2，在Rt△OAE中，42+（r﹣2）2＝r2，解得r＝5，∴OE＝3，∵BF＝，∴F点为BC的中点，作FH⊥CE于H，如图，∴FH为△BCE的中位线，∴FH＝BE＝2，HE＝CE＝1，在Rt△DHF中，tan∠HDF＝＝＝．故答案为．20.如图，P是等边三角形ABC内一点，连接PA、PC，PA＝PC，∠APC＝90°，把线段AP绕点A逆时针旋转120°，得到线段AQ（点P与点Q为对应点），连接BQ交AP于点E．点D为BQ的中点，连接AD、PD，若S△DAP＝2，则AB＝4．【考点】KK：等边三角形的性质；KW：等腰直角三角形；R2：旋转的性质．【专题】558：平移、旋转与对称；69：应用意识．【分析】延长QA到M，使得AM＝AQ，连接BM，PM．首先证明△PAM是等边三角形，证明△MAB≌△PAC（SAS），推出∠AMB＝∠APC＝90°，由AQ＝AM，BD＝DQ，推出AD∥BM，BM ＝2AD，推出AD＝PA，再利用三角形的面积公式构建方方程求出PA即可解决问题．【解答】解：延长QA到M，使得AM＝AQ，连接BM，PM．∵△ABC是等边三角形，∴∠BAC＝60°，∵PA＝PC，∠APC＝90°，∴∠PAC＝∠PCA＝45°，∵∠PAQ＝120°，∴∠PAM＝180°﹣120°＝60°，∵AM＝AQ＝AP，∴△APM是等边三角形，∴∠MAP＝∠BAC＝60°，∴∠MAB＝∠PAC，∵AM＝AP，AB＝AC，∴△MAB≌△PAC（SAS），∴BM＝PC，∠AMB＝∠APC＝90°，∵AQ＝AM，BD＝DQ，∴AD∥BM，BM＝2AD，∴AD＝PA，∴∠QAD＝∠QMB＝90°，∴∠PAD＝∠MAD﹣∠MAP＝90°﹣60°＝30°，∵S△PAD＝2，∴•PA•AD•sin30°＝2，∴•PA•PA•＝2，∴PA＝4，∴AB＝AC＝PA＝4，故答案为4．三、解答题（其中21~22题各7分，23~24题各8分，25~27题各10分，共计60分)21.先化简，再求代数式（1﹣）÷的值，其中x＝2sin60°﹣tan45°．【考点】6D：分式的化简求值；T5：特殊角的三角函数值．【专题】513：分式；55E：解直角三角形及其应用．【分析】先算括号内的减法，把除法变成乘法，算乘法，求出x的值后代入，即可求出答案．【解答】解：（1﹣）÷＝•＝•＝，当x＝2sin60°﹣tan45°＝2×﹣1＝﹣1时，原式＝＝．22.如图，在每个小正方形的边长均为1的方格纸中，线段AB的端点均在小正方形的顶点上．（1）在图中画出以AB为底的等腰三角形ABC，点C在小正方形的顶点上，且△ABC的面积是7.5；（2）在（1）的条件下，在图中画出以AC为斜边的直角三角形ACE（AE＜EC），点E在小正方形的顶点上，且△ACE的面积是5，连接EB，并直接写出tan∠AEB的值．【考点】KJ：等腰三角形的判定与性质；KQ：勾股定理；KS：勾股定理的逆定理；N4：作图—应用与设计作图；T7：解直角三角形．【专题】13：作图题；64：几何直观．【分析】（1）直接利用网格结合等腰三角形的性质得出答案；（2）直接利用直角三角形的性质结合锐角三角函数关系得出答案．【解答】解：（1）如图所示：△ABC即为所求；（2）如图所示：△ACE即为所求，延长EA，交网格于点G，连接BG，tan∠AEB＝＝＝．23.某中学在艺术节期间向全校学生征集书画作品，美术王老师从全校随机抽取了四个班级记作A、B、C、D，对征集到的作品的数量进行了分析统计，制作了如下两幅不完整的统计图．（1）王老师抽查的四个班级共征集到作品多少件？（2）请把图2的条形统计图补充完整；（3）若全校参展作品中有五名同学获得一等奖，其中有三名男生、二名女生．现在要在其中抽两名同学去参加学校总结表彰座谈会，请用画树状图或列表的方法求恰好抽中一名男生一名女生的概率．【考点】V2：全面调查与抽样调查；VB：扇形统计图；VC：条形统计图；X6：列表法与树状图法．【专题】543：概率及其应用；69：应用意识．【分析】（1）用C班的人数除以该班的作品数得到调查的总作品数；（2）计算出B班的作品数，再补全条形统计图；（3）画树状图展示所有20种等可能的结果数，找出恰好抽中一名男生一名女生的结果数，然后根据概率公式计算．【解答】解：（1）5÷＝12，所以抽查的四个班级共征集到作品12件，B班级的作品数为12﹣2﹣5﹣2＝3（件），条形统计图补充为：（2）画树状图为：共有20种等可能的结果数，其中恰好抽中一名男生一名女生的结果数为12，所以恰好抽中一名男生一名女生的概率＝＝．24.在Rt△ABC中，∠ABC＝90°，∠BAC＝30°，将△ABC绕点A顺时针旋转60°，得到△AED，点B、C的对应点分别是E、D．F为AC的中点，连接BF、DF、BE，DF与EA相交于点G，BE与AC相交于点H．（1）如图1，求证：四边形BFDE为平行四边形；（2）如图2，连接CE，在不添加任何辅助线与字母的情况下，请直接写出所有与△AEC 全等的三角形．【考点】KB：全等三角形的判定；KP：直角三角形斜边上的中线；L7：平行四边形的判定与性质；R2：旋转的性质．【专题】553：图形的全等；554：等腰三角形与直角三角形；555：多边形与平行四边形；558：平移、旋转与对称；67：推理能力．【分析】（1）由直角三角形的性质可得BF＝BC，由旋转的性质可得∠BAE＝∠DAC＝60°，CA＝DA，DE＝BC，由“AAS”可证△AFD≌△CBA，可得DF＝AB＝BE，且BF＝DE，即可得四边形BFDE是平行四边形；（2）由“SAS”可证△BAC≌△EAC，△ACE≌△ADE，可求解．【解答】证明：（1）∵点F是边AC中点，∴BF＝AC，∵∠BAC＝30°，∴BC＝AC，∠ACB＝60°，∴BF＝BC，∵将△ABC绕点A顺时针旋转60°，得到△AED，∴∠BAE＝∠DAC＝60°，CA＝DA，DE＝BC，∴DE＝BF，△ACD和△BAE为等边三角形，∴BE＝AB＝AE，∵点F为△ACD的边AC的中点，∴DF⊥AC，∴∠DFA＝∠ABC＝90°，∠DAF＝∠C＝60°，AC＝AD，∴△AFD≌△CBA（AAS），∴DF＝AB，∴DF＝BE，且BF＝DE，∴四边形BFDE是平行四边形；（2）△ADE，△ABC，△ADF与△ACE全等；理由如下：∵∠BAE＝60°，∠BAC＝30°，∴∠BAC＝∠CAE＝30°，且AC＝AC，AB＝AE，∴△BAC≌△EAC（SAS），∵∠CAE＝∠DAE＝30°，AC＝AD，AE＝AE，∴△ACE≌△ADE（SAS），∵△AFD≌△CBA，∴△EAC≌△FDA．25.某超市有甲、乙两种商品，若买1件甲商品和2件乙商品，共需80元；若买2件甲商品和3件乙商品，共需135元．（1）求甲、乙两种商品每件售价分别是多少元；（2）甲商品每件的成本是20元，根据市场调查：若按（1）中求出的单价销售，该超市每天销售甲商品100件；若销售单价每上涨1元，甲商品每天的销售量就减少5件．写出甲商品每天的销售利润y（元）与销售单价（x）元之间的函数关系，并求每件售价为多少元时，甲商品每天的销售利润最大，最大利润是多少？【考点】9A：二元一次方程组的应用；HE：二次函数的应用．【专题】536：二次函数的应用；69：应用意识．【分析】（1）设甲、乙两种商品每件售价分别是a元，b元，根据题意列方程组即可得到结论；（2）由题意列出关于x，y的函数关系式；把函数关系式配方即可得到结果．【解答】解：（1）设甲、乙两种商品每件售价分别是a元，b元，由题意列方程组得：，解得：，答：甲、乙两种商品每件售价分别是30元和25元；（2）由题意得，y＝（x﹣20）[100﹣5（x﹣30）]＝﹣5x2+350x﹣5000，∵y＝﹣5x2+350x﹣5000＝﹣5（x﹣35）2+1125，∴当x＝35时，y最大＝1125，∴销售单价为35元时，甲商品每天的销售利润最大，最大利润是1125元．26.已知：△ABC是⊙O的内接三角形，AB为直径，AC＝BC，D、E是⊙O上两点，连接AD、DE、AE．（1）如图1，求证：∠AED﹣∠CAD＝45°；（2）如图2，若DE⊥AB于点H，过点D作DG⊥AC于点G，过点E作EK⊥AD于点K，交AC于点F，求证：AF＝2DG；（3）如图3，在（2）的条件下，连接DF、CD，若∠CDF＝∠GAD，DK＝3，求⊙O的半径．【考点】MR：圆的综合题．【专题】152：几何综合题；55C：与圆有关的计算；67：推理能力．【分析】（1）连接CO，CE，证∠B＝45°，可依次推出∠AED﹣∠CAD＝∠AED﹣∠CED＝∠AEC＝∠COA＝45°，即可写出结论；（2）连接CO并延长，交⊙O于点N，连接AN，过点E作EM⊥AC于M，证△ADG≌△EAM，△ADG≌△EFM，即可推出AF＝2DG；（3）证△FCD∽△DCA，推出△GFD为等腰直角三角形，设GF＝GD＝a，分别用含a的代数式表示DF，AF，FK，在Rt△FKD中，即可求出a的值，再利用△FCD∽△DCA，求出FC 的值，即可求得AC的值，进一步求出AB的值，即可求得半径．【解答】（1）证明：如图1，连接CO，CE，∵AB是直径，∴∠ACB＝90°，∵AC＝BC，∴∠B＝∠CAB＝45°，∴∠COA＝2∠B＝90°，∵，∴∠CAD＝∠CED，∴∠AED﹣∠CAD＝∠AED﹣∠CED＝∠AEC＝∠COA＝45°，即∠AED﹣∠CAD＝45°；（2）如图2，连接CO并延长，交⊙O于点N，连接AN，过点E作EM⊥AC于M，则∠CAN＝90°，∵AC＝BC，AO＝BO，∴CN⊥AB，∴AB垂直平分CN，∴AN＝AC，∴∠NAB＝∠CAB，∵AB垂直平分DE，∴AD＝AE，∴∠DAB＝∠EAB，∴∠NAB﹣∠EAB＝∠CAB﹣∠DAB，即∠GAD＝∠NAE，∵∠CAN＝∠CME＝90°，∴AN∥EB，∴∠NAE＝∠MEA，∴∠GAD＝∠MEA，又∵∠G＝∠AME＝90°，AD＝EA，∴△ADG≌△EAM（AAS），∴AG＝EM，AM＝DG，又∵∠MEF+∠MFE＝90°，∠MFE+∠GAD＝90°，∴∠MEF＝∠GAD，又∵∠G＝∠FME＝90°，∴△ADG≌△EFM（ASA），∴DG＝MF，∵DG＝AM，∴AF＝AM+MF＝2DG；（3）∵∠CDF＝∠GAD，∠FCD＝∠DCA，∴△FCD∽△DCA，∴∠CFD＝∠CDA＝∠CBA，∵AC＝BC，AB为直径，∴△ABC为等腰直角三角形，∴∠CFD＝∠CDA＝∠CBA＝45°，∴△GFD为等腰直角三角形，设GF＝GD＝a，则FD＝a，AF＝2a，∴＝＝，∵∠FAK＝∠DAG，∠AKF＝∠G＝90°，∴△AFK∽△ADG，∴＝＝，在Rt△AFK中，设FK＝x，则AK＝3x，∵FK2+AK2＝AF2，∴x2+（3x）2＝（2a）2，解得，x＝a（取正值），∴FK＝a，在Rt△FKD中，FK2+DK2＝FD2，∴（a）2+32＝（a）2，解得，a＝（取正值），∴GF＝GD＝，AF＝，∵△FCD∽△DCA，∴＝，∴CD2＝CA•FC，∵CD2＝CG2+GD2，∴CG2+GD2＝CA•FC，设FC＝n，则（﹣n）2+（）2＝（+n）n，解得，n＝，∴AC＝AF+CF＝+＝，∴AB＝AC＝，⊙O的半径为．27.在平面直角坐标系中，点O为坐标原点，抛物线y＝ax2+ax+a（a≠0）交x轴于点A和点B（点A在点B左边），交y轴于点C，连接AC，tan∠CAO＝3．（1）如图1，求抛物线的解析式；（2）如图2，D是第一象限的抛物线上一点，连接DB，将线段DB绕点D顺时针旋转90°，得到线段DE（点B与点E为对应点），点E恰好落在y轴上，求点D的坐标；（3）如图3，在（2）的条件下，过点D作x轴的垂线，垂足为H，点F在第二象限的抛物线上，连接DF交y轴于点G，连接GH，sin∠DGH＝，以DF为边作正方形DFMN，P 为FM上一点，连接PN，将△MPN沿PN翻折得到△TPN（点M与点T为对应点），连接DT 并延长与NP的延长线交于点K，连接FK，若FK＝，求cos∠KDN的值．【考点】HF：二次函数综合题．【专题】556：矩形菱形正方形；55E：解直角三角形及其应用；66：运算能力；67：推理能力．【分析】（1）通过抛物线y＝ax2+ax+a先求出点A的坐标，推出OA的长度，再由tan∠CAO＝3求出OC的长度，点C的坐标，代入原解析式即可求出结论；（2）如图2，过点D分别作x轴和y轴的垂线，垂足分别为W和Z，证△DZE≌△DWB，得到DZ＝DW，由此可知点D的横纵坐标相等，设出点D坐标，代入抛物线解析式即可求出点D坐标；（3）如图3，连接CD，分别过点C，H作F的垂线，垂足分别为Q，I，过点F作DC的垂线，交DC的延长线于点U，先求出点G坐标，求出直线DG解析式，再求出点F的坐标，即可求出正方形FMND的边长，再求出其对角线FN的长度，最后证点F，K，M，N，D共圆，推出∠KDN＝∠KFN，求出∠KFN的余弦值即可．【解答】解：（1）在抛物线y＝ax2+ax+a中，当y＝0时，x1＝﹣1，x2＝4，∴A（﹣1，0），B（4，0），∴OA＝1，∵tan∠CAO＝3，∴OC＝3OA＝3，∴C（0，3），∴a＝3，∴a＝2，∴抛物线的解析式为：y＝﹣x2+x+3；（2）如图2，过点D分别作x轴和y轴的垂线，垂足分别为W和Z，∵∠ZDW＝∠EDB＝90°，∴∠ZDE＝∠WDB，∵∠DZE＝∠DWB＝90°，DE＝DB，∴△DZE≌△DWB（AAS），∴DZ＝DW，设点D（k，﹣k2+k+3），∴k＝﹣k2+k+3，解得，k1＝﹣（舍去），k2＝3，∴D的坐标为（3，3）；（3）如图3，连接CD，分别过点C，H作F的垂线，垂足分别为Q，I，∵sin∠DGH＝，∴设HI＝4m，HG＝5m，则IG＝3m，由题意知，四边形OCDH是正方形，∴CD＝DH＝3，∵∠CDQ+∠IDH＝90°，∠IDH+∠DHI＝90°，∴∠CDQ＝∠DHI，又∵∠CQD＝∠DIH＝90°，∴△CQD≌△DIH（AAS），设DI＝n，则CQ＝DI＝n，DQ＝HI＝4m，∴IQ＝DQ﹣DI＝4m﹣n，∴GQ＝GI﹣IQ＝3m﹣（4m﹣n）＝n﹣m，∵∠GCQ+∠QCD＝90°，∠QCD+∠CDQ＝90°，∴∠GCQ＝∠CDQ，∴△GCQ∽△CDQ，∴＝，∴＝，∴n＝2m，∴CQ＝DI＝2m，∴IQ＝2m，∴tan∠CDG＝＝＝＝，∵CD＝3，∴CG＝，∴GO＝CO﹣CG＝，设直线DG的解析式为y＝kx+，将点D（3，3）代入，得，k＝，∴y DG＝x+，设点F（t，﹣t2+t+3），则﹣t2+t+3＝t+，解得，t1＝3（舍去），t2＝﹣，∴F（﹣，）过点F作DC的垂线，交DC的延长线于点U，则UF＝3﹣＝，DU＝3﹣（﹣）＝，∴在Rt△UFD中，DF＝＝＝，由翻折知，△NPM≌△NPT，∴∠MNP＝∠TNP，NM＝NT＝ND，∠TPN＝∠MPN，TP＝MP，又∵NS⊥KD，∴∠DNS＝∠TNS，DS＝TS，∴∠SNK＝∠TNP+∠TNS＝×90°＝45°，∴∠SKN＝45°，∵∠TPK＝180°﹣∠TPN，∠MPK＝180°﹣∠MPN，∴∠TPK＝∠MPK，又∵PK＝PK，∴△TPK≌△MPK（SAS），∴∠MKP＝∠TKP＝45°，∴∠DKM＝∠MKP+∠TKP＝90°，连接FN，DM，交点为R，再连接RK，则RK＝RF＝RD＝RN＝RM，则点F，D，N，M，K同在⊙R上，FN为直径，∴∠FKN＝90°，∠KDN＝∠KFN，∵FN＝FD＝×＝，∴在Rt△FKN中，∴cos∠KDN＝cos∠KFN＝＝＝．。

2022-2023学年九上数学期末模拟试卷注意事项:1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题(每小题3分,共30分)1．如图，EFO GHO ∆∆，若12,6,4FO HO GH ===，则EF 的长是（ ）A ．4B ．6C ．8D ．10 2．如图，抛物线2( +0)y ax bx c a =+≠的对称轴为直线2x =-，与x 轴的一个交点在()3,0-和(4,0)-之间，下列结论:①40a b -=;②0c <;③ 30a c -+>;④若123531,,,,,222y y y ⎛⎫⎛⎫⎛⎫--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭是该抛物线上的点，则123y y y <<;其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个3．用配方法解一元二次方程x 2﹣4x ﹣5＝0的过程中，配方正确的是（ ）A ．（x +2）2＝1B ．（x ﹣2）2＝1C ．（x +2）2＝9D ．（x ﹣2）2＝94．定义A*B ，B*C ，C*D ，D*B 分别对应图形①、②、③、④：那么下列图形中，可以表示A*D ，A*C 的分别是（）A ．（1），（2）B ．（2），（4）C ．（2），（3）D ．（1），（4）5．以半径为2的圆内接正三角形、正方形、正六边形的边心距为三边作三角形，则（ ）A ．不能构成三角形B ．这个三角形是等腰三角形C ．这个三角形是直角三角形D ．这个三角形是钝角三角形6．关于x 的一元二次方程x 2﹣（k+3）x+2k+2＝0的根的情况，下面判断正确的是（ ）A ．有两个相等的实数根B ．有两个不相等的实数根C ．有两个实数根D ．无实数根 7．方程x 2－4＝0的解是A ．x ＝2B ．x ＝－2C ．x ＝±2D ．x ＝±4 8．如图，在O 中，AB 是直径，点D 是O 上一点，点C 是弧AD 的中点，CE AB ⊥于点E ，过点D 的切线交EC 的延长线于点G ，连接AD ，分别交CE ，CB 于点PQ ．连接AC ，关于下列结论：①BAD ∠= ABC ∠；②GP GD =；③点P 是ACQ ∆的外心，其中正确结论是（ ）A ．①②B ．①③C ．②③D ．①②③9．如图，AB 是⊙O 的直径，CD 是⊙O 的弦，若∠BAD=48°，则∠DCA 的大小为（ ）A ．48B ．42C ．45D ．24 10．若反比例函数y ＝K x （k≠0）的图象经过（2，3），则k 的值为（ ） A ．5 B ．﹣5 C ．6 D ．﹣6二、填空题(每小题3分,共24分)11．如图，ABC ∆中，90BAC ︒∠=，4AB =，5AC =，D 是AC 上一个动点，以AD 为直径的⊙O 交BD 于E ，则线段CE 长的最小值是_________．12．已知反比例函数y ＝k x的图象经过点（3，﹣4），则k ＝_____． 13．已知二次函数()(3)y x a x =-++的图象经过点,M N ，,M N 的横坐标分别为,3b b +，点,M N 的位置随b 的变化而变化，若,M N 运动的路线与y 轴分别相交于点,A B ,且3b a m -=（m 为常数），则线段AB 的长度为_________.14．如图，在⊙O 内有折线DABC ，点B ，C 在⊙O 上，DA 过圆心O ，其中OA ＝8，AB ＝12，∠A ＝∠B ＝60°，则BC ＝_____．15．抛物线()2219y k x k =++-开口向下，且经过原点，则k =________． 16．我国南宋数学家杨辉曾提出这样一个问题：“直田积（矩形面积），八百六十四（平方步），只云阔（宽）不及长一十二步（宽比长少12步），问阔及长各几步．”如果设矩形田地的长为x 步，那么根据题意列出的方程为_____．17．若二次函数2y ax =的图象开口向下，则实数a 的值可能是___________（写出一个即可）18．抛物线()222y x =-+的顶点坐标是____________三、解答题(共66分)19．（10分）阅读以下材料，并按要求完成相应的任务.已知平面上两点A B 、，则所有符合0(PA k k PB=>且1)k ≠的点P 会组成一个圆.这个结论最先由古希腊数学家阿波罗尼斯发现，称阿氏圆.阿氏圆基本解法：构造三角形相似.（问题）如图1，在平面直角坐标中，在x 轴，y 轴上分别有点()(),0,0,C m D n ，点P 是平面内一动点，且OP r =，设OP k OD=，求PC kPD +的最小值.阿氏圆的关键解题步骤：第一步：如图1，在OD 上取点M ，使得::OM OP OP OD k ==；第二步：证明kPD PM =；第三步：连接CM ，此时CM 即为所求的最小值.下面是该题的解答过程(部分)：解：在OD 上取点M ，使得::OM OP OP OD k ==，又,POD MOP POM DOP ∠=∠∴.任务：()1将以上解答过程补充完整.()2如图2，在RtABC 中，90,4,3,ACB AC BC D ∠=︒==为ABC 内一动点，满足2CD =，利用()1中的结论，请直接写出23AD BD +的最小值.20．（6分）已知二次函数y=(x－1)2+n的部分点坐标如下表所示：（1）求该二次函数解析式；（2）完成上表，并在平面直角坐标系中画出函数图象21．（6分）已知点M(2，a)在反比例函数y＝kx（k≠0）的图象上，点M关于原点中心对称的点N在一次函数y＝﹣2x+8的图象上，求此反比例函数的解析式．22．（8分）如图1，在矩形ABCD中，AB＝6cm，BC＝8cm，如果点E由点B出发沿BC方向向点C匀速运动，同时点F由点D出发沿DA方向向点A匀速运动，它们的速度分别为每秒2cm和1cm，FQ⊥BC，分别交AC、BC于点P 和Q，设运动时间为t秒（0＜t＜4）．（1）连接EF，若运动时间t＝23秒时，求证：△EQF是等腰直角三角形；（2）连接EP，当△EPC的面积为3cm2时，求t的值；（3）在运动过程中，当t取何值时，△EPQ与△ADC相似．23．（8分）小李在景区销售一种旅游纪念品，已知每件进价为6元，当销售单价定为8元时，每天可以销售200件．市场调查反映：销售单价每提高1元，日销量将会减少10件，物价部门规定：销售单价不能超过12元，设该纪念品的销售单价为x（元），日销量为y（件），日销售利润为w（元）．（1）求y与x的函数关系式．（2）要使日销售利润为720元，销售单价应定为多少元？（3）求日销售利润w （元）与销售单价x （元）的函数关系式，当x 为何值时，日销售利润最大，并求出最大利润．24．（8分）如图1为放置在水平桌面l 上的台灯，底座的高AB 为5cm ，长度均为20cm 的连杆BC ，CD 与AB 始终在同一平面上．当150ABC ∠=︒，165BCD ∠=︒时，如图2，连杆端点D 离桌面l 的高度是多少？25．（10分）某商城销售一种进价为10元1件的饰品，经调查发现，该饰品的销售量y （件）与销售单价x （元）满足函数20100y x =-+，设销售这种饰品每天的利润为W （元）.（1）求W 与x 之间的函数表达式；（2）当销售单价定为多少元时，该商城获利最大？最大利润为多少？（3）在确保顾客得到优惠的前提下，该商城还要通过销售这种饰品每天获利750元，该商城应将销售单价定为多少？26．（10分）如图，在△ABC 中，点D 在边AB 上，DE∥BC，DF∥AC，DE 、DF 分别交边AC 、BC 于点E 、F ，且32AE EC =． （1）求BF FC的值； （2）联结EF ，设BC =a ，AC =b ，用含a 、b 的式子表示EF ．参考答案一、选择题(每小题3分,共30分)1、C【解析】根据相似三角形对应边成比例即可求解．【详解】∵△EFO ∽△GHO ∴1226=EF FO GH HO == ∴EF=2GH=8故选：C ．【点睛】本题考查了相似三角形的性质，找到对应边建立比例式是解题的关键．2、C【分析】根据抛物线的对称轴可判断①；由抛物线与x 轴的交点及抛物线的对称性可判断②；由x=-1时y ＞0可判断③；根据抛物线的开口向下且对称轴为直线x=-2知图象上离对称轴水平距离越小函数值越大，可判断④． 【详解】∵抛物线的对称轴为直线22b x a =-=-， ∴40a b -=，所以①正确；∵与x 轴的一个交点在（-3，0）和（-4，0）之间，∴由抛物线的对称性知，另一个交点在（-1，0）和（0，0）之间，∴抛物线与y 轴的交点在y 轴的负半轴，即c ＜0，故②正确；∵由②、①知，1x =-时y ＞0，且4b a =，即43a b c a a c a c -+=-+=-+＞0，所以③正确； ∵点152y ⎛⎫- ⎪⎝⎭，与点232y ⎛⎫- ⎪⎝⎭，关于对称轴直线2x =-对称，∴12y y =，∵抛物线的开口向下，且对称轴为直线2x =-，∴当2x >-，函数值随x 的增大而减少， ∵3122-<-， ∴23y y >，∴123y y y =>，故④错误；综上：①②③正确，共3个，故选：C ．【点睛】本题考查了二次函数与系数的关系：对于二次函数()20y ax bx c a =++≠，二次项系数a 决定抛物线的开口方向和大小；一次项系数b 和二次项系数a 共同决定对称轴的位置；常数项c 决定抛物线与y 轴交点；抛物线与x 轴交点个数由24b ac =-⊿决定．3、D【分析】先移项，再在方程两边都加上一次项系数一半的平方，即可得出答案．【详解】解：移项得：x 2﹣4x ＝5，配方得：2224(2)5(2)x x -+-=+-，（x ﹣2）2＝9，故选：D ．【点睛】本题考查的知识点是用配方法解一元二次方程，掌握用配方法解一元二次方程的步骤是解此题的关键．4、B【分析】先判断出算式中A 、B 、C 、D 表示的图形，然后再求解A*D ，A*C ．【详解】∵A*B ，B*C ，C*D ，D*B 分别对应图形①、②、③、④可得出A 对应竖线、B 对应大正方形、C 对应横线，D 对应小正方形∴A*D 为竖线和小正方形组合，即（2）A*C 为竖线和横线的组合，即（4）故选：B【点睛】本题考查归纳总结，解题关键是根据已知条件，得出A 、B 、C 、D 分别代表的图形．5、C【分析】由于内接正三角形、正方形、正六边形是特殊内角的多边形，可构造直角三角形分别求出边心距的长，由勾股定理逆定理可得该三角形是直角三角形，问题得解．【详解】解：如图1，∵OC ＝2，∴OD ＝2×sin30°＝1；如图2，∵OB＝2，∴OE＝2×sin45°＝2；如图3，∵OA＝2，∴OD＝2×cos303，则该三角形的三边分别为：123∵122）232，∴该三角形是直角三角形，故选：C．【点睛】本题主要考查多边形与圆，解答此题要明确：多边形的半径、边心距、中心角等概念，根据解直角三角形的知识解答是解题的关键．6、C【分析】判断一元二次方程根的判别式的大小即可得解.【详解】由题意可可知：△＝（﹣k﹣3）2﹣4（2k+2）＝k2﹣2k+1＝（k﹣1）2≥0，故选：C．【点睛】本题考查一元二次方程ax2+bx+c=0(a≠0)根的判别式：（1）当△=b2﹣4ac＞0时，方程有两个不相等的实数根；（2）当△=b2﹣4ac=0时，方程有有两个相等的实数根；（3）当△=b2﹣4ac＜0时，方程没有实数根.7、C【分析】方程变形为x1=4，再把方程两边直接开方得到x=±1．【详解】解：x1=4，∴x=±1．故选C．8、C【分析】由于AC与BD不一定相等，根据圆周角定理可知①错误；连接OD，利用切线的性质，可得出∠GPD＝∠GDP，利用等角对等边可得出GP＝GD，可知②正确；先由垂径定理得到A为CF的中点，再由C为AD的中点，得到=，根据等弧所对的圆周角相等可得出∠CAP＝∠ACP，利用等角对等边可得出AP＝CP，又AB为直径得到CD AF∠ACQ为直角，由等角的余角相等可得出∠PCQ＝∠PQC，得出CP＝PQ，即P为直角三角形ACQ斜边上的中点，即为直角三角形ACQ的外心，可知③正确；【详解】∵在⊙O中，AB是直径，点D是⊙O上一点，点C是弧AD的中点，∴AC＝CD≠BD，∴∠BAD≠∠ABC，故①错误；连接OD，则OD⊥GD，∠OAD＝∠ODA，∵∠ODA＋∠GDP＝90︒，∠EPA＋∠EAP＝∠EAP＋∠GPD＝90︒，∴∠GPD＝∠GDP；∴GP＝GD，故②正确；∵弦CF⊥AB于点E，∴A为CF的中点，即AF AC=，又∵C为AD的中点，∴AC CD=，∴CD AF=，∴∠CAP＝∠ACP，∴AP＝CP．∵AB为圆O的直径，∴∠ACQ＝90 ，∴∠PCQ＝∠PQC，∴PC＝PQ，∴AP＝PQ，即P为Rt△ACQ斜边AQ的中点，∴P为Rt△ACQ的外心，故③正确；故选C．【点睛】此题是圆的综合题，其中涉及到切线的性质，圆周角定理，垂径定理，圆心角、弧、弦的关系定理，相似三角形的判定与性质，以及三角形的外接圆与圆心，平行线的判定，熟练掌握性质及定理是解决本题的关键．9、B【详解】解：连接BD，∵AB是⊙O的直径，∴∠ADB=90°，∴∠ABD=90°−∠BAD=42°，∴∠DCA=∠ABD=42°故选B10、C【分析】反比例函数图象上的点（x，y）的横纵坐标的积是定值k，依据xy=k即可得出结论．【详解】解：∵反比例函数y＝Kx（k≠0）的图象经过（2，3），∴k＝2×3＝6，故选：C．【点睛】本题主要考查了反比例函数图象上点的坐标特征，熟练掌握是解题的关键.二、填空题(每小题3分,共24分)11、292-【分析】连接AE，可得∠AED=∠BEA=90°，从而知点E在以AB为直径的⊙Q上，继而知点Q、E、C三点共线时CE最小，根据勾股定理求得QC的长，即可得线段CE的最小值．【详解】解：如图，连接AE，则∠AED=∠BEA=90°(直径所对的圆周角等于90°)，∴点E在以AB为直径的⊙Q上，∵AB=4，∴QA=QB=2，当点Q、E、C三点共线时，QE+CE=CQ（最短），而QE长度不变为2，故此时CE最小，∵AC=5，2222=2529QC AQ AC∴=++=，∴292CE QC QE，292．【点睛】本题考查了圆周角定理和勾股定理的综合应用，解决本题的关键是确定E点运动的轨迹，从而把问题转化为圆外一点到圆上一点的最短距离问题．12、-1．【分析】直接把点（3，﹣4）代入反比例函数y＝kx，求出k的值即可．【详解】解：∵反比例函数y＝kx的图象经过点（3，﹣4），∴﹣4＝3k ，解得k ＝﹣1. 故答案为：﹣1．【点睛】本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．13、27【分析】先求得点M 和点N 的纵坐标，于是得到点M 和点N 运动的路线与字母b 的函数关系式，则点A 的坐标为(0，3m -) ，点B 的坐标为(0，273m --) ，于是可得到AB 的长度．【详解】∵()(3)y x a x =-++过点M 、N ，且3b a m -=即3a b m =-，∴()()33y x b m x =-+-+，∴()()33M y b b m b =-+-+，()()3333N y b b m b =--+-++，∵点A 在y 轴上，即0b =，把0b =代入()()33M y b b m b =-+-+，得：3y m =-，∴点A 的坐标为(0，3m -) ，∵点B 在y 轴上，即30b +=，∴3b =-，把3b =-代入()()3333N y b b m b =--+-++，得：273y m =--，∴点B 的坐标为(0，273m --) ，∴()327327AB m m =----=．故答案为：27．【点睛】本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求二次函数的解析式，正确理解题意、求得点A 和点B 的坐标是解题的关键．14、1【分析】作OE ⊥BC 于E ，连接OB ，根据∠A 、∠B 的度数易证得△ABD 是等边三角形，由此可求出OD 、BD 的长，设垂足为E ，在Rt △ODE 中，根据OD 的长及∠ODE 的度数易求得DE 的长，进而可求出BE 的长，由垂径定理知BC =2BE 即可得出答案．【详解】作OE⊥BC于E，连接OB．∵∠A＝∠B＝60°，∴∠ADB＝60°，∴△ADB为等边三角形，∴BD＝AD＝AB＝12，∵OA＝8，∴OD＝4，又∵∠ADB＝60°，∴DE＝12OD＝2，∴BE＝12﹣2＝10，由垂径定理得BC=2BE=1故答案为：1．【点睛】本题考查了圆中的弦长计算，熟练掌握垂径定理，作出辅助线构造直角三角形是解题的关键．15、3【解析】把原点（0，0）代入y=（k+1）x2+k2﹣9，可求k，再根据开口方向的要求检验．【详解】把原点（0，0）代入y=（k+1）x2+k2﹣9中，得：k2﹣9=0解得：k=±1．又因为开口向下，即k+1＜0，k＜﹣1，所以k=﹣1．故答案为：﹣1．【点睛】主要考查了二次函数图象上的点与二次函数解析式的关系．要求掌握二次函数图象的性质，并会利用性质得出系数之间的数量关系进行解题．16、x（x﹣12）＝1【分析】如果设矩形田地的长为x步，那么宽就应该是（x﹣12）步，根据面积为1，即可得出方程．【详解】解：设矩形田地的长为x步，那么宽就应该是（x﹣12）步．根据矩形面积＝长×宽，得：x（x﹣12）＝1．故答案为：x （x ﹣12）＝1．【点睛】本题考查一元二次方程的实际应用，读懂题意根据面积公式列出方程是解题的关键．17、-2（答案不唯一，只要是负数即可）【分析】根据二次函数2y ax =的图像和性质进行解答即可【详解】解：∵二次函数2y ax =的图象开口向下，∴a<0∴取a=-2故答案为：-2（答案不唯一，只要是负数即可）【点睛】本题考查了二次函数的图像和性质，熟练掌握相关知识是解题的关键，题目较简单18、(2,2)【分析】根据顶点式即可得到顶点坐标．【详解】解：∵()222y x =-+，∴抛物线的顶点坐标为（2，2），故答案为（2，2）.【点睛】本题主要考查二次函数的顶点坐标，掌握二次函数的顶点式y=a （x-h ）2+k 的顶点坐标为（h ，k ）是解题的关键．三、解答题(共66分)19、（1（2. 【分析】 ⑴ 将PC+kPD 转化成PC+MP ，当PC+kPD 最小，即PC+MP 最小，图中可以看出当C 、P 、M 共线最小，利用勾股定理求出即可；⑵ 根据上一问得出的结果，把图2的各个点与图1对应代入，C 对应O,D 对应P ，A 对应C ，B 对应M ，当D 在AB 上时23AD BD +为最小值，所以23AD BD + = =【详解】解()1:,MP PD k MP kPD =∴=∴，PC kPD PC MP ∴+=+，当PC kPD +取最小值时，PC MP +有最小值，即,,C P M 三点共线时有最小值，利用勾股定理得()2222222.CM OC OM m kr m k r =+=+=+ ()223AD BD +的最小值为4103， 提示：4AC m ==，2433CD kr ==， 23AD BD ∴+的最小值为224410433⎛⎫+= ⎪⎝⎭. 【点睛】此题主要考查了新定义的理解与应用，快速准确的掌握新定义并能举一反三是解题的关键.20、（1）y=（x-1）2+1；（2）填表见解析，图象见解析．【分析】（1）将（2，2）代入y=（x-1）2+n 求得n 的值即可得解；（2）再由函数解析式计算出表格内各项，然后再画出函数图象即可．【详解】（1）∵二次函数y=（x-1）2+n ，当x=2时，y=2，∴2=（2-1）2+n ，解得n=1，∴该二次函数的解析式为y=（x-1）2+1．（2）填表得x⋯⋯ -1 0 1 2 3 ⋯⋯ y ⋯⋯ 5 2 1 2 5 ⋯⋯ 画出函数图象如图：【点睛】本题考查了待定系数法求二次函数解析式，二次函数的图象与性质，二次函数图象上点的坐标特征，正确求出函数解析式是解题的关键．21、y＝﹣24 x【分析】由点M与点N关于原点中心对称，可表示出点N的坐标，代入一次函数的关系式，可求得a的值，确定点M的坐标，再代入反比例函数的关系式求出k的值即可．【详解】∵点M(2，a)，点M与点N关于原点中心对称，∴N(﹣2，﹣a)代入y=﹣2x+8得：﹣a=4+8，∴a=﹣12，∴M(2，﹣12)代入反比例函数y=kx得，k=﹣24，∴反比例函数的解析式为y=﹣24x．【点睛】本题考查了一次函数、反比例函数图象上点的坐标特征，把点的坐标代入相应的函数关系式是常用的方法．22、（1）详见解析；（2）2秒；（3）2秒或12857秒或12839秒．【分析】（1）由题意通过计算发现EQ＝FQ＝6，由此即可证明；（2）根据题意利用三角形的面积建立方程即可得出结论；（3）由题意分点E在Q的左侧以及点E在Q的右侧这两种情况，分别进行分析即可得出结论．【详解】解：（1）证明：若运动时间t＝23秒，则BE＝2×23＝43（cm），DF＝23（cm），∵四边形ABCD是矩形∴AD＝BC＝8（cm），AB＝DC＝6（cm），∠D＝∠BCD＝90°∵∠D＝∠FQC＝∠QCD＝90°，∴四边形CDFQ也是矩形，∴CQ＝DF，CD＝QF＝6（cm），∴EQ＝BC﹣BE﹣CQ＝8﹣43﹣23＝6（cm），∴EQ＝QF＝6（cm），又∵FQ⊥BC，∴△EQF是等腰直角三角形；（2）由（1）知，CE＝8﹣2t，CQ＝t，在Rt△ABC中，tan∠ACB＝ABBC＝34，在Rt△CPQ中，tan∠ACB＝PQCQ＝PQt＝34，∴PQ＝34t，∵△EPC的面积为3cm2，∴S△EPC＝12CE×PQ＝12×（8﹣2t）×34t＝3，∴t＝2秒，即t的值为2秒；（3）解：分两种情况：Ⅰ．如图1中，点E在Q的左侧．①∠PEQ=∠CAD时，△EQP∽△ADC，∵四边形ABCD是矩形，∴AD∥BC，∴∠CAD=∠ACB，∵△EQP∽△ADC，∴∠CAD=∠QEP，∴∠ACB=∠QEP，∴EQ=CQ，∴CE=2CQ，由（1）知，CQ=t，CE=8-2t，∴8-2t=2t，∴t=2秒；②∠PEQ=∠ACD时，△EPQ∽△CAD，∴PQ EQ AD CD =， ∵FQ ⊥BC ，∴FQ ∥AB ，∴△CPQ ∽△CAB ，∴PQ CQ AB BC =，即68PQ t =， 解得：34PQ t =， ∴348682t t t =--，解得：12857t =； Ⅱ．如图2中，点E 在Q 的右侧．∵0＜t ＜4，∴点E 不能与点C 重合，∴只存在△EPQ ∽△CAD ，可得PQ EQ AD CD =，即638348t t -=， 解得：12839t =； 综上所述，t 的值为2秒或12857秒或12839秒时，△EPQ 与△ADC 相似． 【点睛】 本题是相似形综合题，主要考查矩形的性质和判定，三角函数，相似三角形的判定和性质，用方程的思想解决问题是解本题的关键．23、（1）10280y x =-+；（2）10元；（3）x 为12时，日销售利润最大，最大利润960元【分析】（1）根据题意得到函数解析式；（2）根据题意列方程，解方程即可得到结论；（3）根据题意得到()()()26128010171210w x x x =--+=--+，根据二次函数的性质即可得到结论．【详解】解：（1）根据题意得，()20010810280y x x =--=-+，故y 与x 的函数关系式为10280y x =-+；（2）根据题意得，()()610280720x x --+=，解得：110x =，224x =（不合题意舍去），答：要使日销售利润为720元，销售单价应定为10元；（3）根据题意得，()()()261028010171210w x x x =--+=--+， 100-<，∴当17x <时，w 随x 的增大而增大，当12x =时，960w =最大，答：当x 为12时，日销售利润最大，最大利润960元．【点睛】此题考查了一元二次方程和二次函数的运用，利用总利润=单个利润×销售数量建立函数关系式，进一步利用性质的解决问题，解答时求出二次函数的解析式是关键．24、(1021035)cm ++【分析】作DF ⊥l 于F ，CP ⊥DF 于P ，BG ⊥DF 于G ，CH ⊥BG 于H ．判断四边形PCHG 是矩形， 求出DP ，CH ，再加上AB 即可求出DF ．【详解】解：如图，作DF l ⊥于F ，CP DF ⊥于P ，BG DF ⊥于G ，CH BG ⊥于H ．则四边形PCHG 是矩形，1509060CBH ∠=︒-︒=︒，90CHB ∠=︒，30BCH ∴∠=︒，165BCD ∠=︒，∴45DCP ∠=︒，sin 60103()CH BC cm ∴=︒=，sin 45102()DP CD cm =︒=，(1021035)()DF DP PG GF DP CH AB cm ∴=++=++=.∴连杆端点D 离桌面l 的高度是(1021035)cm .【点睛】本题考查解直角三角形的应用，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．25、（1）221201000=-+-W x x ；（2）销售单价为30时，该商城获利最大，最大利润为800元；（3）单价定为25元【分析】（1）利用利润=每件的利润×数量即可表示出W 与x 之间的函数表达式；（2）根据二次函数的性质即可求出最大值；（3）令750W =,求出x 值即可.【详解】解：（1）2(2100)(10)21201000W x x x x =-+-=-+-（2）由（1）知，22212010002(30)800W x x x =-+-=--+∵20-<，∴当30x =时，W 有最大值,最大值为800元即销售单价为30时，该商城获利最大，最大利润为800元.（3）令750W =，即221201000750x x -+-=解得25x =或35x =因为要确保顾客得到优惠所以35x =不符合题意，舍去所以在确保顾客得到优惠的前提下，该商城还要通过销售这种饰品每天获利750元，该商城应将销售单价定为25元【点睛】本题主要考查二次函数的实际应用，掌握二次函数的图象和性质是解题的关键. 26、 (1)见解析；（2）EF =25b ﹣35a ． 【解析】（1）由32AE EC = 得25EC AC =，由DE//BC 得25BD EC AB AC ==，再由DF//AC 即可得； （2）根据已知可得35CF a =- ，25EC b = ，从而即可得. 【详解】（1）∵32AE EC = ， ∴25EC AC =， ∵DE//BC ，∴25BD EC AB AC ==， 又∵DF//AC ，∴25BF BD BC AB == ； （2）∵25BF BC =，∴35FC BC =， ∵BC a =，CF 与BC 方向相反 ， ∴35CF a =- ，同理：25EC b=，又∵EF EC CF=+，∴2355 EF b a=-.。

道里九年级数学期末试题一、选择题(每题3分，共30分)1．抛物线y=（一2)2+3的顶点坐标是( )(A)(2，3) (B)(-2，3) (C)(2， -3) (D)( -2， -3) 2．下列图形是中心对称图形的是( )3．在Rt △ABC 中，∠C=900，sinA=53 ，则cosA 的值等于( ) (A) 53 (B) 54 (C) 43 (D)55 4．下列几何体中，俯视图是三角形的几何体是( )5．一个袋子里装有8个球，其中6个红球2个绿球，这些球除颜色外，形状、大小质 地等完全相同．搅匀后，在看不到球的条件下，随机从这个袋子中摸出一个是红 概率是( )(A)81 (B) 61 (C) 41 (D) 43 6．如图，E 是平行四边形ABCD 的边BA 延长线上的一点， CE 交AD 于点F ，下列各式中错误的是( ) (A)CF EF AB AE = (B) FC CF BE CD = (C) DF AF AB AE = (D) BCAF AB AE =7．若反比例函数y=xm-3=的图象位于第二、四象限，则m 的取值范围是( ) (A)m>0 (B)m<0 (C)m>3 (D)m<38．将二次函数y=2的图象先向下平移l 个单位，再向右平移3个单位，得到的图象与一次函数y=2+b 的图象有公共点，则实数b 的取值范围是( ) (A)b>8 (B)b>一8 (C)b ≥8 (D)b ≥8 9．如图，在Rt △ABC中，∠C=900，∠A=500,以BC 为 直径的⊙0交AB 于点D ，E 是⊙0上一点，且弧CE=弧CD ，连接0E ，过点E 作⊙0的切线交AC 的延长线于点F ， 则∠F 的度数为( )(A)900(B)1000(C)1100(D)120010．如图，正方形ABCD 的边长为3 cm ，点P 从点A 出发沿AB →BC →CD 以3 cm ／s 的速度向终点D 匀速运动，同时，点Q 从点A 出发沿AD 以 1 cm ／s 的速度向终点D 匀速运动，设P 点运动的时间为ts ，△APQ 的面积为S cm2，下列选项中能表示S 与t 之间函数关系的是( )二、填空题(每题3分，共30分)11．在平面直角坐标系中，点P(1，．2)关于原点的对称点的坐标是 . 12．若△ABC ∽△DEF,DE=2AB ，若△DEF 的面积为20，则△ABC 的面积为 . 13．若反比例函数y=x6的图象经过点A(m,3)，则m 的值是 . 14．一辆汽车行驶的距离S(单位：m)关于行驶时间t(单位：s)的函数解析式是S=9t+221t ，当t=10 s 时，则S= 米.15．如图，四边形ABCD 与四边形EFGH 位似，位似中心是点O ，若43 EA OE ，则BCFG= ． 16．如图，在Rt △ABC 中，∠ACB=900，AC=BC=2．将Rt△ABC 绕A 点逆时针旋转30。

2022-2023学年九上数学期末模拟试卷考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。

选择题必须用2B 铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题(每小题3分,共30分)1．如图，已知A （2，1），现将A 点绕原点O 逆时针旋转90°得到A1，则A1的坐标是（ ）A ．（﹣1，2）B ．（2，﹣1）C ．（1，﹣2）D ．（﹣2，1）2．已知⊙O 的直径为12cm ，如果圆心O 到一条直线的距离为7cm ，那么这条直线与这个圆的位置关系是（ ）A ．相离B ．相切C ．相交D ．相交或相切3．解方程2（5x-1）2=3(5x-1)的最适当的方法是 （ ）A ．直接开平方法．B ．配方法C ．公式法D ．分解因式法4．如图，,PA PB 分别与O 相切于,A B 点，C 为O 上一点，66P ∠=︒，则C ∠=（ ）A ．57︒B ．60︒C ．63︒D ．66︒5．如图，该几何体的主视图是( )A ．B ．C ．D ．6．二次函数223y x =+的顶点坐标为（ ）A ．()2,0B ．()2,3C ．()3,0D ．()0,37．已知二次函数y ＝ax 2＋bx ＋c(a≠0)的图象如图所示，当y ＞0时，x 的取值范围是( )A ．－1＜x ＜2B ．x ＞2C ．x ＜－1D ．x ＜－1或x ＞2 8．已知抛物线C 的解析式为2y ax bx c =++，则下列说法中错误的是（ ）A ．a 确定抛物线的开口方向与大小B ．若将抛物线C 沿y 轴平移，则a ，b 的值不变C ．若将抛物线C 沿x 轴平移，则a 的值不变D ．若将抛物线C 沿直线l ：2y x =+平移，则a 、b 、c 的值全变9．比较cos10°、cos20°、cos30°、cos40°大小，其中值最大的是（ ）A ．cos10°B ．cos20°C ．cos30°D ．cos40°10．⊙O 的半径为15cm ，AB ，CD 是⊙O 的两条弦，AB ∥CD ，AB=24cm ，CD=18cm ，则AB 和CD 之间的距离是（ ）A ．21cmB ．3cmC ．17cm 或7cmD ．21cm 或3cm二、填空题(每小题3分,共24分)11．用配方法解一元二次方程2430x x +-=，配方后的方程为2(2)x n +=，则n 的值为______.12．方程x （x ﹣2）﹣x+2＝0的正根为_____．13．如图，正方形ABCD 的边长为4，E 为BC 上的一点，BE=1，F 为AB 上的一点，AF=2，P 为AC 上的一个动点，则PF ＋PE 的最小值为______________14．若两个相似三角形对应角平分线的比是2:3，它们的周长之和为15cm ，则较小的三角形的周长为_________．15．光线从空气射入水中会发生折射现象，发生折射时，满足的折射定律如图①所示：折射率sin sin n αβ=（α代表入射角，β代表折射角）.小明为了观察光线的折射现象，设计了图②所示的实验；通过细管可以看见水底的物块，但从细管穿过的直铁丝，却碰不上物块，图③是实验的示意图，点A,C,B 在同一直线上，测得7,12,16BC cm BF cm DF cm ===，则光线从空射入水中的折射率n 等于________.16．如果△ABC ∽△DEF ，且△ABC 的三边长分别为4、5、6，△DEF 的最短边长为12，那么△DEF 的周长等于_____．17．不透明袋子中有2个红球和4个蓝球，这些球除颜色外无其他差别，从袋子中随机取出1个球是红球的概率是______________.18．2sin 456cos 603tan 60︒+︒-︒=__________．三、解答题(共66分)19．（10分）如图，D 是等边三角形ABC 内一点，将线段AD 绕点A 顺时针旋转60°，得到线段AE ，连接CD ，BE ． （1）求证：EB =DC ；（2）连接DE ，若∠BED=50°，求∠ADC 的度数．20．（6分）如图，直线11y k x b =+与双曲线22k y x=在第一象限内交于,A B 两点，已知()1,,,1)(2A m B ．（1）求2k 的值及直线AB 的解析式．（2）根据函数图象，直接写出不等式21y y >的解集．（3）设点是线段AB 上的一个动点，过点P 作PD x ⊥轴于点,D E 是y 轴上一点，当PED 的面积为98时，请直接写出此时点P 的坐标．21．（6分）如图，Rt ABC △中，90ABC ∠=︒，以AB 为直径作半圆O 交AC 与点D ，点E 为BC 的中点，连结DE .（1）求证：DE 是半圆O 的切线；（2）若30BAC ∠=︒，2DE =，求AD 的长.22．（8分）我市某校准备成立四个活动小组：A ．声乐，B ．体育，C ．舞蹈，D ．书画，为了解学生对四个活动小组的喜爱情况，随机选取该校部分学生进行调查，要求每名学生从中必须选择而且只能选择一个小组，根据调查结果绘制如下两幅不完整的统计图．请结合图中所给信息，解答下列问题：（1）本次抽样调查共抽查了 名学生，扇形统计图中的m 值是 ；（2）请补全条形统计图；（3）喜爱“书画”的学生中有两名男生和两名女生表现特别优秀，现从这4人中随机选取两人参加比赛，请用列表或画树状图的方法求出所选的两人恰好是一名男生和一名女生的概率．23．（8分）国庆期间电影《我和我的祖国》上映，在全国范围内掀起了观影狂潮．小王一行5人相约观影，由于票源紧张，只好选择3人去A 影院，余下2人去B 影院，已知A 影院的票价比B 影院的每张便宜5元，5张影票的总价格为310元．（1）求A 影院《我和我的祖国》的电影票为多少钱一张；（2）次日，A 影院《我和我的祖国》的票价与前一日保持不变，观影人数为4000人．B 影院为吸引客源将《我和我的祖国》票价调整为比A 影院的票价低a %但不低于50元，结果B 影院当天的观影人数比A 影院的观影人数多了2a %，经统计，当日A 、B 两个影院《我和我的祖国》的票房总收入为505200元，求a 的值．24．（8分）综合与实践在数学活动课上，老师出示了这样一个问题：如图1，在ABC 中，90ACB ∠=︒，6AC =，8BC =，点D 为BC 边上的任意一点．将C ∠沿过点D 的直线折叠，使点C 落在斜边AB 上的点E 处．问是否存在BDE 是直角三角形？若不存在，请说明理由；若存在，求出此时CD 的长度．探究展示：勤奋小组很快找到了点D 、E 的位置．如图2，作CAB ∠的角平分线交BC 于点D ，此时C ∠沿AD 所在的直线折叠，点E 恰好在AB 上，且90BED ∠=︒，所以BDE 是直角三角形．问题解决:（1）按勤奋小组的这种折叠方式，CD 的长度为 ．（2）创新小组看完勤奋小组的折叠方法后，发现还有另一种折叠方法，请在图3中画出来．（3）在（2）的条件下，求出CD 的长．25．（10分）在平面直角坐标系xOy 中，⊙O 的半径为r （r ＞0）．给出如下定义：若平面上一点P 到圆心O 的距离d ，满足1322r d r ≤≤，则称点P 为⊙O 的“随心点”．（1）当⊙O 的半径r =2时，A （3，0），B （0，4），C （32-，2），D （12，12-）中，⊙O 的“随心点”是 ； （2）若点E （4，3）是⊙O 的“随心点”，求⊙O 的半径r 的取值范围；（3）当⊙O 的半径r =2时，直线y=- x+b （b ≠0）与x 轴交于点M ，与y 轴交于点N ，若线段MN 上存在⊙O 的“随心点”，直接写出b 的取值范围 ．26．（10分）已知：二次函数22y x mx m =-+-，求证：无论m 为任何实数，该二次函数的图象与x 轴都在两个交点；参考答案一、选择题(每小题3分,共30分)1、A【解析】根据点（x，y）绕原点逆时针旋转90°得到的坐标为（-y，x）解答即可．【详解】已知A（2，1），现将A点绕原点O逆时针旋转90°得到A1，所以A1的坐标为（﹣1，2）.故选A.【点睛】本题考查的是旋转的性质，熟练掌握坐标的旋转是解题的关键.2、A【分析】这条直线与这个圆的位置关系只要比较圆心到直线的距离与半径的大小关系即可．【详解】∵⊙O的直径为12cm，∴⊙O的半径r为6cm，如果圆心O到一条直线的距离d为7cm，d>r，这条直线与这个圆的位置关系是相离．故选择：A．【点睛】本题考查直线与圆的位置关系问题，掌握点到直线的距离与半径的关系是关键．3、D【详解】解：方程可化为[2（5x-1）-3]（5x-1）=0，即（10x-5）（5x-1）=0，根据分析可知分解因式法最为合适．故选D．4、A【分析】连接OA，OB，根据切线的性质定理得到∠OAP=90°，∠OBP=90°，根据四边形的内角和等于360°求出∠AOB，最后根据圆周角定理解答．【详解】解：连接OA，OB，∵PA，PB分别与⊙O相切于A，B点，∴∠OAP=90°，∠OBP=90°，∴∠AOB=360°-90°-90°-66°=114°，由圆周角定理得，∠C=12∠AOB=57°，故选：A．【点睛】本题考查的是切线的性质、圆周角定理，掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半是解题的关键．5、D【解析】试题分析：根据主视图是从正面看到的图形，因此可知从正面看到一个长方形，但是还得包含看不到的一天线（虚线表示），因此第四个答案正确．故选D考点：三视图6、D【分析】已知二次函数y＝2x2＋3为抛物线的顶点式，根据顶点式的坐标特点直接写出顶点坐标．【详解】∵y＝2x2＋3＝2（x−0）2＋3，∴顶点坐标为（0，3）．故选：D．【点睛】本题考查了二次函数的性质：二次函数的图象为抛物线，则解析式为y＝a（x−k）2＋h的顶点坐标为（k，h），7、D【分析】根据已知图象可以得到图象与x轴的交点是（-1，0），（2，0），又y＞0时，图象在x轴的上方，由此可以求出x的取值范围．【详解】依题意得图象与x轴的交点是（-1，0），（2，0），当y＞0时，图象在x轴的上方，此时x ＜－1或x ＞2，∴x 的取值范围是x ＜－1或x ＞2，故选D ．【点睛】本题考查了二次函数与不等式，解答此题的关键是求出图象与x 轴的交点，然后由图象找出当y ＞0时，自变量x 的范围，注意数形结合思想的运用.8、D【分析】利用二次函数的性质对A 进行判断；利用二次函数图象平移的性质对B 、C 、D 进行判断．【详解】解：A 、a 确定抛物线的开口方向与大小，说法正确；B 、若将抛物线C 沿y 轴平移，则抛物线的对称轴不变，开口大小、开口方向不变，即a ，b 的值不变，说法正确； C 、若将抛物线C 沿x 轴平移，抛物线的开口大小、开口方向不变，即a 的值不变，说法正确；D 、若将抛物线C 沿直线l ：y ＝x ＋2平移，抛物线的开口大小、开口方向不变，即a 不变，b 、c 的值改变，说法错误； 故选：D ．【点睛】本题考查了二次函数图象与几何变换，由于抛物线平移后的形状不变，所以a 不变．9、A【解析】根据同名三角函数大小的比较方法比较即可．【详解】∵10203040︒<︒<︒<︒，∴10203040cos cos cos cos ︒>︒>︒>︒．故选：A ．【点睛】本题考查了同名三角函数大小的比较方法，熟记锐角的正弦、正切值随角度的增大而增大；锐角的余弦、余切值随角度的增大而减小．10、D【分析】作OE ⊥AB 于E ，交CD 于F ，连结OA 、OC ，如图，根据平行线的性质得OF ⊥CD ，再利用垂径定理得到AE=12AB=12cm ，CF=12CD=9cm ，接着根据勾股定理，在Rt △OAE 中计算出OE=9cm ，在Rt △OCF 中计算出OF=12cm ，然后分类讨论：当圆心O 在AB 与CD 之间时，EF=OF+OE ；当圆心O 不在AB 与CD 之间时，EF=OF-OE ．【详解】解：作OE ⊥AB 于E ，交CD 于F ，连结OA 、OC ，如图，∵AB ∥CD ，∴OF ⊥CD ，∴AE=BE=12AB=12cm ，CF=DF=12CD=9cm ， 在Rt △OAE 中，∵OA=15cm ，AE=12cm ，∴22OA AE -，在Rt △OCF 中，∵OC=15cm ，CF=9cm ，∴22OC m CF c -，当圆心O 在AB 与CD 之间时，EF=OF+OE=12+9=21cm （如图1）；当圆心O 不在AB 与CD 之间时，EF=OF-OE=12-9=3cm （如图2）；即AB 和CD 之间的距离为21cm 或3cm ．故选：D ．【点睛】本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理．学会运用分类讨论的思想解决数学问题．二、填空题(每小题3分,共24分)11、7【分析】根据配方法，先移项，然后两边同时加上4，即可求出n 的值.【详解】解：∵2430x x +-=，∴243x x +=，∴2447x x ++=，∴2(2)7x +=，∴7n =；故答案为：7.【点睛】本题考查了配方法解一元二次方程，解题的关键是熟练掌握配方法的步骤.12、x＝1或x＝2【分析】利用提取公因式法解方程即可得答案．【详解】∵x（x﹣2）﹣（x﹣2）＝0，∴（x﹣2）（x﹣1）＝0，∴x﹣2＝0或x﹣1＝0，解得：x＝2或x＝1，故答案为：x＝1或x＝2【点睛】本题考查解一元二次方程，一元二次方程的常用方法有：直接开平方法、配方法、公式法、因式分解法等，熟练掌握并灵活运用适当的方法是解题关键．13、17【详解】试题分析：∵正方形ABCD是轴对称图形，AC是一条对称轴∴点F关于AC的对称点在线段AD上，设为点G，连结EG与AC交于点P，则PF+PE的最小值为EG的长∵AB=4，AF=2，∴AG=AF=2∴EG=221417+=考点：轴对称图形14、6cm【分析】利用相似三角形的周长比等于相似比，根据它们的周长之和为15，即可得到结论．【详解】解：∵两个相似三角形的对应角平分线的比为2：3，∴它们的周长比为2：3，∵它们的周长之和为15cm，∴较小的三角形周长为15×223+=6（cm）．故答案为：6cm．【点睛】本题考查了相似三角形的性质，如果两个三角形相似，那么它们的对应角相等，对应边的比，对应高的比，对应中线的比，对应角平分线的比，对应周长的比都等于相似比；它们对应面积的比等于相似比的平方．15、4 3【分析】过D作GH⊥AB于点H，利用勾股定理求出BD和CD，再分别求出入射角∠PDG和折射角∠CDH的正弦值，根据公式可得到折射率.【详解】如图，过D作GH⊥AB于点H，在Rt△BDF中，BF=12cm，DF=16cm∴2222BF DF=1216++cm∵四边形BFDH为矩形，∴BH=DF=16cm，DH=BF=12cm又∵BC=7cm∴CH=BH-BC=9cm∴2222DH CH=129=15++cm∵入射角为∠PDG，sin∠PDG=sin∠BDH=BH164== BD205折射角为∠CDH，sin∠CDH=CH93== CD155∴折射率sin PDG454 ===sin CDH533η∠⨯∠故答案为：4 3 .【点睛】本题主要考查了勾股定理和求正弦值，解题的关键是找出图中的入射角与折射角，并计算出正弦值.16、1【分析】根据题意求出△ABC的周长，根据相似三角形的性质列式计算即可．【详解】解：设△DEF的周长别为x，△ABC的三边长分别为4、5、6，∴△ABC的周长＝4＋5＋6＝15，∵△ABC∽△DEF，∴415 12x＝，解得，x＝1，故答案为1．【点睛】本题考查的是相似三角形的性质，掌握相似三角形的周长比等于相似比是解题的关键．17、1 3【分析】直接利用概率公式求解．【详解】解：从袋子中随机取出1个球是红球的概率21 243=+=，故答案为：1 3【点睛】本题考查了概率公式：随机事件A的概率P（A）=事件A可能出现的结果数除以所有可能出现的结果数．18【分析】直接代入特殊角的三角函数值进行计算即可．【详解】2sin456cos6060︒+︒-︒12622=⨯+⨯33=-=．【点睛】本题考查了特殊角的三角函数值，熟记特殊角的三角函数值是解题的关键．三、解答题(共66分)19、（1）证明见解析；（2）110°【分析】（1）根据等边三角形的性质可得∠BAC＝60°，AB＝AC，由旋转的性质可得∠DAE＝60°，AE＝AD，利用SAS 即可证出EAB≌DAC△，从而证出结论；（2）根据等边三角形的判定定理可得EAD为等边三角形，从而得出∠AED=60°，由（1）中全等可得∠AEB＝∠ADC，求出∠AEB即可求出结论．【详解】解：（1）∵ABC 是等边三角形，∴∠BAC ＝60°，AB ＝AC ．∵线段AD 绕点A 顺时针旋转60°，得到线段AE ，∴∠DAE ＝60°，AE ＝AD ．∴∠BAD +∠EAB ＝∠BAD +∠DAC ．∴∠EAB ＝∠DAC ．在EAB 和DAC △中，∵AB AC EAB DAC AE AD =⎧⎪∠=∠⎨⎪=⎩，∴EAB ≌DAC △．∴EB ＝DC ．（2）如图，由（1）得∠DAE ＝60°，AE ＝AD ，∴EAD 为等边三角形．∴∠AED ＝60°，由（1）得EAB ≌DAC △，∴∠AEB ＝∠ADC ．∵∠BED ＝50°，∴∠AEB=∠AED+∠BED=110°，∴∠ADC=110°．【点睛】此题考查的是等边三角形的判定及性质、全等三角形的判定及性质和旋转的性质，掌握等边三角形的判定及性质、全等三角形的判定及性质和旋转的性质是解决此题的关键．20、（1）22k =，3y x =-+（2）解集为01x <<或2x >（3）33,22⎛⎫⎪⎝⎭ 【分析】（1）先把B （2，1）代入22k y x=，求出反比例函数解析式，进而求出点A 坐标，最后用待定系数法，即可得出直线AB 的解析式；（2）直接利用函数图象得出结论；（3）先设出点P 坐标，进而表示出△PED 的面积等于98，解之即可得出结论． 【详解】解：（1）：∵点()2,1B 在双曲线22k y x =上， ∴2212k =⨯=， ∴双曲线的解析式为22y x=. ∵()1,A m 在双曲线22y x =， ∴2m =，∴()1,2A .∵直线11:AB y k x b =+过()()1,22,1A B 、两点，∴11221k b k b +=⎧⎨+=⎩，解得113k b =-⎧⎨=⎩∴直线AB 的解析式为3y x =-+（2）根据函数图象，由不等式与函数图像的关系可得：双曲线在直线上方的部分对应的x 范围是：01x <<或2x >，∴不等式21y y >的解集为01x <<或2x >.（3）点P 的坐标为33,22⎛⎫ ⎪⎝⎭. 设点(),3Px x -+，且12x ≤≤， 则22113139()222228S PD OD x x x =⋅=-+=--+. ∵当98S =时， 解得1232x x ==， ∴此时点P 的坐标为33,22⎛⎫⎪⎝⎭. 【点睛】此题是反比例函数综合题，主要考查了一次函数和反比例函数的图象和性质，待定系数法，三角形的面积公式，求出直线AB 的解析式是解本题的关键．21、（1）见解析；（2）1.【分析】（1）连接OD ，OE ，BD ，证△OBE ≌△ODE （SSS ），得∠ODE=∠ABC=90°；（2）证△DEC 为等边三角形，得DC=DE=2.【详解】（1）证明：连接OD ，OE ，BD ，∵AB 为圆O 的直径，∴∠ADB=∠BDC=90°，在Rt △BDC 中，E 为斜边BC 的中点，∴DE=BE ，在△OBE 和△ODE 中，OB OD OE OE BE DE =⎧⎪=⎨⎪=⎩，∴△OBE ≌△ODE （SSS ），∴∠ODE=∠ABC=90°，则DE 为圆O 的切线；（2）在Rt △ABC 中，∠BAC=30°，∴BC= 12AC ， ∵BC=2DE=4，∴AC=8，又∵∠C=10°，DE=CE ，∴△DEC 为等边三角形，即DC=DE=2，则AD=AC-DC=1．【点睛】考核知识点：切线的判定和性质.22、 (1) 50，32；(2)见解析；（3）23【解析】（1）根据D 组的人数及占比即可求出本次抽样调查共抽查的人数，故可求出m 的值；（2）用调查总人数减去各组人数即可求出B 组人数，再补全条形统计图；（3）根据题意列出树状图，再根据概率公式即可求解.【详解】解：（1）1020%50÷=，所以本次抽样调查共抽查了50名学生， 16%32%50m ==，即32m =； 故答案为50，32；（2）B 组的人数为50-6-16-10=18（人），全条形统计图为：（3）画树状图为：共有12种等可能的结果数，其中所选的两人恰好是一名男生和一名女生的结果数为8，所以所选的两人恰好是一名男生和一名女生的概率82=123=． 【点睛】此题主要考查统计调查的应用，解题的关键是根据题意求出调查的样本容量.23、（1）A 影院《我和我的祖国》的电影票为60元一张；（2）a 的值为1．【分析】（1）设A 影院《我和我的祖国》的电影票为x 元一张，由5张影票的总价格为310得关于x 的一元一次方程，求解即可；（2）当日A 、B 两个影院《我和我的祖国》的票房总收入为505200元，得关于a 的方程，再设a%＝t ，得到关于t 的一元二次方程，解得t ，然后根据题意对t 的值作出取舍，最后得a 的值．【详解】解：（1）设A 影院《我和我的祖国》的电影票为x 元一张，由题意得：3x+2（x+5）＝310∴3x+2x ＝300∴x ＝60答：A影院《我和我的祖国》的电影票为60元一张；（2）由题意得：60×4000+60（1﹣a%）×4000（1+2a%）＝505200化简得：2400（1﹣a%）（1+2a%）＝2652设a%＝t，则方程可化为：2t2﹣t+0.105＝0解得：t1＝1%，t2＝35%∵当t1＝1%时，60×（1﹣1%）＝51＞50；当t2＝35%时，60×（1﹣35%）＝39＜50，故t1＝1%符合题意，t2＝35%不符合题意；∴当t1＝1%时，a＝1．答：a的值为1．【点睛】本题考查了一元一次方程和一元二次方程在实际问题中的应用，明确题意正确列式并对一元二次方程采用换元法求解，是解题的关键．24、（1）3；（2）见解析；（3）247 CD=【分析】（1）由勾股定理可求AB的长，由折叠的性质可得AC=AE=6，CD=DE，∠C=∠BED=90°，由勾股定理可求解；（2）如图所示，当DE∥AC，∠EDB=∠ACB=90°，即可得到答案；（3）由折叠的性质可得CF=EF，CD=DE，∠C=∠FED=90°，∠CDF=∠EDF=45°，可得DE=CD=CF=EF，通过证明△DEB∽△CAB，可得DE BDAC BC＝，即可求解．【详解】（1）∵∠ACB=90°，AC=6，BC=8，∴10AB==，由折叠的性质可得：△ACD≌△AED，∴AC=AE=6，CD=DE，∠C=∠BED=90°，∴BE=10-6=4，∵BD2=DE2+BE2，∴（8-CD）2=CD2+16，∴CD=3，故答案为：3；（2）如图3，当DE∥AC，△BDE是直角三角形，（3）∵DE ∥AC ，∴∠ACB=∠BDE=90°，由折叠的性质可得：△CDF ≌△EDF ，∴CF=EF ，CD=DE ，∠C=∠FED=90°，∠CDF=∠EDF=45°，∴EF=DE ，∴DE=CD=CF=EF ，∵DE ∥AC ，∴△DEB ∽△CAB ， ∴DE BD AC BC ＝， ∴886DE DE -＝， ∴DE=247， ∴247CD = 【点睛】此题考查几何变换综合题，全等三角形的性质，折叠的性质，相似三角形的判定和性质，勾股定理等知识，灵活运用这些性质进行推理是解题的关键．25、 (1) A,C ；（2）10103r ≤≤；(3) 1≤b≤32-32-1． 【分析】（1）根据已知条件求出d 的范围：1≤d ≤3，再将各点距离O 点的距离，进行判断是否在此范围内即可，满足条件的即为随心点；（2）根据点E （4，3）是⊙O 的“随心点”，可根据1322r d r ≤≤，求出d=5，再求出r 的范围即可； （3）如图a ∥b ∥c ∥d ，⊙O 的半径r=2，求出随心点范围13d ≤≤，再分情况点N 在y 轴正半轴时，当点N 在y 轴负半轴时，分情况讨论即可.【详解】(1) ∵⊙O 的半径r=2， ∴32r =3，12r =1 ∴1≤d ≤3∵A （3，0），∴OA=3，在范围内∴点A 是⊙O 的“随心点”∵B （0，4）∴OB=4，而4＞3，不在范围内∴B 是不是⊙O 的“随心点”，∵C （32-，2）， ∴OC=32，在范围内 ∴点C 是⊙O 的“随心点”， ∵D （12，12-）， ∴OD=12＜1，不在范围内 ∴点D 不是⊙O 的“随心点”，故答案为：A,C（2）∵点E （4，3）是⊙O 的“随心点”∴OE=5，即d=5若152r =， ∴r=10 若 352r =，103r = ∴10103r ≤≤ (3)∵如图a ∥b ∥c ∥d ，⊙O 的半径r=2，随心点范围1322r d r ≤≤ ∴13d ≤≤∵直线MN 的解析式为y=x+b ，∴OM=ON ，①点N 在y 轴正半轴时，当点M 是⊙O 的“随心点”，此时，点M （-1，0），将M （-1，0）代入直线MN 的解析式y=x+b 中，解得，b=1，即：b 的最小值为1，过点O 作OG ⊥M'N'于G ，当点G 是⊙O 的“随心点”时，此时OG=3，在Rt △ON'G 中，∠ON'G=45°，∴GO=3∴在Rt △GNN ’中，NN '=sin GO GN N '∠=3sin 45=b 的最大值为∴1≤b≤②当点N 在y 轴负半轴时，同①的方法得出--1．综上所述，b 的取值范围是：1≤b≤--1．【点睛】此题考查了一次函数的综合题，主要考查了新定义，点到原点的距离的确定，解（3）的关键是找出线段MN 上的点是圆O 的“随心点”的分界点，是一道中等难度的题目．26、见解析【分析】计算判别式，并且配方得到△=2(2)40m -+>，然后根据判别式的意义得到结论． 【详解】二次函数22y x mx m =-+-∵1a =，b m =-，2c m =-，∴24b ac =-⊿ 2()41(2)m m =--⨯⨯-2444m m =-++2(2)4m =-+，而2(2)40m -+>，∴>0∆，即m 为任何实数时， 方程220x mx m -+-=都有两个不等的实数根，∴二次函数的图象与x 轴都有两个交点．【点睛】本题考查了抛物线与x 轴的交点：把求二次函数2(y ax bx c a b c =++，，是常数，0a ≠)与x 轴的交点坐标问题转化为解关于x 的一元二次方程．。

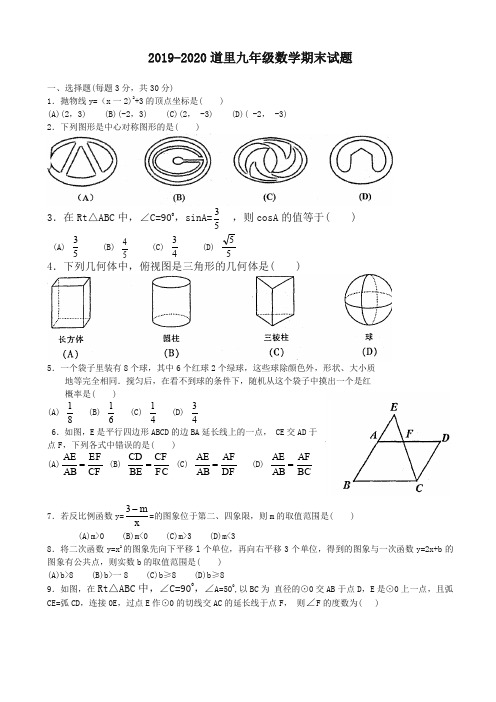
2019-2020道里九年级数学期末试题一、选择题(每题3分，共30分)1．抛物线y=（x 一2)2+3的顶点坐标是( )(A)(2，3) (B)(-2，3) (C)(2， -3) (D)( -2， -3) 2．下列图形是中心对称图形的是( )3．在Rt △ABC 中，∠C=900，sinA=53 ，则cosA 的值等于( ) (A) 53 (B) 54 (C) 43 (D)55 4．下列几何体中，俯视图是三角形的几何体是( )5．一个袋子里装有8个球，其中6个红球2个绿球，这些球除颜色外，形状、大小质 地等完全相同．搅匀后，在看不到球的条件下，随机从这个袋子中摸出一个是红 概率是( )(A)81 (B) 61 (C) 41 (D) 43 6．如图，E 是平行四边形ABCD 的边BA 延长线上的一点， CE 交AD 于点F ，下列各式中错误的是( ) (A)CF EF AB AE = (B) FC CF BE CD = (C) DF AF AB AE = (D) BCAFAB AE =7．若反比例函数y=xm-3=的图象位于第二、四象限，则m 的取值范围是( ) (A)m>0 (B)m<0 (C)m>3 (D)m<38．将二次函数y=x 2的图象先向下平移l 个单位，再向右平移3个单位，得到的图象与一次函数y=2x+b 的图象有公共点，则实数b 的取值范围是( ) (A)b>8 (B)b>一8 (C)b ≥8 (D)b ≥89．如图，在Rt △ABC中，∠C=900，∠A=500,以BC 为 直径的⊙0交AB 于点D ，E 是⊙0上一点，且弧CE=弧CD ，连接0E ，过点E 作⊙0的切线交AC 的延长线于点F ， 则∠F 的度数为( )(A)900(B)1000(C)1100 (D)120010．如图，正方形ABCD 的边长为3 cm ，点P 从点A 出发沿AB →BC →CD 以3 cm ／s 的速度向终点D 匀速运动，同时，点Q 从点A 出发沿AD 以 1 cm ／s 的速度向终点D 匀速运动，设P 点运动的时间为ts ，△APQ 的面积为S cm2，下列选项中能表示S 与t 之间函数关系的是( )二、填空题(每题3分，共30分)11．在平面直角坐标系中，点P(1，．2)关于原点的对称点的坐标是 . 12．若△ABC ∽△DEF,DE=2AB ，若△DEF 的面积为20，则△ABC 的面积为 . 13．若反比例函数y=x6-的图象经过点A(m,3)，则m 的值是 . 14．一辆汽车行驶的距离S(单位：m)关于行驶时间t(单位：s)的函数解析式是S=9t+221t ，当t=10 s 时，则S= 米.15．如图，四边形ABCD 与四边形EFGH 位似，位似中心是点O ，若43=EA OE ，则BCFG= ． 16．如图，在Rt △ABC 中，∠ACB=900，AC=BC=2．将Rt△ABC 绕A 点逆时针旋转30。

道里九年级数学期末试题一、选择题(每题3分，共30分)1．抛物线y=（一2)2+3的顶点坐标是( )(A)(2，3) (B)(-2，3) (C)(2， -3) (D)( -2， -3) 2．下列图形是中心对称图形的是( )3．在Rt △ABC 中，∠C=900，sinA=53 ，则cosA 的值等于( ) (A) 53 (B) 54 (C) 43 (D)55 4．下列几何体中，俯视图是三角形的几何体是( )5．一个袋子里装有8个球，其中6个红球2个绿球，这些球除颜色外，形状、大小质 地等完全相同．搅匀后，在看不到球的条件下，随机从这个袋子中摸出一个是红 概率是( )(A)81 (B) 61 (C) 41 (D) 43 6．如图，E 是平行四边形ABCD 的边BA 延长线上的一点， CE 交AD 于点F ，下列各式中错误的是( ) (A)CF EF AB AE = (B) FC CF BE CD = (C) DFAFAB AE = (D) BCAF AB AE =7．若反比例函数y=xm-3=的图象位于第二、四象限，则m 的取值范围是( ) (A)m>0 (B)m<0 (C)m>3 (D)m<38．将二次函数y=2的图象先向下平移l 个单位，再向右平移3个单位，得到的图象与一次函数y=2+b 的图象有公共点，则实数b 的取值范围是( ) (A)b>8 (B)b>一8 (C)b ≥8 (D)b ≥8 9．如图，在Rt △ABC中，∠C=900，∠A=500,以BC 为 直径的⊙0交AB 于点D ，E 是⊙0上一点，且弧CE=弧CD ，连接0E ，过点E 作⊙0的切线交AC 的延长线于点F ， 则∠F 的度数为( )(A)900(B)1000(C)1100(D)120010．如图，正方形ABCD 的边长为3 cm ，点P 从点A 出发沿AB →BC →CD 以3 cm ／s 的速度向终点D 匀速运动，同时，点Q 从点A 出发沿AD 以 1 cm ／s 的速度向终点D 匀速运动，设P 点运动的时间为ts ，△APQ 的面积为S cm2，下列选项中能表示S 与t 之间函数关系的是( )二、填空题(每题3分，共30分)11．在平面直角坐标系中，点P(1，．2)关于原点的对称点的坐标是 . 12．若△ABC ∽△DEF,DE=2AB ，若△DEF 的面积为20，则△ABC 的面积为 . 13．若反比例函数y=x6的图象经过点A(m,3)，则m 的值是 . 14．一辆汽车行驶的距离S(单位：m)关于行驶时间t(单位：s)的函数解析式是S=9t+221t ，当t=10 s 时，则S= 米.15．如图，四边形ABCD 与四边形EFGH 位似，位似中心是点O ，若43=EA OE ，则BCFG= ． 16．如图，在Rt △ABC 中，∠ACB=900，AC=BC=2．将Rt△ABC 绕A 点逆时针旋转30。

2020-2021学年黑龙江省哈尔滨市道里区九年级（上）期末数学试卷（五四学制）一.选择题（每题3分，共30分）1．（3分）（2020•海南）下列各点中，在反比例函数图象上的是 8y x =()A ．B ．C ．D ．(1,8)-(2,4)-(1,7)(2,4)2．（3分）（2020秋•道里区期末）下列图形中，既是中心对称图形又是轴对称图形的是 ()A ．B ．C ．D ．3．（3分）（2020秋•道里区期末）袋子中装有4个黑球、2个白球，这些球的形状、大小、质地完全相同，即除颜色外无其他差别．在看不到球的条件下，随机从袋中摸出1个球，是白球的概率是 ()A ．B ．C ．D ．131214234．（3分）（2020•安徽）下面四个几何体中，主视图为三角形的是 ()A ．B ．C ．D ．5．（3分）（2020秋•天长市期末）把函数图象向右平移1个单位长度，平移2(1)2y x =-+后图象的函数解析式为 ()A ．B ．C ．D ．22y x =+2(1)1y x =-+2(2)2y x =-+2(1)3y x =--6．（3分）（2020•温州）如图，在离铁塔150米的处，用测倾仪测得塔顶的仰角为，A α测倾仪高为1.5米，则铁塔的高为 AD BC ()A ．米B ．米(1.5150tan )α+150(1.5tan α+C ．米D ．米(1.5150sin )α+150(1.5)sin α+7．（3分）（2020•海南）如图，在中，，，，将Rt ABC ∆90C ∠=︒30ABC ∠=︒1AC cm =绕点逆时针旋转得到△，使点落在边上，连接，则的Rt ABC ∆A Rt AB C ''C 'AB BB 'BB '长度是 ()A ．B ．CD ．1cm 2cm 8．（3分）（2020秋•道里区期末）如图，为的外接圆，已知为，则O ABC ∆ABC ∠130︒的度数为 AOC ∠()A ．B ．C ．D ．50︒80︒100︒115︒9．（3分）（2020秋•道里区期末）如图，在中，点，，分别在，，ABC ∆D E F AB AC上，，，则下列式子一定正确的是 BC //DE BC //EF AB ()A ．B ．C ．D ．AD CE DB AE =CE CF AC BF =AB CE AC BD =DE AE CF EC=10．（3分）（2020秋•道里区期末）如图，抛物线与轴交于点，2(0)y ax bx c a =++≠x (4,0)其对称轴为直线，结合图象给出下列结论：1x =①；0abc <②；420a b c -+=③当时，随的增大而增大；1x >y x ④关于的一元二次方程有一个实数根．x 20ax bx c ++=其中正确的结论有 ()A ．1个B ．2个C ．3个D ．4个二.填空题（每题3分，共30分）11．（3分）（2020秋•道里区期末）在平面直角坐标系中，点关于原点对称的点的坐(3,2)标是 ．12．（3分）（2021•海安市模拟）抛物线的顶点坐标为 ．22(1)3y x =+-13．（3分）（2020秋•道里区期末）一辆汽车行驶的路程（单位：关于时间（单位：s )m t的函数解析式是，经过汽车行驶了 ．)s 2192s t t =+16s m 14．（3分）（2011•盘锦）反比例函数的图象经过点，则的值为 ．k y x=(2,3)-k 15．（3分）（2020•黑龙江）如图，是的外接圆的直径，若，则AD ABC ∆O 40BAD ∠=︒ ．ACB ∠=︒16．（3分）（2020秋•道里区期末）在中，，，，则ABC ∆90C ∠=︒3sin 4A =6BC =的长为 ．AC 17．（3分）（2020秋•道里区期末）若扇形的圆心角为，半径为6，则该扇形的弧长为 45︒．18．（3分）（2020秋•道里区期末）是的弦，，垂足为，连AB O OM AB ⊥M 接．若中有一个角是，，则弦的长为 ．OA AOM ∆30︒3OM =AB 19．（3分）（2020秋•道里区期末）同时掷两个质地均匀的骰子，则两个骰子的点数和是10的概率为 ．20．（3分）（2020秋•道里区期末）如图，的中线与高交于点，ABC ∆AD CE F ，，，则的长为 ．AE EF =2FD =24ACF S ∆=AB三、解答题（60分）21．（7分）（2020秋•道里区期末）先化简，再求代数式值，其中322(1)121x x x x x -+÷--+．3tan 30x =︒22．（7分）（2020秋•道里区期末）如图所示，在每个小正方形的边长均为1的网格中，线段的端点、均在小正方形的顶点上．AB A B （1）在图中画出等腰，点在小正方形顶点上；ABC ∆C（2）在（1）的条件下确定点后，再确定点，点在小正方形顶点上，请你连接，C D D DA ，，使，并直接写出四边形的面积为 ．DC DB 1tan 3ACD ∠=ADBC23．（8分）（2020秋•道里区期末）为了解疫情期间学生网络学习的学习效果，高远中学随机抽取了部分学生进行调查．要求每位学生从“优秀”，“良好”，“一般”，“不合格”四个等次中，选择一项作为自我评价网络学习的效果．现将调查结果绘制成如图两幅不完整的统计图，请结合图中所给的信息解答下列问题（1）这次活动共抽查学生多少名？（2）请通过计算补全条形统计图；（3）若高远中学共有1600名学生，估计该中学“优秀”等次的学生有多少名？24．（8分）（2020秋•道里区期末）如图，在中，，，点Rt ABC ∆90BAC ∠=︒AB AC =是边上一动点，连接，把绕点逆时针旋转，得到，连接，D BC AD AD A 90︒AE CE ．点是的中点，连接．DE F DE CF （1）求证：；CF AF =（2）在不添加任何辅助线的情况下，请直接写出图中所有的等腰直角三角形．25．（10分）（2020秋•道里区期末）某班班主任对在某次中取得优异成绩的同学进行表彰．她到商场购买了甲、乙两种笔记本作为奖品，若购买甲种笔记本15个，乙种笔记本20个，共花费250元；若购买甲种笔记本10个，乙种笔记本25个，共花费225元．（1）求购买一个甲种、一个乙种笔记本各需多少元？（2）班主任决定再次购买甲、乙两种笔记本共35个，如果班主任此次购买甲、乙两种笔记本的总费用不超过300元，求至多需要购买多少个甲种笔记本？26．（10分）（2020秋•道里区期末）内接于，，为的直径，ABC ∆O CA CB =BD O ．30DBC ∠=︒（1）如图1，求证：为等边三角形；ABC ∆（2）如图2，弦交于点，点在上，，求证：；AE BC F G EC BAF GAF ∠=∠FB FG =（3）如图3，在（2）的条件下，弦分别交，于，两点，BH AF AG P Q，，求的长．PO DH ==AC =QG27．（10分）（2020秋•道里区期末）在平面直角坐标系中，点为坐标原点，抛物线O 交轴负半轴于点，交轴正半轴于点，交轴于点，23y ax bx =+-x A x B y C ．32OB OC OA ==（1）如图1，求抛物线的解析式；（2）如图2，点在抛物线上，且点在第二象限，连接交轴于点，若D D BD yE ，求点的坐标；1tan 2EBA ∠=D （3）如图3，在（2）的条件下，点在抛物线上，且点在第三象限，点在上，P P F PB ，过点作轴的垂线，点为垂足，连接并延长交于点，若FC FB =F x G DG BF H ，求的长．DHP CEB ∠=∠BP2020-2021学年黑龙江省哈尔滨市道里区九年级（上）期末数学试卷（五四学制）答案与试题解析一.选择题（每题3分，共30分）1．（3分）（2020•海南）下列各点中，在反比例函数图象上的是 8y x =()A ．B ．C ．D ．(1,8)-(2,4)-(1,7)(2,4)解：、，该点不在函数图象上，故本选项错不合题意；A 1888-⨯=-≠ ∴、，该点不在函数图象上，故本选项不合题意；B 2488-⨯=-≠ ∴、，该点不在函数图象上，故本选项不合题意；C 1778⨯=≠ ∴、，该点在函数图象上，故本选项符合题意．D 248⨯=∴故选：．D 2．（3分）（2020秋•道里区期末）下列图形中，既是中心对称图形又是轴对称图形的是 ()A ．B ．C ．D ．解：、既不是轴对称图形，也不是中心对称图形，故本选项不合题意；A 、不是轴对称图形，是中心对称图形，故本选项不合题意；B 、是轴对称图形，不是中心对称图形，故本选项不合题意；C 、既是轴对称图形，又是中心对称图形，故本选项符合题意．D 故选：．D 3．（3分）（2020秋•道里区期末）袋子中装有4个黑球、2个白球，这些球的形状、大小、质地完全相同，即除颜色外无其他差别．在看不到球的条件下，随机从袋中摸出1个球，是白球的概率是 ()A ．B ．C ．D ．13121423解：袋子中装有4个黑球、2个白球，共有6个球，随机从袋中摸出1个球，是白球的概率是．∴2163=故选：．A 4．（3分）（2020•安徽）下面四个几何体中，主视图为三角形的是 ()A ．B ．C ．D ．解：、主视图是圆，故不符合题意；A A 、主视图是三角形，故符合题意；B B 、主视图是矩形，故不符合题意；C C 、主视图是正方形，故不符合题意；D D 故选：．B 5．（3分）（2020秋•天长市期末）把函数图象向右平移1个单位长度，平移2(1)2y x =-+后图象的函数解析式为 ()A ．B ．C ．D ．22y x =+2(1)1y x =-+2(2)2y x =-+2(1)3y x =--解：二次函数的图象的顶点坐标为，2(1)2y x =-+(1,2)向右平移1个单位长度后的函数图象的顶点坐标为，∴(2,2)所得的图象解析式为．∴2(2)2y x =-+故选：．C 6．（3分）（2020•温州）如图，在离铁塔150米的处，用测倾仪测得塔顶的仰角为，A α测倾仪高为1.5米，则铁塔的高为 AD BC ()A ．米B ．米(1.5150tan )α+150(1.5tan α+C ．米D ．米(1.5150sin )α+150(1.5)sin α+解：过点作，为垂足，如图所示：A AE BC ⊥E 则四边形为矩形，米，ADCE 150AE =米，1.5CE AD ∴==在中，，ABE ∆tan 150BE BE AE α== ，150tan BE α∴=（米，(1.5150tan )BC CE BE α∴=+=+)故选：．A7．（3分）（2020•海南）如图，在中，，，，将Rt ABC ∆90C ∠=︒30ABC ∠=︒1AC cm =绕点逆时针旋转得到△，使点落在边上，连接，则的Rt ABC ∆A Rt AB C ''C 'AB BB 'BB '长度是 ()A ．B ．CD ．1cm 2cm 解：在中，，，， Rt ABC ∆90C ∠=︒30ABC ∠=︒1AC cm =，则．12AC AB ∴=22AB AC cm ==又由旋转的性质知，，，12AC AC AB '==B C AB ''⊥是的中垂线，B C ∴''ABB ∆'．AB BB ∴'='根据旋转的性质知．2AB AB BB cm ='='=故选：．B 8．（3分）（2020秋•道里区期末）如图，为的外接圆，已知为，则O ABC ∆ABC ∠130︒的度数为 AOC ∠()A ．B ．C ．D ．50︒80︒100︒115︒解：作所对的圆周角，如图，AC ADC ∠，180ADC ABC ∠+∠=︒ 而，130ABC ∠=︒，18013050ADC ∴∠=︒-︒=︒．2100AOC ADC ∴∠=∠=︒故选：．C9．（3分）（2020秋•道里区期末）如图，在中，点，，分别在，，ABC ∆D E F AB AC 上，，，则下列式子一定正确的是 BC //DE BC //EF AB ()A ．B ．C ．D ．AD CE DB AE =CE CF AC BF =AB CE AC BD =DE AE CF EC =解：，//DE BC ，所以选项错误；∴AD AE DB CE=A ，//EF AB ，所以选项错误；∴CE CF AC BC =B ，//DE BC ，即，所以选项错误；∴AB AC BD CE =AB BD AC CE=C ，//DE BC ，AED C ∴∠=∠，//EF AB ，A CEF ∴∠=∠，ADE EFC ∴∆∆∽，所以选项正确．∴DE AE CF CE=D 故选：．D10．（3分）（2020秋•道里区期末）如图，抛物线与轴交于点，2(0)y ax bx c a =++≠x (4,0)其对称轴为直线，结合图象给出下列结论：1x =①；0abc <②；420a b c -+=③当时，随的增大而增大；1x >y x ④关于的一元二次方程有一个实数根．x 20ax bx c ++=其中正确的结论有 ()A ．1个B ．2个C ．3个D ．4个解：抛物线开口向上，则，对称轴，则．与轴交于负半轴，0a >12b x a=-=20b a =-<y 则，故，所以①错误；0c <0abc >抛物线对称轴为，与轴的一个交点为，则另一个交点为，于是有1x =x (4,0)(2,0)-，所以②正确；420a b c -+=时，随的增大而增大，所以③正确；1x >y x 抛物线与轴有两个不同交点，因此关于的一元二次方程有两个不相等的x x 20ax bx c ++=实数根，所以④错误；综上所述，正确的结论有：②③，故选：．B 二.填空题（每题3分，共30分）11．（3分）（2020秋•道里区期末）在平面直角坐标系中，点关于原点对称的点的坐(3,2)标是 ．(3,2)--解：点关于原点对称的点的坐标是，(3,2)(3,2)--故．(3,2)--12．（3分）（2021•海安市模拟）抛物线的顶点坐标为　．　．22(1)3y x =+-(1,3)--解：顶点坐标是．(1,3)--故．(1,3)--13．（3分）（2020秋•道里区期末）一辆汽车行驶的路程（单位：关于时间（单位：s )m t 的函数解析式是，经过汽车行驶了　272　．)s 2192s t t =+16s m 解：当时，，16t =21916162722s =⨯+⨯=经过汽车行驶了，∴16s 272m 故272．14．（3分）（2011•盘锦）反比例函数的图象经过点，则的值为 ．k y x =(2,3)-k 6-解：把代入函数中，得，解得．(2,3)-k y x =32k =-6k =-故．6-15．（3分）（2020•黑龙江）如图，是的外接圆的直径，若，则AD ABC ∆O 40BAD ∠=︒　50　．ACB ∠=︒解：连接，如图，BD 为的外接圆的直径，AD ABC ∆O ，90ABD ∴∠=︒，90904050D BAD ∴∠=︒-∠=︒-︒=︒．50ACB D ∴∠=∠=︒故答案为50．16．（3分）（2020秋•道里区期末）在中，，，，则ABC ∆90C ∠=︒3sin 4A =6BC =的长为　AC 解：，，3sin 4BC A AB== 6BC =，8AB ∴=BC ∴===，=故17．（3分）（2020秋•道里区期末）若扇形的圆心角为，半径为6，则该扇形的弧长为　45︒　．32π解：由题意，得该扇形的弧长，45631802ππ⨯==故．32π18．（3分）（2020秋•道里区期末）是的弦，，垂足为，连AB O OM AB ⊥M接．若中有一个角是，，则弦的长为　或OA AOM ∆30︒3OM =AB 解：，OM AB ⊥ ，AM BM ∴=若，30OAM ∠=︒则3tan OM OAM AM AM ∠===，AM ∴=2AB AM ∴==若，30AOM ∠=︒则tan 3AM AM AOM OM ∠===AM ∴=2AB AM ∴==故或．19．（3分）（2020秋•道里区期末）同时掷两个质地均匀的骰子，则两个骰子的点数和是10的概率为 ．112解：易得有种可能，两个骰子的点数和是10的有4，6；5，5；6，4共3种，所6636⨯=以概率是．11220．（3分）（2020秋•道里区期末）如图，的中线与高交于点，ABC ∆AD CE F ，，，则的长为　AE EF=2FD =24ACF S ∆=AB 解：延长至点，使，连接，AD M MD FD =MB 在和中，BDM ∆CDF ∆，BD CD BDM CDF DM FD =⎧⎪∠=∠⎨⎪=⎩．()BDM CDF SAS ∴∆≅∆，．MB CF ∴=M CFD ∠=∠，//EC BM ∴，是的高，EA EF = CE ABC ∆，45EAF EFA ∴∠=∠=︒，//EC BM ，90ABM AEF ∴∠=∠=︒，45M MAB ∴∠=∠=︒，AB MB ∴=，AB CF ∴=是的高，，CE ABC ∆24ACF S ∆=，即，∴1242CF AE ⋅=1242AB AE ⋅=作于，FN BM ⊥N 则四边形是矩形，是等腰直角三角形，EFNB FMN ∆2BE FN FD ∴=====AE AB ∴=-，∴11(2422AB AE AB AB ⋅=-=（负数舍去），AB ∴=故答案为三、解答题（60分）21．（7分）（2020秋•道里区期末）先化简，再求代数式值，其中322(1)121x x x x x -+÷--+．3tan 30x =︒解：原式212(1)(1)()11(1)x x x x x x x -+-=+÷---111(1)x x x x x +-=⋅-+，1x=当时，3tan 303x =︒==原式==22．（7分）（2020秋•道里区期末）如图所示，在每个小正方形的边长均为1的网格中，线段的端点、均在小正方形的顶点上．AB A B （1）在图中画出等腰，点在小正方形顶点上；ABC ∆C （2）在（1）的条件下确定点后，再确定点，点在小正方形顶点上，请你连接，C D D DA ，，使，并直接写出四边形的面积为　4　．DC DB 1tan 3ACD ∠=ADBC解：（1）如图，即为所求作．ABC ∆（2）如图，四边形即为所求作．ADBC ．111331311234222ADBC S =⨯-⨯⨯-⨯⨯-⨯⨯=四边形故答案为4．23．（8分）（2020秋•道里区期末）为了解疫情期间学生网络学习的学习效果，高远中学随机抽取了部分学生进行调查．要求每位学生从“优秀”，“良好”，“一般”，“不合格”四个等次中，选择一项作为自我评价网络学习的效果．现将调查结果绘制成如图两幅不完整的统计图，请结合图中所给的信息解答下列问题（1）这次活动共抽查学生多少名？（2）请通过计算补全条形统计图；（3）若高远中学共有1600名学生，估计该中学“优秀”等次的学生有多少名？解：（1）（名，8040%200÷=)答：这次活动共抽查学生200名；（2）（名，20080406020---=)补全条形统计图如图所示：（3）（名，401600320200⨯=)答：高远中学1600名学生中“优秀”等次的学生大约有320名．24．（8分）（2020秋•道里区期末）如图，在中，，，点Rt ABC ∆90BAC ∠=︒AB AC =是边上一动点，连接，把绕点逆时针旋转，得到，连接，D BC AD AD A 90︒AE CE ．点是的中点，连接．DE F DE CF （1）求证：；CF AF =（2）在不添加任何辅助线的情况下，请直接写出图中所有的等腰直角三角形．（1）证明：，90BAC DAE ∠=∠=︒ ，即．BAC CAD DAE CAD ∴∠-∠=∠-∠BAD CAE ∠=∠在与中，BAD ∆CAE ∆．AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩．()BAD CAE SAS ∴∆≅∆．ABD ACE ∴∠=∠，，AB AC = 90BAC ∠=︒．45ABC ACB ∴∠=∠=︒，45ABD ACE ∴∠=∠=︒．90DCE ACB ACE ∴∠=∠+∠=︒点是的中点，．F DE 90DAE DCE ∠=∠=︒，．12AF DE ∴=12CF DE =；CF AF ∴=（2）解：符合条件的等腰直角三角形有：，，，．ABC ∆ADE ∆ADF ∆AFE ∆理由如下：在中，，，则是等腰直角三角形．ABC ∆AB AC =90BAC ∠=︒ABC ∆在中，，，则是等腰直角三角形．ADE ∆AD AE =90DAE ∠=︒DEA ∆在等腰中，点是的中点，Rt ADE ∆ F DE ，，AD DE ∴⊥12AF DF EF DE ===，都是等腰直角三角形．ADF ∴∆AFE∆25．（10分）（2020秋•道里区期末）某班班主任对在某次中取得优异成绩的同学进行表彰．她到商场购买了甲、乙两种笔记本作为奖品，若购买甲种笔记本15个，乙种笔记本20个，共花费250元；若购买甲种笔记本10个，乙种笔记本25个，共花费225元．（1）求购买一个甲种、一个乙种笔记本各需多少元？（2）班主任决定再次购买甲、乙两种笔记本共35个，如果班主任此次购买甲、乙两种笔记本的总费用不超过300元，求至多需要购买多少个甲种笔记本？解：（1）设购买一个甲种笔记本需元，一个乙种笔记本需元，x y由题意可得：，15202501025225x y x y +=⎧⎨+=⎩解得：，105x y =⎧⎨=⎩答：购买一个甲种笔记本需10元，一个乙种笔记本需5元；（2）设需要购买个甲种笔记本，a 由题意可得：，105(35)300a a +- 解得：，25a 答：至多需要购买25个甲种笔记本．26．（10分）（2020秋•道里区期末）内接于，，为的直径，ABC ∆O CA CB =BD O ．30DBC ∠=︒（1）如图1，求证：为等边三角形；ABC ∆（2）如图2，弦交于点，点在上，，求证：；AE BC F G EC BAF GAF ∠=∠FB FG =（3）如图3，在（2）的条件下，弦分别交，于，两点，BH AF AG P Q，，求的长．PO DH ==AC =QG（1）证明：如图1，连接，CDBDO为的直径，．∴∠=︒90BCD，∠=︒30DBC．9060∴∠=︒-∠=︒BDC DBC．BAC BDC∴∠=∠=︒60，=CA CB为等边三角形；∴∆ABC（2）证明：如图2，为等边三角形，∆ABC．∴∠=∠ABC ACB，∠=∠E ABC．∴∠=∠ACB E，，∠=∠BAF BCE∠=∠BAF GAF．∴∠=∠GAF BCE．∴∠+∠=∠+∠ACB BCE E GAF，∠=∠+∠AGC E GAF．AGC ACG ∴∠=∠．AG AC ∴=为等边三角形，ABC ∆ ．AC AB ∴=．AB AG ∴=，，BAF GAF ∠= AE AF =．()BAF GAF SAS ∴∆≅∆；FB FG ∴=（3）解：如图3，过点作，点为垂足．O OL PH ⊥L点为圆心，O ，BL LH ∴=，BO OD = ．12OL DH ∴=，PO DH = ．12OL PO ∴=在中，．Rt POL ∆1sin 2OL OPL OP ∠==．30OPL ∴∠=︒连接，延长交于点，AH PO AH M 是等边三角形，ABC ∆ ．60ACB ∴∠=︒．60AHB ACB ∴∠=∠=︒．18090PMH AHB OPL ∴∠=︒-∠-∠=︒．OM AH ∴⊥．AM MH ∴=．PA PH ∴=．60AHP ∠=︒ 是等边三角形．AHP ∴∆连接，AD 为的直径，BD O ．90BAD ∴∠=︒是等边三角形，ABC ∆．AB AC ∴==．60ADB ACB ∠=∠=︒在直角内，，∴ABD ∆sin AB ADB BD∠=BD ==为的直径，BD O ．90BHD ∴∠=︒在直角中，，BDH ∆222BD BH DH =+．9BH ∴=，OL PH ⊥ ．92BL LH ∴==在直角中，．POL ∆1cos 2PL OPL PO ∠==．30OPL ∠=︒．32PL ∴==，．6PH ∴=3BP =是等边三角形，AHP ∆ ，．6AP PH ∴==60APH ∠=︒连接，BE ，，60BEA ACB ∠=∠=︒ 60BPE APH ∠=∠=︒．60PBE ∴∠=︒．PBE BPE BEA ∴∠=∠=∠是等边三角形．BPE ∴∆．3PE PB ∴==．9AE ∴=，60AEC ABC BPE ∠=∠=∠=︒ ．//PQ EG ∴．∴QG PE AG AE=AG AC ==QG ∴=27．（10分）（2020秋•道里区期末）在平面直角坐标系中，点为坐标原点，抛物线O 交轴负半轴于点，交轴正半轴于点，交轴于点，23y ax bx =+-x A x B y C ．32OB OC OA ==（1）如图1，求抛物线的解析式；（2）如图2，点在抛物线上，且点在第二象限，连接交轴于点，若D D BD y E ，求点的坐标；1tan 2EBA ∠=D （3）如图3，在（2）的条件下，点在抛物线上，且点在第三象限，点在上，P P F PB ，过点作轴的垂线，点为垂足，连接并延长交于点，若FC FB =F x G DG BF H ，求的长．DHP CEB ∠=∠BP解：（1）二次函数，23y ax bx =+-当时，，，∴0x =3y =(0,3)C -，3OC ∴=，，，32OB OC OA == 3OB =2OA =，，B ∴(3,0)(2,0)A -，∴93304230a b a b +-=⎧⎨--=⎩解得，1212a b ⎧=⎪⎪⎨⎪=-⎪⎩抛物线的解析式为；∴211322y x x =--（2）过点作轴的垂线，点为垂足，设点的横坐标为，则点的纵坐标为D x M D t D ，211322t t --点在第二象限，D ，211322DM t t ∴=--，，OM t =- 3OB =，3MB t ∴=-+在中，，Rt DMB ∆tan DM DBA MB∠=，1tan 2EBA ∠= ，，2DM MB ∴=2112(3)322t t t --=-+解得（舍去），，13t =23t =-点的纵坐标为，∴D 211(3)(3)3322⨯--⨯--=点的坐标为；∴D (3,3)-（3）连接，OF ，，，OB OC = FB FC =OF OF =，()OFB OFC SSS ∴∆≅∆；COF BOF ∴∠=∠过点作轴的垂线，点为垂足，F y T ，FG OB ⊥ ，FT FG ∴=，90BOT OTF FGO ∠=∠=∠=︒ 四边形为矩形；∴OTFG ，FT FG = 四边形为正方形；∴OTFG 取的中点，连接，过点作的垂线交的延长线于点，OM N DN G DN DN R 在中，，Rt OEB ∆1tan 2OE EBO OB ∠==；32OE ∴=，3OM = ，32MN ∴=；MN OE ∴=；3DM OB == ，90DMN EOB ∴∠=∠=︒，()OEB MND SAS ∴∆≅∆，DNM OEB ∴∠=∠，DHP CEB ∠=∠ ，DNM DHP ∴∠=∠，，，DNM DGN NDG ∠=∠+∠ DHP HGB GBF ∠=∠+∠DGN HGB ∠=∠；NDG GBF ∴∠=∠在中，，，，Rt OEB ∆32OE =3BO =222BE OB OE =+BE ∴=，DN ∴=在中，，，Rt DNM ∆tan 2DM DNM MN ∠==DNM GNR ∠=∠在中，，Rt GNR ∆tan 2GR GNR NR∠==；2RG RN ∴=在中，，Rt GNR ∆222NR RG NR +=，NR ∴=四边形为正方形， OTFG 设，，，∴OG GF m ==3BG m =-32NG m =+，，3()2NR m =+3()2RG m =+，NDG GBF ∠=∠ ，tan tan NDG GBF ∴∠=∠在中，Rt DGR ∆tan RG RDG DR ∠=在中，Rt GBF ∆tan FG GBF BG∠=，∴3m m =-解得（舍去），；13m =-21m =．1tan 2GBF ∴∠=过点作轴的垂线，点为垂足，P x W 设点的横坐标为，则点的纵坐标为，P n P 211322n n --点在第三象限，P ，211322PW n n ∴=-++在中，，Rt PWB ∆1tan 2PW PBW BW ∠==，2PW BW ∴=．OW n =- ，3BW n ∴=-+，2112(3)322n n n ∴-++=-+解得（舍去），，13n =21n =-，．4BW ∴=2PW =在中，，Rt PWB ∆222BP PW BW =+BP ∴=。

2021-2022学年黑龙江省哈尔滨市道里区九年级（上）期末数学试卷（五四学制）一、选择题（每题3分，共30分）1．﹣3的绝对值是（）A．﹣3B．3C．-13D．132．下列运算正确的是（）A．（﹣a）2＝﹣a2B．2a2﹣a2＝2C．a2•a＝a3D．（a﹣1）2＝a2﹣13．下列选项中的图形，是轴对称图形、不是中心对称图形的是（）A．B．C．D．4．如图是由4个相同的小正方体组成的几何体，则它的俯视图是（）A．B．C．D．5．把函数y＝（x﹣1）2+2图象向左平移1个单位长度，平移后图象的函数解析式为（）A．y＝x2+2B．y＝（x﹣1）2+1C．y＝（x﹣2）2+2D．y＝（x﹣1）2+36．方程13151x x=+-的解为（）A．x＝1B．x＝2C．x＝3D．x＝47．如图，AB是⊙O的直径，CD是弦，若⊙BCD=34°，则⊙ABD等于（）A．66°B．34°C．56°D．68°8．如图，在Rt⊙ABC中，⊙C＝90°，⊙ABC=30°，ACRt⊙ABC绕点A逆时针旋转得到Rt⊙AB'C'，连接BB'，则BB'的长度是（）A．1B．3CD．9．如图，在ABC中，点D，E，F分别在AB，AC，BC上，//DE BC，//EF AB，则下列式子一定正确的是（）A．AD CEDB AE=B．CE CFAC BF=C．AB CEAC BD=D．DE AECF EC=10．为了让更多的学生学会游泳，少年宫新建一个游泳池，其容积为480m2，打开进水口注水时，游泳池的蓄水量y（m3）与注水时间t（h）之间满足一次函数关系，其图像如图所示，下列说法错误的是（）A ．注水2小时，游泳池的蓄水量为380m 3B ．该游泳池内开始注水时已经蓄水100m 3C ．注水2小时，还需注水100m 3，可将游泳池注满D ．每小时可注水190m 3二、填空题（每题3分，共30分）11．将数13140000用科学记数法表示为 _____． 12．在函数y ＝134x -中，自变量x 的取值范围是 _____． 13．已知反比例函数(0)ky k x=≠的图象经过点(－2，5)，则k =________．14_____． 15．把多项式a 3﹣9ab 2分解因式的结果是 _____． 16．不等式组{2x −5<1x +3<7的解集是 _____．17．一枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，张兵同学掷一次骰子，骰子向上的一面出现的点数是3的倍数的概率是_____．18．点P 为⊙O 外一点，直线PO 与⊙O 的两个公共点为A ，B ，过点P 作⊙O 的切线，切点为C ，连接AC ，若⊙CPO ＝40°，则⊙CAB ＝_____度．19．一个扇形的弧长是9πcm ，圆心角是108度，则此扇形的半径是 _____cm ．20．如图，点E 在正方形ABCD 的边BC 上，BE ＝2CE ，点G 为垂足，若FG ＝2，则DG =_____．三、解答题（60分）21．先化简，再求代数式222211()2111a a aa a a a-+-÷-+--的值，其中a＝3tan30°+1．22．如图所示，在每个小正方形的边长均为1的网格中，线段AB的端点A、B均在小正方形的顶点上．(1)在图中画出等腰△ABC，且△ABC为钝角三角形，点C在小正方形顶点上；(2)在（1）的条件下确定点C后，再画出矩形BCDE，D，E都在小正方形顶点上，且矩形BCDE的周长为16，直接写出EA的长为．23．某校为了解学生对生物知识的掌握情况，从中随机抽取了部分学生的成绩作为样本，把成绩按优秀、良好、及格和不及格四个级别进行了统计，抽调的学生成绩为及格的占抽调学生总人数的30%．(1)求一共抽调多少名学生？(2)请通过计算补全条形统计图；(3)若该校共有学生2400名，请估计该校学生中有多少人的成绩为不及格？24．如图，点C，D在AB上，AC BD=，⊙A＝⊙B，AE＝BF．(1)如图1，求证：DE＝FC；(2)如图2，DE与CF交于点G，连接CE，DF，直接写出图中所有面积相等的三角形．25．某班班主任对在某次考试中取得优异成绩的同学进行表彰．到商场购买了甲、乙两种文具作为奖品，若购买甲种文具12个，乙种文具18个，共花费420元；若购买甲种文具16个，乙种文具14个，共花费460元；(1)求购买一个甲种、一个乙种文具各需多少元？(2)班主任决定购买甲、乙两种文具共30个，如果班主任此次购买甲、乙两种文具的总费用不超过500元，求至多需要购买多少个甲种文具？26．四边形ABCD为矩形，点A，B在⊙O上，连接OC、OD．(1)如图1，求证：OC＝OD；(2)如图2，点E在⊙O上，DE⊙OC，求证：DA平分⊙EDO；(3)如图3，在（2）的条件下，DE与⊙O相切，点G在弧BF上，弧FG＝弧AE，若BG＝，DF＝2，求AB的长．27．在平面直角坐标系中，点O为坐标原点，抛物线y＝ax2+bx﹣3交x轴负半轴于点A，交x轴正半轴于点B，交y轴于点C，点D（4，3）在抛物线上，连接AC，AD，tan⊙BAC＝32．(1)如图1，求抛物线的解析式；(2)如图2，点P在抛物线上，点P在第四象限，点P的横坐标为t，过点P作y轴的平行线交AD于点E，设线段PE的长为d，求d与t之间的函数关系式，不要求写出自变量t的取值范围；(3)如图3，在（2）的条件下，点F在OB上，AF=OB，PE交线段BF于点G，过点F作AE 的垂线，点H为垂足，点Q在射线FH上，连接QE，EF，EO，FP，若⊙AEO=⊙FEO，⊙QEF+⊙EAC=180°，求点P与点Q的距离．1．B【分析】根据负数的绝对值是它的相反数，可得出答案．【详解】根据绝对值的性质得：|-3|=3．故选B．【点睛】本题考查绝对值的性质，需要掌握非负数的绝对值是它本身，负数的绝对值是它的相反数．2．C【分析】根据乘方的意义，合并同类项，同底数幂的乘法，完全平方公式逐项分析即可．【详解】解：A.（﹣a）2＝a2，故不正确；B. 2a2﹣a2＝a2，故不正确；C. a2•a＝a3，正确；D.（a﹣1）2＝a2﹣2 a +1，故不正确；故选C．【点睛】本题考查了整式的运算，熟练掌握运算法则是解答本题的关键．同底数的幂相乘，底数不变，指数相加；合并同类项时，把同类项的系数相加，所得和作为合并后的系数，字母和字母的指数不变．完全平方公式是(a±b)2=a2±2ab+b2．3．C【分析】轴对称图形的定义：如果一个平面图形沿着一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形；中心对称图形：把一个图形绕着某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，据此逐项判断即可．【详解】解：A中图形既是轴对称图形，也是中心对称图形，不符合题意；B中图形既是轴对称图形，也是中心对称图形，不符合题意；C中图形是轴对称图形，不是中心对称图形，符合题意；D中图形既是轴对称图形，也是中心对称图形，不符合题意，故选：C．【点睛】本题考查轴对称图形和中心对称图形的判断，理解定义，找准对称轴和对称中心是解答的关键．4．B【分析】根据俯视图是从上面看到的图形解答即可．【详解】解：从上面看有2行，上面一行是横放2个正方形，右下角一个正方形．故选：B．【点睛】本题考查了三视图的知识，从正面看到的图是正视图，从上面看到的图形是俯视图，从左面看到的图形是左视图．5．A【分析】根据表达式y＝（x﹣1）2+2得到抛物线的顶点为（1，2），根据相应的平移得到新抛物线的顶点，利用平移不改变二次项的系数及顶点式可得新抛物线．【详解】解：⊙原抛物线的顶点为（1，2），⊙向左平移1个单位后，得到的顶点为（0，2），⊙平移后图象的函数解析式为y=x2+2．故选：A．【点睛】本题考查了二次函数图象与几何变换．由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．6．B【分析】先将分式方程化为整式方程，然后解整式方程即可求解．【详解】解：去分母，得：5x－1=3(x+1)，去括号，得：5x－1=3x+3，移项、合并同类项，得：2x=4，解得：x=2，经检验，x=2是原分式方程的解．故选：B．【点睛】本题考查解分式方程，熟练掌握分式方程的解法步骤是解答的关键，注意要检验根．7．C【分析】由题意根据AB为⊙O的直径，可以得出AB所对弧为半圆，可以得出⊙DCB+⊙ABD=90°，即可得出答案．【详解】解：⊙AB为⊙O的直径，⊙⊙ADB=90°，⊙⊙DAB+⊙ABD=90°，⊙⊙DAB=⊙BCD=34°，⊙⊙ABD=90°-34°=56°.故选：C．【点睛】本题主要考查圆周角定理的推论，根据已知可以得出⊙DCB+⊙ABD=90°是解决问题的关键．8．D【分析】先根据含30°角的直角三角形的性质求得⊙BAC=60°，AB⊙BAB'=⊙BAC=60°，AB=AB'，根据等边三角形的判定与性质证明⊙ABB'是等边三角形即可求解．【详解】解：⊙在Rt⊙ABC中，⊙C＝90°，⊙ABC=30°，AC⊙⊙BAC=90°－⊙ABC=60°，AB=2AC⊙将Rt ⊙ABC 绕点A 逆时针旋转得到Rt ⊙AB 'C '， ⊙⊙BAB '=⊙BAC =60°，AB =AB '， ⊙⊙ABB '是等边三角形， ⊙BB '=AB故选：D ． 【点睛】本题考查含30°角的直角三角形性质、旋转的性质、等边三角形的判定与性质，熟练掌握旋转的性质和等边三角形的判定是解答的关键． 9．D 【分析】根据平行线分线段成比例的性质判断选项的正确性． 【详解】 解：⊙//DE BC ， ⊙AD AEDB EC=，故A 错误， ⊙//EF AB ， ⊙CE CFAC BC=，故B 错误， ⊙//DE BC ， ⊙AB ACBD CE =，即AB BD AC CE=，故C 错误， ⊙//DE BC ，//EF AB ， ⊙四边形BDEF 是平行四边形， ⊙DE BF =， ⊙//EF AB ， ⊙BF AE CF EC=，即DE AECF EC =，故D 正确．故选：D ． 【点睛】本题考查平行线分线段成比例的性质，解题的关键是熟练运用这个性质得到线段的比例关系． 10．D 【分析】根据图象中的数据逐项判断即可解答．【详解】解：A 、由图可知，注水2小时，游泳池的蓄水量为380m 3，正确，故选项A 不符合题意；B 、由图象可知，当t =0时，y =100，即该游泳池内开始注水时已经蓄水100m 3，正确，故选项B 不符合题意；C 、由图象可知，480－380=100（m 3），即注水2小时，还需注水100m 3，可将游泳池注满，正确，故选项C 不符合题意，D 、由（380－100）÷2=140（m 3），即每小时可注水140m 3，故选项D 错误，符合题意； 故选：D ．【点睛】本题考查一次函数的应用，能从图象中获取有效信息是解答的关键．11．71.31410⨯【分析】用科学记数法表示较大的数时，一般形式为10n a ⨯，其中11|0|a ≤＜，n 为整数． 【详解】71.1313140400001=⨯．故答案为：71.31410⨯【点睛】本题考查了科学记数法，科学记数法的表示形式为10n a ⨯的形式，其中11|0|a ≤＜，n 为整数．确定n 的值时，要看把原来的数，变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值10≥时，n 是正数；当原数的绝对值1＜时，n 是负数，确定a 与n 的值是解题的关键．12．x ≠43【分析】根据分式分母不为0列出不等式，解不等式得到答案．【详解】解：由题意得：3x −4≠0，解得：x ≠43，故答案为：x ≠43． 【点睛】本题考查的是函数自变量的取值范围的确定，掌握分式分母不为0是解题的关键． 13．-10【详解】解：将（-2,5）代入函数解析式，可得52k =-，所以10k =- 14【详解】解：原式=15．a （a +3b ）（a -3b ）【分析】根据题意直接提取公因式a ，再利用平方差公式分解因式得出答案．【详解】解：a 3-9ab 2=a （a 2-9b 2）=a （a +3b ）（a -3b ）．故答案为：a （a +3b ）（a -3b ）．【点睛】本题主要考查提取公因式法以及公式法分解因式，正确运用平方差公式分解因式是解题的关键．16．x ＜3【分析】由题意分别求出每一个不等式的解集，进而根据口诀：同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集．【详解】解：解不等式2x -5＜1，得：x ＜3，解不等式x +3＜7，得：x ＜4，⊙不等式组的解集为x ＜3.故答案为：x＜3．【点睛】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．17．1 3【分析】共有6种等可能的结果数，其中点数是3的倍数有3和6，从而利用概率公式可求出向上的一面出现的点数是3的倍数的概率．【详解】解：掷一次骰子，向上的一面出现的点数是3的倍数的有3，6，故骰子向上的一面出现的点数是3的倍数的概率是：21=63．故答案为13．【点睛】本题考查了概率公式：随机事件A的概率P（A）=事件A可能出现的结果数除以所有可能出现的结果数．18．25或65【分析】由切线性质得出⊙OCP=90°，根据圆周角定理和等腰三角形的性质以及三角形的外角性质求得⊙CAB或⊙CBA的度数即可解答．【详解】解：如图1，连接OC，⊙PC是⊙O的切线，⊙OC⊙PC，即⊙OCP=90°，⊙⊙CPO=40°，⊙⊙POC =90°－40°=50°，⊙OA =OC ，⊙⊙CAB =⊙OCA ，⊙⊙POC =2⊙CAB ，⊙⊙CAB =25°，如图2，⊙CBA =25°，⊙AB 是⊙O 的直径，⊙⊙ACB =90°，⊙⊙CAB =90°－⊙CBA =65°，综上，⊙CAB =25°或65°．【点睛】本题考查圆周角定理、切线的性质、等腰三角形的性质、三角形的外角性质、直角三角形的两锐角互余，熟练掌握切线性质和等腰三角形的性质是解答的关键．19．15【分析】由题意直接根据弧长计算公式列方程求解即可．【详解】解：设扇形的半径为r cm ，由题意得，1089180r ππ=， 解得：r =15（cm ）.故答案为：15．【点睛】本题考查弧长的计算，熟练掌握弧长的计算方法是正确计算的前提．20．92【分析】先通过⊙ADF ⊙⊙BAE 求得AF =BE ，FD =AE ，再通过⊙AGF ⊙⊙ABE ，对应线段成比例求得AE 长度用x 的表达式，最后通过勾股定理建立等式，解出x 即可．【详解】在正方形ABCD 中：AD =AB =BC =CD⊙DAB =⊙B =⊙C =⊙ADC =90°⊙⊙1+⊙3=90°⊙DF ⊙AE⊙⊙DGE =⊙DAF =90°⊙⊙2+⊙3=90°又⊙1+⊙3=90°⊙⊙2=⊙1在⊙ADF 和⊙BAE 中2190AD ABDAB B ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩⊙⊙ADF ⊙⊙BAE （ASA ）⊙AF =BE⊙BE =2CE设CE =x ，则BE =2x ，BC =3x ，AF =2x ，BF =x⊙⊙1=⊙2，⊙AGF =⊙B =90°⊙⊙AGF ⊙⊙ABE ⊙=FG AF BE AE ⊙222x x AE= ⊙AE =2x ²在R t⊙ABE 中，AB ²+BE ²=AE ²⊙（3x ）²+（2x ）²=（2x ²）²⊙224944x x x +=⊙22134x x =⊙x ≠0⊙2134x =x ∴=x ∴= 132AE ∴=AF =在⊙AGF ⊙⊙ABE 中AF FG AE BE=2=⊙FG =2⊙DG =DF -GF =139222-= 【点睛】本题考查全等三角形的判定和性质，相似三角形的判定和性质，勾股定理的应用，掌握这些是本题关键．21．11a -【分析】先利用提公因式和公式法因式分解、分式的混合运算法则化简分式，再由特殊角的三角函数值求得a 值，代入化简式子中求解即可．【详解】 解：222211()2111a a a a a a a -+-÷-+-- =()()()()()2211211111a a a a a a a a ⎡⎤+----⨯⎢⎥+--⎢⎥⎣⎦=2(1)(1)(1)(1)a a a a a a +-⨯-+ =11a -，⊙a ＝1，⊙原式=． 【点睛】本题考查分式的化简求值、因式分解、完全平方公式、平方差公式、特殊角的三角函数值，熟练掌握分式的混合运算法则是解答的关键．22．(1)见解析(2)【分析】（1）作出腰为5且⊙ABC 是钝角的等腰三角形ABC 即可；（2）作出边长分别为5，3的矩形ABDE 即可．（1）解：如图，AB =BC ，⊙ABC>90°，所以⊙ABC 即为所求；（2）解：如图，矩形BCDE 即为所求．AE =．【点睛】本题考查作图-应用与设计作图，等腰三角形的判定，矩形的判定，勾股定理等知识，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型．23．(1)一共抽调100名学生；(2)见解析；(3)该校学生中有240人的成绩为不及格【分析】（1）根据及格人数和及格人数所占的百分比求解即可；（2）求出良好人数即可补全条形统计图；（3）由总人数乘以样本中不及格人数所占的比例即可求解．（1）解：30÷30%=100（名），答：一共抽调100名学生；（2）解：100－10－30－20=40（名），补全条形统计图如图所示：（3）解：2400×10100=240（人）， 答：该校学生中有240人的成绩为不及格【点睛】本题考查条形统计图、用样本估计总体，能正确从图中获取有效信息是解答的关键． 24．(1)见解析(2)面积相等的三角形有4对，分别为ACE BDF ，；AED BFC ，；ECG FDG ，；ECD FDC ，【分析】（1）由AC BD =可得AD BC =，进而根据SAS 即可证明AED BFC △≌△，从而证明DE ＝FC ；（2）根据题意找出4对全等三角形即可(1) 证明：AC BD =AC CD CD DB ∴+=+∴AD BC =在AED △与BFC △中AE BF A B AD BC =⎧⎪∠=∠⎨⎪=⎩∴AED BFC △≌△∴ DE ＝FC ；(2),,AC BD A B AE BF =∠=∠=ACE BDF ∴≌EC FD ∴=AED BFC ≌,ADE BCF ED FC ∴∠=∠=CG GD ∴=ED FC =EG GF ∴=ECG FDG ≌同理可得ECD FDC ≌∴面积相等的三角形有4对，分别为ACE BDF ，；AED BFC ，；ECG FDG ，；ECD FDC ，【点睛】本题考查了全等三角形的性质与判定，等角对等边，掌握全等三角形的性质与判定是解题的关键．25．(1)甲种文具需要20元，一个乙种文具需要10元(2)20【分析】（1）设购买一个甲种文具需要x元，一个乙种文具需要y元，然后根据若购买甲种文具12个，乙种文具18个，共花费420元；若购买甲种文具16个，乙种文具14个，共花费460元，列出方程组求解即可；（2）设需要购买m个甲种文具，则购买（30﹣m）个乙种文具，然后根据购买甲、乙两种文具的总费用不超过500元，列出不等式求解即可．(1)解：设购买一个甲种文具需要x元，一个乙种文具需要y元，依题意得：1218420 1614460x yx y+=⎧⎨+=⎩，解得：2010xy=⎧⎨=⎩，答：购买一个甲种文具需要20元，一个乙种文具需要10元．(2)解：设需要购买m个甲种文具，则购买（30﹣m）个乙种文具，依题意得：20m+10（30﹣m）≤500，解得：m≤20．答：至多需要购买20个甲种文具．【点睛】本题主要考查了二元一次方程组和一元一次不等式的实际应用，解题的关键在于能够准确理解题意列出式子求解．26．(1)见解析；(2)见解析；【分析】（1）连接OA、OB，则OA=OB，根据矩形的性质和等腰三角形的性质证得⊙DAO=⊙CBO，AD=BC，进而利用SAS证明⊙AOD⊙⊙BOC即可证得结论；（2）过O作OM⊙CD于M，则OM⊙AD，根据等腰三角形的三线合一性质证得⊙DOM =⊙COM =12⊙COD ，根据平行线的性质证得⊙ODA =⊙DOM =12⊙COD =12⊙EDO ，进而证得结论；（3）连接OB 、OG 、AG 、OE 、EF ，设EF 与AD 相交于H ，利用切线性质可得OE ⊙DE ，进而得到OC ⊙OE ，利用弦切角定理和角平分线定义得到⊙AHE =45°，根据平行线的性质证得⊙DAG =⊙AHE =45°，再利用圆周角定理和勾股定理求得圆的半径和DE 长，过D 作DN ⊙OC 于N ，利用矩形的判定与性质可得DN =OE =3，ON =DE =4，再利用勾股定理求得CD 即可求得AB 长．（1）证明：如图1，连接OA 、OB ，则OA =OB ，⊙⊙OAB =⊙OBA ，⊙四边形ABCD 是矩形，⊙⊙BAD =⊙ABC =⊙ADC =90°，AD =BC ，AB =CD ，⊙⊙DAO =⊙CBO ，在⊙AOD 和⊙BOC 中，OA OB DAO CBO AD BC =⎧⎪∠=∠⎨⎪=⎩，⊙⊙AOD ⊙⊙BOC （SAS ），⊙OC =OD ；（2）证明：过O 作OM ⊙CD 于M ，则⊙OMD =90°，⊙⊙ADC =⊙OMC =90°，⊙OM ⊙AD ，⊙OM ⊙CD ，OC =OD ，⊙⊙DOM =⊙COM =12⊙COD ，⊙OM ⊙AD ，DE ⊙OC ，⊙⊙COD =⊙EDO ，⊙DOM =⊙ODA ，⊙⊙ODA =12⊙EDO ，⊙DA 平分⊙EDO ；（3）解：连接OB 、OG 、AG 、OE 、EF ，设EF 与AD 相交于H ，⊙DE 与⊙O 相切，⊙OE ⊙DE ，又OC ⊙DE ，⊙OC ⊙OE ，⊙⊙EOD +⊙ODE =90°，即12⊙EOD +12⊙EDO =45°，由（2）结论知，⊙EDA =12⊙EDO ，⊙⊙DEF 为弦切角，⊙⊙DEF = 12⊙EOD ，⊙⊙AHE =⊙DEF +⊙EDA =45°，⊙弧FG ＝弧AE ，⊙EF ⊙AG ，⊙⊙DAG =⊙AHE =45°，又⊙BAD =90°，⊙⊙BAG =90°－⊙DAG =45°，⊙⊙BOG =2⊙BAG =90°，在Rt ⊙BOG 中，OB =OG ，BG ＝ 由勾股定理得：22232（）OB OG ，即2218OB ，⊙OB =3，⊙OE =OF =3，又DF ＝2，⊙OD =OF +DF =3+2=5，⊙DE =，过D 作DN ⊙OC 于N ，则四边形EOND 为矩形，⊙DN =OE =3，ON =DE =4，⊙OC =OD =5，⊙CN =OC －ON =5－4=1，在Rt ⊙CDN 中，CD = 22231CN = ，⊙AB =CD =【点睛】本题考查圆的综合知识，涉及矩形的判定与性质、角平分线的判定与性质、等腰三角形的性质、全等三角形的判定与性质、平行线的判定与性质、切线性质、弦切角定理、三角形外角性质、圆周角定理、勾股定理等知识，综合性强，熟练掌握相关知识的联系与运用，通过添加辅助线联系相关知识求解是解答的关键．27．(1)211322y x x =-- (2)2142d t t =-++(3)【分析】（1）根据题意先求出点C 的坐标，得到OC 的长度，然后结合tan ⊙BAC 的值求得OA 的长，进而得到点A 的坐标，最后将点A 和点D 的坐标代入函数解析式求得二次函数的解析式； （2）根据题意先求出直线AD 的解析式，然后用含有t 的式子表示点P 的坐标和点E 的坐标，最后求得线段PE 的长度，即可得d 与t 的函数关系式；（3）由题意先令y =0求得点B 的坐标，进而结合AF =OB 求得点F 的坐标，记直线AD 与y 轴的交点为点R ，通过直线AD 的解析式求得点R 的坐标，从而得到OK =OL ，过点O 作OK ⊙AD 于点K ，过点O 作OL ⊙EF ，交EF 的延长线于点L ，然后结合⊙AEO =⊙OEF 得到OK =OL ，从而得证⊙OKR ⊙⊙OLF ，进而得到⊙KRO =⊙LFO ，然后得到⊙EFG =⊙KRO ，即可得到tan ⊙EFG =tan ⊙KRO =AO OR=2，然后通过点E 的坐标表示出EG 和FG 的长，进而求得t 的值，得到点E 的坐标和点P 的坐标，记直线FQ 与y 轴的交点为点S ，然后通过证明⊙FGP ⊙⊙FOS 得到点S 的坐标，进而得到直线FQ 的解析式，然后可知点P 在直线FQ 上，即点P 、点F 、点Q 三点共线，过点Q 作QV ⊙x 轴于点V ，过点E 作EN ⊙QV 于点N ，通过⊙QEF +⊙EAC =180°得到⊙QEN =⊙ACO ，然后利用tan ⊙QEN =tan ⊙ACO =23AO OC =，设点Q 的坐标，然后表示出QN 和EN 的长度，进而求得点Q 的坐标，最后求得PQ 的长度．(1)解：当x =0时，y =-3，⊙点C （0，-3），⊙OC =3，⊙tan ⊙BAC =32OC OA =， ⊙OA =2，即A （-2，0），将点A 和点D 的坐标代入函数解析式，得423016433a b a b --=⎧⎨+-=⎩，解得：1212a b ⎧=⎪⎪⎨⎪=-⎪⎩， ⊙二次函数的解析式为：211322y x x =--． (2) 解：设直线AD 的解析式为y =kx +b ，则2043k b k b -+=⎧⎨+=⎩，解得：121k b ⎧=⎪⎨⎪=⎩， ⊙直线AD 的解析式为：112y x =+， ⊙点P 的横坐标为t ，过点P 作y 轴的平行线交AD 于点E ，⊙点P （211322t t t --，），点E （112t t +，），⊙2211111(3)42222d t t t t t =+---=-++. (3) 解：对211322y x x =--，令y =0，2113022x x --=， 解得：x =0，或x =3，⊙点B 的坐标为（3，0），即OB =3，⊙AF =OB ，⊙点F 的坐标为（1，0），如图3，记直线AD ：112y x =+与y 轴的交点为点R ，则x =0时，y =1，⊙点R 的坐标（0，1），即OR =1，过点O 作OK ⊙AD 于点K ，过点O 作OL ⊙EF ，交EF 的延长线于点L ，则⊙OKR =⊙OLF =90°， ⊙⊙AEO =⊙OEF ，⊙OK =OL ，在Rt ⊙OKR 和Rt ⊙OLF 中，OK OL OR OF=⎧⎨=⎩， ⊙Rt ⊙OKR ⊙Rt ⊙OLF （HL ），⊙⊙KRO =⊙LFO ，⊙⊙EFG =⊙KRO ，⊙tan ⊙EFG =tan ⊙KRO =AO OR=2，⊙EG FG=2，即EG =2FG ， 由（2）知，点P （211322t t t --，），点E （112t t +，）， 记PE 与x 轴的交点为点G ，则1112EG t FG t =+=-，， ⊙12t +1=2（t -1），解得：t =2，⊙E （2，2），P （2，-2），⊙FG =OF =1，PG =2，⊙tan ⊙PFG = PG FG =2， 记直线QF 与y 轴的交点为点S ，⊙HF ⊙AD ，⊙⊙HF A +⊙HAF =90°，又⊙⊙HAF +⊙ARO =90°，⊙⊙HF A =⊙ARO ，⊙tan ⊙HF A =tan ⊙ARO =21AO OR ==2， ⊙OS OF=2，⊙HF A =⊙PFG ， ⊙OS =2，⊙S （0，2），设直线QF 的解析式为y =mx +n ，则{n =2m +n =0，解得：22m n =-⎧⎨=⎩， ⊙直线QF 的解析式为y =-2x +2，过点Q 作QV ⊙x 轴于点V ，过点E 作EN ⊙QV 于点N ，则EN ⊙AB ，四边形ENVG 是矩形， ⊙⊙NEA =⊙EAG ，⊙NEG =90°，⊙⊙QEF +⊙EAC =180°，⊙⊙QEN +⊙NEA +⊙AEF +⊙EAG +⊙OAC =180°，又⊙⊙ARO =⊙EFG ，⊙AOR =⊙EGF =90°，⊙⊙EAG =⊙FEG ，⊙⊙QEN+⊙NEA+⊙AEF+⊙FEG+⊙OAC=180°，即⊙QEN+⊙NEG+⊙OAC=180°，⊙⊙QEN+⊙OAC=90°，又⊙⊙OAC+⊙OCA=90°，⊙⊙QEN=⊙ACO，⊙tan⊙QEN=tan⊙ACO=23 AOOC=，设点Q（a，-2a+2），则QN=-2a，EN=2-a，⊙2223 QN aEN a-=-＝，解得：a=-1，⊙点Q的坐标为（-1，4），⊙PQ=【点睛】本题考查二次函数的性质、角平分线的性质定理、解直角三角形、求一次函数的解析式、全等三角形的判定与性质、矩形的判定与性质，解题的关键是准确作出辅助线构造全等三角形和熟练应用解直角三角形求线段的长度．。