下载文档原格式
2013年崇武学区“广海杯”小学生知识竞赛理科试卷（满分75分，答卷时间75分钟）数学科试题（60分） 成绩__________一、填空题（每一处1分共18分）1、 2小时35分=( ) 分2、 O.4=( )÷25=36 ：( ) = ( )％= ( )成3、一个棱长1米的正方体可以切成( )个棱长是1分米的小正方体。
4、用8个同样大小的小正方体拼成一个大正方体，那么原来每个小正方体的）（）（表面积的表面积是这个大正方体 。
5、一本书有a 页，芳芳平均每天看16页，看了b 天，还剩下( )页没看。
()）个。
有（）中可以填写的自然数的（、 54 7 21 6〈〈7、在长为180厘米，宽为120厘米的纸板上，能裁出( )个半径为20厘米的圆；每个圆的面积约是( )平方厘米．. 60198））和（，原来是（倒数的和等于、已知互质的两个数的9、某月有五个星期三，但这个月的第一天和最后一天都不是星期三，这个月的1日是星期（ ）10、甲、乙两数的平均数是16，乙、丙两数的平均数是15，已知甲数正好是甲、乙、丙三数之和的41，甲数是( )，丙数是( )。
11、一根钢管长6米，把它锯成每段长60厘米需要53小时，如果锯成每段长100厘米的钢管需（ ）小时。
12、从运动场的一端到另一端全长100米，从一端起到另一端止每隔4米插一面小红旗。
现在要改成每隔5米插一面，有( )面小红旗不用移动。
二、选择题（每题1分，共6分）1、一种微型零件长0.5毫米，画在一幅图上长为5cm ，这幅图的比例尺是（ ）【A ．1:10 B.10:1 C.1:100 D.100:1】2、减数是被减数的73，差和减数的比是( )。
【A ．4:7 B ．4:3 C ．7:4】 3、圆锥的高缩小3倍,半径扩大3倍,则圆锥的体积( )。
【A. 扩大3倍;B. 缩小3倍;C.不变;D.扩大9倍】4、某商品原价为a 元，春节促销，降价20%，如果节后恢复到原价，则应将现售价提高（ ）A 、15%B 、20%C 、25%D 、30%5、小红早晨起床后，在家刷牙洗脸要用3分钟，用电饭锅浇早饭要用15分钟，读英语单词要用12分钟，吃早饭要用6分钟，她经过合理安排，起床后用( )分钟就能去上学。
2017年浙江高中数学竞赛一，填空题（每题8分，共80分）1. 在多项式()()610321x x x 的展开式+-的系数为______.2. 已知()5log35log172+=-a a ，则实数a=_________.3. 设()[]1,02在b ax x x f ++=中有两个实数根，则b a 22-的取值范围是___________.4. 设()1sin sin sin cos cos cos sin ,,222222=+-+-∈y x yx y x x x R y x 且，则=-y x _______. 5.已知两个命题，命题()()0log :>=x x x f p a 函数单调递增；命题函数:q ()012>++=ax x x g ()R x ∈,q p q p ∧∨为真命题，若为假命题，则实数a 的取值范围为____.6. 设S 是⎪⎭⎫ ⎝⎛850，中所有有理想的集合，对简分数()1,,=∈q p S pq，定义函数,1p q p q f +=⎪⎪⎭⎫ ⎝⎛则()32=x f 在S 中根的个数为___________.7. 已知动点P ,M,N 分别在x 轴上，圆()()12122=-+-y x 和圆()()34322=-+-y x 上，则PN PM +的最小值为__________.8. 已知棱长为1的正四面体P —ABC,PC 的中点为D,动点E 在线段AD 上，则直线与平面ABC 所成的角的取值范围为__________.9.已知平面向量0.10,321,,,=⋅<<===c b c b a ρρρρρ若λ()c b λλ---1所有取不到的值的集合为____________.10. 已知()()()0421212,0.1,0,2222=---+-+⎩⎨⎧≥-<-=x a x x f x x f x x x x x f 方程有三个根.321x x x <<若()12232x x x x -=-，则实数a=_______.二. 解答题11. （本题满分20分）设()()()，⋯=+=+=+,2,1,316,322121n x f x x f x x f n n 对每个n ，求()x x f n 3=的实数解。
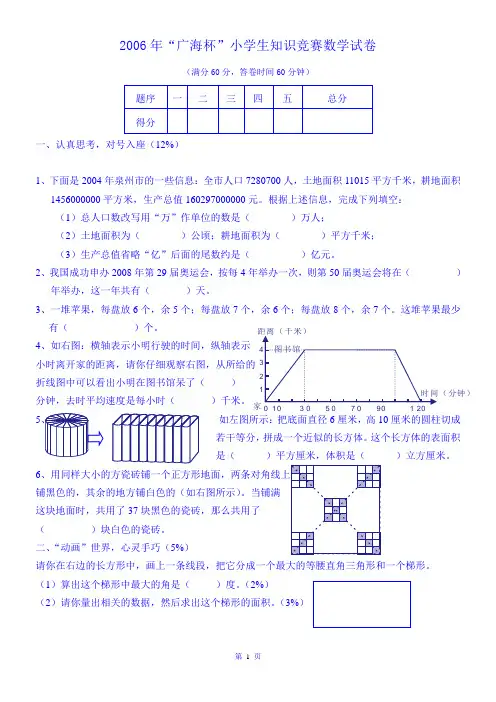
2006年“广海杯”小学生知识竞赛数学试卷（满分60分，答卷时间60分钟）题序 一 二 三 四 五 总分 得分一、认真思考，对号入座（12%）1、下面是2004年泉州市的一些信息：全市人口7280700人，土地面积11015平方千米，耕地面积1456000000平方米，生产总值160297000000元。
根据上述信息，完成下列填空： （1）总人口数改写用“万”作单位的数是（ ）万人；（2）土地面积为（ ）公顷；耕地面积为（ ）平方千米； （3）生产总值省略“亿”后面的尾数约是（ ）亿元。
2、我国成功申办2008年第29届奥运会，按每4年举办一次，则第50届奥运会将在（ ）年举办，这一年共有（ ）天。
3、一堆苹果，每盘放6个，余5个；每盘放7个，余6个；每盘放8个，余7个。
这堆苹果最少有（ ）个。
4、如右图：横轴表示小明行驶的时间，纵轴表示小时离开家的距离，请你仔细观察右图，从所给的 折线图中可以看出小明在图书馆呆了（ ）分钟，去时平均速度是每小时（ ）千米。
5、 如左图所示：把底面直径6厘米，高10厘米的圆柱切成若干等分，拼成一个近似的长方体。
这个长方体的表面积 是（ ）平方厘米，体积是（ ）立方厘米。
6、用同样大小的方瓷砖铺一个正方形地面，两条对角线上 铺黑色的，其余的地方铺白色的（如右图所示）。
当铺满 这块地面时，共用了37块黑色的瓷砖，那么共用了 （ ）块白色的瓷砖。
二、“动画”世界，心灵手巧（5%）请你在右边的长方形中，画上一条线段，把它分成一个最大的等腰直角三角形和一个梯形。
（1）算出这个梯形中最大的角是（ ）度。
（2%） （2）请你量出相关的数据，然后求出这个梯形的面积。
（3%）0 10 30 50 7090 1204321家图书馆距离（千米）时间（分钟）三、反复比较，慎重选择（5%）1、从上面观察这个几何体，看到的应该是第（）幅图的①②③④2、用2、3、4这三个数字任意摆一个三位数，这个三位数能被2整除的可能性是（）。
第3届“海都杯”数学竞赛五年级决赛试卷1、早晨4:20的时候，钟面上长针与短针所夹的锐角的角度是（）度。
2、已知2※3=2+3+4，5※2=5+6，2※5=2+3+4+5+6，则5※5=（）。
3、一个正方形的边长增加5厘米，它的面积就会增加225平方厘米，原来的正方形的面积是（）平方厘米。
4、一个正三角形的周长与一个正六边形的周长相等。
若此正三角形的面积为4，则这个正六边形的面积为（）。
5、某超市为庆祝元旦，准备将毛巾类商品做促销：儿童毛巾5元3条，大人毛巾4元1条。
明明的妈妈花了39元购买了15条毛巾。
那么他购买了（）条儿童毛巾和（）条大人毛巾。
6、有三个质数的和是50，则这三个质数的积最大是（）。
7、在一个纸盒中装有红色、绿色及黄色的弹珠。
已知盒子里的弹珠除了38颗之外都是红色的弹珠，除了33颗之外都是绿色的弹珠，除了35颗之外都是黄色的弹珠。
那么盒子中总共装有（）颗弹珠。
8、有A、B、C、D四个点从左向右依次排在一条直线上，以这四个点为端点，可以数出6条线段。
已知这6条线段的长度分别是12、18、30、32、44、62（单位：厘米），那么线段BC的长度是（）厘米。
9、如下图，甲、乙两图形都是正方形，它们的边长分别是20厘米和12厘米，则三角形AEG的面积为（）平方厘米。
10、通信班举行10分钟汉字输入大赛，全班平均成绩为每分钟120字，男生平均成绩比全班平均成绩少18字，女生平均成绩比男生平均成绩多27字，则这个班女生的人数是男生的（）倍。
11、一个整数，如果它的各位上的数字之和再加上它的各位数字之积，恰好等于这个数，我们就称这个数为“海都数”，例如39=3+9+3×9就是一个“海都数”。
两位数中这样的“海都数”一共有（）个。
12、依次写下整数1，2，3，4，…，998，999，则得到的整数123456789101112…998999，这个整数左起第2018位上的数字是（）。
13、在桌面上摆有一些大小一样的正方体木块，从正面看如下（图1），从右面看如下（图2），要摆出这样的图形至少需要（）块正方体木块。
2018年“广海杯”综合知识邀请赛数学试卷解析版
一、填空题：32%（每题2分）
1．（2分）4吨50千克＝ 4.05吨，1.05立方分米＝1050立方厘米．【解答】解：4吨50千克＝4.05吨
1.05立方分米＝1050立方厘米
故答案为：4.05；1050．
2．（2分）如果3A＝5B，那么A：B＝5：3
【解答】解：如果3A＝5B，那么A：B＝5：3．
故答案为：5、3．
3．（2分）已知A和B都是非零自然数，并且A+B＝60，A和B积的最大值是900，最小值是59．
【解答】解：（1）当两个因数都是30时积最大；
30×30＝900；
（2）当一个因数是1时积最小；
60﹣1＝59；
59×1＝59；
故答案为：900，59．
4．（2分）在比例尺1：600000的地图上，量得甲、乙两地之间的距离是15厘米，甲乙两地的实际距离是90千米．
【解答】解：15÷
1
600000
=15×600000＝9000000（厘米），
9000000厘米＝90千米，
答：甲乙两地的实际距离是90千米．故答案为：90．
5．（2分）将3
55
表示为小数形式，小数点后第2018位上的数是5．
【解答】解：3
55
=3÷55＝0.05454…
循环节是2位数，
（2018﹣1）÷2＝1008 (1)
第1 页共12 页。
2012年“广海杯”小学生知识竞赛理科试卷（满分75分，答卷时间70分钟）数学科试题（60分）一、填空。
（每题2分，共12分）1．a＝2×3×m，b＝3×7×m（m是自然数且m≠0），如果a和b的最大公约数是27，则m是（），a和b的最小公倍数是（）。
2．学校编码时，最后一位数字表示性别，1是男生，2是女生。
小红今年读三（2）班，她是2009年入学的，学号是36号，她的编码是200903362，小刚今年读五（1）班，学号是15号，他的编码是（）。
3．数手指：伸出你的左手，按下面的顺序数：拇指1、食指2、中指3、无名指4、小指5、无名指6、中指7、食指8、拇指9、食指10……这样的顺序数，2012这个数是（）指。
4．学校体育馆买排球12个，篮球9个，共用去756元，后来又买了同样的排球7个，篮球3个共用去351元，那么排球的单价是（）元，篮球的单价是（）元。
5．淘气和笑笑同时从学校出发步行到西湖公园，淘气每分钟走65米，笑笑每分钟走50米。
结果淘气先到，并在公园门口等了12分钟笑笑才赶到，学校到公园距离是（）米。
6．甲、乙两油库存油数的比是7:5，从甲库运出60桶放入乙库，甲、乙两库油数比是4:5，乙库原有油（）桶。
二、选择正确答案的题号填在括号里。
（每题1分，共6分）1．六（3）班有学生50人，上午出勤率是98﹪，下午又有3人请假。
下午的出勤率是（）。
A．92﹪ B．94﹪ C．96﹪ D．98﹪2．在内壁长30厘米，宽20厘米，深15厘米的长方体容器内，倒入6升水，水位线离这个容器上边的距离是（ ）。
A ． 5厘米B ． 10厘米C ．15厘米D ．20厘米 3．（如下图）小正方形的51未被阴影覆盖，大正方形的101未被阴影覆盖，大小正方形的阴影部分面积之比是 （ ）。
A ．8:9B ． 9:8C ．1:2D ．2:14．A 、B 两人分别从长200米的直线跑道两端出发来回跑步，A 每秒跑2米，B 每秒跑3米，匀速跑了20分钟，那么在这段时间内，A 、B 两人共相遇（ ）次。
2017年全国初中数学联合竞赛试题参考答案和评分标准（1）2017年全国初中数学联合竞赛试题参考答案及评分标准说明：评阅试卷时，请依据本评分标准.第一试，选择题和填空题只设7分和0分两档；第二试各题，请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同，只要思路合理，步骤正确，在评卷时请参照本评分标准划分的档次，给予相应的分数.第一试(A)一、选择题：（本题满分42分，每小题7分）1．已知实数,,abc满足213390abc，3972abc，则32bcab??＝（）A.2．B.1．C.0．D.1?．【答】B.已知等式可变形为2(2)3(3)90abbc，3(2)(3)72abbc，解得218ab??，318bc??，所以32bcab1.2．已知△ABC的三边长分别是,,abc，有以下三个结论：（1）以,,abc为边长的三角形一定存在；（2）以222,,abc为边长的三角形一定存在；（3）以||1,||1,||1abbcca为边长的三角形一定存在.其中正确结论的个数为（）A．0．B．1．C．2．D．3．【答】C.不妨设abc??，则有bca??.（1）因为bca??，所以2bcbca，即22()bca??（），即bca??，故以,,abc为边长的三角形一定存在；（2）以2,3,4abc为边长可以构成三角形，但以2224,9,16abc为边长的三角形不存在；（3）因为abc??，所以||11,||11,||11ababbcbccaac，故三条边中||1ca??大于或等于其余两边，而||1||111abbcabbc（）（）（）（）111||1acacca=，故以||1ab??，||1bc??，||1ca??为边长的三角形一定存在.3．若正整数,,abc满足abc??且2()abcabc，则称(,,)abc为好数组.那么，好数组的个数为（）A.1．B．2．C．3．D．4．【答】C.若(,,)abc为好数组，则2()6abcabcc，所以6ab?.显然，a只能为1或2.若a＝2，由6ab?可得2b?或3，2b?时可得4c?，3b?时可得52c?（不是整数）；若a＝1，则2(1)bcbc，于是可得(2)(2)6bc，可求得(,,)abc ＝（1，3，8）或（1，4，2017年全国初中数学联合竞赛试题参考答案及评分标准第1页（共7页）5）.综合可知：共有3个好数组，分别为（2，2，4），（1，3，8）和（1，4，5）.4．设O是四边形ABCD的对角线AC、BD的交点，若180BADACB，且3BC?，4AD?，5AC?，6AB?，则DOOB＝（）A.109．B.87．C.65．D.43．【答】A.过B作//BEAD，交AC的延长线于点E，则180ABEBAD ACB??，所以△ABC∽△AEB，所以ACBCABEB?，所以631855ABBCEBAC.再由//BEAD，得4101895DOADOBBE.5．设A是以BC为直径的圆上的一点，ADBC?于点D，点E在线段DC上，点F在CB的延长线上，满足BAFCAE.已知15BC?，6BF?，3BD?，则AE＝（）A.43．B.213．C.214．D.215．【答】B.如图，因为BAFCAE，所以BAFBAECAEBAE，即90FAEBAC.又因为ADBC?，故2ADDEDFDBDC.而639DFBFBD，15312DCBCBD，所以29312ADDE，所以6AD?，4DE?.从而222264213AEADDE.6．对于正整数n，设na是最接近n的整数，则1232001111aaaa（）A.1917．B.1927．C.1937．D.1947．【答】A.对于任意自然数k，2211()24kkk不是整数，所以，对于正整数n，12n?一定不是整数.设m是最接近n的整数，则1||2mn??，1m?.易知：当1m?时，1||2mn2211()()mnm??221144mmnmm.于是可知：对确定的正整数m，当正整数n满足221mmnmm时，m是最接近n的整数，即nam?.所以，使得na＝m的正整数n的个数为2m.注意到2213131822001414210，因此，12200,,,aaa?中，有：2个1，4个2，6个3，2017年全国初中数学联合竞赛试题参考答案及评分标准第2页（共7页）EOCBADCBFDE8个4，……，26个13，18个14.所以123200111111111191246261812313147aaaa.二、填空题：（本题满分28分，每小题7分）1．使得等式311aa成立的实数a的值为_______．【答】8.由所给等式可得32(11)aa.令1xa??，则0x?，且21ax??，于是有322(1)(1)xx，整理后因式分解得2(3)(1)0xxx，解得10x?，23x?，31x??（舍去），所以1a??或8a?.验证可知：1a??是原方程的增根，8a?是原方程的根.所以，8a?.2．如图，平行四边形ABCD中，72ABC，AFBC?于点F，AF交BD于点E，若2DEAB?，则AED?＝_______．【答】66?.取DE的中点M，在Rt△ADE中，有12AMEMDEAB.设AED，则1802AME，18ABM.又ABMAMB，所以180218，解得66.3．设,mn是正整数，且mn?.若9m与9n的末两位数字相同，则mn?的最小值为．【答】10.由题意知，999(91)mnnmn是100的倍数，所以91mn??是100的倍数，所以9mn?的末两位数字是01，显然，mn?是偶数，设2mnt??（t是正整数），则29981mntt.计算可知：281的末两位数字是61，381的末两位数字是41，481的末两位数字是21，581的末两位数字是01.所以t的最小值为5，从而可得mn?的最小值为10.4．若实数,xy满足3331xyxy，则22xy?的最小值为．【答】12.因为333322031()(1)333xyxyxyxyxyxy22(1)[()()(1)(1)]3(1)xyxyxyxyxy2017年全国初中数学联合竞赛试题参考答案及评分标准第3页（共7页）MEFCBDA22(1)(1)xyxyxyxy2221(1)[()(1)(1)]2xyxyxy，所以1xy或1xy??.若1xy，则22xy?＝2.若1xy??，则22222111[()()][1()]222xyxyxyxy，当且仅当12xy??时等号成立.所以，22xy?的最小值为12.第一试(B)一、选择题：（本题满分42分，每小题7分）1．已知二次函数2(0)yaxbxcc的图象与x轴有唯一交点，则二次函数3233yaxbxc的图象与x轴的交点个数为（）A．0．B．1．C．2．D．不确定．【答】C.因为二次函数2yaxbxc的图象与x轴有唯一交点，所以2140bac，所以240bac??.故二次函数3233yaxbxc的判别式323363623211()4(4)()1616bacbacbb61516b?0?，所以，二次函数3233yaxbxc的图象与x轴有两个交点.2．题目和解答与（A）卷第1题相同.3.题目和解答与（A）卷第3题相同.4．已知正整数,,abc满足26390abc，260abc，则222abc??＝（）A.424．B.430．C.441．D.460．【答】C.由已知等式消去c整理得22(9)3(1)75ab，所以23(1)75b??，又b为正整数，所以16b??.若b＝1，则2(9)75a??，无正整数解；若b＝2，则2(9)72a??，无正整数解；若b＝3，则2(9)63a??，无正整数解；若b＝4，则2(9)48a??，无正整数解；若b＝5，则2(9)27a??，无正整数解；若b＝6，则2(9)0a??，解得9a?，此时18c?.2017年全国初中数学联合竞赛试题参考答案及评分标准第4页（共7页）因此，9a?，b＝6，18c?，故222abc＝441.5．设O是四边形ABCD的对角线AC、BD的交点，若180BADACB，且3BC?，4AD?，5AC?，6AB?，则DOOB＝（）A.43．B.65．C.87．D.109．【答】D.解答过程与（A）卷第4题相同.6．题目和解答与（A）卷第5题相同.二、填空题：（本题满分28分，每小题7分）1．题目和解答与（A）卷第1题相同.2．设O是锐角三角形ABC的外心，,DE分别为线段,BCOA的中点，7ACBOED，5ABCOED，则OED?＝_________.【答】10?.如图，设OEDx??，则5ABCx??，7ACBx??，DOC??18012BACx，10AOCx??，所以1802AODx，180(1802)ODExxx，所以1122ODOEOAOC，所以60DOC，从而可得10x??.3.题目和解答与（A）卷第3题相同.4.题目和解答与（A）卷第4题相同.第二试（A）一、（本题满分20分）已知实数,xy满足3xy??，221112xyxy，求55xy?的值.解由221112xyxy可得2233222()xyxyxyxyxy.设xyt?，则222()292xyxyxyt，332()[()3]3(93)xyxyxyxyt，代入上式可得22(392)3(93)tttt，解得1t?或3t?.……………………10分当3t?时，3xy?，又3xy??，故,xy是一元二次方程2330mm的两实数根，但易知此方程没有实数根，不合题意.……………………15分当1t?时，1xy?，又3xy??，故,xy是一元二次方程2310mm的两实数根，符合题意.此时552233222()()()(92)[3(93)]3123xyxyxyxyxyttt.……………………20分2017年全国初中数学联合竞赛试题参考答案及评分标准第5页（共7页）DEOBAC二、（本题满分25分）如图，△ABC中，ABAC?，45BAC，E 是BAC?的外角平分线与△ABC的外接圆的交点，点F在AB上且EFAB?.已知1AF?，5BF?，求△ABC的面积.解在FB上取点D，使FD＝AF，连接ED并延长，交△ABC的外接圆于点G.由EF⊥AD，AF＝FD知△AED是等腰三角形，所以∠AED＝1802??∠EAD＝∠BAC，……………………10分所以??AGBC?，所以??ACBG?，所以AC＝BG (15)分又∠BGE＝∠BAE＝∠ADE＝∠BDG，所以BG＝BD，所以AC＝BD ＝5－1＝4，……………………20分△ABC的AB边上的高sin4522hAC.所以，△ABC的面积116226222SABh (25)分三、（本题满分25分）求所有的正整数数对(,)ab，使得34938ba.解显然，4938b??为奇数，所以a为奇数.又因为33493849385ba，所以5a?.……………………5分由34938ba可得38493ba，即22(2)(24)73baaa.……………………10分设2(2,24)aaad，则d为奇数.注意到224(2)(4)12aaaa，所以|12d，所以d＝1或3.……………………15分若d＝1，则有22 27, 243,b aaa或22 23, 247, ba aa均无正整数解.……………………20分若d＝3，则有221237,243,baaa?或12223,2437,baaa解得11a?，3b?.所以，满足条件的正整数对只有一个，为（11，3）.……………………25分第二试（B）一、（本题满分20分）已知实数,,abc满足abc??，16abc，22211284abcabc，求c的值.解设abx??，aby?，依题意有2212(16)(16)1284xyxyx，整理得21(8)(8)8xyx，所以8x?或8(8)yx??.……………………10分2017年全国初中数学联合竞赛试题参考答案及评分标准第6页（共7页）FEABCD（1）若8x?，则8ab??，此时c＝8.（2）若8(8)yx??，即8(8)abab，则(8)(8)0ab，所以8a?或8b?.当8a?时，结合abc??可得24abc，与16abc矛盾.当8b?时，结合abc??及16abc可得0a?，8c?.综合可知：8c?.……………………20分二、（本题满分25分）求所有的正整数m，使得21221mm 是完全平方数.解当m＝1时，212211mm是完全平方数.……………………5分当1m?时，设212221mmn（n为正整数）.注意到2112112122212(2)221(21)(2)mmmmmm，故可得12122(21)(2)mmn，……………………10分所以22212112(21)(21)(21)mmmmnnn.……………………15分设121mxn，121myn，则xy?，222mxy??，所以,xy均为2的方幂.……………………20分又22myx被4除余数为2，所以，只可能2x?，2my?，故22222mm，解得3m?.综上可知：满足条件的正整数m有两个，分别为1和3.……………………25分三、（本题满分25分）如图，O为四边形ABCD内一点，OADOCB，OAOD?，OBOC?.求证：2222ABCDADBC.证明由题设条件可知90AODBOC，又OADOCB，所以△AOD∽△COB，……………………5分所以ODAOOBCO?，从而OCAOOBOD?.……………………10分又AOCAOBBOCAOBAODDOB，所以△AOC∽△DOB，所以OACODB.……………………15分设AC和BD交于点P，则90APDAOD，所以ACDB?，……………………20分所以222222222222()()()()ABCDAPPBPDPCAPPDPBPCADBC .……………………25分2017年全国初中数学联合竞赛试题参考答案及评分标准第7页（共7页）PDAO CB。
2017年数学竞四川赛区（非数学类）试题评分标准及参考答案一 1. 已知可导函数满足, 则()f x解： 在方程两边求导得'()c o s +()s i n f x x f x x =,'()+()tan sec f x f x x x =.从而tan tan ()sec xdx xdx f x e xe dx c -⎛⎫⎰⎰=+ ⎪⎝⎭⎰l nc o sl n c o s211==cos cos cos x x e e dx c x dx c x x --⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭⎰⎰ ()=c o s t a n =s i n co s xx c x cx ++ 由于(0)1f =，故()sin cos f x x x =+。
2．求()n n n +∞→22sin lim π解 由于 ()=+n n 22sin π()ππn n n -+22sin=2sin 1⎛⎫→。
3. 设(,)w f u v =具有二阶连续偏导数，且==+u x cy v x cy -，，其中c 为非零常数。
则21xx yy w w c-=_________。
解: 12+x w f f =，1112222xx w f f f =++，21()y w c f f =-，()()()22111122122111222=2yy w cf f c cf cf cf cf c f f f y∂=-=--+-+∂。
所以1221=4xx yy w w f c-。
4. 设()f x 有二阶导数连续，且(0)'(0)0,"(0)6f f f ===，则24(s i n )l i m x f xx →=______解：21()(0)'(0)"()2f x f f x f x ξ=++，所以241(sin )"()sin 2f x f x ξ=。
这样244400(sin )"()sin lim=lim 32x x f x f xx x ξ→→=。
