下载文档原格式
国开形成性考核《建筑力学》形考任务(1-4)试题及答案（课程ID：00883，整套相同，如遇顺序不同，Ctrl+F查找，祝同学们取得优异成绩！）形考任务1一、单项选择题（每小题2分，共20分）题目：1、1．约束反力中含有力偶的约束为（C）。
【A】：可动铰支座【B】：光滑接触面【C】：固定支座【D】：固定铰支座题目：2、2．只限制物体沿任何方向移动，不限制物体转动的支座是（C）。
【A】：可动铰支座【B】：固定支座【C】：固定铰支座【D】：光滑接触面题目：3、3．若刚体在三个力作用下处于平衡，则此三个力的作用线必（C）。
【A】：不在同一片面内，且汇交于一点【B】：不在同一平面内，且互相平行【C】：在同一平面内，且汇交于一点【D】：在同一平面内，且互相平行题目：4、4．力偶可以在它的作用平面内（C），而不改变它对物体的作用。
【A】：既不能移动也不能转动【B】：任意转动【C】：任意移动和转动【D】：任意移动题目：5、5．平面一般力系可以分解为（B）。
【A】：一个平面力偶系【B】：一个平面汇交力系和一个平面力偶系【C】：无法分解【D】：一个平面汇交力系题目：6、6．平面汇交力系的合成结果是（B）。
【A】：一个力偶和一个合力【B】：一个合力【C】：一个合力偶【D】：不能确定题目：7、7．平面力偶系的合成结果是（C）。
【A】：一个力偶和一个合力【B】：主矢【C】：一个合力偶【D】：一个合力题目：8、8．平面一般力系有（A）个独立的平衡方程，可用来求解未知量。
【A】：3【B】：2【C】：4【D】：1题目：9、9．由两个物体组成的物体系统，共具有（C）独立的平衡方程。
【A】：4【B】：5【C】：6【D】：3题目：10、10．力的可传性原理只适用于（C）。
【A】：固体【B】：任何物体【C】：刚体【D】：弹性体二、判断题（每小题2分，共20分）题目：11、1．若两个力大小相等，则这两个力等效。
（X）题目：12、2．在任意一个已知力系中加上或减去一个平衡力系，会改变原力系对变形体的作用效果。
江苏开放大学形成性考核作业学号姓名课程代码110011课程名称建筑力学评阅教师第 4 次任务共 4 次任务1．判断题（每小题表述是正确的在括号中打√，错误的在括号中打×）（1）力法的基本未知量是多余约束力。
（√）（2）力法典型方程是根据变形协调条件可建立的。
（√）（3）力法基本结构可以是几何瞬变体系。
（×）（4）力法可用来求解超静定桁架。
（√）（5）力法可用来求解任意超静定结构。
（×）（6）力法的基本未知量一定是支座约束力。
（×）（7）多余约束力后的运算与静定结构运算相同。
（√）（8）三铰刚架不能作为力法基本结构。
（×）（9）力法基本结构只能从原结构中解除多余约束得出。
（×）(10) 力法典型方程中的系数和自由项值都是基本未知量的位移。
（√）2．单项选择题（在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内）（1）撤除一根支承链杆相当于解除（A）个约束。
A. 1B. 2C.3D. 4（2）撤除切断一根结构内部链杆相当于解除（C）个约束。
A. 1B. 2C.3D. 4（3）将刚性连接改为单铰连接，相当于解除（A）个约束。
A. 1B. 2C.3D. 4（4）将固定端约束改为固定铰支座，相当于解除（A）个约束。
A. 1B. 2C.3D. 4（5）撤除一个固定铰支座，相当于解除（B）个约束。
A. 1B. 2C.3D. 4（6）撤除一个固定端约束，相当于解除（C）个约束。
A. 1B. 2C.3D. 4（7）二次超静定结构力法典型方程有（A）个自由项。
A． 2 B． 3 C． 4 D． 6（8）二次超静定结构力法典型方程有（A）个主系数。
A． 2 B． 3 C． 4 D． 6（9）二次超静定结构力法典型方程有（A）个副系数。
A． 2 B． 3 C． 4 D． 6（10）将固定端约束改为固定铰支座，是（B）形式的多余约束力。
一、单项选择题（每小题2分，共10分）1．在图乘法中，欲求某点的竖向位移，则应在该点虚设（）。
正确答案是：任意方向单位力2．在图乘法中，欲求某点的转角，则应在该点虚设（）。
正确答案是：单位力矩3．在图乘法中，欲求某两点的相对转角，则应在该点虚设（）。
正确答案是：一对反向的单位力矩4．平面刚架在荷载作用下的位移主要是由（）产生的。
正确答案是：弯曲变形5．作刚架内力图时规定，弯矩图画在杆件的（）。
正确答案是：受拉一侧二、判断题（每小题2分，共20分）1．在使用图乘法时，两个相乘的图形中，至少有一个为三角图形。
正确的答案是“错”。
2．图乘法的正负号规定为：面积Aω与纵坐标y c 在杆的同一侧时，乘积Aωy C 应取正号；面积Aω与纵坐标y c 在杆的不同侧时，乘积Aωy C 应取负号。
正确的答案是“对”。
3．单位荷载法就是将两个弯矩图的图形进行简单拼合。
正确的答案是“错”。
4．一次截取两个结点为研究对象，来计算桁架杆件轴力的方法称为结点法。
正确的答案是“错”。
5．桁架中内力为零的杆件是多余杆件，应该撤除。
正确的答案是“错”。
6．桁架中的内力主要是剪力。
正确的答案是“错”。
7．多跨静定梁基本部分承受荷载时，附属部分不会产生内力。
正确的答案是“对”。
8．刚架在刚结点处联结的各杆杆端弯矩相等。
正确的答案是“对”。
9．轴线是曲线的结构称为拱。
正确的答案是“对”。
10．三铰拱的支座反力中水平推力与拱高成反比，与拱轴曲线形状无关。
正确的答案是“对”。
三、计算题（共70分）1．试作图示静定多跨梁的剪力图和弯矩图。
（10分）（1.1）梁的弯矩图如（）所示（5分）正确答案是：（1.2）梁的剪力图如（）所示（5分）正确答案是：2．试作图示刚架的内力图。
（10分）（2.1）刚架的弯矩图如（）所示（5分）正确答案是：（2.2）刚架的剪力图如（）所示（5分）正确答案是：3．试作图示刚架的内力图。
（10分）（3.1）刚架的弯矩图如（）所示（5分）正确答案是：（3.2）刚架的剪力图如（）所示（5分）正确答案是：4．试计算图示桁架各杆的轴力。
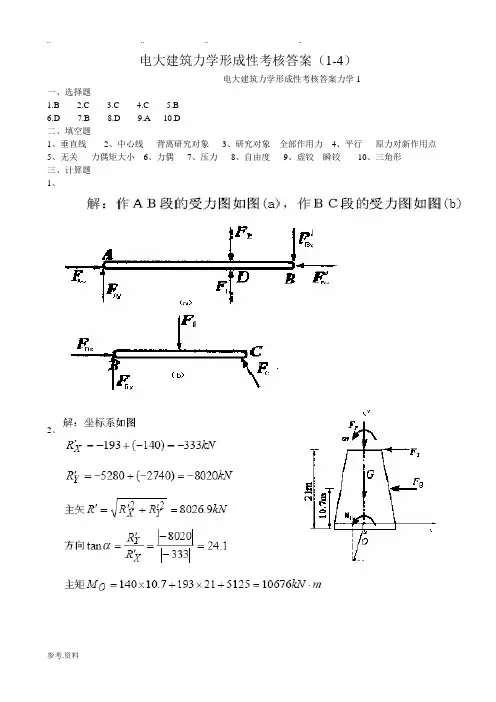
最新资料，word文档，可以自由编辑！！精品文档下载【本页是封面，下载后可以删除!】建筑力学作业答案 一、选择题1．D 2．C 3．B 4．D 5．A 6．C 7．B 8．B 9．D 10．C二、填空题1．轴向拉压、剪切、扭转和弯曲。
2．扭矩 M n 扭矩矢量指向与截面外法线一致 3．杆件轴线方向4．剪力 弯矩 5．零杆6．水平直 斜直 7．斜直 抛物 8．剪力 集中力 9．弯矩 集中力偶 10．弯矩三、计算题1．解：（1）用1-1截面将杆截开，保留左段，受力如图：由xF=0∑ N1F 2F =0- N1F 2F()=拉再用2-2截面将杆截开，保留左段，受力如图： 由xF=0∑ N2F 2F+2F =0-N2F =0最后用3-3截面将杆截开，保留左段，受力如图： 由xF=0∑ N3F 2F+2F F =0-- N3F =F （拉） 作轴力图：2FABD∙∙C2FF1 122332F A1 1F N12FAB∙2F22F N22FAB∙∙C2F F33F N32F F N 图⊕⊕F（2）用1-1截面将杆截开，保留左段，受力如图： 由xF=0∑ N1F 10=0-N1F 10kN()=拉再用2-2截面将杆截开，保留左段，受力如图： 由xF=0∑ N2F 10+30=0- N2F 20kN()=-压最后用3-3截面将杆截开，保留右段，受力如图： 由xF=0∑ N3F 40=0-- N3F =40kN()-压 作轴力图：10kNABD∙∙C1 1 22 3320kN30kN40kN10kNA1 1F N110kNAB∙22F N230kND 3340kNF N310F N 图（kN ）⊕Ө2040（3）用1-1截面将杆截开，保留右段，受力如图： 由x F =0∑ N1F 604010=0-++- N1F =90kN()拉再用2-2截面将杆截开，保留右段，受力如图：由xF=0∑ N2F 4010=0-+- N2F =30kN()拉最后用3-3截面将杆截开，保留右段，受力如图： 由xF=0∑ N3F 10=0-- N3F =10kN()-压作轴力图：2．解：（1）求支座反力， 由AM=0∑ B F 440220420-⨯-⨯⨯= B F 60k N ()=↑ 由xF=0∑ Ax F 400+= Ax F 40kN()=-←ABD∙∙C60kN1 1 223310kN 40kNBD∙∙C60kN1 110kN 40kNF N1 D∙C2210kN 40kN F N2D33 10kN F N390 F N 图（kN ） ⊕Ө3010由yF=0∑ Ay F 602040+-⨯= Ay F 20kN()=↑分别作出AC 、CD 、DB 各段受力平衡图如下：作F Q 图、M 图、F N 图如下：40kN C 20kN/m2m 2m4mA DB 40kN AC40kN20kN20kN 80kN/m C20kN/mD20kN 80kN/m60kN B D60kN60kNC A DB ⊕Ө⊕ 20 40 60F Q 图（kN ） C ADB8040M 图（kN ∙m ）8080（2）求支座反力，由力偶的平衡，得：B M F =()l ↑ A M F =()l↓ 作分段平衡受力图：作F Q 图、M 图、F N 图如下：C A DBӨ 20 60 F N 图（kN ） ӨC AB l l M CA MM Ml MlM l MlCBM C A B F Q 图 ӨM l C A BM 图 M3．解：（1）求支座反力， 由AM=0∑ B F 485420--⨯⨯= B F 12k N ()=↑ 由yF=0∑ A F 12540+-⨯= A F 8k N ()=↑ 作F Q 图，计算弯矩极值M D ： 由yF=0∑ 85x =0- x =1.6mD M =8 1.65 1.60.8 6.4k N m ⨯-⨯⨯= 作M 图，C A BF N 图M l ⊕ 5kN/mD C8kN ∙mA B4m2m⊕ Ө1.6m8F Q 图（kN ）125kN/m DAM Dx 8kN6.4M 图（kN ∙m ）8（2） B M =4010130k N m -⨯= A M =40104103 1.545kN m -⨯-⨯⨯=-作F Q 图、M 图如下：（3）求支座反力， 由BM=0∑ A F 42020210630--⨯+⨯⨯= -A F 30kN()=↑由yF=0∑ B 30F 106200+-⨯-= B F 50k N ()=↑ 作F Q 图计算弯矩极值M E ： 由y F =0∑ 502010(x 2)0--⨯-=x =5mE M =503205103 1.55kN m ⨯-⨯-⨯⨯= A M =2010210-⨯⨯= B M =20240kN m -⨯=- 作M 图10kNDC 40kN ∙mAB 1m 3m1m10kN/mӨF Q 图（kN ）1040 204045M 图（kN ∙m ）10kN/mDC 20kN ∙mA B4m2m 2m20kN10kN/mECM EB x20kN 50kNӨF Q 图（kN ）1020 Ө2030⊕⊕ 40205M 图（kN ∙m ）4．解：求支座反力，由整体平衡条件，得：yF=0∑ C F F F F 0---= C F 3F ()=↑用Ⅰ-Ⅰ截面将桁架截开，保留右边部分，受力如图：由yF=0∑ N2F sin 45F F+3F 0︒--= N2F 2F()=-压 由DM=0∑ N1F a F a +3F a 0-= N1F 2F()=-压 由xF=0∑ N 1N 2N 3F F c o s 45F 0--︒-= N3F 3F()=拉 由零杆判别法，可知：N4F 0=1 2 3a ABCFDaaa4F FⅠ Ⅰ C DFFF N1 F N2 F N33F。
国开（电大）《建筑力学》形成性考核作业1-4参考答案形考作业1一、单项选择题(每小题2分,共20分)1.约束反力中含有力偶的约束为（）。
A.固定铰支座B.固定支座C.可动铰支座D.光滑接触面2.只限制物体沿任意方向移动,不限制物体转动的支座是（）。
A.固定铰支座B.固定支座C.可动铰支座D.光滑接触面3.若刚体在三个力作用下处于平衡,则此三个力的作用线必（）。
A.在同一平面内,且互相平行B.不在同一平面内,且互相平行C.在同一平面内,且汇交于一点D.不在同一片面内,且汇交于一点4.力偶可以在它的作用平面内（）,而不改变它对物体的作用。
A.任意移动B.任意转动C.任意移动和转动D.既不能移动也不能转动5.平面一般力系可以分解为（）。
A.一个平面汇交力系B.一个平面力偶系C.一个平面汇交力系和一个平面力偶系D.无法分解6.平面汇交力系的合成结果是（）。
A.一个合力偶B.一个合力C.一个力偶和一个合力D.不能确定7.平面力偶系的合成结果是（）A.一个合力偶B.一个合力C.一个力偶和一个合力D.主矢8.平面一般力系有（）个独立的平衡方程,可用来求解未知量。
A.1B.2C.3D.49.由两个物体组成的物体系统,共具有（）独立的平衡方程。
A.3B.4C.5D.610.力的可传性原理只适用于（）A.固体B.刚体C.弹性体D.任何物体二、判断题(每小题2分,共20分)1.若两个力大小相等,则这两个力等效。
（×）2.在任意一个已知力系中加上或减去一个平衡力系,会改变原力系对变形体的作用效果。
（×）3.作用力与反作用力公理只适用于刚体。
（×）4.合力的数值一定比分力数值大。
（×）5.力沿坐标轴方向上的分力是矢量,力在坐标轴上的投影是代数量。
（√）6.力的三要素是大小、方向、作用点。
（√）7.由n个物体组成的系统,若每个物体都受平面一般力系的作用,则共可以建立3n个独立的平衡方程。
国开电大《建筑力学》形成考核册4答案形考任务四1.在图乘法中，欲求某点的竖向位移，则应在该点虚设（）。
正确答案是：任意方向单位力2在图乘法中，欲求某点的转角，则应在该点虚设（）。
正确答案是：单位力矩3．在图乘法中，欲求某两点的相对转角，则应在该点虚设（）。
正确答案是：一对反向的单位力矩4．平面刚架在荷载作用下的位移主要是由（）产生的。
正确答案是：弯曲变形5．作刚架内力图时规定，弯矩图画在杆件的（）。
正确答案是：受拉一侧1．在使用图乘法时，两个相乘的图形中，至少有一个为三角图形。
正确的答案是“错”。
2．图乘法的正负号规定为：面积Aω与纵坐标yc 在杆的同一侧时，乘积AωyC 应取正号；面积Aω与纵坐标yc 在杆的不同侧时，乘积AωyC 应取负号。
正确的答案是“对”。
3．单位荷载法就是将两个弯矩图的图形进行简单拼合。
正确的答案是“错”。
4．一次截取两个结点为研究对象，来计算桁架杆件轴力的方法称为结点法。
正确的答案是“错”。
5．桁架中内力为零的杆件是多余杆件，应该撤除。
正确的答案是“错”。
6．桁架中的内力主要是剪力。
正确的答案是“错”。
7．多跨静定梁基本部分承受荷载时，附属部分不会产生内力。
正确的答案是“对”。
8．刚架在刚结点处联结的各杆杆端弯矩相等。
正确的答案是“对”。
9．轴线是曲线的结构称为拱。
正确的答案是“对”。
10．三铰拱的支座反力中水平推力与拱高成反比，与拱轴曲线形状无关。
正确的答案是“对”。
1．试作图示静定多跨梁的剪力图和弯矩图。
（10分）（1.2）梁的剪力图如（）所示（5分）2．试作图示刚架的内力图。
（10分）（2.2）刚架的剪力图如（）所示（5分）3．试作图示刚架的内力图。
（10分）（3.2）刚架的剪力图如（）所示（5分）4．试计算图示桁架各杆的轴力。
（10分）5．试计算图示桁架结构的指定杆件1、2、3杆的轴力。
（10分）（5.2）2杆的轴力FN2=（）所示（3分）（5.3）3杆的轴力FN3=（）所示（4分）6．求图示简支梁A 端角位移及跨中C 点的竖向位移。
请认真阅读完再下载：预览的题目顺序完全和您自己的试题顺序完全相同再下载！建筑力学＃形考四-0001浙江广播电视大学形成性测评系统课程代码：3309027 参考资料试卷总分：100判断题(共30题,共60分)1.(2分)（）力法基本结构：去掉多余约束后得到的静定结构作为基本结构，同一结构可以选取多个不同的基本结构。
√×参考答案：√2.(2分)（）由于位移法的计算过程主要是建立和求解位移法方程，而位移法方程是平衡条件，故位移法校核的重点是平衡条件。
√×参考答案：√3.(2分)（）只要有结点位移，就有位移法基本未知量，所以位移法可求解超静定结构，但是不可以求解静定结构。
√×参考答案：×4.(2分)（）力矩分配法的三个基本要素为：转动刚度、分配系数和传递系数。
√×参考答案：√5.(2分)（）位移法中角位移的数目不等于结构中刚结点的数目。
√×参考答案：×6.(2分)（）力法典型方程中全部系数和自由项都是基本结构的位移，所以，求系数和自由项的实质就是求静定结构的位移。
√×参考答案：√7.(2分)（）力矩分配法中规定：杆端弯矩对杆以顺时针转向为负。
√×参考答案：×8.(2分)（）单位多余未知力单独作用时所引起的沿其他未知力方向上的位移在力法方程中称为主系数。
√×参考答案：×9.(2分)（）在力矩分配法的计算过程中，总是重复一个基本运算，即单结点的力矩分配。
√×参考答案：√10.(2分)（）求位移的单位荷载法是由叠加原理推导出来的。
√×参考答案：×11.(2分)（）静定结构的静力特征是：满足平衡条件内力解答是唯一的，即仅由平衡条件就可求出全部内力和反力。
√×参考答案：√12.(2分)（）超静定结构的静力特征是：满足平衡条件内力解答有无穷多种，即仅由平衡条件求不出全部内力和反力，还必须考虑变形条件。
国家开放大学《工程力学》形成性作业1-4参考答案
形成性作业1
一、单项选择题（每小题2分，共30分）在每小题的四个备选答案中选出一个正确答案，并将其代号填在题干后面的括号内。
不选、错选或多选者，该题无分。
1．三刚片组成几何不变体系的规则是（）
A. 三链杆相连，不平行也不相交于一点
B. 三铰两两相连，三铰不在一直线上
C. 三铰三链杆相连，杆不通过铰
D. 一铰一链杆相连，杆不通过铰
2．在无多余约束的几何不变体系上增加二元体后构成（）
A. 可变体系
B. 瞬变体系
C. 无多余约束的几何不变体系
D. 有多余约束的几何不变体系
3．图示体系为（）
A. 瞬变体系
B. 常变体系
C. 有多余约束的几何不变体系
D. 无多余约束的几何不变体系
4．下图所示平面杆件体系是何种杆件体系（）
A. 常变
B. 瞬变
C. 不变且无多余联系
D. 不变且有一个多余联系
5．图示桁架有几根零杆（）
A. 0
B. 2
C. 4
D. 6
6．图1所示结构的弯矩图形状应为（）
A. A
B. B
C. C
D. D
7．图示结构中C截面弯矩等于（）
A. A
B. B
C. C
D. D
8．图示刚架杆端弯矩MBA等于（）。
最新资料，word文档，可以自由编辑！！
精
品
文
档
下
载
【本页是封面，下载后可以删除!】
一、选择题
1．B 2．D 3．D 4．C 5．A 6．C 7．C 8．C 9．B 10．C
二、填空题 1．直杆 2．位移
3．轴力 N P N
F F l EA
∆=∑
4．单位荷载 实际荷载 5．反 反 6．位移 7．结点位移 8．单跨梁 9．位移法 10．转动
三、计算题
*1．解：取图示坐标，分段积分，有： 右段：
21
P qx M 2
=-
1M =x -
1l (0x )2
≤≤ 左段：
P 21
M qlx 8=-
2M =x 1
-2
2(0x l )≤≤ C 端竖向位移：
q
C
A
B
l
l/2 q
C A
B
x 2
x 1
1
C
A
B
x 2
x 1
P C M(x)M (x)
Δ=dx EI
∑⎰
2
221
11l
2
00l 43
l 122
00444x qlx qx ()()(x )()282dx dx EI EI
x x q ql =[][]2EI 416EI 3
ql ql +
128EI 48EI 11ql ()384EI
=++==↓⎰⎰----
2．解：（1）作M P 图，
（2）作M 图，
（3）计算横梁中点位移
2
c P P ωy F l F l 11l l ()EI EI 24216EI
∆==⨯⨯=↓∑
C
l
A
D
B
l F P
C A D
B
F P M P 图 F P l
F P l C
A
D
B
1
M 图
l/4
3．⑴解：（1）刚架为一次超静定结构，取基本结构如下图所示： X 1为多余未知力。
（2）写出力法方程如下：
δ11 X 1+Δ1P = 0
（3）计算系数δ11及自由项Δ1P
作1M 图和M P 图如下：
C 11ωy 112144
δ==6662EI EI 23EI ⨯⨯⨯⨯⨯⨯=∑
C 1P ωy 1211080
==6906EI EI 32EI
∆⨯⨯⨯⨯⨯=∑
（4）求解多余未知力：
1P 111
1080
Δ
EI X =7.5kN 144δEI
-=-=-
（5）由式M= 1M X 1+ M p 按叠加法作出M 图如下：
20kN /m
EI=常量 6m 6m
6m
A B
C
D X 1 20kN /m EI=常量
A
B
C D 基本结构 1
1M 图 A B C D 6
M P 图（kN ∙m ） A B
C
D 90 M 图（kN ∙m ）
A
B C
D (90) 45
67.5
3．⑵解：（1）这是二次超静定结构，取基本结构如下图所示，X 1 、X 2为多余未知力。
（2）写出力法方程如下：
δ11 X 1+δ12 X 2+Δ1P = 0
δ21 X 1+δ22 X 2+Δ2P = 0
（3）计算系数及自由项：
作1M 图、2M 图和M P 图如下：
q
EI=常量 l l l A B C D E q
EI=常量
A B C
D
E X 1 X 2 基本结构 { A
B C
D
E
1
l l
1M 图
A B
C
D E
1
l
2M 图
A
B
C
D
E
21ql 8
M P 图
3
C 11ωy 112l 2l δ==l l 2EI EI 233EI ⨯⨯⨯⨯⨯=∑
3
C 22ωy 112l 2l δ==l l 2EI EI 233EI ⨯⨯⨯⨯⨯=∑ 3C 1221ωy 11l l
δ=δ=l l E I E I 236E I =⨯⨯⨯⨯=∑ 4
2C 1P ωy 121l ql ==l ql EI EI 38224EI
∆⨯⨯⨯⨯=∑ 4
2P
1P ql Δ24EI
=∆=
（4）求解多余未知力：
将系数和自由项代入力法方程，得：
334
122l l ql X +X +03EI 6EI 24EI = 334
12l 2l ql X +X +06EI 3EI 24EI
= 解得： 121
X =X ql 20
=- （5）作最后弯矩图
由式M= 1M X 1+2M X 2+ M p 得： 2
BA
1ql M =l(ql)002020-++=-
2
BC
1ql M =l(ql)002020-++=-
2
CB
1ql M =0l(ql)02020+-+=-
2
CE
1ql M =0l(ql)02020
+-+=-
C D D C A B E C M M =M =M 0==
{
4．⑴解：结构有2个结点角位移，1个线位移。
见位移法基本结构：
4．⑵解：结构有2个结点角位移，2个线位移。
见位移法基本结构：
5．⑴解：（1）计算分配系数，
B A B A BA BA B
C BA BC EI 24S 4i 863μ===0.47EI EI 23S +S 4i +3i 17
4+36434
⨯
===⨯⨯+ B C B A
89μ1μ=10.531717
=--==
A B C D E
2
1ql 8
M 图
2ql 20 2ql 20 2ql 20
2
3ql 40
基本结构 基本结构
（2）计算固端弯矩，
F A B P 11
M F l =100675kN m 88=--⨯⨯=-
F B A
P 1M F l 75k N m 8
== F 22BC
11M ql =30460kN m 88
=--⨯⨯=- F
CB M 0=
（3）分配与传递计算（列表），
（4）作M 图。
30kN/m
C
A B
3m
4m
3m 100kN
EI
EI
C
A B
78.53 51.76
67.95
26.02
(60)
(150)
M 图（kN ∙m ） 0.47 分配系数
固端弯矩 分配与传递最后弯矩 0.53 -75 75
-60
-7.05 -7.95 -3.53
-78.53
-67.95
67.95 0
单位（kN ∙m ）
5．⑵解：（1）计算分配系数， B A B A
BA BA BC BA BC
0.75EI 14S 4i 66μ=
=
=0.40.75EI 1.5EI 11S +S 4i +4i 4+46864
⨯
==⨯⨯+
B C B A
μ1μ
=10.40.
6=--= C B C B
CB CB CD CB CD
1.5EI
4S 4i 1.58μ=
=
=0.61.5EI EI S +S 4i +3i 2.54+386
⨯
==⨯⨯
C D C B
μ1μ
=10.60.
4=--= （2）计算固端弯矩， 22F
P AB
22F ab 4524M
=40kN m l 6⨯⨯=--=-
22F
P BA
22
F a b 4524M
=20kN m l 6
⨯⨯=-= F 22BC 11
M ql =15880kN m 1212=-
-⨯⨯=- F
2CB
1M ql 80kN m 12== F
C D P
33M F l =40645kN m 1616
=--⨯⨯=- F DC M 0=
（3）分配与传递计算（列表），
（4）作M图。
15kN/m
C
A
B
8m
4m
2m
45kN
0.75I
40kN
3m3m
D
1. 5I I
0.4
分配系数固端弯矩
最后弯矩
6.36
36
-400
-2.86
单位（kN∙m）
-50.99
-31.8
50.980
分配与传递
0.4
0.60.6
20-8080-45
24
1218
-21.2
-15.9
9.54
3.18
4.77
-1.91
-1.43
0.570.86
0.290.43
-0.26-0.1
-0.13
0.050.08
0.030.04
-0.02-0.02
-0.01
-24.5-68.3
68.3
C
A
B
D
50.98
68.3
26.68
(60)
(120)
M图（kN∙m）
(60)
24.5
25.85
60.66。
